Динамика асослари
ЎЗБЕКИСТОН РЕСПУБЛИКАСИ ОЛИЙ ВА ЎРТА МАХСУС ТАЪЛИМ ВАЗИРЛИГИ
ФАРОНА ПОЛИТЕХНИКА ИНСТИТУТИ
“МЕХАНИКА” ФАКУЛЬТЕТИ
“Амалий механика ва материаллар аршилиги” КАФЕДРАСИ
“НАЗАРИЙ МЕХАНИКА” ФАНИДАН
Бажарди: 23-12 ТМЖ гурух талабаси
С. Тожиматова
абул илди: асс. О. Хайдарова
ФАРОНА-2013
МАВЗУ: Динамика асослари.
РЕЖА:
I.Кириш.
II. Асосий исм.
1. Динамика онунлари
2.Моддий нута динамикасининг икки асосий масаласи
3.Моддий нута аракатининг дифферциал тенгламалари
4. Моддий нута динамикасининг биринчи асосий масаласини ечиш
5. Моддий нута динамиканинг иккинчи асосий масаласини ечиш
6. Назорат саволлари.
III. Хулоса.
IV. Фойдаланилган адабиётлар.
Кириш
Динамика юнонча «dynamics» бўлиб, куч деган маънони билдиради. Динамикада моддий нута, моддий нуталар системаси ва абсолют жисмнинг аракати шу аракатни вужудга келтирувчи кучлар билан биргаликда ўрганилади.
Статикада асосан ўзгармас кучлар ўрганилган динамикада эса, ўзгармас кучлар билан биргаликда мидор ва йўналиш жиатдан ўзгарувчи кучлар таъсири ам ўрганилади. Механикада кучларнинг табиати ўрганилмайди. Бундай масала билан физиканинг электродинамика, атти жисм назарияси ва боша бўлимларида ўрганилади. Ишаланиш кучи тушунчаси киритилганда, баъзан тинч турган жисмга куч таъсир этса ам у аракатга келмайди. ар андай жисмнинг аракати унга тасир этувчи кучлардан ташари, материянинг асосий усусиятларидан бири исобланган жисмнинг инертлиги ёки инерцияга боли бўлади. Куч таъсир этмаганда жисмнинг ўз олатини ёки аракатини салашида, куч таъсир этганида эса ўз аракатини бирданига эмас, балки жисм ташкил топган модданинг мидорига боли равишда аста-секин ўзгартиришида бу усусият номоён
бўлади.
СИ бирликлар системасида масса килограмм (кг) билан ўлчанади. Жисмнинг аракати унга таъсир этувчи кучлардан ташари жисмнинг шаклига, яъни жисм массасининг андай тасимланганига ам боли бўлади.
Динамикада дастлаб моддий нутанинг аракати ўрганилади. Сўнгра олинган натижалар моддий нуталар системаси ва атти жисмга татби илинади.
Динамика онунлари
1.Инерция онуни. Таши муитдан ажратилган моддий нута ташаридан куч таъсир этмагунча ўзининг тинч олатини ёки тўри чизили ва тенг ўлчовли аракатини салашга интилади.
Шуни таъкидлаб ўтиш керакки,битта куч таъсирида бўлган моддий нута (жисм) бир хил ват орасида турли масофага силжийди ва тезлиги ар хил бўлади.Демак,моддий нуталар битта куч таъсирида ўзларининг тезлигини тез ёки секин ўзгартиради.Бу хусусият моддий нутанинг инертлиги дейилади. Моддий нутанинг инертлик ўлчови физик мидор бўлиб,у (m) масса деб аталади.
Тўри чизили ва тенг ўлчовли аракат моддий нутанинг инерцияси бўйича аракатидан иборат.Бу одисани таърифловчи онун динамиканинг биринчи онуни деб юритилади.
Динамиканинг биринчи онуни аноатлантирадиган сано системаси инерциал система дейилади.Инерция онуни бажарилмайдиган сано система инерциал бўлмаган система деб аталади.
Маркази уёш билан устма-уст тушувчи,ўлари эса мос равишда танлаб олинган юлдузларга томон йўналган сано системанинг инерциал эканлиги тажрибада аниланган.Кўпинча,техник масалаларни ечишда,Ер билан макам боланган система инерциал сано системаси деб аралади. Бу олда Ернинг ўз ўи атрофидаги айланма аракати амда уёш ва юлдузларга нисбатан аракати исобга олинмайди.
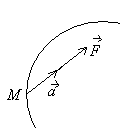
2.Динамиканинг асосий онуни.Моддий нутанинг аракатлантирувчи куч таъсиридан олган тезланиши шу куч йўналишида бўлиб,мидори мазкур куч мидорига пропорционалдир (117-расм).Бу онуннинг математик ифодаси уйидагича ёзилади:
1-расм (1.1)
бу ерда - аракатлантирувчи куч, - нутанинг массаси,-нута тезланиши.
(1.1) вектор тенглама моддий нута динамикасининг асосий тенгламаси дейилади. (1.1)дан кўрамизки, муайян куч таъсирида моддий нутанинг оладиган тезланиши фаат куч катталигигагина боли бўлмай,балки нута массасига ам боли.
Агар моддий нута фаат ўзининг G оирлик кучи таъсирида Ерга эркин тушса, F=G ,a=g бўлиб,(1.1) ифода
G=mg (1.2)
кўринишни олади.Демак,моддий нутанинг оирлик кучи билан массаси ўзаро (1.2) тенглик билан боланган экан.
Агар моддий нутанинг оирлик кучи ани бўлса,унинг массасини (1.2) га кўра
(1.3)
формуладан топиш мумкин.
Халаро бирликлар системаси (СИ) да масса бирлиги учун кг, ват бирлиги илиб секунд (1с), узунлик учун метр (1м) абул илинган.
Бинобарин,куч бирлиги уйидагича бўлади:
Демак,массаси 1кг бўлган моддий нутага 1м/с2 тезланиш бера оладиган куч Нютон деб аталади.
3.Таъсир ва акс таъсир онуни. ар бир таъсир ўзига тенг ва арама-арши йўналишдаги акс таъсирни вужудга келтиради.Бошача айтганда,иккита жисмнинг бир-бирига таъсирлари ўзаро тенг ва арама-арши йўналган (2-расм).А жисмнинг В жисмга кўрсатган таъсири бўлса,учинчи онунга кўра,В нинг А га кўрсатган таъсири бўлади.Бу онундан жисмлар мувозанатда деган хулоса келиб чимайди,чунки кучлар ар хил жисмларга ўйилган.Мазкур онун иккита жисмнинг ўзаро таъсирини характерлайди.
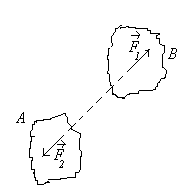
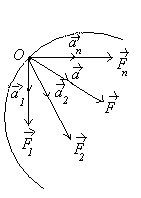
2-расм 3-расм
4.Кучларнинг эркинлик онуни. Моддий нутанинг бир анча куч тенг таъсир этувчиси туфайли олган тезланиши ар айси кучнинг алоида таъсиридан осил бўлган тезланишларининг геометрик йииндисига тенг,(3-расм) яъни:
(1.4)
(1.4) тенгликни икки томонини m га кўпайтирамиз:
Демак,
(1.5)
(1.5) ифода бир анча куч таъсиридаги моддий нута учун динамиканинг асосий тенгламасидир.
(1.5) ифодани (1.1) билан таослашдан кўрамизки,моддий нутага бир неча куч ўйилган бўлса,(1.1) даги ни шу кучларнинг тенг таъсир этувчиси деб араш керак.
Моддий нута динамикасининг икки асосий масаласи
Динамика масалаларини иккита асосий турга ажратиш мумкин. Бу масалалар эркин моддий нута учун уйидагича:
Динамиканинг биринчи асосий масаласида моддий нута массаси ва унинг аракат онуни берилган бўлиб,аракатлантирувчи кучни топиш сўралади.
Динамиканинг иккинчи асосий масаласи эса моддий нута массаси ва унга таъсир этувчи куч маълум бўлганда,шу куч таъсиридан осил бўладиган кинематик элементларни топишдан иборат.
Техникада эрксиз (боланишдаги) моддий нута аракатини текширишга доир кўплаб масалаларни ечишга тўри келади. Бундай олларда нутага ўйилган боланиш уни ўзалмас сирт ёки чизи устида аракат илишга мажбур этади.
Эрксиз моддий нута аракатига доир масалаларни ечишда мазкур нута боланишдан утарилиб,ўйилган боланиш реакция кучи билан алмаштирилади.
Натижада моддий нута динамикасининг асосий тенгламаси уйидагича ёзилади:
(2.1)
бунда - боланиш реакция кучи.
Демак, эрксиз моддий нута динамикасининг биринчи асосий масаласида моддий нута массаси ва унинг аракат онуни амда мазкур нутага таъсир илувчи куч маълум бўлганда реакция кучи аниланади; иккинчи масалада эса моддий нута массаси ва унга таъсир этувчи куч маълум бўлганда моддий нутанинг аракат онуни билан реакция кучини анилаш керак.
Моддий нута аракатининг дифферциал тенгламалари
Эркин моддий нута куч таъсирида аракатланаётган бўлсин (4-расм).Бу олда динамиканинг асосий тенгламаси (1.1) кўринишда ёзилар эди.(1.1) тенгламадаги тезланиш векторини радиус-вектори орали ифодалаймиз:
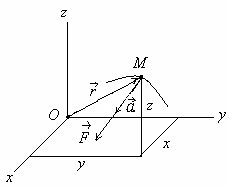
(3.1)
4-расм
(3.1) ни (1.1) га ўйсак:
(3.2)
келиб чиади.
(3.2) тенглама эркин моддий нута аракати диффенциал тенгламасининг вектор ифодасидир.
(3.2) нинг Декарт координата ўларидаги проекциялари уйидагича бўлади:
(3.3)
бу ифодаларда билан кучнинг координата ўларидаги проекциялари белгиланган; x,y,z эса радиус-векторнинг проекциялари,яъни М нутанинг координаталаридир.
(3.3) тенгламалар эгри чизили аракатдаги моддий нута аракати дифференциал тенгламаларининг координата усулидаги кўриниши дейилади.
Агар моддий нутанинг аракат йўналиши билан куч йўналиши бир тўри чизи бўйича бўлса,нута аракати тўри чизили бўлади.Бу олда нутанинг аракат йўналиши учун Ox ўни олсак,унинг дифференциал тенгламаси уйидагича ёзилади:
(3.4)
Агар моддий нута аракати текисликда бўлса, (3.3) тенгламаларнинг биринчи иккитаси (аракат Оху текислигида) ёзилади.
(3.1) нинг табиий координата ўларидаги проекциялари уйидагича бўлади (5-расм):
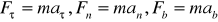
(3.5)
Кинематикадан маълумки:
(3.6)
(3.6) ни (3.5) га ўйсак,
(3.7)
келиб чиади.
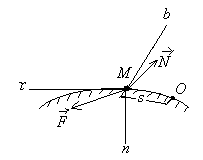
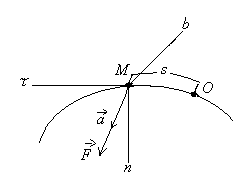
5-rasm 6-rasm
(3.7) тенгламалар моддий нута аракати дифферциал тенгламаларининг табиий усулда ифодаланишидир.
Айтайлик,моддий нута ўзалмас силли чизи устида аракатланаётган бўлсин (6-расм).
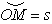
Сано системаси бошини О, М нутанинг эгри чизили координатасини деб абул иламиз. ўзалмас силли чизининг нутага таъсири реакция кучи билан алмаштирилиб,нутани боланишдан утарамиз.
Натижада эрксиз моддий нута динамикасининг асосий тенгламаси уйидагича ёзилади:
ёки (3.8)
Бу тенгламани Декарт координата ўларига проекцияласак,эрксиз моддий нута аракати дифференциал тенгламаларининг координата усулдаги ифодаси келиб чиади:
,, ( 3.9)
(3.8) ни табиий координата ўларига проекциялаймиз:
ўзалмас чизи силли бўлганлиги учун нинг уринмадаги проекцияси нолга тенг:
Демак,
(3.10)
(3.10) моддий нутанинг ўзалмас cилли чизи устидаги аракати дифференциал тенгламасини табиий усулда ифодалашдан иборат.
Хусусий олда куч уринма текисликда ётса, Fb =0 бўлиб, нормал реакция траекториянинг бош нормали билан бир йўналишда бўлади.
Моддий нута динамикасининг биринчи асосий масаласини ечиш
Моддий нутанинг аракат онуни маълум бўлса, динамиканинг биринчи масаласини ечиш жуда осон.Бу масала уйидаги тартибда ечилади:
1.Агар масала шартида сано системаси берилмаган бўлса,у танлаб олинади.
2.Моддий нутага таъсир илувчи кучлар расмда тасвирланади.
3.Агар нута боланишда бўлса,у боланишдан утарилади ва боланиш реакция кучлари расмда кўрсатилади.
4.Танлаб олинган сано системасида моддий нута аракатининг дифференциал тенгламалари тузилади.
5.Берилган аракат онунидан фойдаланиб моддий нута тезланишининг танлаб олинган системадаги проекциялари аниланади.
6.Тезланишнинг топилган проекциялари дифференциал тенгламаларга ўйилиб номаълум куч аниланади.
1-масала. Массаси m=2кг бўлган М жисм (м) онунга кўра куч таъсирида тўри чизили аракат илмода. куч модулининг энг катта иймати анилансин (123-расм).
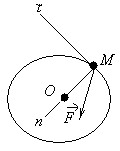
7-расм 8-расм
Ечиш.Масала шартига кўра М жисм тўри чизили аракат илади. Жисмни моддий нута деб араб,сано системаси учун Ох ўни оламиз (7-расм). М жисмга фаат кучи таъсир илади.
М жисм аракатининг дифференциал тенгламаси уйидагича бўлади:
(4.1)
Жисмнинг аракат онунидан ват бўйича иккинчи тартибли осила исоблаймиз:
(4.2)
(4.2) ни (4.1) га ўйсак:
бу ерда Fx куч мидори sin2t=-1 бўлганда энг катта ийматга эришади.
Демак,
Fx =80Н
бўлади.
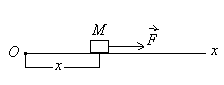
2-масала.Массаси m =1кг бўлган моддий нута радиуси r=2м бўлган айлана бўйлаб =2t (м/с) тезлик билан аракат илади. t=1 секунд бўлганда моддий нутага таъсир этувчи кучнинг тенг таъсир этувчиси топилсин (8-расм).
Ечиш. Сано системасини 8-расмдагидек танлаймиз.Моддий нутанинг аракати табиий усулда берилгани учун аракат дифференциал тенгламалар уйидагича ёзилади:
(4.3)
Моддий нутанинг тезлиги ўзгариш онунидан ват бўйича осила оламиз:
Сон ийматларни (4.3) га ўйсак,
келиб чиади.
3-масала.Горизонт билан бурчак осил илувчи ия текисликда М массага эга бўлган сувли бак турибди. Бакдаги сув сирти ия текисликка параллел бўлиши учун бакни ия текисликка параллел бўлган андай куч билан аракатга келтириш керак? Бакнинг таги билан ия текислик ўртасидаги ишаланиш коэффициенти f га тенг (9-расм).
Ечиш.Бак аракатининг йўналиши ия текислик бўйлаб содир бўлгани сабабли, Ox ўни 9-расмдагидек танлаймиз.ўйилган масалани ал этиш учун аввал суюлик заррачаси аракатини текширамиз.
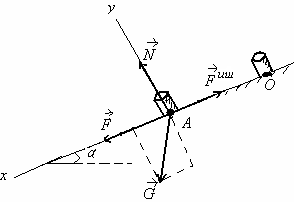
9- расм 10-расм
Заррачага таъсир илувчи куч оирлик кучи ва суюлик сиртига перпендикуляр бўлган босим кучидан иборат.Суюлик сирти ия текисликка параллел.Суюлик заррачаси учун динамиканинг асосий тенгламаси
бўлади.Бу ерда суюлик заррачасининг массаси , тезланиши эса .Сувли бак тезланиши ax ам тезланишга эга бўлиши керак.Демак:
(4.4)
Энди сувли бакни А моддий нута деб араймиз.Бакка оирлик кучи , тортиш кучи , ишаланиш кучи амда ия текисликнинг нормал реакцияси таъсир илади.Бак аракати тўри чизили бўлгани учун динамиканинг асосий тенгламаси уйидагича бўлади:
(4.5)
бунда М – сувли бак массаси, унинг тезланиши.
9-расмдан :
бу ерда
N ни топиш учун моддий нута аракати дифференциал тенгламасининг Oy ўидаги проекциясини тузамиз:
бўлгани учун
Шундай илиб, ва
(4.6)
(4.4) ва (4.6) ни (4.5) га ўямиз:
(4.7)
G=Mg бўлгани учун (66.7) уйидаги кўринишга келади:
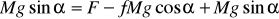
бу тенгликдан
келиб чиади.
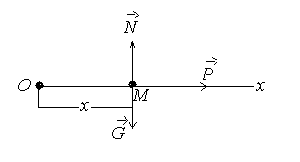
4-масала. Будой ўрувчи комбайннинг пичои онунга кўра тўри чизили аракат илади (t-секундлар, x-метрлар исобида). Пичони аракатга келтирувч куч анилансин.Пичо оирлиги G=100Н . Эркин тушиш тезланиши деб абул илинсин.
Ечиш. Масала шартига кўра пичо тўри чизили аракат илади.Пичони моддий нута деб араб, сано системаси учун Ox ўни оламиз (10-расм).
Пичонинг бошланич олати О нутада бўлсин. Пичоа оирлик кучи , аракатга келтирувчи куч амда реакция кучи таъсир илади.
Пичо аракатининг дифференциал тенгламаси уйидагича бўлади:
(4.8)
Пичонинг аракат онунидан ват бўйича осила исоблаймиз:
(4.9)
(4.9) ни (4.8) га ўйсак,
(4.10)
келиб чиади. m=G/g бўлгани сабабли (66.10) уйидагича ёзилади:
Масала шартидаги берилганларни эътиборга олсак,
келиб чиади.
Динамиканинг иккинчи асосий масаласини ечиш
Техникага оид кўпгина масалаларни ечиш динамиканинг иккинчи асосий масаласини ал илишга келтирилади.
Динамиканинг иккинчи асосий масаласини ечишда нутага ўйилган куч андай характерда ўзгаришига араб дифференциал тенгламаларни ечишнинг турли усуллари ўлланилади.
Энг содда ол куч ўзгармас бўлган олдир. Баъзи олларда куч ватнинг,ёки нута олатининг, ёки нута тезлигининг функцияси бўлиши мумкин. Шунингдек, куч бир йўла ват,йўл,тезлик ва атто тезланиш функциясидан иборат оллар ам учрайди.
Динамиканинг бу асосий масаласини ечиш учун (3.2), (3.3), (3.7) –(3.10) кўринишдаги иккинчи тартибли дифференциал тенгламалардан бирини тузиш ва уни интеграллаш керак.Интеграллаш натижасида ихтиёрий ўзгармаслар осил бўлади.
ар бир конкрет масалани ечишда ихтиёрий ўзгармасларни анилаш керак. Бу ўзгармасларни анилашда моддий нутанинг бошланич пайтдаги олати ва тезлигини ифодаловчи бошланич шартлардан фойдаланилади.
Динамиканинг иккинчи асосий масаласи дифференциал тенгламаларни ечиб,яъни функцияни дифференциаллашга тескари йўлни ўллаб ал илингани учун у динамиканинг тескари масаласи деб ам аталади.
Динамиканинг тескари масаласи уйидаги тартибда ечилади.
1. Агар масала шартида сано системаси берилмаган бўлса, у танлаб олинади.
2. Расмда моддий нутанинг ихтиёрий олати белгиланиб,унга таъсир илувчи кучлар тасвирланади.
3. Агар нута боланишда бўлса,уни боланишдан утариб,боланиш реакция кучлари расмда кўрсатилади.
4. Моддий нута аракатининг бошланич шартлари ёзиб олинади.
5. Моддий нута аракатининг танлаб олинган сано системасидаги дифференциал тенгламалари тузилади.
6. Тузилган дифференциал тенгламалар интегралланади.
7. Бошланич шартлардан фойдаланиб интеграллаш натижасида осил бўлган ўзгармаслар аниланади.
8. Аниланган моддий нутанинг аракат тенгламасидан керак бўлган номаълумлар топилади.
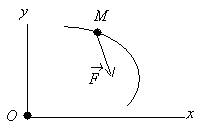
5-масала. m=5кg бўлган моддий нутага кучлар таъсир илади. Моддий нута тезланишининг Ox ўдаги проекцияси анилансин (11-расм).
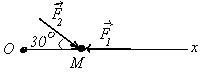
11-расм 12-рacм
Ечиш.Масала шартига кўра сано системаси берилган бўлиб,таъсир илувчи кучлар расмда кўрсатилган.Моддий нутанинг аракати дифференциал тенгламасини Ox ўидаги проекциясини ёзиб оламиз:
(5.1)
11-расмдан:
(67.2)
(5.2) ни (5.1) га ўямиз:
бу ердан:
Сон ийматларни ўйсак, келиб чиади.
6-масала. Массаси m=2кг бўлган нута Oxy текислигида кучлар таъсирида аракат илади. Мазкур нутанинг t=1 секунддаги тезлиги топилсин (128-расм).Бошланич пайтда нута тинч бўлган.
Ечиш.Масала шартига кўра моддий нута Oxy текислигида аракат илади.Шунинг учун сано системаси 128-расмдагидек бўлади.Мазкур нутага Fx , Fy кучлар таъсир илади.
Бошланич ватда нута тинч тургани учун x=0, y=0,=0, =0 бўлади.
Моддий нутанинг дифференциал тенгламаси уйидагича ёзилади:
бу ердан
ёки (5.3)
келиб чиади.
(5.3) ни бошланич шартлардан фойдаланиб интегралласак:
Сон ийматларни ўйсак, келиб чиади.
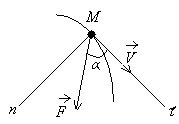
7-масала. Массаси m=16кг бўлган моддий нута текисликдаги эгри чизили траектория бўйлаб тенг таъсир этувчиси F=0,3t (Н) бўлган куч таъсирида аракатланади.Мазкур куч тезлик вектори билан бурчак ташкил илади. t=20 секунд бўлганда эгрилик радиуси.Моддий нутанинг тезлиги анилансин (12-расм).
Ечиш. Моддий нута аракатини табиий координаталар системасига нисбатан текширамиз.
Нутага расмда кўрсатилган куч таъсир этади.
13-расм
Моддий нута тезлигини анилаш учун (3.7) тенгламани иккинчисини тузамиз:
(5.4)
13-расмдан: (5.5)
(5.5) ни (5.4) га ўямиз:
бу ердан
Сон ийматларни ўйсак, келиб чиади.
8-масала. Дон отувчи аппаратдан отилган будойнинг бошланич тезлиги . тезликнинг горизонт билан осил илган бурчаги андай бўлганда будой энг узоа бориб тушади? Муит аршилиги исобга олинмасин (14-расм).
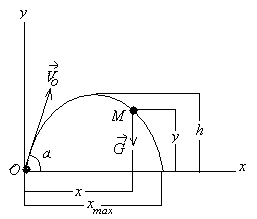
Ечиш. Будой аракатини Декарт координаталар системасига нисбатан текширамиз. Координаталар боши O ни M (будой) нутанинг бошланич отилиш олатида олиб, Oxy текисликни орали ўтказамиз. Бу олда будой аракати Oxy текислигида бўлади. Будойга фаат оирлик кучи таъсир илади.
14-расм
Бошланич пайтда будойнинг координаталари x=0, y=0; тезлигининг координата ўларидаги проекциялари эса
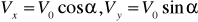
M нута аракатининг дифференциал тенгламалари:
ёки
(5.6)
(5.6) ни икки марта интегралласак
(5.7)
осил бўлади.
Бошланич шартларни (5.7) га ўйсак,
келиб чиади.
Демак,будой аракатининг параметрик тенгламалари
,
(5.8)
бўлади.
(5.8) тенгламалардан ватни йўатсак,будой аракатининг траектория тенгламаси келиб чиади,яъни:
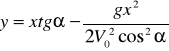
(5.9)
(5.9) парабола тенгламаси бўлиб,унинг ўи Oy ўига параллелдир.
Энди будойнинг энг узоа бориб тушиш масофасини топамиз. Бунинг учун (67.9) ни нолга тенглаштириб ,
(5.10)
ни осил иламиз.
(5.10) даги x координата максимум бўлиши учун бўлиши керак.
Хулоса
Динамика асосида тажриба ва кузатишлар воситасида аниланган онунлар ётади . Бу онунлар XVII асрда Г.Галилей ва И. Ньютон кашф илинган амда Ньютоннинг “Натурал фалсафанинг математик асослари ” асарида баён илинган.
Классик механиканинг биринчи онуни Галилей томонидан кашф илинган бўлиб, жисмларнинг инертлик хусусиятини ифодалайди ва инерция онуни дейилади.
Тажрибаларнинг кўрсатишича,координаталар боши уёш марказида олинган ва ўлари учта “ўзалмас” юлдузлар томонга йўналган гелиоцентрик системани инерциал система деб араш мумкин. Техникада учрайдиган кўпгина масалаларни ечишда инерциал система учун Ер билан боланган координаталар системаси олинади.Бунда Ернинг суткалик айланиши амда уёш атрофида эгри чизили орбита бўйлаб аракати эътиборга олинмайди.
Назорат саволлари
1. И.Ньютоннинг биринчи онунини айтинг.
2. И.Ньютоннинг иккинчи онунини айтинг.
3. И.Ньютоннинг учинчи онунини айтинг.
4. Куч нинг механик катталиги СИ (Халаро бирликлар
системаси) да андай бирликда ўлчанади?
5. Нута динамикасининг биринчи масаласини изоланг.
6. Нута динамикасининг иккинчи масаласини айтинг.
7. СИ (Халаро бирликлар системаси) да тезланиш катталиги андай бирликда ўлчанади?
8. СИ (Халкаро бирликлар системаси) да масса (m) катталиги андай бирликда ўлчанади?
9. Эркин моддий нута аракат дифференциал тенгламаси неча хил усулда берилади?
10. Эркин моддий нута аракатининг вектор усулдаги дифференциал тенгламасини ёзинг.
11. Эркин моддий нута аракатининг Декарт координата ўларидаги дифференциал тенгламаларини ёзинг.
12. Эркин моддий нута аракатининг табиий координата ўларидаги диффференциал тенгламаларини ёзинг.
Фойдаланилган ва тавсия этиладиган адабиётлар.
1. Азиз-ориев С.. Янгуразов Ш.Х. Назарий механикадан массалалар ечиш методикаси (Статика ва кинематика). айта ишланган 2-нашри. –Т.: Ўитувчи, 1974.
2. Азиз-ориев С.. Янгуразов Ш.Х. Назарий механикадан массалалар ечиш методикаси (Динамика). –Т.: Ўитувчи, 1967.
3. Айзенберг Т.Б.,Воронков И.М., Осецкий В.Н. Руководство к решению задач по теоретической механике.-6 е стереотип. Изд. –М,: Высшая школа, 1968
4. Бать М.И., Джанелидзе Г,Ю., Кельзон А.С. теоретической механике в примерах и задачах. -7-е изд., доп. М.: Наука, 1975, т.1;-6-е изд., доп.- М.: Наука,1975, 11;-М.: Наука, 1973, т. Ш.
5. Бражниченко Н.А., Кан В.Л., Минцбург Б.Б. [и др.]. Сборник задач по теоретической механике. -3-е изд.прераб, и доп. –М.: Высшая школа, 1974.
6. Т.Р. Рашидов, Ш. Шозиётов, .Б. Мўминов.”Назарий механика асослари”.
Динамика асослари