Бизнес-прогнозирование с помощью моделей временных рядов

Бизнес-прогнозирование с помощью моделей временных рядов

Оглавление

1 Понятие временного ряда. Компоненты временного ряда………………….......…4

2 Сглаживание временных рядов…………………………………………………….11

3 Анализ периодических колебаний во временных рядах………………………...20

4 Сезонность. Аддитивная и мультипликативная модели…………………………...21

5 Понятие о стационарных временных рядах……………………………………….23

6 Понятие белого шума в моделях динамики временных рядов…………………..28

7 Модель случайного блуждания…………………………………………………….32

8 Понятие оператора лагового сдвига……………………………………………….32

9 Оценка и вывод среднего, автокорреляционной и частной автокорреляционной функций………………………………………………………………………………..35

Литература………………………………………………………………………….….38

Бизнес-прогнозирование с помощью моделей временных рядов

1 Понятие временного ряда. Компоненты временного ряда

Статистическое описание развития экономических процессов во времени осуществляется с помощью временных рядов.

Ряд наблюдений (или ), анализируемой случайной величины , произведенных в последовательные моменты времени называется временным рядом. Отдельные наблюдения временного ряда называются уровнями этого ряда. Уровни ряда могут принимать детерминированные или случайные значения.

Временные ряды делятся на моментные и интервальные. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные интервалы (периоды) времени.

В общем случае модель временного ряда имеет следующий вид:

,

где - систематическая (детерминированная) составляющая ряда;

- случайная составляющая ряда с нулевым математическим ожиданием и дисперсией .

Детерминированная составляющая временного ряда различается в зависимости от типа факторов, под влиянием которых она формировалась.

В общем случае в практике эконометрических исследований на основе временных рядов различают составляющие трех видов.

Долговременная (вековая) составляющая, формирующая общую в длительной перспективе тенденцию в изменении анализируемого признака . Обычно эта тенденция описывается с помощью той или иной неслучайной функции - , как правило, монотонной. Эту функцию называют функцией тренда или просто — трендом.

Сезонная составляющая – , формирующаяся под влиянием сезонных колебаний экономического показателя в течение заданного периода времени, обычно года.

Циклическая (конъюнктурная) оставляющая – , формирующая изменения анализируемого признака в связи с действием долговременных циклов экономической, демографической или астрофизической природы (волны Кондратьева, демографические «ямы» и пики, циклы солнечной активности и т.п.).

Естественно, что перечислить все факторы, которые прямо или косвенно оказывают влияние на интересующий нас показатель, мы не можем, хотя бы просто потому, что их бесконечно много. Именно с этим связывают возникновение стохастической (случайной) составляющей временного ряда, она является предметом серьезных исследований.

Очевидно, что в процессе формирования значений каждого временного ряда не обязательно участвуют одновременно факторы всех четырех типов. Однако во всех случаях предполагается непременное участие случайных (эволюционных) факторов . В научной литературе их также именуют «белым шумом», в отличие от простых остаточных компонент исследуемого ряда.

Если временной ряд представляется в виде суммы соответствующих компонент, то полученная модель носит название аддитивной (1), если в виде произведения - мультипликативной (2) или смешанного типа (3):

(1)

(2)

(3)

где - уровни временного ряда;

-трендовая составляющая;

- сезонная компонента;

- циклическая компонента;

- случайная компонента.

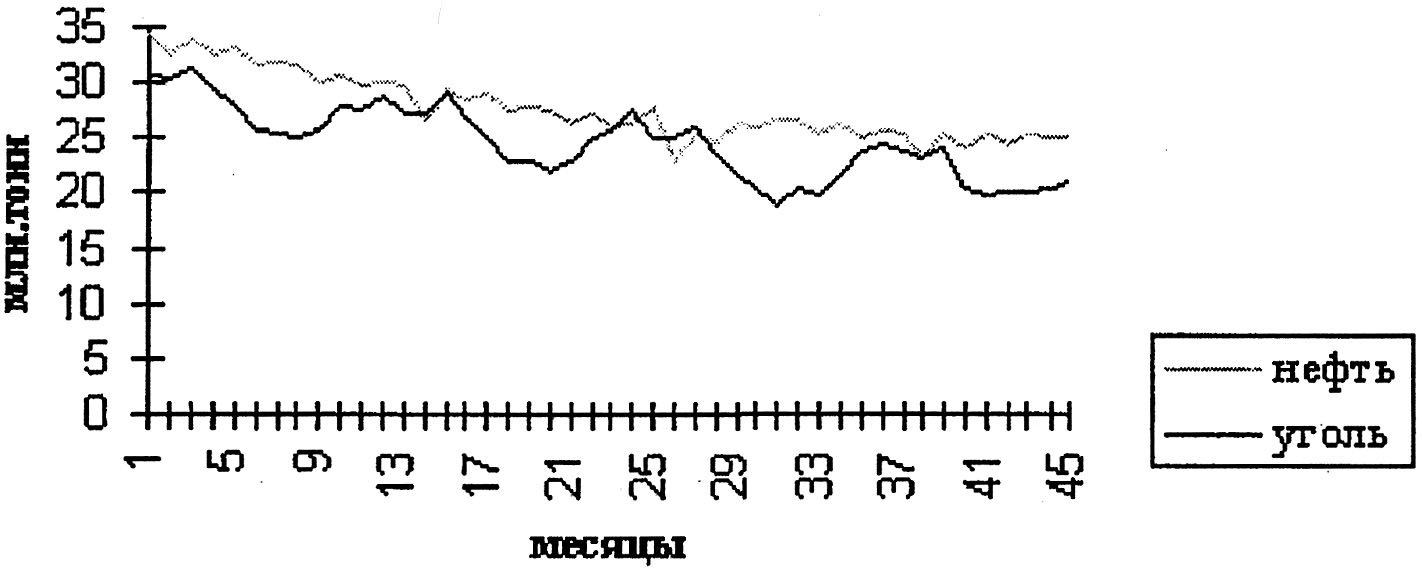
Рисунок 1 - Месячная динамика производства отдельных видов промышленной продукции в натуральном выражении

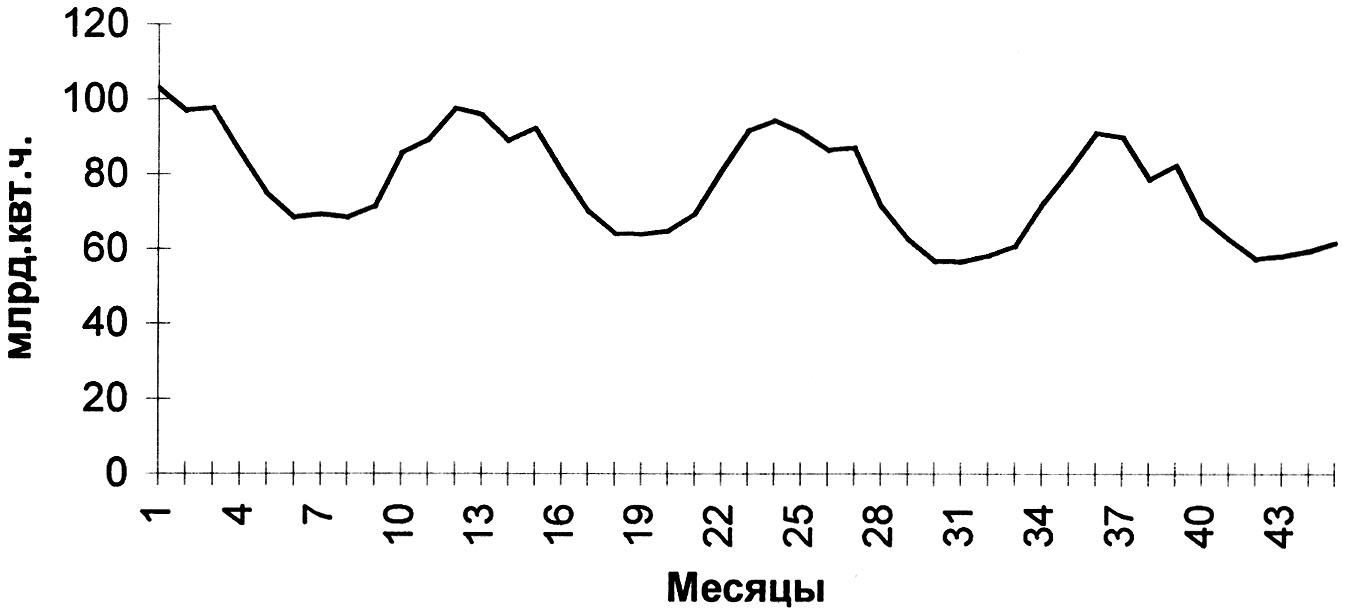
Рисунок 2 - Месячная динамика производства электроэнергии

На рисунках 1 и 2 приведены примеры временных рядов, иллюстрирующие присутствие в них указанных компонент. Графики месячных временных рядов производства промышленной продукции наглядно демонстрируют устойчивые сезонные колебания при снижающемся тренде, причем на последнем участке темпы падения производства заметно снижаются.

Решение любой задачи по анализу и прогнозированию временных рядов начинается с построения графика исследуемого показателя, тем более что современные программные средства предоставляют пользователю большие возможности для этого. Не всегда при этом четко прослеживается присутствие тренда во временном ряду. В этих случаях прежде, чем перейти к определению тенденции и выделению тренда, нужно выяснить, существует ли вообще тенденция в исследуемом процессе. Основные подходы к решению этой задачи основаны на статистической проверке гипотез. Критерии выявления компонент ряда основаны на проверке гипотезы о случайности ряда.

Рассмотрим наиболее часто используемые на практике критерии проверки "наличия-отсутствия" тренда: критерий серий, основанный на медиане выборки и метод Фостера - Стюарта.

Критерий серий, основанный на медиане выборки, реализуется в виде следующей последовательности шагов:

1. из исходного ряда длиной n образуется ранжированный (вариационный) ряд : , где - наименьшее значение ряда .
2. определяется медиана этого вариационного ряда Me.В случае нечетного значения , в противном случае .
3. Образуется последовательность из плюсов и минусов по следующему правилу:

(4)

Если значение равно медиане, то это значение пропускается.

г) подсчитывается v(n) - число серий в совокупности , где под серией понимается последовательность подряд идущих плюсов или минусов. Один плюс или один минус тоже будет считаться серией.

Определяется - протяженность самой длинной серии.

д) проверка гипотезы основывается на том, что при условии случайности ряда (при отсутствии систематической составляющей) протяженность самой длинной серии не должна быть слишком большой, а общее число серий - слишком маленьким. Поэтому для того, чтобы не была отвергнута гипотеза о случайности исходного ряда (об отсутствии систематической составляющей) должны выполняться следующие неравенства (для 5% уровня значимости)

(5)

Если хотя бы одно из неравенств нарушается, то гипотеза об отсутствии тренда отвергается.

Квадратные скобки в правой части неравенства означают целую часть числа. Напомним, что целая часть числа А – [А] - это целое число, ближайшее к А и не превосходящее его.

Другой способ проверки гипотезы о наличии тенденции процесса основывается на методе Фостера-Стюарта. Этот метод может быть реализован в виде следующей последовательности шагов:

1. каждый уровень ряда сравнивается со всеми предшествующими, при этом определяются значения вспомогательных характеристик и :

Таким образом, =, если больше всех предшествующих уровней, , если меньше всех предшествующих уровней.

б) вычисляется , для всех .

Очевидно, что величина может принимать значения 0; 1; -1.

в) находится характеристика .

г) с помощью критерия Стьюдента проверяется гипотеза о том, что можно считать случайной разность D-0 (т.е. ряд можно считать случайным, не содержащим тренд).

Для этого определяется:

где - средняя квадратическая ошибка величины D:

Значения затабулированы.

Таблица 1 Значения стандартных ошибок для для n от 10 до 100

n		n		n		n
10	1,964	35	2,509	60	2,713	85	2,837
15	2,153	40	2,561	65	2,742	90	2,857
20	2,279	45	2,606	70	2,769	95	2,876
25	2,373	50	2,645	75	2,793	100	2,894
30	2,447	55	2,681	80	2,816

Расчетное значение сравнивается с критическим значением, взятым из таблицы t-распределения Стьюдента для заданного уровня значимости а и числа степеней свободы k=n-1. Если |, то гипотеза об отсутствии тренда отвергается.

Пример

Изменения курса акций промышленной компании в течение месяца представлены в таблице 2:

Таблица 2 Курс акций (дол.)

t		t		t		t
1	509	6	515	11	517	16	510
2	507	7	520	12	524	17	516
3	508	8	519	13	526	18	518
4	509	9	512	14	519	19	524
5	518	10	511	15	514	20	521

Проверить утверждение об отсутствии тенденции в изменении курса акций двумя способами:

а) с помощью метода Фостера - Стюарта;

б) используя критерий серии, основанный на медиане выборки.
Доверительную вероятность принять равной 0,95.

Решение