БУЧЕНИЕ УЧАЩИХСЯ ЭЛЕМЕНТАМ КОМБИНАТОРИКИ КАК СРЕДСТВО РАЗВИТИЯ У НИХ КРИТИЧЕСКОГО МЫШЛЕНИЯ

PAGE \* MERGEFORMAT 42

ОБУЧЕНИЕ УЧАЩИХСЯ ЭЛЕМЕНТАМ КОМБИНАТОРИКИ КАК СРЕДСТВО РАЗВИТИЯ У НИХ КРИТИЧЕСКОГО МЫШЛЕНИЯ

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ…………………………………………………………………….	3
1 ФОРМИРОВАНИЕ ОСНОВ КРИТИЧЕСКОГО МЫШЛЕНИЯ У ШКОЛЬНИКОВ НА УРОКАХ МАТЕМАТИКИ……………………………	6
1.1 Понятие и цели внедрения технологии критического мышления……………………………………………………………………….	6
1.2 Этапы технологии развития критического мышления…………………	15
1.3 Методические приемы развития критического мышления учащихся...	23
1.4 Использование технологии развития критического мышления у школьников……………………………………………………………………..	28
2 ИЗУЧЕНИЕ КОМБИНАТОРИКИ КАК СРЕДСТВА РАЗВИТИЯ У ШКОЛЬНИКОВ КРИТИЧЕСКОГО МЫШЛЕНИЯ ………………………...	31
2.1 Основные понятия комбинаторики………………………………………	31
2.2 Анализ школьных учебников…………………………………………….	42
2.3 Развитие комбинаторного мышления школьников при изучении комбинаторики в 5-7 классах……………………………………………...….	55
2.4 Формирование критического мышления при использовании элементов комбинаторики в обучении математики……………………………………..	72
ЗАКЛЮЧЕНИЕ…………………………………………………………………	79
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ ………………………………	82

ВВЕДЕНИЕ

В условиях развития Российского образования педагоги используют эффективные методики обучения, отвечающие требованиям современной педагогики. В связи с этим завоевывают известность методики обучения, повышающие мотивацию обучения, увеличивающие познавательный интерес к дисциплине, помогающие традиционными и инновационными способами научить с максимальной эффективностью основным приемам и навыкам учащихся. В наше время имеется множество различных педагогических технологий, заслуживающих внимания педагогов.

Технология формирования критического мышления позволяет:

- активизировать мыслительную деятельность учащихся,

- научить выделять главное, анализировать ситуацию,

- устанавливать причинно-следственные связи,

- стимулировать творческую деятельность,

- проявлять креативные способности,

- выполнять исследования и делать умозаключения.

Необходимость применения данной технологии определена принадлежностью к развивающему обучению, современным подходом к образованию, перспективой воспитания нравственных основ личности школьников.

Элементы технологии критического мышления применяются давно, но интерес к данной методике обучения увеличился только в настоящее время в связи с модернизацией системы образования в общем и изменением личности учащегося и педагога в частности.

Объект исследования: процесс развития критического мышления учащихся в процессе обучения математике.

Предмет исследования: условия развития критического мышления учащихся при обучении их элементам комбинаторики.

Цель: выявить методические приемы и условия, способствующие развитию критического мышления у учащихся при обучении комбинаторике.

Задачи:

1. При анализе психологической, педагогической и методической литературы уточнить понятие критического мышления и изучить технологию развития критического мышления;

2. Проанализировать учебно-методическую литературу по математике;

3. Выявить особенности развития критического мышления при изучении математики в частности при изучении элементов комбинаторики;

Актуальность исследования: Рассмотрение научной литературы и педагогического опыта позволил выявить ряд противоречий в развитии математического мышления школьников:

- между увеличившимися требованиями к уровню развития мыслительной деятельности выпускников общеобразовательной школы и отсутствием в школьной практике специальной работы, ориентированной на развитие мышления учащихся;

- между необходимостью организации специальной работы, ориентированной на развитие математического мышления учащихся и отсутствием научно-методического обеспечения этой работы;

- между необходимостью использования в процессе обучения основ логики, комбинаторики и их практическим отсутствием в профессиональной компетентности учителей математики;

- между широкими возможностями формирования комбинаторно-критического мышления учащихся на уроках математики и недостаточной разработанностью методических направлений, учебно-методических комплексов, обеспечивающих развитие комбинаторно-критического мышления.

Хотя вопросам формирования мыслительной деятельности ученика уделяется достаточно большое внимание, тем не менее, необходимо отметить крайне низкое усвоение способов комбинаторно-критического мышления как в рамках школьной, так и социальной среды.

Поэтому одной из важнейших задач образования остается задача развития мышления учащихся, в котором одной из главных составляющих является комбинаторно-критическое мышление.

Под комбинаторно-критическим мышлением будем понимать продуктивный процесс, в результате которого происходит выбор необходимых знаний, способов и методов, направленных на разрешение различным числом вариантов, как частных конкретных задач, так и поиск общих закономерностей посредством модельно-мыслительных рассуждений.

Критическое мышление, то есть творческое, помогает человеку установить собственные приоритеты в личной и профессиональной жизни, предполагает принятие индивидуальной ответственности за сделанный выбор, формирует умение анализировать и делать самостоятельные выводы, прогнозировать последствия своих решений и отвечать на них, позволяет развивать культуру диалога в совместной деятельности. [28]

Современного ученика трудно мотивировать к познавательной деятельности, к поиску пути к цели в поле информации и коммуникации. Это происходит потому, что дети часто испытывают серьезные затруднения в восприятии учебного материала по всем школьным предметам. [1] Причиной этого является недостаточно высокий уровень развития мышления, в том числе критического. А это очень важно для человека в современном мире, который живет в новом веке с новым обликом познавательной культуры.

1 Формирование основ критического мышления у школьников на уроках математики

1.1 Понятие и цели внедрения технологии критического мышления.

Технология критического мышления занимает значительную часть в педагогической практике, так как помогает добиться лучших результатов для освоения универсальных учебных действий школьников. А именно, обращают на себя внимание следующие «плюсы» данной образовательной технологии:

- формируется собственное мнение обучающихся,

- совершается обдуманный выбор между различными мнениями,

- самостоятельно решаются проблемы,

- учит аргументировано спорить,

- ценится совместная деятельность, в которой возникает общее решение,

- воспитывается умение ценить чужую точку зрения и сознание, что восприятие человека и его отношение к любому вопросу формируется под влиянием многих факторов.

Критическое мышление - это тип мышления о знании, каком-либо предмете, содержании или проблеме, при котором думающий улучшает качество его мышления с помощью умелого использования структур и интеллектуальных стандартов, присущих мышлению.

Критическое мышление (англ. critical thinking) - система суждений, которая используется для анализа вещей и событий с формулированием обоснованных выводов и позволяет выносить обоснованные оценки, интерпретации, а также корректно применять полученные результаты к ситуациям и проблемам. [25]

В общем значении под критическим мышлением подразумевается мышление более высокого уровня, чем составление вопросов.

В качестве результата внедрения критического мышления можно разобрать критерии для человека, обучающегося с помощью данной образовательной технологии.

Данная методика:

- поднимает актуальные проблемы и вопросы, формулируя их ясно и четко;

- собирает и аккумулирует относящуюся к делу информацию, используя абстрактные идеи, чтобы эффективно их интерпретировать;

- подводит к обоснованным заключениям и решениям, проверяя их по критериям и стандартам;

- предлагает задуматься непредубежденно в пределах альтернативных систем мышления, распознавая и допуская, по необходимости, их предположения, причастность и практическое соответствие;

- помогает эффективно общаться с другими при выработке решения.

Критическое мышление, коротко, - это самонаправляемое, самодисциплинируемое, самооценивающее и самокорректирующее мышление. Это предполагает соглашение со строгими стандартами, что влечет за собой эффективную коммуникацию и способность решать проблемы и обязательство преодолевать наш природный эгоцентризм и социоцентризм.

При планировании и проведении урока с элементами критического мышления преподаватель ставит перед собой три цели обучения: образовательные, воспитательные и развивающие. Каждая составляющая имеет свое направление воздействия на учащихся, но они тесно переплетаются и, как правило, могут быть реализованы только в совокупности. Критическое мышление является частью развивающего обучения. Поэтому развивающие цели весьма важны при проведении учебных занятий, ведь развитие должно прослеживаться на каждом шаге учебной деятельности.

К основным развивающим целям технологии критического мышления относятся:

- развитие памяти, внимательности, усидчивости;

- формирование умения выделять главное;

- увеличение степени развивающего воздействия на формирование личностных качеств обучаемых;

- формирование умений сравнивать, обобщать, контролировать, оценивать, анализировать, делать выводы;

- развитие познавательных возможностей, творческих способностей, креативности личностных качеств;

- организация способности общения (живого, виртуального, обоюдного, группового и т.д.);

- развитие самостоятельности, трудолюбия, специфичных способностей;

- развитие логического мышления;

-формирование эстетического восприятия окружающей действительности;

- развитие инициативы, познавательного интереса;

- обучение методам исследовательского поиска;

- развитие мыслительной деятельности;

- развитие практической направленности изучаемого материала;

- развитие интеграционных связей с другими дисциплинами;

- проведение анализа межпредметных связей;

- опора на морально-нравственные ценностные ориентиры;

- увеличение развивающих способностей;

- развитие нестандартного мышления;

- использование личностного и субъектного опыта;

- стимулирование «я - концепции»;

- внедрение ситуации «успеха» в образовательный процесс;

- развитие индивидуальных особенностей учащихся.

При проведении уроков математики с элементами технологии критического мышления, к развивающим целям можно добавить следующие:

- введение элементов опережающего обучения;

-развитие умений применять математические знания для решения практических задач;

- решение задач повышенной сложности;

- решение задачи разными способами;

- развитие математического мышления через методы активного обучения;

- развитие вычислительных навыков, кругозора школьников;

- формирование информационной культуры, овладение анализа информации и навыками поиска;

- развитие математической интуиции, логического мышления, применение знаний в нестандартных ситуациях, умения анализировать;

- привитие любви к математике,

- развитие у учащихся коммуникативных компетентностей (культуры общения, умения работать в группах),

- обучение самостоятельной деятельности по овладению знаниями.

Понятие «критическое мышление» является важной категорией для всей темы критического мышления. Под критическим мышлением в отечественной психологии принято понимать - основной канальный фактор для подрыва взглядов не только деструктивных культов, но и любых других попыток манипуляторной эксплуатации недостатков человеческой психики и мышления.

К конкретным инструментальным чертам относятся:

- Взвешенное суждение,

- Оценивающее суждение,

- Допущение,

- Классификация,

- Формулирование суждений на основе критериев,

- Понимание принципов,

- Предложение мнений с аргументами,

- Построение гипотезы,

- Логическое формулирование выводов. [3]

Г. В. Сорина считает, что критическое мышление предполагает наличие навыков рефлексии относительно собственной мыслительной деятельности, умение работать с суждениями, понятиями, вопросами, умозаключениями, развитие способностей к аналитической деятельности, а также к оценке аналогичных возможностей других людей.

Критическому мышлению в целом свойственна практическая ориентация. В силу этого оно может быть проинтерпретировано как форма практической логики, рассмотренной внутри и в зависимости от контекста рассуждения и индивидуальных особенностей рассуждающего субъекта.

Вместе с тем одна из главных особенностей критического мышления заключается в том, что оно учит конструированию рассуждений и анализу, получению знания вне зависимости от профессиональной сферы деятельности.

Критическое мышление ориентируется на анализ «естественных» рассуждений, не стремясь подогнать их под стандартные структуры формальной логики. [31]

В зарубежной психологии термин «критическое мышление» был одним из главных в философии Карла Поппера. Согласно его эволюционной эпистомеологии любой живой организм работает как решатель проблемы. При этом данные из окружающего мира используются для подтверждения или опровержения гипотез, которые живой организм предварительно задает. Не только организм, но и знание, которое он несет и хранит, адаптируется к окружающей среде путем естественного отбора. Знание всегда есть результат устранения плохо приспособленных гипотез или адаптаций. Если перед организмом встает проблема, то она ищет попытки решения с помощью выдвижения пробных теорий. Пробные теории подвергаются критическому процессу устранения ошибок. Как подчеркивал Поппер, все организмы, чрезвычайно активны в приобретении знания. [26]

Д. Клустер определял критическое мышление через 5 пунктов:

1. Критическое мышление есть мышление самостоятельное. Следовательно, мышление может быть критическим только тогда, когда оно носит индивидуальный характер.

2. Информация является отправным, а отнюдь не конечным пунктом критического мышления. Знание создает мотивировку, без которой человек не может мыслить критически.

3. Критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить.

4. Критическое мышление стремится к убедительной аргументации. Критически мыслящий человек находит собственное решение проблемы и подкрепляет это решение разумными, обоснованными доводами. Под всеми названными элементами аргументации - утверждением, доводами и доказательствами - лежит четвертый элемент: основание.

Основание - это некая общая посылка, точка отсчета, которая является общей для оратора или писателя и его аудитории и которая дает обоснование всей аргументации.

5. Критическое мышление есть мышление социальное. Всякая мысль проверяется и оттачивается, когда ею делятся с другими. Когда мы спорим, читаем, обсуждаем, возражаем и обмениваемся мнениями с другими людьми, мы уточняем и углубляем свою собственную позицию. [9].

Р. У. Поль писал: «Люди просто не должны доверять своим инстинктам. Они, несомненно, не должны доверять тому, что спонтанно происходит с ним. Они не должны принимать за истинное все, что преподносится как истинное. Они не должны предполагать, что их опыт необъективен. Они нуждаются в том, чтобы быть сформированными, они не рождены со стандартами, априорными нормами, суждениями, претендующими на абсолютную истинность, законность. Они должны вырастить в себе привычки и черты, которые объединят эти стандарты в их жизни». Критическое мышление - это размышление о мышлении, когда вы размышляете с целью улучшить своё мышление… При этом два момента имеют определяющее значение: критическое мышление - это влекущее за собой самоусовершенствование; и это усовершенствование приходит с навыками использования стандартов корректной оценки мыслительного процесса использования стандартов корректной оценки мыслительного процесса» [25].

Одна из самых популярных концепций критического мышления принадлежит американскому педагогу Р. Эннису, который одним из первых разработал систему установок или готовностей к критическому мышлению, или, другими словами, внутренних мотиваций, влияющих на «качество» мышления. Согласно концепции Р. Энниса критически мыслящий человек должен:

1. Заботиться о том, чтоб его решения, взгляды, были четко обоснованы, а для этого ему необходимо:

• Стремиться к поиску новых гипотез, альтернативных объяснений источников, выводов;
• Быть хорошо информированным;
• Рассматривать точки зрения, отличные от своих собственных;
• Расширять свой кругозор, стремиться к разносторонней осведомленности.

2. Быть способным четко представлять, как свою позицию, так и позицию других;

• Ясно и точно понимать сказанного и написанного, принимая во внимание особенности ситуации;
• Концентрироваться на выводе или вопросе, стремиться придерживаться основной темы;
• Искать и предлагать доводы (обоснования);
• Принимать во внимание всю ситуацию в целом;
• Осознавать собственные убеждения;

3. Уважать мнение и достоинства собеседника, т.е.:

• Уметь слушать и слышать других;
• Избегать критических замечаний, принимая во внимание чувства собеседника, быть восприимчивым и стремиться к пониманию чужих чувств, уровня познаний и глубины суждений;
• Быть внимательным к состоянию другого человека.

В основу современных концепций, описывающих интеллектуальные умения критического мышления, положены идеи американского исследователя Э. Глейзера. Он первым изложил набор определённых умений, которые, по его мнению, относятся именно к критическому мышлению: умение распознавать проблему и находить пути её решения, собирать и упорядочивать необходимую информацию, распознавать неподтверждённые предположения и оценки; точность и избирательность в использовании и восприятии языковых средств; умение истолковывать факты и информацию, давать оценку доказательствам, обнаруживать существование или отсутствие логических связей между суждениями, делать правомерные выводы и обобщения и подвергать их сомнению, перестраивать собственную систему убеждений и формировать правильные суждения о явлениях повседневной жизни.

Описанные Э. Глейзером интеллектуальные умения и навыки получили своё развитие в исследованиях Р. Энниса, Р. Пола, С. Норриса, А. Фишера. Вопрос о наборе тех или иных умений, которые относятся именно к умениям критического мышления, до сих пор остаётся «открытым», т.к. каждый из авторов предлагает свою систему, ровно, как и определение самого понятия «критическое мышление». Так, Р. Эннис выделяет 12 основных умений критического мышления, в то время как в концепции Р. Пола их число достигает 35. Выделим наиболее существенные, на наш взгляд, мыслительные умения, которые нашли отражение в большинстве современных концепций критического мышления:

• Оценка надёжности источников информации;
• Умение выделить необходимую информацию и способность к дальнейшей её обработке;
• Ясность изложения собственной позиции, точность в выборе языковых средств;
• Анализ и оценка высказываний, предположений, выводов, аргументов, гипотез, убеждений;
• Рассмотрение проблемы с различных углов зрения и сравнение различных позиций и подходов;
• Умение задавать вопросы с целью получения более точной информации или её проверки;
• Принятие решений и умение обосновать свой выбор.

Использование данных умений в повседневной жизни и на учебном занятии имеет место при наличии уже накопленных знаний и опыта. Критическое мышление - это своего рода «мышление о знании», которое позволяет «использовать ранее приобретённые знания, чтобы создавать новые». При этом понятие «знание» употребляется в самом широком смысле слова. По мнению автора книги «Критическое мышление и обучение» М.Мейсона знаниевый компонент критического мышления это - «…определённый объём знаний, будь то знание основных понятий, относящихся к критическому мышлению, или знание той или иной научной дисциплины, к которой критическое мышление может быть в последствии применено». Так, например, Р. Эннис полагает, что критическое мышление, являясь междисциплинарной и над предметной категорией, носит дедуктивный характер: учащийся овладевает интеллектуальными умениями критического мышления вне конкретной научной дисциплины и может применять их в различных областях знаний. В то время как Дж. Мак Пэк подчёркивает индуктивный характер критического мышления, полагая, что оно неотделимо от конкретной научной области и что необходимым условием критического рассмотрения проблем той или иной научной дисциплины является глубокое знание этой самой дисциплины. «Мы не можем критически рассматривать проблемы ядерной физики, не зная самой ядерной физики», - пишет автор.

Цель критического мышления - тестирование предложенных идей: применимы ли они, как можно их усовершенствовать и т. п. Чтобы провести соответствующий отбор надлежащим образом, необходимо, во-первых, соблюдать известную дистанцию, т. е. уметь оценивать свои идеи объективно, и, во-вторых, учитывать критерии, или ограничения, определяющие практические возможности внедрении новых идей.

Еще одной целью данной технологии является проверка предложенных решений с целью определения области их возможного применения, выявляющее их недостатки и дефекты. [15]

Для установления исходного уровня склонности к критическому мышлению использовался тест – «Бытовые Рассуждения» («Everyday Reasoning») - созданный в Калифорнийским университете, выявляющий склонность к критическому мышлению.

Западная психолого-педагогическая традиция располагает целым рядом отдельных исследований (П. Фэкайон, Н. Фэкайон, С. Джанкарло, Р. Эннис, С. Норрис, Г. Саломон), посвящённых изучению установок на критическое мышление, методик их развития и диагностики.

1.2 Этапы технологии развития критического мышления

Критическое мышление, есть мышление самостоятельное, носит индивидуальный характер, и означает, что человек пытается самостоятельно, независимо от остальных, сформулировать идею или дать оценку ситуации. Критическое мышление осуществляется в ситуации реально значимой для человека, определяемой его потребностями и целями.

Технология представляет собой совокупность приемов, направленных на то, чтобы заинтересовать ученика, пробудить его к деятельности, создать условия для обобщения информации, способствовать развитию критического мышления, навыков самоанализа и рефлексии. На основе этой технологии можно обучить школьников добывать информацию из различных источников.

Выполняя задание в группе, между собой общаясь, учащиеся принимают участие в добывании информации для решения вопроса, в построении знаний. Школьники приобретают новое качество, характеризующее развитие интеллекта на новом этапе, способность критически мыслить.

Выделяют следующие признаки критического мышления:

- мышление продуктивное, в ходе которого формируется позитивный опыт из всего, что происходит с человеком;

- самостоятельное, ответственное;

- аргументированное, поскольку убедительные доводы позволяют принимать продуманные решения;

- многогранное, так как оно проявляется в умении рассматривать явление с разных сторон;

- индивидуальное, ибо оно формирует личностную культуру работы с информацией;

- социальное, поскольку работа осуществляется в парах, группах; основной прием взаимодействия - дискуссия.

Критическое мышление начинается с вопросов и проблем, а не с ответов на вопросы преподавателя. Человек нуждается в критическом мышлении, которое помогает ему жить среди людей, социализироваться.

Основу технологии данного мышления составляет трехфазный процесс:

• Вызов,
• Осмысление содержания,
• Рефлексия,

Данную технологию можно использовать для учащихся любого возраста и применять на любой дисциплине школьной программы.

1. Стадия вызова.

Происходит выявление первоначальных представлений учащихся о теме обсуждения. Школьник ставит перед собой вопрос "Что я знаю?" по данной проблеме.

Задачи этапа:

• Актуализация имеющихся знаний;
• Пробуждение интереса к пробуждению новой информации;
• Постановка учеником собственных целей обучения;
• Определение вопросов, на которые необходимо найти ответы.

Можно предложить школьнику работу с вопросами по проблеме. Данная работа может проходить в два этапа: парная ("я сам"), групповая работа ("мы вместе"). Также может использоваться прием - "мозговая атака". На стадии вызова у ребенка должно сформироваться представление, чего же он не знает, "Что хочу узнать?"

Это побуждает школьников вспомнить, что они уже знают по этой теме, привести имеющиеся знания в определенную систему, а также поделиться своими знаниями. На стадии вызова целесообразно сочетать индивидуальную и групповую формы обучения.

На стадии вызова можно предложить каждому из учащихся начертить в тетради таблицу 1, и после проведения фронтальной беседы о познавательном объекте, заполнить колонки «Знаю», «Хочу узнать».

Таблица 1 – Выявление имеющихся знаний у учащихся.

Знаю	Хочу узнать	Узнал
Записываются знания, которыми владеют учащиеся. Пополняется после групповой работы по обмену знаниями.	Обозначаются вопросы, знаний по которым не достаточно.	После работы записываются те знания, которые ученик индивидуально «Узнал» после работы с учебным текстом.

Информация, полученная на стадии вызова, выслушивается, записывается, обсуждается. Работа ведётся индивидуально, в группах или парах.

Таблица 2 – Деятельность на стадии вызова.

Деятельность учителя	Деятельность учащихся	Приёмы и методы
Направлена на вызов у учащихся имеющихся знаний по изучаемой теме, вопросу; активизацию их деятельности; мотивация к дальнейшей работе.	Вспоминает, что известно по изучаемому, делает предложения, систематизирует информацию до изучения нового материала, задаёт вопросы, на которые хочет получить ответы.	Составление списка «известной информации»: Рассказ-предположение; Кластеры, таблицы; Словарь понятий, терминов; Ключевые понятия; Логические цепочки;

2. Стадия осмысления.

Эта стадия начинается вместе с подачей новой информации. На этой стадии происходит соприкосновение учащихся с новыми знаниями, понятиями, идеями. Новая информация может быть представлена в виде текста, лекции, видеофильма. Здесь происходит соотнесение новой информации с той, которой ранее располагали учащиеся.

Задачи стадии:

• Корректировка учеником поставленных целей обучения;
• Получение новой информации;
• Корректировка первоначальных знаний по теме.

Во время этой фазы урока учащиеся работают самостоятельно. Задачей учителя является поддержка активности учащихся, которая была достигнута на стадии вызова.

На данной стадии школьник под руководством учителя и с помощью своих товарищей ответит на те вопросы, которые сам поставил перед собой на первой стадии (что хочу знать).

Здесь может быть предложена работа с текстом: прочитать, пересказать, растолковать соседу (группе), заполнение матричной таблицы, чтение с пометками текста (“V” - уже знаю; “+” - новое; “-” - противоречит взглядам; “?” - “хочу узнать подробнее”), выписка из текста. Например, при использовании метода перестановок при решении комбинаторных задач возможно следующее деление на части:

Таблица 3 – Прием «Инсерт»

Значки	Ключевые слова
	Понятие множества
+	С множествами можно делать действия, использовать основные свойства
–	Не думал, что для работы с множествами возможны формулы, думал, что такие задачи решаются перебором решений
?	Как решаются практические задачи

В ходе работы с учебным текстом, каждый ученик индивидуально заполняет колонку «Узнал».

Осуществляется непосредственный контакт с новой информацией (текст, фильм, лекция, материал параграфа, рассказ).

Работа ведётся индивидуально, в парах или группах.

Таблица 4 – Деятельность на стадии осмысления

Деятельность учителя	Деятельность учащихся	Приёмы и методы
Направлена на сохранение интереса к теме при непосредственной работе с новой информацией, постепенное продвижение от знания «старого» к «новому».	Ученик читает или слушает текст, используя предложенные учителем активные методы чтения, делает пометки на полях или ведёт записи по мере осмысления новой информации.	Методы активного чтения: инсерт; двухчастные и трёхчастные дневники; бортовые журналы; таблицы «З-Х-У» фишбоун; кластеры, зигзаг…

На этой стадии можно провести чтение текста с пометками, что позволяет не только проанализировать текст повторно, но и учит школьников переводить обширную информацию из текстовой в табличную форму. Смысл используемых знаков необходимо оговорить заранее.

Используемые приемы: изучение текста и его отдельных частей, просмотр видеофильма, прослушивание лекций учителя.

3. Стадия рефлексии.

На завершающем этапе урока проводится фронтальная беседа с опорой на те новые знания, которые получены в ходе работы с текстом и проведения лабораторных и практических работ. Осуществляется окончательная коррекция колонки «Узнал» в таблице 1.

Задачи этапа:

• Размышление;
• Рождение нового знания;
• Постановка учеником новых целей.

Размышление и обобщение того, “что узнал” ребенок на уроке по данной проблеме. На этой стадии может быть составлен опорный конспект в тетради учащегося. Кроме того, могут быть осуществлены: а) возврат к стадии вызова; б) возврат к ключевым словам; в) возврат к перевернутым логическим цепочкам; г) возврат к кластерам.

На стадии рефлексии осуществляется анализ, творческая переработка, интерпретация изученной информации. Работа ведется индивидуально, в парах или в группах.

Таблица 5 – Деятельность на стадии рефлексии

Деятельность учителя	Деятельность учащихся	Приёмы и методы
Учителю следует вернуть учащихся к первоначальным записям; внести корректировку, дополнения; дать творческие, исследовательские или практические задания на основе изученной информации.	Учащиеся соотносят «новую» информацию со «старой», используя знания, полученные на стадии осмысления содержания.	Кластеры, таблицы. Причинно-следственные связи. Возврат к ключевым словам. Ответы на поставленные вопросы. Организация круглых столов, дискуссий. Творческие работы, исследования.

Завершается урок составлением кластера, который продемонстрирует взаимосвязь основных понятий рассмотренных на уроке.

Используемые приемы: составление схемы, таблицы обсуждения, дискуссия, краткое сочинение, карты познания, кластер, синквейн, рисунок и т.д.

Представим основные характеристики критического мышления, в виде схемы 2: [37]

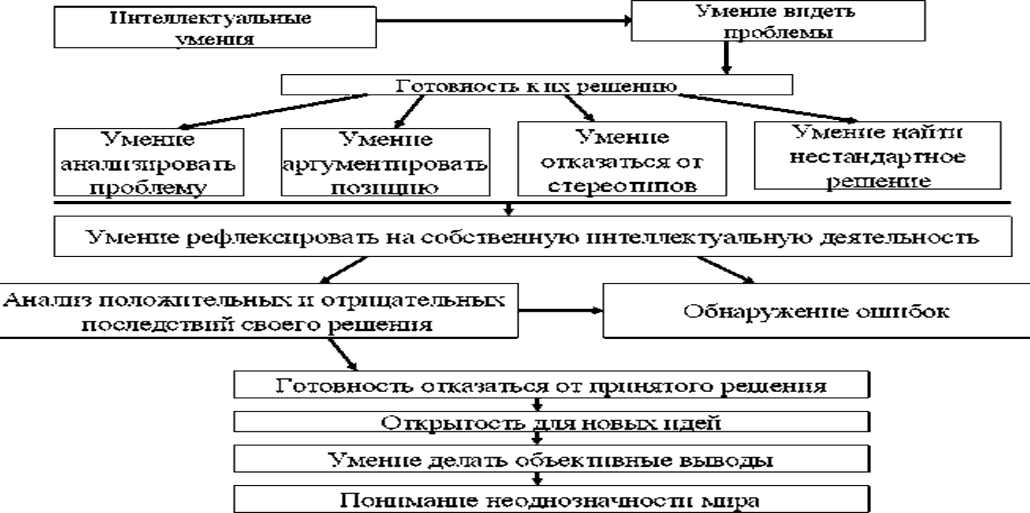
Схема 2- Характеристика критического мышления

При использовании технологии критического мышления происходит формирование нравственных качеств личности школьников, они показаны на схеме 3. [37]

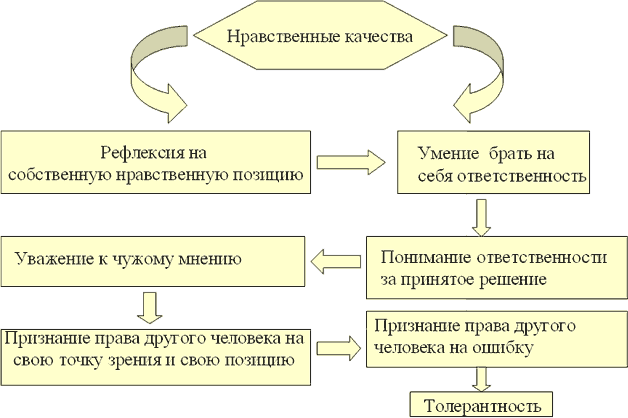
Схема 3– Формирование нравственных качеств личности школьника

1.3 Методические приемы развития критического мышления учащихся

Технология критического мышления предполагает групповую, командную формы работы, которые формируют коллективную, коммуникативную формы работы. Рассмотрим схему 4, на которой показаны составляющие понятия «команды» и назначение составляющих этого понятия.

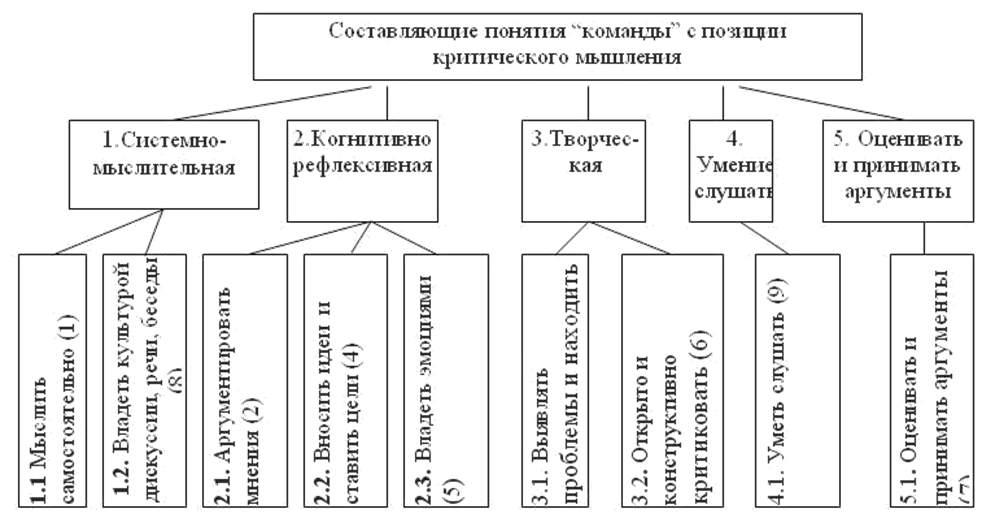
Схема 4 – Составляющие понятия «команды» с позиции критического мышления

Для каждой стадии реализации критического мышления характерны свои методические приемы, перечисленные далее.

1 - Вызов

- Индивидуальная, парная и групповая мозговая атака.

- Работа с ключевыми терминами.

- Перевёрнутые логические цепи (связать последовательность элементов информации в нужной последовательности).

- Свободное письмо (задаётся тема, а способ воплощения - нет; пишите всё, что приходит в голову: это может быть связанный текст, или опорные словосочетания).

- Разбивка на кластеры (построение логографа-выделение блоков идей).

- Механизм ЗХУ (знаю, хочу узнать, узнал).

2 - Стадия осмысления

- Маркировочная таблица («5» - я так и думал, «+» - новая информация, «+!» - очень ценная информация, «-» - у меня по-другому, «?» - не очень понятно, я удивлён).

- Взаимоопрос и взаимообучение (например, задать друг другу вопросы).

- Двойной дневник (страница делиться на две части: слева - что понравилось, запомнилось, справа - почему, какие ассоциации).

3 - Рефлексия

- Возврат к стадии вызова (обсудить, что совпадает с началом).

- Возврат к ключевым словам.

- Возврат к перевернутым логическим цепочкам.

- Возврат к кластерам (их заполнение).

- Возврат к ЗХУ.

Дополнительные приемы

А) Трёхчастный дневник (В третьей колонке - письмо учителю, описание впечатлений, предложения).

Таблица 6 - Трехчастный дневник

Вопросительные слова	Основные понятия темы	Описание впечатлений, предложения
…	…	…

Б) Графическая организация материала (Концептуальная таблица).

Рисунок 1 – Концептуальная таблица

В) Кубик.

Дать описание граней.

Сравнить с чем-нибудь.

Проассоциируй (на что похоже).

Проанализируй (из чего состоит).

Применить это.

Привести примеры.

Рисунок 2- Кубик

Г) Синквейн - способ творческой рефлексии - “стихотворение”, написанное по определенным правилам:

1 строка - одно существительное,

2-я - два прилагательных,

3-я - три глагола,

4-я - крылатая фраза,

5-я - одно существительное, которое выражает суть.

"Критическое мышление" можно смело отнести к инновационным технологиям, так как она соответствует основным параметрам инновационного образования. Например, синквейн комбинаторики:

Комбинаторика 
Интересная, непознанная.
Изучать, понимать, перебирать.
Присутствует во всех областях.
Вариативность.

Д) Интеллект – карта.

Е) Составление кластера

Например, способы решения комбинаторных задач.

Комбинаторика

Перестановки Сочетания Размещения

с повторениями без повторения с повторениями без повторения

Схема 5 – кластер способы решения комбинаторных задач.

Ж) Перепутанные логические цепочки.

Учитель предлагает учащимся ряд утверждений, среди которых есть верные, а есть и неверные. Учащиеся работают индивидуально, читают текст, отмечают перепутанные цепочки. Обсуждают свои результаты в группе, уточняют, исправляют.

З) Ассоциативные игры, направленные на закрепление материала.

Хокку (или хайку) – японская стихотворная форма в три строки. Хокку обычно выражает первое впечатление писателя от предмета, окружающего мира или события.

И) Прием «Фишбоун» («Рыбная кость»)

Рисунок 3 – прием «Фишбоун»

К) Понятийное колесо.

Его можно использовать по-разному: либо повторить определение каждого понятия по очереди, либо использовать игровой момент с той же целью.

Рисунок 4 - Понятийное колесо

Существуют приемы по развитию навыков ведения дискуссии, к ним относятся:

• Ролевая игра
• Перекрестная дискуссия
• Спор-диалог
• Метод углов (учащиеся расходятся по углам в соответствии с определенными взглядами. Аргумент одной группы – контраргумент другой. Учащиеся могут переходить в другой угол. Колеблющиеся сидят в центре класса, в процессе дискуссии могут подключиться к той или иной группе)

1.4 Использование технологии развития критического мышления у школьников

Для учащихся подросткового возраста актуальны следующие вырабатываемые навыки, которые относятся к технологии развития критического мышления у школьников:

- Готовность к планированию;

- Гибкость;

- Настойчивость;

- Готовность исправлять свои ошибки;

- Осознание;

- Поиск компромиссных решений.

Существует мнение, что критическое мышление – западная технология. Одной из задач «Национального комитета в сфере образования США» является повышение доли выпускников колледжей, способных критически мыслить, работать в коллективе и решать поставленные задачи.

Анализируя различные источники, можно сделать вывод, что американские и российские педагоги давно говорят об актуальности методики развития критического мышления, каждый своими словами, но об одном и том же. Например:

1) «Умение отличить возможное от невозможного, выделять основное, использовать аргументы при доказательстве или опровержении своих и чужих суждений и предположений, «узнавать» несообразности и «нелепости» в рассуждениях». П.П.Блонский.

2) «Процесс, при помощи которого разум перерабатывает информацию, чтобы понять установившиеся идеи, создать новые идеи или решить проблемы». Д.Х.Кларк, А.У.Бидл.

3) «Искусство думать о том, как вы думаете, когда думаете о том, чтобы думать более ясно, точно, четко, осмысленно, последовательно; искусство конструктивного скептицизма; искусство обнаружения и преодоления предубеждений и одномерности мышления; искусство целенаправленного и глубокого размышления».

Критическое мышление включает умение решать проблемы. Учащиеся вовлекаются во множество процессов, которые помогают им развить и продемонстрировать умение решать проблемы и мыслить критически.

Одним из механизмов формирования навыков критического мышления, стимулирования мышления является задавание вопросов. Для этого используется таксономия уровней познания Блума.

Большая часть вопросов, которые задают в школе, требуют лишь мышления низкого порядка на уровне воспроизведения и понимания. Знания и понимание являются преобладающими навыками мышления и служат базой для формирования навыков мышления более высокого порядка. На каждом последующем уровне навыки мышления становятся более сложными и используются реже.

Существует прямая связь между вопросами, которые мы задаем и уровнями мышления, на которые выходим при ответе на них.

Вопросы низкого уровня подходят для:

• Оценки подготовленности ученика и его понимания материала;
• Определения сильных и слабых сторон ученика;
• Повторения и /или обобщения материала.

Вопросы высокого уровня необходимы для:

• Мотивирования учеников мыслить глубоко и критически;
• Решения проблем;
• Организации дискуссий;
• Поощрения учеников к самостоятельному поиску информации.

2 Изучение комбинаторики как средства развития у школьников критического мышления

2.1 Основные понятия комбинаторики

Дискретная математика (конечная математика) – раздел математики, занимающийся изучением свойств объектов конечного характера. К их числу могут быть отнесены конечные множества, графы, некоторые математические модели.

В математике некоторые понятия являются неопределяемыми (первичными). К ним относится понятие множества (например, в «Алисе в стране чудес»: «- Множество чего? – А ничего, просто множество»).

Множества можно составлять из различных объектов, как материальных, так и абстрактных (числа, геометрические фигуры и т.д.), объединённых на основе самых различных признаков, содержащих различное количество элементов. Под элементами множества в математике понимают объекты, составляющие множество. Обычно множества обозначают прописными латинскими буквами: А, В, С и т.д., а элементы – малыми: а, b, с и т.д. Принадлежность элемента множеству записывают, а А.

Оказывается удобным считать множеством пустое множество, т. Е. множество, не содержащее ни одного элемента. Пустое множество обозначается .

Рассмотрим некоторые примеры множеств.

1) Множество натуральных чисел: {1,2,3…}. Множество содержит бесконечное число элементов.

2) Множество всех делителей числа 12: {1,2,3,4,6,12}. Конечное множество, содержащее 6 элементов.

3) Множество всех выпуклых четырёхугольников. Множество содержит бесконечное число элементов. Несчётное множество.

4) Множество действительных чисел, являющихся корнями уравнения

х2 = -1. Уравнение не имеет действительных корней, поэтому множество его решений – пустое.

Порядком множества называется число его элементов. Если множество состоит из конечного числа элементов, то его порядком называется количество элементов. Если множество содержит бесконечное число элементов, оно называется бесконечным. Из бесконечных множеств можно выделить множества, элементы которых можно пронумеровать (множество натуральных чисел, множество, состоящее из членов арифметической или геометрической прогрессии и т. Д.) – счётные множества.

Множества можно задавать характеристическим свойством.

Например, Q = {т/п | т Z; п N} – множество рациональных чисел, состоящее из дробей, в числителе которых стоит целое число, а в знаменателе – натуральное.

Наглядную иллюстрацию множеств дают диаграммы Эйлера-Венна, в которых элементы множеств изображаются точками некоторых кругов.

Множество А называется подмножеством множества В (А В), если любой элемент множества А принадлежит множеству В.

Любое множество есть подмножество самого себя, пустое множество является подмножеством любого множества. Если А В и В А, то множества А и В состоят из одинаковых элементов и называются равными (А = В). Если А – непустое подмножество множества В и А В, то А называют собственным подмножеством множества В. Подмножество множества на рисунке 5:

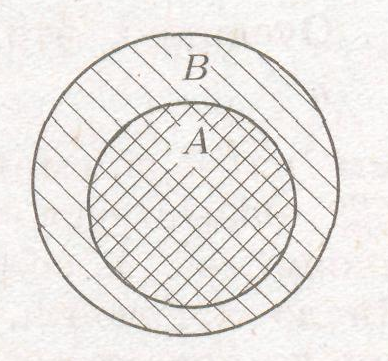
Рисунок 5 – Подмножество множества

Рассмотрим действия с множествами.

Пусть даны множества А и В.

1. Объединением множеств А и В (A U В) называется множество С (A U В = С), элементы которого являются элементами А или элементами В.

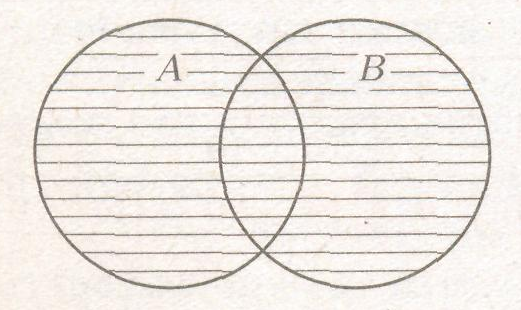
Рисунок 6 – Объединение двух множеств

2) Пересечением множеств А и В (А В) называется множество С (А В = С), элементы которого являются элементами А и элементами В одновременно.

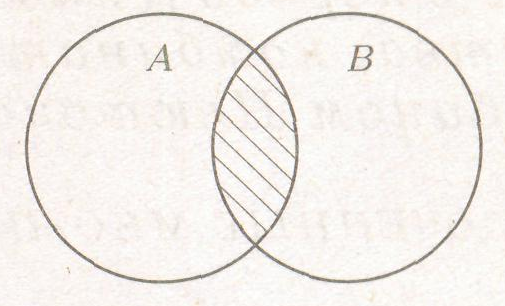
Рисунок 7 – Пересечение двух множеств

3) Разностью множеств А и В (А\СВ) называется множество С (А\ В = С), элементы которого являются элементами А и не принадлежат В.

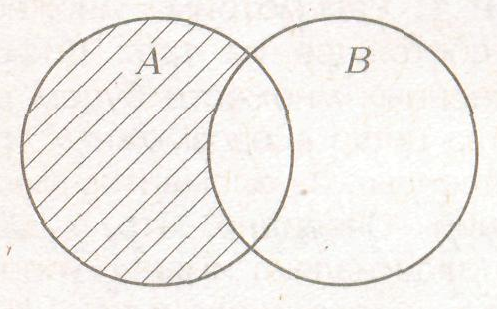
Рисунок 8 – Разность двух множеств

4) Декартовым произведением множеств А и В называется множество упорядоченных пар (х, у), где х А, у В: А х В = {(х, у) | х А, у В}.

Рассмотрим еще некоторые примеры множеств.

1. Множество целых чисел есть объединение множества натуральных чисел, множества чисел, противоположных натуральным и множества, состоящего из числа 0:

N U {-n | n N} U {0} = Z.

2) Пересечением двух прямых (не обязательно различных) в пространстве может быть пустое множество (параллельные или скрещивающиеся прямые), точка (пересекающиеся прямые) или бесконечное множество точек (прямая, совпадающая с двумя заданными).

3) Разностью множества точек отрезка АВ и множества точек, одинаково удалённых от точек А и В (плоскость, перпендикулярная АВ и проходящая через его середину) являются все точки отрезка АВ, кроме его середины.

4) Координатная плоскость является декартовым произведением двух координатных прямых: R х R = R2.

5) Функцией с областью определения D и множеством значений Е называется любое подмножество декартова произведения D х Е, удовлетворяющее условию функциональности (если F – подмножество D x E:

F D х Е и пары (x, y1); (х, у2) F, то у1 = у2).

Множества могут быть заданы по-разному. Например, описанием элементов, арифметическими действиями с числами, перечислением и т.д. Но чаще всего они представляются графической схемой.

Графическое задание множеств происходит с помощью диаграмм Эйлера-Венна. Замкнутая линия-круг Эйлера – ограничивает множество, а рамка – универсальное пространство Е. Заданы два множества: А = {a, b, c} и B = {b, d, e, f}. Если элементов множеств немного, то они могут на диаграмме указываться явно (показано на рисунке 9).

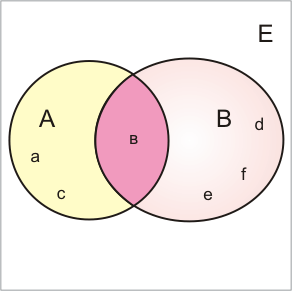
Рисунок 9 – Графическое задание множеств

Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами:

1. Коммутативность.

A B=B A

A B=B A

1. Ассоциативность.

(A B) C=A (B C)

(A B) C= A (B C)

1. Дистрибутивность.

(A B) C = (A C) (B C)

(A B) C= (A C) (B C)

1. A A=A, A A=A
2. A = A, A =
3. Законы де Моргана (законы двойственности).
   1. C (A B)= C A C B
   2. C (A B)= C A C B

Доказательство данных свойств проводится на основе определения равенства двух множеств.

Под множеством понимается набор, совокупность, собрание каких-либо объектов (которые называются элементами множества). Множество, все элементы которого изолированы друг от друга, называется дискретным. Элементы дискретного множества представляют собой конкретные конечные значения чего-либо. Для измерения степени изолированности элементов данного множества вводится понятие расстояния между элементами. Таким расстоянием для чисел может быть, например, модуль разности между ними; для точек на плоскости – геометрическое расстояние.

Дискретное множество определяется как множество объектов, расстояние между которыми не меньше некоторой наперед заданной величины L.

Разница между дискретным и непрерывным представлением информации хорошо видна на примере часов. В электронных часах с цифровым циферблатом информация представляется дискретно – цифрами, каждая из которых четко отличается друг от друга. В механических часах со стрелочным циферблатом информация представляется непрерывно – положениями двух стрелок, причем два разных положения стрелки не всегда четко отличимые (особенно, если на циферблате нет минутных делений). Вообще, любое представление информации с помощью конечного множества символов (букв, цифр, знаков препинания, математических знаков) дискретно; графическое представление (рисунок, чертеж) непрерывно.

Типичный пример дискретного устройства - электронно – вычислительная машина (компьютер), состояние памяти которой представляется последовательностью двоичных цифр: нулей и единиц, все операции в ней производятся с дискретными представлениями информации.

Типичные примеры аналоговых устройств – измерительные приборы, представляющие информацию положением стрелки (вольтметр, спидометр), непрерывной кривой, выдаваемой на экран (осциллограф) или на бумагу (кардиограф) и т.д. Переход от аналоговых представлений информации к цифровым (например, ввод результатов измерений ЭВМ) и обратно в технике осуществляется специальными устройствами: аналого-цифровыми и цифро-аналоговыми преобразователями.

Другой пример, измерение температуры больного – работа с дискретными величинами, так как каждая конкретная температура – это отдельная дискретная величина. А создание кардиограммы сердца – это исследование непрерывной величины, вследствие того, что линия кардиограммы – величина непрерывная.

В школьную математику не так давно включили элементы комбинаторики. Этот раздел – комбинаторика, “наука о способах подсчета вариантов”. Эта наука имеет примерно 300 летний возраст. Комбинаторика –изучает простейшие соединения. Как и в древней, в современной статистике невозможно обойтись, без навыков просчитывать в уме или, по крайней мере, быстро, по простым формулам, варианты событий, размещений предметов, значений величин и т.п.

Рассмотрим пример решения практического вопроса с использованием правил комбинаторики:

Решается вопрос об установлении электронной связи между 8 предприятиями фирмы по следующему принципу – каждое предприятие должно иметь отдельный канал связи со всеми остальными. Сколько таких каналов придется установить в фирме?

Для решения задачи можно нарисовать выпуклый 8-угольник и провести в нем все диагонали, пересчитав в конце их число и не забыв добавить число сторон. Человек, знающий комбинаторику, укажет верный ответ – всего требуется 28 каналов.

Рисунок 10 – Иллюстрация решения задачи

Можно рассуждать по-другому. Первое предприятие установит 7 каналов, второе – 6, третье – 5 и т.д. Значит нужно найти сумму:

7 + 6 + 5 + 4 + 3 + 2 + 1 = 28

Для изучения наиболее популярных применений комбинаторики, рассмотрим ее основные понятия - перестановки, размещения и сочетания.

Перестановками называют операции над упорядоченным рядом из n различных объектов, в процессе которых “списочный состав” ряда не изменяется, но “места” объектов в этом ряду изменяются от варианта к варианту. Количество перестановок – это количество новых упорядоченных множеств, составленных из данного множества с тем же количеством элементов.

Попробуем найти число перестановок для множества из 1, 2 и 3 предметов.

Воспользуемся для этого простенькой схемой:

n=1 A 1 вариант.

N=2 AB BA 12= 2 варианта.

N=3 ABC ACB BCA BAC CAB CBA 123= 6 вариантов.

Можно доказать строго, что в общем случае число перестановок в ряду из n элементов составит

Pn = n! = 123 … (n – 1) n

n! – факториал числа,

n – произведение последовательных натуральных чисел от 1 до n.

Свойства перестановок: 1! = 1; 0! = 1.

Рассмотрим пример.

Дано множество А = {1, 2, 3}.

Составим все перестановки чисел этого множества: 123, 132, 213, 231, 312, 321. Их 6.

Вычислим по формуле P3 = 3! = 123= 6.

Размещениями из n элементов по m элементам Anm называют конечные упорядоченные множества, содержащие m элементов, выбранных из n элементов множества А. То есть, количество размещений – это количество новых упорядоченных множеств, составленных из данного множества с другим количеством элементов. Число всевозможных размещений вычисляется по формуле Аmn =

Свойства размещений: А1n = n; Аon = 1; Аnn =n!

Рассмотрим пример.

Дано множество А = {1, 2, 3}.

Составим все размещения двух чисел этого множества: 12, 21, 13, 31, 23, 32. Их 6.

Вычислим по формуле

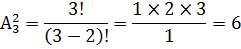
Сочетаниями называют операции над множеством из n различных объектов, в процессе которых образуют подмножества из k элементов, взятых из исходного множества, так, чтобы варианты подмножеств отличались друг от друга хотя бы одним элементом. То есть, количество размещений – это количество новых неупорядоченных множеств, составленных из данного множества с другим количеством элементов.

Опустим доказательство формулы для расчета числа сочетаний из n по k в общем виде и приведем лишь примеры для числа сочетаний из 3 по 2 и из 5 по 3.

Если элементы исходного множества A, B, C.

Варианты подмножеств: AB, AC, BC – всего три.

Если элементы исходного множества A, B, C, D, E.

Варианты подмножеств: ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE – всего десять.

Если опыт состоит в выборе m элементов без возвращения и без упорядочивания, то различными исходами следует считать m – элементные подмножества, имеющие различный состав. Получаемые при этом комбинации элементов (элементарные исходы) носят название сочетание из n элементов по m, а их общее число определяется по формуле:

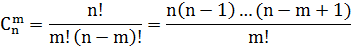
Свойства сочетаний: С1n = n; Сon = 1; Сnn =1.

Рассмотрим пример.

Дано множество А = {1, 2, 3}.

Составим все сочетания двух чисел этого множества: 1 и 2, 2 и 3, 1 и 3. Их 3.

Вычислим по формуле

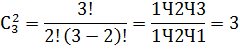
Существует еще один способ вычисления числа сочетаний из n по m – с использованием коэффициентов в развернутой форме бинома Ньютона (p+q)n. В самом деле, например, при n = 3 коэффициенты при степенях разложения составляют 1, 3, 3, 1 – а это и есть сочетания из 3 по 0, 1, 2, 3 и 4 элементов.

С помощью сочетаний рассчитывается треугольник Паскаля, который заполняется значениями , если m n.

Таблица 6 – Треугольник Паскаля

n m	0	1	2	3	4	5	6
0	1
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1

Проверяется треугольник Паскаля просто: первый элемент любого основания равен 1, второй – номеру основания, а все последующие – сумме двух «вышестоящих» (верхнего и левого).

Для чисел Cnm , называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:

Cnm = Cnn – m (свойство симметрии);

Cn + 1k = Cnk + Cnk – 1 ; Cn0 = 1 (рекуррентное соотношение);

Cn0 + Cn1 + . . . + Cnn = 2n (следствие биномиальной формулы Ньютона).

Для любого натурального n верна формула, называющаяся биномом Ньютона:

(a + b)n = Cno an + Cn1 an-1b + … + Cnm an-mbm + … + Cnn bn .

Коэффициенты Cnm, равные числу сочетаний из n элементов по m, называются биномиальными коэффициентами. Частные случаи бинома Ньютона (n = 2; 3) входят в список формул сокращенного умножения:

a2 + 2ab + b2 = (a + b) 2

a2 – 2ab + b2 = (a – b) 2

a3 + 3a2b + 3ab2 + b3 = (a + b) 3

a3 – 3a2b + 3ab2 – b3 = (a – b) 3

Таблица 7 - «Основные формулы комбинаторики»

Понятия	Формулы для вычисления	Основные свойства
Перестановки	Рn = n! = 1 2 3 … n	1! = 1; 0! = 1
иРазмещения	Аmn =	А1n = n; Аon = 1; Аnn =n!
Сочетания	Сmn =	С1n = n; Сon = 1; Сnn =1

2.2 Анализ школьных учебников с точки зрения содержания комбинаторной линии

Рассмотрим учебники «Математика 5», «Математика 6», «Математика 7» под редакцией Г.В Дорофеева и И.Ф Шарыгина. [19, 20, 21]

В 5 классе представлены комбинаторные задачи на размещения, сочетания, перестановки с повторением и без повторения элементов. Однако ни сами эти термины, ни соответствующие формулы не рассматриваются. Используется естественный, доступный детям этого возраста метод решения комбинаторных задач с помощью непосредственного перебора возможных вариантов (комбинаций). Этот метод целесообразен в тех случаях, когда число вариантов невелико.

На первоначальном этапе освоения решить комбинаторную задачу — это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи. Цель пункта состоит в том, чтобы в процессе решения системы задач учащиеся встретились с необходимостью перебора различных по своей сути и составу комбинаций.

При решении каждой задачи ставится один и тот же вопрос: как организовать перебор вариантов, чтобы не пропустить ни один из них и в тоже время избежать повтора?

Среди других способов перебора в теоретической части пункта предлагается осуществление перебора с помощью специальной схемы — дерева возможных вариантов, задающего удобную опорную схему для перебора.

Пример. В алфавите племени УАУА имеются только две буквы – «а» и «у». Сколько различных слов по три буквы в каждом можно составить, используя алфавит этого племени?

Решение. В этой задаче одна и та же буква может встречаться в слове как один, так два или три раза. И нужно рассмотреть все варианты.

Заметим, что очень удобно процесс перебора осуществлять путем построения специальной схемы, которая называется деревом возможных вариантов. Рассмотрим построение дерева возможных вариантов для данной задачи: сначала нужно выбрать первую букву – это могут быть буквы «а» или

«у», поэтому в «дереве» из корня проведем две веточки с буквами «а» и «у» на концах. Вторая буква может быть опять как «а» так и «у», поэтому из каждой веточки выходит еще по две веточки и т.д.

Первая буква

Вторая буква

Третья буква

Полученное

слово ааа аау ауа ауу уаа уау ууа ууу

Рисунок 11 – Дерево возможных вариантов

Теперь, проходя по веточкам дерева, по порядку выписываем нужные нам сочетания букв - «слова»:

ааа; аау; ауа; ауу; уаа; уау; ууа; ууу.

Дерево помогает увидеть путь решения, учесть все варианты и избежать повторений. Нужно обратить внимание, что дерево возможных вариантов позволяет нам подсчитывать упорядоченные наборы.

В 6 классе для изучения элементов комбинаторики выделяется два параграфа: логика перебора и правило умножения. В данном учебнике, как и в 5 классе, продолжается решение задач путем систематического перебора возможных вариантов. Однако при этом учащиеся имеют дело с большим количеством элементов и в более сложных ситуациях. Они знакомятся с кодированием как способом представления информации, который позволяет упростить записи. Продвижением вперед является знакомство на содержательном уровне с комбинаторным правилом умножения. Задачи решаются как с опорой на зрительный образ, которым служит дерево, изображенное на бумаге или представленное мысленно, так и с помощью только логических рассуждений. 

При введении правила умножения на наглядно-содержательной основе учащимся предлагаются задачи с большим числом вариантов решения, когда построение дерева оказывается технически трудоемким. При этом обращается внимание на то, что, если дерево симметричное или, как говорят, «правильное», его легко представить себе по отдельному фрагменту. Подсчитав число решений для выделенного фрагмента, нетрудно с помощью умножения определить число всех возможных вариантов решения. Термин «правило умножения» здесь не вводится, и какое-либо формальное правило действия не предлагается. Учащиеся остаются на уровне содержательного подхода.

Пример. На обед в школьной столовой предлагается 2 супа, 3 вторых блюда и 4 разных сока. Сколько различных вариантов обеда из трех блюд можно составить по предложенному меню?

Решение. В меню указано 2 супа с каждым из них можно взять любое из трех вторых блюд. Получим 23=6 вариантов выбора супа и второго блюда. Каждому из шести вариантов можно взять любой из четырех соков. Получаем, 64=24 варианта обеда из трех блюд.

Данную задачу можно решить построением дерева:

*

1 2

1 2 3 1 2 3

1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4

Рисунок 12 – дерево вариантов

В 7 классе тема «Комбинаторика» рассматривается в двух параграфах. В одном из параграфов снова обращаемся к решению комбинаторных задач, которые решаются с помощью рассуждений и правила умножения. В данном пункте дается формулировка правила умножения. Задачи более сложные. В следующем параграфе рассматриваются перестановки, где также дается определение перестановки и формула перестановки для решения задач, в этом же пункте вводится термин и обозначение «факториал». Также в учебнике имеется дополнительная информация о круговой перестановке.

Пример. В расписании 7 класса на четверг должно быть шесть предметов: русский язык, литература, алгебра, география, физика, физкультура. Сколькими способами можно составить расписание, на этот день?

Решение. Число способов, которыми можно составить расписание, равно числу перестановок из шести элементов: Р6=6!=123456=720.

 И.И. Зубарева, А.Г. Мордкович «Математика 5», «Математика 6» [7, 8]

В 5 классе в главе «Введение в вероятность» во втором параграфе рассматриваются комбинаторные задачи, решаемые методом перебора возможных вариантов. Дается понятие «комбинация». По-нашему мнению, рассматриваемые комбинаторные задачи, решаемые методом перебора возможных вариантов, взяты не совсем удачно. Для первого знакомства с задачами на перебор возможных вариантов лучше взять более простые задачи.

Пример. Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов – белого, красного, синего. Сколько стран могут использовать такую символику при условии, что у каждой страны – свой флаг?

Решение. Предположим, что первая полоса (верхняя) – белого цвета (Б). Тогда вторая полоса (средняя) – может быть синей (С) или красной (К), а третья (нижняя) полоса, соответственно, красной (К) или синей (С). Получилось 2 варианта цвета полос: белая, синяя, красная (БСК) или белая, красная, синяя (БКС).

Пусть теперь первая полоса синего цвета (С). Тогда вторая полоса может быть белой (Б) или красной (К), а третья полоса, соответственно, красной (К) или белой (Б). Получилось два варианта: синяя, белая, красная (СБК) или синяя, красная, белая (СКБ).

Пусть, наконец, первая полоса красного цвета (К). Тогда вторая полоса может быть белой(Б) или синей (С), а третья полоса, соответственно, синей (С) или белой (Б). Получилось 2 варианта: красная, белая, синяя (КБС) или красная, синяя, белая (КСБ).

Таким образом, всего получилось 6 комбинаций. Значит, указанную символику при выборе государственного флага могут использовать 6 стран.

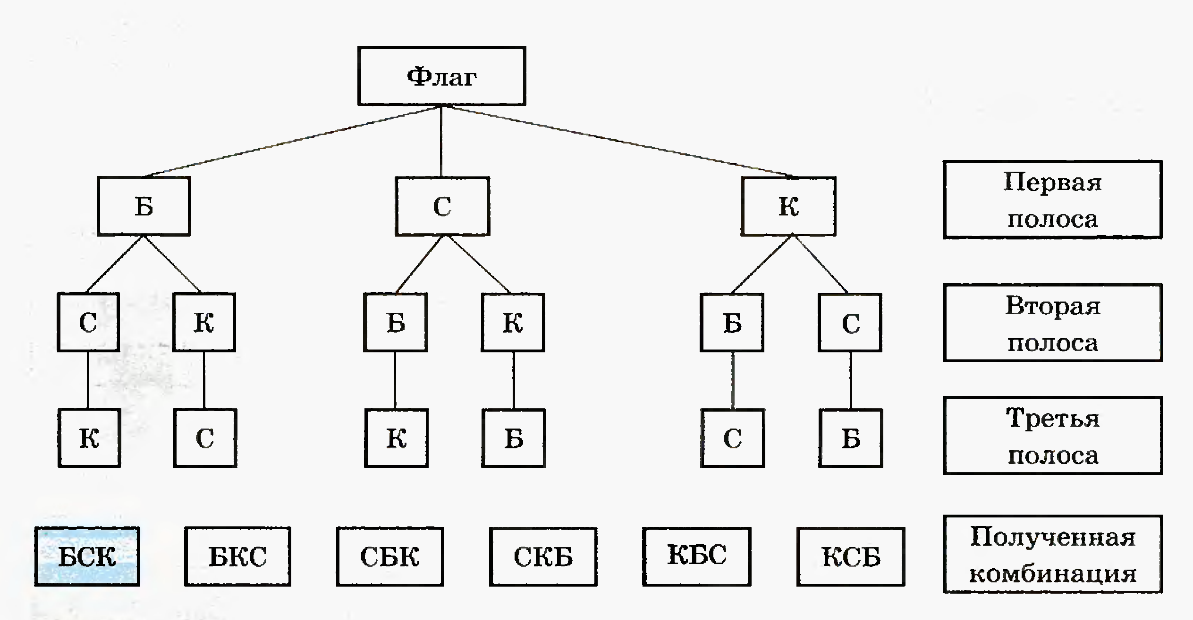
Рисунок 13 – Дерево возможных вариантов

В 6 классе, рассматриваются задачи, в которых для вычисления вероятности используют комбинаторное правило умножения.

Пример. Собрание для проведения тайного голосования по важному вопросу избрало счетную комиссию, в состав комиссии вошли Антонов, Борисова и Ващенко. Члены счетной комиссии должны распределить обязанности: председатель, заместитель, секретарь. Сколькими способами они могут это сделать?

Решение. Для того чтобы решить задачу необходимо осуществить перебор возможных вариантов. Построим дерево возможных вариантов, используя кодировку: А-Антонов, Б-Борисова, В-Ващенко; кроме того, порядок расположения букв будет соответствовать распределению функциональных обязанностей: первая буква – председатель, вторая – заместитель, третья – секретарь.

Рисунок 14 – Дерево возможных вариантов

Итого получилось 6 вариантов распределения обязанностей между членами комиссии.

Также эту задачу можно решить, используя логические рассуждения и здравый смысл.

Если председатель выбран, то заместителем может быть любой из двух оставшихся членов комиссии (два варианта), а секретаря уже выбирать не из кого, им будет оставшийся член комиссии. Итого 321=6 вариантов.

Е.А. Бунимович «Математика-5», «Математика-6» [22, 23]

Учащиеся знакомятся с приемом решения комбинаторных задач путем перебора возможных вариантов, в том числе, с помощью дерева возможных вариантов. Материал органично включен в курс, изложен с акцентом на практическое применение к реальным ситуациям. Кроме того, формируется умение работать с информацией. В 6 классе вводится также предусмотренное стандартом понятие множества и рассматриваются диаграммы Эйлера. Теоретико-множественный язык и символика органично включаются в основное содержание курса

С.А.Козлова,А.Г.Рубин «Математика – 5», «Математика – 6».[10, 11]

В учебнике для 5 класса тема «Комбинаторик» рассматривается на решении простейших комбинаторных задач путем перебора возможных вариантов, с помощью построения дерева возможных вариантов, число всех возможных пар, а также число пар, соответствующих определенным требованиям.

Пример. У путешественников есть три лески – красная, желтая и зеленая, и два крючка – большой и маленький. Им нужно сделать удочку, состоящую из лески и крючка. Сколькими способами они могут это сделать?

Решение. Одним из возможных подходов к решению задачи такой:

Изобразим в верхнем ряду три точки, соответствующие лескам: К, Ж и З, а в нижнем ряду две точки, соответствующие крючкам: Б и М.

Тогда каждой удочке соответствует отрезок, один конец которого лежит в верхнем ряду, а второй – в нижнем.

К Ж З

Б М

Рисунок 15 – Графическая иллюстрация задачи

Из рисунка 15, легко подсчитать, что соединить 3 лески и 2 крючка, можно шестью способами.

В 6 классе тема «Комбинаторика» начинает рассматриваться с повторения материала изученного в 5 классе. После чего предлагается формулировка правила умножения, дается определение и обозначение «факториала». Также в данном пункте вводится формула для вычисления количества различных пар на множестве из n элементов, и формула для вычисления количества различных троек на множестве из n элементов.

Пример. Сколькими способами можно построить в ряд 5 человек?

Решение. Первым в ряду можно выбрать любого из 5 человек, т.е. первого человека можно выбрать 5 различными способами. После того как первый человек выбран, второго можно выбрать четырьмя способами. Рассуждая аналогично, устанавливаем, что третьего в ряду можно выбрать тремя способами, четвертого – двумя способами, пятого – единственным способом.

Применим правило умножения, подсчитаем количество способов:

54321= 120 или 5! = 120.

Ю.Н. Макарычев, Н.Г. Миндюк «Алгебра: элементы статистики и теории вероятностей» под редакцией С.А.Теляковского. [16]

Это учебное пособие предназначено для учащихся 7-9 классов, оно дополняет учебники: Ю.Н. Макарычев. Н.Г. Миндюк, К.И. Нешков, С.Б.Суворова «Алгебра 7», «Алгебра 8», «Алгебра 9», под редакцией С.А.Теляковского.

Книга состоит из четырех параграфов. В каждом пункте содержатся теоретические сведения и соответствующие упражнения. В конце пункта приводятся упражнения для повторения. К каждому параграфу даются дополнительные упражнения более высокого уровня сложности по сравнению с основными упражнениями.

Наибольший объем материала приходится на 9 класс. Например, §3 «Элементы комбинаторики» содержит четыре пункта: примеры комбинаторных задач, перестановки, размещения, сочетания.

1. Примеры комбинаторных задач. На простых примерах демонстрируется решение комбинаторных задач методом перебора возможных вариантов. Этот метод иллюстрируется с помощью построение дерева возможных вариантов. Рассматривается правило умножения.

2. Перестановки. Вводится само понятие и формула подсчета перестановок.

3. Размещения. Понятие вводится на конкретном примере. Выводится формула числа размещений.

Пример. Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?

Решение. Любое расписание на один день, составленное из 4 различных предметов, отличается от другого либо предметами, либо распорядком следования предметов. Значит, в этом примере речь идет о размещении из 8 элементов по 4. Имеем, А48= 8765=1680.

Расписание можно составить 1680 способами.

4. Сочетания. Понятие и формула числа сочетаний.

В данном пособии некоторые элементы вводятся таким же образом, как и в учебном комплекте Г.В. Дорофеева. Но теории и практических упражнений по комбинаторике содержится больше. По-нашему мнению, комбинаторика предлагается к изучению слишком поздно. Как уже отмечалось выше, начинать обучать комбинаторике лучше, как можно раньше.

Методические рекомендации к данному учебнику даны в ряде статей Ю.Н.Макарычева и Н.Г. Миндюка [17, 18], а также некоторые критические замечания по данному учебному пособию содержатся в статье В.Н.Студенецкой и О.М.Фадеевой [29], которые помогут учителю не допустить ошибок при работе с данным учебником.

М.В.Ткачева «Элементы статистики и вероятность». [31]

Это учебное пособие для 7-9 классов и оно дополняет учебники Ш.А.Алимова «Алгебра 7,8,9».

Первая глава «Введение в комбинаторику» в 7 классе начинается с исторических комбинаторных задач о магических и латинских квадратах и другие. Затем рассматриваются пункт различные комбинации из трех элементов, где рассматриваются сочетания, перестановки и размещения, но вводить сами термины при этом не обязательно. Рассматривается таблица подсчета вариантов, которая подводит к правилу умножения. Также рассматриваются графы, но лишь как средство подсчета возможных вариантов. Эта глава имеет и дополнительные параграфы – перестановки и разбиение на две группы, выдвижение гипотез.

В конце учебника содержатся краткие методические рекомендации для учителя. Также методические рекомендации к первой главе данного учебного пособия можно найти в статье М.В. Ткачевой. [33]

Пример. Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?

Решение. С помощью полного графа с четырьмя вершинами А, Б, В, Г, обозначенными по первым буквам имен каждого из четырех мальчиков (Рис.).

В полном графе проводятся все возможные ребра. В данном случае отрезки-ребра обозначают шахматные партии, сыгранные каждой парой мальчиков. Граф имеет шесть ребер, значит, и партий было сыграно шесть.

Рисунок 16 – граф к задаче

На данный момент одним из действующих учебников в школе является учебник А.Г.Мордковича, к нему также имеются дополнительные главы для 7-9 классов:

А.Г.Мордкович, П.В.Семенов «События, вероятности, статистическая обработка данных». [24]

Первые два параграфа посвящены комбинаторике. Начинается изучение комбинаторики с рассмотрения простых комбинаторных задач, рассматривается таблица возможных вариантов, которая показывает принцип правила умножения. Затем рассматриваются деревья возможных вариантов и перестановки. После теоретического материала идут упражнения по каждому из подпунктов.

Следующий параграф – выбор нескольких элементов, в котором рассматриваются сочетания. Сначала выводится формула для двух элементов, затем для трех, а потом общая для п элементов.   

По комбинаторике материал изложен более удачно.  Замечания по данному учебному пособию содержатся в статье В.Н.Студенецкой и О.М.Фадеевой «Новое пособие по теории вероятностей для основной школы». [29]

В данном пособии не комбинаторика изучается как математический аппарат, нужный для анализа некоторых вероятностных схем решения задач, а наоборот, теория вероятностей изучается для развития комбинаторного мышления.

При формулировке комбинаторного правила умножения авторы заводят речь о каких-то испытаниях и их исходах, о независимости испытаний, а второй параграф о комбинаторике заканчивают подробными рассуждениями о соотношении между реальными «жизненными» ситуациями и их математическими моделями.

Комбинаторика, как и вся математика, имеет дело только с моделями количественных отношений и пространственных форм действительного мира, но отношение этих моделей к действительности в простейших случаях никаких вопросов не вызывает.

Таким образом, изложение элементов комбинаторики в пособии А.Г. Мордковича и П.В.Семенова представляет собой странное смешение комбинаторной и вероятностно-статистической проблематики. Возможно, авторы хотели таким образом подготовить учащихся к введению понятия вероятности на основе комбинаторных представлений.

На взгляд В.Н. Студенецкой и О.М.Фадеевой, авторы пособия этим только усложнили дело и внесли определенную путаницу в понимание того, какими же задачами занимается комбинаторика.

Пример. Встретились 6 друзей и каждый пожал руку каждому своему другу. Сколько было рукопожатий?

Решение. Условно пронумеруем друзей. Первый поздоровался со вторым, третьим, …, шестым. Всего пять рукопожатий. Для второго неучтенного оказались рукопожатия с третьим, четвертым, пятым, шестым. Всего четыре рукопожатия и т.д.

Получаем, что рукопожатий было всего 5+4+3+2+1=15.

1 2 1 2 1 2

3 3 3

6 5 4 6 5 4 6 5 4

пять рукопожатий четыре рукопожатия три рукопожатия

Ю.Н. Тюрин, А.А. Макаров и др.   «Теория вероятностей и статистика». [35]

Это пособие для учащихся 7-9 классов.

В блоке комбинаторики рассматриваются правило умножения, перестановки, сочетания, формулы числа перестановок и сочетаний, а затем с их помощью решаются задачи на вычисление вероятностей.

Приложение включает в себя вопросы: формула Бинома-Ньютона, треугольник Паскаля, также имеется несколько самостоятельных и контрольных работ, по предложенному материалу.

 Комбинаторные формулы в данном пособии рассматриваются, как средство для подсчета вероятности и даются после определения вероятности. Но основной целью изучения комбинаторики является развитие мышления, и ее нельзя рассматривать только как средство для подсчета вероятности.

Пример. Предположим, что имеется белый хлеб, черный хлеб, сыр, колбаса, варенье. Сколько видов бутербродов можно приготовить?

Решение. Выпишем сначала бутерброды с хлебом. Это бутерброд с сыром (БС), с колбасой (БК) и вареньем (БВ). Столько же бутербродов можно приготовить и с черным хлебом: ЧС, ЧК, ЧВ. Всего получается 6 бутербродов. Это число можно найти с помощью, так называемого комбинаторного правила умножения.

2.3 Развитие комбинаторного мышления школьников при изучении комбинаторики в 5-7 классах

Комбинаторика (комбинаторный анализ) - раздел математики, в котором изучаются задачи выбора и расположения элементов из некоторого основного (обычно конечного) множества в соответствии с заданными правилами.

При изучении элементов комбинаторики в 5 классе основными задачами являются:

- Формирование умений и навыков в составлении, выборе и упорядочении комбинаторных наборов;

- Формирование умений подсчета комбинаторных объектов методом непосредственного перебора;

- Необходимо показать, что такое дерево возможных вариантов, показать его использование как один из методов решения комбинаторных задач.

В 5 классе предлагаются простейшие комбинаторные задачи, при решении которых должна вестись либо работа по перебору возможных вариантов, либо по упорядочиванию, либо их объединение - перебор и упорядочивание вместе. В нашей жизни часто возникают такие задачи, которые имеют несколько различных решений, и перед нами встает проблема рассмотреть все возможные варианты решения. Для этого нам нужно найти удобный способ перебора, при котором будут рассмотрены всевозможные варианты, и они не повторялись бы.

На первом месте перед учителем стоит задача по формированию навыков систематического перебора. Начинать нужно с простых задач, где не так много элементов, важна сама суть перебора всех вариантов.

Задача. Три друга, Антон, Борис и Виктор, приобрели два билета на футбольный матч. Сколько существует различных вариантов похода на футбол?

Решение. Здесь необходимо перебрать всевозможные пары мальчиков.

а) Антон и Борис б) Антон и Виктор в) Борис и Виктор

Теперь добавим условие, при котором, решая задачу, учтем еще и место, на котором будет сидеть тот или иной мальчик, то есть учитывается порядок элементов в наборе.

Задача. Три друга, Антон, Борис и Виктор, приобрели два билета на футбольный матч на 1-е и 2-е места первого ряда стадиона. Сколько существует способов занять эти два места на стадионе?  Записать все эти варианты.

Решение. Здесь мы можем использовать результаты предыдущей задачи. В ней мы не учитывали порядок, а теперь необходимо учитывать порядок, на каком месте будет сидеть тот или иной мальчик.  Рассмотрим тот вариант, когда на матч пошли Антон и Борис, в этом случае возможно два варианта занять места на матче: 1-ое место – Антон, 2-ое место - Борис и наоборот 1-ое место Борис, а 2-ое Антон. То есть упорядочить два элемента мы можем двумя способами. Таким образом, решение предыдущей задачи дало нам два решения для этой задачи. Аналогично на каждый вариант предыдущей задачи мы получаем еще один вариант решения, итого 6 вариантов.

После этого можно добавить условие, при котором, решая задачу, учитываем еще и место, на котором будет сидеть тот или иной мальчик, то есть учитывая порядок элементов в наборе.

Задача. Антону, Борису и Виктору повезло, они купили 3 билета на футбол на 1-е, 2-е и 3-е места первого ряда стадиона. Сколькими способами могут занять мальчики эти места?

Решение. В данной задаче, как и в предыдущей важно на каких местах сидят мальчики, то есть нам нужно рассмотреть, сколько существует вариантов рассадить трех мальчиков на три разных места. Пусть на первом месте сидит Антон, тогда на оставшиеся два места двух оставшихся мальчиков мы можем усадить двумя способами, аналогично для случаев, когда на первом месте сидит Борис и Виктор. В результате получим 6 вариантов, то есть упорядочить 3 элемента мы можем шестью способами.

В предыдущих задачах, не учитывая порядка перебора, не сложно перечислить все возможные варианты, так как их не так много, но часто при переборе возможных вариантов их может быть столько, что сложно оценить все ли возможные решения мы учли и не пропустили ли хотя бы одно из них. В этом случае необходимо упорядочить процедуру перебора, то есть перебирать возможные варианты в некотором порядке, определенном заранее, который позволяет не допускать повторений решений и пропускать возможные решения.

Задача. Сколько двузначных чисел можно составить, используя цифры  1,2 и 3?

Решение. Выпишем возможные двузначные числа. Но мы не будем выписывать эти числа как попало, а договоримся выписывать их в порядке возрастания, что позволит нам не пропускать числа и не повторяться. В процессе решения этой задачи может возникнуть такой вопрос, а может ли одна и та же цифра повторяться в числе два раза? (Если не возникнет, то учитель может сам обратить на это внимание). Так как в данной задаче это условие не оговорено, то решим ее для обоих случаев, и увидим, что в каждом из них число решений различно. Из чего делаем вывод, что данное условие при решении задач необходимо учитывать.

Задача. В 5«А» классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?

Решение. В данной задаче у нас имеется 4 предмета и необходимо выписать возможные варианты расписания на один день, учитывая те условия, что каждый урок должен обязательно присутствовать в расписании, и встречаться там всего один раз (для упрощения записи предлагается каждый предмет обозначит его заглавной буквой). Таким образом, нам необходимо подсчитать сколькими способами мы можем упорядочить 4 элемента. Пусть первым будет урок математики, тогда оставшиеся 3 предмета мы можем упорядочить 6-ью способами (из ранее рассмотренных задач). Аналогично для оставшихся трех предметов. Итого получим 24 способа упорядочить 4 предмета.

При изучении элементов комбинаторики в 6 классе основными задачами являются:

- Отработка умений и навыков в составлении и подсчете числа комбинаторных наборов.

- Показать учащимся как можно решать комбинаторные задачи с помощью рассуждений. Знакомство учащихся с правилом умножения при подсчете числа возможных вариантов, сформировать умения по его применению.

- знакомство с правилом суммы

- Формирование умений строить дерево возможных вариантов.

В 6 классе в теме «Комбинаторика» продолжаем рассматривать комбинаторные задачи, на первый план выходят задачи по подсчету числа возможных вариантов.

Существует несколько подходов к преподаванию комбинаторики: теоретико-множественный, лексико-графический и теоретико-вероятностный.  В школе преимущество отдается теоретико-множественному подходу, но будет полезным частично обратиться и к лексикографическому подходу. При таком подходе все определения опираются на представление об алфавите, словах, длине слов и др. 

Решая задачи, иногда очень удобно использовать кодирование, то есть обращение к лексикографическому подходу.

 Рассмотрим задачу.

Задача. Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов – белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны – свой флаг.

Решение. Мы можем записывать наше решение следующим образом: «1 вариант: первая полоса – красная, вторая – синяя, третья – белая.» и т.д. Но это очень долго и неудобно, записывая так, сложно сориентироваться все ли варианты мы записали, и не повторились ли мы где-нибудь. Поэтому очень удобно ввести кодирование, т.е. некоторое условное обозначение перебираемых в задаче объектов. В нашем случае мы заменим первой буквой каждый цвет полосы. Белый соответственно – «Б», красный – «К» и синий – «С».  

Введя кодирование, запись решения задачи очень упрощается. Мы имеем множество из трех элементов {Б, К, С}. Нужно составить различные комбинации из трех элементов, при этом порядок элементов учитывается. Например, запись «БКС» будет обозначать, что первая полоса флага – белая, вторая – красная, третья – синяя.  Подобные задачи мы уже решали методом непосредственного перебора и построением дерева возможных вариантов. 

Задача. При встрече 8 приятелей обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Решение. Данную задачу можно решать методом непосредственного перебора, и уже в самом начале заметим, что довольно сложно перебирать все возможные варианты и не запутаться, не говоря уже о записи решения этой задачи. Но, введя определенные обозначения - кодирование, решение будет очень легко представить. 

Каждому приятелю даем номер от 1 до 8, а рукопожатия закодируем следующим образом: например число 24 означает что 2-ой приятель пожал руку 4-му. Причем число 35 и 53 означают одно и то же рукопожатие, и брать будем меньшее из них. Коды рукопожатий мы можем оформить следующей таблицей:

12, 13, 14, 15, 16, 17, 18,

23, 24, 25, 26, 27, 28,

34, 35, 36, 37, 38,

45, 46, 47, 48,

56, 57, 58,

67, 68,

78.

Таким образом, у нас получилось 1+2+3+4+5+6+7=28 рукопожатий.

После того как учащиеся научились составлять всевозможные наборы, на первый план выдвигается задача подсчета числа возможных вариантов.

Задача. Группа туристов планирует осуществить поход по маршруту Антоново – Борисово – Власово – Грибово. Из Антоново в Борисово можно сплавиться по реке или дойти пешком. Из Борисово во Власово можно пройти пешком или доехать на велосипедах. Из Власово в Грибово можно доплыть по реке, доехать на велосипедах или пройти пешком. Сколько всего вариантов похода могут выбрать туристы? Сколько вариантов похода могут выбрать туристы при условии, что хотя бы на одном из участков маршрута они должны использовать велосипеды?

Решение. Построим для этой задачи дерево возможных вариантов:

Пусть у нас «П» -обозначает путь пешком; «Р» - сплавиться по реке; «В» - доехать на велосипедах.

Рисунок 17 – Дерево возможных вариантов

Ответ на второй вопрос также хорошо просматривается по дереву возможных вариантов.

Но эту задачу можно решить по-другому, с помощью рассуждений. Из Антоново в Борисово у нас 2 варианта каким образом продолжать путь, из Борисово во Власово тоже 2 варианта, т.е. на каждый вариант первого участка пути у нас есть по 2 варианта второго участка пути и того на данном этапе у нас будет 2*2=4 варианта выбора способа передвижения. На каждый из этих 4 вариантов существует по 3 варианта способа передвижения по третьему участку пути из Власово в Грибово, т.е.  4*3=12. Ответ в этой задаче мы получили умножением.

Такой способ подсчета называется правилом умножения, он возможен, если дерево возможных вариантов является «правильным»: из каждого узла выходит одно и то же число веток.

Такой способ подсчета называется правилом умножения, он возможен, если дерево возможных вариантов является «правильным»: из каждого узла выходит одно и то же число веток.

Задача. От турбазы к горному озеру ведут 4 тропы. Сколькими способами туристы могут отправиться в поход к озеру, если они не хотят спускаться по той же тропе, по которой поднимались?

Решение. Занумеруем тропы числами от 1 до 4 и построим дерево возможных вариантов:

Рисунок 18 – дерево вариантов

Чтоб подняться у нас есть четыре тропы (четыре варианта) и на каждую из нее есть по три оставшихся тропы (три варианта), чтобы спуститься, т.е. 43=12 маршрутов подхода к озеру. А теперь представим, что к озеру ведут не четыре, а 10 троп. Сколько в этом случае существует маршрутов, если по-прежнему решено спускаться не по той тропе, по которой поднимались? Изобразить дерево возможных вариантов в такой ситуации очень сложно. Гораздо легче решить эту задачу с помощью рассуждений. Подняться к озеру можно по любой из 10 троп, а спускаться по любой из оставшихся 9 троп. Таким образом, всего получим 109=90 различных маршрутов похода.

Обе эти задачи мы решили, используя правило умножения, которое звучит следующим образом: пусть необходимо выполнить к независимых действий, если первое действие мы можем выполнить п1 способами, после чего второе действие можем выполнить п2 способами и т.д. до k-го действия, которое можно выполнить пk способами, тогда выполнить все k действия в указанном порядке можно п1 п2… пk способами. Следует обратить внимание, что, применяя правило умножения, мы учитываем порядок действий. То есть правило умножения применяется для подсчета упорядоченных наборов.

Рассмотрим две задачи.

Задача 1. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать капитана команды для математических соревнований и его заместителя?

На роль капитана может быть выбран любой из 30 учащихся, а его заместитель – любой из 29 оставшихся учеников. Таким образом, получаем 3029 = 870 способов.

Задача 2. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать двоих для участия в математической олимпиаде?

Нам не важно, кто капитан, а кто заместитель, нам нужны всего лишь два участника, поэтому получаем, что у нас каждая пара учащихся в произведении повторяется два раза. Поэтому ответом для второй задачи будет (3029):2.

Еще одним способом подсчета комбинаторных наборов является использование правила суммы.

Задача. Из класса нужно выделить одного дежурного, мальчика или девочку. Сколько существует способов для выбора дежурного, если в классе 22 девочки и 18 мальчиков?

Решение. Выбрать одну девочку из 22 мы можем 22-мя способами, а одного мальчика из 18 можно 18-тью способами. Тогда выбрать одного дежурного мальчика или девочку можно (18+22) способами.

Для подсчета вариантов мы использовали здесь правило суммы, которое можно сформулировать так: если два действия взаимно исключают друг друга, причем одно из них можно выполнить п способами, а другое – m способами, то какое-либо одно из них можно выполнить n+m способами. В нашем примере действия исключают друг друга, так как мы должны выбрать либо мальчика из одного множества, либо девочку из другого.

Основной задачей при изучении элементов комбинаторики в 7 классе является: введение понятия перестановки и вывод формулы числа перестановок.

К 7 классу учащиеся уже должны иметь навыки систематического перебора и быть знакомы с основными методами подсчета возможных вариантов. В 7 классе продолжаем решать задачи на подсчет возможных вариантов различными способами, а также вводим понятие перестановки.

Ранее учащиеся уже сталкивались с перестановками, когда подсчитывали сколькими способами можно упорядочить несколько (2,3 или 4) элементов, но само понятие перестановки еще не вводилось.

На данный момент мы уже знаем, количество перестановок для 2, 3 и 4-ех элементных множеств. 

Задача. В турнире участвуют четыре человека. Сколькими способами могут быть распределены места между ними?

Решение. Решим эту задачу, используя правило умножения. Первое место может занять любой из четырех участников. При этом второе место может занять любой из трех оставшихся, третье – любой из двух оставшихся, а на четвертом месте остается последний участник. Значит, места между участниками могут быть распределены 4321 = 24 способами.

Мы искали, сколько различных упорядоченных наборов мы можем составить, имея некоторое число элементов, каждый из таких упорядоченных наборов, есть перестановка. В рассмотренном примере мы фактически нашли число перестановок для четырех элементов.

А что если множество состоит не из четырех, а например, из десяти элементов? Тогда всего будет 10987654321=3 628 880 перестановок. Т.е. произведение первых 10 натуральных чисел. Но для еще большего количества элементов уже будет сложно подсчитать число перестановок.  В математике есть специальное обозначение для краткой записи произведения нескольких первых натуральных чисел. Произведение, например, первых десяти натуральных чисел обозначают 10! – и читается как «десять факториал». 0!=1 по определению.

Рассуждения, использованные в примере, показывают, что число перестановок для множества из четырех элементов равно 4!, точно также для множества, например, из 10 элементов число перестановок равно 10!, и вообще: число перестановок для множеств из n элементов равно n!.

Задача. Сколькими способами можно составить маршрут путешествия, проходящего через семь городов.

Решение. У нас есть семь городов и нужно составить маршрут по этим городам, то есть фактически, нам нужно рассмотреть все перестановки этих семи городов. Мы уже знаем формулу, поэтому получаем 7!.

Нужно дать учащимся несколько упражнений на вычисление выражений с факториалами, чтоб они лучше овладели навыками работы с ними.

1) Верно ли, что:

а) 10!=109!         б) 10!=2!5!           в) 12!:11!=12?

2) найдите значения выражения 16! : 14! 3!

В некоторых задачах на подсчет числа перестановок накладываются дополнительные условия, и для решения задачи кроме подсчета числа перестановок необходимо произвести другие действия.

Задача. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?

Решение. Число всех возможных перестановок цифр 0, 2, 4, 6 будет 4!, но нужно обратить внимание учащихся на 0 и из этого числа перестановок нужно исключить те числа, которые начинаются с 0. Это всевозможные перестановки цифр 2, 4, 6, их количество равно 3!. Таким образом, число искомых чисел будет равно 4!-3!.

Задача. Имеется девять различных книг, четыре из которых – учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?

Решение. Сначала рассмотрим все учебники как одну книгу. Тогда на полке надо расставить не девять, а шесть книг. Это можно сделать 6! способами.  В каждой из полученных комбинаций можно выполнить 4! перестановок учебников. Значит, искомое число способов расположения книг на полке равно произведению 6!4!.

Рассмотрим книгу В.С. Лютикас «Факультативный курс по математике. Теория вероятностей».

Обычно рассматривают правило произведения и «дерево» вариантов.

Список возможных задач по теме «Перестановки».

1. Сколько можно записать двузначных чисел? (90)
2. Сколько различных 5-значных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что ни одна цифра не повторяется. (120)
3. Сколько разных 3-значных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что ни одна цифра не повторяется. (60)
4. Сколько можно составить 3-значных чисел из цифр 1, 2, 3, 4 и 5, если цифры могут повторяться. (125)
5. Сколько 4-значных чисел можно составить из цифр 1 и 2? (16)
6. Сколько 5-значных чисел можно образовать из цифр 0 и 1? (16)
7. Сколько автомашин можно обеспечить 6-значными номерами? (106)
8. В классе 30 учеников. Необходимо избрать старосту, заместителя и организатора внеклассных мероприятий класса. Сколькими способами можно организовать эту руководящую тройку, если одно лицо может занимать только один пост? (24360)
9. Сколько стартовых шестерок можно организовать из числа 10 волейболистов? (210)
10. В кружке юных математиков 25 членов. Необходимо избрать председателя кружка, его заместителя, редактора стенгазеты и секретаря. Сколькими способами можно организовать эту руководящую четверку, если одно лицо может занимать только один пост? (303 600)
11. Игрок сначала бросает белую игральную кость, потом черную. Сколько может быть случаев, когда число очков, появившихся на белой кости, больше числа очков, появившихся на черной? (15)

Можно предложить следующее планирование по курсу в 7 классе (7 уроков).

Таблица

№	Тема	Содержание
1.	Наука о подсчете числа комбинаций – комбинаторика.	Определение, виды выборок (перестановки, размещения, сочетания). Правило суммы и правило произведения. Пример решения задачи.
2.	Решение задач.	№ 1–5
3.	Решение задач.	№ 6–11
4.	Геометрия и комбинаторика.	Решение задач из учебника (различные варианты, их анализ).
5.	Повторение.	Обобщение изученного.

Задачи на пересечение и объединение множеств

Пример 1. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро - фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?

Можно, конечно, «угадать» в процессе замысловатых рассуждений, можно - посредством вот таких действий:

1. 6 + 5 = 11.
2. 11 - 2 = 9.

Но как грамотно обосновать их? Как ответить на вопрос, что получилось в результате первого действия? Коротко - не получится, длинно - язык «сломаешь» и мысль «размажешь».

А ведь еще в XVIII в. великий Леонард Эйлер придумал очень красивый способ решения таких задач.

Изобразим два круга, так как у нас два вида цветов (впрочем, если это будут не совсем круги - не страшно). В одном будем фиксировать владелиц кактусов, в другом - фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть (так как эту задачу можно предлагать на ранних стадиях обучения, то и слова надо употреблять простые, понятные детям, а не теоретико-множественные термины). В этой общей части (на рисунке затемненной) ставим цифру 2 (т.к. кактусы и фиалки у двоих). В оставшейся части «кактусового» круга ставим цифру 4 (всего кактусы - у шестерых, а двух мы уже учли). В свободной части «фиалкового» круга ставим цифру 3 (5 - 2 = 3). А теперь сам рисунок подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Кактусы

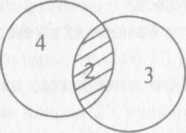
Фиалки

Рисунок 19 –

Пример 3. Я живу в девятиэтажном доме, где на первом этаже нет квартир, а на всех остальных - по 4 квартиры. И в каждой квартире (кроме моей) есть какая-нибудь «живность». В 15 квартирах живут кошки, в 13 - собаки и в 13 - попугайчики. В одной квартире обитают и кошки, и собаки, в четырех - кошки и попугаи, а в одной - и кошки, и собаки, и попугаи. Сколько семей держат собак и попугаев?

Обратимся за помощью к тем же кругам Эйлера.

Остальное, как говорится, дело техники.

11 +0 + 3 + 1 + 13 - (1 +х) + х + + 13 - (3 + 1 + х) = 9 - 14, откуда следует, что х = 5, т. е. попугайчики мирно «уживаются» с собаками в 5 + 1 = 6 квартирах.

Решено три задачи. И хотя это не было заявлено официально, а было преподнесено в «легком жанре» (на предмет показа органичного введения элементов занимательности), все здесь было сделано с учетом основных принципов дидактики (начиная с перехода от простого к сложному и т. д.) и жизненного опыта.

Последняя из этих задач рассчитана на шестиклассника, но и умный пятиклассник может сообразить, как найти выход из создавшегося затруднительного положения (речь идет о решении получившегося уравнения).

Вспомнив, что собаки живут в 13 квартирах (т. е. выделенный круг содержит в себе 13 голов), можно сделать уравнение проще, а именно:

13+11 +3 + 13 - (4 + х) = 31

Рисунок 20 -

Такое уравнение пятикласснику под силу, как и следующие 10 задач.

№ 1. Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?

№ 2. Из 40 учащихся нашего класса 32 любят молоко, 21 - лимонад, а 15 - и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

№ 3. 12 моих одноклассников любят читать детективы, 18 - фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

№ 4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

№ 5. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом - 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

№ 6. 65 % дедушкиных кроликов любят морковку, 10 % любят и морковку, и капусту. Сколько процентов кроликов не прочь полакомиться капустой?

№ 7. В ясельной группе 11 деток любят манную кашу, 13 - гречневую и 7 малышей - перловую. Четверо любят и манную кашу, и гречневую, 3 - манную и перловую, 6 - гречневую и перловую, а двое с удовольствием «уплетают» все три вида каши. Сколько детей в этой группе, если в ней нет ни одного ребенка, вовсе не любящего кашу?

№ 8. В группе 29 студентов. Среди них 14 любителей классической музыки, 15 - джаза и 14 - народной музыки. Классическую музыку и джаз слушают 6 студентов, народную музыку и джаз - 7, классику и народную - 9. Пятеро студентов слушают всякую музыку, а остальные не любят никакой музыки. Сколько их?

№ 9. В воскресенье 19 учеников нашего класса побывали в планетарии, 10 - в цирке и 6 - на стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион - 3; цирк и стадион - 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?

№ 10. Если я не ошибаюсь, в нашем садово-огородном обществе только я не выращиваю орехов. Гуляя по улице, я насчитала на 19 участках фундук, на 40 - грецкий орех, на 34 - арахис. На 11 участках я обнаружила и фундук, и арахис; на 6 - фундук и грецкий орех; на 20 - арахис и грецкий орех. А мой сосед выращивает все три вида орехов. Всего у нас в обществе 56 участков. Верно ли это?

Остальные задачи с равным успехом можно предлагать и шестикласснику, и абитуриенту.

№ 11. В одном классе 25 учеников. Из них 7 любят груши, 11 - черешню. Двое любят груши и черешню; 6 - груши и яблоки; 5 - яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

№ 12. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 - умных и 9 - добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

№ 13. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике - 12; по истории - 23. По русскому и математике - 4; по математике и истории - 9; по русскому языку и истории - 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

№ 14. Из 100 человек 85 знают английский язык, 80 - испанский, 75 - немецкий. Все владеют, nb крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

№ 15. Из сотрудников фирмы 16» побывали во Франции, 10 - в Италии, 6 - в Англии; в Англии и Италии - 5; в Англии и Франции - 6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

№ 16. Учитель задал на уроке сложную задачу. В результате количество мальчиков, решивших задачу, оказалось равно количеству девочек, ее не решивших. Кого в классе больше - решивших задачу или девочек?

№ 17. В поход отправились учащиеся 5 и 6 классов. Мальчиков было 16; шестиклассников и шестиклассниц всего 24; пятиклассниц столько, сколько мальчиков из 6 класса. Сколько всего детей отправилось в поход?

№ 18. В салоне небольшого самолета было 42 пассажира. Некоторые из них были москвичами, остальные - иногородние. Среди москвичей было 9 мужчин. Некоторые из пассажиров были артистами, но ни одна из иногородних женщин артисткой не была. Всего иногородних мужчин было 18. Из них 13 не были артистами. Среди пассажиров, не являющихся артистами, было 16 мужчин и 11 женщин. 5 москвичей не были артистами. Сколько всего артистов было в самолете?

№ 19. Получил я посылку от своих друзей из Сочи с яблоками и грушами. Одни плоды были большие, другие маленькие. Да и по цвету, они отличались: часть была желтого цвета; часть - зеленого. Среди плодов не было маленьких груш и не было маленьких зеленых яблок. Яблок было 25. Груш было 17. Больших плодов было 32. Желтых плодов было 28. Зеленых яблок было на 2 больше, чем зеленых груш. Сколько больших желтых яблок было в этой посылке?

№ 20. Наш класс изготовил кубики для детского сада. Несколько кубиков мы склеили из картона, а остальные сделали из дерева. Кубики были только двух размеров: большие и маленькие. Когда кубики были готовы, мы покрасили их: несколько кубиков в зеленый цвет, а остальные - в красный. Получилось 16 зеленых кубиков. Зеленых кубиков большого размера было 6. Больших зеленых кубиков из картона - 4. Красных кубиков из картона было 8, а красных кубиков из дерева - 9. Больших деревянных кубиков было 7, а маленьких деревянных кубиков было 11. Сколько всего кубиков мы изготовили?

Ответы: № 1. 89 семей. № 2. 2 ученика. № 3. Не менее 28 учеников. № 4. 7 одноклассников. № 5. 9 футболистов; 9 теннисистов. № 6. 45 %. № 7. 20 ребятишек. № 8. 3 студента. № 9. 20 учеников. № 10. Ошибаюсь! № 11. 14 учеников. № 12. 1 девушка. № 13. 4 ученика. № 14. 70 человек. № 15. 7 сотрудников. № 16. Поровну. № 17. 40 учеников. № 18. 15 артистов. № 19. 3 больших желтых яблока. № 20. 33 ящика.

2.4 Формирование критического мышления при использовании элементов комбинаторики в обучении

Одна из основных задач современного обучения состоит в развитии личности учащихся и подготовке к получению образования на основе профильного изучения математики. Эта задача требует развития математической культуры учащихся, основным компонентом которого является математическое мышление.

На основе изучения логического и комбинаторного мышления как видов мышления, анализа психолого-педагогической литературы сформулировано определение комбинаторно-критического мышления и его развития как синтеза двух видов мышления.

Комбинаторно-критическое мышление - мышление, реализуемое посредством мыслительных операций, направленного на выделение конечных вариантов рассматриваемых явлений и понятий, дальнейшего процесса преобразования числа выделенных выборов в зависимости от субъектного опыта ученика.

Чтобы развивать комбинаторно-критический стиль мышления у старшеклассников необходимо чтобы:

- учащиеся умели находить и видели, как можно больше вариантов подхода к одной и той же проблеме, а также могли выбрать наиболее оптимальный, исходя из поставленных целей и задач;

- учащиеся умели рассматривать собственные действия и действия других с различных точек зрения, развивая тем самым критическую и рефлексивную компоненты;

- учащиеся умели, применяя ряд мыслительных операций, переформулировать задачу, подходить к ее решению и оформлению решения с различных позиций;

- учащиеся смогли осуществить выбор способа саморазвития, выстраивания своей профессиональной карьеры.

Умение решать задачи, разрабатывать стратегию их решения, выдвигать и доказывать гипотезы, прогнозировать результаты своей деятельности, анализировать и находить рациональные способы решения задачи путем оптимизации, различных вариантов перебора с использованием логических операций позволяют судить об уровне развития комбинаторно-критического мышления школьников.

Необходимость поиска новых эффективных средств развития комбинаторно-критического мышления школьников обусловлена его значимостью для дальнейшей самореализации личности в современном обществе. Умение логически рассуждать, вариативно мыслить является показателем общей культуры мышления человека.

Чтобы развивать комбинаторно-критический стиль мышления у старшеклассников необходимо чтобы:

- учащиеся умели находить как можно больше вариантов подхода к одной и той же проблеме, а также могли выбрать наиболее оптимальный вариант, исходя из поставленных целей и задач;

- учащиеся умели рассматривать собственные действия и действия других с различных точек зрения, развивая тем самым критическую и рефлексивную компоненты;

- учащиеся умели, применяя ряд мыслительных операций, переформулировать задачу, подходить к ее решению и оформлению решения с различных позиций;

- учащиеся смогли осуществить выбор способа саморазвития, выстраивания своей профессиональной карьеры.

Предлагается следующая система педагогических условий, помогающих организовать деятельность по формированию и развитию комбинаторно-критического мышления старшеклассников.

Первое условие.

Специально разработанное содержание (например, элективных курсов по математике), направленных на развитие комбинаторно-критического мышления старшеклассников.

Выделим принципиальные условия к разработке метода развития комбинаторно-критического мышления:

1. Содержание должно носит циклический характер, так как к наиболее важным типологиям задач (логическим, комбинаторным) следует периодически возвращаться на новом витке познания и понимания;
2. Обучение на высоком уровне позволяет каждому ученику осуществить очередной этап собственного развития;
3. Обучение, которое включает в себя все четыре уровня действия: физическое, физиологическое, уровень действия субъекта, уровень действия личности.

Второе условие.

Специально предложенная типология задач, направленных на развитие комбинаторно-критического мышления старшеклассников, реализацию ближней и дальней целей ученика.

В ходе исследования были определены основные требования к заданиям, направленным на развитие комбинаторно-критического мышления:

1. Задания должны способствовать развитию комбинаторно-критического мышления учащихся. Так как задания многие старшеклассники преломляют через призму дальнейшей профессиональной карьеры, через важность и необходимость реализации ближней (итоговая аттестация) и дальней (продолжение образования) цели, то компенсировать данную особенность можно за счет повышенной мотивации, интересных подходов к организации учебного процесса, а также за счет учета возрастных особенностей;
2. Задания должны быть предложены на каждом из основных этапов формирования приемов умственной деятельности учащихся:

- система заданий должна быть личностно-ориентированной, построенной исходя из субъектного опыта ученика;

- задания должны быть симбиозом всех представленных нами требований к заданиям, направленным на развитие комбинаторно-критического мышления учащихся.

Третье условие.

Развитие комбинаторно-критического мышления старшеклассников органично соединяется с развитием предметных умений, тем самым отражается на успеваемости по предмету.

Четвертое условие.

Реализация прямого (изучение операций мышления, их классификации и способов применения, основных разделов «комбинаторики») и косвенного путей (умение применять мыслительные операции, комбинаторные, логические, общенаучные методы через предмет) развития комбинаторно-критического мышления старшеклассников.

В рамках реализации системы факультативных курсов и уроков предусмотрено рассмотрение основных разделов комбинаторики: перемещение, сочетание, размещение, а также приема определения различий между понятиями «сочетание» - «размещение». Кроме изучения операций мышления, основных разделов комбинаторики, изучаются общенаучные, логические и комбинаторные методы.

Методика изучения основных методов представлена поэтапно:

1. Пропедевтический этап. Весь процесс обучения, так или иначе, ведет к тому, что к старшей школе учащиеся отчасти в явном виде (метода замены переменной, графический метод и т.д.) или неявном виде имеют представление о методе;
2. Формирующий этап. Через разработку моделей известных учащимся специальных методов и их применение осуществляем переход к проблемной ситуации - к выходу на общенаучные, логические, комбинаторные методы. На основе работы в проектном режиме и результатов работы в проекте вырабатывается новая модель (на основе известных) основных методов, разбираются основные характеристики метода, демонстрируются образцы применения каждого метода;
3. Абстрагирующий вариант. Узнавание метода, применение его в задачах - первый этап абстрагирования. Второй этап абстрагирования будет считаться реализованным, если ученик осуществляет применение изученного метода в житейских ситуациях.

Пятое условие.

Индивидуальная педагогическая поддержка. Педагогическая поддержка всей группы учащихся осуществляется за счет: эмоционального настроя; субъект-субъектных отношений; использования инновационных технологий, при реализации которых создаются ситуации: взаимообучения, диалогичности общения, позитивной оценки достижений.

Индивидуально-личностная поддержка учащихся осуществляется за счет: диагностики индивидуального развития, обученности, воспитанности, выявления личных проблем ученика; отслеживания процесса развития (вводные, промежуточные и итоговые диагностические данные), так как диагностические данные дают возможность дозировать педагогическую помощь, основанную на индивидуальных особенностях ученика; создания ситуации успеха.

Шестое условие.

Специально разработанные модели системы уроков реализуемых посредством технологизации (педагогическая мастерская, метод проектов, моделирование при информационно-компьютерной поддержке) образовательного процесса.

Седьмое условие.

Обеспечение единства содержательного, мотивационного, критического, корректирующего, контролирующего, рефлексивного, творческого компонентов.

Мотивационный компонент ориентирует на создание благоприятной среды выявления личностных качеств учащихся. В основе компонента лежит управление педагогическим влиянием на положительную мотивацию посредством создания условий, востребующих ее деятельность как личностной структуры, опосредованно влияющей на математическую культуру.

Содержательный компонент определяет новые или практически новые знания, а также процесс познания как процесс отражения и воспроизведения в человеческом сознании действительности, начинающейся с ощущений и восприятий, с помощью которых познаются единичные предметы и их свойства, которые доступны чувственному восприятию.

Корректирующий компонент ориентирует на создание ситуаций, где возможно осуществление осмысления достигнутого уровня развития самим учеником и его учителем. Главная цель корректирующего компонента: корректировка содержания изучаемого материала в зависимости от «зоны ближайшего развития» каждого ученика и корректировку самой «зоны развития».

Контролирующий компонент содержит оценочный материал и условия для возможности корректировки содержательной линии, для осуществления качественного перехода на новый виток развития.

Рефлексивный компонент даёт возможность каждому старшекласснику перейти на новый виток «собственного» развития. Рефлексивный компонент направлен на формирование установки осознания сущностей и смыслов явлений, составляющих предмет изучения, соотнесение изучаемого материала с собственными размышлениями, сомнениями по данному вопросу.

Критический компонент определяет содержание как основу для осмысления любого факта на предмет его соответствия или несоответствия поставленным целям и задачам, современным ценностям и т.д., ориентирует на развитие сильной позиции критичности.

Творческий компонент составляет основу для конструирования собственных отношений к изучаемому событию, содержит материал, требующий экспертной оценки и условия для перевода обучаемых в позицию экспертов, а также осуществляется переход на исследовательский этап обучения.

Восьмое условие.

Специальные материалы для оценки и коррекции умений (уровневые тесты).

Девятое условие.

Педагогическая деятельность учителя, направленная на развитие комбинаторно-критического мышления старшеклассников.

При обучении школьников решению задач учитель сталкивается с некоторыми проблемами. Многие учащиеся, даже старших классов не умеют анализировать условие трудных задач, осуществлять поиск решения, тем более поиск и оформление нескольких способов решения.

ЗАКЛЮЧЕНИЕ

Технология критического мышления реализует следующие цели и задачи системы образования:

- формирование нового стиля мышления,

- развитие таких базовых качеств личности, как критическое мышление, коммуникативность, креативность, мобильность,

- развитие аналитического, критического мышления,

- формирование культуры чтения, включающей в себя умение ориентироваться в источниках информации,

- стимулирование самостоятельной поисковой творческой деятельности, запуск механизмов самообразования и самоорганизации.

Технология дает ученику:

- повышение эффективности восприятия информации;

- повышение интереса как к изучаемому материалу, так и к самому процессу обучения;

-умение критически мыслить;

- умение ответственно относиться к собственному образованию;

- умение работать в сотрудничестве с другими;

- повышение качества образования учеников;

- желание и умение стать человеком, который учится в течение всей жизни.

Технология дает учителю:

- умение создать в классе атмосферу открытости и ответственного сотрудничества;

- возможность использовать модель обучения и систему эффективных методик, которые способствуют развитию критического мышления и самостоятельности в процессе обучения;

- стать практиками, которые умеют грамотно анализировать свою деятельность;

- стать источником ценной профессиональной информации для других учителей.

Использование технологии развития критического мышления на уроках позволяет сформировать умения и навыки работы с информацией:

• находить, осмысливать, использовать нужную информацию;
• анализировать, систематизировать, представлять информацию в виде схем, таблиц, графиков.
• сравнивать исторические явления и объекты, при этом самостоятельно выявлять признаки или линии сравнения;
• выявлять проблемы, содержащиеся в тексте, определять возможные пути решения, вести поиск необходимых сведений, используя различные источники информации.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Абрамова Г.С. Возрастная психология: Учебное пособие для вузов. – М.: Академический проект, 2000. – 624 стр.
2. Башмаков М.И. Планирование учителем своей деятельности //Вестник СЗО РАО "Образование и культура Северо – Запада России", Вып. 1, СПб, 1996. с. 140 – 147.
3. Волков Е.В. Развитие критического мышления: Опыт неспортивного, но здорового и полезного ориентирования в реальности и в себе // Тренинг, 2005.
4. Гусев В.А. Психолого-педагогические основы обучения математике – М.: ООО “Издательство “Вербум-М”, ООО “Издательский центр “Академия”, 2003.
5. Занимательная математика. 5 – 11 классы. Автор – составитель Т. Д. Гаврилова. – Волгоград: Учитель, 2005. – 96с.
6. Зинченко В.П. Психологические основы педагогики (Психолого-педагогические основы построения системы развивающего обучения Д.Б. Эльконина, В.В. Давыдова): Учеб. Пособие. - М.: Гардарики, 2002.- 431с., с.110-111).
7. Зубарева, И.И. Математика: учебник для 5 класса общеобразовательных учреждений. / И.И.Зубарева, А.Г.Мордкович.– М.: Мнемозина, 2003.- 267 с.
8. Зубарева, И.И. Математика: учебник для 6 класса общеобразовательных учреждений. И.И.Зубарева, А.Г. Мордкович.– М.: Мнемозина, 2009. - 264 с.
9. Клустер Д. Что такое критическое мышление? (Международный журнал о развитии мышления через чтение и письмо) «Перемена» 2001, № 4.
10. Козлова С.А. Математика. 5 класс: учеб. для общеобразоват. учреждений: в 2 ч. Ч.1 /С.А.Козлова, А.Г.Рубин. – 2-е изд. – М.: Баласс, 2013. – 208 с.
11. Козлова С.А. Математика. 6 класс: учеб. для общеобразоват. учреждений: в 2 ч. Ч.2 /С.А.Козлова, А.Г.Рубин. – 2-е изд. – М.: Баласс, 2013. – 208 с.
12. Кузьмин О.В. Перечислительная комбинаторика: учебное пособие. М.: Дрофа, 2005
13. Кузьмин О.В. Комбинаторные методы решения логических задач: учебное пособие, М.: Дрофа, 2006
14. Кузьмин, О.В., Попова, Т.Г. О важности комбинаторно-логического мышления/ Проблемы учебного процесса в инновационных школах. Вып.12: Сб. научн. тр./ Под ред. О.В. Кузьмина.- Иркутск: Иркут. ун-т, 2007.- С. 113-123.
15. Линдсей Г., Халл К.С. Томсон Р.Ф. Творческое и критическое мышление. // Познавательные психические процессы / Сост. и общая редакция А.Г.Маклакова. – СПб: Питер, 2001. – (Серия «Хрестоматия по психологии»)
16. Макарычев, Ю.Н. Алгебра: элементы статистики и теории вероятностей: учебное пособие для учащихся 7-9 классов общеобразовательных учреждений / Ю.Н.Макарычев, Н.Г.Миндюк. Под ред. С.А.Теляковского – М.: Просвещение. – 2005. С. 37-50.
17. Макарычев, Ю.Н. Элементы комбинаторики / Ю.Н.Макарычев // Математика в школе. – 2004. – №6.- с.59 – 64.
18. Макарычев, Ю.Н. Начальные сведения из теории вероятностей в школьном курсе алгебры / Ю.Н. Макарычев // Математика в школе. – 2004. – №7. - с. 24 – 27.
19. Математика: Учебник для 5 класса общеобразовательных учреждений / Г.В.Дорофеев, И.Г.Шарыгин и др.; под ред. Г.В.Дорофеева, И.Г.Шарыгина. – М.: Просвещение, 2011. – 303 с.
20. Математика: Учебник для 6 класса общеобразовательных учебных заведений / Г.В.Дорофеев, И.Г.Шарыгин, С.Б.Суворова и др.; под ред. Г.В.Дорофеева, И.Г.Шарыгина. – М.: Просвещение, 2010. – 303 с.
21. Математика: Учебник для 7 класса общеобразовательных учебных заведений / Г.В.Дорофеев, С.Б.Суворова и др.; под ред. Г.В.Дорофеева, И.Г. Шарыгина. – М.: Просвещение, 2010. – 254 с.
22. Математика. Арифметика. Геометрия. 5 класс: учеб. для общеобразоват. учреждений/ Е.А. Бунимович, Г.В.Дорофеев, С.Б. Суворова и др., - М.: Просвещение, 2010.
23. Математика. Арифметика. Геометрия. 6 класс: учеб. для общеобразоват. учреждений/ Е.А. Бунимович, Г.В.Дорофеев, С.Б. Суворова и др., - М.: Просвещение, 2010.
24. Мордкович А.Г, Семенов П.В. События. Вероятности. Статистическая обработка данных: дополнительные параграфы к курсу алгебры 7-9кл. общеобразоват. учреждений. - М.: Мнемозина, 2003.
25. Полат Е.С. Современные педагогические и информационные технологии в системе образования: Учеб. пособие для студентов высшего учебного заведения./ Е.С.Полат, М.Ю. Бухарина. – М.: Изд. «Академия», 2007. – 368 с.
26. Поль Р.У. Критическое мышление: Что необходимо каждому для выживания в быстро меняющемся мире. 1990.
27. Попова Т.Г. Педагогическая мастерская на уроках математики. Сборник научных трудов “Вопросы преподавания математики и информатики в школе и ВУЗе”, филиал ИГПУ, 2005 г., 5 стр.
28. Поппер К. Логика научного исследования: Пер. с англ. / Под общ. ред. В.Н. Садовского. — М.: Республика, 2004. — 447 с.
29. Студенецкая, В.Н. Новое пособие по теории вероятностей для основной школы / В.Н.Студенецкая  // Математика в школе. - 2004. - №7. – с. 66-71.
30. Студенецкая, В.Н. Статистика и теория вероятностей на пороге основной школы / В.Н.Студенецкая // Математика в школе. - 2004. - №6. – с. 64 – 65.
31. Сорина Г.В. Критическое мышление: история и современный статус. Вестник Московского университета. Серия 7. Философия. №6. 2003. С. 97-110.
32. Ткачева, М.В. Элементы статистики и вероятность: учебное пособие для учащихся 7-9 классов общеобразовательных учреждений / М.В.Ткачева, Н.Е.Федорова. – М.: Просвещение, 2005.- 112 с.
33. Ткачева, М.В. Элементы стохастики в курсе математики VII-IX классов основной школы / М.В. Ткачева // Математика в школе. - 2003.-№3. – с. 36 – 47.
34. Ткачева М.В., Федорова Н.Е. Элементы стохастики в курсе математики VII-IX классов основной школы. [текст] // Математика в школе. - 2003.-№3
35. Тюрин Ю.Н. Теория вероятностей и статистика [текст] / Ю.Н.Тюрин, А.А.Макаров, И.Р.Высоцкий, И.В.Ященко - М.:МЦНМО: АО «Московские учебники», 2004.
36. Халпер Д. Психология критического мышления – М., 2000
37. http://school41-saransk.narod.ru/page/krit_mi.htm - схемы

а

а

а

а

а

а

а

у

у

у

у

у

у

у

*

КОМИССИЯ

В

А

Б

Председатель

В

Б

В

Б

А

А

Заместитель

А

Б

А

В

Б

В

Секретарь

ВБАА

ВАБ

БАВ

АВБ

АБВ

БВА

Полученная комбинация

Б

А

В

Г

Из Антоново в Борисово

Из Борисово во Власово

Из Власово в Грибово

П

П

П

Р

В

В

Р

В

П

Р

В

П

Р

В

П

Р

В

П

*

*

Подъем

Спуск

1

3

4

2

2

3

4

1

3

4

1

2

4

1

2

3

*

БУЧЕНИЕ УЧАЩИХСЯ ЭЛЕМЕНТАМ КОМБИНАТОРИКИ КАК СРЕДСТВО РАЗВИТИЯ У НИХ КРИТИЧЕСКОГО МЫШЛЕНИЯ