Lobachevskiy geometriyasi uchun Puankare modeli

O‘ZBEKISTON RESPUBLIKASI XALQ TA’LIMI VAZIRLIGI
NAVOIY DAVLAT PEDAGOGIKA INSTITUTI
Fizika-matematika fakulteti
Umumiy matematika kafedrasi
Mavzu: Lobachevskiy geometriyasi uchun Puankare modeli
Bajardi: matematika-informatika
yo`nalishi 4-kurs talabasi
U.Ramonov
Ilmiy rahbar: f.-m.f.n. S.X.Abjalilov
Navoiy – 2010
Reja:
|
Kirish ………………………………………………………..
|
|
1. Noyevklid geometriyalar haqida ………………………………
|
|
2. Lobachevskiy geometriyasi uchun Puankare modeli ………...
|
|
2.1. Ortogonal aylanalar va ortogonal to`g`ri chiziqlarni yasash ……
|
|
2.2. Inversiya va inversion almashtirishlar ……………….
|
|
2.3. Puankare modeli ……………………………………….
|
|
2.4. Cheksiz uzoqlikdagi nuqta ……………………………
|
|
Xulosa ………………………………………………………
|
|
Foydalanilgan adabiyotlar………………………………….
|
Vatanimizning kalajagi, xalqimizning ertangi kuni, mamlakatimizning jahon hamjamiyatidagi obro`-etibori, avalambor, farzandlarimizning unib-o`sib, ulg`ayib, qanday inson bo`lib hayotga kirib borishiga bog`liqdir. Biz bunday o`tkir haqiqatni hech qachon unutmasligimiz kerak …
“Yuksak ma’naviyat - yengilmas kuch” asaridan.
I.Karimov
Hech qaysi bir geometriya boshqasi bilan
taqqoslanganda haqiqatga yaqinroq emas…
Anri Puankare
Kirish
Prezidentimiz Islom Karimov tashabbusi bilan 2010 yil “Barkamol avlod yili” deb e’lon qilindi. Mamlakatimizning barcha jabhalarida amalga oshirilayotgan keng ko‘lamli islohotlar, huquqiy demokratik davlat va erkin fuqorolik jamiyatini qurish zamirida, avvalambor, inson manfaatlari, uning intelektual salohiyatini yuzaga chiqarish, kasb mahoratini oshirish uchun zarur shart-sharoit vazifalari mujassam. Bu borada barkamol avlodni tarbiyalash, umumta’lim maktablari, oliy va o`rta maxsus ta’lim sohasida yuqorimalakali kadrlarni tayyorlash, ilm-fan, ta’lim hamda ishlab chiqarish o`rtasidagi o`zaro hamkorlikni yanada rivojlantirishga alohida e’tibor qaratilmoqda.
Davlat ta’limini rivojlantirish davlat umummilliy dasturi doirasida 2005-2009 yillar davomida jami 8541 ta umumta’lim maktabi mebel, o`quv labaratoriya asbob-uskunalari, kom’yuter mexakanikalari, sport anjomlari va maxsus jihozlar bilan ta’minlandi. Buning uchun Moliya vazirligi huzuidagi byudjetdan tashqari maktab ta’limi jamg`armasi hisobidan jami 463, 8 milliard; (2005 yili 41,9 milliard; 2006 yili 53,6 milliard; 2007 yili 101,3 millard; 2008 yili 136,8 milliard; 2009 yili 130,2 milliard.) so`m mablag` ajratildi.
O`quv jarayonida samaradorlikka erishish uchun zamonaviy ilg`or pedagogik texnologiyalar, noan’anaviy dars usullari va o`zaro faol o`quv jarayonini tadbiq qilish lozim. O`zaro faol usullarni o`quv jarayoniga qo`llash uchun esa o`tiladigan mavzuni talabalar, o`quvchilar o`zlari mustaqil tayyorlab kelishlari talab etiladi. Jarayonning samaradorligini oshirish maqsadida innovatsion usullarini qo`llashda endi biz – pedagoglar “O`quvchlarni o`qitmaymiz, balki kitobni o`qishga o`rgatamiz” shiorini amalga oshiramiz. Buning sabababi shundaki, agarda talaba va o`quvchilar darsga tayyor holda kelmasalar, hech qanaqa faol usuldan samarali foydalanib bo`lmaydi. Natijada o`qituvchi yana o`z-o`zidan an’anaviy shaklda dars o`tishiga to`g`ri keladi.
Buning uchun talaba yoshlarimiz erkin fikrlash madaniyatiga ega bo`lishlari zarur. Bu masalalar tizimini yaratish talabalarda erkin fikrlash madaniyatini tarbiyalashning tamoyillarini Nizomiy nimidagi Toshkent davlat pedagogika universiteti professori, p.f.n. R.Niyozmetova quyidagilarga ajratdi:
Tarixiylik tamoyili masalalarni tarixiy bilimlarda foydalanib yechish imkoniyatini beradi. Bu esa ilmiy dunyoqarashning, ijodiy fikrning shakllanishi, bitta dalilning o`ziga nisbati turli nuqtai nazarlar mantig`ini va kurashini hisobga olish, sabab-oqibat bog`lanishlarini aniqlashga imkon beradi. Ba’zi tarixiy dalillar ta’lim jarayoniga qiziqarlilik elementini olib kirishi mumkinligi, bu ham erkin fikrlashning rivojlanishiga olib keladi;
Fanlar ichki aloqalarini amalgam oshirish tamoyili bitta fanni o`rganishning turli bosqichlarida masalani yechishda uning turli bo`limlari orasidagi zaruriy aloqalarni aniqlashdan iborat. Bunda, bir tomondan, talabalar o`qitishning ma’lum bosqichida yechiladigan masala qachon va qayerda foydalanilishini hisobga olishlari, ikkinchi tomondan esa yangi masalani yechishda ilgari o`rganilgan qaysi materialga tayanish mumkinligini bilishari zarur;
Fanlararo aloqalarni amalga oshirish tamoyilini turli o`quv fanlarida bilish faoliyati aspektida qarash va shu asosda yaxlit masalalar struktura sini yaratish mumkin. Bu esa pirovard natijada, erkin fikrlashning rivojlanishiga jiddiy ta’sir etadi. Kasbiy yo`nalganlik tamoyilidan erkin fikrlashni rivojlantirish jarayonida foydalanishdan bosh maqsad – bo`lajak pedagog faoliyatning ma’lum sifatlarini rivojlantirishga yo`naltirishni ko`zda tutadi. Talabalarda kasbga yo`nalganlikni rivojlantirish – bu ularda bo`lajak kasbiga munosabat, qiziqish, unga bo`lgan maxsus qobilyatlarini mustahkamlash demakdik;
Mustaqil o`qib bilim orttirish tamoyili shaxsning o`zi tomonidan boshqariladigan maqsadga yo`nalgan bilim faoliyatini ta’minlaydi. Qo`yilgan masalaning o`z yechimini izlash maqsadlarini aniqlash, mustaqil xulosalar qilishga intilish, fan, texnika, madaniyatning turli sohalarida izchil bilim olish shaxs tomonidan erkin fikrlash madaniyati rivojlanganligining yuqori darajasiga erishilganligi haqida guvohlik beradi.
Talaba yoshlarimiz ilmiy va ommabop adabiyotlardan mustaqil foydalanishni, ya’ni mustaqil bilim olish madaniyatiga ega bo`lishi kerak. Fanlardan o`zlashtirishda darslik bilan bir qatorda qo`shimcha adabiyotlardan foydalanish talab etiladi.
Geometriya insoniyat paydo bo`lishi tarixi davomidagi eng qadimiy fanlardan biri hisoblanadi. Fanning tizimli ravishda rivojlanishida (abstraklashuvida) eramizdan avvalgi III asrda yashab ijod qilgan grek olimi Yevklidning “Negizlar” nomli asari sabab bo`ldi. Bu asar 13 ta kitobdan iborat bo`lib, unda Yevklid dastlab ta’riflar, postulotlar (Yevklid bu terminnni geometrik tushunchalar uchun ishlatgan bo`lsa, aksoimalarni algebraik munosabatlar uchun ishlatgan).
Insoniyat tarixida inson yaratgan kitoblar orasida eng ko`p marta qayta nashrdan chiqarilgan ushbu kitobda Yevklid geometriyasini aksiomatik qurilishini bayon etib, nuqta, to`g`ri chiziq va tekislik kabi asosiy tushunchar yordamida keyingi figuralar ta’rifi, ularni bog`lovchi munosabatlat, teoremalar va ularni izchil isbotlash tarzida tizimga solindi.
1826 yil Qozon davlat universiteti professori N.I.Lobachevskiy tomonidan noyeyklid geometriyaga asos solindi. Bu yerda dastlabki to`tta aksiomani o`z o`rnida qoldirib (bu to`rt aksioma o`rinli bo`lgan geometriya absolyut geometriya deb yuritiladi) beshinchi parallellik aksiomasini almashtirish bilan yangi geometriya hosil qilindi.
Yevklidning beshinchi postulotining ingliz pedagogi Pleyfer tomonidan yaratilgan ekvivalanti:
Tekislikda to`gri chiziqdan tashqaridagi nuqtadan u bilan kesishmaydigan yogona to`g`ri chiziq o`tadi.
Ushbu postulotni lobachevskiy quyidagi bilan almashtirdi:
Tekislikda to`gri chiziqdan tashqaridagi nuqtadan u bilan kesishmaydigan kamida ikkita to`g`ri chiziq o`tadi.
Lobachevskiyning deyarli barcha zamondoshlari uning yaratgan geometriyasi xatolikkka ega deb hisoblashar edi. Ular bu geometriyani biz yashab turgan fazoda qo`llab bo`lmasligi bilan birga, bu geometriya qachonlardir ichki qarama-qarshilikka uchraydi deb hisoblashar edi.
Noyevklid geometriya tarafdorlari uchun bu geometriyani zidsiz ekanini asoslash, boshqalarni bunga o`rgatish uchun biror usul yoki yevklid geometriyasi doirasida ushbu geometriyani tushuntira biladigan uning modellarini yaratish zarurati bor edi.
Bunday modellardan biri Keli-Kleyn modeli bo`lib hisoblanadi. Bu model doira va uning oxirlari hisobga olinmagan vatarlari yordamida tushuntiriladi.
Ikkinchi model fransuz matematigi Puankare tomonidan Lobachevskiy geometriyasi uchun taklif qilingan modeldir. Bu model doira va uning ichki nuqtalari Lobachevskiy tekisligi deb olinib, Lobachevskiy tekisligidagi nuqta doira ichidagi nuqtaga, to`g`ri chiziq esa ushbu doiraga orthogonal aylananing doira ichidagi yoyi tushuniladi.
Bu ikki model ham Lobachevskiy geometriyasining keyingi rivojlanishga katta xizmat qilgan modellardir.
Referat mavzusi ana shunday muhim masalani o`rganishni o`z oldiga maqsad qilib qo`ygan. Olingan maqsadga ko`ra referat kirish, ikkita paragraf va xulosa shaklida bajarish rejalashtirildi.
Birinchi paragrafda noyevklid geometriyalar haqida umumiy ma’lumot berildi. Bu yerda noyevklid geometriyalarni asoslash va uni barcha uchun tushunarli tilda bayon etish maqsadida modellari yaratilishi zarurati bor ekanligi va ularning ushbu geometrlarni o`rganishdagi ahamiyati haqida so`z yuritildi.
Ikkinchi paragraf Lobachevskiy geometriyasining Puankare modelini izohlashga bag`ishlandi. Ushbu model uchun zarur bo`lgan ortogonal aylanalar va ularni yasash, inversiya va inversion almashtirishlar kabi tushunchalar bayon etildi. Shundan so`ng “Puankarening sehrli dunyosi” deb ataluvchi modeli kiritildi. Ushbu model yordamida cheksiz uzoqlikdagi nuqta tushunchasi o`z aksini topdi.
Xulosa qismida olingan natijalar tahlil qilingan. Referatni bajarishda foydalanilgan adabiyotlar ro`yxati keltirilgan.
1. Noyevklid geometriyalar haqida
Geometriyani aksomatik qurilishi tizimli ravishda eramizdan avvalgi III asrda Yevklidning “Negizlar” asari orqali kiritilga edi. Yevklidning parallellar haqidagi mashhur postulotini teorema sifatida qabul qilib isbotlashga bo`lgan o`rinishlar, postulotga teskari jumlani qabul qilib undan xulosa chiqarishga bo`lgan harakatlar noyevklid geometriyalarni yaratilishiga olib keldi.
Noyevklid geometriya tarafdorlariga bu geometriyaning zidsizligi va real fazodagi aniq tadbiqini ko`rsatish muammosi turar edi. Biz yashab turgan fazoni Yevklid geometriyasi to`la ifodalab beradi. Noyevklid geometriyalar qanday fazoni ifoda etadi?
Nemis matematigi K.F.Gauss geometriyaning matematikani boshqa sohalaridan (mexanika singari eksprimental fanlardan) ajratish tarafdori edi. Bu yerda Gauss va u singari Lobachevskiy va Boyyailarga birinchidan, “xayoliy geometriyani” fizik reallikdan holi ravishda mantiqiy qurish mumkinligi, ikkinchidan astranomik masshtablarda bu davrda Yevklid geometriyasining ustunligini olib tashlashni taklif qilish foydasizligi ma’lum edi.
Eramizdan avvalgi ikkinchi asrgacha Evklidning o`n uch tomlik “Negizlar” asari asosida geometriyaning aksiomatik qurilishi o`z nihoyasiga yetgan edi. Amaliy ehtijojlar natijasida hosil qilinan burchakni, uzunlik va yuzani o`lchash izchil matematik nazariyalar aksioma, postulot, teorema, ta’rif va isbotlar yordamida o`z tasdig`ini topdi. Geometriyaning asosiy elementlari nuqta, to`g`ri chiziq va tekislik tushunchalari yuzaga chiqdi.
Shu davrdagi inson amaliy ehtiyojlari uchun foydalaniladigan tushunchalar abstract qiyofasini topgan edi. Bu yerda cheksiz uzoqlikdagi to`g`ri chiziq qanday ifodaga ega bo`ladi degan savol mavjud emas edi. Balkim shuning uchun parallellik haqidagi V postulot Evklid tomonidan juda ehtiyotlik bilan bayon etilgandir: agar to`g`ri chiziq ikki to`g`ri chiziqni kesib o`tsa, bu to`g`ri chiziqlar ichki bir tomonli burchaklari yig`indisi ikkita to`g`ri burchak yig`indisidan kichik bo`lgan tarafda kesishadi.
Qadimgilar yerni juda katta o`lchamdagi (o`lchashning hech iloji bo`lmagan) tekis disk sifatida tasavvur etishgan. Geografik kashfiyotlar natijasida bu chegara masofalar yanada uzoqlashdi. Tevarak atrofdagi borliq haqidagi bilimlarning oshib borishi bilan geometriya ham taraqqiy eta boshladi. XVIII asrda ingliz pedagogi Pleyfer kitobida V postulotning zamonaviy shakli bayon etildi: to`g`ri chiziqdan tashqaridagi nuqtadan u bilan bir tekislikda yotuvchi va kesishmaydigan faqat bitta to`g`ri chiziq o`tkazish mumkin.
XIX asrning yigirmanchi yillarida1 Lobachevskiy geometriyasi dunyuga keldi. Bu yerda Evklidning V postulotidan boshqa barch postulotlari saqlangan holda V postulotga quyidagicha o`zgartirish kiritdi: to`g`ri chiziqdan tashqaridagi nuqtadan u bilan bir tekislikda yotuvchi va kesishmaydigan kamida ikkita to`g`ri chiziq o`tkazish mumkin.
N.I.Lobachevskiy 1792 yil 2 dekabrda Nijniy Novgorod (hozirgi Gorkiy shaxrida) to‘g‘ilgan. U Qozon universiteti qoshidagi gimnaziyani, undan keyin Qozon universitetini bitirib, shu yerda o‘qituvchi bo‘lib ishga qoldirilgan. U 1816 yilda professor, 1827 yildan 1846 yilgacha shu universitetning rektori bo‘lib ishlagan. N. I. Lobachevskiy 1856 yil 24 fevralda vafot etgan.
N. I. Lobachevskiy shu universitetda ishlagandan boshlab V postulatni isbotlashga qattiq harakat qilgan. U safdoshlarining urinishlari samaraisizligi, V postulatni isbotlash uchun avvalgi postulatlardan foydalanish yetarli emas degan xulosaga kelgan. Buni isbotlash uchun Yevklidning asosiy yo‘nalishlarini saqlagan holda, V postulatni rad qilib, uni teskarisiga almashtirib, mantiqiy tizimni qurdi. Bu mantiqiy sxema yangi geometriyani, Yevklid geometriyasi kabi muvofaqqiyatlarga olib keladi degan xulosaga kelgan.
N.I.Lobachevskiy 1826 yil 7 fevralda Qozon universitetining fizika-matematika fakultetiga uzining “Geometriya qoidalari haqida” degan ma’ruzasini topshirgan. 1829 yilda “Geometriyaning boshlanishi haqida” degan maqolasini “Qozon universiteti olimlarining ishlari” turkumiga kiritgan. Bu esa uning yangi geometriya haqida eng birinshi ishi edi. Keyingi yillarda N.I.Lobachevskiy geometriya haqida ko‘p ishlarni o‘rgandi. Bu ishlarida u V postulatni yevklidning qolgan aksiomalaridan keltirib chiqarib bo‘lmaydi deb asoslagan va aniq ta’rif bergan.
Lobachevskiy o`zining geometriyasini tekislikda va fazoda trigonometrik formulalarni kiritgan holda takomillashtirgan. Bu geometriyani u “hayoliy geometriya” deb atagan.
Yangi-yangi dalillarni ochishda Lobachevskiy o`zining geometriyasida mantiqiy qarama-qarshilikni uchratmadi. Bu geometriyani hech qashon qarama-qarshiliklarga olib kelmasligini ko‘rsatishni xoxlagan Lobachevskiy uzining geomeriyasida analitik tekshirishlar olib boradi va zidsizlik muammosini hal qiladi.
Lobachevskiyning deyarli barcha zamondoshlari uning geometriyasi xatolikka ega deb hisoblashar edi. Ular nafaqat bu geometriyaning tashqi olamda qo``llanilmasligi, balki bu geometriyaning keyingi rivojlanishi davomida o`z-o`zida ichki qarama-qarshilik kelib chiqadi deb hisobashgan.
Lobachevskiy geometriyasi bilan bog`liq murakkab savollarni tahlil qilmasakda uning amaliy tadbiqini aytib o`tish mumkin. Lobachevskiy geometriyasi XX asrning boshlarida yaratilgan nisbiylik nazariyasini chuqur va izchil ochib bera oladi.
Lobachevskiy geometriyasining to`g`ri ekanligiga tushunib yetgan olimlar oldida yana bir masala turardi: “qanday qilib Lobachevskiy geometriyasiga qo`yilgan qarama-qarshilik aybini olib tashlash mumkin”.
Shu maqsadda birinchi model 1868 yilda E.Beltrami tomonidan qurildi. Shuningdek nemis matematigi F.Kleyn va fransuz matematigi Anri Puankare modellari mavjud.
2. Lobachevskiy geometriyasi uchun Puankare modeli
1882 yillarda fransuz matematigi Anri Puankare Lobachevskiy geometriyasining modelini qurdi. Buning uchun u oddiy aylanadan foydalangan.
2.1. Ortogonal aylanalar va ortogonal to`g`ri chiziqlarni yasash
Ikkita chiziq, aylana yoki to`g`ri chiziq ortogonal bo‘lishi uchun ular to`g`ri burchk ostida kesishishlari kerak. Maktab matematikasidan ma’lumki, ikki aylana orasidagi burchak deyilganda ularning kesishish chizig`idan o`tuvchi urinmalari orasidagi burchak tushunilsa, to`g`ri chiziq va aylana orasidagi burchak deyilganda to`g`ri chiziq va kesishish nuqtasidan o`tkazilgan urinma orasidagi burchak tushuniladi.
Bizga ma’lumki to`g`ri chiziq aylanaga ortogonal bo`lsa, u aylana markazidan o`tadi. Shu bilan birga ikki ortogonal aylanalar kesishgan nuqtasidan har bir aylanaga o`tkazilgan urinmalar ikkinchining markazidan o`tadi (1-chizma). Bu tasdiqlar quyidagi ikki muhim masalalarni yechishda qo`l keladi.
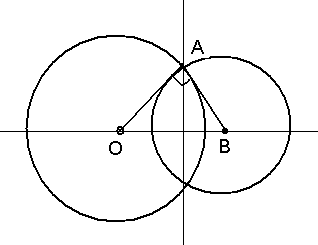
1-chizma
1-masala. aylananing A va B nuqtalaridan unga ortogonal aylana o`tkazing.
Yechish. Izlanayotgan aylana markazi aylananing markazi O nuqtadan AB to`g`ri chiziqqa tushirilgan perpendikulyar va OA to`g`ri chiziqqa A nuqtasidan o`tkazilgan perpendikulyarlar kesishgan nuqtada bo`ladi (1-chizma). Agar perpendikulyarlar kesishsa yechim yagona bo`ladi. Yechimga ega bo`lmaydigan holat bu A va B nuqtalar diametral qarama-qarshi nuqtalar bo`lganida ya’ni AB to`g`ri chiziqning o`zi berilgan aylanaga ortogonal bo`lgan hollar tushuniladi.
2-masala. aylana va bu aylana tashqarisida O1 nuqta berilgan. O1 markazli va berilgan aylanaga orthogonal aylana o`tkazing.
Yechish. A nuqta OO1 diametrli aylananing berilgan aylana bilan kesishgan nuqtalaridan biri bo`lsin. U holda (O1,O1A) – aylana izlangan aylana bo`ladi.
Puankare modelini o`rganishda iversiya va uning xossalarini bilish muhim ahamiyat kasb etadi.
2.2. Inversiya va inversion almashtirishlar
(O,r) inversiya deb (yoki O markazli r radiusli aylanaga nisbatan simmetriya) tekislikning istalgan M nuqtasiga OM nurda yotuvchi va
shartni qanoatlantiruvchi M/ nuqtani mos keltiruvchi almashtirishga aytiladi. O - nuqta inversiya markazi (tekislikda obrazi aniqlanmagan yagona nuqta), r - inversiya radiusi, (O,r) – inversiya aylanasi deyiladi.
Inversiyaning asosiy xossalari:
- aylana ichidagi nuqtalar aylana tashqarisidagi nuqtalarga va aksincha aylana tashqarisidagi nuqtalar aylana ichidagi nuqtalarga akslanadi;
- inversiya aylanasiga tegishli nuqtalar o`z-o`ziga akslanadi;
- inversiya markazidan o`tuvchi to`gri chiziq oz-oziga akslanadi;
- inversiya markazidan o`tuvchi aylana to`g`ri chiziqqa akslanadi;
- inversiya markazidan o`tmagan aylana aylanaga akslanadi;
- inversiyada chiziqlar orasidagi burchak kattaligi saqlanadi;
- inversiya tekislikdagi boshqa simmetriyalar singari uni ikki marta bajarish bilan ayniy almashtirishga aylanadi.
Yuqorida aytib o`tilgan xossalar isboti to`g`ridan-to`g`ri hosil qilinadi. Bu xossalar isboti pedagogika oliy o`quv yurtlari Geometriya kursida o`rganiladi.
- istalgan inversiya aylanasiga ortogonal aylana o`z-o`ziga akslanadi.
Isbot. berilgan aylana 4-xossaga asosan inversiyada aylanaga akslangan bo`lsin. 2-xossaga ko`ra aylana inversiya aylanasi bilan A va B nuqtalarda kesishgan bo`lsin. Bu nuqtalarning obrazi yana shu nuqtalarning o`zi bo`ladi. aylana ham ushbu nuqtalardan o`tadi. 5- xossaga asosan aylana inversiya aylanasiga ortogonal bo`ladi. Ammo 1-masalaga asosan A va B nuqtalardan aylanaga yagona ortogonal aylana o`tkazish mumkin edi. Demak, va aylanalar ustma-ust tushadi.
9) inversiya aylanasi bilan ustma-ust tushmagan aylana o`z-o`ziga akslansa, bu aylana inversiya aylanasiga ortogonal bo`ladi.
Isbot. 1-xossaga ko`ra berilgan aylana inversiya aylanasini (2-xossa asosida) o`z-o`ziga akslanuvchi A va B nuqtalarda kesib o`tadi. Inversiya markazi O va A nuqtadan OA to`g`ri chiziq o`tkazamiz. Agar A nuqta OA va aylanalarning yagona umumiy nuqtasi bo`lmasa, ularning yana qandaydir D umumiy nuqtasi mavjud bo`lib, D nuqtaning obrazi D/ nuqtasida ham kesishishi kerak bo`ladi. Ammo to`g`ri chiziq va aylana uchta umumiy nuqtaga ega bo`la olmaydi. Demak, A nuqta aylana va OA to`g`ri chiziqning yagona umumiy nuqtasi bo`ladi va OA to`g`ri chiziq aylanaga A nuqtada urinar ekan.
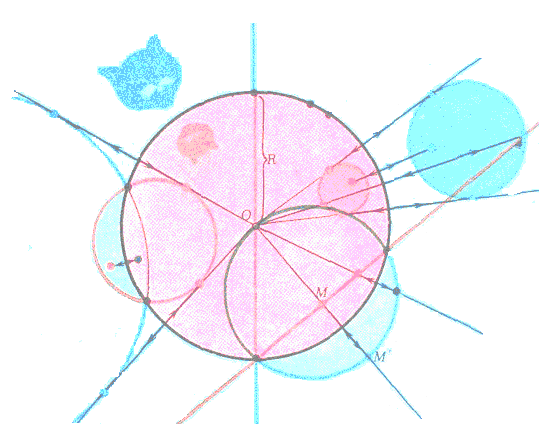
2-chizma
Inversiya puakare modelida siljitish vazifasini bajaradi. Shuning uchun model mohiyatini o`rganish uchun inversion yasashga doir masalalarni bilish muhim ahamiyatga ega.
3-masala. Q marqazli aylana ichidagi X nuqta berilgan. aylanaga orthogonal shunday aylana yasangki, bunda X va Q nuqtalar simmetrik bo`lsin.
Yechish. QX to`gri chiziqqa perpendikulyar to`g`ri chiziq aylana bilan A nuqtada kesishadi. A nuqtadan QA ga perpendikulyar to`g`ri chiziq QX to`g`ri chiziqni O nuqtada kesib o`tadi. (O,OA) aylana izlangan aylana bo`ladi (3-chizma).
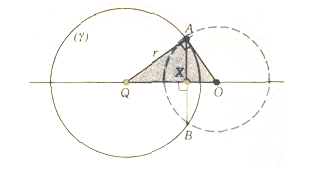
3-chizma
4-masala. Berilgan ikki aylanaga orthogonal aylanalar uchun aylanaga orthogonal va aylanalar simmetrik bo`lgan to`g`ri chiziq yoki aylana yasang.
Yechish. A1 , B1 va A2, B2 nuqtalar mos ravishda va , va aylanalarning kesishgan nuqtalari bo`lsin. Agar A1A2 va B1B2 to`g`ri chiziqlar parallel bo`lsa, aylanalar aylana dimetriga nisbatan simmetrik bo`ladi. Agarda A1A2 va B1B2 to`g`ri chiziqlar O nuqtada kesishsa, 2-masalaga asosan O markazli aylanaga orthogonal aylana o`tkazish mumkin (4-chizma). Bu aylana izlangan aylana bo`ladi.
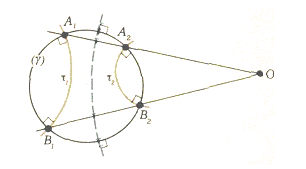
4-chizma
Eslatma. aylanalardan biri aylanaga orthogonal to`g`ri chiziq bo`lsa, u holda uning diametri bo`ladi.
2.3. Puankare modeli
Bu yerda Lobachevskiy geometriyasining asosiy tushunchalari o`rnida odatiy bo`lmagan nuqta, to`g`ri chiziq, yevklid geometriyasini siljitish yoki ko`proq maxsus tushunchalar ishlatiladi. Bu modelni berish uchun Lobachevskiy geometriyasi asosiy tushunchalarin Yevklid geometriyasidagi maxsus tanlangan tushunchalari orasida “Lo`g`at” tuzib olish kerak bo`ladi.
Puankare modeli uhun bu lo`g`at ushbu ko`rinishda bo`ladi.
Lobachevskiy tekisligi deganda Yevklid tekisligining Q markazli ayalana bilan chegaralangan doirasi ichki qismi tushuniladi. Lobachevskiy tekisligining nuqtasi doiraning ichki nuqtasi bo`ladi. To`g`ri chiziq deganda aylanaga orthogonal aylananing doira ichidagi qismi tushuniladi (demak, aylana diametr bilan ustma-ust tushmagan vatarlari to`g`ri chiziq hisoblanmaydi). Lobachevskiy tekisligida siljitish deganda doiraning ushbu asosiy almashtirishlari tusuniladi:
1) doiraning uning markazi Q nuqta atrofida istalgan burchakka burish;
2) doirani diametriga yoki aylanaga orthogonal istalgan aylanaga nisbatan simmetrik almashtirish.
Shuningdek bu almashtirishlarning kompozitsiyalari.
Bu kabi “nuqta”, “to`g`ri chiziq”, “tekislik”, “tekislikni siljitish” so`zlarni olish bilan Lobachevskiy geometriyasining barcha aksiomalari bajariladi. Demak, Lobachevskiy geometriyasi qarama-qarshiliksiz ya’ni zidsiz geometriya ekan. Bu haqida model muallifi Anri Puankare quyidagi so`zlarni aytgan edi: “Lobachevskiy teoremasini olib uni o`zimiz tuzgan lo`g`at bo`yicha xuddi biror tekstni fransuz tilidan ingliz tiliga tarjima qilgan kabi o`tkazamiz. Natijada biz Yevklid geometriyasida inkor etib bo`lmaydigan natijalarni ko`ramiz.”
Bu o`girish Yevklid geometriyasining zidsizligidan lobachevskiy geometriyasining zidsizligini ko`rsatildi. Shuning uchun ham Anri Puankare: “Hech qaysi bir geometriya boshqasiga qaraganda haqiqatga yaqinroq bo`lishi mumkin emas”, - degan edi.
Aksiomalarni tekshirish
- Istalgan siljitish “tekislik” ni o`z-o`ziga o`tkazadi, shu bilan birga to`g`ri chiziqni to`g`ri chiziqqa o`tkazadi.
- Istalgan ikki “nuqta”dan bitta va faqat bitta to`g`ri chiziq o`tadi.
- “tekislikni siljitish”da “to`g`ri chiziqlar” orasidagi burchak kattaligi saqlanadi.
- Istalgan ikki “to`g`ri chiziq” kongurent, ya’ni ulardan birini ikkinchiga o`tkazuvchi “tekislikni siljitish” mavjud.
- “to`g`ri chiziq”qa tegishli bo`lmagan istalgan “nuqta”dan “to`g`ri chiziq” bian umumiy nuqtaga ega bo`lmagan kamida ikkita “to`g`ri chiziq” o`tkazish mumkin.
Bu aksiomalarni isbotlarini qarab chiqaylik.
I. doirani o`z markazi atrofida burish, yoki bu doirani o`z diametriga nisbatan simmetrik almashtirish uni o`z-o`ziga o`tkazadi. Tekislikda iltalgan aylanani inversiya aylanasi sifatida olib, unga orthogonal aylanani inversion almashtirilganda aylana o`z-o`ziga almashadi. Ya’ni doirani aylana ajratgan qismlar o`rinlarini almashtiradi. Umuman olganda doira o`zida qolar ekan.
II. Buning o`rinli ekanligi 5-masaladan ko`rinadi.
III. Bu barcha siljitishlar uchu o`rinli, jumladan ularning kompozitsiyalari uhun ham o`rinli bo`ladi.
IV. Bu 4-masaladan kelib chiqadi.
V. Berilgan to`g`ri chiziq ni A va B nuqtalarda kesib o`tgan bo`lsin. Dastlab xususiy holni qaraymiz P va A nuqtalarni o`z ichiga oluvchi va aylanaga orthogonal aylana yagona bo`lib, P va B nuqtalarni o`z ichiga oluvchi aylanaga orthogonal aylana ham yagona bo`ladi. “Lo`g`at” bo`yicha bu aylanalar berilgan to`g`ri chiziq bilan kesishmaydigan to`g`ri chiziqlar hisoblanadi. Bu yerda A va B nuqtalar Lobachevskiy tekisligiga tegishli emasligini ta’kidlash lozim.
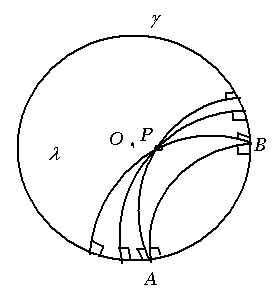
5-chizma
2.4. Cheksiz uzoqlikdagi nuqta
Puankare modelining yana bir ajoyib xususiyataridan biri Yevklid geometriyasi nuqtai nazaridan Lobachevskiy geometriyasining cheksiz uzoqlikdagi nuqtasini korish mumkin.
aylana Lobachevskiy tekisligining cheksiz uzoqlikdagi aylanasi ekanligini ko`rsatamiz. Buning uchun odatiy Yevklid tekisligida berilgan figurani boshlang`ich holatidan mumkin qadar uzoklika siljitamiz. Bu masalani quyidagicha amalgam oshiramiz. Yevklid tekisligida ikki ustma-ust tushmagan parallel to`g`ri chiziqlarni olamiz va tekislikda ga nisbatan simmetrik almashtirish bajaramiz. Bunda chiziq chiziqqa almashadi. to`g`ri chiziqqa simmetrik almashtirish bajarish bilan to`g`ri chiziqqa simmetrik bo`lgan to`g`ri chiziq hosil qilinadi. Bu jarayonni davom ettirish bilan to`g`ri chiziqqa parallel cheksiz uzoqlashgan to `g`ri chiziqlar topiladi (6-rasm).
Xuddi shunga o`xshash ishlarni Lobachevskiy tekisligida ham davom ettirsak, aylanaga orthogonal aylanalar aylanasi nuqtasiga yaqinlasha boradi. Demak, cheksiz uzoqlashgan nuqtalar aylana ustidagi nuqtalar bo`lar ekan.
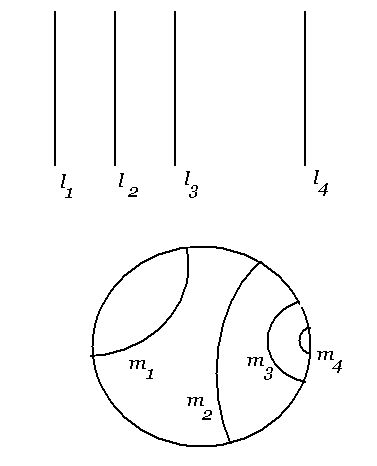
6-chizma
Xulosa
Uzluksiz ta’lim tizimida ta’lim sifati va samaradorligini oshirish xozirgi kunning muhim talablaridan biri hisoblanadi. Darsni tashkil etishda zamonaviy yangi pedagogik texnologiyalardan foydalanish, turli faol usullarni qo`llash ijobiy natija beradi. Oquvchilarni darsga bo`lgan qiziqishlarini orttirish maqsadida ularning erkin fikrlash madaniyatiga ega bo`lishlariga ko`mak berish lozim. Agar o`qituvchi va shu bilan birga o`quvchi darsga tayyor bo`lmas ekan hech qanaqa faol usulni qo`llash imkoniyati paydo bo`lmaydi.
Dars davomida tarixiy ma’lumotlardan foydalanish, buyuk matematik olimlar hayoti va ijodidan lavhalar keltirish, ular olgan ilmiy xulosalarning fan va jamiyat rivojlanishi uchun qanchalik katta ahamiyati to`grisida aniq faktlar keltirish o`quvchilarda bilim olishga ishtiyoqni ortishiga sabab bo`ladi.
Sinfdan tashqari mashg`ulotlar uchun mo`ljallangan materiallarni tayyorlashda sinfda o`tiladigan mashg`ulotlarga mos keluvchi ma’lumotlardan foydalanish muhim ahamiyat kasb etadi.
Shu maqsadda ushbu bajarilgan referat natijalaridan foydalanish mumkin.
Referat noyevklid Lobachevskiy geometriyasi va uni sodda holda tushunish imkonini beruvchi modellar haqidagi qiziqarli va dolzarb mavzug bag`ishlandi.
Referat kirish, ikkita paragraf va xulosa qismlari shaklida bajarish rejalashtirildi.
Birinchi paragrafda noyevklid geometriyalarning yaratilishi, bu geometriyalarni juda kamchilik qabul qilganligi, ana shu kamchilik olimlar qanday qilib bu geometriyalarni boshqalarga tushuntirishi mumkinligi haqidagi muammolar haqida so`z yuritildi. Ana shu kabi harakatlar va izlanishlar mahsuli sifatida dunyoga kelgan, yevklid geometriyasi doirasida bemalol tushunish imkonini beruvchi modellar haqida ma’lumotlar berildi.
Ikkinchi paragraf fanda “Puankarening sehrli dunyosi” nomi bilan mashhur bo`lgan model haqida mulohazalar yuritilgan. Ushbu modelni o`rganishdan avval orthogonal aylanalar va ortogonal to`g`ri chiziqlarni yasash metodikasi, inversiya va inversion almashtirishlar bo`yicha to`liq malumot berib o`tilgan. So`ngra ular yordamida Puankare modeli kiritilgan va ushbu model orqali Lobachevskiy geometriyasi faktlari oddiy tushuntirildi.
Referat ma’lumotlaridan o`qituvchilar, talabalar va o`quvhcilar darsdan tashqari mashg`ulotlarida foydalanishlari mumkin.
Foydalanilgan adabiyotlar
- I.A.Karimov, Yuksak ma’naviyat yengilmas kuch T. “Ma’naviyat” 2008 y., 176 bet.
- I.A.Karimov, Jahon moliyaviy iqtisodiy inqirozi, O‘zbekiston sharoitida uni bartaraf etishning yo‘llari va choralari T. “O‘zbekiston” 2009 y. 56 bet.
- А.В.Погорелов, Геметрия 7-11 синф дарслиги, “Ўитувчи” нашриёти, T. 1991й.
- N.G‘aybullayev, A.Ortiqboyev Geometriya, 7-sinf uchun o‘quv qo‘llanma, Toshkent “O‘zbekiston” 2001.
- А.Я.Нарманов, А.С.Шарипов, Геометрия асослари, Т. Университет, 2004. – 88б.
- N.D.Dadajonov, M.Sh.Jo‘rayeva Geometriya I qism, “O‘qituvchi” nashriyoti, T. 1982y., 368 bet.
- А.Д.Александров и др. Геометрия для 10-11 классов, Учебное пособие для учащихся школ и классов с углубленным изучением математики./ А.Д.Александров, А.Л.Вернер, В.И.Рыжик. - 3-е изд., перераб.-М.: Просвещение, 1992.- 464с.
- С.Гиндикин Волшебный мир Анри Пуанкаре, «Квант», №12, 1975г., kvant.mccme.ru.
- К.Л.Самаров, В.М.Уроев Модель Пуанкаре, kvant.mccme.ru.
- А.Ширшов, Модель Кэли-Клейна геометрии Лобачевского, «Квант», № 3, 1976г.
- www.edu.uz, www.ziyonet.uz, www.pedagog.uz
1 1826 yil Qozon universiteti ilmiy kengashida
Lobachevskiy geometriyasi uchun Puankare modeli