Изучение кинетики гравитационного осаждения
Изучение кинетики гравитационного осаждения
ЦЕЛЬ РАБОТЫ
Целями лабораторной работы являются:
• экспериментальное определение скорости осаждения твердых частиц под действием силы тяжести в зависимости от диаметра частиц и физических свойств частицы и жидкости;
• сопоставление полученных экспериментальных данных с расчетными.
Теория
Рассмотрим процесс осаждения твердой шарообразной частицы диаметром d , плотность которой Т , в жидкости с плотностью ж. В данном случае примем Т > ж. Если частицу вводят в жидкость и начальная скорость ее движения будет равна нулю, то она вначале будет двигаться ускоренно, и баланс сил, действующих на нее (рис. 1.1.1), можно представить уравнением
T – A – R = J
где - сила тяжести, действующая на частицу;
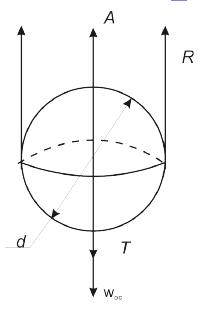
Рисунок 1 - Силы, действующие на частицу, осаждающуюся в гравитационном поле
- выталкивающая сила, равная по закону Архимеда весу объема вытесненной частицей жидкости;
- сила сопротивления, отнесенная к поперечному сечению частицы
– сила инерции.
где: m – масса частицы; – коэффициент сопротивления;
– скорость осаждения частицы; – время.
С увеличением в начальный момент скорости возрастает сила сопротивления, которая уменьшает ускорение частицы. Через некоторый момент времени можно считать ускорение практически равным нулю.
При условии постоянства скорости осаждения уравнение (1) действующих на частицу сил будет иметь вид
T – A – R = 0
Можно с достаточной для технических расчетов точностью период движения частицы с ускорением исключить из дальнейшего рассмотрения, так как начальный промежуток времени движения с ускорением мал по сравнению с общей длительностью процесса осаждения.
Из уравнения можно получить скорость осаждения
Скорость осаждения твердой частицы непосредственно из уравнения рассчитать нельзя, так как неизвестно значение коэффициента сопротивления , который зависит от режима осаждения.
Исследования показывают, что можно выделить три режима осаждения: ламинарный, переходный и турбулентный. Каждый режим осаждения имеет свой характер обтекания твердой частицы жидкостью.
Область существования того или иного режима осаждения определяют величиной критерия Рейнольдса
Режим осаждения частицы можно определить и по значению критерия Архимеда.
Так, верхней границей ламинарного режима осаждения служит значение Re = 1,85, что соответствует значению Ar = 33. Следовательно, при выполнении условия 33 Ar имеет место ламинарный режим осаждения. Верхнее предельное значение критерия Архимеда для переходного режима, соответствующее значению Re = 500, определяется по уравнению (1.1.14) и равно 8,3·104.
Переходный режим осаждения ограничивается изменением значений критерия Ar в следующих пределах
33 < Ar < 8,3·104
ОПИСАНИЕ УСТАНОВКИ
Установка состоит из трех стеклянных цилиндров, заполненных разными жидкостями: водой, трансформаторным маслом и глицерином.
В верхней и нижней части каждого цилиндра имеются метки, фиксирующие расстояние, которое частица проходит в процессе осаждения.
Замеряя время, в течение которого частица проходит расстояние между метками, можно определить скорость осаждения частицы. С целью исключения влияния начального ускоренного участка движения частицы в жидкости, верхняя метка расположена на 30–40 мм ниже поверхности жидкости.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Шарики известного или замеренного диаметра помещают над поверхностью жидкости и отпускают. Время прохождения частицы между метками фиксируют секундомером. Каждый замер дублируют. Результаты опытов заносят в таблицу.
Всего проводят не менее 5 опытов, в каждом по 3-4 замера. Если частица коснулась стенки сосуда или к частице прилип пузырек воздуха, результаты таких опытов (замеров) не учитывают и производят повторные опыты.
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
На основе экспериментальных данных вычисляют:
1) скорость осаждения в каждом замере, исходя из известной длины пути и времени осаждения (графа 9 таблицы по форме 1.1). Значение скорости осаждения вносят в графу 10. По данным 3-4-х замеров определяют скорость осаждения (графа 11);
2) подсчитывают для каждого опыта значения критериев Re и Ar ;
3) сопоставляют полученные экспериментальные значения критериев Re и Ar со значениями, получаемыми по уравнениям (1.1.13) –(1.1.15), и анализируют причины отклонений экспериментальных данных от расчетных значений.
Таблица 1.1
|
№ опыта
|
№ замера
|
Частицы
|
Жидкость
|
|
|
|
Материал
|
d
мм
|
кг/м
|
Название
|
кг/м
|
Па-с
|
|
1
|
1
|
Стальной шарик
|
4мм.
|
7850
|
Вода
|
1000
|
|
|
1
|
2
|
Стальной шарик
|
4мм.
|
7850
|
Глицерин
|
1240
|
1,5
|
|
1
|
3
|
Стальной шарик
|
4мм.
|
7850
|
Трансформаторное масло
|
893
|
|
|
1
|
4
|
Стеклянный шарик
|
3мм.
|
2450
|
Глицерин
|
1240
|
1,5
|
|
1
|
5
|
Стеклянный шарик
|
6мм.
|
2450
|
Глицерин
|
1240
|
1,5
|
|
1
|
6
|
Стеклянный шарик
|
6мм.
|
2450
|
Трансформаторное масло
|
893
|
|
|
1
|
7
|
Стеклянный шарик
|
4мм.
|
2450
|
Трансформаторное масло
|
893
|
|
Таблица 1.1 Продолжение
|
Время осаждения
|
Скорость осаждения
|
Ar
|
Re
|
Примечание
|
|
|
|
|
|
|
|
|
0,5с
|
0,9
|
0,14
|
4300704
|
3608,4
|
|
|
3,8с
|
0,04
|
0,018
|
2,29
|
0,1
|
|
|
0,9с
|
0,73
|
0,095
|
23807
|
204,7
|
|
|
22,8с
|
0,004
|
0,003
|
0,18
|
0,008
|
|
|
17,2с
|
0,02
|
0,004
|
1,41
|
0,063
|
|
|
2с
|
0,4
|
0,035
|
17982
|
167,5
|
|
|
0,8с
|
0,25
|
0,088
|
5328
|
70,2
|
|
Для опыта 1 определяем значения Ar и Re
Режим турбулентный т.к.
м/с
Определяем среднюю скорость осаждения по пройденному пути и времени
где =0,07м – расстояния осаждения шариков
- время осаждения (берем из опыта)
м/с
Для 2 опыта
Режим ламинарный
м/с
Определяем среднюю скорость осаждения по пройденному пути и времени
м/с
Для опыта 3
Режим переходный так как
м/с
Определяем среднюю скорость осаждения по пройденному пути и времени
м/с
Для опыта 4
Режим ламинарный
м/с
Определяем среднюю скорость осаждения по пройденному пути и времени
м/с
Для опыта 5
Режим ламинарный
м/с
Определяем среднюю скорость осаждения по пройденному пути и времени
м/с
Для опыта 6
Режим переходный так как
м/с
Определяем среднюю скорость осаждения по пройденному пути и времени
м/с
Для опыта 7
Режим переходный так как
м/с
Определяем среднюю скорость осаждения по пройденному пути и времени
м/с
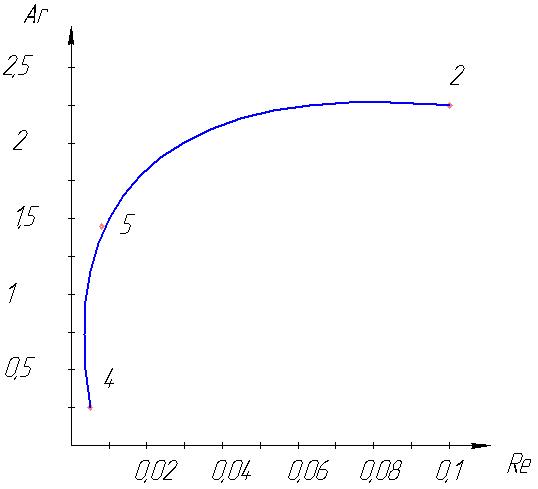
Рисунок 2 - график зависимости Re=f(Ar) для глицерина для опытов (2, 4, 5)
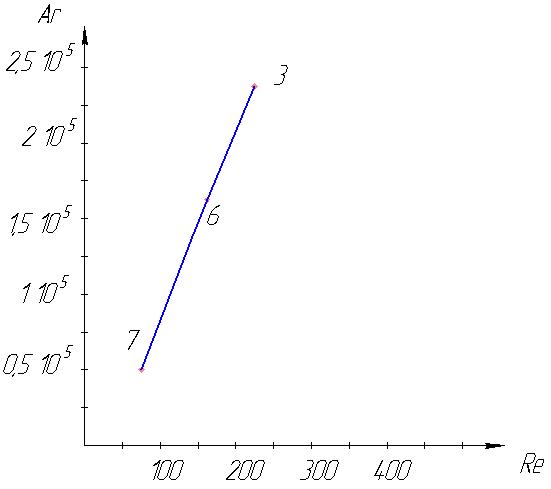
Рисунок 3 - график зависимости Re=f(Ar) для трансформаторного масла (3, 6, 7)
Вывод: как видно из проведенных опытов скорости расчетные совпадают с практическими скоростями при проведении лабораторной работы, что подтверждает правильность использования формул при расчете скорости осаждения. Исключение составляет первый и седьмой опыт, это можно объяснить сложностью измерения времени осаждения так как время осаждения занимает меньше 1 секунды и наоборот в случае, где длительное время осаждения результаты опыта и расчетов совпадают.
1) Какой закон использован для записи уравнения (1.1.1)
Т – А – R = 0
Данное уравнение составлено на основании закона Ньютона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел.
2) Каким образом можно рассчитать скорость осаждения частиц по уравнению (1.1.4)?
Данное уравнении нельзя рассчитать из-за , необходимо преобразовать в критериальное
где зависит от критерия Рейнольдса
При ламинарном движении
3) Дайте характеристику режимов осаждения.
При малых числах Re жидкость плавно «обтекает» частицу без образования вихрей в кормовой части. Коэффициент сопротивления в этой области описывают уравнением
Эта зависимость хорошо аппроксимирует опытные данные при Re 1,85. В этой области сила сопротивления определяется, в основном, сопротивлением трения на поверхности частицы, и она пропорциональна первой степени скорости.
Вторая область – область переходного режима осаждения частицы – лежит в пределах изменения 1,85 < Re < 500. С увеличением числа Re в кормовой части осаждающейся частицы образуется зона, в которой существует замкнутое циркуляционное (вихревое) движение. Пока значения числа Re невелики, вихри устойчивы. При дальнейшем увеличении числа Re возрастает интенсивность движения вихрей, течение становится неустойчивым и начинает наблюдаться периодический срыв вихрей с поверхности частицы, которые образуют вихревой след. Если в начале переходной области основная часть сопротивления приходится на силы трения, то в конце основную часть составляет лобовое сопротивление.
Коэффициент сопротивления в этой области может быть рассчитан по уравнению
При увеличении числа Re выше 500 коэффициент сопротивления остается практически постоянным, не зависящим от числа Re (автомодельная область).
В этом случае в кормовой части частицы наблюдается регулярный отрыв вихрей. Такой режим осаждения называется турбулентным. Сила сопротивления в этом случае пропорциональна скорости во второй степени. Коэффициент сопротивления определяется, в основном, лобовым сопротивлением и составляет
4) Почему прибегают к критериальным уравнениям для расчета скорости осаждения?
Расчет скорости осаждения без использования критериального уравнения приведет к расчету методом последовательных приближений, оченть трудоемкий расчет.
5) Как определить коэффициент формы ?
Коэффициент формы представляет собой отношение поверхности частицы сферической формы fщ к поверхности частицы произвольной формы fч того же веса (объема). Для сферических частиц = 1 (так как fш = fч ), а для частиц любой иной формы < 1. С учетом коэффициента уравнения (1.1.13) – (1.1.15) имеют вид
6) Раскройте физический смысл критериев Re и Ar. От каких параметров и каким образом зависит скорость осаждения?
Критерий Рейнольдса является мерой отношения инерционных сил в жидкостном потоке (в данном случае при обтекании частицы) и вязкостных сил. При малых значениях Re наблюдается преобладание вязкостных сил над силами инерции и при обтекании частицы не происходит образования вихрей. При больших значениях Re, наоборот, преобладает действие инерционных сил. Возмущения жидкостного потока, возникшие при обтекании частицы, вязкостные силы погасить не могут, и за частицей возникает цепочка вихрей.
Критерий Архимеда является мерой отношения подъемной силы (являющейся разностью силы тяжести и архимедовой силы) к вязкостным силам. Таким образом, критериальные уравнения учитывают не только действующие на частицу в процессе осаждения силы (уравнение (1.1.2)), но и характерные особенности обтекания частицы жидкостью
7) Как изменится скорость осаждения сферической частицы в ламинарном режиме, если ее диаметр увеличится в 2 раза?
При ламинарном движении
Таким образом, при увеличении скорости осаждения сферической частицы раза.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. http://www.engineer-oht.ru/ - информационный ресурс по расчету ПАХТ
2. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу ПАХТ: Учебное пособие для вузов/ Под редакцией чл-корр. АН СССР П.Г. Романкова. -9-е изд., перераб. и доп. -Л.: Химия, 1981. - 560с., ил.
2. Лащинский А.А., Толчинский А.Р. Основы конструирования и расчёта химической аппаратуры. Л.: Машиностроение, 1970. - 752 с.
3. Основные процессы и аппараты химической технологии. Пособие по проектированию/ Под ред. Ю.И. Дытнерского. - М.: Химия, 1983-272с., ил.
4. Рамм В.М. Абсорбция газов. М. : Химия, 1975. 655 с.
5. Дытнерский Ю.И. Процессы и аппараты химической технологии: Учебник для вузов. Изд. 3-е. В 2-х кн.: Часть 2. Массообменные процессы и аппараты. М.: Химия, 2002. - 368с.: ил.
PAGE 11
Изучение кинетики гравитационного осаждения