Определение оптимального размера заказа
Содержание
1. Определение оптимального размера заказа…..………............................................................3
2. Практическая часть………………………………………..……………………………………9
Список использованной литературы……..…………………………………………………….15
1. Определение оптимального размера заказа
Оптимальный размер партии поставляемых товаров и, соответственно, оптимальная частота завоза зависят от следующих факторов:
- объем спроса (оборота);
- транспортно-заготовительные расходы;
- расходы на хранение запаса.
В качестве критерия оптимальности выбирают минимум суммы расходов транс-портно-заготовительных и на хранение.
Транспортно-заготовительные расходы при увеличении размера заказа уменьшаются, так как закупки и перевозки товаров осуществляются более крупными партиями и, следовательно, реже.
Расходы по хранению растут прямо пропорционально размеру заказа.
Для решения данной задачи необходимо минимизировать функцию, представляющую сумму расходов транспортно-заготовительных и на хранение, т. е. определить условия, при которых
Собщ = Схран + Странсп,
где Собщ – общие затраты на транспортировку и хранение; Схран – затраты на хранение запаса; Стсп – транспортно-заготовительные расходы.
Предположим, что за определенный период времени величина оборота составляет Q. Размер одной заказываемой партии S. Допустим, что новая партия завозится после того, как предыдущая полностью закончилась. Тогда средняя величина запаса составит S/2. Введем размер тарифа (М) за хранение товара. Он измеряется долей, которую составляют издержки по хранению за период Т в стоимости среднего запаса за тот же период.
Стоимость хранения товаров за период Т можно рассчитать по следующей формуле:
Схран = М (S/2).
Размер транспортно-заготовительных расходов за период Т определится по формуле:
Схран = K(Q/S)
где К – транспортно-заготовительные расходы, связанные с размещением и доставкой одного заказа; Q/S – количество заказов за период времени. Подставив данные в основную функцию, получим:
Со6щ = М (S/2) + K (Q/S).
Минимум Собщ имеется в точке, в которой ее первая производная по S равна нулю, а вторая производная больше нуля.
Найдем первую производную:
После того как сделан выбор системы пополнения запасов, необходимо количест-венно определить величину заказываемой партии, а также интервал времени, через который повторяется заказ.
Оптимальный размер партии поставляемых товаров и, соответственно, оптимальная частота завоза зависят от следующих факторов:
- объем спроса (оборота);
- расходы по доставке товаров;
- расходы по хранению запаса.
В качестве критерия оптимальности выбирают минимум совокупных расходов по доставке и хранению.
Рис. 1. Двухбункерная система контроля за состоянием запасов
И расходы по доставке и расходы по хранению зависят от размера заказа, однако характер зависимости каждой из этих статей расходов от объема заказа, разный. Расходы по доставке товаров при увеличении размера заказа очевидно уменьшаются, так как перевозки осуществляются более крупными партиями и, следовательно, реже.
График этой зависимости, имеющей форму гиперболы, представлен на рис. 1.
И расходы по доставке и расходы по хранению зависят от размера заказа, однако характер зависимости каждой из этих статей расходов от объема заказа, разный. Расходы по доставке товаров при увеличении размера заказа очевидно уменьшаются, так как перевозки осуществляются более крупными партиями и, следовательно, реже.
График этой зависимости, имеющей форму гиперболы, представлен на рис. 2.
Расходы по хранению растут прямо пропорционально размеру заказа. Эта зависи-мость графически представлена на рис. 3.
Рис. 2. Зависимость расходов на транспортировку от размера заказа
Рис. 3. Зависимость расходов на хранение запасов от размера заказа
Сложив оба графика, получим кривую, отражающую характер зависимости совокуп-ных издержек по транспортировке и хранению от размера заказываемой партии (рис. 4). Как видим, кривая суммарных издержек имеет точку минимума, в которой суммарные издержки будут минимальны. Абсцисса этой точки Sопт дает значение оптимального размера заказа.
Рис. 4. Зависимость суммарных расходов на хранение и транспортировку от размера заказа. Оптимальный размер заказа S опт
Таким образом, задача определения оптимального размера заказа, наряду с графи-ческим методом, может быть решена и аналитически. Для этого необходимо найти урав-нение суммарной кривой, продифференцировать его и приравнять вторую производную к нулю.
В результате получим формулу, известную в теории управления запасами, как формулу Уилсона, позволяющую рассчитать оптимальный размер заказа:
где Sопт - оптимальный размер заказываемой партии;
О - величина оборота;
Ст - издержки, связанные с доставкой;
Сх - издержки, связанные с хранением.
Полученная формула, позволяющая рассчитать оптимальный размер заказа, в теории управления запасами известна как формула Уилсона.
Задача определения оптимального размера заказа может быть решена графическим методом и аналитическим. Рассмотрим аналитический метод.
«Для этого необходимо минимизировать функцию, представляющую сумму транс-портно-заготовительных расходов и расходов на хранение от размера заказа, т.е. определить условия, при которых:
С общ. = С хран. + трансп. Min
где, С общ. - общие затраты на транспортировку и хранение запаса;
С хран. - затраты на хранение запаса;
С трансп. - транспортно - заготовительные расходы.
Предположим, что за определенный период времени величина оборота составляет Q. Размер одной заказываемой и доставляемой партии S. Допустим, что новая партия заво-зится после того, как предыдущая полностью закончилась. Тогда средняя величина запаса составит S/2.
Введем размер тарифа М за хранение запаса. М измеряется долей, которую состав-ляют издержки по хранению за период Т в стоимости среднего запаса за этот же период.
Например, если М = 0,1, то это означает, что издержки по хранению запаса за период составили 10 % от стоимости среднего запаса за этот же период. Можно сказать также, что издержки по хранению единицы товара в течение периода составили 10 5 от ее стоимости.
Теперь можно рассчитать, во что обойдется хранение товаров за период Т:
С хран. = М х S/2
Размер транспортно - заготовительных расходов за период Т определится умноже-нием количества заказов за этот период на величину расходов, связанных с размещением и доставкой одного заказа.
С трансп. = К х Q/S
где К - транспортно - заготовительные расходы, связанные с размещением и достав-кой одного заказа; Q/S - количество завозов за период времени.
Выполнив ряд преобразований, найдем оптимальный размер единовременно доставляемой партии (S опт.), при котором величина суммарных затрат на хранение и завоз будет минимальной.
С общ. = М х S/2 + К х Q/S
Далее находим значение S, обращающее производную целевой функции в ноль, откуда выводится формула, позволяющая рассчитать оптимальный размер заказа, в теории управления запасами известная как формула Уилсона.
Рассмотрим пример расчета оптимального размера заказываемой партии. В качестве исходных данных примем следующие величины.
Стоимость единицы товара - 40 руб. (0,04 тыс. руб.).
Месячный оборот склада по данной товарной позиции:
Q = 500 единиц/мес. или Q = 20 тыс. руб./мес.
Доля затрат на хранение товара составляет 10 % от его стоимости, т.е. М = 0,1.
Транспортно - заготовительные расходы, связанные с размещением и доставкой одно-го заказа: К = 0,25 тыс. руб.
Тогда оптимальный размер завозимой партии составит:
Очевидно, что товар в течение месяца целесообразно завозить дважды:
20 тыс. руб. / 10 тыс. руб. = 2 раза.
В этом случае транспортно - заготовительные расходы и расходы по хранению:
С общ. = 0,1 10/2 + 0,25 20/10 = 1 тыс. руб.
Игнорирование полученных результатов приведет к завышенным расходам.
Ошибка в определении объема заказываемой партии на 20% в нашем случае увеличит месячные расходы предприятия на транспортировку и хранение на 2%. Это соизмеримо со ставкой депозитного вклада.
Другими словами, названная ошибка равносильна недопустимому поведению финан-систа, продержавшего без движения деньги в течение месяца и не давшего им «поработать» на депозитном вкладе».
Точка возобновления заказа определяется по формуле:
Тз = Рз х Тц + Зр
где, Рз - средний расход товара в расчете на единицу продолжительности заказа;
Тц - продолжительность цикла заказа (временной интервал между размещением заказа и его получением);
Зр - размер резервного (гарантийного) запаса.
Рассмотрим пример расчета точки возобновления заказа.
Предприятие закупает у поставщика хлопчатобумажную ткань. Годовой объем спроса ткани составляет 8 200 м. Принимаем, что годовой спрос равен объему закупок. На предприятии ткань расходуется равномерно, и требуется резервный запас ткани, равный 150 м. (Примем в расчете, что в году 50 недель).
Средний расход ткани на единицу продолжительности заказа составит:
Рз = 8 200 м. / 50 недель = 164 м.
Точка возобнавления заказа будет равна:
Тз = 164 м. Х 1 нед. + 150 м. = 314 м.
Это означает, что когда уровень запаса ткани на складе достигает 314 м., то следует сделать очередной заказ поставщику.
Стоит отметить, что у многих предприятий есть доступная и очень важная инфор-мация, которая может быть использована при контроле ТМЗ. Группировки материальных затрат должны проводиться для всех видов ТМЗ в целях выявления среди них наиболее значимых.
В результате ранжирования по стоимости отдельных видов сырья и материалов среди них может быть выделена конкретная группа, контроль за состоянием которой имеет перво-очередное значение для управления оборотными средствами предприятия. Для наиболее значимых и дорогостоящих видов сырья целесообразно определить наиболее рациональный размер заказа и задать величину резервного (страхового) запаса.
Необходимо сопоставить экономию, которую может получить предприятие за счет оптимального размера заказа, с дополнительными транспортными затратами, которые возникают при реализации этого предложения.
Например, ежедневная поставка сырья и материалов может потребовать содержания значительного парка грузовых автомашин. Транспортно-эксплуатационные издержки могут превысить экономию, которую дает оптимизация размеров запасов.
При этом возможно создание консигнационного склада используемого сырья поблизости от предприятия.
В управлении запасами продукции на складе могут быть использованы такие же приемы, как и при управлении ТМЦ, в частности метод АВС.
При помощи представленных выше методик, а также на основе анализа запросов потребителей и производственных возможностей может быть определен наиболее рацио-нальный график поступления готовой продукции на склад и размер страхового запаса.
Затраты на хранение, учет и другие расходы, связанные с обеспечением ритмичности поставки произведенной продукции, необходимо сопоставить с преимуществами, которые дает бесперебойное снабжение традиционных покупателей и выполнение периодических срочных заказов.
2. Практическая часть
Задача 1
Постройте кривую АВС-анализа для следующего множества:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Вклад объекта |
30 |
100 |
200 |
350 |
50 |
120 |
80 |
240 |
60 |
70 |
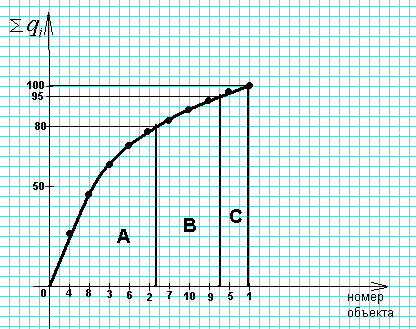
Упорядочим в таблице все объекты по доле объекта в общем вкладе, при этом рассчитаем долю объекта нарастающим итогом. Разделим все материалы на группы следующим образом: объекты относятся к группе А, пока удельный вес нарастающим итогом не достигнет 80%; в группе В – 95%, остальные объекты отнесем к группе С.
Анализ АВС
Первичный список |
Упорядоченный список |
Группа |
|||||
|
№ объекта |
Вклад объекта |
Доля объекта в общем вкладе, % |
№ пози-ции |
Вклад объекта |
Доля объекта в общем вкладе, % |
Доля нараста-ющим итогом, % |
|
|
|
30 |
2,31 |
4. |
350 |
26,92 |
26,92 |
А |
|
|
100 |
7,69 |
8. |
240 |
18,46 |
45,38 |
|
|
|
200 |
15,38 |
3. |
200 |
15,38 |
60,77 |
|
|
|
350 |
26,92 |
6. |
120 |
9,23 |
70,00 |
|
|
|
50 |
3,85 |
2. |
100 |
7,69 |
77,69 |
|
|
|
120 |
9,23 |
7. |
80 |
6,15 |
83,85 |
В |
|
|
80 |
6,15 |
10. |
70 |
5,38 |
89,23 |
|
|
|
240 |
18,46 |
9. |
60 |
4,62 |
93,85 |
|
|
|
60 |
4,62 |
5. |
50 |
3,85 |
97,69 |
С |
|
|
70 |
5,38 |
1. |
30 |
2,31 |
100,00 |
Задача 2
Годовой спрос D единиц, стоимость подачи заказа рублей/заказ, закупочная цена, C рублей/единицу, годовая стоимость хранения одной единицы составляет a % ее закупочной цены. Время доставки 6 дней, в году 300 рабочих дней. Найти оптимальный уровень заказа, издержки, уровень повторного заказа, число циклов за год, расстояние между циклами. Сравнить две модели: основную и с дефицитом (заявки выполняются).
|
D |
C |
a |
|||
|
800 |
75 |
65 |
25 |
20 |
17 |
Решение:
- Основная модель управления запасами.
Оптимальный уровень заказа:
Таким образом, в течение каждого цикла заказа необходимо подавать заказ на 86 единиц продукции.
Годовая общая переменная стоимость заказов определяется в соответствии с формулой:
Объём продажи за 6 дней доставки составит:
Уровень повторного заказа 16 единиц.
То есть, подача нового запаса производится, когда уровень запасов равен 16 единиц.
Число циклов за год
Расстояние между циклами
2) Рассмотрим модель с дефицитом (заявки выполняются).
Плановый дефицит
Оптимальный уровень заказа:
В данной ситуации необходимо подавать заказы размером в 116 единиц.
Максимальный размер дефицита:
Общая переменная стоимость за год определяется следующим образом:
По сравнению с основной моделью величина экономии составляет
1396,42-1073,26=323,16 рублей в год.
Таким образом, если использовать модель планирования дефицита, то можно достичь экономии общей переменной стоимости запасов, равной 323,16 рублей в год.
Задача 3
В таблице приведены координаты восьми потребителей, указан месячный грузообо-рот каждого из них. Найти координаты снабжающего центра.
|
№ потребителя |
Координата Х |
Координата У |
Грузооборот |
|
1 |
19 |
12 |
15 |
|
2 |
13 |
17 |
10 |
|
3 |
18 |
24 |
10 |
|
4 |
17 |
17 |
5 |
|
5 |
21 |
15 |
10 |
|
6 |
25 |
12 |
5 |
|
7 |
23 |
19 |
25 |
|
8 |
29 |
17 |
20 |
Задачу выбора места расположения снабжающего центра решим для распре-делительной системы, включающей один снабжающий центр. Основным фактором, влияю-щим на выбор места расположения снабжающего центра, является размер грузооборота каждого из восьми потребителей. Минимизировать затраты можно, разместив снабжающий центр в окрестностях центра тяжести грузопотоков.
Координаты центра тяжести грузовых потоков (Хцентр, Yцентр), т.е. - точки, в которой может быть размещен распределительный склад, определятся по формулам:
где Гi г грузооборот i-гo потребителя;
Xi, Yj г координаты i-гo потребителя.
Точка территории, обеспечивающая минимум транспортной работы по доставке, в общем случае не совпадает с найденным центром тяжести, но, как правило, находится где-то недалеко. Подобрать приемлемое место для снабжающего центра позволит последующий анализ возможных мест размещения в окрестностях найденного центра тяжести. При этом необходимо оценить транспортную доступность местности, размер и конфигурацию возможного участка, а также планы местных властей в отношении намеченной территории.
Выполним чертеж к заданию.
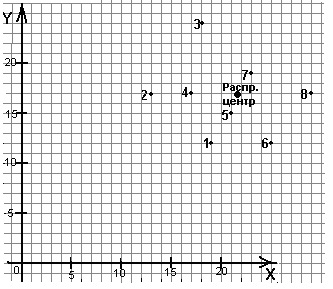
Найдем координаты центра тяжести грузовых потоков.
Xцентр = 21,7
Yцентр = 17
Нанесем точку с такими координатами на чертеж.
Задача 4
Осуществить выбор поставщика, если известна динамика цен на поставляемые товары. Данные приведены в таблице.
Динамика цен на поставляемые товары
|
Поставщик |
Квартал |
Товар |
Объем поставки |
Цена за единицу |
|
№1 |
1-й 1-й 1-й |
А В С |
2009 1009 1509 |
19 14 17 |
|
№1 |
2-й 2-й 2-й |
А В С |
1209 1209 1609 |
20 15 19 |
|
№2 |
1-й 1-й 1-й |
А В С |
9009 6009 8009 |
18 13 21 |
|
№2 |
2-й 2-й 2-й |
А В С |
7009 10009 10009 |
19 15 22 |
Темп роста цены на i-ю разновидность товара у j-го поставщика
где Cij2 – цена i-го товара у j-го поставщика во втором квартале;
Cij1 – цена i-го товара у j-го поставщика в первом квартале.
В условиях данной задачи для первого поставщика по товарам А, В и С соответственно
Для второго поставщика по товарам А, В и С соответственно
Доля i-го товара в общем объеме поставок j-го поставщика
где Sij – сумма, на которую поставлен товар i-го вида j-м поставщиком;
Gij – объем поставки товара i-го вида j-м поставщиком;
Sij – сумма, на которую поставлены все товары j-м поставщиком.
Доля товара вида А в общем объеме поставок первого поставщика
Доля товара вида В в общем объеме поставок первого поставщика
Доля товара вида С в общем объеме поставок первого поставщика
Доля товара вида А в общем объеме поставок второго поставщика
Доля товара вида В в общем объеме поставок второго поставщика
Доля товара вида С в общем объеме поставок второго поставщика
Средневзвешенный темп роста цен у j-го поставщика
Тогда средневзвешенный темп роста цен у первого поставщика.
Средневзвешенный темп роста цен у второго поставщика.
Темп роста цены отражает увеличение негативной характеристики поставщика, поэтому предпочтение очевидно следует отдать тому из них, чей рейтинг ниже. В данном примере предпочтение следует отдать поставщику №1.
Список использованной литературы
1. Аникин, Б.А. Логистика: Учебник [Текст] / Б.А. Аникин. М.: ИНФРА – М, 2008.
2. Гаджинский, А.М. Логистика: Учебник [Текст] / А.М. Гаджинский – М.: «Дашков и Ко», 2008. – 484 с.
3. Неруш, Ю.М. Логистика: Учебник [Текст] / Ю.М. Неруш. – М.: Проспект, ТК Велби, 2008. – 520 с.
4. Практикум по логистике / Под ред. Б.А. Аникина. – М.: ИНФРА – М, 2007. – 280 с.
5. Чудаков, А.Д. Логистика [Текст]: Учебник / А.Д. Чудаков. – М.: Издательство РДЛ, 2003. – 480 с.
PAGE \* MERGEFORMAT 2
Определение оптимального размера заказа