Амплитудно-импульсная модуляция и ее свойства

Реферат

Содержание

1 Разновидности АИМ. Спектральные характеристики

2 Интегральные характеристики напряжения с АИМ-3

3 Улучшение спектрального состава напряжения с АИМ-3

4 Применение функций Уолша для реализации сложных законов модуляции

Литература

1 Разновидности АИМ. Спектральные характеристики

В настоящее время сигналы с АИМ делятся на пять родов.

В АИМ первого рода выборка производится в тактовые моменты времени, вершина импульсов постоянна (рис.1). В АИМ второго рода параметры импульса определяются текущим значением функции . В АИМ третьего рода выборка производится в некоторый момент времени внутри импульса. В АИМ четвертого рода выборка определяется функционалом от функции , определенном на интервале импульса. В АИМ пятого рода выборка определяется функционалом на тактовом интервале. На практике на наибольшее распространение получила АИМ первого, второго и третьего родов.

По аналогии с ШИМ АИМ любого рода могут делиться на ОНМ, ОРМ и ДРМ.

Рассмотрим спектральную характеристику на примере с АИМ-2 ОНМ. Зададим закон модуляции в виде:

. (1)

Тогда модулированная последовательность импульсов будет иметь вид:

, (2)

где - э.д.с. немодулированной последовательности импульсов.

Диаграмма формирования сигнала с АИМ

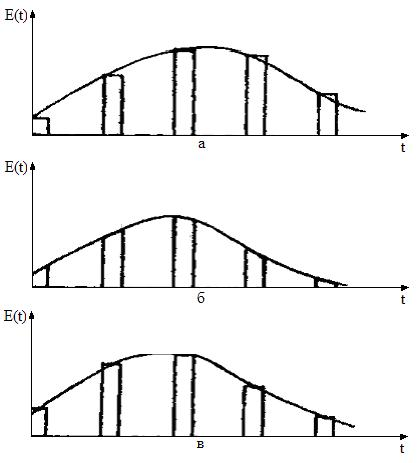
а) АИМ-1; б) АИМ-2; в) АИМ-3;

Рис.1

Ранее было получено:

. (3)

Тогда

. (4)

(5)

где - индекс модуляции;

Проведем анализ полученного выражения:

в сигнале есть постоянная составляющая (рис.2);
есть составляющая с частотой сигнала ;
сохранена составляющая и арочный закон ее изменения;
каждая составляющая окружена парой боковых гармоник, амплитуды которых одинаковы и пропорциональны ;
при амплитуды боковых гармоник в два раза меньше, чем амплитуда с частотой .

Спектр сигнала с АИМ-2(ОНМ)

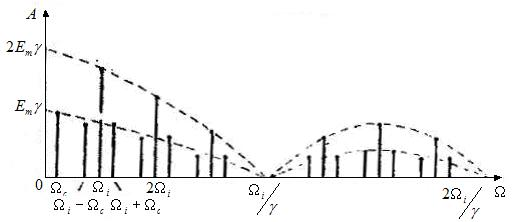
Рис.2

Рассмотрим второй пример для АИМ-2 ОРМ. Зададим закон модуляции в виде:

. (6)

Тогда выражение, описывающее спектр этого сигнала, примет следующий вид:

. (7)

По этому выражению можно сделать следующие выводы:

в сигнале отсутствует постоянная составляющая;
есть составляющая с частотой ;
отсутствует составляющая с частотой ;
боковые гармоники имеют равную амплитуду и пропорциональны (рис.3).

Спектр сигнала с АИМ-2 (ОРМ)

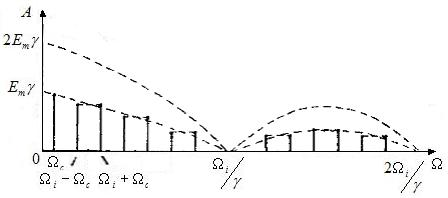
Рис.3

Полученные спектры АИМ-2 при ОНМ и ОРМ наглядно иллюстрируют сущность теоремы Котельникова В.А. Из ряда диаграмм (см.рис.2 и 3) видно, что между гармониками и должно быть расстояние, иначе они сольются, т.е. необходимо получить или . Спектр с АИМ-1 дадим без вывода формулы. Главное отличие АИМ-1 от АИМ-2 при ОНМ в том, что амплитуды боковых гармоник неодинаковы и определяются огибающей спектральных линий (рис.4).

Спектр сигнала с АИМ-1 (ОНМ)

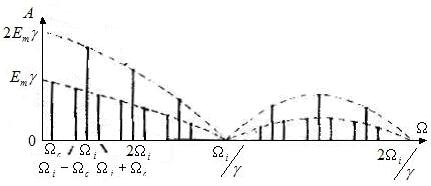
Рис.4

В качестве третьего примера рассмотрим АИМ-3, заданную по синусоидальному закону.

Зададим закон модуляции (рис.5):

где - амплитуда m-ого импульса;

- количество интервалов разбиения на полупериоде, q = 2i ;

- момент выборки (в пределах такта).

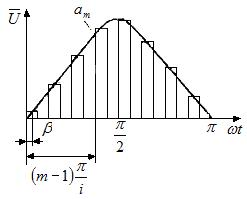
Рис.5

В представленном на рис.5 случае I – целое число. Выражение, описывающее спектр сигнала с АИМ-3, имеет вид:

, (8)

где k – номер гармоники.

Строго доказывается, что только при

, (9)

где S = 0,1,2,… - текущий индекс.

Умножим левую и правую части выражения (9) на :

. (10)

С учетом того, что и , получим:

, (11)

т.е. номера гармоник те же, что и в спектре у АИМ-2 ОРМ.

Рассматривая выражение (8), сделаем следующие выводы:

каждая боковая гармоника имеет свою амплитуду;
нет гармоник на частоте квантования и кратных ей;
амплитуды гармоник зависят от и , но не зависят от , т.е. от правила выбора амплитуд.

2 Интегральные характеристики напряжения с АИМ-3

Действующее значение напряжение при АИМ-3 определяется только длительностью импульсов, и не зависит от их количества и правила выбора амплитуд. При действующее значение напряжения с АИМ равно действующему значению синусоидальной функции построения. Выражение для определения действующего значения:

. (12)

Для определения коэффициента гармоник вспомним, что

, (13)

и подставляя (8), (12) в (13), получим:

, (14)

т.е. при АИМ определяется только количеством и шириной импульсов. Количественная оценка дается рис.6.

График зависимости от величины при различных

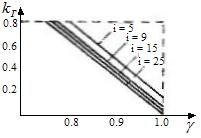
Рис.6

3 Улучшение спектрального состава напряжения с АИМ-3.

При прочих равных условиях под этим понимается исключение как можно большего количества гармоник, близлежащих к основной, т.к. в этом случае существенно облегчается фильтрация. С этих позиций наилучшими свойствами обладает напряжение при и , но надо помнить, что увеличение существенно усложняет схему и ведет к увеличению потерь. Поэтому возникает вопрос об оптимальном ступенчатом напряжении.

Ступенчатая кривая с числом ступеней «n» может быть представлена совокупностью прямоугольников (рис.7) с координатами ;.

Основываясь на многочисленных расчетах в институте электродинамики АН УССР получены аппроксимирующие выражения, которые позволяют с большей точностью посчитать и :

; (15)

. (16)

Для того, чтобы определить необходимое количество ступеней «n», которые обеспечивают заданный , этим же институтом предложена формула:

, (17)

где представляется в процентах.

Вариант формирования ступенчатого напряжения

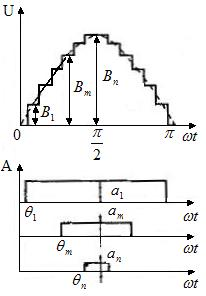
Рис.7

4 Применение функций Уолша для реализации сложных законов модуляции

Функции Уолша представляют собой специально подобранную систему прямоугольник импульсов, удовлетворяющих условию ортогональности, согласно которому

(18)

(вспомните свойство ортогональности рядов Фурье). Это система функций найдена в 1900г. Барретом и описана математически в 1923г. Уолшем. Система функций Уолша сроится из ортогональных элементов , , . Аналогично тому как элементы рядов Фурье , могут быть заменены функцией , так и функции Sal и Cal могут быть заменены функцией Уолша (Wal). При этом действует правило:

для четных функций – ;

для нечетных функций – .

Умножение двух функций Уолша дает третью функцию Уолша, т.е.

где .

Для нахождения «r», «h» и «k» представляются в виде двоичных чисел и складываются без переноса единицы в старший разряд. Например: ,

т.к.

На рис.8 представлены временные диаграммы первых восьми элементов Уолша.

Характерно, что четные элементы не имеют особенностей и представляют собой периодические последовательности разнополярных прямоугольных импульсов разной частоты. Эта система функций носит название функций Родемахера.

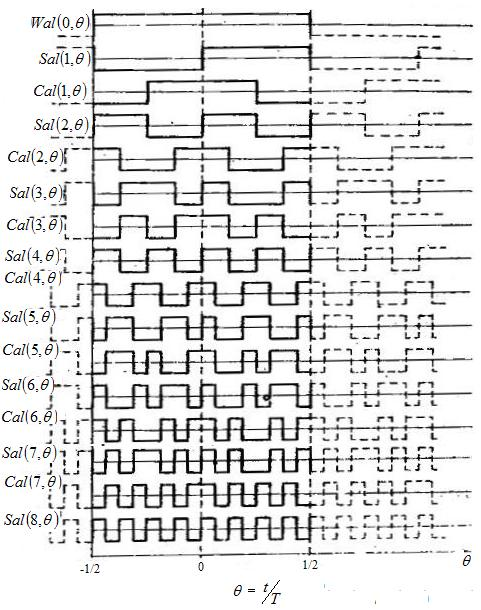
Рис.8

Чтобы функции Уолша использовать для реализации законов модуляции, производится разложение сложной импульсной кривой в ряд Уолша. При этом как и для любой системы ортогональных функций можно записать:

, (19)

Для того, чтобы найти формулы коэффициентов разложения, необходимо воспользоваться свойством ортогональности функций Уолша. Умножим, например, левую и правую часть (19) на и проинтегрируем:

. (20)

В силу свойства ортогональности, заданного выражением (18), в правом интеграле останется только , а все остальные слагаемые будут равны нулю. Тогда

Аналогично можно получить:

и т.д.

Поскольку сложная импульсная функция известна, то по указанным формулам мы найдем амплитуды функций Уолша. Заметим, что для сложных импульсных сигналов ряды Уолша сходятся гораздо быстрее, чем ряды Фурье. Покажем это на примере по рис.9.

Диаграмма сигнала с АИМ

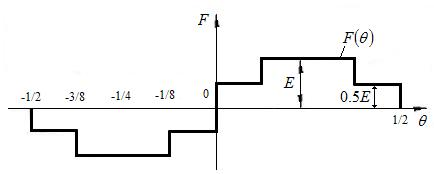
Рис.9

;

Амплитуды всех остальных гармоник равны нулю.

Таким образом, получили:

Точно представление кривой (см.рис.9) достигнуто двумя гармониками Уолша, в то время как при разложении этой кривой в ряд Фурье количество гармоник равно бесконечности.

Литература

Ямпурин Н.П.: Электроника. - М.: Академия, 2011

Воронков Э.Н.: Твердотельная электроника. - М.: Академия, 2010

Гуртов В.А.: Зарядоперенос в структурах с диэлектрическими слоями. - Петрозаводск: ПетрГУ, 2010

Дрейзин В.Э.: Управление качеством электронных средств. - М.: Академия, 2010

Институт СВЧ полупроводниковой электроники РАН: Наногетероструктуры в сверхвысокочастотной полупроводниковой электронике. - М.: Техносфера, 2010

Прянишников В.А.: Электроника. - СПб.: КОРОНА-Век, 2010

рец.: С.П. Вихров, О.А. Изумрудов: Твердотельная электроника. - М.: Академия, 2010

Ямпурин Н.П.: Основы надежности электронных средств. - М.: Академия, 2010

Под ред. А.А. Орликовского ; Рец.: А.Ф. Александров, А.А. Горбацевич: Наноэлектроника. - М.: МГТУ им. Н.Э. Баумана, 2009

Под ред.: А.А. Кураева, Д.И. Трубецкого ; А.В. Аксенчик и др.: Методы нелинейной динамики и теории хаоса в задачах электроники сверхвысоких частот. - М.: ФИЗМАТЛИТ, 2009

Шишкин Г.Г.: Электроника. - М.: Дрофа, 2009

А.Н. Диденко и др. ; Под ред. И.Б. Фёдорова: Вакуумная электроника. - М.: МГТУ им. Н.Э. Баумана, 2008

Лебедев А.И.: Физика полупроводниковых приборов. - М.: Физматлит, 2008

Шматько А.А.: Электронно-волновые системы миллиметрвого диапазона. - Харьков: ХНУ им. В.Н. Каразина, 2008

Московский гос. ин-т стали и сплавов, Саратовский гос. ун-т им. Н.Г. Чернышевского ; под ред. Л.В. Кожитова: Оборудование, технологии и аналитические системы для материаловедения, микро- и наноэлектроники. - М.: МИСиС, 2007

Федеральное агентство по образованию, Московский гос. ин-т стали и сплавов (Технологический ун-т), Саратовский гос. ун-т им. Н.Г. Чернышевского ; под ред. Л.В. Кожитова ; авт-сост.: В.П. Менушенков и др.: Оборудование, технологии и аналитические системы для материаловедения, микро- и наноэлектроники. - М.: МИСиС, 2007

Амплитудно-импульсная модуляция и ее свойства