Єконометрические модели производственной функции и ее анализ в среде Excel
Содержание
Введение……………………………………………………………………..….…2
1 Виды производственных функций………………………………………….….3
2. Статистический анализ по выборке…………………………………………...5
2.1 Определение числовых характеристик выборки с помощью инструмента «Описательная статистика»……………………………………………………....5
2.2 Выполнение корреляционного анализа однофакторной, двухфакторных линейной и мультипликативной производственных функций с помощью функции «Корреляция» из пакета «Анализ данных»…………………………..9
2.3 Выполнение дисперсионного анализа производственных функций процедурой двухвыборочногоF-теста для дисперсий на двухстороннем уровне значимости =0,025………………………………………………..……15
3. Проведение регрессионного анализа исходных данных и выбор аналитической формы записи производственной функции……………….….20
3.1 Выполнение расчетов однофакторной степенной зависимости с использованием статистической функции «Линейн» и проведение статистического анализа………………………………………………….….….20
3.2 Построение модели множественной регрессии для двухфакторных линейной и мультипликативной производственных функций с помощью инструмента «Регрессия» пакета «Анализ данных» и проведение статистического анализа………………………………………...........................22
4 Выполнение экономического анализа в выбранной регрессионной модели на основе коэффициентов эластичности Эj.........................................................29
Заключение…………………………………………………………………….…30
Список использованной литературы……………………………………….…..31
Введение
Производственная функция занимает важное место в экономической теории как модель, непосредственно относящаяся не к процессу обмена, а к процессу производства, который связан с потреблением различных ресурсов (сырье, энергия, труд, оборудование и т.д.).
Построение производственных функции, то есть выявление фактических технологических взаимосвязей в производстве, является одной из важнейших эконометрических задач. Экономический анализ производства исследует отношение между затратами и выпуском. Это отношение и определяет максимальный объём выпуска при определенных комбинациях факторов производства.
Актуальность данной темы состоит в том, что с помощью производственных функций можно планировать производство, составлять экономический анализ, прогнозировать и моделировать макро- и микроэкономику.
Цель данной работы – научиться строить эконометрические модели производственной функции и анализировать ее в среде Excel.
Основные задачи данной курсовой работы:
- Выполнение статистического анализа по выборке
- Проведение регрессионного анализа исходных данных и выбор аналитической формы записи производственной функции
- Выполнение экономического анализа в выбранной регрессионной модели на основе коэффициентов эластичности Эj
1 Виды производственных функций
Производственной функцией называется зависимость между объемами затрачиваемых в производстве ресурсов (независимые переменные x1, x2, .., xn, число которых n равно числу ресурсов) и объемом выпускаемой продукции Y.
Основными производственными ресурсами являются труд L и капитал K.
В общем виде функция может быть записана в виде:
где Y - выпуск продукции;
- факторы, определяющие величину выпуска продукции (затраты труда, материалов и т.д.).
Зависимость между затратами различных видов ресурсов и объемом выпуска продукции должна быть выражена уравнением множественной регрессии.
С помощью производственных функций решаются задачи:
· оценки отдачи ресурсов в производственном процессе;
· прогнозирования экономического роста;
· разработки вариантов плана развития производства;
· оптимизации функционирования хозяйственной единицы при условии заданного критерия и ограничений по ресурсам.
В микроэкономике используется большое количество самых разнообразных функций производства, но чаще всего — двухфакторные функции, которые легче анализировать в силу их графического представления.
Среди двухфакторных функций наибольшую известность получила функция Кобба-Дугласа, имеющая вид:
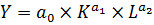
где а0, а1, а2 - параметры ПФ.
Часто а1 и а2 таковы, что а1+а2=1;
Линейная двухфакторная производственная функция относится к классу аддитивных ПФ и имеет вид:
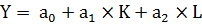
где а0 = 0.
Однофакторная степенная производственная функция
Если сумма показателей степени в ПФКД
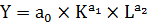
равна 1 (a1+a2 = 1), то ее можно записать в несколько другой форме :
,
где - производительность труда, - капиталовооруженность труда.
2. Статистический анализ по выборке
2.1 Определение числовых характеристик выборки с помощью инструмента «Описательная статистика»
Имеются следующие данные:
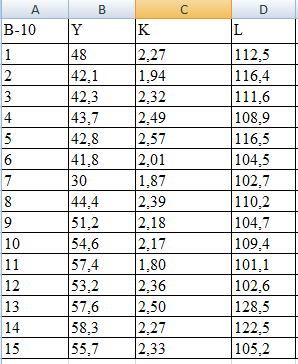
Выполняем линеаризацию переменных для функции Кобба-Дугласа и степенной модели путем логарифмирования обеих частей уравнения.
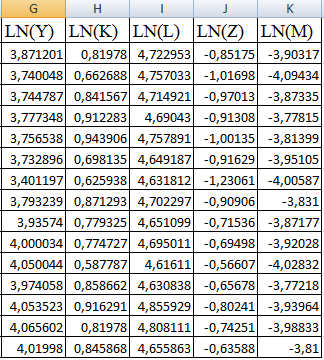
Чтобы определить числовые характеристики полученных выборок, воспользуемся инструментом анализа «Описательная статистика» программы Excel:
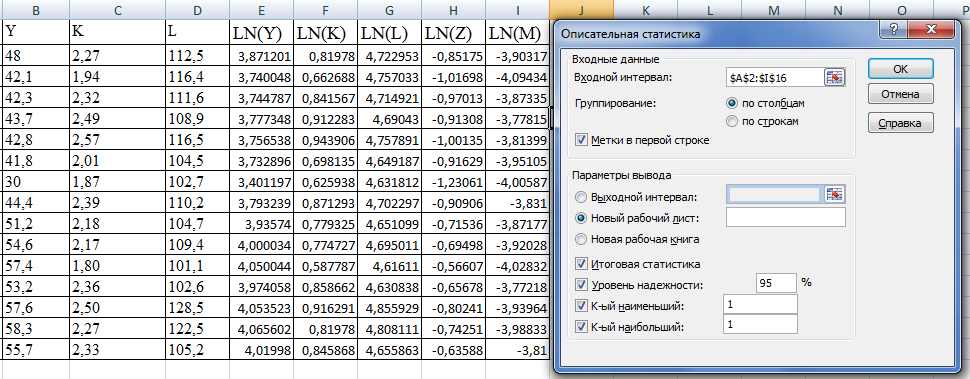
Это средство анализа служит для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
К показателям описательной статистики относятся: среднее, стандартная ошибка, медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет.
Среднее значение — среднее арифметическое, которое вычисляется путем суммирования набора чисел, а затем деления суммы на число, равное количеству этих чисел.
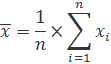
xi—варианты;
n-частоты вариант.
Медиана — число, которое является серединой ряда чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Медиана для упорядоченной, нечетной выборки рассчитывается по формуле:
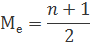
Мода — наиболее часто повторяющееся число в группе.
Минимум и максимум – это минимальное и максимальное значения выборки.
Асимметрия является мерой несимметричности распределения. Если этот коэффициент значительно отличается от 0, распределение является асимметричным, т.е. несимметричным.
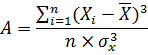
А-показатель асимметрии;
Xi – фактическое значение показателя;
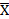- среднее значение показателя;
n – количество измерений;
x – среднеквадратическое отклонение.
Эксцесс измеряет остроту пика распределения. Коэффициент эксцесса равен нулю, если наблюдения подчиняются нормальному распределению.
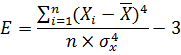
Е - показатель эксцесса.
Стандартное отклонение – это корень квадратный из дисперсии. Показывает абсолютное отклонение измеренных значений от среднеарифметического.
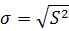
Дисперсия выборки - среднее арифметическое квадратов отклонений значений от их среднего.
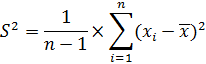
Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.
Стандартная ошибка оценивает меру ошибки рассчитан ного на основе сформированной выборки среднего значения и снижается при увеличении массива отобранных данных.
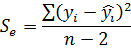
Где: - вариация переменной y, которая не объяснятся уравнением регрессии
Счет – объем выборки.
Коэффициент вариации - это отношение среднего квадратичного отклонения среднему значению, выраженное в процентах. Чем ближе он к 1, тем больше случайностей. Если значение рассчитанного V < 33%, то совокупность по рассчитанному признаку можно считать однородной.
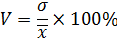
В результате указанных действий MicrosoftExcel осуществляет вывод таблицы описательных статистик:
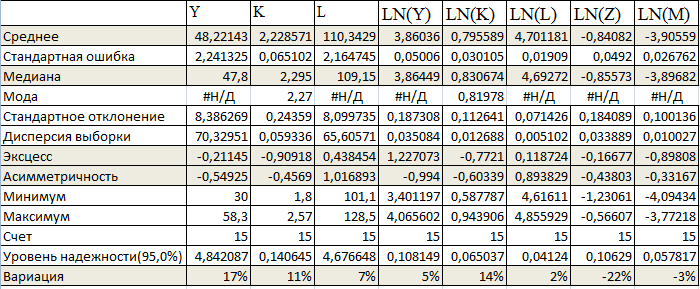
По данным таблицы можно сделать следующие заключения: среднее значение не сильно отличается от медианы, а значения эксцесса и ассиметричности близки к нулю, поэтому можно сказать о том, что распределение нормальное.
Значения вариации меньше 33%, значит, совокупность по рассчитанному признаку можно считать однородной.
2.2 Выполнение корреляционного анализа однофакторной, двухфакторных линейной и мультипликативной производственных функций с помощью функции «Корреляция» из пакета «Анализ данных»
Корреляционный анализ – это раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами.
Основной целью корреляционного анализа является уста новление характера влияния факторной переменной на ис следуемый показатель и определение тесноты их связи с тем, чтобы с достаточной степенью надежности строить модель развития исследуемого показателя.
Проведение корреляционно го анализа сводится к расчету коэффициентов парной корре ляции (R), значения которых помогут судить о характере и тес ноте связи между исследуемым показателем и каждой отоб ранной факторной переменной.
Коэффициенты парной корреляции используются для измерения силы линейных связей различных пар признаков из их множества. Для множества признаков получают матрицу коэффициентов парной корреляции. Вычисляем её инструментом «Корреляция» пакета «Анализ данных». Она симметрична относительно главной диагонали (ryk = rky, ryl = rly, rkl = rlk):
Матрица коэффициентов парной корреляции R линейной модели:
|
|
Y
|
K
|
L
|
|
Y
|
1
|
0,20471
|
0,242453
|
|
K
|
0,2047111
|
1
|
0,478371
|
|
L
|
0,2424532
|
0,47837
|
1
|
Матрица производственной функции Кобба-Дугласа:
|
|
LN(Y)
|
LN(K)
|
LN(L)
|
|
LN(Y)
|
1
|
0,25837
|
0,23581
|
|
LN(K)
|
0,258374
|
1
|
0,48469
|
|
LN(L)
|
0,235809
|
0,48469
|
1
|
Матрица степенной однофакторной модели:
|
|
LN(Z)
|
LN(M)
|
|
LN(Z)
|
1
|
0,19049
|
|
LN(M)
|
0,19049
|
1
|
Одной корреляционной матрицей нельзя полностью описать зависимости между величинами. В связи с этим в многомерном корреляционном анализе рассматриваются задачи:
1 Определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ; решается с помощью коэффициента множественной корреляции.
Квадрат коэффициента множественной корреляции называют выборочным множественным коэффициентом детерминации (R2); он показывает, какую долю вариации исследуемой величины Xj объясняет вариация остальных случайных величин.
2. Определение тесноты связи между двумя величинами при фиксировании или исключении влияния остальных величин; решается с помощью выборочного частного коэффициента корреляции.
Для модели парной регрессии коэффициент парной корреляции вычисляется функцией КОРРЕЛ, указав столбцы чисел – LN(Z) и LN(M).
Выборочный коэффициент множественной детерминации находим по формуле:
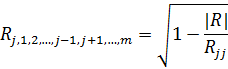
где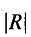 
-определитель матрицы коэффициентов парной корреляции R;
Rjj - алгебраическое дополнение элемента rjj той же матрицы R.
Для линейной двухфакторной модели вычисляем множественный коэффициент корреляции Y на K и Y на L (Y-1, K-2,L-3) по формуле:
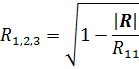
где - определитель матрицы R; R11 - алгебраическое дополнение первого диагонального элемента r11 той же матрицы R:
|
|
|
|
|
|
|
1
|
0,204711
|
0,242453
|
|
|R|=
|
0,2047111
|
1
|
0,478371
|
|
|
0,242453
|
0,478371
|
1
|
Определители матриц вычисляются с помощью функции МОПРЕД(массив).
Коэффициенты частной корреляции находим по формулам:
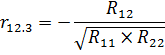
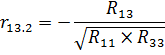
где R12, R13 - алгебраические дополнения элементов r12, r13 матрицы, а R22 и R33 -алгебраические дополнения второго и третьего диагональных элементов.
Коэффициент Пирсона характеризует тесноту связи изучаемых явлений и находится с помощью функции PEARSON.
Критерий Стьюдента определяет оценку значимости коэффициентов корреляции и рассчитывается по формуле:
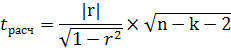
r – коэффициент корреляции
n – число измерений (пар наблюдений)
k=0 при парном коэффициенте корреляции
k=1 при частном коэффициенте корреляции
Рассчитанное значение критерия Стьюдента сравниваем с табличным:
tтабл(; n- k-2), где:
- уровень значимости;
n- k-2 - число степеней свободы.
Данное табличное значение рассчитывается с помощью:
СТЬЮДРАСПОБР(; n- k-2).
Если tрасч>tтабл, то полученное значение коэффициента корреляции признается значимым (т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
Все коэффициенты линейной функции и функции Кобба-Дугаласа объединяем в таблицу для того, чтобы сделать предварительные выводы:
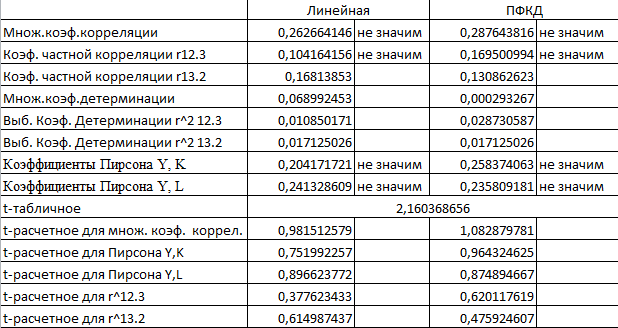
Мы можем сделать следующие заключения по результатам рассчитанных коэффициентов линейной модели:
Коэффициенты Пирсона небольшие по своей величине (Y,K =0,204), (Y,L=0,241). Мы можем сделать вывод, что между показателем результата Y и факторными показателями K и L, скорее всего, низкая степень линейной зависимости.
Множественный коэффициент корреляции R1,2,3 = можно оценить по шкале Чеддока: связь изучаемых явлений является слабой.
Значение r212.3=0,011 говорит о том, что включение в модель фактора "Производственные фонды" приводит к сокращению остаточной дисперсии на 1% от исходной величины.
Значение r213.2 =0,028 говорит о том, что включение в модель фактора "Затраты труда" приводит к сокращению остаточной дисперсии на 3% от исходной величины.
С помощью проведенного t-критерия Стьюдента множественной регрессии мы получили, что tрасч<tтабл, что говорит о статистической незначимости коэффициентов.
Мы можем сделать следующие заключения по результатам рассчитанных коэффициентов ПФКД:
Коэффициенты Пирсона небольшие по своей величине (Y,K =0,258), (Y,L=0,236). Мы можем сделать вывод, что между показателем результата Y и факторными показателями K и L, скорее всего, низкая степень линейной зависимости.
Множественный коэффициент корреляции R1,2,3 = можно оценить по шкале Чеддока: связь изучаемых явлений является слабой.
Значение r212.3=0,028 говорит о том, что включение в модель фактора "Производственные фонды" приводит к сокращению остаточной дисперсии на 3% от исходной величины.
Значение r213.2=0,017 говорит о том, что включение в модель фактора "Затраты труда" приводит к сокращению остаточной дисперсии на 2% от исходной величины.
С помощью проведенного t-критерия Стьюдента множественной регрессии мы получили, что tрасч<tтабл, что говорит о статистической незначимости коэффициентов.
Коэффициенты парной корреляции и парной детерминации степенной функции:
|
|
Степенная
|
|
Коэф. парной корреляции
|
0,1904891
|
не значим
|
|
Коэф парной детерминации
|
0,0362861
|
|
|
t табл
|
1,77093338
|
|
|
t расчет
|
0,69962889
|
|
Данные коэффициенты корреляции и детерминации показывают, что связь изучаемых явлений является слабой. Также мы получили, что tрасч<tтабл, что говорит о статистический незначимости коэффициентов.
2.3 Выполнение дисперсионного анализа производственных функций процедурой двухвыборочногоF-теста для дисперсий на двухстороннем уровне значимости =0,025
Целью дисперсионного анализа является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.
Задача дисперсионного анализа – установить, является ли фактор причиной изменчивости случайной величины.
Оценка влияния факторов на результирующий признак проводится двухвыборочнымF-тестом для дисперсии( «Анализ данных», ДвухвыборочныйF-тест для дисперсии). Он применяется для сравнения дисперсий двух генеральных совокупностей.
Результаты двухвыборочного F-теста линейной функции:
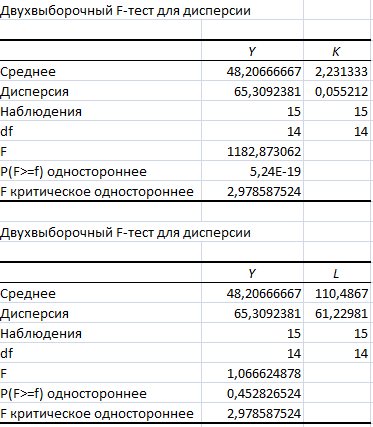
F критическое одностороннее соответствует двухстороннему критерию с 5% уровнем значимости, т.е. значение альфа, вводимое в диалоговом окне инструмента, равнялось 0,025.
Результаты двухвыборочного F-теста функции Кобба-Дугласа:
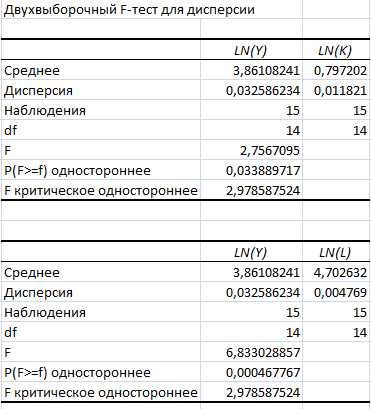
Результаты двухвыборочного F-теста степенной модели:
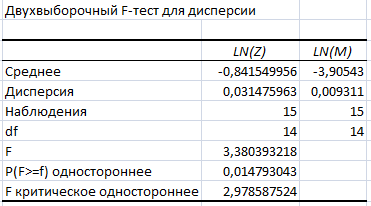
Результаты дисперсионного анализа линейной модели:
|
|
Y, K
|
Y, L
|
|
F
|
1182,873062
|
1,066624878
|
|
P(F>=f) одностороннее
|
5,24E-19
|
0,452826524
|
|
F критическое одностороннее
|
2,978587524
|
2,978587524
|
Двухстороннее значение р в первом случае равно 1,05E-18, что соответствует случаю значительного влияния факторов на зависимую переменную LN(Y). Во втором случае р равно 0,905653048, что не соответствует случаю значительного влияния факторов на зависимую переменную LN(Y). Вычисленная F-статистика для уровня значимости 5% в первом случае превосходит критическое значение 2,978587524, а во втором случае не превосходит, поэтому мы можем отвергнуть нулевую гипотезу равенства дисперсии.
Результаты дисперсионного анализа функции Кобба-Дугласа:
|
|
LN(Y), LN (K)
|
LN (Y), LN (L)
|
|
F
|
2,7567095
|
6,833028857
|
|
P(F>=f) одностороннее
|
0,033889717
|
0,000467767
|
|
F критическое одностороннее
|
2,978587524
|
2,978587524
|
Двухсторонние значения р равны 0,067779434 и 0,000935534, что не соответствует случаю значительного влияния факторов на зависимую переменную LN(Y). Вычисленная F-статистика для уровня значимости 5% в первом случае не превосходит критического значения 2,978587524, а во втором случае превосходит, поэтому мы можем отвергнуть нулевую гипотезу равенства дисперсии.
Результаты дисперсионного анализа степенной модели:
|
|
LN(Z), LN(M)
|
|
F
|
3,380393218
|
|
P(F>=f) одностороннее
|
0,014793043
|
|
F критическое одностороннее
|
2,978587524
|
Двухстороннее значение р равно0,029586087 , что не соответствует случаю значительного влияния факторов на зависимую переменную LN(Y). Вычисленная F-статистика для уровня значимости 5% превосходит критическое значение 2,978587524, поэтому мы можем отвергнуть нулевую гипотезу равенства дисперсии.
На данном этапе лучшей моделью по дисперсионному анализу является линейная модель.
3. Проведение регрессионного анализа исходных данных и выбор аналитической формы записи производственной функции
3.1 Выполнение расчетов однофакторной степенной зависимости с использованием статистической функции «Линейн» и проведение статистического анализа
Для оценки параметров уравнения степенной модели используем функцию «Линейн».
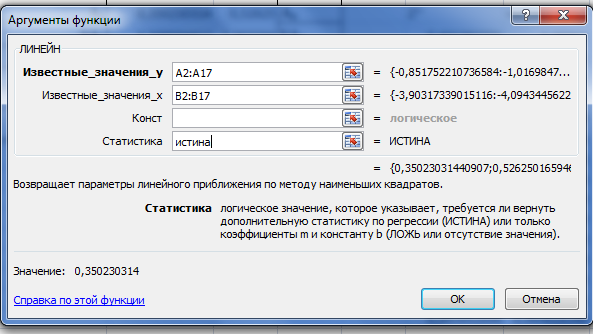
Основные характеристики степенной модели
|
А1
|
0,350230314
|
0,52625
|
А0
|
|
SА1
|
0,500594412
|
1,955594
|
SА0
|
|
R2
|
0,036286096
|
0,180741
|
E
|
|
F
|
0,489480589
|
13
|
n-p
|
|
TSS-ESS=RSS
|
0,015989958
|
0,424674
|
ESS
|
А1, А0– коэффициенты модели. Находятся по формулам:
,
SА1 , SА0 - среднеквадратические отклонения коэффициентов А1, А0 от своих математических ожиданий. Находятся по формулам:
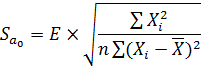
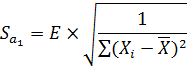
R2 - коэффициент детерминации;
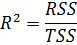
Е – ошибка модели или среднеквадратическое отклонение остатков;
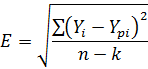
F- критерий Фишера;
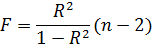
n-p – число степеней свободы для остатков модели;
р – количество коэффициентов в модели, включая свободный коэффициент;
TSS-ESS=RSS – сумма квадратов отклонений Y, обусловленных регрессией;
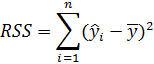
TSS – общая вариация переменной y;
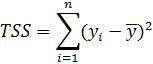
ESS–сумма квадратов отклонений остатков.
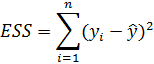
Выполняем потенцирование уравнения :
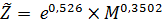
Значение e0,526 = а0 получим с использованием функции EXP( ): а0 =1,6926 . Получим следующее уравнение степенной модели регрессии:
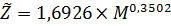
Чтобы провести статистический анализ, находим индекс корреляции , который характеризует тесноту связи изучаемых переменных:
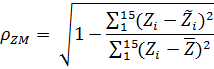
3.2 Построение модели множественной регрессии для двухфакторных линейной и мультипликативной производственных функций с помощью инструмента «Регрессия» пакета «Анализ данных» и проведение статистического анализа
Задача регрессионного анализа состоит в построении модели, позволяющей получать оценки значений результирующей (так называемой зависимой) переменной по значениям объясняющих (так называемых независимых) показателей.
Чтобы проанализировать взаимосвязь между факторами, воспользуемся функцией «Регрессия». Множественный регрессионный анализ с помощью этого инструмента можно выполнить в двух формах:
1) при выполнении регрессии имеется свободная переменная, или константа уравнения регрессии
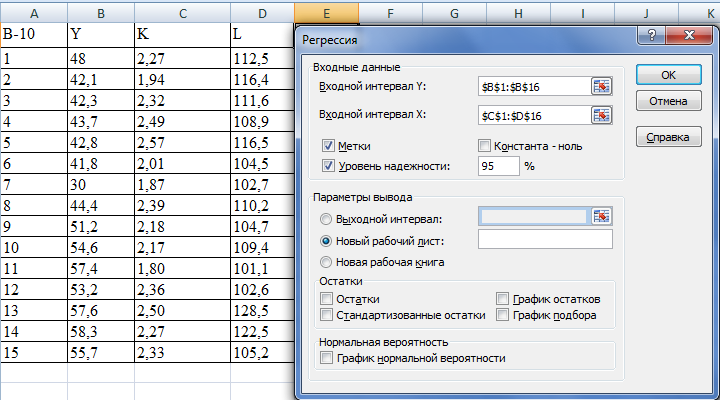
2) уравнение регрессии не содержит эту константу
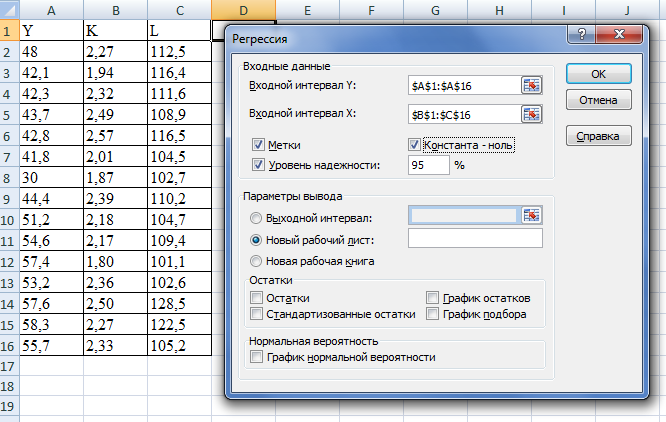
Результаты регрессионного анализа двухфакторной линейной модели, не содержащей константу:
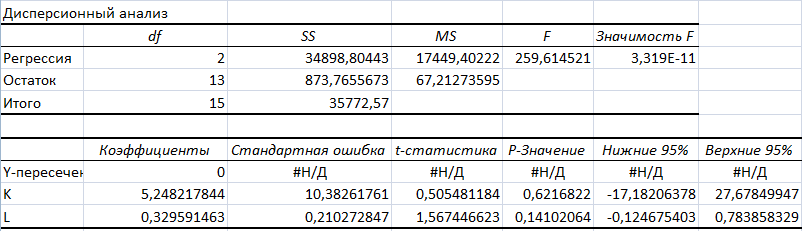
Результаты регрессионного анализа линеаризованной функции Кобба-Дугласа без константы:
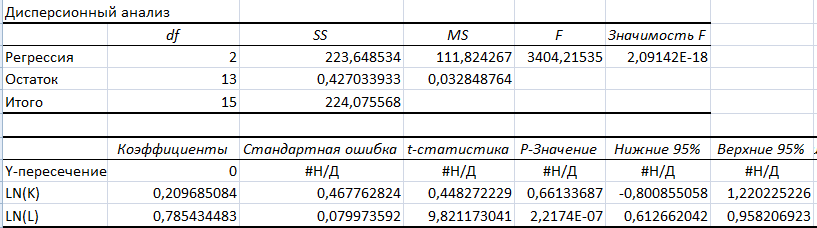
Результаты регрессионного анализа двухфакторной линейной модели, содержащая константу:
Результаты регрессионного анализа функции Кобба-Дугласа, содержащая константу:
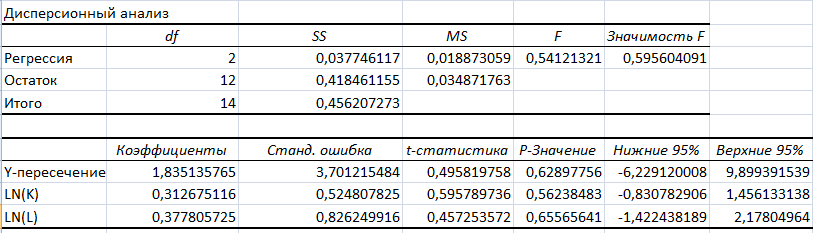
Характеристика значений первой таблицы:
df - число степеней свободы;
SS– сумма квадратов отклонений;
MS – дисперсия, равная вариации деленной на соответствующее число степеней свободы;
F – критерий Фишера.
Характеристика значений второй таблицы:
Значимость F – вероятность совершить ошибку при отклонении нулевой гипотезы: модель является недостоверной, если значение больше 0,05.
Коэффициенты-значения параметров уравнения регрессии;
Стандартная ошибка - стандартные ошибки коэффициентов уравнения регрессии;
t-статистика – расчетные значения t-критерия, используемые для проверки значимости коэффициентов уравнения регрессии;
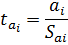
Р-значение (значимость t) – уровень значимости, соответствующий вычисленной t-статистике. Если Р-значение меньше 0,05 - стандартного уровня значимости, - то соответствующий коэффициент статистически значим;
Нижние 95% и Верхние 95% - нижние и верхние границы 95%-х доверительных интервалов для коэффициентов теоретического уравнения регрессии.
В таблице «Вывод остатка» приводятся вычисленные (предсказанные) по модели значения зависимой переменной y и значения остаточной компоненты е (остатки).
Регрессия указывает число степеней свободы (df) для RSS.
Итого указывает число степеней свободы для TSS.
Остаток указывает число степеней свободы для ESS.
По F-значимости определяется множественный R и R квадрат.
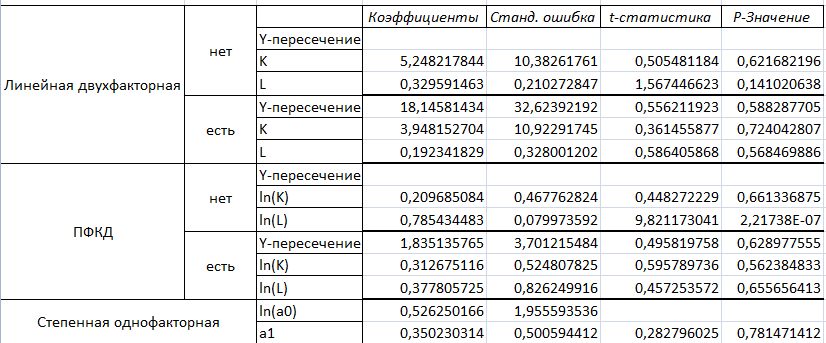
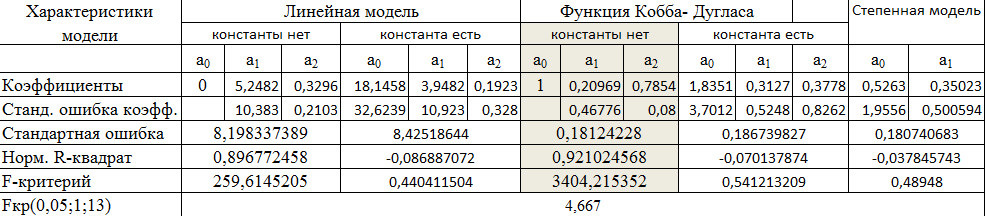
Полученные результаты обобщаем в таблицу.
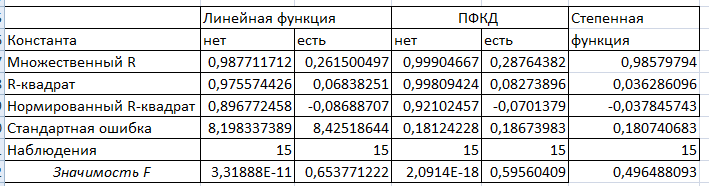
Множественный R – коэффициент множественной корреляции
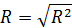
R–квадрат – коэффициент детерминации, R2
Нормированный R-квадрат – скорректированный R2 ; если значение отрицательное, то это говорит о том, что с ростом K и L убывает Y.
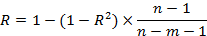
Стандартная ошибка – среднеквадратическое отклонение от модели
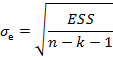
Значимость F для линейной модели без константы равна 3,319Е-11, а для ПФКД без константы равна 2,09142Е-18, что меньше 0,05, поэтому данные модели являются достоверными.
Значимость F для линейной модели с константой равна 0,645, а для ПФКД с константой равна 0,596, для степенной модели равна 0,496, что больше 0,05, поэтому данные модели являются недостоверными.
Выводы по полученным таблицам:
У линейной двухфакторной модели без константы очень высокие коэффициенты корреляции (0,988 ) и детерминации (0,976). F-критерий равен 259,615, это говорит о том, что данная модель статистически значима с вероятностью случайности 3,31888Е-11. Стандартная ошибка модели (8,198) и одного из двух коэффициентов (10,383 и 0,21) довольно высокие.
У линейной двухфакторной модели с константой низкие коэффициенты корреляции (0,262) и детерминации (0,07). F-критерий равен 0,44, это говорит о том, что модель статистически незначима. Также у этой модели довольно высокие стандартные ошибки модели (8,425) и коэффициентов (32,624, 10, 923 и 0,328).
У ПФКД без константы очень высокие коэффициенты корреляции (0,999) и детерминации (0,998). F - критерий равен 3404,215, что говорит о том, что модель статистически значима. Также у этой модели относительно низкие стандартные ошибки модели (0,181) и ее коэффициентов (0,468 и 0,08).
На этапе дисперсионного анализа линейная модель была лучшей, но результаты регрессионного анализа говорят о том, что ПФКД является лучшей.
У ПФКД с константой низкие коэффициенты корреляции (0,288) и детерминации (0,083). F-критерий равен 0,541, что говорит о том, что модель статистически незначима. Также у этой модели относительно невысокие стандартные ошибки модели (0,187) и ее коэффициентов (3,701, 0,525 и 0,826).
У степенной однофакторной модели высокий коэффициент корреляции (0,986) и низкий коэффициент детерминации (0,036). F- критерий равен 0,489, что говорит о том, что модель статистически незначима. Также у этой модели относительно невысокие стандартные ошибки модели и ее коэффициентов.
4 Выполнение экономического анализа в выбранной регрессионной модели на основе коэффициентов эластичности Эj
a1 – эластичность выпуска по основным фондам, она равна 0,2097, т.е при увеличении фондов на 1% выпуск увеличится на 0,21%;
а2 – эластичность выпуска по труду, она равна 0,785, т.е. при увеличении численности работников на 1% выпуск увеличится на 0,785%.
Так как а1<а2, то это характеризуется как фондосберегающий (экстенсивный) рост.
Относительная эластичность по фондам и труду равна:
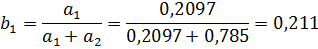
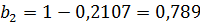
За анализируемый период выпуск вырос в 1,16 раза (=1,16), основные фонды – в 1,026 раза (=1,026), а численность промышленно-производственного персонала снизилась в 0,935 раза (=0,935).
Частная эффективность ресурсов соответственно равна:
,
Обобщенный показатель эффективности:
Масштаб производства:
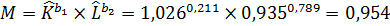
Таким образом, на основании расчетов рост объема выпуска за анализируемый период произошел за счет повышения эффективности производства в 1,217 раза и за счет масштаба производства в 9,54 раза.
Производственная функция имеет вид:
.
Заключение
В данной курсовой работе был выполнен статистический анализ по выборке, был проведен регрессионный анализ исходных данных и был сделан выбор аналитической формы записи производственной функции. Также был выполнен анализ в выбранной регрессионной модели на основе коэффициентов эластичности.
Выбранная модель – ПФКД без константы - имеет вид: .
При оценке качества модели мы отметили, что все основные характеристики говорят о хорошем качестве этой модели. Так, коэффициент детерминации R2=0,998, следовательно, более 99% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов. Расчетное значение F-критерия (3404,215) также подтверждает хорошее качество модели.
В процессе написания курсовой работы были достигнуты ранее поставленные цели, а именно построение эконометрических моделей производственной функции и анализ ее в среде Excel.
Список литературы:
1) Валентинов В. А. Эконометрика: Практикум. 3-е изд. - М.: Издательско-торговая корпорация «Дашков и К», 2010. – 436 с.
2) Валентинов В. А. Эконометрика: Учебник . 2-е изд. – М.: Издательско-торговая корпорация «Дашков и К», 2010. – 448 с.
3) Вуколов Э. А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXCEL.- М.: Форум, 2012.
4) Елисеева И.И. Практикум по эконометрике: Учеб. пособие. –Мю: Финансы и статистика, 2005. – 192 с.: ил.
5) Ефимов. В. В. Статистические методы в управлении качеством. Учебное пособие.-Ульяновск: УлГТУ. - 134 с., 2003
6) Орлова И. В. , Половников В. А. Экономико- математические методы и модели: компьютерное моделирование. - М.: Вузовский учебник, 2009.
Электронные ресурсы:
7) http://studopedia.net – Студопедия
8) https://ru.wikipedia.org/ - Википедия
PAGE \* MERGEFORMAT1
Єконометрические модели производственной функции и ее анализ в среде Excel