ОТКРЫТЫЕ ОПТИЧЕСКИЕ РЕЗОНАТОРЫ ЛАЗЕРОВ И ИХ СВОЙСТВА

Контрольная работа

Содержание

Введение

1. Принципы создания резонатора оптического диапазона

2. Пассивный ООР в приближении плоской волны.

3. Устойчивость ООР

4. Типы колебаний (моды) пассивного ООР

5. Моды активного ООР (лазера). Влияние вида уширения линии на модовый состав излучения лазера

6. Мощность на выходе лазера, оптимальное пропускание выходного зеркала

7. Методы селекции мод

8. Одночастотный режим работы лазера

Литература

Введение

Оптический резонатор является неотъемлимой и принципиально важной частью квантовых генераторов и усилителей ”резонаторного” типа, работающих в УФ, видимой, ИК и субмиллиметровой частях спектра. Он обеспечивает многократное прохождение волны через активную среду (положительная обратная связь в генераторе), накопление энергии в стоячей волне на строго определённых собственных резонансных частотах (модах) в пределах контура усиления активной среды, определяет частотно-пространственную структуру излучения лазера. Изменяя параметры резонатора можно управлять и частотно-временной структурой излучения лазера.

1. Принципы создания резонатора оптического диапазона.

Необходимость создания открытых оптических резонаторов (ООР) возникла из невозможности использования закрытых объёмных резонаторов (ЗОР) СВЧ-диапазона в оптическом диапазоне. В самом деле, будем исходить из того, что размеры СВЧ-ЗОР–L порядка длины волны СВЧ-излучения L~СВЧ. Если перенести такой резонатор в оптический диапазон, сохраняя соотношение между его размерами и длиной волны, то размеры “оптического” ЗОР должны быть порядка длины волны в оптическом диапазоне L~опт, т.е порядка мкм, а объем V~3опт–порядка (мкм)3, что накладывает неприемлемые ограничения на объём заполняющей резонатор активной среды квантового генератора, который также должен быть порядка (мкм)3. При подобном масштабировании снижается и добротность резонатора. В самом деле, добротность Q металлических ЗОР СВЧ-диапазона определяется как , где – толщина скин-слоя, ~–1/ Так как L при переходе в оптический диапазон изменилась как L~опт~–1, а как ~ –1/2, то Q будет зависеть от как Q~–1/2, и при увеличении - в 104 раз снизится в 102 раз, что также неприемлемо, хотя потери резонансных свойств (перекрытия резонансных контуров) при этом может и не произойти.

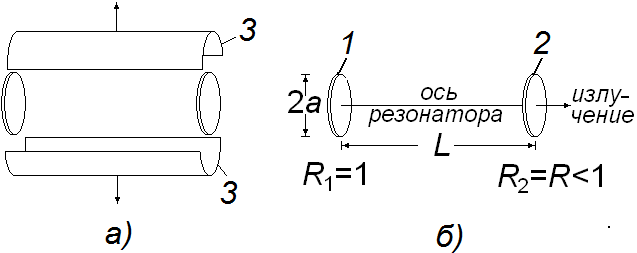
Рис. 1. Образование ООР из закрытого объёмного цилиндрического резонатора (применяемого в СВЧ диапазоне) а–удаление “боковых” стенок 3 у исходного резонатора; б – ООР с двумя противоположными круглыми отражателями (зеркалами) 1 и

Рассмотрим другой способ–использование СВЧ-ЗОР в оптическом диапазоне без изменения его размеров. При этом объём активной среды остаётся достаточным, однако резонансные свойства при таком переносе резко ухудшаются. В самом деле, зная число резонансов М, приходящихся на единичный спектральный интервал (1), можно определить интервал частот между соседними резонансами :

Получаем, что при переходе в оптический диапазон, при росте частоты в 104 раз, мм снижается в 108 раз, при этом ширина каждого резонанса , возрастает в 102 раз. То есть происходит расширение и «наложение» резонансов, и резонансные свойства теряются. В целом второй путь можно считать более перспективным, если избавиться от части резонансов. Этого можно достичь, оставив только две противоположные стенки резонатора и убрав обе других пары (“боковых”) стенок (если СВЧ-ЗОР – прямоугольный параллелепипед), и оставив только два донышка–если ЗОР является полым цилиндром (рис. 1). В результате получаем резонатор, образованный только двумя противоположными (в данном примере–параллельными) отражателями, и СВЧ-ЗОР после описанного изменения становится отрытым оптическим резонатором (ООР). Заметим, что при плоских отражателях ООР представляет собой хорошо известный в оптике интерферометр Фабри-Перо.

Таким образом, пассивный ООР – это система из двух (линейный ООР) и более двух («изломанный» кольцевой ООР) обращенных друг к другу отражающих поверхностей, в которой могут возбуждаться электромагнитные колебания оптического диапазона. В отличие от объёмных СВЧ-резонаторов геометрические размеры оптического резонатора во много раз превышают длину волны излучения, и он является “открытым”, т.е. резонатором без боковых стенок. В качестве отражателей ООР используют полностью или частично отражающие зеркала на нужный спектральный диапазон (с металлическими и диэлектрическими отражающими покрытиями), призмы полного внутреннего отражения, дифракционные решётки, грани кристалла и др.

2. Пассивный ООР в приближении плоской волны.

Очевидно, что для ООР (рис. 1) в наиболее благоприятные условия попадает волна (луч), распространяющаяся строго по оси резонатора, волновой фронт такой волны плоский. “Приближение плоской волны” является самым простым, и позволяет найти набор собственных резонансных частот и добротность ООР. Условие резонанса имеет вид

, , (1)

где L – расстояние между отражателями (зеркалами), n – показатель преломления, q –целое число, номер продольной моды – количество вариаций поля стоячей волны на длине L. Из (1) можно получить значения частот для “соседних” q и q+1 мод

и . (2)

Частотный интервал между соседними резонансами (модами q и q+1) будет

(3)

Найдем добротность ООР, пользуясь её классическим определением

, (4)

где р–ширина резонанса на частоте , U0–запасённая в резонаторе энергия, Рп – мощность потерь за период колебаний.

Пусть коэффициент отражения левого зеркала “1” радиусом a: R1=1; а правого “2”, частично прозрачного, предназначенного для вывода излучения: R2=R<1 (рис. 1). Тогда, поскольку излучение распространяется в обоих направлениях, , . Подставляя U0 и Рп в (4), получим

, (5)

где — эффективная длина резонатора – путь, который проходит излучение до выхода через частично прозрачное зеркало “2”. — постоянная времени нахождения излучения в резонаторе, а линейный коэффициент “активных” потерь 1 на два прохода луча в резонаторе:

. (6)

В то же время энергия может накапливаться не только на волнах, распространяющихся строго по оси ООР, но и на волнах, распространяющихся под малыми углами к оси, если число отражений и проходов для таких волн будет достаточно большим. Ограничимся значением , при этом . Пренебрегая дифракционными потерями, можно получить, что перекрытия резонансов не происходит, если выполняется условие

, (7),

где –число Френеля. Для геометрической оптики NF >>1, а для волновой оптики NF~1. Можно показать, что в приближении плоской волны резонансные свойства ООР сохраняются для всего видимого и ИК-диапазонов.

3. Устойчивость ООР.

Однако оказывается, что при удалении боковых стенок излучение начинает частично покидать ООР не только за счет пропускания зеркала “2”, но и за счет явления дифракции света на краях обоих зеркал (т.наз. дифракционные потери). Чтобы скомпенсировать эти принципиально неустранимые потери и сохранить излучение в резонаторе, т.е. сделать резонатор устойчивым, внутреннюю поверхность одного или обоих зеркал делают вогнутой, обычно – сферической. Обозначим через r1 и r2 – радиусы кривизны зеркал и примем, что для вогнутых зеркал (если смотреть «изнутри» резонатора) r>0, а для выпуклых r<0.

Если ввести параметры для каждого из зеркал: и , то теория дает критерий устойчивости ООР в виде

0 < q1q2 < 1. (8)

Геометрическое место точек, даваемое уравнением (8) (область устойчивости), заштриховано на диаграмме q1(q2) (рис. 2,в), незаштрихованные поля на диаграмме отвечают неустойчивым резонаторам, для которых q1q2<0 и q1q2>1; а оси координат и ветви гиперболы–резонаторам, находящимся «на границе устойчивости»: q1q2=0 и q1q2=1.

Наиболее часто используются следующие конфигурации резонаторов (см., также рис. 2):

– "плоско-плоский" резонатор (r1=r2=);

– "почти" плоско-плоский резонатор (L r1=r2=r <);

– “плоско-вогнутый” резонатор (r1=, r2=L);

– “вогнуто-вогнутый” резонатор (r1, r2>0; r1, r2 ~L);

– "конфокальный" резонатор (r1=r2= r =L), в нём совпадают точки фокуса зеркал;

– "почти конфокальный" резонатор, у которого не включается точка r1=r2= r =L, т.е. L < r и L > r;

– “полуконфокальный” резонатор, (r2=, L = r1/2), данный резонатор обеспечивает минимальную расходимость выходного излучения при использовании плоского зеркала «2» в качестве выходного;

– "концентрический" резонатор, совпадают центры кривизны зеркал (L=r1+r2 или L=2r);

– “выпукло-вогнутый” резонатор (r1>0, r2<0 );

– “выпукло-выпуклый” резонатор (r1>0, r2<0 ).

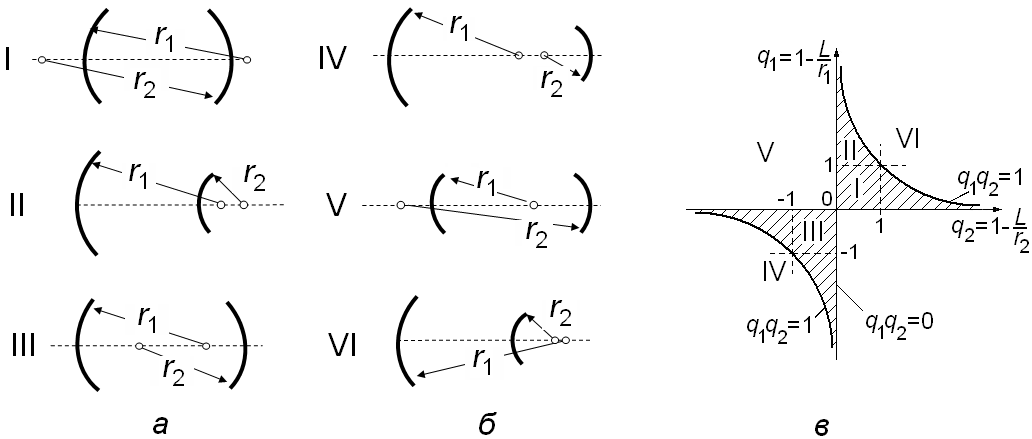
Рис. 2 Некоторые устойчивые (а) и неустойчивые (б) конфигурации ООР, составленного двумя сферическими зеркалами с радиусами кривизны r1 и r2 и расстоянием между ними L: r1>L, r2>L ( I ); r1>L, r2<0, (r1–L)<r2 ( II );– L/2<r1<L, L/2<r2<L ( III ); L/2<r1<L, 0<r2< L/2, (r1+ r2)<L( IV ); 0<r1<L, r2>L( V ); r1>L, r2<0, (r1–L)>r2 ( VI ). Соответствующие точки нанесены на диаграмму устойчивости (в).

Эпюра поля световой стоячей волны в “вогнуто-вогнутом” резонаторе имеет между зеркалами сужение пучка–“перетяжку”, радиус которой и расстояние до зеркала зависят от r1, r2 и L [1].

4. Типы колебаний (моды) пассивного ООР.

Остановимся на особенностях волн, распространяющихся в устойчивых ООР. Будем исходить из того, что световая электромагнитная волна – строго поперечная: , где – волновой вектор, и обозначается как ТЕМmnq (ТЕМ–аббревиатура «Transverse Electro-Magnetic»).

Индекс “q” обозначает число вариаций поля в продольном направлении (по оси резонатора–для “плоской” волны), а индексы “m” и “n” – в поперечном направлении.

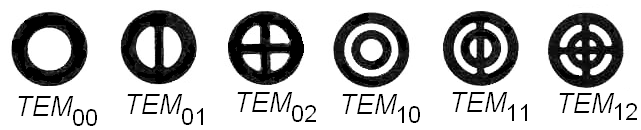
Совокупность волн с одними и теми же “m” и “n”, но различными “q”, образует поперечную моду ТЕМmn, например, ТЕМ00, ТЕМ11 ТЕМ12 и др. Поперечная мода ТЕМ00 называется низшей или основной модой, дифракционные потери для неё минимальны, т.к. распределение поля в ней по радиусу–гауссово и выглядит как пятно, расположенное на оси резонатора (см., рис. 3). Для этой моды возможна фокусировка луча в пятно минимального размера (порядка ).

Рис. 3. Эпюры поля на зеркале резонатора для продольной основной моды ТЕМ00 и различных поперечных мод высших порядков – ТЕМmn.

Мода ТЕМmnq называется “q-ой” продольной модой поперечной моды ТЕМmn. Таким образом, например, основная поперечная мода представляет собой совокупность продольных мод: …ТЕМ00q–1, ТЕМ00q, ТЕМ00q+1, ТЕМ00q+2 и др., и частотный интервал между ними (“межмодовый” интервал) выражается формулой (3).

В реальных условиях структура светового поля представляет собой суперпозицию нескольких поперечных мод. Интерференция волн на зеркалах приводит для каждой моды к специфическому распределению поля, имеющего m и n вариаций по x- и y-координатам (прямоугольные зеркала) или по радиусу и азимуту (круглые зеркала) (рис. 3). Частотный интервал между ближайшими модами ТЕМmnq и ТЕМm+1nq, например, при m=n=0: ТЕМ00q и ТЕМ10q можно найти из формулы, которую нетрудно получить в т.наз.”приближении СВЧ-объёмного резонатора”:

, (9)

где (мм)продмм в (3).

5. Моды активного ООР (лазера). Влияние вида уширения линии на модовый состав излучения лазера.

Пространство между двумя отражателями можно полностью или частично заполнить активной средой. ООР, внутрь которого помещена активная среда с инверсией населенностей, из “пассивного” превращается в “активный”, обеспечивает положительную обратную связь, и вместе с устройством накачки активной среды представляет собой оптический квантовый генератор (лазер). Расстояние между отражающими поверхностями резонатора L определяется размерами применяемой активной среды и колеблется от долей миллиметра (у полупроводниковых лазеров) до нескольких метров у мощных газовых лазеров.

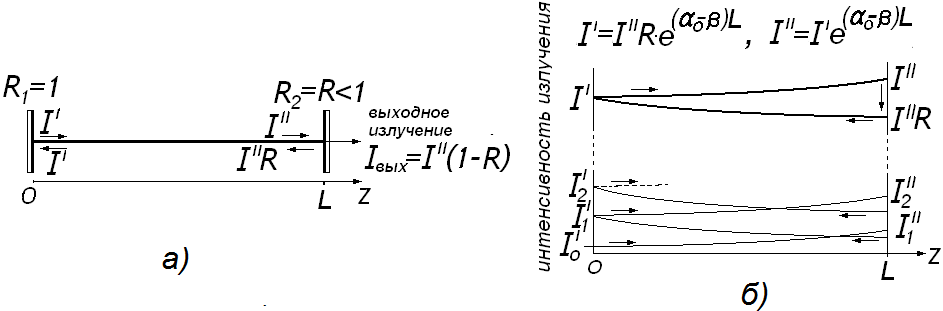
Динамика развития генерации лазера следующая (рис.4). Начало процессу генерации даёт спонтанное испускание фотона одной из частиц на лазерном переходе в направлении, совпадающем с осью ООР. На диаграмме интенсивности лучей (рис. 4) величина такого излучения обозначена как I0'. Этот сигнал, пройдя слева направо через активную среду длиной L, усиливается до величины I1'', далее частично выходит через правое зеркало и отражается в обратном направлении (интенсивность I1''R), далее пройдя через среду опять усиливается (до I1'), отражается от левого зеркала и так далее–до насыщения, когда увеличение интенсивности луча за два прохода через активную среду равно мощности излучения, покидающего резонатор через зеркало 2 (условие самовозбуждения).

Рис. 4. Схема (а), динамика развития генерации и условие самовозбуждения (б) в активном ООР (лазере). I''(1–R)=Iвых – интенсивность выходного излучения лазера при насыщении; R1=1 и R2=R–коэффициенты отражения зеркал ООР.

Параметры активного ООР (конфигурация резонатора, распределение коэффициента усиления и показателя преломления по радиусу среды и др.) определяют частотно-пространственные параметры генерируемого излучения, такие как распределение амплитуды и фазы в поперечном сечении, угловую расходимость излучения, выходящего из резонатора, общую генерируемую мощность (энергию), частотный спектр и состояние поляризации.

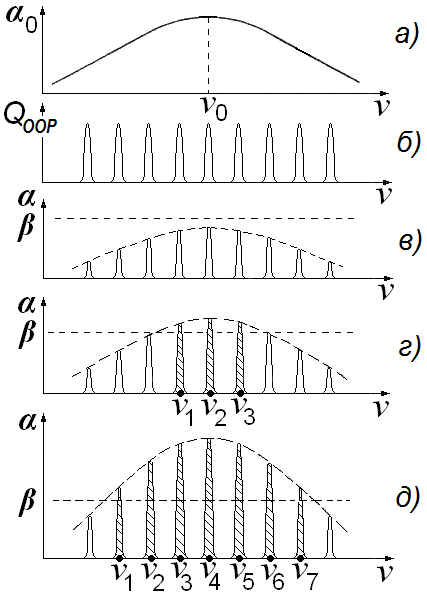
В активном ООР генерируются только те моды пассивного резонатора, которые находятся в частотном интервале, задаваемом активной средой (рис. 5), и для которых значение ненасыщенного коэффициента усиления будет превышать потери резонатора 0()>. Очевидно, что чем ниже уровень потерь относительно 0(), тем выше интенсивность генерации на данной моде. Ширина каждого резонанса пассивного резонатора определяется его добротностью (5), а активного ООР – добротностью генератора в целом. Очевидно, что наилучшим образом достоинства лазера как источника с наивысшей монохроматичностью излучения будут проявляться при генерации на одной продольной моде ТЕМ00q основной поперечной моды ТЕМ00. Выделить моду (00q) из спектра многомодовой генерации при неоднородно уширенной линии можно методами внутрирезонаторного управления спектральными характеристиками излучения, а именно–методами селекции мод, которые будут рассмотрены ниже.

Таким образом, ЛАЗЕР – это источник когерентного электромагнитного излучения оптического диапазона, использующий для усиления и генерации света явление индуцированного (вынужденного) излучения атомов, ионов или молекул, составляющих активную среду, помещённую в ООР. Лазер содержит три основных компонента: активную среду, в которой создают инверсию населённостей для какой-либо одной или нескольких пар уровней; устройство накачки для создания и поддержания инверсии в активной среде и открытый оптический резонатор – устройство для формирования частотно-пространственных характеристик генерируемого излучения и осуществления положительной обратной связи.

Проанализируем как влияет тип уширения квантового рабочего перехода активной среды (однородного и неоднородного)–на модовый состав излучения лазера. При плотности энергии излучения и плотности потока мощности (интенсивности) волны в резонаторе и I, насыщение коэффициента усиления активной среды будет происходить в резонаторе уже не до нулевого уровня, а до уровня потерь =1+2, складывающихся из активных потерь 1 на пропускание зеркала, через которое излучение выводится из резонатора (формула (6)) и пассивных потерь 2, вызываемых не связанным с рабочим переходом поглощением в оптических элементах внутри ООР, рассеянием и другими причинами.

Рис.5. Процесс формирования частотного спектра излучения лазера с неоднородно уширенным контуром усиления при различном соотношении усиления и потерь: а–контур усиления, б–спектр собственных частот пассивного резонатора (мода ТЕМ00), в–ненасыщенный коэффициент усиления 0 меньше уровня потерь ; г и д– 0>, заштрихованы моды активного резонатора (лазера).

Рис.6. Процесс насыщения контура усиления перехода при различных интенсивностях излучения в резонаторе: а – при однородном уширении контура, б – при неоднородном уширении за один проход, в – провалы Беннета в неоднородно уширенном контуре усиления в активном многопроходном резонаторе, симметричные относительно центральной частоты 0.

5.1. Однородное уширение. Поскольку при однородном уширении все частицы ансамбля вносят одинаковый вклад в формирование всего лоренцевого контура усиления, очевидно, что и каждая частица будет участвовать в насыщении его во всем частотном диапазоне 0(). При этом будет генерироваться одна мода, для которой значение {0()–} будет максимальным. “Проседание” кривой усиления при этом происходит во всей полосе частот (рис. 6,а)

5.2 Неоднородное уширение. При неоднородном уширении “в резонансе” с собственными резонансными частотами резонатора находятся различные группы частиц, для которых излучение и производит насыщение населенности уровней перехода, и в кривой ненасыщенного усиления 0() при одном проходе излучения возникает “провал” на резонансной частоте резонатора p=', при достигающий уровня потерь (рис.6,б).

Рассмотрим процесс насыщения за два прохода. Предположим, что существует резонанс резонатора на частоте p=', причём <0 для контура ненасыщенного усиления 0(). В резонансе с волной данной частоты, распространяющейся слева направо, будут частицы среды, движущиеся со скоростью <0, т.е. справа налево-”навстречу” волне, (см., рис.1.3). Для этих частиц происходит насыщение квантового перехода, населенности начинают выравниваться и усиление на частоте снижается в пределе до уровня потерь. В результате в кривой ненасыщенного усиления возникает (говорят: «выжигается») провал на частоте , ширина (на половине «глубины») которого равна одн.

После отражения от правого зеркала волна движется уже справа налево, и с ней взаимодействуют частицы также движущиеся ей навстречу со скоростью +u, а данные частицы формируют кривую усиления на частоте =0+(0–), ”симметричной” относительно 0. Это взаимодействие приводит к насыщению перехода для второй группы частиц на частоте , и в контуре усиления возникает второй провал с теми же параметрами, что и первый (рис. 6,в). Такая пара симметричных провалов в кривой ненасыщенного усиления возникающих в активном резонаторе при неоднородном уширении перехода, называется провалами Беннета.

При взаимодействии с волной, частицы активной среды при индуцированных переходах излучают энергию, получаемую ими от источника накачки. Далее, будет показано, что мощность, излучаемая средой и “подпитывающая” волну при её движении в одном направлении, пропорциональна площади провала, который она “выжигает”, а за два прохода–пропорциональна сумме площадей провалов, т.е. двойной площади одного провала.

До сих пор речь шла об устойчивом резонаторе. Неустойчивые резонаторы несмотря на неустойчивую модовую структуру поля стоячей волны имеют привлекательные особенности и также применяются в квантовых приборах. Световое поле неустойчивого резонатора и резонатора, работающего «на границе устойчивости», не стремится сосредоточиться вблизи оси, как в устойчивом резонаторе, и поэтому энергия стоячей волны в течение коротких промежутков времени может быть снята с большего объёма среды: как с приосевых, так и с периферийных участков её сечения. Неустойчивые резонаторы используются на практике в лазерах с коротким временем существования инверсии, а также–в лазерах с высоким усилением, таких как полупроводниковые, некоторые типы газовых, и состоят из плоских либо сферических отражателей.

6. Мощность на выходе лазера, оптимальное пропускание выходного зеркала.

Теоретический анализ выполним для случая однородного уширения перехода. Из выражения (1.44) для насыщенного коэффициента усиления н при однородном уширении, получим выражение для интенсивности, связанной с величиной :

, (10)

где Is-параметр насыщения. Так как при насыщении н==1+2, для выходной мощности лазера Рвых можно записать

. (11)

Найдем оптимальное значение коэффициента потерь 1, откуда воспользовавшись выражением (6), можно легко отыскать коэффициент пропускания выходного зеркала R2= R. Оптимизация 1 сводится к отысканию условий, при которых функция РВЫХ (1) имеет экстремум (максимум). Для этого необходимо найти из (11) и приравнять нулю производную , в результате чего получим

. (12)

Подставляя (12) в (11) получим выражение для максимальной выходной мощности

. (13)

Найдем выражение для , в практически важном случае, а именно: при значительном превышении ненасыщенного коэффициента усиления над коэффициентом пассивных потерь, т.е. 0>>2; а также при и при . Тогда (13) после подстановки в него выражения для IS из (1.44,б) будет

. (14)

То есть в идеальном случае, для которого и получено выражение (14), вся мощность накачки превращается в энергию лазерного излучения.

Чтобы пояснить вывод, сделанный нами в разделе 5.2, преобразуем (13) не раскрывая 0, в случае когда в резонаторе формируется излучение, частота которого совпадает с центральной частотой однородно уширенного перехода 0:

. (15)

Из (15) получим значение излучаемой средой мощности при насыщении и при формировании провалов Беннета на частотах и :

и . (16)

Видно, что 0(') и 0('') являются величиной превышения усиления над уровнем потерь, т.е.–«глубиной» провала Беннета, а одн является «шириной» провала, таким образом, и получается, что при неоднородном уширении перехода мощность, излучаемая лазером в одной моде за два прохода в резонаторе, пропорциональна удвоенной площади «выжигаемых» излучением провалов Беннета. .

7. Методы селекции мод

Методы селекции (выделения) мод применяются с целью улучшения частотно-пространственных характеристик излучения многомодового и многочастотного лазера с неоднородно уширенной линией, и подразделяются на селекцию одной поперечной моды ТЕМmn и селекцию одной продольной моды ТЕМmnq.

7.1. Селекция поперечной моды (пространственная). Легче всего осуществить выделение основной (низшей) поперечной моды ТЕМ00. Метод основан на различии в дифракционных потерях для моды ТЕМ00 и для поперечных мод высших порядков, имеющих существенно различающиеся распределения поля на зеркале в поперечном (радиальном) направлении (см., например, рис. 3). Задача–сделать так, чтобы потери для поперечных мод высших порядков оказались бы выше уровня потерь для выделяемой моды ТЕМ00. Наиболее просто это делают введением внутрь резонатора диафрагмы (непрозрачного “экрана” с отверстием на оси резонатора) (рис.7,а-в).

7. Селекция одной продольной моды ТЕМ00q (частотная). Самый простой и очевидный метод выделения одной продольной моды–искусственное увеличение потерь резонатора или снижения коэффициента усиления активной среды (см., например, рис.5), не является приемлемым, т.к. при таком способе мощность генератора снижается. Поэтому селекцию обычно проводят в два этапа: сначала осуществляют селекцию одной поперечной моды ТЕМ00 (“пространственную”), а затем–селекцию одной продольной моды ТЕМ00q (“частотную”). Сравним возможные методы частотной селекции для газового лазера, имеющего наиболее узкие линии. Поскольку доплеровская ширина контура усиления имеет порядок ~1 ГГц, сопоставимый с межмодовым интервалом, то применение поглощающих, поляризационных фильтров или дисперсионных элементов может выделить лишь группу продольных мод, внося при этом и для них достаточно высокие потери. Зачастую неприемлема и селекция центральной продольной моды путём увеличения межмодового интервала при уменьшении длины резонатора L (см., формулу (3)), что требует уменьшения продольного размера активной среды и, как следствие, – снижения усиления и мощности лазера. Поставленная задача может быть решена лишь применением устройств высокой разрешающей силы: многозеркальных связанных резонаторов, интерференционных фильтров и др.:

а) трёхзеркальный связанный резонатор. Схема этого метода селекции показана на рис.7,а. В резонатор, образованный зеркалами 1 и 2 вводится дополнительное зеркало 3. Для того, чтобы зеркало 3 не вносило в резонатор существенных потерь, его коэффициент отражения обычно выбирается небольшим, т.е. R3<<1. В результате можно рассматривать два связанных резонатора 1-2 и 1-3, спектры собственных частот которых показаны на рис. 7,в и 7,г. Межмодовый интервал для резонатора 1-3 оказывается бльшим, чем для резонатора 1-2 (см., формулу (3)), а добротность–меньшей (см., формулу (5)), и резонанс р–более широким. В результате в лазере генерируется только та продольная мода, частота которой удовлетворяет условиям резонанса одновременно для обоих резонаторов (рис. 7,е). Подобным образом действуют и четырёхзеркальные связанные резонаторы (типа интерферометров Майкельсона, Фокса-Смита и др.)

б) введение в резонатор интерференционного элемента. Таким элементом может служить двухзеркальный интерферометр (эталон) Фабри-Перо с малой базой. Схема селекции показана на рис 7,б. Условия резонанса в интерферометре подобны условиям для резонатора 1-3 в предыдущем методе (рис. 7,в,д,е). В результате в лазере генерируется продольная мода, частота которой удовлетворяет условиям резонанса одновременно для резонатора 1-2 и интерферометра 3-4. Подобным селектирующим элементом является и вводимая в резонатор тонкая диэлектрическая “плёнка Троицкого”.

Рис.7. Частотная селекция моды ТЕМ00q в излучении лазера с неоднородно уширенным контуром усиления в трехзеркальном резонаторе 1–2–3, (а), и с эталоном Фабри-Перо 3–4 внутри двухзеркального резонатора 1–2 (б). в–спектр активного резонатора 1–2 после селекции моды ТЕМ00 с помощью диафрагмы Д; г–спектр собственных частот резонатора 1–3; д–спектр собственных частот эталона Фабри-Перо 3–4; е–заштрихована мода ТЕМ00q активного резонатора (лазера) после частотной селекции.

8. Одночастотный режим работы лазера

8.1. Ширина линии генерации лазера. Очевидно, что ширина линии излучения будет минимальной для газового лазера и при минимальных потерях активного ООР. Исходя из специфики квантовых переходов и структуры генератора понятно, что принципиально неустранимыми у лазера остаются два вида потерь: потери на спонтанное излучение рабочего перехода РСП* и активные потери на пропускание выходного зеркала 1 (6). Ширину линии генерации поэтому рассчитаем для идеального лазера, не имеющего пассивных потерь излучения (2=0), в котором излучает одна группа активных частиц (одночастотный лазер с однородно уширенным контуром усиления).

Ширину резонанса такого генератора г можно найти из записи выражений для добротности: через отношение запасённой энергии U0 к энергии потерь РП=РСП*, и через отношение центральной частоты линии излучения к её ширине (4):

, (17)

откуда для г получим

. (18)

Для U0 и РСП* (в одной моде) можно записать:

(19)

. (20)

Выражение для с можно найти из (5): , где – ширина резонансной кривой резонатора. Подставляя (19) и (20) в (18) получим

. (21)

Оценки для минимальной ширины линии излучения лазера г дают величину порядка 10–3 Гц, что недостижимо для других источников оптического излучения, имеющих на 10…12 порядков более широкие линии.

Таким образом, одночастотный режим генерации лазера (работа на одной продольной моде ТЕМ00q) позволяет реализовать два важнейших преимущества лазера перед другими источниками оптического излучения: предельно высокие монохроматичность и когерентность излучения. Его линия излучения оказывается на много порядков уже не только контура усиления, но и резонанса р ООР. При этом оказывается возможной и стабилизация излучения лазера на моде ТЕМ00q по частоте.

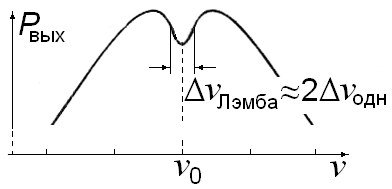
8.2 “Провал” Лэмба. Провалом Лэмба называют локальный минимум в частотной зависимости для мощности излучения одночастотного лазера с неоднородно уширенным контуром усиления, наблюдаемый на центральной частоте перехода 0 (рис.8).

Рис. 8. “Провал” Лэмба на центральной частоте 0 в гауссовом контуре лазера, работающего в одночастотном режиме

В самом деле, перестраивая моду генерации лазера по частоте в пределах контура усиления, оказывается, что при отстройке от 0 на величину большую, чем одн, вклад в энергию излучения вносят две группы активных частиц среды, а, как показано в разделе 6, мощность лазера оказывается пропорциональной удвоенной площади провала Беннета. Иначе обстоит дело, когда частота моды генератора совпадает с центральной частотой перехода 0. При этом взаимодействие волны, имеющей частоту, равную 0, происходит только с одной группой частиц, имеющих , и только от этой единственной группы волна получает энергию. В этом случае ' и '' совпадают: '=''=0, провалы Беннета в контуре усиления «перекрываются» и превращаются в один провал, и мощность лазера оказывается пропорциональной площади только одного провала Беннета, т.е. для центральной частоты 0 происходит её снижение (рис. 8).

Провал Лэмба используется для стабилизации резонансной частоты р ООР лазера, работающего в одночастотном режиме излучения, в точке р=0. Такой лазер можно использовать в качестве стандарта частоты в оптическом диапазоне, а также в уникальных оптических лазерных стандартах единицы длины (метра).

Отметим, что известны и оптические резонаторы специального назначения: волноводный, волноводный с распределённой обратной связью и др.

Литература

Ямпурин Н.П.: Электроника. - М.: Академия, 2011

Воронков Э.Н.: Твердотельная электроника. - М.: Академия, 2010

Гуртов В.А.: Зарядоперенос в структурах с диэлектрическими слоями. - Петрозаводск: ПетрГУ, 2010

Дрейзин В.Э.: Управление качеством электронных средств. - М.: Академия, 2010

Институт СВЧ полупроводниковой электроники РАН: Наногетероструктуры в сверхвысокочастотной полупроводниковой электронике. - М.: Техносфера, 2010

Прянишников В.А.: Электроника. - СПб.: КОРОНА-Век, 2010

рец.: С.П. Вихров, О.А. Изумрудов: Твердотельная электроника. - М.: Академия, 2010

Ямпурин Н.П.: Основы надежности электронных средств. - М.: Академия, 2010

Под ред. А.А. Орликовского ; Рец.: А.Ф. Александров, А.А. Горбацевич: Наноэлектроника. - М.: МГТУ им. Н.Э. Баумана, 2009

Под ред.: А.А. Кураева, Д.И. Трубецкого ; А.В. Аксенчик и др.: Методы нелинейной динамики и теории хаоса в задачах электроники сверхвысоких частот. - М.: ФИЗМАТЛИТ, 2009

Шишкин Г.Г.: Электроника. - М.: Дрофа, 2009

А.Н. Диденко и др. ; Под ред. И.Б. Фёдорова: Вакуумная электроника. - М.: МГТУ им. Н.Э. Баумана, 2008

Лебедев А.И.: Физика полупроводниковых приборов. - М.: Физматлит, 2008

Шматько А.А.: Электронно-волновые системы миллиметрвого диапазона. - Харьков: ХНУ им. В.Н. Каразина, 2008

Московский гос. ин-т стали и сплавов, Саратовский гос. ун-т им. Н.Г. Чернышевского ; под ред. Л.В. Кожитова: Оборудование, технологии и аналитические системы для материаловедения, микро- и наноэлектроники. - М.: МИСиС, 2007

Федеральное агентство по образованию, Московский гос. ин-т стали и сплавов (Технологический ун-т), Саратовский гос. ун-т им. Н.Г. Чернышевского ; под ред. Л.В. Кожитова ; авт-сост.: В.П. Менушенков и др.: Оборудование, технологии и аналитические системы для материаловедения, микро- и наноэлектроники. - М.: МИСиС, 2007

Филачёв А.М.: Твердотельная фотоэлектроника. - М.: Физматлит, 2007

Захвалинский В.С.: Электроника. - Белгород: БелГУ, 2006

Смоликов А.А.: Наноматериалы. - Белгород: БГТУ, 2006

Смоликов А.А.: Наноматериалы. - Белгород: БелГУ, 2006

Горошков Б.И.: Электронная техника. - М.: Академия, 2005

Гуртов В.А.: Твердотельная электроника. - М.: Техносфера, 2005

Гусев В.Г.: Электроника и микропроцессорная техника. - М.: Высшая школа, 2005

Жаворонков М.А.: Электротехника и электроника. - М.: Академия, 2005

Келим Ю.М.: Вычислительная техника. - М.: Академия, 2005

Кучумов А.И.: Электроника и схемотехника. - М.: Гелиос АРВ, 2005

ОТКРЫТЫЕ ОПТИЧЕСКИЕ РЕЗОНАТОРЫ ЛАЗЕРОВ И ИХ СВОЙСТВА