Материалы и элементы электронной техники
Контрольная работа
МАТЕРИАЛЫ И элементы электронной техники
Содержание
1. ОСНОВЫ ФИЗИКИ ПОЛУПРОВОДНИКОВ
2. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ И УРОВНИ ПОЛУПРОВОДНИКА
3. РАСПРЕДЕЛЕНИЕ НОСИТЕЛЕЙ В ЗОНАХ
4. ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
5. РЕКОМБИНАЦИЯ НОСИТЕЛЕЙ
6. ПОЛУПРОВОДНИК В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
7. ДВИЖЕНИЕ НОСИТЕЛЕЙ В ПОЛУПРОВОДНИКАХ
8. КОНТАКТНЫЕ ЯВЛЕНИЯ В ПОЛУПРОВОДНИКАХ
9. КОНТАКТЫ МЕТАЛЛА С ПОЛУПРОВОДНИКОМ
10. КОНТАКТЫ МЕЖДУ ПОЛУПРОВОДНИКАМИ С ОДИНАКОВЫМИ ТИПАМИ ПРОВОДИМОСТИ
Литература
1. ОСНОВЫ ФИЗИКИ ПОЛУПРОВОДНИКОВ
Физика полупроводников представляет собой теоретическую основу полупроводниковой электроники.
Следует начать с того, что все вещества в природе по электрофизическим свойствам могут быть разделены на три больших класса: металлы, полупроводники и диэлектрики. Они обладают различными величинами удельного сопротивления (у металлов = 106 – 104 Омсм, у полупроводников = 104 – 1010 Омсм, у диэлектриков > 1010 Омсм). Однако значения при переходе от одного класса веществ к другому перекрываются и поэтому такой параметр не может служить однозначным критерием для классификации веществ.
Рис.1
Зависимость удельного сопротивления от температуры (рис.1) дает более четкую границу. У металлов (химически чистых) зависимость пропорциональна абсолютной температуре Т
= ОМ(1 + Т) (1)
в то время, как у невырожденных полупроводников, для некоторого интервала температур
= 0е/Т или для проводимости = 0е-/Т, (2)
где ОМ удельное сопротивление металла при 0оС, термический коэффициент сопротивления, равный 1/273 (Т0 = 273), 0, некоторые постоянные для данного интервала температур величины, характерны для каждого полупроводника.
Однако и этот критерий не абсолютен, т.к. в некотором интервале температур Т полупроводник может вести себя подобно металлам, хотя здесь и прослеживается положительный температурный коэффициент удельной проводимости
/ = (2 1)/(Т2 – Т1) > 0. (3)
Однозначным является характер этой зависимости при понижении температуры до абсолютного нуля. У металлов при этом проводимость растет, а у ряда металлов и сплавов наступает сверхпроводящее состояние. Тогда как у полупроводников удельная проводимость с понижением температуры уменьшается, а при абсолютном нуле они приближаются к диэлектрикам.
Из этого следует, что в полупроводнике свободные носители заряда возникают при проведении к нему тепловой энергии. Эти носители называют тепловыми или равновесными. Свободные носители могут появляться также при освещении, облучении ядерными частицами, при наложении на полупроводник электрического поля, при изменении внешнего давления. Возникающие носители заряда в этом случае называются неравновесными и процесс их образования существенно зависит от структуры полупроводника, наличия в нем примеси и пр.
Таким образом, полупроводник это такое вещество, которое при комнатной температуре имеет удельную проводимость в интервале 1010 – 104 Ом1см1, зависящую от структуры вещества, вида и количества примеси и внешних условий: температуры, давления, освещенности, облучения частицами, электрического и магнитного полей.
Существуют два типа проводников электрического тока: электронные и ионные. Металлы – электронные проводники, электролиты – ионные. Полупроводники могут быть как электронные, так и ионные, но мы будем рассматривать лишь электронные полупроводники (это такие вещества, как: бор В, углерод С, кремний Si, фосфор Р, сера -S, германий Ge, мышьяк As, серое олово -Sn, сурьма -Sb, селен Se (красный), теллур Те, йод J, ряд сложных соединений карбиды (SiC), антимониды (AlSb, GaSb, SnSb), арсениды (GaAs, SnAs), фосфиды (GaP, SnP), теллуриды (РbТе), окиси (ZnO), сульфиды (CdS, ZnS, PbS), селениды (СdSe) и др.
Рассмотрим механизм электропроводимости полупроводников на основе элементарных полупроводников. Здесь электроны распределены по состояниям следующим образом:
С(6) (1s2, 2s2, 2p2);
Si(14) (1s2, 2s2, 2p6, 3s2, 3p2);
Ge(32) (1s2, 2s2, 2p6, 3s2, 3p6, 3d10, 4s2, 4p2),
причем внешняя оболочка электронов заполнена частично, и содержит четыре валентных электрона. При образовании кристалла четыре валентных электрона каждого атома из состояния 3s2, 3p2 переходят в гибридное состояние 3p3 с не спаренными спинами и образуют четыре пространственно-эквивалентные связи. Каждый атом при этом окружен четырьмя ближайшими соседями и находится в центре тетраэдра – свойственного кристаллической решетке алмаза, поэтому свойства полупроводника зависят от плоскости скола кристалла – плоскости Миллера. Все полупроводники имеют решетку типа “алмаза”: если вложить 2 кубические, гранецентрированные решетки друг в друга и сместить на часть диагонали куба. По типу элементарной ячейки и типу центрирования различают 14 видов решеток Бравэ.
Если единицей длины принять параметры элементарной ячейки рис.2 a = b = c = 1, то координатами узла станут числа m, n, p, причем
,
где [m, n, p] – индексы узла,
направления.
Рис.2
Если выбрать направление по осям координат, то обозначение направления определяется индексами узла. Для описания плоскостей элементарной ячейки используют индексы Миллера: если плоскость отсекает на осях координат отрезки m, n, p, то уравнение плоскости будет
,
hx + ky + lz = 0,
{h, k, l} – индексы Миллера.
В идеальном полупроводнике все электроны связаны и электрический ток в таком полупроводнике при помещении в электрическое поле (ЭП) не возникает т.к. нет свободных носителей заряда. При воздействии внешних возмущений (тепло) происходит разрыв валентных связей и электроны становятся свободными – этот процесс называется генерацией (превращение связанного электрона в свободного).
На месте ушедшего электрона образуется незавершенная связь, имеющая положительный заряд. Это вакантное место в валентной связи получило название – дырка.
В целом кристалл остается электронейтральным и в нем произвольно происходят как генерационные так и обратные процессы – рекомбинации.
Полупроводник в котором в результате разрыва валентных связей образуется равное количество свободных электронов и дырок, называется собственным (концентрация носителей в нем при комнатной температуре составляет для германия порядка 1013 см3, для кремния 1010 см-3).
Свободные носители заряда (тока) будут хаотически перемещаться по кристаллу полупроводника из-за столкновений с дефектами кристаллической решетки. Расстояние, проходимое свободными носителями заряда между двумя столкновениями, называется длинной свободного пробега, а усредненное значение всех отрезков пути – средняя длина свободного пробега.
Время между двумя соударениями и его усредненное значение называют временем свободного пробега и средним временем свободного пробега.
Средняя длина свободного пробега и среднее время свободного пробега связаны отношением
= 0, (4)
где 0 средняя скорость теплового движения свободного носителя заряда (среднее значение модуля скорости), которая имеет порядок 107 см/с.
В отсутствии внешнего ЭП суммарный заряд переносимый свободными электронами и дырками в любом направлении, равен нулю и беспорядочное тепловое движение не дает тока. Под воздействием ЭП свободные электроны полупроводника будут приобретать скорость, направленную против поля. При этом вся совокупность получает некоторую скорость направленного движения называемая дрейфовой скоростью, а само движение – дрейф. В этом случае средняя скорость движения не равна нулю и через полупроводник течет ток, обусловленный свободными носителями – электронами.
В чистом полупроводнике (не содержащем примеси) осуществляется электронная и дырочная электропроводность. Следовательно, электрический ток в собственном полупроводнике определяется двумя составляющими – электронным и дырочным токами, текущими в одном направлении. Электроны против ЭП, дырки – по ЭП.
Мы отметили, что в полупроводнике имеется два типа свободных носителей и следовательно проводимость обусловлена парными носителями теплового происхождения которая называется собственной проводимостью. В отличие от неё, проводимость обусловленную примесями, называют – примесной проводимостью.
Для кремния характерны примеси замещения, здесь примесный атом (пятивалентный: фосфор, сурьма, мышьяк и др.) превращается в неподвижный ион с единичным положительным зарядом. При этом проводимость полупроводника становится преимущественно электронной, т.к. обусловлена свободным электроном пятивалентного примесного атома. Такая примесь называется – донором (отдающим электрон), а полупроводник n-типа (negative).
При введении трехвалентной примеси получаем незаполненную валентную связь – дырку. При этом атом примеси становится неподвижным ионом с единичным отрицательным зарядом. Дырки примесного происхождения добавляются к собственным и проводимость становится преимущественно дырочной. Такие полупроводники называют дырочными или р-типа (positive), а примесь ее обуславливающую – акцепторной. (Собственную проводимость и собственный полупроводник обозначают буквой i (intrinsiс)).
Отрыв «лишнего» электрона от донора и «недостающего» для акцептора требует некоторой энергии – энергии ионизации или активации примеси. Поэтому при Т = 00К ионизация отсутствует, но в рабочем диапазоне температур ( 600С и выше) и, в частности, при комнатной температуре примесные атомы в кремнии и германии ионизированы практически полностью.
Поскольку в примесных полупроводниках концентрация электронов и дырок резко различны, принято называть носители преобладающего типа основными, а носители другого – не основными.
2. ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ И УРОВНИ ПОЛУПРОВОДНИКА
Как было отмечено в курсе физики, одиночный атом имеет дискретный спектр разрешенных уровней, находящихся на расстоянии h друг от друга. Причем, чем дальше находится от атома электрон, тем большей энергией он обладает. В устойчивом состоянии все электроны занимают минимально возможные энергетические уровни (состояния) и атом имеет минимальную потенциальную энергию. При получении дополнительной энергии электроны переходят на более высокие энергетические уровни – уровни возбуждения, и в случае, если энергии достаточно для преодоления притяжения ядра – электрон становится свободным.
Подтверждением дискретности энергетических уровней является то, что атомы различных веществ излучают или поглощают энергию в виде колебания строго определенной частоты. При этом частота излучения связана с дискретными уровнями атома соотношением
= (Еn –En-1)/h,
где En энергия электрона на n-ом уровне, h = 6,621027 эргсек.
В кристалле, вследствие взаимодействия атомов энергетические уровни (разрешенные для электронов одиночного атома) расщепляются, образуя зоны разрешенных уровней. Между разрешенными зонами находятся запрещенные, внутри которых нет энергетических уровней, дозволенных для электронов квантовыми законами.
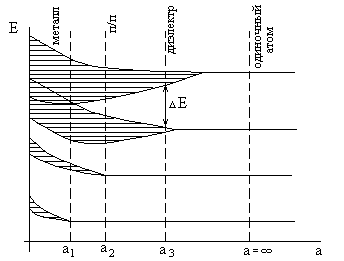
Рис.3
Структура энергетических зон зависит от рассояния между атомами (постоянной решетки “а”) рис.3, при уменьшении которго и наблюдается расщепление уровней. Нижние энергетические уровни практически не расщепляются, более высокие уровни одиночного атома расщепляются и при слабом взаимодействии атомов, образуя перекрещивающиеся зоны уровней. При этом запрещенные уровни энергии электронов отсутствуют.
Энергетические “расстояния” между разрешенными зонами (ширина запрещенной зоны) определяются энергией связи электронов с атомами решетки. Таким образом, кристалл с конкретным межатомным расстоянием характеризуется определенной зонной диаграммой, в которой разрешенные (уровни) зоны чередуются с запрещенными.
При Т = 0 К, для металлов (а), собственных полупроводников (б) и диэлектриков (в) зонные диаграммы можно представить следующим образом рис.4.
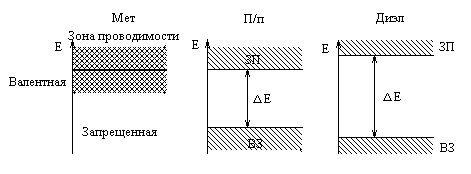
Рис.4
Верхняя разрешенная зона называется зоной проводимости, а расположенная под ней – валентной. При нулевой абсолютной температуре валентная зона полностью заполнена электронами, тогда как зона проводимости либо заполнена только в нижней части, либо полностью пуста.
Проводимость в твердых телах возможна только в случае, когда возможен переход электронов на ближайший энергетический уровень, причем в проводимости могут участвовать только электроны тех зон, в которых есть свободные уровни. Такие разрешенные уровни всегда имеются в верхней разрешенной зоне – ее и назвали зоной проводимости.
При температуре отличной от нуля, в валентной зоне (в верхней ее части), образуются свободные уровни, и эта зона также может обусловить проводимость.
Таким образом, все существенные процессы в полупроводнике и, следовательно, приборах на их основе можно изучать, рассматривая только две смежные зоны: зону проводимости и валентную зону.
Зона проводимости практически сплошная, энергия электрона в ней может меняться непрерывно, как у изолированного электрона в вакууме, поэтому электроны в этой зоне называются свободными (аналогично и для дырок в валентной зоне).
В случае примесных полупроводников зонные диаграммы иные рис.5,а. Здесь в запрещенной зоне имеются энергетические уровни донорной и акцепторной примесей. Следует отметить, что примесные уровни не сливаются с зонами и не расщепляются, т.к. концентрация примесей обычно мала, а значит расстояние между примесными атомами настолько велики, что взаимодействие их, необходимое для оьразования зон, практически отсутствует.
В собственном полупроводнике при температуре, отличной от абсолютного нуля, часть электронов переходит из валентной зоны на более высокие уровни – в зону проводимости, образуя носители (заряда) тока. Энергия необходимая для такого перехода, определяется шириной запрещенной зоны Е. Образовавшиеся в валентной зоне дырки – незаполненные энергетические уровни – могут заполняться другими электронами валентной зоны, что равносильно движению дырок в валентной зоне.
а б
Рис.5
Возврат электронов на незаполненный уровень валентной зоны из зоны проводимости – означает рекомбинацию электрона и дырки. В равновесном состоянии скорости термогенерации и рекомбинации одинаковы.
В примесных полупроводниках процесс образования свободных носителей при повышении температуры происходит иначе: в полупроводнике n-типа наряду с термогенерацией электронно-дырочных пар имеет место перехода электронов с донорных уровней в ближайшую зону проводимости, а в полупроводнике р-типа – из валентной зоны на близлежащие уровни акцепторов. Соответственно в полупроводнике n-типа образуются избыточные электроны, а в р-типа – дырки. Т.к. донорные и акцепторные уровни мелкие, то их энергия активации намного меньше энергии активации электронов валентной зоны.
Обычно в полупроводниках присутствует примесь как донорная, так и акцепторная, но в разных концентрациях. Разность Na Nд (или обратную) называют эффективной концентрацией соответствующей примеси и обозначают для кратности Nд* или Nа*.
Если в полупроводник введено равное количество донорной и акцепторной примеси, то такой полупроводник называют компенсированным (рис.5, б).
Для количественной оценки энергии (ширины запрещенной зоны – энергии активации) учтем, что в термодинамике для оценки энергии элементарных прпоцессов, используется величина kТ, где Т- абсолютная температура, k – постоянная Больцмана равная 1,380510-23 Дж/0С. Величина kТ близка к средней кинетической энергии свободных электронов (3/2 kТ), обусловленной их хаотическим движением в твердом теле.
В полупроводниковой электронной технике энергию электронов оценивают величиной q, где - разность потенциалов, которую прошел электрон, q - элементарный заряд, равный 1,61019Кл. Эту энергию принято измерять в электрон-вольтах (эта энергия, которую приобретает электрон пройдя разность потенциалов 1В, 1 эВ = 1,602101019Дж.)
Энергия, выраженная в электрон-вольтах, численно совпадает с соответствующей разностью потенциалов.
Выражая энергию kТ в эВ, приравняв их (kТ = q), получим одну из фундаментальных величин полупроводниковой физики и техники – температурный потенциал
T = kT/q T/11600. (5)
Несложно показать, что при комнатной температуре (Т = 293 К) температурный потенциал равен
Т = 0,025 В или 25 мВ.
Аналогично приведению kТ можно любую энергию Е, фигурирующую на зонных диаграммах, характеризовать энергетическим потенциалом , поделив Еi на q. Тогда энергетические уровни дна зоны проводимости и потока валентной зоны будем обозначать C и V, а их разность – ширину запрещенной зоны З т.е.
З = С - V (6)
З определяет энергию, необходимую для образования электронно- дырочных пар.
В случае полупроводников З = (0,2 – 1,5)В, для диэлектриков З > (2 – 3) В, а для полуметаллов (вырожденных полупроводников) З < (0,1 0,05) В.
Следует отметить, что ширина запрещенной зоны существенно зависит от температуры
З = ЗО ЗТ, (7)
где ЗО - ширина запрещенной зоны при нулевой температуре, З (В/0С) - температурная чувствительность (для кремния ЗО = 1,21 и З = 3104 В/0С, что дает при комнатной температуре З = 1,12 В).
Энергию, соответствующую середине запрещенной зоны, характеризуют электростатическим потенциалом полупроводника
Е = 0,5(С + V)
который часто принимают за начало отсчета других энергетических потенциалов.
3. РАСПРЕДЕЛЕНИЕ НОСИТЕЛЕЙ В ЗОНАХ
Разрешенные зоны содержат огромное количество уровней (1022 1023 в см3), на каждом из которых могут находиться электроны. Фактическое количество электронов зависит от концентрации доноров и от температуры. Чтобы оценить концентрацию носителей, необходимо знать распределение энергетических уровней и вероятность заполнения этих уровней.
Для невырожденных полупроводников вероятность заполнения уровня в зоне проводимости определяется распределением Максвелла-Больцмана:
,
где F - потенциал, характеризующий так называемый уровень Ферми. Этот уровень есть электрохимический потенциал системы частиц. С формальной точки зрения его можно определить как энергетический уровень вероятность заполнения, которого равна 0,5.
Вероятность наличия дырки в валентной зоне на уровне определяется аналогичной функцией
.
Если плотность уровней в зоне проводимости вблизи уровня обозначим через Р(), тогда Р()d будет количество уровней в диапазоне d. Умножая это количество уровней на вероятность заполнения уровней Fn() или Fp(), получим концентрацию свободных носителей с энергиями от до + d. Полную концентрацию свободных электронов n в интервале от с до сmax получим путем интегрирования по всей ширине зоны проводимости
.
Если принять зависимость P() ~ ()0,5, то полная концентрация свободных электронов :
, (10)
где Nc эффективная плотность уровней (состояний) в зоне проводимости
(11)
где mn эффективная масса электрона, m масса свободного электрона, равная 910-31кг.
Для концентрации дырок в валентной зоне получаем аналогично:
, (12)
где эффективная плотность уровней в валентной зоне
(13)
где mр – эффективная масса дырки. (Для кремния =2,8)
Учитывая закон действующих масс , путем перемножения (10) и (12) получаем