Метод аддитивной аппроксимации данных выборки ограниченного объема

Контрольная работа

Содержание

1. Мониторинг выбросов случайных процессов контролируемых параметров

2. Оценка критического объема выборок при традиционном подходе обработки стохастических массивов

3. Принципы обработки статистических данных в базисе аддитивной аппроксимации стандартными распределениями

4. Разработка методов аппроксимирующих вкладов значений выборки

5. Разработка метода имитационного моделирования для идентификации вероятностных моделей параметров на основе статистик малых выборок

6. Оценка моментов стохастического массива малой выборки

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Мониторинг выбросов случайных процессов контролируемых параметров

Мониторинг выбросов случайных процессов контролируемых параметров РТС предлагается осуществлять с использованием подхода, суть которого заключается в том, что с помощью квантования по уровню случайной функции xi(t, , S), характеризующей изменение во времени диагностируемого параметра, реальный процесс ухудшения функционирования РТС, выражающийся в отклонении (наличии выброса) значения параметра до j-го уровня квантования, моделируется дискретным процессом, как это показано на рисунке 1.

Рисунок 1 – Измерение характеристик выбросов хi параметра в диапазоне посредством квантования на q уровней

Состояние РТС отображается совокупностью N непрерывных контролируемых независимых параметров xi(t, , S) с соответствующими значениями допусков нижнего и верхнего уровней, которое можно представить в матричной форме:

. (1.1)

Постепенный отказ ТО сопровождается выходом значений k контролируемых параметров за пределы своих допусковых зон, тогда, применив пороговый оператор П(х) к каждой строке матрицы (1.1):

, (2)

где , получим булеву матрицу S состояний N контролируемых параметров:

. (3)

С помощью порогового оператора (2) состояние i-го параметра отображается трехместным кодовым вектором с одной единичной компонентой, положение которой в кодовом векторе определяет характер порядкового соотношения между текущим xi(t, , S) значением i-го параметра и его допусковых уровней. Для каждого параметра формируется дизъюнктивный индикатор выхода i-го параметра за допусковые уровни , множество которых образует вектор состояния ТО:

, (4)

число ненулевых компонент которого отображает число параметров, значения которых в текущий момент времени находятся за пределами допусковых зон.

Квазиматрица может быть представлена согласно посредством логического определителя в виде ряда упорядоченной последовательности:

. (5)

Упорядоченный кодовый вектор имеет только одну единичную компоненту, определяющую адрес каждого из k вышедших за допусковые зоны параметров. Пронумеруем соответствующие им векторы (ситуации) в произвольном, но фиксированном порядке и обозначим соответственно. Значения параметров в области, определяемой ситуацией , обозначим . Очевидно, что совпадает с переменной . Индекс этой переменной обозначим и введем депороговой оператор .

Поставим в соответствие каждой ситуации -мерный вектор . Тогда для любой ситуации выполняются равенства:

Положение единичной компоненты вектора меняется в зависимости от ситуации. Эти ситуации можно отобразить бинарной матрицей G, строки которой соответствуют номеру ситуации, а столбцы – координатам вектора .

. (6)

Матрица G однозначно определяет функцию . В том случае, когда выброс -го параметра контролируется по q уровням квантования диапазона допусковой зоны (см. рисунок 1), пороговый оператор сопоставляет непрерывно меняющимся переменным (параметрам) q-мерный вектор

а пороговый оператор сопоставляет времени пребывания значения контролируемого параметра над уровнем допуска t- мерный вектор :

Поскольку вектор будет функционально определяющим адрес i-го параметра, то представим матрицу состояний ТО в виде бинарной матрицы B, строки которой соответствуют ситуациям, а столбцы – компонентам вектора .

. (7)

Будем рассматривать столбцы матрицы В как независимые булевы переменные, а строки – как различные наборы этих переменных. При этом каждый столбец матрицы G (6) будет определять булеву функцию переменных , которая по наборам принимает значение . При на наборах значений переменных , не вошедших в матрицу В, матрица считается равной нулю.

Представив по табличному заданию булеву функцию в ДНФ для всех j, получим выражение переменных через :

Учитывая то, что при условии, что:

(8)

получим:

(9)

Таким образом, всякую непрерывно-логическую функцию f(x), можно реализовать посредством последовательного применения порогового П(x) и депорогового операторов и преобразования двоичных векторов.

Итак, в момент времени , где k – число ненулевых координат депороговых операторов , формируется максимальный элемент ранжированного ряда:

, (10)

то есть с помощью поканального () применения депорогового оператора в момент времени и элементарной операции раскрытия логического определителя выделяется экстремальный (максимальный) контролируемый параметр , поскольку кодовый вектор имеет только один ненулевой элемент:

(11)

Координаты i-го параметра , вышедшего за допусковые зоны, определяются ненулевой компонентой вектора или единичным элементом матрицы G как:

. (12)

В свою очередь может быть представлен двоичным вектором размерности с помощью функции кодопреобразования вектора :

где

Текущее значение i-го параметра представляется двоичным вектором посредством оператора аналого-цифрового преобразования:

Для разнородных параметров предварительно указанным процедурам должны предшествовать операции масштабирования и нормирования:

Таким образом, мониторинг значений диагностических параметров, представленных в виде непрерывных функций xi(t, , S) , осуществляется посредством квантования диапазонов , по уровню и последовательного применения порогового и депорогового операторов, что позволяет:

любую непрерывно-логическую функцию xi(t, , S) представить дискретным процессом, а именно: массивами амплитуд A(хi)={A1,..., An} и длительностей (хi)={1,..., n} выбросов значений диагностических параметров за допусковые зоны;
упорядочивать диагностические параметры по значимости (величине отклонения от заданных допусковых зон);
определять адреса параметров, значения которых вышли за допусковые зоны ;
наделять контролируемые параметры приоритетами в процессе диагностического мониторинга в зависимости от фактического состояния ТО.

2. Оценка критического объема выборок при традиционном подходе обработки стохастических массивов

Традиционные методы обработки статистических массивов ориентированы на обработку выборок большого объема для получения приемлемого по точности результата. Статистические погрешности зависят от трех параметров, с которыми оперируют при построении функции плотности и интегральной функции распределения, один из этих параметров - объем выборки n. Величина n должна выбираться по возможности большей. Так, например, при n =200 для средней по оси ординат части распределений относительные статистические погрешности составляют 20-40% .

При диагностике сложных ТО в нештатных режимах всегда приходиться иметь дело с предельно ограниченным объемом выборок значений выбросов контролируемых параметров. Поэтому возникает необходимость в обосновании и определении того минимального объема статистических данных, который обеспечивает достаточную для практики точность полученных результатов. Необходимый объем выборки определяют, используя неравенство Чебышева к выборочному среднему:

(14)

где Х - эмпирическое среднее; Dx - дисперсия случайной величины Х; mx - математическое ожидание величины Х; >0 - вероятность расхождения величин Х и mx.

Из (14) получают соотношение, позволяющее определить необходимый объем выборки:

(15)

где - среднеквадратическое отклонение случайной величины Х; - доверительная вероятность.

Графическое решение (15) представлено на рисунке 2. Следует отметить, что использование неравенства Чебышева при вычислении объема выборки дает завышенную оценку для n, однако порядок объема выборки остается достаточно большим.

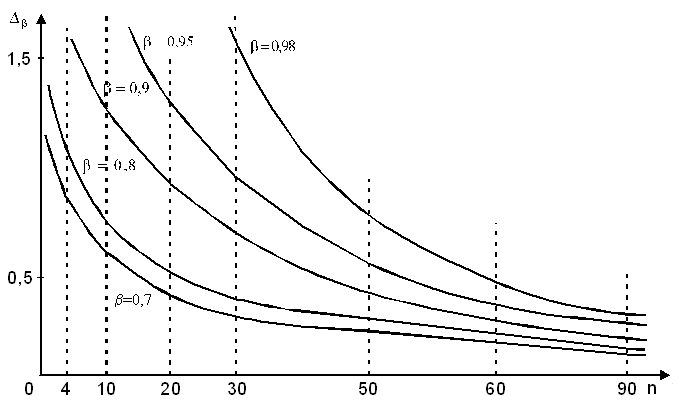
Рисунок 2 – График зависимости объема выборки n от и

В случаях, когда для аппроксимации функции распределения используется один из известных законов распределения, задача определения объема выборки n решается методами статистической проверки гипотез . Объем выборки определяется при заданной погрешности оценки ср, доверительной вероятности и коэффициента вариации V. Так, для экспоненциального распределения, справедливо:

(16)

где - Хи-квадрат распределение для уровня значимости =1- с числом степеней свободы 2n.

Решение уравнения (16) представлено на рисунке 3.

Для нормального распределения случайной величины объем выборки определяется по формуле:

, (17)

где - распределение Стьюдента для доверительной вероятности с n-1 степенями свободы.

График зависимости (17) приведен на рисунке

Рисунок 3 – График зависимости n=F(ср) для экспоненциального закона распределения

Рисунок 4 – График зависимости объема выборки n от коэффициента вариации V, погрешности оценки ср и доверительной вероятности для нормального закона

Можно выделить несколько недостатков методов обработки статистического материала, если объемы выборок значительны. Статистическая обусловленность, или достоверность эмпирического распределения неодинакова в различных зонах (в зависимости от степени нарушения предпосылок закона больших чисел):

наибольшей статистической обусловленностью обладает зона больших частот;
«хвосты» эмпирического распределения обусловлены хуже (так как приходящееся на них общее число событий относительно мало);
зоны усечения эмпирического распределения (соответствующие отсутствующим наблюдениям) имеют нулевую обусловленность.

Анализ соотношений (14)(17) и рисунков 24 свидетельствует, что традиционные методы оказываются неприемлемыми для обработки данных о выбросах, представленных, как правило, крайне немногочисленными статистическими данными (не более 10 выбросов), и необходимо привлечение специального математического аппарата по обработке статистик малых выборок.

Патентный поиск в области устройств по идентификации законов распределения по малому числу данных класса G 06 F за последние 15 лет позволяет сделать следующие выводы: известные алгоритмы является узкоспециализированными на идентификацию только одного вида закона распределения, не делается вывод о виде закона распределения измеряемой случайной величины.

Таким образом, для получения приемлемых по достоверности результатов обработки статистических данных традиционные методы требуют объемов выборок в сотни значений, при этом классические методы неизбежно приводят к потере части информации, имеющейся в выборке. При малом числе данных эти методы несостоятельны, что зачастую приводит к отказу от обработки статистического материала, который может нести важнейшую информацию о ТО. Поэтому традиционные методы и разработанные на их основе ИВК и статистические анализаторы не могут отвечать требованиям функционального диагностирования сложных ТО в нештатных режимах, для которых характерны быстрое изменение состояния и недопустимость длительного пребывания в предаварийном режиме. Очевидно, что для обработки эмпирических данных о выбросах случайных процессов контролируемых параметров необходимо использование математического аппарата статистик малых выборок.

3. Принципы обработки статистических данных в базисе аддитивной аппроксимации стандартными распределениями

Выборку следует считать малой, если при ее обработке методами, основанными на группировке наблюдений, нельзя достичь заданных точности и достоверности. Выборку можно считать большой, если при ее обработке имеется возможность перейти к группировке наблюдений без ощутимой потери информации. При этом должны достигаться заданные точность и достоверность. Но самым существенным, что следует из определения малой выборки, является необходимость при обработке малой выборки индивидуального подхода к каждой отдельной реализации.

Получение оценки функции плотности. При решении задачи оценивания плотности или функции распределения по малой выборке используются некоторые приемы как гистограммного и метода полигональных оценок, так и вообще традиционного подхода: приписывание некоторой функции каждой реализации случайной величины, так и "распределение" некоторой элементарной вероятности по всему интервалу существования функции .

Именно эти приемы использовались для получения оценки плотности распределения f*(x) непосредственно по выборке. В работе данная оценка называется эмпирической компонентой полной оценки.

Поскольку информация, заложенная в малой выборке, ограничена, то очевидно, для повышения эффективности оценивания, как отмечалось выше, необходимо привлекать дополнительную информацию, которая содержится в априорных данных. По априорным данным также можно отыскать оценку плотности f0(x).

В целом, получение полной оценки плотности распределения будет состоять из следующих этапов:

анализ и формализация априорного массива в виде оценки f0(x);
накопление и формализация в виде оценки fn(x) эмпирического массива;
объединение априорной и эмпирической информации, получение полной оценки f*(x).

Априорная компонента. Выбранная f0(x) должна полностью соответствовать уровню знаний о случайной величине X. Для этого при выборе f0(x) надо потребовать, чтобы она имела максимально возможную энтропию при заданных условиях в виде конкретных априорных данных. При заданных условиях f0(x) должна быть выбрана такой, чтобы обеспечивался максимум функционала

. (18)

Задача сводится к отысканию f0(x) как функции от x, обеспечивающей экстремум интеграла

, (19)

где G – функционал.

При этом могут накладываться ограничивающие условия вида:

; (20)

где О1, О2,..., Оn - заданные ограничения, g1, g2,..., gn - некоторые функции.

Известно, что f0(x), обеспечивающая экстремум интеграла (19), может быть найдена из уравнения

(21)

где - неопределенные множители, которые вычисляются с помощью подстановки f0(x), удовлетворяющей уравнению (21) в равенствах (20).

Допустим, что известен интервал изменения случайной величины и существует единственное условие

Тогда, учитывая, что , вычислим для составления уравнения (21) частные производные функций G(x,f0) и g1(x,f0) и, подставив их в уравнение (21), получим:

, (22)

то есть максимум энтропии Н0 обеспечивается при . Подставив f0(x) в (22), получим

(23)

Таким образом, априорным данным в виде интервала изменения случайной величины (a,b) адекватна априорная компонента f0(x) оценки плотности распределения f*(x) в форме плотности равномерного распределения (23).

Эмпирическая компонента. Пусть f(x) - неизвестная плотность распределения вероятностей случайной величины X, заданная на действительной оси R. Задана конечная совокупность реализаций , случайной величины X, то есть имеется эмпирический массив данных. Необходимо по заданному массиву построить fn(x) - эмпирическую компоненту оценки плотности f(x). Оценка должна быть состоятельной, несмещенной и эффективной. Априорно полагается, плотность f(x) – непрерывная или хотя бы кусочно-непрерывная функция и удовлетворяет условию f(x)>0 на интервале .

Эмпирическая компонента fn(x) строится путем графического суммирования упорядоченных значений выборки x1,...,xn с построением вокруг каждого значения выборки некоторого элементарного распределения, называемого вкладом или ядром.

Выражение для эмпирической оценки в этом случае примет вид:

(24)

где d - полуинтервал диапазона изменения величины X, C(d) - амплитуда или высота вклада.

Высота вклада C(d) может быть вычислена следующим образом:

, (25)

где (d,x) - ядро вклада при xi=0.

Полная оценка функции плотности распределения определяется с учетом (24) и (25) следующим выражением:

(26)

где - вероятность полного получения оценки по априорным данным; - коэффициент нормировки i-ой реализации.

Использование методов, основанных на аддитивной композиции, наталкивается на достаточно серьезные теоретические затруднения. Эмпирическая функция распределения (26) – аддитивная конструкция из стандартных (симметричных) распределений, а на основании центральной предельной теоремы в различных формах в доказательстве А. М. Ляпунова предрешена быть описанной нормальным законом. Следовательно, возможность идентификации статистических массивов малых выборок законами распределений, отличных от нормального, является весьма сомнительной. Докажем, что при невыполнении условий центральной предельной теоремы, возможна идентификация не только нормальным законом, а семейством бесконечно делимых предельных распределений.

Теоретические предпосылки аппроксимации вероятностных функций распределений аддитивной композицией стандартных распределений. Различные формы закона больших чисел утверждают одно: факт сходимости по вероятности тех или иных случайных величин (с.в.) к определенным постоянным. Все формы центральной предельной теоремы посвящены установлению условий, при которых возникает нормальный закон распределения. Так как эти условия на практике весьма часто выполняются, нормальный закон является самым распространенным из законов распределения, наиболее часто встречающимся в случайных явлениях природы. Он возникает во всех случаях, когда исследуемая случайная величина может быть представлена в виде суммы достаточно большого числа независимых (или слабо зависимых) элементарных слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму.

Долгое время нормальный закон считался единственным и универсальным законом ошибок. В настоящее время взгляд на нормальный закон как на единственный и универсальный должен быть пересмотрен. Опыт показывает, что в ряде процессов измерения и производства наблюдаются законы распределения, отличные от нормального. Это утверждение чисто опытного характера, однако существуют и теоретические обоснования анормальности многих наблюдаемых явлений.

Кажущаяся незыблемость предельных теорем зачастую заставляет многих авторов обходить молчанием явления, утверждения и даже математически доказанные теоремы, опровергающие их абсолютность. Тем не менее, работы в данной области ведутся давно и требуют на данном этапе развития техники тщательного изучения. Стоит обратить внимание на следующие математические факты.

Предельные теоремы отличаются той особенностью, что доставляемая ими аппроксимация оказывается тем менее действенной, чем меньше вероятность р. Оказалось, что в случае малых р для приближений надо привлекать не нормальное, а другое распределение (теорема Пуассона):

(27)

где распределение Пуассона. Чебышевым была доказана теорема - закон больших чисел и тогда же поставлен вопрос об уточнении предельных аппроксимаций распределений Yn и предложено это делать за счет добавления к нормальному распределению конечной части некоторого зависящего от n ряда. Тот ряд, который использовал Чебышев, впоследствии действительно оказался хорошей основой для построения уточненных аппроксимаций (ряд Чебышева-Крамера или разложение Эджворта-Крамера).

Теорема Ляпунова и построенные Марковым примеры последовательностей независимых случайных величин, для которых центральная предельная теорема неверна, естественно ставят вопрос о построении предельных теорем, связанных не с нормальным предельным законом, а с какими-либо другими. На разумность такой постановки вопроса указывает и теорема Пуассона.

Леви дал описание класса всех функций распределения G(x), появляющихся в качестве предельных в соотношении:

(28)

где выбором положительных постоянных Вm можно распоряжаться по своему усмотрению (символ означает слабую сходимость распределений). Описание класса осуществляется в терминах характеристических функций, соответствующих распределениям G(x). G(x) называется классом устойчивых законов (сейчас называют строго устойчивых).

Колмогоровым и Гнеденко показано, множество U всех распределений, которые могут появиться в качестве предельных для распределений сумм Snm, совпадает с множеством всевозможных распределений на вещественной оси. Чтобы убедиться в том, что любая функция распределения U(x) может выступать в качестве предельной, достаточно рассмотреть последовательность серий случайных величин {Xnj}, n=1,2,..., в которых Xn1 подчинены распределению U(x), при любых n, а Xnj=0 с вероятностью 1 для всех j 2, n1. Кроме того, следует ввести в постановку задачи разумные общие ограничения: специфические свойства предельных функций распределения должны определяться тем, что они являются предельными для сумм возрастающего числа независимых случайных величин, причем роль каждого отдельного слагаемого должна быть при n исчезающе малой.

Обширность класса предельных законов при такой постановке вызывает сомнение до настоящего времени. Однако еще де Финетти ввел понятие безгранично делимых распределений и дал описание в терминах характеристических функций небольшой части класса этих распределений, а Колмогоров описал все распределения из с конечной дисперсией. Полное описание класса дали Леви и Хинчин, Хинчин доказал, что U совпадает с . Обобщающие теоремы Ляпунова и Линдеберга содержат некоторые достаточные условия сходимости распределений сумм Sn к предельному закону без условия предельной пренебрегаемости.

В работах Кароблиса, посвященных проблеме асимптотических приближений распределений сумм независимых случайных величин, развивается постановка вопроса, в которой аппроксимирующим является не одно распределение, а параметрическое семейство распределений.

Помимо (27), (28) и других теоретических заключений, на возможность аппроксимации не только нормальным распределением указывает и неравенство Берри - Эссеена, которое оценивает расхождение суммы независимых с.в.: для некоторого А>0 и независимых с.в. X1,...,Xn с нулевым математическим ожиданием, конечной дисперсией справедливо:

(29)

где Ф(X) – функция нормального распределения.

Причем порядок оценки (29) нельзя улучшить, не вводя дополнительных предположений о распределениях рассматриваемых случайных величин. До сих пор нет единого мнения по выбору величины А, в некоторых работах указывается А=0.82, при которой выполняется неравенство. Однако очевидна зависимость величины расхождения суммы с.в. от числа слагаемых. При малом числе слагаемых, например, величина оказывается существенной 0,259, то есть расхождение с нормальным законом велико, и целесообразно в качестве предельного использовать другое распределение. Как было показано выше, при аппроксимации эмпирических распределений в качестве предельных необходимо использовать целый класс безгранично делимых распределений .

Итак, современная теория суммирования случайных величин предполагает коррекцию результатов классических предельных теорем и вводит свой специфичный аппарат для доказательства того факта, что в качестве предельных необходимо рассматривать не одно (нормальное) распределение, а целый класс распределений, при этом неравенство Берри - Эссеена позволяет получить количественную оценку расхождения аддитивной аппроксимации с нормальным распределением.

Статистический эксперимент. Для опытной оценки степени расхождения суммы независимых случайных величин от нормального закона при невыполнении условий центральной предельной теоремы, был проведен эксперимент, заключающийся в генерации двух массивов нормальных чисел по формуле:

, (30)

где Ri - равномерно распределенное число.

Как видно из (30), данный метод генерации основан на центральной предельной теореме.

Первый массив чисел генерировался стандартным способом по формуле (30). В качестве Ri были взяты равномерно распределенные числа с математическим ожиданием Mx=0,5 и 2=1/12. Второй ряд чисел генерировался также по (30), но математическое ожидание равномерных чисел варьировалось по различным законам, что нарушает условия центральной предельной теоремы. Степень нормальности этих массивов проверялась критериями Шапиро-Уилкса, Смирнова-Мизеса-Крамера. Графики зависимости величины критерия нормальности от объема выборки для некоторых распределений, полученные с помощью разработанного пакета программ, приведены в Приложении А. По оси ординат отложены значения статистики критерия Мизеса-Смирнова-Крамера, по оси абсцисс – количество чисел в выборке. Из графиков видно, что при невыполнении условий центральной предельной теоремы нормальность полученного распределения нарушается, и степень расхождения растет с ростом числа чисел в массиве, что подтверждает возможность аппроксимации статистических данных различными законами распределений.

4. Разработка методов аппроксимирующих вкладов значений выборки

Метод вкладов основан на:

а) использовании дополнительной, кроме самой выборки, априорной информации о случайной величине Х;

б) индивидуальном подходе к каждой реализации выборки;

в) «распределении» информации, полученной от отдельной реализации выборки, на конечном интервале d.

Априорной информацией может быть предположение относительно истинной плотности распределения f(x) случайной величины Х. Пусть функция f(x) удовлетворяет следующим условиям:

1) f(x) 0 при a x b;

f(x) 0 при x<a и x>b, (31)

где [a, b] - интервал возможных значений Х.

2) f(x) - непрерывная функция и внутри [a, b] не имеет очень крутых подъемов и спадов.

В зависимости от того, какой конкретный вид f(x) будет выбран, различают метод прямоугольных вкладов, метод треугольных вкладов, метод гауссовых вкладов и т.д.

Метод прямоугольных вкладов Наличие априорной информации вида (31), даже при отсутствии реализаций Х, позволяет построить оценку плотности f*(x). На имеющемся уровне знаний ни одной из возможных реализаций внутри интервала [a, b] нельзя отдать предпочтение.

Такой особенностью обладает равномерное распределение:

(32)

Индивидуальный подход к каждой отдельной реализации хi выборки заключается в том, что каждой реализации приписывается элементарная плотность, то есть имеет место прямоугольная форма ядра или функция вклада будет иметь следующий вид:

(33)

где d - ширина функции вклада.

Функция вклада задается симметрично относительно xi на конечном интервале длиной d (рисунок 5).

Рисунок 5 – График функции вклада xi(x)

Линейное суммирование с заданными весами априорной плотности (32) и вкладов (33) для всех n элементов выборки приводит в итоге к искомой оценке плотности:

(34)

В выражении (34) с помощью весового коэффициента 1/(n+1) осуществляется нормирование оценки плотности f*(x).

Для построения оценки f*(x) необходимо установить интервал изменения случайной величины. Общее правило, справедливое для всех исследуемых законов распределения и для всех методов, состоит в вычислении границ интервалов из соотношения P{a<x<b}=0.9970.999. Формула (26) еще не дает приемлемой эмпирической функции плотности по n значениям случайной величины Х, так как что для некоторых значений xi функции вклада xi(x) будут выходить за пределы области [a, b] и, значит, функция fn(x) будет отлична от нуля и вне этой области. Последнее же противоречит априорному условию. Поэтому выходящую за пределы [a, b] часть площади данного вклада xi(x) будем отбрасывать, а над оставшимся основанием прямоугольника, лежащим внутри [a, b], равномерно надстраивать площадь, равную отброшенной. На рисунке 6 изображены диаграммы построения эмпирической функции плотности вероятности для пяти значений выборки.

В методе прямоугольных вкладов в качестве функции вклада используется равномерное распределение. Использование этого вклада упрощает построение эмпирической функции распределения, но данный вклад не является единственно возможным и оптимальным.

Рисунок 6 – Диаграммы построения эмпирической функции распределения f*(x) методом прямоугольных вкладов

Метод треугольных вкладов. В качестве функции вклада не обязательно использовать прямоугольник, тем более, что при применении прямоугольного вклада не выделяется точка xi, которая зафиксирована при конкретном измерении величины Х. Действительно, нет необходимости приписывать точке xi абсолютное значение, но считать в этой точке плотность вклада максимальной по сравнению с другими в интервале d вполне целесообразно. Этому больше всего будет отвечать функция вклада в виде элементарного распределения Симпсона (треугольника). Распределение Симпсона симметрично, а элементарное распределение берется шириной d и высотой h. Метод треугольных вкладов отличается от метода прямоугольных вкладов только формой функции вклада:

(35)

На рисунке 7 изображен график функции вклада Симпсона xi(x).

Рисунок 7 – График функции вклада Симпсона xi(x)

Когда нет ни одной реализации случайной величины, учитывая предварительные условия, можно записать плотность распределения в виде, не противоречащем имеющейся информации о Х:

(36)

где c=(b+a)/2.

Аналогично методу прямоугольных вкладов линейное суммирование с заданными весами априорной плотности (3.48) и вкладов (35) для всех n элементов выборки приводит в итоге к искомой оценке плотности (34). При алгоритмической реализации для построения (34) все обрабатываемые значения упорядочивают по возрастанию, и как таковое, суммирование осуществляется только в точке пересечения вкладов – результатов предыдущего суммирования и нового вклада. Таким образом, построение происходит "внахлест" – меньшая площадь вклада накладывается на большую – результат предыдущего суммирования. Затем проводится сглаживающая ломаная, соединяющая вершины вклада, так как это делается при построении полигональной оценки.

На рисунке 8 изображены диаграммы построения эмпирической функции плотности вероятности методом треугольных вкладов для тех же пяти значений выборки, что и для прямоугольных вкладов на рисунке 6. Аналогично выходящую за пределы [a, b] часть площади данного вклада xi(x) отбрасывают и равномерно надстраивают площадь, равную отброшенной, над оставшимся основанием прямоугольника, лежащим внутри [a, b].

Метод гауссовых вкладов. В качестве функции вклада можно использовать нормальное распределение, которое является симметричным. Поскольку дисперсия вклада d должна быть конечной, то, строго говоря, в качестве функции вклада необходимо использовать усеченное нормальное распределение, то есть функция вклада имеет вид:

Рисунок 8 – Диаграммы построения эмпирической функции распределения f*(x) методом треугольных вкладов

,(37)

где с=[F(3)-F(-3)]-11.0028, - функция нормального распределения.

На рисунке 9 изображен график функции гауссова вклада xi(x).

Априорная функция вклада:

,(38)

где c=(b+a)/2.

Линейное суммирование с заданными весами априорной плотности (38) и гауссовых вкладов (37) для всех n элементов выборки приводит в итоге к искомой оценке плотности (36).

На рисунке 10 изображены диаграммы построения эмпирической функции плотности вероятности для тех же пяти значений выборки, что и для прямоугольных и треугольных вкладов на рисунках 6, 8. Аналогично выходящую за пределы [a, b] часть площади данного вклада xi(x) отбрасывают и равномерно надстраивают площадь, равную отброшенной, над оставшимся основанием прямоугольника, лежащим внутри [a, b].

Рисунок 9 – График функции гауссова вклада xi(x)

Рисунок 10 – Диаграммы построения эмпирической функции распределения f*(x) методом гауссовых вкладов

Таким образом, независимо от вида функции вклада в результате геометрических построений получают эмпирическую функцию плотности вероятности (26), которую теперь необходимо отнести к какой-либо теоретической функции распределения. Для этого интервал [a, b] разбивается на k равных интервалов, и вычисляются частные площади Si, то есть площади секторов, ограниченные пределами i-го интервала, i = 1,2, ... , k (см. рисунок 6). Следующий шаг - это получение значений оценки функции плотности вероятности по формуле:

(39)

где S* - площадь, ограничиваемая эмпирической функцией распределения (26); pi* - есть вероятность того, что реализации данной выборки, будут иметь значения, находящиеся в i-ом интервале диапазона [a, b].

Для того чтобы отнести полученную функцию распределения к одному из теоретических законов распределения надо для каждой теоретической функции распределения получить значения pi(x) и, используя одним из критериев согласия, определить меру расхождения между теоретическим и эмпирическим распределением.

Следует отметить, что нельзя применять общераспространенные критерии согласия (критерий 2, критерий Колмогорова), так как для их использования необходимо знать объем выборки n, а в процессе работы метода происходит равномерное «размазывание» случайной реализации по сектору, значит использовать конкретное значение объема выборки нельзя. Тогда целесообразно воспользоваться методом наименьших квадратов для того, чтобы отнести полученную оценку (26) к одной из теоретических функций распределения:

, (40)

где - эмпирическое и теоретическое значения вероятностей i-го () разряда соответственно.

Статистику (40) вычисляют для набора наиболее распространенных на практике законов распределений. Полученные значения критерия согласия в результате одновременной идентификации эмпирического распределения одним из набора теоретических распределений задают отношение порядка вероятностей соответствия статистических моделей в виде неубывающего упорядоченного ряда:

. (41)

Основываясь на сравнительном анализе членов ранжированного ряда (41) и выделяя максимальный (первый) элемент, делают вывод о соответствии эмпирического закона распределения тому или иному, например, j-му стандартному распределению с вероятностью Pj(V).

Укрупненный алгоритм аддитивной аппроксимации эмпирического распределения методом вкладов приведен на рисунке 11.

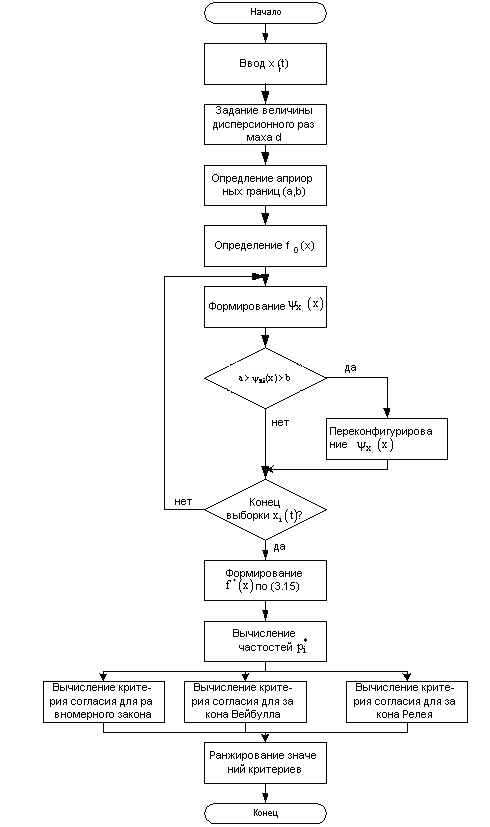
Рисунок 11 – Укрупненный алгоритм аддитивной аппроксимации эмпирического распределения методом вкладов

Рассмотренные выше алгоритмы и методы аддитивной аппроксимации малой выборки являются графическими методами. Альтернативным решением при обработке статистических массивов малой выборки является использование метода имитационного моделирования.

Идея алгоритма состоит в следующем: как и в методе вкладов используется некоторая дополнительная информация относительно неизвестного истинного распределения и при построении эмпирической функции распределения учитывается флуктуационный характер реализующихся в опыте значений случайной величины Х и поэтому не придается осуществившимся событиям некоторая абсолютная значимость.

Метод имитационного моделирования основан:

на использовании дополнительной, кроме самой выборки, априорной информации о случайной величине Х;
на индивидуальном подходе к каждой реализации выборки;
на «распределении» информации, полученной от отдельной реализации выборки, на конечном интервале d.

Если априорно ни одной из возможных реализаций внутри интервала [a, b] не придается предпочтение, то в качестве функции вклада можно использовать равномерное распределение (32). Поэтому индивидуальный подход к каждому случайному значению xi случайного процесса Х состоит в генерации равновероятно распределенных псевдослучайных чисел в d-окрестностях значений xiХ, (рисунок 12).

Рисунок 12 – Представление элемента хi совокупностью значений

Если границы d-окрестностей выходят за пределы отрезка [a, b], то получаемые при генерации числа равномерно распределяются в диапазоне [a, xi+d/2] или [xi-d/2, b]. Количество генерируемых при поступлении очередного значения хi чисел определяется из условия требуемой достоверности. Использование генерации равномерно распределенных чисел не является единственно возможной (например, аналогично методу треугольных вкладов нет необходимости случайному значению хi придавать абсолютного значения, но считать в этой точке плотность максимальной по сравнению с другими в интервале d вполне целесообразно, поэтому можно генерировать числа с плотностью возрастающей к xi и убывающей к xi-d/2, и xi+d/2).

Таким образом, осуществляется переход от малой выборки (n=510) к выборке стандартного объема данных, представляющей собой аддитивную суперпозицию (n+1) псевдореализаций, причем основная из них ограничена диапазоном [a,b] с математическим ожиданием 0.5[b+a]. Такая модель выборки позволяет строить эмпирическую гистограмму с применением известных классических методов и приемов, определять оценки среднеквадратичного отклонения и среднего значения процесса Х, коэффициенты асимметрии и эксцесса, другие моменты. Для полной характеристики эмпирического распределения производится его идентификация одним из стандартных законов распределения в дифференциальной и интегральной формах.

С целью повышения достоверности идентификации диагностических данных малого объема целесообразно осуществлять параллельную обработку несколькими методами с последующим ранжированием результатов идентификации и принятием окончательного решения на основе мажоритарного принципа.

6. Оценка моментов стохастического массива малой выборки

Пусть имеется непрерывная случайная величина X с неизвестной F(x) и выполнена серия наблюдений, результатом которой служит малая выборка. В качестве точечной оценки математического ожидания величины X по принципу максимального правдоподобия, обычно берется среднее арифметическое наблюдений

(42)

Эта оценка обладает свойствами состоятельности, несмещенности и эффективности. Однако для малой выборки самым существенным свойством оценки является ее эффективность. Для выборок малого объема оценка вида (42) не обеспечивает удовлетворительной точности. Интервальная оценка также не может использоваться в оценивании закона распределения, например, при вычислении критерия Пирсона.

Для повышения эффективности оценивания необходимо перейти от (42) к процедуре, основанной на формальном определении математического ожидания:

(43)

согласно которой требуется первоначально построение оценки f*(x) плотности распределения f(x), а для построения f*(x) необходимо реализовать один из алгоритмов вычисления оптимальной оценки, изложенный в предыдущих пунктах.

При конечном объеме выборки для получения точечной оценки дисперсии, удовлетворяющей условиям состоятельности, несмещенности и эффективности, используют следующую формулу

(44)

Однако, как и при определении оценки математического ожидания формула (44) недостаточно точна, поэтому рекомендуется воспользоваться следующей формулой:

(45)

Оценки по формулам (43) и (45) имеют меньшую дисперсию по сравнению с (42), (44), а следовательно, являются более эффективными.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ