ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ

Контрольная работа

ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ

Содержание

1. О гипотезе квантов света

2. Виды переходов между энергетическими уровнями в квантовых системах

3. Переходы с излучением и поглощением, их вероятность

4. Связь между коэффициентами Эйнштейна

5. Релаксационные переходы

6. “Форма” и ширина спектральных линий

7. Виды уширения спектральных линий

8. Интегральная вероятность перехода с учётом формы линии

9. Поглощение излучения средой. Эффект насыщения поглощаемой мощности

10. Коэффициент поглощения, влияние насыщения на форму контура линии поглощения

11 Инверсия населённостей уровней. Коэффициент усиления

12. Насыщение коэффициента усиления

13. Принцип усиления света квантовой системой

Литература

1. О гипотезе квантов света

Гипотеза об излучении света квантами была выдвинута в 1900 г. М.Планком и в дальнейшем развита А.Эйнштейном при построении теории излучения. Напомним читателю, что законы Кирхгофа, Стефана-Больцмана и Вина, а также закон Релея-Джинса (в области малых частот излучения) для поведения объёмной спектральной плотности излучения “абсолютно черного” тела ([] = Дж·см-3·с) удавалось объяснить, используя аппарат и законы термодинамики. В то же время экспериментально наблюдаемое снижение величины при росте частоты излучения объяснить не удавалось. Из термодинамических представлений и модели излучения как совокупности гармонических осцилляторов со средней энергией =kT (T–температура тела, k–постоянная Больцмана) можно было получить только увеличение при росте , что было названо «ультрафиолетовой катастрофой». М. Планку первому удалось устранить это противоречие, предположив, что свет излучается порциями (квантами) с различными энергиями, кратными 0=h (h=6,62·10-34 Дж·с–постоянная Планка), а непрерывный спектр излучения нагретых тел является суперпозицией этих квантов. Используя законы статистики, он нашел, что как функция и Т имеет вид

. (1)

где M'= определяет число типов колебаний (мод) в единице объёма и в интервале частот от до +d, если излучение происходит в объёме, превышающем длину волны излучения .

Из выражения (1) вытекают все законы излучения. В самом деле, интегрируя его по можно получить, что ~Т4 (закон Стефана-Больцмана); тот факт, что зависит от /Т, приводит к закону Вина «смещения» максимума (): макс·Т=const (или макс/Т=const), а в пределе малых и больших (по обе стороны от экстремума зависимости () получаем снижение (закон Релея-Джинса).

В соответствии с квантовой теорией, квант электромагнитного излучения, или фотон, является элементарной квазичастицей, имеющей нулевую массу покоя и движущейся в вакууме с максимальной скоростью движения элементарных частиц материи (с3·108 мс1), а электромагнитное излучение оптического диапазона (свет) представляет собой поток фотонов. Момент количества движения (спин) фотона равен =h/2, и к фотонам применима статистика Бозе-Эйнштейна (фотоны являются “бозонами”), а для бозонов, в противоположность фермионам (например, электронам в атоме), не существует ограничений в числе частиц, занимающих данное квантовое состояние. Это допускает неограниченное число фотонов в световой волне и любую величину её энергии.

Квантовая электроника (как и квантовая радиофизика) имеет дело, как правило,– со связанными электронами, входящими в состав атомов, молекул, кристаллов, которые, наряду с другими способами накопления энергии (колебания, вращение молекул и др.) и определяют значения внутренней потенциальной энергии этих частиц и систем в целом.

2. Виды переходов между энергетическими уровнями в квантовых системах

Рассматриваемые нами квантовые системы представляют собой ансамбль квантовых частиц (атомов, молекул и др.), при этом каждая частица обладает набором дискретных стационарных энергетических (квантованных) состояний, между которыми возможны квантовые переходы. В состоянии термодинамического равновесия (ТДР) распределение частиц по уровням энергии в ансамбле описывается законом Больцмана, например, для уровней «1» и «2», если E2>E1:

. (2)

где Статистический вес – степень “вырождения” уровня g, обозначает число возможных состояний с различными квантовыми числами, имеющих одно и то же значение энергии (g=1–для невырожденных, а g=2, 3 и т.д.–для вырожденных уровней). Отметим, что во внешнем магнитном поле (для атомов) и в электрическом поле (для молекул) вырождение уровней снимается, и они «расщепляются» на соответствующее число компонент (эффекты Зеемана и Штарка).

Энергетические состояния изолированных частиц (атомов, молекул) и переходы между ними подразделяются на: электронные (между уровнями, отвечающими различным состояниям электронов), колебательные (для атомов в кристаллической решетке, молекул в газе и др.), вращательные (для молекул), а также–на уровни и переходы тонкой структуры (ТС) и сверхтонкой структуры (СТС) атомов (Таблица 1).

Таблица 1 Значение граничных энергий Е, эВ, для переходов различных типов.

(1эВ=1,6·1019 Дж)

Тип уровней (переходов между уровнями)	Диапазон значений энергии перехода Е = Е2 – Е1, эВ	Спектральный диапазон излучательного перехода
Электронные	10 и более 3…10 1,5…3 0,1…1,5	Рентгеновский оптический (УФ) оптический (видимый) оптический (ИК)
Колебательные	0,01…0,1	оптический, (ИК)
Вращательные	0,001…0,01	СВЧ (мм)
тонкой структуры (ТС) атома	10-4…10-2	СВЧ (мм, см)
сверхтонкой структуры (СТС) атома	10-5…10-4	СВЧ (см, дм)

3. Переходы с излучением и поглощением, их вероятность

Рассмотрим квантовую частицу (атом) с двумя энергетическими уровнями: «1»–нижний и «2»–верхний. Для такой частицы возможны три вида радиационных переходов между уровнями: спонтанное излучение, поглощение и индуцированное (вынужденное) излучение (рис. 1 и Таблица 2). Излучательный квантовый переход–это переход, совершаемый квантовой системой (атомом, ионом, молекулой и др.) из состояния с большей энергией Е2 в состояние с меньшей Е1, сопровождается испусканием кванта электромагнитного излучения (фотона), с частотой v21, удовлетворяющей соотношению hv21=Е=Е2–Е Вероятности излучательных переходов определяются правилами отбора, величиной Е и другими свойствами энергетических уровней. Очевидно, что структура энергетических уровней квантовой частицы определяет совокупный спектр излучаемых фотонов.

Рис. 1 Виды переходов между уровнями

Спонтанное (самопроизвольное) излучение происходит независимо от внешних воздействий на квантовую систему, при этом испускается фотон с энергией h=Е2–Е1 и частотой , поляризация и направление излучения которого произвольны. Момент спонтанного перехода принципиально не может быть предсказан, и потому можно говорить лишь о вероятности такого перехода Wc, которая определяется исключительно свойствами самой системы:

Wc = A21, (3)

где A21 – коэффициент Эйнштейна для спонтанного излучения, характеризует число переходов в расчёте на одну частицу за 1с, размерность [Wc]=[A21]=c– Заметим, что число W, в отличие от математической вероятности, может принимать любые значения, и обычно в оптическом диапазоне значительно превышает единицу. Случайность спонтанных переходов приводит к тому, что различные атомы (квантовые системы) излучают независимо и несинхронно. Поэтому спонтанное излучение ненаправленно, некогерентно, неполяризованно и немонохроматично. Такое излучение в оптическом диапазоне испускают все источники света (лампы накаливания, люминесцентные лампы, электрические разряды в газах и др.).

Следующие два вида переходов – поглощение и индуцированное (вынужденное) излучение происходят только под действием внешнего излучения–фотонов с частотой Ф=, находящихся “в резонансе” с рассматриваемым переходом hф=Е2–Е

При поглощении частица, находящаяся в состоянии «1», захватывает фотон, увеличивает свою внутреннюю (потенциальную) энергию, и переходит в состояние «2». Вероятность поглощения Wп зависит от плотности энергии излучения и свойств частицы, определяющих величину коэффициента Эйнштейна для поглощения B12:

Wп = ·B12. (4)

При индуцированном (вынужденном) излучении с внешним фотоном взаимодействует атом, находящийся на уровне «2». Фотон может вызвать («спровоцировать») переход из состояния «2» в «1», при этом будет излучаться еще один фотон, по частоте, направлению и поляризации совпадающий с падающим фотоном, и препятствий для этого не существует, т.к. фотоны являются бозонами. Существование индуцированного излучения было постулировано А. Эйнштейном в 1916 г. при теоретическом анализе процессов теплового излучения с позиций квантовой теории, и позднее было подтверждено экспериментально. Вероятность индуцированного излучения выражается через коэффициент Эйнштейна для индуцированного излучения B21:

Wи = ·B21, (5)

Очевидно, что размерность коэффициентов B12 и B21: [B12]=[B21]=Дж–1см3с–2, отличается от размерности коэффициента А2

Таблица 2. Виды связанных с излучением переходов в квантовых системах и их параметры

Тип перехода Параметр перехода	Без внешнего излучения	С внешним (резонансным) излучением
	Спонтанное излучение	Поглощение	Вынужденное (индуцированное) излучение
Вероятность, с-1
Скорость перехода, см–3с–1				(6)
Удельная мощность, Вт.см–3				(7)
Полная мощность, Вт.				(8)

Итак, индуцированное излучение это электромагнитное излучение, испускаемое квантовой системой, находящейся в возбужденном, неравновесном состоянии, под действием внешнего (вынуждающего) электромагнитного излучения. При индуцированном излучении частота, фаза, поляризация и направление распространения испущенной электромагнитной волны полностью совпадают с соответствующими характеристиками волны вынуждающей, поэтому индуцированное излучение полностью когерентно с вынуждающим излучением.

Для всех трёх процессов в ансамбле рассматриваемых квантовых частиц можно ввести (Таблица 2):

–скорость процесса (6): Fc, Fп и Fи, представляющую собой число переходов в единице объёма за 1с и имеющей размерность [см–3с–1]. В (6) n1 и n2–населённости уровней, определяемые как число частиц в единице объёма и имеющие размерность [см3];

–удельную мощность (7): Pc, Pп и Pи, полученную умножением F из (6) на энергию фотона h;

–полную мощность (8): , и , полученную умножением P из (7) на объём ансамбля частиц V.

4. Связь между коэффициентами Эйнштейна.

Рассмотрим ансамбль частиц, находящийся в состоянии ТДР. Балансное (или кинетическое) уравнение для концентрации частиц, находящихся на уровне «2», в стационарном случае будет

. (9)

Из (9), используя формулу Больцмана (2), для можно получить

. (10)

С учётом того, что h=Е2–Е1, формула (10) будет иметь вид (1), если

(11,а)

и , (11,б)

Выражения (11,а) и (11,б) дают связь между коэффициентами Эйнштейна. В (11,б), как и в формуле Планка (1), использована величина –число возможных типов колебаний (мод) в единице объёма свободного пространства и в единичном спектральном интервале.

Расчеты показывают, что коэффициенты B12 и B21, выражающиеся через квадрат матричного элемента квантово-механического оператора перехода: , не являются функцией частоты , откуда следует, что коэффициент А21 пропорционален третьей степени частоты (А21~).

Для всего многообразия переходов в видимой части оптического спектра ( порядка 1014 Гц), коэффициент Аik(с-1)~(10–39…10–34)· (Гц), что даёт для нижней границы диапазона изменений : Аik~103 с–1 (запрещённые переходы), а для верхней границы: Аik~108 с–1 (разрешённые электрические дипольные переходы). В то же время для СВЧ-диапазона величина Аik ничтожно мала: Аik<<

5. Релаксационные переходы.

К релаксационным относят переходы, происходящие без внешнего излучения. Это – рассмотренные выше спонтанные переходы (вероятность Wс) и столкновительные безызлучательные (вероятность wст). Переходы последнего типа могут происходить при столкновении квантовой частицы, например, находящейся в состоянии «2»–A(«2»), с какой-либо другой частицей В. В результате первая квантовая частица переходит, например, в состояние «1», а высвобождаемая при этом потенциальная энергия Е=Е2–Е1 превращается в энергию другого вида – в кинетическую энергию одной или обеих частиц:

A(«2») + В A(«1») + В + {Eкин=Е}.

Полная вероятность релаксационных переходов Wрел в нашем примере будет:

Wрел=А21 + w21ст. (12)

Оценивая вероятность wст как <VQ>NВ (где Q – эффективное сечение столкновений, V–относительная скорость частиц при столкновении, NВ–концентрация частиц В), получим, что wст (с–1)~ (104…106)·p(Тор). Для диапазона частот видимого спектра найдём, что А21 порядка wст. В то время в дальнем ИК и СВЧ-диапазонах: А21<<wст, и в этих случаях релаксация уровней происходит преимущественно столкновениями.

Ансамбль частиц, выведенный из состояния ТДР, в отсутствие внешнего излучения, за счёт релаксационных переходов возвращается в это состояние с постоянной времени i , являющейся по определению временем жизни уровня “i”:

. (13)

6. “Форма” и ширина спектральных линий

6.1 Понятие оптического спектра. Оптическим спектром называют совокупность частотных составляющих, на которые может быть разложено оптическое излучение ансамбля квантовых частиц; т.е. спектр представляет собой распределение энергии оптического излучения по длинам волн (частотам). Спектр можно получить с помощью спектрального прибора как результат обработки спектрограммы. В зависимости от того, какой тип квантового перехода связан с исследуемым оптическим излучением квантовой системы, различают спектры испускания (эмиссионные) и поглощения (абсорбционные). Оптический спектр отдельных атомов является линейчатым, т.е. состоящим из отдельных “спектральных линий”, каждой из которых соответствует дискретное значение длины волны (частоты). (Принятое в спектроскопической практике понятие "спектральная линия" обусловлено тем, что монохроматическое изображение входной щели, формируемое в фокальной плоскости спектрального прибора, имеет вид линии). Энергия линии сосредоточена в некотором интервале частот (говорят, что линия “уширена”). Этот интервал обычно много меньше абсолютного значения частоты 0, соответствующей максимальному значению интенсивности излучения линии. Конечная ширина («размытость» по энергии) линии, вытекает хотя бы из соотношения неопределенностей E·~, где конечно и определяется релаксационными процессами (13). Конечность и E ведет и к конечной ширине частотной зависимости вероятности W() перехода. Вид уширения линии играет в квантовой электронике важную роль. Как будет показано ниже, помимо релаксационных процессов существуют и другие причины уширения.

Спектр может состоять и из отдельных групп тесно расположенных спектральных линий, образующих полосы, либо быть сплошным (непрерывный спектр).

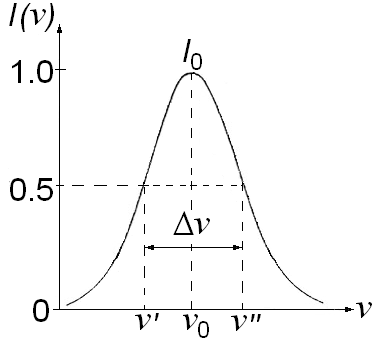
Рис. 2. Параметры спектральной линии

6.2. Параметры спектральной линии. Под формой линии понимают частотную зависимость интенсивности излучения на данном квантовом переходе–I(). Интенсивность излучения I определяется как поток мощности излучения или как энергия, проходящая через площадку в 1 см2 в 1 с, и имеет размерность [I]=Дж·см–2·с–1=Вт·см–2.

Для типичной спектральной линии, имеющей, как говорят «колоколообразную» симметричную форму, можно обозначить следующие ее параметры и характерные точки (рис.2):

0–центральная частота, соответствующая максимуму спектральной интенсивности линии: ;

' и '' – значения частоты, соответствующие половине интенсивности, т.е. I(')=I('')=I(0)/2;

=''–' – ширина линии на уровне I(0)/2 (“на полувысоте”), или коротко: ширина линии.

Введя интегральную интенсивность линии I как: , спектральную интенсивность (“форму” линии) можно выразить аналитически двумя способами, через функцию формы линии (или ”форм-фактор”) двух видов: и (Таблица 3). Условие нормировки (15) для функции может быть получено путём интегрирования , а для функции – путем вычисления при =0.

Таблица 3. Представление формы спектральной линии

	используя “функцию формы” линии	используя “функцию формы” линии
Представление	(14,а)	(14,б)
Условие нормировки “функции формы” линии	(15,а)	(15,б)
Представление данной функции через другую	(16,а)	(16,б)
Значение “функции формы” линии при =0	(17,а) (однородное уширение) (17,б) (неоднородное уширение)	(17,в)

7. Виды уширения спектральных линий

Спектральные линии ансамбля квантовых частиц испытывают уширение двух видов–однородное и неоднородное.

7. Однородное уширение. При однородном уширении спектральных линий функции формы линии (форм-факторы) для каждой частицы и всего ансамбля совпадают. Однородное уширение является следствием релаксационных процессов (см., раздел 5) и бывает естественным, столкновительным, пролётным и др., первые два типа обычно преобладают, и ширина однородно уширенной линии

.

Естественное (или радиационное) уширение , которое является нижней границей , возникает за счёт конечного времени жизни уровней «1» и «2»: 1 и 2 (13). Точное значение даёт квантово-механический подход. В самом деле, используя соотношение неопределённостей для обоих уровней:

E1·1 ~ и E2·2 ~ ,

можно найти значение ширины уровней E1 и E2, откуда можно получить

. (18)

Столкновительное уширение с достаточной точностью можно найти, воспользовавшись моделью классического осциллятора, фаза колебания которого испытывает скачок в момент столкновения излучающей частицы с другими частицами, со стенкой кюветы с газом и др., откуда

, (19)

где ст–интервал времени между двумя последовательными столкновениями излучающей частицы с другими частицами, со стенками кюветы и др.

В результате будет

, (20)

где через j обозначены , и . Важно, что не зависит от частоты перехода .

Функции формы линии излучения при однородном уширении могут быть получены методами электродинамики, и являются функциями Лоренца:

и . (21)

Из (21) легко получить значение функции при =0 (ф-ла (17,а) в Таблице 3).

7.2. Неоднородное уширение. При неоднородном уширении форм-факторы каждой частицы и всего ансамбля различны, а именно, форм-фактор ансамбля является суперпозицией форм-факторов всех частиц. Причиной неоднородного уширения может быть любой процесс, приводящий к различным условиям возбуждения и (или) излучения различных частиц или их групп. Примерами неоднородного уширения являются уширение за счет эффекта Доплера при хаотическом тепловом движении частиц в газе, а также уширение за счет эффекта Штарка в кристаллах.

Специальная теория относительности дает следующее выражение для сдвига частоты , регистрируемой наблюдателем, если источник, излучающий на частоте 0, движется относительно наблюдателя со скоростью (эффект Доплера):

, (22)

где – единичный вектор, указывающий направление на наблюдателя, с – скорость света. Из (22) легко получить выражение для в нерелятивистском случае (при малых скоростях, когда u<<c):

(23)

Видно, что движение излучающей частицы «к наблюдателю» приводит к сдвигу частоты излучения в сторону б'ольших , а «от наблюдателя»–меньших , причем контур излучения каждой частицы является лоренцевым с шириной, равной одн (см., рис. 3). Неподвижные (с u=0) или движущиеся с =0 () частицы, вносят вклад в суммарный контур ансамбля на центральной частоте 0; с <0–на частотах '<0, а с >0–на частотах ''>0. Функцию формы линии при распределении частиц по скоростям, описываемым законом Максвелла-Больцмана, можно получить, исходя из того, что в соответствии с (23) вклад в излучение в частотном интервале …+d дают частицы, имеющие скорости в интервале u…u+du. Число таких частиц определяется вероятностью p(u) в распределении Максвелла-Больцмана, т.е.

Рис. 3. Уширение спектральной линии за счет эффекта Доплера. Заштрихованные контура–однородно уширенные и относящиеся к одной группе частиц. a – вклад частиц со скоростью u·k·cos=0, б – вклад частиц со скоростью u·k·cos<0, в – то же при u·k·cos>0.

. (24)

Подставляя в (24) p(u), получим

, (25)

где – средняя тепловая скорость частиц. Продифференцировав (23), найдём связь между du и d,: , и подставив её в (25), получим гауссовский профиль линии :

,(26)

где

– ширина неоднородно уширенной линии. В последней, “расчётной”, формуле 0–в Гц, Т – в К, – масса частицы в а.е.м.

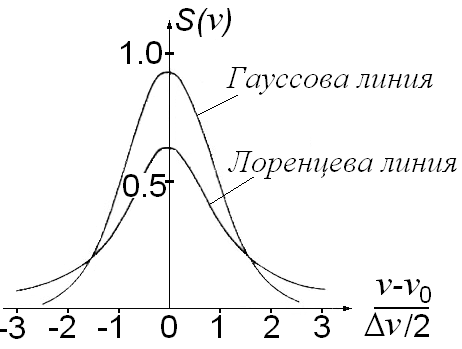
Важно, что в отличие от однородного, при неоднородном уширении зависит от центральной частоты перехода 0. Значение приведено в Таблице 3 (формула (17,б). Сравнение лоренцевского и гауссовского контуров (рис. 4) при одинаковых интегральной интенсивности и ширине линий показывает, что лоренцевский контур имеет более пологие «крылья».

Рис. 4. Сравнение форм-факторов S() для лоренцевой (при однородном уширении) и гауссовой (при неоднородном уширении) линий.

Другим типом неоднородного уширения является уширение за счёт эффекта Штарка в кристаллах. В кубических кристаллах преобладает механизм однородного уширения линий, а в стёклах–механизм неоднородного уширения. В примесном кристалле основными причинами неоднородного уширения могут быть: при низких температурах–неоднородные внутренние напряжения, обусловленные низкой симметрией кристалла (чем ближе реальная решетка кристалла к идеальной кубической, тем меньше вклад неоднородного уширения в ширину линии); а при высоких температурах–электрон-фононные взаимодействия.

8. Интегральная вероятность перехода с учётом формы линии.

А.Эйнштейном вводились вероятности (3)–(5) без учёта частотной зависимости вероятности перехода. Теперь зная форму линии, можно вычислить интегральные вероятности спонтанных и индуцированных переходов, а также переходов с поглощением. Для интегральной вероятности спонтанного перехода получим тот же, что и без учёта формы линии, результат:

. (27)

Интегральная вероятность поглощения и индуцированного излучения зависит, кроме S() линии, ещё и от частотной зависимости плотности энергии падающего излучения . В Таблице 4 приведены выражения для интегральной вероятности поглощения и индуцированного излучения в двух случаях: для медленно (по сравнению с S()) изменяющейся –случай теплового излучения («абсолютно чёрного тела»), а также–для монохроматического излучения, когда является быстро изменяющейся функцией частоты. В последнем случае монохроматическое излучение может действовать как на произвольной частоте ', так и на центральной частоте перехода .

Таблица 4. Интегральные вероятности индуцированных переходов.

–медленно изменяющаяся функция частоты (непрерывный спектр)	–быстро изменяющаяся функция частоты (монохроматическое излучение на частоте )
(28,а)	, (28,б) (при ) (28,в)
(29,а)	, (29,б) (при ) (29,в)

Очевидно, что здесь и далее приобретает смысл и размерность объёмной плотности энергии падающего излучения, т.е. [] = Дж·см–3.

9. Поглощение излучения средой. Эффект насыщения поглощаемой мощности

Если на ансамбль квантовых частиц, находящийся в состоянии ТДР, падает внешнее излучение, частота которого находится в резонансе с энергией E квантового перехода, то, поскольку N1>N2 (если g1=g2), скорость поглощения превосходит скорость индуцированных переходов: Fп > Fи (Табл. 2), и в целом имеет место поглощение этого излучения средой. В процессе поглощения происходит уменьшение числа частиц на нижнем уровне «1» и увеличение – на верхнем уровне «2», т.е. имеет место выравнивание населённости уровней, и, как следствие,–снижение эффекта поглощения. Очевидно, что в предельном случае, при это выравнивание становится полным, т.е. n1n2, поглощение прекращается, и падающее излучение будет проходить через среду без потерь. Такая ситуация называется насыщением населённости уровней «1» и «2». С другой стороны, т.к. спонтанные переходы, не связанные с наличием внешнего излучения, продолжают опустошать уровень «2», пропорциональная часть падающего излучения всё же будет поглощаться и затем сразу же излучаться спонтанными переходами с верхнего уровня – на нижний уровень.

Пусть на ансамбль частиц, первоначально находящийся в состоянии ТДР, падает монохроматическое излучение, частота которого находится в резонансе с квантовым переходом («попадает» в его контур поглощения), например, . Найдем значение мощности этого излучения Р, поглощаемой средой, и зависимость этой мощности от плотности энергии падающей волны. Обозначим через Рпогл – удельную мощность при переходах с поглощением, а Ринд –удельную мощность, выделяемую при индуцированных переходах под действием того же излучения. Вследствие преобладания скорости поглощения над скоростью индуцированного излучения, для величины эффективной удельной поглощаемой мощности, можно записать

. (30,а)

В (30,а), в соответствии с (29): , и введено обозначение: .

Положим для простоты, что , и обозначив , получим

. (30,б)

Поскольку теперь n = n1–n2, а n1+n2=n0 — суммарная концентрация частиц на рассматриваемых уровнях в ансамбле, n2 найдём из стационарного кинетического уравнения:

.

И тогда для n получим:

, (31),

а так как , найдём, что с ростом падающего излучения разность населённостей уровней n снижается.

Введём параметр насыщения для плотности энергии падающего излучения: , и тогда для (31) получим:

. (32, а)

Очевидно, что при =0, величина n снижается вдвое. Переходя от плотности энергии – к интенсивности излучения (плотности потока мощности) I=·vгр (где vгр–групповая скорость распространения излучения, для газов vгрс), получим выражение, подобное (32, а):

, (32, б)

где –параметр насыщения для интенсивности излучения. Видно, что 0 и I0 определяются параметрами квантового перехода и не зависят от . Видно также, что величина n стремится к нулю (то есть происходит выравнивание населённостей на уровнях «1» и «2») с ростом как , так и I.

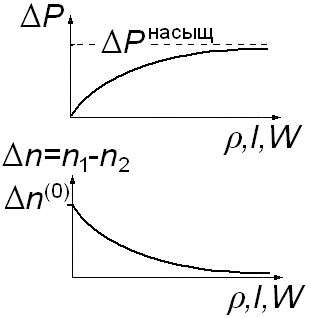
Рис.5. Зависимость мощности Р, поглощаемой квантовой системой, от плотности энергии падающего излучения (интенсивности I, вероятности поглощения W)

С учётом (31) поглощаемая мощность (30,б) будет:

. (33)

Графики зависимостей n() и Р() показаны на рис. 5. Проанализируем предельные случаи. Когда 2W2<<1, что происходит при малых и I, поглощаемая мощность Р~~I, т.е. зависимости Р() и Р(I) растут линейно. Когда , I велики так, что 2W2>>1 (в том числе и когда и I), получим, что

, (34)

т.е. величина поглощённой мощности достигает предельной величины () и далее не возрастает. Отсюда следует вывод, что ансамбль частиц может поглотить только такую мощность, которую может излучить за счёт релаксационных переходов (в данном примере–путём спонтанного излучения с вероятностью А21).

Таким образом, в двухуровневой системе повышение (и I) приводит в выравниванию населённостей уровней: n1 и n2 стремятся к n0/2. При этом для всех возможных значений падающей мощности, в том числе и бесконечно больших, n положительно, откуда следует важный для практики вывод о том, что в двухуровневой системе с помощью внешнего излучения невозможно сделать соотношение населённостей уровней обратным (по отношению к состоянию ТДР).

10. Коэффициент поглощения, влияние насыщения на форму контура линии поглощения