Исследование устойчивости системы при использовании типовых регуляторов
PAGE \* MERGEFORMAT1
ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра “Электропривод и
автоматизация промышленных установок”
ПояснИТЕЛЬНАЯ записка
к курсовому проекту
по дисциплине «Теория автоматического управления»
на тему: «Исследование устойчивости системы при использовании типовых регуляторов»
КП 6.050702-15-260.06.00.00 ПЗ
Выполнил ст. гр. СПУ-12 ______________ Хмара А.О.
(подпись, дата ) ( Ф.И.О.)
Руководитель проекта ______________ Розкаряка П.И.
(подпись, дата ) ( Ф.И.О.)
Нормоконтролер ______________ Розкаряка П.И.
(подпись, дата ) ( Ф.И.О.)
Донецк - 2015
РЕФЕРАТ
Пояснительная записка содержит: 41 страницу, 22 рисунка, 3 источника.
Объектом расчета и исследования в данной курсовой работе является система автоматического регулирования.
Цель работы – исследование устойчивости системы при использовании типовых регуляторов П, И, ПИ.
При определении устойчивости замкнутой системы используется алгебраический критерий устойчивости Гурвица. Выбор передаточных функций регулятора проводится по условиям настройки на технический и модульный оптимум. Определение запаса устойчивости замкнутой системы производится с помощью логарифмических частотных характеристик в разомкнутом состоянии.
РЕГУЛЯТОР, ОБЪЕКТ РЕГУЛИРОВАНИЯ, ПОСТОЯННАЯ ВРЕМЕНИ, СТАНДАРТНЫЕ НАСТРОЙКИ СИСТЕМЫ, СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
СОДЕРЖАНИЕ
Перечень условных обозначений……………………………………………….......4
Вступление…………………………………………………………………………...5
Задание…………………………………………………………………………….….6
- Исследование системы с П-регулятором……………………………………7
- Исследование системы с И-регулятором………………………………..…13
- Исследование системы с ПИ-регулятором……………………………...…22
- Оценка характера переходных процессов…………………….…………...28
- Модель с программой.………………………………………………………30
Заключение…………………………………………………………………….……39
Список использованной литературы……………………………………………...40
Приложение А. Перечень замечаний нормоконтролера……………………...….41
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
ОР – объект регулирования;
ПФ – передаточная функция;
П – регулятор – пропорциональный регулятор;
И – регулятор – интегральный регулятор;
ПИ – регулятор – пропорционально-интегральный регулятор;
ТО – технический оптимум;
СД – среднее демпфирование;
КД – критическое демпфирование;
ЛАЧХ – логарифмическая амплитудная частотная характеристика;
ЛФЧХ – логарифмическая фазовая частотная характеристика;
W(р) – передаточная функция разомкнутой системы;
Gp.(р) – характеристический полином замкнутой системы;
Wp.(р) – передаточная функция регулятора;
h(t) – переходная характеристика;
k1, k2 – коэффициенты усиления объекта регулирования;
Т1, Т2 – постоянные времени объекта регулирования;
– перерегулирование;
tc – время первого достижения переходным процессом установившегося значения;
k р – коэффициент усиления П-регулятора;
Ти – постоянная времени И-регулятора;
Тf, То – постоянные времени ПИ-регулятора;
- коэффициент демпфирования;
– запас устойчивости по фазе;
A – запас устойчивости по амплитуде;
ВСТУПЛЕНИЕ
Теория автоматического управления (ТАУ) — научная дисциплина, изучающая процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию.
Является составной частью технической кибернетики и предназначена для разработки общих принципов автоматического управления, а также методов анализа (исследования функционирования) и синтеза (выбора параметров) систем автоматического управления (САУ) техническими объектами.
ЗАДАНИЕ
Исследовать показатели устойчивости системы, базовая структурная схема которой приведена на рис. 1, при известных параметрах объекта регулирования (ОР) (табл.1) при использовании типовых регуляторов пропорционального (П-), интегрального (И-) и пропорционально-интегрального (ПИ-) типа.
Рисунок 1 – Структурная схема системы
Таблица 1 – Исходные данные
|
Параметры
|
Номер варианта
|
|
|
6
|
|
k1
|
12
|
|
k2
|
15
|
|
T1, мc
|
8
|
|
T2, мc
|
30
|
Исследования для случая использования каждого из перечисленных регуляторов выполнить в соответствии с рекомендованным содержанием:
- Определение условий устойчивости замкнутой системы с использованием алгебраического критерия устойчивости (Гурвица);
- Выбор передаточных функций регулятора из условия обеспечения стандартных настроек системы (настройка на «критическое» демпфирование, настройка на технический оптимум);
- Исследование характера переходного процесса в замкнутой системе в зависимости от степени её удаленности от границы устойчивости;
- Определение запаса устойчивости замкнутой системы при стандартных настройках с помощью логарифмических частотных характеристик системы в разомкнутом состоянии.
1. Исследование системы с П-регулятором
Передаточная функция П-регулятора:
Передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы:
Характеристический полином замкнутой системы:
Чтобы определить устойчивость системы для любых Kp>0, необходима положительность всех коэффициентов характеристического полинома.
По условию устойчивости Гурвица:
, где - коэффициенты .
Условия устойчивости согласно критерию: Определим значение коэффициента усиления регулятора , при котором настройке системы на «критическое демпфирование» (КД). Приравняв дискриминант к нулю, находим значение , при котором =0.
Найдем значение коэффициента kp.a
WP(p)=Kp
1) >0
\
Находим при D=0
Рисунок 2– Переходная и импульсная характеристики системы с настройкой на КД
При изменении параметров в пределах определяем зависимость перерегулирования переходной характеристики от коэффициента усиления Kp.
Таблица 2 – Устойчивость системы с П-регулятором
|
|
|
2
|
2.5
|
3
|
3.5
|
3.7
|
4
|
4.4
|
4.8
|
5
|
|
tc, мc
|
114
|
52.8
|
42
|
35.6
|
31.3
|
29.9
|
28.1
|
26
|
24.4
|
23.6
|
|
, %
|
0
|
0.6
|
1.5
|
2.6
|
3.8
|
4.3
|
5
|
6
|
7
|
7.4
|
Для автоматизации исследований необходим цикл, параметром которого коэффициент . Получаем зависимости:
Рисунок 3 –Графики зависимостей ,
Следовательно оптимальной настройкой, для достаточно быстрой реакции с приемлемым перерегулированием на рисунке 3, первый график, определим значение , при котором имеет место настройка на ТО, при 4,3 %,
=3,7.
Таблица 3 – Параметры системы с П-регулятором
|
Параметр
|
Значение
|
|
Передаточная функция разомкнутой системы
|
|
|
Характеристический полином замкнутой системы
|
|
|
Условие устойчивости
|
|
|
Настройка на КД достигается при
|
|
|
Настройка на ТО достигается при
|
=3,7
|
Для строим переходную и весовую характеристики замкнутой системы, ЛАЧХ и ЛФЧХ разомкнутой системы.
Рисунок 4 – Переходная и импульсная характеристики системы с настройкой на ТО
Рисунок 5 – ЛАЧХ и ЛФЧХ разомкнутой системы с настройкой на ТО
Из рисунка 5 заметно, что запасы устойчивости системы П-регулятора при настройке на ТО составляют A = 95.2 дБ, = 100° это удовлетворяет частотным критериям устойчивости.
2 Исследование системы с И-регулятором
Передаточная функция И-регулятора:
Передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы:
Характеристический полином замкнутой системы:
=
Из критерий устойчивости Гурвица, определяем значение постоянной времени , при которой система пребывает на границе устойчивости. Это условие можем получить из равенства нулю второго определителя Гурвица.
Найдем значение
1) >0
2) >0
Условие устойчивости по критерию Гурвица:
,
после подстановки параметров ОР получаем:
.
Рисунок 6– Переходные и весовые характеристики замкнутой системы при
Рисунок 7– ЛАЧХ и ЛФЧХ разомкнутой системы при
Рисунок 8– Переходные и весовые характеристики замкнутой системы при
Рисунок 9– ЛАЧХ и ЛФЧХ разомкнутой системы при
Рисунок 10– Переходные и весовые характеристики замкнутой системы при
Рисунок 11– ЛАЧХ и ЛФЧХ разомкнутой системы при
Из рисунков 6 и 7 видим, что система при постоянной времени имеет колебательный процесс и отрицательные значения запаса по амплитуде и фазе следовательно находится на границе устойчивости. На рисунках 8 и 9 при мы наблюдаем затухающий характер переходных и импульсных характеристик, то есть является благоприятным условием для И-регулятора. Но система не удовлетворяет частотным критериям устойчивости САР хоть и имеет положительные значения запаса по амплитуде и фазе. Использование регулятора с постоянной времени не удовлетворяет условиям устойчивости системы. Так как имеет расходящийся процесс, наблюдаем на рисунках 10 и 11.
На основании таковых выводов, необходимо экспериментально определить значения и постоянной времени И-регулятора, при которых достигается настройка системы на КД (=0) и на ТО (4,3 %).
Таблица 4 – Устойчивость системы з И-регулятором
|
,
мс
|
1140
|
1400
|
2100
|
2800
|
4000
|
5000
|
6200
|
7500
|
|
tc, мc
|
30
|
34
|
41.4
|
48.5
|
60
|
69
|
80
|
93.2
|
|
, %
|
92
|
82
|
64
|
53
|
39
|
31
|
24
|
18.5
|
|
9000
|
10500
|
11800
|
13900
|
15000
|
16000
|
17000
|
18000
|
19000
|
|
108.6
|
112.5
|
141.9
|
172.7
|
192.2
|
212
|
235.5
|
263.2
|
297
|
|
13.5
|
10
|
7
|
4,3
|
3
|
2
|
1.5
|
1
|
0
|
Рисунок 12– Переходные характеристики при настройке на КД и ТО
Рисунок 13– Весовые характеристики при настройке на КД и ТО
Рисунок 14– Графики зависимостей ,
Из зависимостей , рисунок 14 следует с увеличением постоянной времени перерегулирование уменьшается, что вызывает снижение быстродействия системы.
Для случая настройки системы на ТО изобразим ее ЛАЧХ и ЛФЧХ, определив запасы устойчивости по амплитуде и по фазе:
Рисунок 15– ЛАЧХ и ЛФЧХ системы при настройке на ТО
Bp из графика на рисунке 15 при настройке на ТО запас по амплитуде А и по фазе системы составляют: А=21.8дБ, =64.4°,следовательно удовлетворяет частотному критерию устойчивости САР.
Таблица 5 – Параметры системы з И-регулятором
|
Параметр
|
Значение
|
|
Передаточная функция разомкнутой системы
|
|
|
Характеристический полином замкнутой системы
|

|
|
Граница стойкости
|
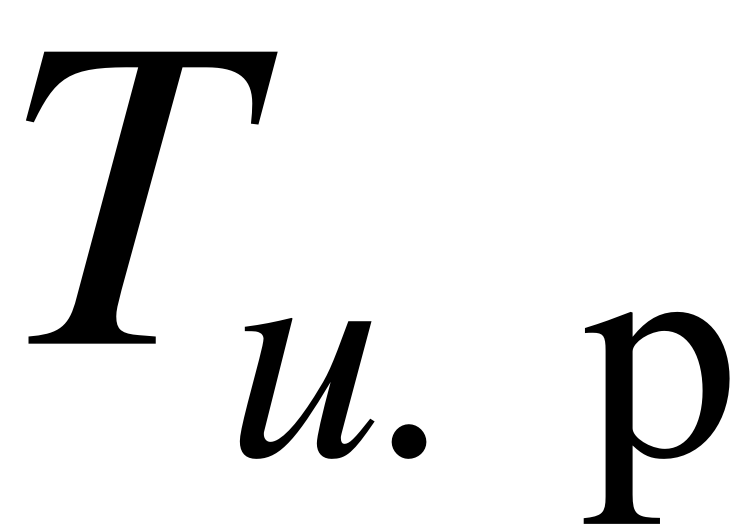 =1140мс =1140мс
|
|
Условия стойкости
|
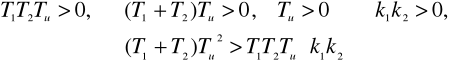
|
|
Настройка на КД достигается при
|
мс
|
|
Настройка на ТО достигается при
|
мс
|
3 Исследование системы з ПИ-регулятором
Передаточная функция ПИ-регулятора:
Передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы
Характеристический полином замкнутой системы:
Используя критерий устойчивости Гурвица, найдем условие устойчивости замкнутой системы с ПИ-регулятором. Соответствующее условие может быть получено из проверки положительности второго определителя Гурвица:
-коэффициенты характеристического полинома
.
Выполнив подстановку параметров ОР получим:
.
В дальнейшем принимаем значение .
По критерию устойчивости Гурвица, необходимо доказать, что при выборе система будет устойчивой. Необходимо проверить положительность всех коэффициентов характеристического полинома замкнутой системы:
передаточная функция замкнутой системы:
характеристический полином для замкнутой системы:
;
условие устойчивости: 0, 0.
Расчет величин: , , коэффициенты демпфирования =1 (настройка на КД), = (настройка на ТО), =0,5 (настройка на СД).
=5760 мс, =2880 мс, =1440 мс.
Таблица 6 – Параметры системы з ПИ- регулятором
|
Параметр
|
Значение
|
|
Передаточная функция разомкнутой системы
|
|
|
Характеристический полином замкнутой системы
|
|
|
Условие устойчивости
|
|
|
Настройка на КД (=1) достигается при
|
мс
|
|
Настройка на ТО (=) достигается при
|
мс
|
|
Настройка на СД (=0,5) достигается при
|
мс
|
Рисунок 16– Переходные характеристики при настройке на КД ,ТО,СД
Рисунок 17– Импульсные характеристики при настройке на КД ,ТО,СД
Рисунок 18– ЛАЧХ и ЛФЧХ при настройке на КД
Рисунок 19– ЛАЧХ и ЛФЧХ при настройке на ТО
Рисунок 20– ЛАЧХ и ЛФЧХ при настройке на СД
Из представленных графиков при настройке системы с ПИ-регулятором на КД, ТО и СД следует, что при настройке системы на КД система имеет максимально быструю реакцию на управляющее воздействие при условии отсутствия перерегулирования, настройка на ТО имеет достаточно быструю реакцию при некотором перерегулировании. Настройка на СД – самая быстродействующая, однако имеет наибольшее перерегулирование из выше представленных характеристик. Запасы устойчивости по амплитуде и по фазе в каждом из представленных случаев удовлетворяют частотному критерию устойчивости, однако при большем перерегулировании имеет место меньшее значение запаса устойчивости как по амплитуде A, так и по фазе .
- Оценка характера переходных процессов
Оценим характер переходных процессов при использовании исследуемых регуляторов, отобразив их переходные функции в одних координатах.
Рисунок 21 – 1) – h(t) без регулятора; 2)- П-регулятор (КД, ТО);
3)– И-регулятор (КД, ТО); 4) – ПИ-регулятор (КД, ТО) .
Семейство характеристик h(t) при исследовании системы с разными регуляторами отображает реакцию системы с каждым из регуляторов на управляющее воздействие. Так, при использовании П- и ПИ-регуляторов длительность переходных процессов значительно меньше, чем при использовании И-регулятора, что соответствует повышенному быстродействию контура. При сравнении системы без регулятора, можно сделать вывод о том, что время достижения установившегося значения в случае отсутствия регулятора больше, чем при наличии П- и ПИ-регуляторов, что свидетельствует о необходимости их применения.
Рисунок 22-Модель регуляторов в математическом пакете Matlab
Программа для исследования П-регулятора
close all, clear all,
k1=12;k2=15;
T1=8e-3;T2=30e-3;
Kpa=0.003;
Ti_gr=1140e-3;Tf=T2;kcx=1;Ti=1;To=1;
kp=3.7*Kpa;r=3.7*Kpa*k1*k2/(1+3.7*Kpa*k1*k2);
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y9,t]=step(sys,3*(T1+T2));
plot(t,y9/r,'r'),grid on,zoom on
kp=3.7*Kpa;
r=3.7*Kpa*k1*k2/(1+3.7*Kpa*k1*k2);
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(2)
subplot(211)
step(sys/r,5*(T1+T2)),grid on
subplot(212)
impulse(sys/r,5*(T1+T2)),grid on
figure(3)
obrs=0;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
kp=Kpa;r=Kpa*k1*k2/(1+Kpa*k1*k2);obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(4)
[y9,t]=step(sys,3*(T1+T2));
plot(t,y9/r,'r'),grid on,zoom on
for i=1:1:20
kr=Kpa*i;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(5)
[y1,t]=step(sys,3*(T1+T2));
subplot(211)
plot(t,y1/r),grid on
subplot(212)
[y2,t]=impulse(sys,5*(T1+T2));
plot(t,y2),grid on
sigma=[0 0.6 1.5 2.6 3.8 4.3 5 6 7 7.4];
ts=[114 52.8 42 35.6 31.3 29.9 28.1 26 24.4 23.6];
figure(6)
subplot(211)
plot(sigma(i),kr,'o'),grid on,hold on
xlabel('\sigma');ylabel('kr');
subplot(212)
plot(ts(i),kr,'o'),grid on, hold on
xlabel('ts, ms'); ylabel('kr')
end
Программа для исследования И-регулятора
close all, clear all,
k1=12;k2=15;
T1=8e-3;T2=30e-3;
Kpa=0.003;
Ti_gr=1140e-3; Tf=T2;kcx=2;kp=1;To=1;
Ti=Ti_gr;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(5)
subplot(211)
step(sys,15*(T1+T2)),grid on
subplot(212)
impulse(sys,15*(T1+T2)),grid on
figure(6)
obrs=0;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
Ti=2*Ti_gr;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(7)
subplot(211)
step(sys,15*(T1+T2)),grid on
subplot(212)
impulse(sys,15*(T1+T2)),grid on
figure(8)
obrs=0;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
Ti=Ti_gr/2;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(9)
subplot(211)
step(sys,15*(T1+T2)),grid on0
subplot(212)
impulse(sys,15*(T1+T2)),grid on
figure(10)
obrs=0;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
% настройка на КД и ТО
Ti=19000e-3; %Tu.a=19000
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(11)
subplot(211)
step(sys,15*(T1+T2)),grid on
subplot(212)
impulse(sys,15*(T1+T2)),grid on
Ti=13900e-3; %Tu.опт=13900
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(12)
subplot(211)
step(sys,15*(T1+T2)),grid on
subplot(212)
impulse(sys,15*(T1+T2)),grid on
% ЛАЧХ ЛФЧХ для ТО
obrs=0;
figure(13)
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
for i=1:1:20
Tu=Ti_gr*i;
sigma=[92 82 64 53 39 31 24 18.5 13.5 10 7 4.3 3 2 1.5 1 0];
ts=[30 34 41.4 48.5 60 69 80 93.2 108.6 112.5 141.9 172.7 192.2 212 235.5 263.2 297];
figure(14)
subplot(211)
plot(sigma(i),Tu,'o'),grid on,hold on
xlabel('\sigma');
ylabel('Ti, ms');
subplot(212)
plot(ts(i),Tu,'o'),grid on, hold on
xlabel('ts, ms');
ylabel('Ti, ms');
end
Программа для исследования ПИ-регулятора
close all, clear all,
k1=12;k2=15;
T1=8e-3;T2=30e-3;
Kpa=0.003;
Tf=T2;kcx=3;Ti=1;kp=1;
To=5760e-3;
To_opt=2880e-3;
Toc=1440e-3;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(15)
subplot(211)
[y1,t]=step(sys,5*(T1+T2));
plot(t,y1),grid on
subplot(212)
impulse(sys,5*(T1+T2)),grid on
figure(16)
obrs=0;
[a,b,c,d]=linmod('tau');
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
To=To_opt;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(17)
subplot(211)
[y2,t]=step(sys,5*(T1+T2));
plot(t,y2),grid on
subplot(212)
impulse(sys,5*(T1+T2)),grid on
figure(18)
obrs=0;
[a,b,c,d]=linmod('tau');
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
To=Toc;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(19)
subplot(211)
[y3,t]=step(sys,5*(T1+T2));
plot(t,y3),grid on
subplot(212)
impulse(sys,5*(T1+T2)),grid on
figure(20)
obrs=0;
[a,b,c,d]=linmod('tau');
bode(a,b,c,d)
[Mag,Phase,w]=bode(a,b,c,d);
margin(Mag,Phase,w);
Программа для построения h(t) без регулятора; 2)- П-регулятор (КД, ТО);
3)– И-регулятор (КД, ТО); 4) – ПИ-регулятор (КД, ТО)
close all, clear all,
k1=12;k2=15;
T1=8e-3;T2=30e-3;
Kpa=0.003; Ti_gr=1140e-3; Tf=T2;kcx=1;Ti=1;To=1;
% p_Regl
kp=Kpa;r=Kpa*k1*k2/(1+Kpa*k1*k2);% коэффициент ошибок
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y1,t]=step(sys,15*(T1+T2));
plot(t,y1/r,'k'),grid on, hold on,zoom on
kp=3.7*Kpa;r=3.7*Kpa*k1*k2/(1+3.7*Kpa*k1*k2);obrs=1;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y2,t]=step(sys,15*(T1+T2));
plot(t,y2/r,'m'),grid on, hold on,zoom on
% I-Regl
Ti=19000e-3; %Tu.a=19000
kcx=2;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y3,t]=step(sys,15*(T1+T2));
plot(t,y3,'b'),grid on, hold on,zoom on
Ti=13900e-3; %Tu.опт=13900
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y4,t]=step(sys,10*(T1+T2));
plot(t,y4,'r'),grid on, hold on,zoom on
%PI_Regl
kcx=3;Ti=1;kp=1;
To=5760e-3; To_opt=2880e-3; Toc=1440e-3;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y5,t]=step(sys,15*(T1+T2));
plot(t,y5),grid on, hold on,zoom on
To=To_opt;
obrs=1;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y6,t]=step(sys,15*(T1+T2));
plot(t,y6,'g'),grid on, hold on,zoom on
kcx=4; Ti=1;To=1;kr=1;obrs=1;kcx=4;
[a,b,c,d]=linmod('tau');
sys=ss(a,b,c,d);
figure(1)
[y7,t]=step(sys,15*(T1+T2));
plot(t,y7/179,'b'),grid on, zoom on
ЗАКЛЮЧЕНИЕ
В данной курсовой работу были изучены показатели устойчивости системы при известных параметрах объекта регулирования.
Для П- И- ПИ-регуляторов были определены передаточные функции из условия настройка на «критическое» демпфирование, настройка на технический оптимум.
Исследован характер переходного процесса в зависимости от степени ее удаленности от границы устойчивости при замкнутой системе.
Выбирались регуляторы проводился при стандартных настройках, из определения запаса устойчивости для замкнутой системы.
Регулятор убирает отклонения регулируемой величины, следовательно улучшаются свойства объекта регулирования.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Гейлер, Л.Б. Введение в теорию автоматического регулирования / Л.Б. Гейлер. - М.: Минск: Наука и техника, 1981. - 528 c.
Современные системы управления/ Р. Дорф., Р. Бишоп. Пер. с англ. Б.И.Копылова. – Москва:Лаборатория Базовых Знаний, 2002.-832с.
Теория систем автоматического регулирования./ В. А. Бесекерский,
Е. П.Попов – М.: Наука, 1975.-768с
ПРИЛОЖЕНИЕ А
Перечень замечаний нормоконтролера к курсовому проекту
ст. гр. СПУ-12 Хмара А.О.
|
Назначение документа
|
Документ
|
Условные обозначения
|
Содержание замечаний
|
|
|
|
|
|
Нормоконтролер _____________ __________ __________
(Ф.И.О.) Подпись Дата
Исследование устойчивости системы при использовании типовых регуляторов