Элементы алгебры логики

PAGE 6

Элементы алгебры логики

В цифровой технике для передачи информации используются кодовые слова, состоящие из набора логических «0» и «1», которые поступают на вход каждого узла ЭВМ, а на выходе при этом образуется новое кодовое слово, представляющее собой результат обработки входных слов. Поэтому можно говорить, что выходное слово есть функция, для которой входной сигнал является аргументом. Такие функции называются функциями алгебры логики (ФАЛ).

Классификация логических цифровых устройств

Устройства, предназначенные для формирования функций алгебры логики, называются логическими цифровыми устройствами. Цифровые устройства или узлы можно делить на типы по различным признакам.

По способу ввода и вывода кодовых слов различают логические устройства последовательного, параллельного и смешанного действия.

На входы устройства последовательного действия символы кодовых слов поступают не одновременно, а последовательно по времени, символ за символом (в последовательной форме) (рис. 1):

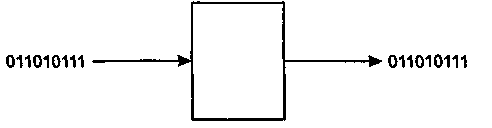
Рис. 1. Схема последовательной подачи импульсов
на вход логического устройства

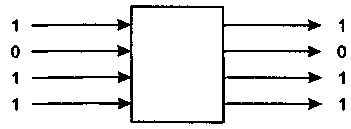
На входы устройства параллельного действия все символы подаются одновременно (в параллельной форме). В такой же форме формируется машинное слово на выходе (рис. 2):

Рис. 2. Схема параллельной подачи импульсов
на выход логического устройства

В устройствах смешанного действия входные и выходные слова представляют в разных формах, например входные слова — в последовательной форме, а выходные — в параллельной (рис.3):

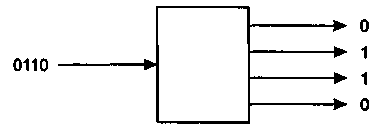
Рис.3. Схема работы устройства смешанного действия

По способу функционирования логические устройства и их системы делят на два класса: комбинационные и последовательные.

В комбинационных устройствах (автоматы без памяти) каждый символ на выходе определяется лишь действующими сигналами, поступающими на вход, и не зависит от того, какие символы поступали ранее.

В последовательных системах (автоматы с памятью) выходной сигнал определяется не только набором символов, действующих на входах в данный момент времени, но и внутренним состоянием устройства, зависящим от того, какие символы действовали до этого времени.

В классической математике для задания функции обычно используют два способа: аналитический (запись формулой) и табличный (таблицами значений функций). Подобными способами задают и логические функции.

При табличной форме задания функции строят таблицу истинности, в которой приводятся всевозможные сочетания значений аргументов и соответствующие им значения логических функций. Так как число таких комбинаций конечно, то таблица истинности позволяет определять значение функции для любых значений аргументов.

Аналитический способ позволяет определять эти значения функций лишь для отдельных комбинаций аргументов (табл.).

Таблица 1.

Таблица истинности для логических функций для одного аргумента

Аргумент х	F0(x)	F1(x)	F2(x)	F3(x)
0	0	0	1	1
1	0	1	0	1

F0(x) = 0, F1(x) = x, F2(x) = НЕx, F3(x) = 1, т. е. существует только четыре функции одного аргумента.

Если число аргументов равно п и число различных сочетаний (наборов) значений аргументов равно двум, то число различных функций n-аргументов — 2n.

Основы алгебры логики

Поскольку цифровые вычислительные машины оперируют только информацией, представленной в виде «0» и «1», то и действия, выполняемые над ней, отличаются от общепринятых. Основы алгебры логики, разработанные математиком Д. Булем, базируются на использовании только двух переменных — a и b.

1. Логическое сложение a и b — логическая «ИЛИ»-дизъюнкция:

а + b = у, 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 1.

2. Логическое умножение а и b — логическая «И»-конъюнкция:

а * b = у, 0*0 = 0, 0*1=0, 1*0 = 0, 1*1 = 1

3. Инверсия (отрицание) а или b — логическое «НЕ», когда значение переменной изменяется на обратное (противоположное).

Элементы, выполняющие одну или одновременно несколько перечисленных функций, называются логическими. Таким образом, выделяют следующие базовые элементы: «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ», «И-ИЛИ-НЕ» и т.д., принцип работы которых поясняется таблицей истинности, указывающей значение функции при заданных переменных.

Законы преобразования над переменными

В алгебре логики используются разнообразные законы, позволяющие выполнять преобразования над переменными:

1. Переместительный — от изменения мест переменных значение функции не меняется:

x v y = yvx; x*y = y * x

2. Сочетательный — от изменения первоочередности вычислений значение функции не меняется:

х v ( у v г) = (х v у ) v z ; (x*y)*z = x*(y*z)

3. Распределительный:

(x v y)*z = x*y v x*z; x v (y*z) = (x v y)*(x v z)

4. Правила де Моргана:

НЕ( х v у ) = НЕ х * НЕ у ; НЕ( х * у ) = НЕ х v НЕ у.

5. Идемпотенции:

х v х = х ; х * х = х

6. Поглощения:

xv(x*y) = x; x*(xvy) = x

7. Склеивания:

(x*y) v(НЕ x*y) = y (x v y)*(НЕ x v y) = y

8. Операция над переменной и ее инверсией:

x v НЕ х = 1 ; x * НЕ х = 0.

9. Операции с константами:

x v 0 = x, x v 1 = 1; x *l = x, x * 0 = 0

10. Двойное отрицание:

НЕ-НЕ х = х.

Устройства, с помощью которых осуществляются логические и арифметические преобразования, называются логическими элементами.

Общий принцип обозначения логических элементов

Рис.4. Логический элемент

Рис. 5. Элемент с инверсным выходом

Рис.6. Элемент с инверсным входом

Обозначение элементов, реализующих логические функции

Рис. 7. Повторитель

Рис.8. Инвертор

Рис. 9. Конъюнктор «И»

Рис. 10. Дизъюнктор «ИЛИ»

Рис.11. Элемент «И-НЕ» (элемент Шеффера)

Рис. 12. Элемент «ИЛИ-НЕ» (элемент Пирса)

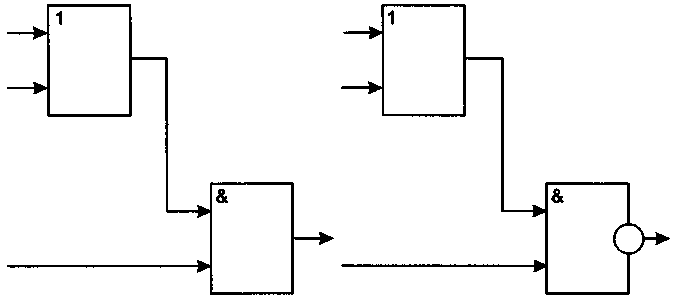
Рис.13. Элемент «И-ИЛИ» Рис.14. Элемент «И-ИЛИ-НЕ»

Так как логические элементы являются техническими устройствами, они обладают рядом параметров.

Коэффициент объединения по входу определяет число входов элемента, предназначенных для подачи логических переменных. Элемент с большим коэффициентом объединения имеет большие функциональные возможности.

Нагрузочная способность (коэффициент разветвления по выходу) определяет количество входов аналогичных элементов, которое может быть подключено к выходу данного элемента. Чем выше нагрузочная способность элементов, тем меньше требуется элементов при построении цифрового устройства.

Быстродействие оценивается задержкой распространения сигнала от входа к выходу элемента.

Помехоустойчивость определяется максимальным значением помехи, не вызывающей нарушения работы элемента. Для количественной оценки помехоустойчивости пользуются передаточной характеристикой логического элемента.

Передаточная характеристика логического элемента — это зависимость выходного элемента от входного.

Выводы

1. Результатом кодирования является выходное слово, которое представляет собой функцию алгебры логики (ФАЛ).
2. Устройства, предназначенные для формирования ФАЛ, называются логическими элементами последовательного, параллельного или смешанного действия.
3. Для задания ФАЛ используют либо аналитический, либо табличный способы представления информации.
4. Для выполнения операций над ФАЛ применяют тождества и законы алгебры логики.
5. Логические элементы, предназначенные для выполнения ФАЛ, характеризуются набором параметров: коэффициент объединения по выходу; нагрузочная способность; быстродействие; помехоустойчивость и передаточная характеристика.

Элементы алгебры логики