ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДАМИ ЛЯПУНОВА

Контрольная работа

Содержание

1. Понятие возмущенного и невозмущенного движения

2. Метод первого приближения

3. Метод функций Ляпунова

4. Исследование систем методом функций Ляпунова

5. Построение функций Ляпунова

6. Об исследовании качества нелинейных систем

Литература

1. Понятие возмущенного и невозмущенного движения

Любая динамическая система способна совершать множество движений, вызываемых теми или иными причинами. Среди этого множества существуют движения, которые система должна совершать в соответствии со своим назначением. Это движение Ляпунов предложил называть невозмущенным движением [20]. Для обеспечения работоспособности систем управления и других динамических систем необходимо, чтобы это движение было устойчивым.

В настоящее время это движение системы чаще называют эталонным, желаемым или номинальным движением [3, 25]. Все другие движения системы, отличающиеся от невозмущенного, называются возмущенными движениями.

В общем случае движения нелинейной системы описываются некоторой системой дифференциальных уравнений

, (1)

где – нелинейная вектор-функция, – вектор состояния системы, – вектор начальных условий, а – некоторая нелинейная вектор-функция, удовлетворяющая условиям существования и единственности решения [5, 20, 25].

Решением системы (1) является вектор . На рис. 1 показаны графики возможных движений некоторой динамической системы. На этом рисунке кривые соответствуют невозмущенному движению, а кривые и описывают возмущенные движения при различных начальных условиях и . Причем на рис. 1,а показаны графики движений системы при устойчивом невозмущенном движении , а на рис. 1, б – графики движений системы с неустойчивым невозмущенным движением . Здесь и в дальнейшем – обобщенное входное воздействие, а – начальные условия, при которых возникает невозмущенное движение системы; – другие начальные условия.

Рис. 1

В дальнейшем невозмущенное движение будет обозначаться

. (2)

При этом функция (2) является решением системы дифференциальных уравнений (1). К невозмущенному обычно относят движение системы при номинальных значениях параметров и воздействий, желаемое движение системы или её экстремальное движение.

Аналогично, функция

(3)

описывает возмущенные движения динамической системы и также

является решением системы нелинейных дифференциальных уравнений (1).

По предложению Ляпунова при исследовании устойчивости рассматриваются не все возмущенные движения, а лишь те, которые вызываются начальными условиями при условии, что . Поэтому в дальнейшем будут рассматриваться возмущенные движения только вида .

С тем, чтобы упростить задачу исследования устойчивости невозмущенного движения, обычно рассматриваются отклонения возмущенного движения от невозмущенного . С этой целью вводится вектор отклонений. .

Чтобы получить уравнения движения системы в отклонениях, продифференцируем по времени и учтем, что и вектор , и вектор удовлетворяют уравнению (1), так как являются его решениями. Тогда с учетом (3) будем иметь

или

, (4)

где . При этом, очевидно, всегда выполняются условия

, (5)

. (6)

Уравнение (4) и есть нелинейное уравнение в отклонениях возмущенных движений исследуемой системы (1). Его решение описывает невозмущенное движение этой системы. Другими словами, в переменных состояния невозмущенное движение описывается выражением или, как часто говорят, нулевым, тривиальным решением системы (4). Последнее, в силу условия (6), соответствует положению равновесия системы (4). Остальные решения 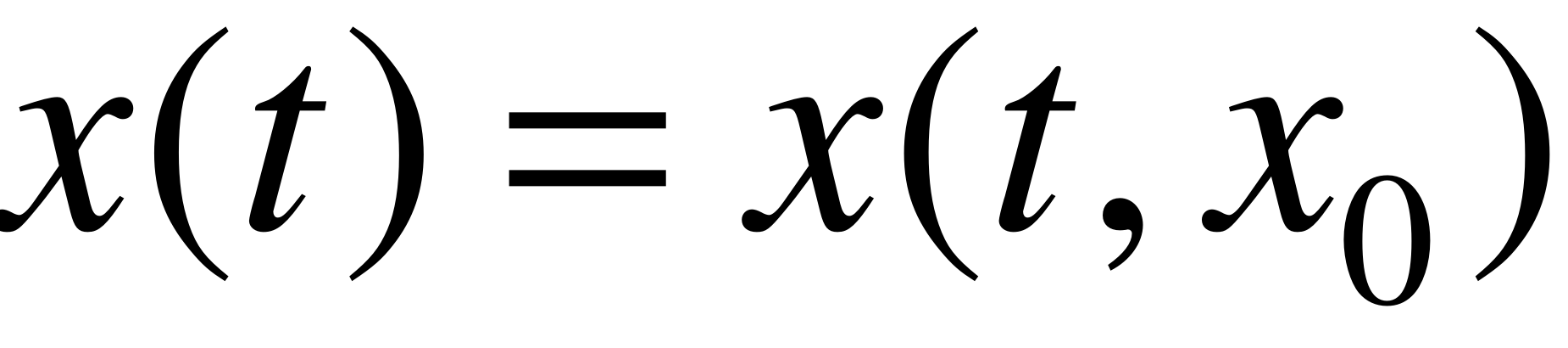этой системы описывают возмущенные движения исследуемой системы (1) или эквивалентной ей системы (4). Решение 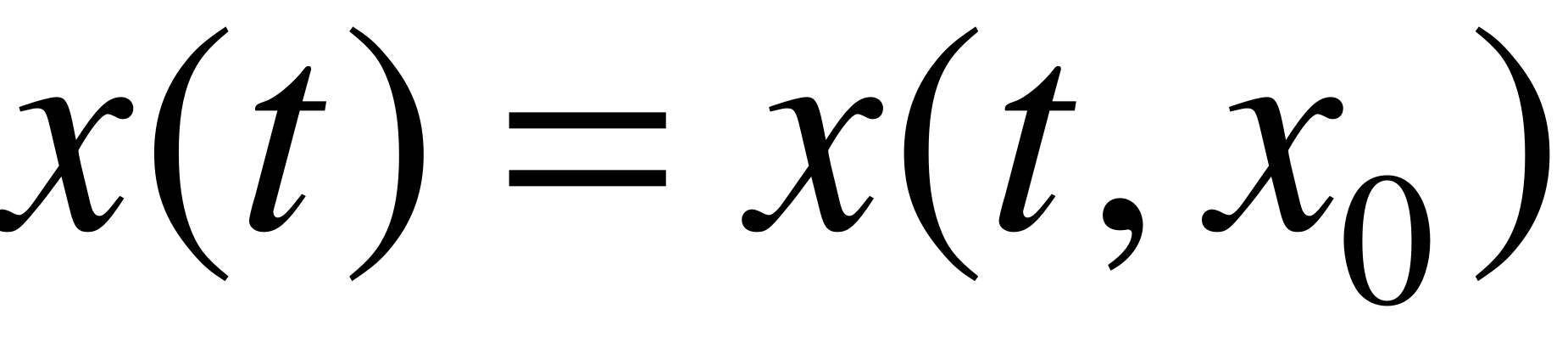, очевидно, описывает свободное движение системы (4).

Таким образом, задача исследования устойчивости движений нелинейных динамических систем достаточно общего вида (1) сведена Ляпуновым к задаче исследования устойчивости положения равновесия нелинейной дифференциальной системы (4) и состоит в изучении характера общего решения этой системы. Для решения этой задачи А. М. Ляпуновым было предложено два метода. Первый из них заключается в линеаризации системы (4), т.е. в изучении свойств системы первого приближения [3, 5, 25], а второй в применении специальных функций Ляпунова.

2. Метод первого приближения

Ляпунов в своей докторской диссертации, в частности, нашел и теоретически обосновал условия применимости уравнений первого приближения (применявшихся и ранее) для исследования устойчивости движений нелинейных систем. Эти уравнения строятся по уравнению (4) и имеют вид:

(7)

где

(8)

Ляпуновым были доказаны теоремы, позволяющие установить устойчивость или неустойчивость невозмущенного движения нелинейной системы (1) или, что то же самое (4), путем исследования её системы первого приближения (7), (8).

Обычно этот способ называют или первым методом Ляпунова, или методом первого приближения, или методом линеаризации.

Он может быть применен к исследованию нелинейной системы (4), если только – непрерывная, дифференцируемая вектор-функция, а отклонения малы по норме, т.е. , где - некоторое малое число.

Далее под нормой будет пониматься одно из следующих выражений:

или . (9)

Уравнения (7) часто называются линейными уравнениями в отклонениях системы (1) или (4).

Теоремы Ляпунова метода первого приближения. Обозначим через , собственные числа матрицы , т.е. корни уравнения . А. М. Ляпунов доказал следующие теоремы [20].

Теорема 1 (об асимптотической устойчивости). Если вещественные части всех собственных чисел матрицы системы первого приближения (7) строго меньше нуля, т.е.

, (10)

то невозмущенное движение нелинейной системы (1) и положение равновесия системы (4) асимптотически устойчивы.

Под асимптотической устойчивостью понимается следующее. Если , где – достаточно малое число, то выполняются условия

, , (11)

где – некоторое число, зависящее от .

Ситуация, соответствующая условиям (11), показана на рис. 2.

Определение. Область начальных значений, при которых выполняются условия (11), называется областью притяжения или областью асимптотической устойчивости.

Рис. 2.

Например, областью притяжения на рис. 3 является внутренняя область замкнутой кривой, показанной пунктирной линией. Само положение равновесия (0,0) в данном случае называется аттрактором (притягивающим положением равновесия).

Рис. 3

Определение. Если областью притяжения положения равновесия некоторой системы является все фазовое пространство, то она называется асимптотически устойчивой в целом.

Отметим, что матрица А, собственные числа которой удовлетворяют условию (10), называется устойчивой матрицей [10, 21]. При этом система (7) является асимптотически устойчивой в целом.

Теорема 2 (о неустойчивости по первому приближению). Если среди собственных чисел матрицы системы первого приближения (7) найдется хотя бы одно число с положительной вещественной частью, т.е.

, , (12)

то невозмущенное движение нелинейной системы (1) и положение равновесия системы (4) являются неустойчивыми, т. е. условия (11) не выполняются.

Теорема 3 (о невозможности исследования устойчивости по первому приближению). Если среди корней характеристического уравнения системы первого приближения имеется один или несколько с нулевыми вещественными частями, а остальные корни имеют отрицательную вещественную часть, то об устойчивости или неустойчивости невозмущенного движения нелинейной системы (1) и положения равновесия системы (4) сказать ничего нельзя.

Пример 1. Исследовать зависимость устойчивости положения равновесия от параметра системы, описываемой уравнениями

Решение. Прежде всего, построим систему первого приближения (7) в окрестности заданного положения равновесия. С этой целью найдем коэффициенты матрицы с помощью соотношений (8):

, ,

Следовательно, система первого приближения в данном случае имеет вид

Собственные числа матрицы , очевидно, равны , .

Применяя теперь теоремы Ляпунова, приходим к следующим выводам:

а) при , все собственные числа имеют отрицательную вещественную часть. Поэтому, в соответствии с теоремой 1, положение равновесия исследуемой нелинейной системы асимптотически устойчиво;

б) при , одно из собственных чисел имеет положительную вещественную часть. В соответствии с теоремой 2, положение равновесия исследуемой нелинейной системы является неустойчивым;

в) при , в соответствии с теоремой 3, нельзя сделать каких либо заключений об устойчивости положения равновесия рассматриваемой нелинейной системы (устойчиво оно или неустойчиво).

Большим преимуществом первого метода Ляпунова является простота процедуры исследования устойчивости этим методом, так как к исследованию нелинейных систем можно применять критерии устойчивости линейных систем. Однако метод первого приближения применим, если только нелинейности системы являются дифференцируемыми функциями по всем своим аргументам.

Недостатком метода первого приближения является также и то, что приведенные выше теоремы оценивают устойчивость лишь в сколь угодно малой области отклонений вектора состояний от положения равновесия. При этом величина этой области не определяется.

3. Метод функций Ляпунова

Этот метод не имеет ограничений по виду правых частей системы (1) или (4), кроме условий существования и единственности решения. Он может быть применен для исследования устойчивости движений любых систем дифференциальных уравнений, но, к сожалению, вплоть до настоящего времени не разработан общий метод построения функций Ляпунова, необходимых для решения вопросов устойчивости движения нелинейных систем.

При исследовании устойчивости движений нелинейных систем типа (1) этим методом также рассматривается система дифференциальных уравнений в отклонениях (4). Задача состоит в определении условий на вектор-функцию , при которых положение равновесия этой системы асимптотически устойчиво. Как отмечалось выше, положение равновесия системы (4) устойчиво асимптотически, если её вектор состояния удовлетворяет условиям (11).

Если положение равновесия системы устойчиво асимптотически, то расстояние изображающей точки от начала координат с течением времени убывает, возможно, немонотонно, как для примера показано на рис. 4. Если же особая точка системы не является асимптотически устойчивой, то это расстояние не уменьшается при .

Идея второго метода Ляпунова заключается в построении некоторой функции , зависящей от вектора состояния исследуемой системы, положительной и монотонно убывающей с уменьшением . Если эта функция при будет стремиться к нулю, подобно расстоянию изображающей точки от положения равновесия, то, очевидно, соответствующее положение равновесия будет асимптотически устойчивым.

Рис. 4

Другими словами, устойчивость или неустойчивость невозмущенного движения системы можно установить, исследовав характер изменения функции с течением времени.

Такие функции получили название функций Ляпунова. Функции Ляпунова обычно всегда больше нуля и имеют отрицательную производную по времени (в случае устойчивости положения равновесия), определенную на траекториях исследуемой системы.

В связи с этим рассмотрим понятие знакоопределенных функций, т. е. положительно (отрицательно) определенных и знакопостоянных положительно (отрицательно) полуопределенных функций, а также понятие производной по времени вдоль траекторий динамической системы.

Рассмотрим функцию . Пусть эта функция дифференцируема, т.е. её частные производные существуют при всех .

Определение. Функция называется положительно-определенной, если при любом

а при

Положительно-определенная функция обозначается . Положительно-определенными функциями при являются, например, функции

; .

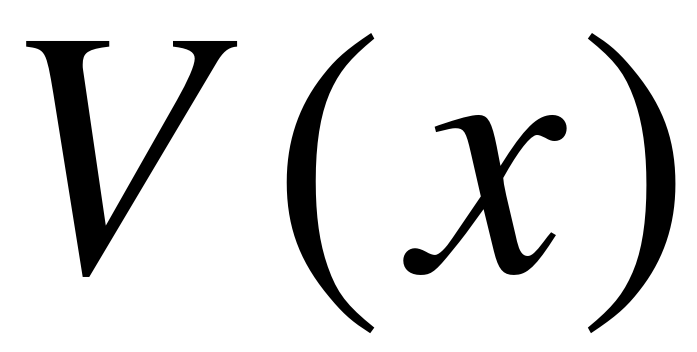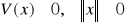
Определение. Функция называется положительно полуопределённой, если

Положительно полуопределенная функция обозначается . Положительно полуопределенной функцией при является, например, функция

Отрицательно-определенная функция определяется так:

где

Отрицательно-определенная функция обозначается , а отрицательно полуопределенная .

Определение. Функция 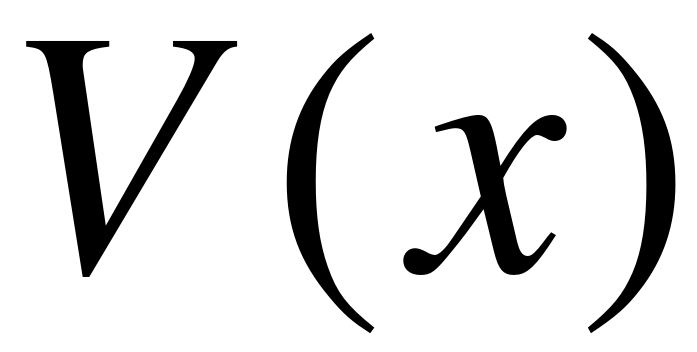называется бесконечно большой, если для любого числа найдется такое, что вне сферы имеет место неравенство .

Квадратичные формы. Часто в качестве знакоопределенных функций используются квадратичные формы, т. е. функции вида

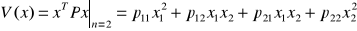(13)

или

Матрицы Р квадратичных форм обычно являются симметрическими матрицами, т. е. такими, у которых

. (14)

Условия положительной определенности квадратичной формы с симметрической матрицей состоят в следующем.

Критерий Сильвестра. Для положительной определённости квадратичной формы (13), (14) необходимо и достаточно, чтобы все диагональные миноры матрицы Р были строго больше нуля.

Матрицы Р, удовлетворяющие критерию Сильвестра, называют положительно-определенными и также обозначают.

Пусть матрица Р симметрическая, т. е.

Для оценки знакоопределенности этой матрицы найдем следующие определители :

Тогда в соответствии с критерием Сильвестра матрица , если

. (15)

Определение производной по времени вдоль траектории системы. Эта производная играет большую роль при исследовании устойчивости движений динамических систем методом функций Ляпунова. Рассмотрим некоторую функцию , определенную на переменных состояниях системы (4). Найдем её производную по времени вдоль траекторий этой системы. По общему правилу дифференцирования сложной функции находим

. (16)

Однако в силу уравнения (4) . Поэтому производная по времени от функции V(x) вдоль траектории системы (4) определяется выражением

. (17)

Пример 2. Пусть , а уравнения системы имеют вид: . Найти производную по времени функции вдоль траекторий заданной системы.

Решение. По формулам (16), (17) находим

или с учетом заданных уравнений для и :

Как видно, производная является отрицательно-определенной. Это указывает на то, что функция монотонно затухает, уменьшаясь по величине при . Так как может уменьшаться лишь при уменьшении , то норма решения рассматриваемой системы, очевидно, стремится к нулю при . Причем это имеет место при любых начальных условиях. Следовательно, положение равновесия рассматриваемой системы является асимптотически устойчивым в целом.

Заметим, что этот вывод сделан без решения дифференциальных уравнений заданной нелинейной системы, и каких-либо других математических операций над ними.

Основу второго метода Ляпунова для исследования движений динамических систем составляют следующие теоремы [2, 20].

Теорема 4 (об асимптотической устойчивости). Если при

всех существует положительно-определенная функция такая, что её производная по времени вдоль траекторий системы (4) является отрицательно-определенной функцией, то положение равновесия этой системы асимптотически устойчиво в целом.

Теорема 5 (о неустойчивости). Если при всех , существует положительно-определенная функция такая, что ее производная по времени вдоль траекторий системы (2) также является положительно-определенной функцией, то положение равновесия такой системы неустойчиво.

Теорема 6 (Барбашина-Красовского). Если при всех существует бесконечно большая положительно-определенная функция такая, что ее производная по времени вдоль траекторий системы (4) является отрицательно полуопределенной функцией, но обращается в нуль на множестве, не содержащем целых траекторий, (кроме положения равновесия) системы (4), то положение равновесия системы (4) асимптотически устойчиво в целом.

Положительно-определенная функция , удовлетворяющая какой-либо теореме об устойчивости или неустойчивости по отношению к некоторой системе, называется функцией Ляпунова данной системы. Отметим также, что если функция Ляпунова удовлетворяет условиям некоторой теоремы об устойчивости не во всем пространстве, а лишь в некоторой области, включающей положение равновесия, то эта область является областью притяжения соответствующего положения равновесия.

Приведем примеры исследования устойчивости движений нелинейных систем методом функций Ляпунова.

4. Исследование систем методом функций Ляпунова

Пример 3. Исследовать устойчивость положения равновесия системы

Решение. Возьмем функцию . Ее производная вдоль траекторий рассматриваемой системы, согласно (16), (17), определяется выражением

или

Полученная функция является определенно-отрицательной при всех . Следовательно, функция является функцией Ляпунова для рассматриваемой системы. Причем она удовлетворяет условиям теоремы 1 при всех , . Поэтому положение равновесия рассматриваемой системы асимптотически устойчиво в целом.

Пример 4. Исследовать методом функций Ляпунова устойчивость линейной системы, уравнение свободного движения которой имеет вид

. (18)

В данном случае можно говорить об устойчивости системы, поскольку она всегда имеет единственное положение равновесия, которое в отклонениях соответствует точке .

Решение. В данном случае функция Ляпунова ищется обычно в виде квадратичной формы

где – симметрическая матрица.

Если матрица удовлетворяет условию (15) критерия Сильвестра, то . Найдем ее производную по времени на траекториях системы (18):

В соответствии с выражением (16) и уравнением (18) находим , поэтому

, (19)

где – симметрическая, причем положительно-определенная матрица, т.е. .

Из выражения (19) вытекает следующее равенство:

. (20)

Это выражение называется матричным уравнением Ляпунова. В нём и – симметрические матрицы, причем также положительно-определенная матрица.

При исследовании устойчивости линейных систем в уравнении Ляпунова обычно задаются матрицей , а матрицу находят как решение этого уравнения.

Ляпунов доказал следующее утверждение.

Теорема 7. Если решение уравнения (20) – матрица является положительно-определенной, то линейная система (18) асимптотически устойчива в целом. Справедливо и обратное утверждение. Если же матрица Р окажется отрицательно-определенной, то система (18) будет неустойчивой.

Отметим, что математическое обеспечение современных ЦВМ имеет специальные программы для решения уравнения Ляпунова. Например, в системе MATLAB это программа “Lyap”.

Уравнение Ляпунова (20) часто применяется для исследования устойчивости и построения области притяжения (рис. 5) положения равновесия нелинейных систем вида

, (21)

где А – устойчивая матрица, – нелинейная вектор функция, причём . Если , то ее производная вдоль траекторий системы (21) определяется выражением

. (22)

Здесь матрицы и из уравнения Ляпунова (20).

Если удается показать, что модуль первого слагаемого в (22) в некоторой области, включающей точку пространства состояний системы (см. рис. 5, не заштрихованная область), больше модуля второго слагаемого, то в этой области, очевидно, будут выполнены условия теоремы 1, и, следовательно, при всех начальных условиях из этой области свободное движение исследуемой системы будет затухающим.

В этом случае положение равновесия нелинейной системы (21) будет асимптотически устойчивым в большом. Указанная область (рис. 5) будет областью устойчивости или областью притяжения положения равновесия рассматриваемой нелинейной системы (21).

Рис. 5

Пример 5. Исследовать устойчивость положения равновесия системы, показанной на рис. 6, двумя (первым и вторым) методами Ляпунова, если , а y – отклонение выходной переменной.

Рис. 6

Решение. Прежде всего, найдем уравнения заданной системы в переменных состояния. В соответствии с рис. 6 имеем равенства, , . Переходя к оригиналам, получим . Отсюда , так как .

Пусть , тогда . Следовательно, уравнения рассматриваемой системы в форме (4) имеют вид

(23)

Первый метод Ляпунова. Здесь необходимо сначала построить уравнения первого приближения. По формулам (8) находим:

, , , .

Итак, уравнение первого приближения (7) заданной системы

(23) имеет вид

Характеристический полином этой системы

а его корни , . Так как один из корней равен нулю, то сделать какое-либо заключение об устойчивости или неустойчивости системы (23) по уравнениям первого приближения нельзя.

Второй метод Ляпунова. В качестве функции Ляпунова возьмем функцию . Ее производная по времени вдоль траекторий системы (23) определяется следующим образом:

Очевидно, функции и не удовлетворяют ни первой, ни второй теоремам Ляпунова, а удовлетворяют теореме Барбашина-Красовского. При этом функция обращается в нуль при 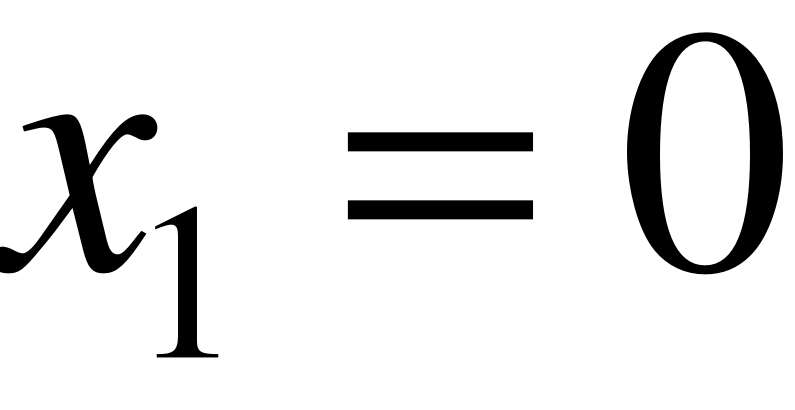и любом . Подставим эти значения в уравнения системы (23). В результате получим систему

траектории которой не принадлежат множеству , .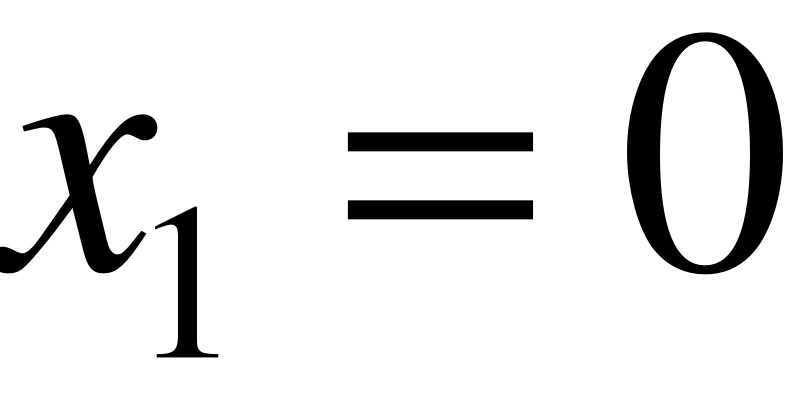

Следовательно, в силу теоремы Барбашина-Красовского положение равновесия исследуемой нелинейной системы асимптотически устойчиво в целом.

Часто нелинейная система имеет устойчивую линейную часть и одну нелинейность , где , причем

и . (24)

В этих случаях в качестве кандидата в функции Ляпунова можно брать сумму

(25)

Пример 6. Рассмотрим нелинейную систему

Функция расположена в первом и третьем квадрантах, как показано на рис. 7. Исследовать устойчивость положения равновесия данной системы.

Рис. 7

Решение. В данном случае нелинейность удовлетворяет условиям (24), поэтому в соответствии с выражением (25) в качестве функции Ляпунова возьмем функцию . Её производная по времени вдоль траекторий заданной системы

Итак, в силу первой теоремы Ляпунова данная система имеет асимптотически устойчивое в целом положение равновесия.

Градиентное управление. С помощью функции Ляпунова в виде квадратичной формы (13), построенной для устойчивой линейной части нелинейной системы типа (21), можно синтезировать так называемое градиентное управление. Это управление обеспечивает асимптотическую устойчивость в целом положения равновесия при наличии аддитивной с управлением ограниченной нелинейности. Покажем процедуру построения такого управления на примере.

Пример 7. Допустим, синтезируемая нелинейная система описывается уравнением

, (26)

где А – устойчивая матрица, – скалярная нелинейность такая, что

, , (27)

причем, если , то положение равновесия системы (26) – неустойчиво; – управление. Вектор x – измеряется.

Необходимо найти управление , при котором замкнутая система асимптотически устойчива в целом.

Решение. Пусть матрица является решением уравнения (20) при А из (26) и некоторой . Положим

, (28)

где – подлежащая определению функция.

Так как произведение является градиентом функции , то управление (28) называется градиентным.

Найдем условие выбора функции , определяющей интенсивность градиентного управления (28), при котором замкнутая система (26), (28) является асимптотически устойчивой в целом.

С этой целью найдем производную в силу указанной системы. На основе приведённых выше соотношений находим

С учетом того, что матрица Р является решением уравнения Ляпунова (20), а матрица А – устойчивой, отсюда следует равенство

, (29)

где матрица .

Рассмотрим два случая.

Пусть . Тогда в силу (28) , и из (29) вытекает соотношение

Пусть теперь . Тогда, подставляя из (28) в (29), получим

. (30)

Произведение можно представить в виде

Поэтому из равенства (30) выводим

. (31)

Из условия (27) на нелинейность следует, что значение разности в квадратных скобках соотношения (31) является строго положительным, если функция удовлетворяет условию

, (32)

где – положительно-определенная функция.

Таким образом, при условии (32) положительно-определенная функция имеет отрицательно-определенную производную по времени вдоль траекторий системы (33), (35) во всей области изменения вектора состояния . Следовательно, синтезированная система с градиентным управлением (28), (32) является асимптотически устойчивой в целом.

Условие может выполняться лишь на некоторой гиперповерхности, в которой не могут лежать целые траектории системы (26), (28) (кроме начинающихся в точке ). Поэтому из выражений (30) и (32) следует, что почти во всех точках траекторий рассматриваемой системы выполняется условие

, .

На основе этого неравенства можно заключить, что путем изменения положительно-определенной функции можно изменять скорость затухания функции Ляпунова, а, следовательно, и скорость затухания нормы решения нелинейной системы с градиентным управлением.

Рассмотрим еще один пример применения функций Ляпунова в виде квадратичной формы для обоснования устойчивости положения равновесия нелинейной системы. При синтезе системы управления здесь используется квазилинейное представление модели нелинейной системы, а также полиномиальный подход, изложенный применительно к линейным системам в восьмой главе.

Квазилинейная модель. Рассмотрим нелинейную управляемую систему, которая описывается уравнением

, (33)

где – доступный измерению вектор состояния системы; – непрерывная вектор-функция, причем

, , (34)

при . Здесь – некоторая область простран-

ства . В этих условиях уравнение (33) допускает квазилинейное [2] представление

, (35)

где и – функциональные n-вектор и непрерывная -матрица, элементы которых определяются [2] выражениями:

, ,

где , – символ транспонирования.

Управление ищется в виде , где . Поэтому с учетом (35) уравнение системы (33) принимает вид

, (36)

. (37)

Обозначим – решение системы (33), (35) или (36). При этом , , а область такова, что при всех и решение .

Необходимо найти непрерывный вектор из (37), при котором

, (38)

т.е. обеспечивается асимптотическая устойчивость положения равновесия замкнутой системы (33) или, что то же самое, системы (36) в некоторой области . Здесь – положительные постоянные.

Следующая теорема определяет условия существования области притяжения положения равновесия системы (36).

Теорема 8. Если матрица является непрерывной, а коэффициенты её характеристического полинома – постоянными числами, и этот полином удовлетворяет критерию Гурвица, то существует некоторая область , такая, что при всех и выполняется неравенство (6) при , .

Здесь – решение системы (36); – корни характеристического полинома матрицы (37); – достаточно малое число.

Справедливость теоремы вытекает из следующих фактов. В силу непрерывности матрицы и постоянства коэффициентов её гурвицевого характеристического полинома, матрица стремится при к постоянной матрице , которая является устойчивой. Поэтому существует симметрическая положительно-определенная матрица такая, что производная по времени функции на траекториях нелинейной системы (36) при достаточно малых является отрицательно-определенной функцией.

Поскольку теорема 8 не гарантирует асимптотической устойчивости в целом нелинейных гурвицевых систем типа (36), то необходимо всегда оценивать область притяжения их положения равновесия . Для этой цели целесообразно использовать метод численного моделирования с помощью ЭВМ, так как аналитические методы (например, на основе равенства (22)) дают слишком грубые оценки область притяжения. Область начальных условий , в которой решения системы (36) будут затухающими, и будет являться искомой областью притяжения.

Характеристический полином матрицы (37), согласно [7], определяется выражением

, (39)

где

, (40)

, (41)

где , , , .

Пусть

(42)

– желаемый гурвицевый полином матрицы системы (36). На основе полиномов (40), (41) составляется [8] система

, (43)

где , .

В (43) аргументы нелинейных функций из (40) и (41) опущены для сокращения записи. Решение системы уравнений (43) определяет искомый вектор , зависящий только от вектора , при котором решение системы (36) удовлетворяет (37) в некоторой области .

Замечание. Соотношения (40) – (43) могут использоваться для определения коэффициентов модального управления (7.4) и при постоянных матрице A и векторах b, c и k.

Пример 8. Найти управление, стабилизирующее частоту синхронного генератора при постоянном напряжении возбуждения и отсутствии насыщения в магнитных цепях. Синхронный генератор и турбина описываются уравнениями

, ,

, (44)

где – угол поворота ротора относительно синхронной оси вращения, – скольжение, – отклонение механической мощности турбины, , – конструктивные постоянные, , – дифференцируемые нелинейности, удовлетворяющие (34).

Решение. В квазилинейном представлении (35) уравнений (44) матрица и вектор определяются выражениями

, .

Здесь , , .

По формулам (39), (40) определяются полиномы: , , и , где , .

Пусть в качестве желаемого выбран полином , удовлетворяющий критерию Гурвица. Система (43) в данном случае имеет решение: , , .

Следовательно, искомое управление для заданной системы (44) определяется равенством: .

Подставляя найденные выражения для функций , в равенство (37), найдем матрицу . Нетрудно установить, что её характеристический полином совпадает с выбранным выше полиномом , т.е. в соответствии с теоремой 8 нелинейная система (44) при найденном управлении асимптотически устойчива при . Область может быть найдена, как отмечалось выше, методом компьютерного моделирования.

5. Построение функций Ляпунова

Основной сложностью второго метода Ляпунова является отсутствие общего метода построения функций Ляпунова для заданной нелинейной системы. В общем случае функция Ляпунова определяется решением нелинейного дифференциального уравнения в частных производных. Известные методы позволяют решить эту задачу лишь в отдельных частных случаях. При этом решение дифференциальных уравнений в частных производных для построения функции Ляпунова значительно осложняется требованием знакоопределенности самой функции Ляпунова и ее производной по времени на траекториях исследуемой системы.

В настоящее время известно много различных приемов или методов, которые позволяют решить задачу построения функций Ляпунова, но лишь в некоторых частных случаях [2, 4, 11, 21].

Рассмотрим в качестве примера метод деления переменных, предложенный Е.А. Барбашиным [2]. Это один из часто используемых методов построения функций Ляпунова для систем второго порядка. Применим он для систем, описываемых уравнением следующего вида:

. (45)

В этом методе предполагается построение в виде суммы двух функций

(46)

каждая из которых зависит лишь от одного переменного и .

Пусть , Тогда уравнения системы принимают вид

Производная по времени функции (46) вдоль траекторий этой системы определяется выражением

Барбашин предложил выбирать функции и так, чтобы

. (47)

Тогда

(48)

Раскрывая соотношение (47) в виде пропорции и приравнивая последнюю к единице, получим

Отсюда следуют равенства

Подставляя найденные выражения для и в

(45) и (48), получим

(49)

Из условий

можно найти условия на функции , , , при которых будут выполняться условия теоремы Барбашина-Красовского и при которых положение равновесия системы будет устойчиво.

Пример 9. Исследовать устойчивость положений равновесия судна, уравнение бортовой качки которого на «тихой» воде имеет вид

(50)

где – момент инерции судна, – коэффициент вязкого трения, – восстанавливающий момент. Возможные зависимости его от угла крена судна приведены на рис. 8 и 9. На этих рисунках угол соответствует положению судна «килем вверх».

Рис. 8

Решение. Сравнивая уравнение бортовой качки судна (50) с уравнением (45), заключаем, что имеют место соответствия

Следовательно, для построения функции Ляпунова можно воспользоваться методом Барбашина.

Подставляя соответствующие функции в равенства (49), найдем искомую функцию Ляпунова и её производную по времени вдоль

траекторий системы (50):

(51)

Здесь возможны два варианта. Если зависимость восстанавливающего момента от угла крена имеет вид, показанный на рис. 8, то функции (51) удовлетворяют условиям теоремы Барбашина-Красовского в окрестности положения равновесия . Следовательно, положение равновесия в этом случае будет асимптотически устойчивым в области , где , причем коэффициент зависит от значений .

Рис. 9

Если же зависимость восстанавливающего момента от угла имеет вид, показанный на рис. 9, то в окрестности основного положения равновесия уравнение (50) будет иметь ещё два положения равновесия и . При этом в соответствии с той же теоремой и приведенными выражениями (51) положения равновесия и будут устойчивыми, а основное положение равновесия будет неустойчивым. В этом случае судно будет двигаться с креном либо на левый, либо на правый борт.

6. Об исследовании качества нелинейных систем

В силу невыполнимости принципа суперпозиции в нелинейных системах известные критерии качества переходных процессов, такие как время регулирования, перерегулирование, колебательность, определяемые по переходной функции системы при нулевых начальных условиях, строго говоря, теряют свой смысл, так как при различных начальных условиях указанные показатели в случае нелинейных систем будут принимать различные значения. Поэтому качество нелинейных систем чаще всего оценивают либо с помощью интегральных оценок, определяя их максимальное значение по всей области притяжения, либо ограничиваются определением минимального или максимального времени регулирования. Для этой цели часто используются функции Ляпунова [2]. Особенно удобными для этой цели являются квадратичные формы.

Очень часто нелинейные системы синтезируются как оптимальные по быстродействию, т. е. управление определяется таким образом, чтобы при любых начальных условиях из области притяжения время регулирования (или длительность переходного процесса) было минимальным [15, 22]. Практически это значит, что при различных начальных условиях длительность переходного процесса будет различна, но время переходного процесса при оптимальном управлении будет меньше, чем при любом другом управлении.

В связи с большой сложностью получения аналитических решений уравнений нелинейных САУ оценка качества синтезированных систем чаще всего осуществляется путем моделирования. Для этой цели удобнее всего использовать цифровые вычислительные машины при достаточно малом периоде квантования переменных по времени. Если используется программа без автоматического выбора (по заданной точности решения) шага квантования по времени, то его необходимо выбирать следующим образом.

Определяется некоторый достаточно малый период квантования по времени , при котором переходные процессы моделируемой устойчивой системы являются затухающими. Затем период квантования уменьшается в два раза, и сравниваются процессы, полученные при и . Уменьшение периода квантования продолжается до тех пор, пока процесс, получаемый при , не будет отличаться от процесса, получаемого при , на величину, меньшую заданной погрешности моделирования непрерывной динамической системы. Дальнейшие расчеты проводятся при .

Литература

под ред. Н.Ш. Кремера: Математика для экономистов: от арифметики до эконометрики. - М.: Юрайт, 2012

под ред. А.С. Поспелова: Сборник задач по высшей математике. - М.: Юрайт, 2011

под ред. С.Я. Казанцева ; рец.: Р.З. Матиев, Г.Е. Корчагин: Математика для юридических специальностей. - М.: Академия, 2011

Шапкин А.С.: Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями. - М.: Дашков и К, 2011

Атурин В.В.: Высшая математика. - М.: Академия, 2010

Баврин И.И.: Высшая математика. - М.: Академия, 2010

Бурмистрова Е.Б.: Линейная алгебра, дифференциальное исчисление функций одной переменной. - М.: Экономика, 2010

под ред. Н.Ш. Кремера ; рец.: Каф. математики Финансовой Академии при Правительстве РФ, В.З. Партон: Высшая математика для экономистов. - М.: ЮНИТИ, 2010

Соболь Б.В.: Практикум по высшей математике. - Ростов н/Д: Феникс, 2010

Баранова Е.С.: Практическое пособие по высшей математике. - СПб.: Питер, 2009

Боревич З.И.: Определители и матрицы. - СПб. ; М. ; Краснодар: Лань, 2009

Гельфанд И.М.: Лекции по линейной алгебре. - М.: Добросвет : КДУ, 2009

Красс М.С.: Математика для экономистов. - СПб.: Питер, 2009

под ред. Н.Ш. Кремера ; рец.: Каф. математики Финансовой Академии при Правительстве РФ, В.З. Партон: Высшая математика для экономистов. - М.: ЮНИТИ-ДАНА, 2009

Шафаревич И.Р.: Линейная алгебра и геометрия. - М.: ФИЗМАТЛИТ, 2009

Бутузов В.Ф.: Линейная алгебра в вопросах и задачах. - СПб ; М. ; Краснодар: Лань, 2008

PAGE \* MERGEFORMAT1

ИССЛЕДОВАНИЕ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДАМИ ЛЯПУНОВА