Статистический анализ рисковых активов. Нелинейные модели
Контрольная работа
Статистический анализ рисковых активов. Нелинейные модели
Содержание
1. Условно – гауссовские модели финансовых индексов
2. Авторегрессионная модель условной неоднородности (ARCH)
3. Модель GARCH
4. Модели EGARCH, TGARCH, HARCH
5. Модель стохастической волатильности
6. Оценка волатильности
7. Устойчивые распределения
8. Условно-устойчивые распределения
9. Безгранично делимые распределения
10. Нелинейные хаотические модели
14 Литература
1.Условно – гауссовские модели финансовых индексов
Рассмотрим следующую модель эволюции стоимости рискового актива (акции).
|
, . |
(1) |
Величины принято считать случайными. Наиболее привлекательным с точки зрения анализа и развитой статистики является гауссовский закон совместного распределения величин . Гауссовский закон совместного распределения приводит к линейным моделям временных рядов таких как скользящее среднее авто-регрессия, которые подробно рассмотрены в [1]. Однако реальные данные для многих финансовых временных рядов показывают, что линейные модели не всегда адекватно отражают истинную картину поведения цен.
Если иметь ввиду разложение Дуба [2], в котором привлекаются условные математические ожидания , вполне естественным является предположение о том, что условные распределения являются гауссовскими:
|
. |
(2) |
В (2) - предсказуемые случайные величины. Из представления (2) следует, что существует условное математическое ожидание и условная дисперсия
|
. |
(3) |
Безусловный закон распределения является смесью гауссовских законов и получается интегрированием по распределению , что позволяет говорить о разнообразии этого класса распределений.
Рассмотрим последовательность
|
. |
(4) |
Эта последовательность также является условно-гауссовской последовательностью со стандартным нормальным распределением . Отсюда следует, что , поэтому последовательность - последовательность независимых стандартных нормальных случайных величин. Из этого рассуждения следует, что условно-гауссовская последовательность представима в виде
|
, |
(5) |
где последовательность независимых стандартных нормальных случайных величин – белый шум.
Условно-гауссовские последовательности позволяют достаточно просто решать задачи прогноза цены. Так условный точечный прогноз с минимальной дисперсией ошибки для - . Условный доверительный интервал для - , где - решение уравнения , - условная доверительная вероятность, а - функция стандартного нормального распределения. Отсюда для цены условный точечный прогноз
|
(6) |
Условный доверительный интервал с условной доверительной вероятностью
|
. |
(7) |
Ясно, что более подробное описание условно-гауссовских последовательностей зависит от конкретизации структуры величин . Именно этому и посвящено изложение, причем внимание уделяется нелинейным моделям.
2. Авторегрессионая модель условной неоднородности (ARCH).
Здесь и далее мы будем предполагать, что белый шум является единственным источником случайности, то есть фильтрация , . Модель ARCH была впервые введена в работе Р.Энгля [3], который поставил перед собой цель объяснить возникновение кластерности (группировки) больших или малых значений . В этой модели
|
, |
(8) |
с , и начальными значениями , которые могут быть случайными величинами, независящими от , но обычно считают их постоянными. Из (8) видим, что волатильность является (предсказуемой) функцией от . При этом в силу особенности модели если были большими, то это приводит к большому значению , что в свою очередь приводит к большому значению . Если были малыми, то большое значение может появиться только за счет большого значения . Таким образом, становится понятным, почему ARCH-модель объясняет явления кластерности. Это в свою очередь оправдывает название модели - Авторегрессионая модель условной неоднородности, в которой волатильность ведет себя весьма неоднородно в зависимости от прошлых значений .
Отметим, что модель (8) может быть переписана в виде
|
. |
(9) |
На рисунке 1. представлена машинная реализация ARCH-модели второго порядка.
Остановимся на рассмотрении ряда статистических свойств последовательности , которая описывается ARCH-моделью первого порядка. Использование модели первого порядка, обусловлено желанием упростить изложение.
Для модели первого порядка формула (9) приобретает вид
|
. |
(10) |
Прежде всего, определим математическое ожидание и дисперсию . Математическое ожидание
|
, |
(11) |
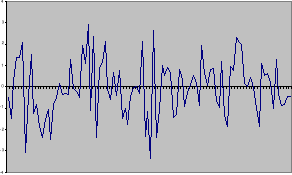
Рис. 1. График компьютерной реализации последовательности , подчиняющейся ARCH-модели второго порядка с .
Дисперсия
|
((12) |
В предположении рекуррентное уравнение (12) имеет единственное стационарное решение (решение независящее от )
|
. |
(13) |
Вычислим ковариацию - . Пусть . Ковариация
|
. |
(14) |
Однако свойство (14) не означает, что случайные величины независимы, поскольку совместный закон распределения не является гауссовским. Чтобы установить факт зависимости рассмотрим корреляционную зависимость между и . В стационарном случае ковариация
Отсюда . Вычислим Непосредственно вычисляем . Далее
При условии, что и , единственное стационарное решение последнего рекуррентного уравнения - . Отсюда . Следовательно . Отсюда
|
. |
(15) |
Нетрудно показать, что дисперсия . Теперь можно определить автокорреляционную функцию
Покажем, что ARCH – модель тесным образом связана с авторегрессионной моделью. Действительно, пусть имеется ARCH – модель (9), из которой следует, что . Обозначим через . Поскольку , то последовательность является мартингал-разностью. Тогда
|
. |
(16) |
Таким образом, величины удовлетворяют авторегрессионной модели с шумом , являющимся мартингал-разностью.
Для модели первого порядка
|
. |
(17) |
Рассмотрим авторегрессионную модель первого порядка со случайными коэффициентами
|
, |
(18) |
где и две независимые стандартные гауссовские последовательности. Рассмотрим условный закон распределения . Нетрудно убедиться в том, что
|
. |
(19) |
Напомним, что для ARCH – модели . Сопоставив с , получим, что устроены точно также, что и при условии, что .
Для ARCH – модели -го порядка эквивалентная с точки зрения распределения авторегрессионная модель со случайными коэффициентами модель:
|
, |
(20) |
где - независимые стандартные гауссовские последовательности, при .
Рассмотрим несколько более сложную модель:
|
, |
(21) |
в которой сочетается ARCH и AR – модели.
На рисунке 2. представлена компьютерная реализация модели.
Условно-гауссовский характер модели позволяет представить плотность совместного распределения величин при
|
. |
(22) |
Применим метод максимального правдоподобия для получения оценок параметров аторегрессионной составляющей модели. Не вдаваясь подробно в
Рис. 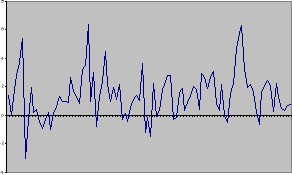
2. График компьютерной реализации последовательности , подчиняющейся ARCH, AR - модели второго порядка с .
сущность метода максимального правдоподобия, отметим, что в нашем случае для получения оценок максимального правдоподобия требуется найти
|
, . |
(23) |
Рассмотрим вопрос о предсказании будущего движения цен, считая, что последовательность подчинена ARCH – модели.
Поскольку последовательность является мартингал разностью, то оптимальная в среднеквадратическом смысле оценка . Тривиальность этой оценки говорит о том, что ARCH – модель непригодна для получения точечных оценок. Поэтому целесообразно говорить об оценках нелинейных функций от - или .
Рассмотрим оценку с целью в дальнейшем получить доверительный интервал для цены. Вычислим
Отсюда следует, что оценка . По индукции получаем
Отсюда
|
. |
(24) |
Если , то при оценки сходятся с вероятностью единица к значению .
Остановимся на прогнозировании цены. Если подчиняется ARCH – модели, то одношаговый точечный прогноз для цены:
|
. |
(25) |
Парадоксальность ситуации заключается в том, что при любых обстоятельствах точеный одношаговый прогноз предвещает рост цены.
Одношаговый доверительный интервал
|
. |
(26) |
Рассмотрим многошаговый прогноз цены, а именно рассмотрим построение доверительного интервала в первом приближении.
Поскольку
|
, |
(27) |
то нам необходимо найти условное математическое ожидание
|
(28) |
и условную дисперсию
|
(29) |
При вычислении дисперсии использовалось некоррелированность
Таким образом, условный доверительный интервал: