Общая характеристика нагрева материалов

Контрольная работа

Общая характеристика нагрева материалов

Содержание

1 Общая характеристика нагревания лазерным излучением

2. Теплопроводностные механизмы отвода тепла

3. Термические эффекты, сопровождающие лазерный нагрев

4. Диффузионно-химические явления и фотохимические методы

5. Эмиссионные процессы

6. Основные предпосылки для построения квантовой теории фотоэффекта

7. Фотоэлектрический эффект под действием ЛИ

8. Термоэлектронная эмиссия

9. Особенности действия ЛИ в жидкости и в вакууме

10. Лазерное плавление поверхности

Литература

1 Общая характеристика нагревания лазерным излучением

Рассмотрим тепловые эффекты в конденсированных средах и основные особенности температурной кинетики при лазерном воздействии.

При рассмотрении процессов воздействия ЛИ на материалы необходимо знать энергетические характеристики: поглощенную долю падающего потока, максимальную плотность мощности ЛИ, длительность импульса, длину волны, пространственное распределение плотности мощности и условия фокусировки. Указанные параметры источника ЛИ зависят от типа лазера, активного вещества, метода накачки и конструкции осветителя, используемого типа резонатора и оптической фокусирующей системы и т.д. с одной стороны, и оптических свойств обрабатываемого материала с другой.

Для описания тепловых источников (при известных пространственно-временных характеристиках ЛИ ОКГ), возникающих в непрозрачных для излучения ОКГ данной длины волны материалах, нужно знать коэффициенты отражения, позволяющие оценить долю поглощенной энергии.

Коэффициент отражения R для плотностей потока много меньше 106 Вт/см2 может быть оценен с помощью известных из электродинамики формул Френеля [1], которые существенно зависят от состояния поверхности (класса шероховатости, обработки, наличия пленки окислов). Увеличение плотности потока до 106 107 Вт/см2 приводит к уменьшению коэффициента отражения для большинства материалов.

Экспериментальные данные показывают, что увеличение плотности потока ЛИ до 1010 Вт/см2 приводит к резкому уменьшению R от френелевского значения до величины 0,1 от нормального (рис. 1). Вследствие заметной пространственно-временной неоднородности импульса излучения измеренные на опыте значения коэффициента отражения относятся к некоторому усредненному значению плотности потока ЛИ.

Рис.1 Качественная зависимость коэффициента отражения Rфр от плотности потока излучения Q [2]

Поэтому целесообразно описывать сложные пространственно-временные зависимости плотности мощности ЛИ более простыми закономерностями. В частности, достаточно удачным является использование для описания пространственного распределения мощности излучения, закона нормального распределения.

Такое приближение при тепловых расчетах дает возможность использовать ряд преимуществ теории тепловых источников [3], разработанной для процессов сварки, резки и др. С другой стороны, опытные данные [4] и теоретические соображения приводят к выводу о близости пространственного распределения мощности источника, создаваемого ЛИ, к закону нормального распределения.

В расчетах тепловых процессов обычно используют два типа пространственного распределения удельного теплового потока: гауссовское и равномерное (по пятну нагрева радиусом rf).

Для гауссовского распределения справедливо равенство

(1)

где kc коэффициент сосредоточенности в см2, определяющий степень «остроты» источника.

Для равномерного распределения мощности по пятну нагрева радиусом rf имеем

(2)

Связь между распределениями (1) и (2) может быть установлена через коэффициент сосредоточенности kc [3] в законе Гаусса:

Здесь В* численный множитель, зависящий от способа определения rf в законе Гаусса. Если определить rf как расстояние от центра пятна, при котором мощность падает в е раз, то В* = Расчеты показывают, что в зоне воздействия ЛИ при Q0 ~ 106 Вт/см2 разница между этими типами распределения по оси симметрии источника порядка ~10 % и становится существенной на краю области распределения при r rf [5].

Отметим особенности задач теплофизики при нагреве материалов ЛИ [6]. Для воздействия импульсных лазеров с продолжительностью импульса порядка единиц миллисекунд и плотностью мощности ЛИ Q0 ~ 104 106 Вт/см2 характерно следующее:

в большинстве случаев потерями теплоты с помощью лучеиспускания и конвекции с нагреваемой поверхности можно пренебречь;

в ряде случаев учет температурной зависимости теплофизических и оптических постоянных не вносит большого изменения в конечное положение зоны обработки, что позволяет рассматривать более простые задачи с постоянными, не зависящими от температуры коэффициентами;

учет теплоты фазовых переходов (плавление, кристаллизация, испарение) наиболее важен в тех задачах обработки материалов, где испарение и движение продуктов выноса газообразной и конденсированной фаз являются определяющими с энергетической точки зрения. Когда плавление является основным итогом действия луча, что наблюдается в процессах сварки, существенным может быть учет теплоты плавления. Тогда становится необходимым рассматривать одну из разновидностей задачи Стефана [4] с фазовым переходом на движущейся границе;

теплофизическая постановка задачи по описанию воздействия ЛИ справедлива только для плотностей мощности ~ 108 109 Вт/см2. При дальнейшем росте плотности мощности одним из основных методов рассмотрения явлений в зоне воздействия излучения становится теория взрыва, сопровождающегося генерацией ударных волн, проходящих через объем материала. Роль взрывчатого вещества в этом случае играет узкий поверхностный слой вещества, в котором происходит энерговыделение. При этом на свободных поверхностях тонких пластин возможен откол, если амплитуда ударных волн превосходит предел прочности вещества на разрыв [7]. Амплитуды ударных волн для мощных импульсных лазеров с Q0 ~ 1012 1014 Вт/см2 достаточны для развития в веществе процессов, сопровождающихся структурными изменениями и фазовыми переходами.

Отметим основные методы решения теплофизических задач. Если задачи обработки материалов формулируются в линейной постановке, то обычно используют методы источников (функций Грина), методы Фурье, конечные и бесконечные интегральные преобразования по пространственным переменным.

Остановимся на связи выбора метода решения рассматриваемой задачи с конкретной информацией, которую необходимо получить при решении задачи.

Для решения трехмерных задач нагрева полуограниченных тел практически при любой продолжительности воздействия наиболее универсальным является метод источников, который в сочетании с принципом местного влияния [3] дает возможность в общем виде рассмотреть характерные закономерности изменения температурного поля в объеме материала.

При анализе температурных полей составных тел удобно использовать преобразование Лапласа по временной переменной, позволяющее найти варианты решения, справедливые для малых времен действия источника и для установившегося температурного поля.

Использование конечных интегральных преобразований по пространственным переменным становится целесообразным, когда существенно различие теплофизических свойств соединяемых или нагреваемых материалов (например, в случае стыковой сварки листовых материалов или при нагреве двухслойных ограниченных пластин).

Применение классического метода Фурье в сочетании с методами интегральных преобразований может быть полезным при решении задач нагрева, когда температура поверхности близка к установившемуся состоянию [8, 9].

В значительном числе задач лазерного нагрева материалов необходимо учитывать температурную зависимость теплофизических коэффициентов. Общих аналитических методов решения таких задач не разработано, поэтому в каждом конкретном случае необходим детальный анализ возможностей того или иного подхода [10, 11].

Оценим количественные параметры механизмов поглощения света и перехода этой энергии в тепло.

Если падающий на поверхность материала световой поток частично отражается, а остальная его часть проходит вглубь объема тела и поглощается в нем, то внутри и на поверхности тела, начиная с некоторого времени, действует тепловой источник, распределенный в пространстве и времени определенным образом. Плотность поглощенной мощности ЛИ для большинства реальных случаев изменяется внутри объема твердого тела по закону Бугера [1]:

Q(z) = Q0(1 R)e, (3)

где Q(z) и Q0 соответственно объемные плотности мощности излучения в Вт/см3 на расстоянии z от поверхности и на поверхности тела; (1 R) и соответственно поглощательная способность и коэффициент поглощения света в см

Оптические свойства металлов опишем классической моделью свободных электронов [12], в соответствии с которой световой поток (за вычетом отраженной части) полностью поглощается при взаимодействии с электронами проводимости в поверхностном слое толщиной ~ 104 105 см. Процесс поглощения квантов света электронами проводимости происходит как при поглощении или испускании фононов, так и при столкновении электронов между собой и т.д.

2. Теплопроводностные механизмы отвода тепла

Уравнение теплопроводности, начальное и граничные

условия

Известно, что поглощение света повышает энергию электронов. Часть этой энергии электроны передают решетке, однако эффективность передачи невелика вследствие большой разницы масс электронов и ионов. Поэтому электронный газ значительно перегревается по сравнению с решеткой. Процесс разогрева электронного газа и передачу поглощенной энергии решетке рассмотрим на основе решения кинетического уравнения для функции распределения по энергиям электронного газа [13].

Электронный газ и решетка в металле две слабо взаимодействующие подсистемы. Частоты релаксации для электронного газа и ионов (еe и ii) существенно больше частоты релаксации для обмена энергией между ними еi, если

еe >> еf (4)

и ii >> ei , (5)

где еe и ii соответственно, частоты столкновений электрон электрон и ион ион; еf частота столкновения электронов с фотонами; еi частота электронно-ионных столкновений, то в этом случае электронный газ и решетку можно характеризовать в отдельности электронной Те и решеточной Ti температурами. Выполнение условия (4) означает быстрое перераспределение поглощенной энергии между электронами проводимости, а (5) означает, что энергия, передаваемая решетке электронами, быстро перераспределяется между ионами.

Рассмотрим последовательно выражения для частот релаксаций еf, ee, еi, ii, соотношения между которыми существенно определяют характер процессов в металлах при поглощении излучения. Частота столкновений электронов с фотонами еf пропорциональна плотности мощности Qs и может быть оценена с помощью соотношения [14]

ef = Qs/hn, (6)

где Qs поверхностная плотность мощности в эрг/см2с; h энергия кванта в эрг; n число электронов, поглощающих излучение в см3.

Для видимого участка спектра, h >> kcTe, где Te температура электронов ~ 103 К. Тогда n nh/F, где n ~ 51022 см3 число электронов проводимости в единице объема; F энергия Ферми;

F = h(32)1/3n2/3/8m2,

где h постоянная Планка; m масса электрона; F 5 10 эВ.

Частота межэлектронных столкновений ee в металле преимущественно определяется количеством электронов в области размытости Ферми и вычисляется с помощью соотношения [14]

ee = Feen(kTe/F)2, (7)

где F скорость электрона на поверхности Ферми ~ 108 см/с; ee резерфордовское сечение взаимодействия электрон электрон; ee 51016 см2; kTe область размытости Ферми. Тогда при Те ~ 103 К величина ee 1014 с1, а время установления равновесного распределения электронного газа ee ~ 1ee ~ 1014с. Скорость передачи энергии электронного газа решетке и температура определяются источником тепла и коэффициентом теплоотдачи от электронов решетке kei.

Анализ задачи об обмене энергией между электронами и решеткой [13] показывает, что рождению фонона при квантово-механическом описании соответствует черепковское излучение звуковых волн сверхзвуковыми электронами (F ~ 109 см/с, скорость звука s ~ 105 см/с) при классическом рассмотрении.

В этом случае при i > D (D температура Дебая) ei ~ 1/T (ei время свободного пробега электрона до столкновения с фононами).

Количество энергии, получаемое решеткой от электронного газа в единице объема в единицу времени:

= kei(Te Ti), kei = 2m*s2n/[Dei(D)], (8)

где m* эффективная масса электрона.

Поскольку по теоретическим оценкам [13] Dei(D) = const, то для металлов среднего атомного веса Dei(D) 1011 сград. Тогда коэффициент теплообмена между электронами и решеткой kei ~ 1017 эрг/(см3сград), или ~1010 Вт/(см3град).

Частота электронно-ионной релаксации ei может быть выражена через коэффициент теплообмена

ei = kei/(ici ) или ei = 2m*F nkcs2/(30i ci а0 F), (9)

где ici объемная теплоемкость решетки в эрг/см3град [107 Втс/(см3град)]; a0 постоянная решетки ~ 108 см. Подстановка численных значений дает ei ~ 1011 с1 и ei ~ 1011 с.

Частоту ii можно оценить по формуле

ii kc20Ti/(a0Мis), (10)

где 0 параметр Грюнайзена; Мi масса иона ~ 1022 г; при Ti ~ 103 К, ii~ 1013 с1 и ii ~ 1013 с.

Сравнивая равенства (6) и (7), можно показать, что при плотностях потока излучения Q0 109 Вт/см2 условие (5) выполняется всегда и электронный газ в металле характеризуется температурой Те. Аналогично выполняется условие (6), и для описания теплового состояния решетки можно ввести температуру Ti. Для моментов времени t < ei (ei ~ 1011 с) в металле разогревается только электронный газ, температура же решетки мало изменяется. Это обусловлено тем, что время релаксации электронного газа существенно меньше времени релаксации температуры решетки.

Величина T = (Те Тi) зависит от соотношения частот ef и ei, поскольку разность T тем меньше, чем больше величина ei по сравнению с ef, и когда ef < ei, то Те Ti. Однако повышение температуры электронного газа происходит до тех пор, пока количество энергии, передаваемой решетке, не сравняется с количеством энергии, получаемой от внешнего источника [15]. Интенсивная передача энергии электронного газа решетке наступает при t > ei , когда разность Те Ti максимальна. В дальнейшем разность Те Ti уменьшается, стремясь к некоторому пределу, который равен общей температуре металла. Для металлов при постоянной плотности мощности излучения понятие общей температуры металла Т можно ввести, начиная с времени t >> 100ei ~ 109 с.

Поглощенная энергия передается от зоны воздействия ЛИ внутрь вещества с помощью различных механизмов теплопроводности электронной, фононной и лучистой.

В интервале температур от сотен до нескольких тысяч градусов перенос энергии в металлах осуществляется с помощью электронной проводимости. Фононная теплопроводность, играющая существенную роль при низких температурах, в указанном интервале температур мала по сравнению с электронной. Лучистая теплопроводность играет существенную роль в процессах переноса энергии при температурах выше ~ 104 К.

В общем случае движущихся сред (или перемещающегося источника теплоты) задача о нагреве полубесконечного тела (в пренебрежении лучистой теплопроводностью и конечностью скорости распространения тепловой энергии) описывается системой дифференциальных уравнений [15]

(11)

(12)

где вектор поля скоростей; Q объемное тепловыделение в системе, обусловленное действием источника тепла.

Коэффициенты объемной теплоемкости с и электронной теплопроводности ke являются функциями температуры, поэтому система (11), (12) нелинейна. Из-за математических трудностей приходится делать упрощающие предположения. В частности, обычно для металлов считают, что температурная зависимость теплофизических коэффициентов не оказывает существенного влияния на температурное поле. Если, кроме того, среда неподвижна, а поглощение излучения происходит в тонком поверхностном слое, величина которого ~1 ( коэффициент поглощения), то система (11), (12) упрощается:

(13)

где k* = ke/(c) коэффициент температуропроводности [см2/с].

Совместно с краевыми условиями

T/z = 0 при z = 0; (14)

T= 0 при z = ;

= 0 (15)

система (11) (15) описывает нагрев полубесконечного тела, начиная со времени i > 109 с. Граничное условие (14) справедливо только в том случае, если плотность потерь тепла с поверхности с помощью лучеиспускания (по закону Стефана-Больцмана), конвекции (по закону Ньютона) или испарения мала по сравнению с величиной плотности потока ЛИ. Если это условие не выполняется, то соотношение (14) должно быть изменено. При этом Т/z > 0 при потерях теплоты на лучеиспускание или конвекцию и Т/z 0 при испарении. Здесь Т является функцией пространственных координат х, у, z и времени .

Рассмотрим общую задачу о скорости установления равновесия между электронами и решеткой [16].

Электроны в металле, вносящие заметный вклад в передачу энергии решетке, движутся со скоростями порядка фермиевской F ~ ~~108 см/с (F энергия Ферми, m масса электрона), которая значительно превышает скорость звука в металле, равную примерно 3105 см/с. Поэтому передачу энергии от электронов решетке можно рассматривать как черенковское излучение звуковых волн сверхзвуковыми электронами.

Согласно теории упругости смещение , вызванное силой

= U( t)

(U постоянная взаимодействия электрона с решеткой, входящая в выражение для времени свободного пробега), с которой электрон действует на решетку [14, 17], рассматриваемую как упругий континуум, удовлетворяет волновому уравнению

2/t2 – s2= U( t)/, (16)

где плотность металла и s скорость звука. Разлагая смещение и -функцию в интеграл Фурье и подставляя в (16), можно получить для смещения выражение

=. (17)

Потери энергии электроном вычисляются далее, как работа силы, с которой электрон действует на упругую среду:

(18)

После подстановки в (13) производной по времени от (17) вычисление d/dt сводится к квадратурам. Не останавливаясь на деталях этого вычисления, приведем окончательный результат [13]:

(19)

Здесь km максимальное значение составляющей волнового вектора k, перпендикулярной к направлению движения электрона. Появление этого параметра связано с тем, что для очень коротких волн кристалл нельзя рассматривать как сплошную среду.

Для вычисления энергии, теряемой электронами в единице объема за единицу времени, выражение (19) следует просуммировать по всем электронам. С учетом того, что в передаче энергии принимают участие только электроны, находящиеся на краю распределения Ферми, получаем следующее выражение для передаваемой энергии:

(20)

где n число электронов в единице объема (~ 61022 см3), а0 постоянная решетки. Последнюю формулу удобно переписать, используя выражение для времени свободного пробега электрона [14, 17]

(21)

где е(Т) – время свободного пробега, при вычислении которого температуры электронов и решетки предполагаются одинаковыми и равными Т. Так как при температуре выше дебаевской время релаксации обратно пропорционально температуре, то вместо (20) и (21) можно написать

(22)

где коэффициент теплообмена электронов с решеткой kei практически не зависит от температуры и равен

Чтобы оценить численное значение kei, можно взять величину Te из данных по электропроводности. Здесь воспользуемся сравнительно грубой оценкой [17] (дающей правильный порядок величины электропроводности для большинства металлов) Tе (Т) 1011 сград, из которой следует приближенное выражение для коэффициента теплообмена:

kei 1016 ns2. (23)

Численное значение kei в типичном случае n = 61022 см3, s = 3105 см/с равно

kei 1016 ns2 = 51017 эргсм3с1град1 [51010 Вт/(см3 град)].

Если теперь обозначить через ci теплоемкость решетки, рассчитанную на единицу объема, то величина р = сi/kei будет играть роль характерного времени изменения решеточной температуры, связанного с обменом энергией между электронами и решеткой. Величина е= =сe/kei играет аналогичную роль для электронов. Из-за малой величины теплоемкости вырожденного электронного газа е при температуре порядка тысячи градусов оказывается в несколько десятков раз меньше, чем р (типичные значения р ~ 1010, е ~ 1012 с).

Выясним теперь вопрос о том, как влияет электрон-решеточная релаксация на температуропроводность металла.

Выше отмечалось, что в интервале температур от сотен до десятков тысяч градусов Кельвина основным механизмом переноса энергии является электронная теплопроводность. Существенная при низких температурах фононная теплопроводность в указанном интервале температур меньше электронной по крайней мере на порядок [14, 18]. Лучистый перенос энергии начинает играть заметную роль при температурах, значительно больших, чем 104 К, которые мы пока не будем рассматривать.

При температурах выше дебаевской коэффициент электронной теплопроводности ke составляет несколько единиц Вт/(смград) [14]. Этому значению ke соответствует коэффициент температуропроводности k* = = порядка 0,1 1,0 см2/с. Такая температуропроводность характерна для медленных процессов, постоянная времени которых много больше, чем р, так что в металле успевает установиться равновесие между электронами и решеткой и «работает» полная теплоемкость (сi + се). Если же характерное время изменения теплового потока мало по сравнению с р, так что отсутствует равновесие между электронами и решеткой, процесс характеризуется «высокочастотным» коэффициентом температуропроводности , который в несколько десятков раз больше, чем приводимый обычно в таблицах коэффициент k*. В этом случае имеет место заметная разница между температурами решетки и электронов.

Для определения температуры металла, поглощающего световой импульс, необходимо решить задачу теплопроводности для электронов и решетки, рассматриваемых как отдельные подсистемы со своими температурами, и учесть теплообмен между ними, описываемый соотношением (19). Такой подход пригоден, очевидно, при том условии, что время установления равновесия в подсистемах много меньше времени установления равновесия между ними.

Система уравнений, описывающая распределение температур в металле, может быть записана в виде

(24)

В (24) F(,t) есть энергия, получаемая электронами в результате поглощения света, отнесенная к единице объема.

Система уравнений (24) нелинейна, ее коэффициенты зависят от температуры. Наиболее существенно учесть температурную зависимость электронной теплоемкости, которая дается выражением [18]

(25)

Решая систему уравнений (11), можно исследовать характер изменения со временем электронной и решеточной температур [16]. Чтобы избежать вычислительных осложнений (учет которых не дает ничего принципиально нового), упростим задачу в соответствии с условиями эксперимента. Во-первых, будем считать, что поток света плотностью Q(t) равномерно распределен по поверхности х = 0 металла, занимающего полупространство x > 0. Такое допущение правильно, если размер площадки, на которую фокусируется ЛИ, а также толщина образца, много больше, чем расстояние, на которое распространяется в металле тепло за время действия светового импульса. Эти условия практически всегда оказываются выполненными ввиду малой продолжительности импульсов.

Во-вторых, будем считать, что поглощение света происходит в бесконечно тонком слое вблизи поверхности металла, т.е. положим F(,t) = =Q(t)(x). Как будет видно далее, это предположение хорошо выполняется, начиная с моментов времени порядка cе(Тн)/kei ~ 1012 с (Тн начальная температура металла), и потому является вполне приемлемым.

Прежде чем приступить к решению системы (24), обсудим качественный характер изменения температур Ti и Те. До времени порядка е(Tн) = сe(Тн)/kei теплообмен с решеткой никак не сказывается на температуре электронов. В течение этого времени электроны как бы теплоизолированы, и их температура быстро растет. Поскольку решетка при этом остается холодной вплоть до времени порядка р = сi/kei, то рост электронной температуры продолжается до тех пор, пока поток энергии к ионам kei (Те Тi) keiТе не сравняется с поглощаемым световым потоком. В дальнейшем электроны будут передавать решетке практически всю поглощаемую энергию, и их собственная внутренняя энергия будет меняться очень мало. Выравнивание электронной и решеточной температур происходит за время, превышающее р, после чего металл характеризуется одной температурой Т и низкочастотной температуропроводностью k*.

Таким образом, при t решение системы уравнений (24) должно стремиться к решению обычной задачи теплопроводности для полупространства. Отметим, что так, как описано выше, процесс протекает только в том случае, когда внешний поток Q(t) изменяется не слишком быстро. Напомним, кроме того, что под Q(t) мы здесь понимаем поглощенную часть светового потока.

Перейдем теперь к решению системы уравнений (24). Рассмотрим сначала времена, много большие, чем се/kei. При этом, как было отмечено выше, изменение энергии электронного газа незначительно, се(Те/t) << ci(), и им можно пренебречь. В результате задача существенно упрощается, поскольку уравнения с хорошей точностью можно считать линейными. В дальнейшем мы получим решение нелинейной задачи, правильное при малых временах, и установим пределы применимости линейного решения. С учетом сказанного система (24) при t >> ce/kei преобразуется к виду

(26)

Искомое решение должно удовлетворять следующим начальному и граничным условиям:

(27)

Для решения задачи (26), (27) воспользуемся преобразованием Лапласа по времени. Обозначая

и выполняя стандартные вычисления, придем к обыкновенному дифференциальному уравнению второго порядка для функции (х,s). Интегрируя это уравнение и обращая решение с использованием теоремы о свертке, получим следующее выражение для температуры решетки на поверхности x = 0:

(28)

где I0(z) функция Бесселя нулевого порядка от мнимого аргумента.

Выражения для электронной температуры и разности температур (Те Ti) можно получить из (28), заменив под интегралом функцию Q(t) соответственно на

Q + р dQ/dt и рdQ/dt.

Как было отмечено, при изучении действия ЛИ на металлы представляют интерес два режима освещения: моноимпульс длительностью порядка 108 с (генерируемый при модулировании добротности) и последовательность импульсов («пичков») длительностью порядка 108 с каждый, составляющих вместе импульс длительностью порядка 103 104 с (режим свободной генерации). В обоих этих случаях характерное время изменения плотности светового потока значительно превосходит время релаксации решеточной температуры р, что позволяет упростить выражение (28). Используя асимптотическое разложение функции I0(z) при больших z [19] получим вместо (28) выражение

(29)

которое совпадает с решением обычной «низкочастотной» задачи тепло-проводности.

Из (28) и (29) следует, что изменение со временем температуры поверхности будет запаздывать относительно изменения плотности светового потока. По порядку величины это запаздывание совпадает с характерным временем изменения плотности светового потока.

Рассмотрим теперь поведение решения (28) при малых временах tр.

Из сказанного выше о виде функции Q(t) следует, что за времена порядка р плотность светового потока меняется мало, поэтому в рассматриваемом интервале ее можно аппроксимировать линейной функцией времени: Q(t) = const(t). Вычисляя интеграл в (28), получаем

(30)

Для электронной температуры в этом случае получается выражение

(31)

В предельном случае t << р (но в то же время, конечно, t >> ce/kei) из (30) и (31) получаем

т.е. температура электронов много больше, чем температура решетки.

При малых временах разность между электронной и решеточной температурами практически равна первой из них и линейно растет со временем в пределе t << 0,5i. По мере нагревания решетки, рост разности температур (Te – Ti) замедляется и вблизи максимума функции Q(t) достигает своего наибольшего значения. Чтобы оценить его, заменим реальный импульс треугольным с полушириной, равной длительности импульса t0 = i. После несложных вычислений получим

(32)

Полагая, например, t0 = 108 с, k* = 1 см2/c, получим

(Te Ti)max 107 Qmax (Q – в Вт/см2).

Как следует из постановки задачи, при высоких (Qmax 109 Вт/см2) плотностях потока такая оценка должна быть несколько завышенной, поскольку она не учитывает потерь энергии на термоэлектронную эмиссию, а также изменения коэффициента поглощения в результате нагревания и движения среды, уже заметного к моментам времени порядка t ~ 108 с. Тем не менее при потоке порядка 109 Вт/см2 и длительности импульса порядка 108 с максимальная разность между электронной и решеточной температурами оказывается порядка нескольких сотен градусов, и ею нельзя пренебрегать, ссылаясь лишь на малость времени электрон-решеточной релаксации. При более коротких импульсах разность температур будет, очевидно, еще больше. В то же время в режиме свободной генерации эта разность температур, по крайней мере, на порядок меньше, и, как правило, ее можно не учитывать.

Если известна точная форма импульса, то зависимость от времени электронной и фононной температур металла можно получить путем численного интегрирования в формуле (32).

На рис. 2 приведены в качестве примера результаты расчета электронной температуры для осциллограммы лазерного импульса, взятой из работы [20].

Рис. 2. Импульс излучения (1) и электронная температура (2) на поверхности металла

Изложенное выше решение системы уравнений (24) получено в пренебрежении изменением внутренней энергии электронного газа, се(Те/t). Чтобы выяснить пределы применимости этого приближения, обратимся к полной нелинейной задаче.

Найдем ее решение для времен t < р, когда температура решетки еще заметно меньше электронной температуры, и сравним результат с формулами (30) и (31).

Если Ti << Te, то из системы (24) можно выделить уравнение для электронной температуры

(33)

В граничные условия, как и при выводе формул (30) и (31), подставим поток, линейно зависящий от времени:

(34)

(С некоторая постоянная), поскольку интересующие нас времена меньше чем t, и много меньше чем характерное время изменения Q(t). Тогда решение уравнения (33) имеет вид

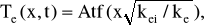
где А = 2keiF(2nk2)-1 1,61014 град/с некоторая постоянная, а безразмерная функция f() удовлетворяет уравнению

(35)

Налагаемое на f() граничное условие при = 0 таково:

, (36)

кроме того, f() должна стремиться к нулю при 0.

Интегрируя (35) с использованием (36), получаем кубическое уравнение для f0 f(0):

(37)

Значения f0 для нескольких значений m приведены в табл. 1 [16].

Таблица 1

m	0,01	0,10	1,00	10,0
f0	0,0099	0,097	0,8	4,9

Решение уравнения (35) выражается через элементарные функции, но для дальнейшего анализа оно не нужно. Отметим только, что температура электронов заметно отличается от нуля в слое вблизи поверхности, толщина которого порядка (ke/kei)0,5, что составляет (2-3)105 см. Пространственное распределение электронной температуры, в отличие от линейного случая, не изменяется со временем. Размер нагретого слоя значительно больше длины свободного пробега электронов (составляющей при температуре плавления меньше, чем 106 см) [14], поэтому рассмотрение вопроса с помощью уравнения теплопроводности вполне корректно.

Учитывая данную выше оценку времени релаксации р, можно ожидать, что полученное решение будет верным до времен порядка 1010с. Оценим исходя из этого, какая электронная температура может быть достигнута при холодной решетке.

Полагая t = 1010 с, получим Te 1,6104 f0. Если выбрать в качестве С среднюю скорость возрастания плотности потока, а полуширину импульса, как и раньше, принять равной 108 с, то в результате получим значения электронной температуры Те (табл. 2).

Таблица 2

Qmax , Bт/см2	3109	31010	31011	31012
Те , К	175	1700	14000	80000

Отметим, что высокие электронные температуры соответствуют уже таким плотностям светового потока, при которых происходит заметное разрушение металла, поэтому последние два столбца должны рассматриваться как ориентировочные.

Уменьшение длительности лазерного импульса при том же максимальном значении плотности потока приводит к примерно пропорциональному увеличению температуры. Поэтому при полуширине импульса, равной 1 нс, приведенные значения Те возрастут примерно на порядок.

Возвратимся теперь к уравнению (37), определяющему электронную температуру. При значениях параметра m << l, как видно из (37), f0 m, а слагаемым, содержащим f03, можно пренебречь. Это как раз и соответствует пренебрежению членом се(Те/t) в исходных уравнениях (24). Полагая f0 = m, получим формулы

(38)

которые были получены выше как предельный случай (30) и (31) при t << р. Таким образом, условие применимости линейного приближения выражается неравенством m << 1, или, после подстановки численных значений постоянных в выражение для m (36)

Qm << 5109 Вт/см2.

3. Термические эффекты, сопровождающие лазерный нагрев

Термомеханические эффекты

Термомеханические эффекты являются следствием поглощения световой энергии (энергии квантов света и импульса фотонов), причем энергия квантов, поглощенная атомами решетки, изменяет температуру вещества, а импульс создает пондеромоторную силу, которая в ЛИ интенсивностью 108 Вт/см2 может придать диэлектрической сфере диаметром 1 мкм, имеющей отражательную способность 10 %, ускорение до 105 g. Кроме пондеромоторной силы следует учитывать и возбуждаемые расширяющимся веществом акустические волны, изменяющие параметры и характеристики прозрачных сред. Следовательно, ЛИ можно использовать для ускорения, замедления, управления положением, охлаждения или локализации небольших частиц, включая атомы, молекулы и ионы. Указанные свойства ЛИ не относятся к нелинейной оптике и наблюдаются в значительном количестве различных сред.

Экспериментально была исследована зависимость изменения передаваемого образцу импульса от интенсивности ЛИ, при этом импульс, передаваемый сфокусированным пучком рубинового лазера простому маятнику в виде сферы из исследуемого материала, подвешенной на нити в вакуумной камере, измерялся через окно камеры при помощи калиброванного микроскопа [20]. Изменение удельного передаваемого импульса в зависимости от интенсивности ЛИ для различных металлов показано на рис. 3. Удельный передаваемый импульс (или просто удельный импульс) определяется как отношение передаваемого импульса к энергии.

Рис. 3. Удельный импульс, передаваемый различным металлам рубиновым лазером, работающим в режиме модуляции добротности

Пиковые давления, достигнутые в металлических материалах, которые облучались импульсами мощных лазеров на неодимовом стекле, работающих в режиме модуляции добротности, составляют десятки килобар. Импульс давления может оказаться достаточным для того, чтобы вызвать откол на обратной поверхности тонких металлических листов.

Пондеромоторные силы

В случае диэлектрической среды сила, действующая со стороны излучения на единицу объема, определяется как

. (39)

Здесь – максвелловский тензор давления, а плотность электромагнитного импульса в вакууме, причем

(40)

где р – давление в среде, плотность среды, – вектор Пойнтинга. С помощью уравнений Максвелла после подстановки (40) в (39) получаем [21]

(41)

В однородной среде это выражение принимает вид

(42)

Второй член в (42) есть просто электрострикционная сила, а третий связан с изменением плотности электромагнитного импульса.

Обычно нас интересует только среднее по времени <>. В стационарном случае, несмотря на то, что в среде , излучение оказывает давление на поверхность границы раздела, где происходит отражение и преломление света. Полная сила, действующая на макроскопический диэлектрический объект, погруженный в жидкость, определяется интегралом

, (43)

который, согласно закону сохранения импульса, должен быть равен интегралу по поверхности, окружающей объект, где ns – нормаль к поверхности, среднее по времени от плотности электромагнитного импульса, переданного объекту в единицу времени через поверхность раздела между двумя средами, причем = = есть плотность электромагнитного импульса (или псевдоимпульс) в среде с диэлектрической проницаемостью . Справедливость этого утверждения можно доказать также, используя выражение (42) для f.

Пусть прозрачная диэлектрическая сфера с = Н погружена в жидкость с = L и смещена в сторону от оси пучка лазера, как показано на рис. 4. Предположим, что справедливо приближение геометрической оптики. Тогда давление на единицу поверхности сферы, оказываемое со стороны луча, падающего на входную поверхность вдоль прямой а, определяется формулой

,

где , и плотности импульсов падающей, отраженной и преломленной волн соответственно. Можно записать, что

<> = , причем 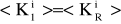, откуда

(44)

Вектор направлен вдоль внутренней нормали к сфере, а имеет компоненту вдоль направления + и компоненту, направленную к оси пучка, если Н > L (как на рис. 4), и от оси пучка, если Н< L.

Сила давления со стороны излучения на сферу вследствие отражения и преломления на выходной поверхности луча, падающего на сферу вдоль прямой а, рассчитывается аналогично. Поэтому можно вновь написать

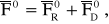
Вектор направлен вдоль внутренней нормали к сфере, а имеет компоненту направления + и компоненту, направленную к оси пучка, если Н > L, и от оси пучка, если Н < L. Сумма i и 0 дает результирующую cилу, действующую вдоль направления +, и силу, направленную к оси пучка, если Н > L. Такой же анализ для луча b, расположенного симметрично по отношению к лучу а относительно оси сферы, как показано на рис. 4, дает результирующую силу, имеющую компоненту, действующую на сферу вдоль направления +, и компоненту, направленную от оси пучка, если Н > L.

Рис. 4. Диэлектрическая сфера смещена относительно оси А лазерного пучка, имеющего моду ТЕМ00

Однако, поскольку волна, распространяющаяся вдоль а, имеет большую интенсивность, чем волна, распространяющаяся вдоль b, сила, оказываемая первой из них, будет больше. Следовательно, полная сила давления излучения на сферу, получающаяся интегрированием по всей сфере, будет иметь составляющую вдоль направления + и составляющую, направленную к оси пучка, если Н > L (от оси пучка, если Н < L). Этот результат легко понять исходя из того, что диэлектрическая сфера, помимо перемещения вперед под действием потока фотонов, должна перемещаться в положение, в котором свободная энергия системы будет минимальной.

Возьмем в качестве примера шарик из латекса (н)0,5 = 1,58, погруженный в воду (L)0,5 = 1,33. Пусть шарик имеет радиус r и находится на оси сфокусированного луча аргонового лазера. Полная сила давления излучения на сферу, действующая вдоль и получающаяся интегрированием по сфере, равна (полн)z 4QPr2/W02, где Р – мощность лазера, W0 – радиус сфокусированного пучка на уровне е2, а Q 0,6. При Р = 1 Вт и r W0(2)0,5 = 514 нм полная сила, действующая на сферу, составляет приблизительно 4105 дин, а получаемое при этом сферой плотностью 1 г/см3 ускорение будет примерно 108 см/с2 или 105g. Эта оценка показывает, что давление со стороны ЛИ действительно можно использовать для управления частицами микронного размера.

В общем случае из закона сохранения импульса можно рассчитать полную силу давления излучения на макроскопическую частицу, а также вращательный момент, передаваемый частице лазерным пучком, имеющим круговую или эллиптическую поляризацию. Индуцированное светом вращение частицы является интересным эффектом, еще до конца не исследованным.

Рассмотрим теперь действие излучения на атомы и молекулы. Пусть – дипольный момент, наводимый у атома ЭМП. Тогда сила, действующая на атом, будет просто силой Лоренца, действующей на диполь [21]:

(45)

Принимая во внимание, что = p, = (1/с), а также равенство = 0,52 (), уравнение (45) можно переписать в виде

. (46)

Легко видеть, что (46) есть не что иное, как микроскопический аналог (42), поскольку для атома р = 0 и = 1 + 4p*. Первый член в (46) соответствует силе электрострикции в случае макроскопической среды. Его называют дипольной силой, когда рассматривают только реальную часть поляризуемости р* = р + iр:

(47)

Поскольку дип прямо пропорциональна р, она имеет наибольшую величину и испытывает сильную дисперсию вблизи резонансов. При р > 0 (вблизи, но ниже по частоте сильного резонанса) эта сила втягивает атом в область с большей интенсивностью, а при р< 0 (выше сильного резонанса) она выталкивает атом в области с меньшей интенсивностью. Если атом можно рассматривать как эффективную двухуровневую среду, то выражение для поляризуемости можно вывести, пользуясь методом матрицы плотности в пределе отсутствия возмущений:

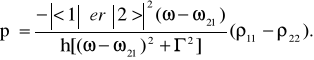(48)

В (48) разность населенностей между двумя уровнями 1> и 2> определяется соотношением

(49)

где 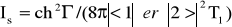интенсивность насыщения, I – интенсивность лазера, 0 – разность населенностей при тепловом равновесии, а g() = Г/{[( 11)2 + Г2]} – резонансный контур в отсутствие насыщения. Поляризуемость можно записать в виде

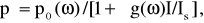(50)

где 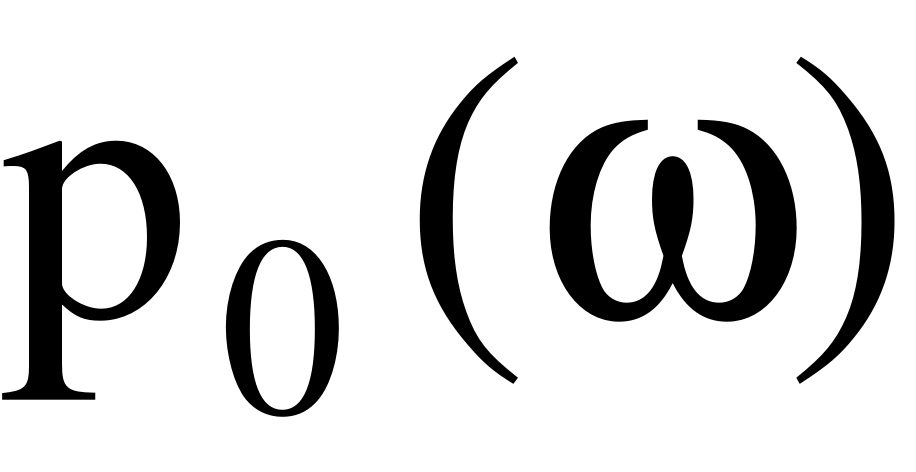реальная часть поляризуемости при отсутствии насыщения. Тогда, согласно (47), усредненная по времени дипольная сила определяется выражением

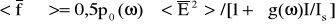(51)

или

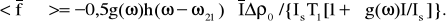(52)

Откуда следует, что в пределе сильного насыщения, несмотря на то, что остается конечной и возрастает с увеличением отстройки ( 21). При < 21, когда р > 0, пучок моды ТЕМ00 стремится втянуть атом вдоль радиуса внутрь и удерживать его на оси благодаря действию дипольной силы. Энергия такого захвата в радиальном направлении возрастает с увеличением мощности лазера даже в пределе насыщения. Кроме дипольной силы никакие другие члены в выражении (46) не дают вклада в среднее по времени от <атом>.

Сила давления со стороны излучения может также возникать вследствие изменения импульса при поглощении или излучении атомом фотонов. Иногда эту силу называют силой отдачи [21]. При поглощении одного фотона атом приобретает импульс , который в следующем затем процессе спонтанного излучения фотона излучается с равными вероятностями во всех направлениях, поэтому в среднем при спонтанном излучении не возникает изменения импульса атома.

Если атом можно рассматривать как двухуровневую среду, то сила отдачи определяется числом фотонов, поглощения в единицу времени, умноженным на :

(53)

В пределе сильного насыщения это выражение сводится к соотношению

<от> = /(2T1),

как и следовало ожидать из физических соображений. Сила отдачи направлена по линии распространения пучка и стремится увлечь атом вдоль пучка.

Для молекул импульс отдачи будет намного меньшим из-за более слабых резонансных переходов вследствие того, что силы осцилляторов «размазаны» по многим колебательно-вращательным линиям, а также из-за большего времени Т Однако дипольная сила все еще может играть заметную роль, так как она не критична к наличию резонансов.

Механическое воздействие ЛИ на атомы вещества

При исследованиях воздействия ЛИ на микрочастицы вещества прежде всего обращают внимание на ЭМ-характер воздействия, приводящий, в частности, и к передаче энергии излучения во внутренние степени свободы микрочастиц, однако помимо этого существует и прямое механическое воздействие, рассмотренное выше, которое обычно считается слабым, но в определенных условиях способное проявиться реально [22].

Квантовая природа ЛИ позволяет рассматривать фотон как квазичастицу, обладающую энергией и импульсом ( = 2 круговая частота излучения, – волновой вектор, постоянная Планка).

Величина волнового вектора связана с длиной волны излучения соотношением k = 2/. При поглощении фотона частицей вещества последней передается импульс . В случае оптической (или более длинноволновой) области спектра величина импульса фотона мала по сравнению с характерным значением импульса, которым обычно обладает частица вещества (например, из-за теплового движения). Так, если в качестве частицы вещества выступает атом массы М со скоростью теплового движения 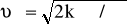(kБ постоянная Больцмана, Т температура), то отношение импульса фотона к импульсу такого атома есть

(54)

Даже в случае атома водорода при комнатной температуре оптический квант ( = 0,5 мкм) при поглощении чрезвычайно слабо меняет состояние его движения и отношение (54) составляет 3104. Разумеется, чем тяжелее атом (молекула), тем слабее это влияние. Однако эффект может накапливаться, если частица вещества испытывает многократные акты поглощения направленного излучения. В обычных условиях приобретенный частицей импульс через определенное время теряется за счет взаимодействия ее с окружением и эффект остается слабым, если не использовать специальные источники излучения. Источники излучения “до лазерной” эпохи не могли обеспечить яркого проявления эффекта, и, кроме того, для его наблюдения требовалось высокое экспериментальное искусство. Существуют специфические условия, реализуемые в космических просторах в окрестностях звезд, где атомы и молекулы вещества могут находиться в свободном состоянии (без столкновений друг с другом) исключительно долгое время, да и само излучение здесь достаточно интенсивное. В ряде случаев интенсивность излучения звезды достаточно высока для того, чтобы сила светового давления преодолела силу гравитационного притяжения. Тогда происходит накопление частицей импульса, направленного от звезды, и она с ускорением покидает окрестность звезды. Это теоретически показано в подразд. 2 и является хорошо известным и часто наблюдаемым эффектом звездного ветра.

С появлением лазеров резко расширился круг возможностей воздействия ЛИ на вещество, в том числе и механического действия на микрочастицы. К настоящему времени в этом направлении достигнуты уникальные результаты, отмеченные Нобелевской премией 1997 года (американцы Steven Chu и William D. Phillips и француз Claude Cohen-Tannoudji).

Световое давление, ускорение и торможение атомов

Резко усилить эффект светового давления позволило одно из уникальных свойств ЛИ – возможность сосредоточивать его энергию в узкой спектральной области и настроить эту область в резонанс с квантовым переходом внутри атома (резонансное световое давление).

Величина этой энергии на несколько порядков выше той, которая могла быть достигнута с помощью резонансных спектральных источников, использованных в экспериментах П.Н. Лебедева и более поздних экспериментах С.Э. Фриша. Чтобы эффект светового давления мог накапливаться, используют камеры с высоким вакуумом. Атомы исследуемого элемента либо находятся в малом количестве в этих камерах в равновесных условиях, либо инжектируются в виде атомного пучка при постоянно действующей вакуумной откачке. В любом случае обеспечиваются условия, при которых атом может пролететь расстояние порядка метра с тепловой скоростью без столкновений с другими атомами. Частота излучения настраивается в резонанс с квантовым переходом атома из основного энергетического состояния (обозначим это состояние индексом 0) в первое возбужденное состояние (ему припишем индекс 1). Все остальные внутренние состояния (уровни энергии) атома не принимают участия в процессе. На такой простой (двухуровневой) модели вполне можно уяснить главные черты явления.

Рассмотрим прежде всего случай бегущей монохроматической волны излучения. Примем следующие начальные условия: атом находится в основном состоянии, а частота излучения близка (в системе координат, связанной с атомом) к частоте 10 квантового перехода в атоме. Механическое действие излучения на атом в данной ситуации развивается следующим образом. Атом поглощает квант излучения и, как следствие, воспринимает квант импульса , при этом атом оказывается в возбужденном состоянии. Акт поглощения фотона происходит тем быстрее, чем выше интенсивность излучения. Дальнейшая судьба атома реализуется альтернативно по одному из двух сценариев: атом испускает либо точно такой же фотон, что и поглощенный ранее, т. е. с теми же энергией и импульсом, либо фотон с той же энергией, но равновероятно во всех направлениях. Первый вариант соответствует процессу вынужденного испускания и вероятность его тем выше, чем выше интенсивность вынуждающего его внешнего излучения. Во втором случае происходит процесс самопроизвольного (спонтанного) испускания, вероятность которого никак не зависит от интенсивности внешнего излучения (в частности, поэтому равновероятны все направления спонтанно испущенных фотонов). После испускания фотона (как спонтанно, так и индуцировано) атом опять оказывается в основном энергетическом состоянии. На этом завершается единичный цикл, который затем будет повторяться снова и снова.

Отметим принципиальное отличие процессов вынужденного и спонтанного испускания фотона с точки зрения передачи импульса со стороны излучения атому. Если цикл реализовался по каналу поглощение – вынужденное испускание, то импульс атома целиком восстановился, поскольку как перед началом, так и в конце цикла имеется в наличии фотон с одним и тем же импульсом . Таким образом, за счет процесса вынужденного испускания атом не получает систематического приращения импульса. Максимум, что может передать излучение атому в данном случае, это импульс в среднем по времени: при достаточно большой интенсивности излучения атом половину времени проводит в возбужденном состоянии, неся в себе при этом импульс фотона . Совсем иное дело, когда цикл завершается спонтанным испусканием. В этом случае из-за различия направлений поглощенного и испущенного фотонов в атоме остается ненулевой импульс. При многократном повторении такого типа циклов сумма импульсов отдачи со стороны спонтанно испущенных фотонов в силу изотропности этого процесса близка к нулю, тогда как принимаемый атомом импульс от поглощенных фотонов направленного излучения есть N, где N – число циклов. Это и есть итоговый импульс, который, как видим, способен накапливаться в атоме. Это накопление можно характеризовать средней силой , действующей со стороны излучения на атом. Используем соотношение =d/dt (сила есть импульс, передаваемый атому в единицу времени). Последний легко подсчитать, зная число актов спонтанного испускания в единицу времени. Оно есть = /, где – вероятность нахождения атома в возбужденном состоянии, – так называемая константа спонтанной релаксации, равная обратному времени жизни возбужденного состояния (это время жизни как раз и обусловливается спонтанным испусканием фотона). Таким образом

=. (55)

Итак, в бегущей волне излучения основная сила, действующая на атом, возникает благодаря изотропному спонтанному испусканию. Чтобы отличить эту силу от других видов сил (о них будет речь дальше), ее стали называть силой спонтанного светового давления, причем она генетически связана с той силой, которую измерял еще П.Н. Лебедев.

Оценим, насколько сильно может повлиять ЛИ на состояние движения атома. При относительно слабых интенсивностях излучения величина пропорциональна интенсивности. В поле интенсивного излучения происходит насыщение (величина перестает расти). Максимальное значение, которого в принципе может достигать величина , равно 0,5. Оно реализуется в таких условиях, когда за время порядка атом много раз попеременно бывает то в основном, то в возбужденном состоянии вследствие вынужденных переходов. Примечателен тот факт, что эти условия легко осуществить за счет фокусировки излучения с помощью любого (мощностью в несколько милливатт) лазера, если частота излучения настроена в резонанс с квантовым переходом в атоме.

Максимально возможная сила спонтанного светового давления создает максимальное ускорение

amax = 0,5/M.

При таком ускорении атом приобретает скорость, сопоставимую со скоростью теплового движения vт за время

.

В числовой оценке здесь использованы характерное для атомов значение ~ 108 с-1, масса атома М = 25 атомных единиц, Т = 300 К, = 0,5 мкм, т.е. для разгона атома до значительных скоростей требуется небольшое время. При старте с нулевого значения скорости за это время атом переместится на расстояние

не зависящее от массы атома, а его значение вполне устраивает с точки зрения эксперимента.

Приведенные оценки свидетельствуют о том, что ЛИ способно эффективно ускорять или замедлять свободные атомы вещества. Однако вероятность пребывания частицы в возбужденном состоянии не остается неизменной по мере изменения скорости атома. Если при какой-то скорости атома частота излучения находится в резонансе с частотой 10 квантового перехода в атоме, то по мере изменения скорости резонансные условия нарушаются и излучение практически перестает взаимодействовать с атомом. Происходит это из-за эффекта Доплера. Излучение с частотой (в лабораторной системе координат) эффективно взаимодействует только с такими атомами, скорость которых близка к резонансному значению, определенному условием

= 10.

Величину называют доплеровским сдвигом частоты. Оче-видно, что реально важна лишь проекция vx скорости на направление волнового вектора . Резонансное значение vx, таким образом, есть

, = 10 , (56)

где величину называют отстройкой частоты излучения от резонансной (в лабораторной системе координат). Разумеется, существует некоторый интервал vx в окрестности , в котором взаимодействие излучения с атомами сопоставимо с резонансным. Этот интервал задается величиной

vx = /k, (57)

что связано с известным квантово-механическим принципом неоп-ределенности энергии: конечность времени жизни возбужденного состояния атома приводит к неопределенности энергии этого состояния, уровень энергии имеет конечную ширину, равную . Как правило, vx << vт, так что при фиксированном значении изменение скорости за счет спонтанного светового давления довольно быстро выводит атом из резонанса с излучением. Эта ситуация может быть преодолена, и одна из возможностей – использование излучения с достаточно широким спектром. В данном случае при каждом значении скорости атома найдется спектральная компонента излучения, которая окажется в резонансе с атомным переходом. Очевидно, что при этом полная интенсивность излучения должна быть существенно выше, чем в случае монохроматического резонансного излучения, если мы хотим добиться максимального эффекта. Другая возможность – использовать монохроматическое излучение, но в процессе разгона (замедления) атома нужно синхронно подстраивать частоту излучения в резонанс согласно условию (56). Поскольку в (56) реально входит разность частот 10, то (в качестве варианта) можно менять не частоту излучения, а частоту атомного перехода 10, воздействуя на атомы дополнительно ЭП или МП. Фактически в многочисленных экспериментах по резонансному световому давлению реализовалась каждая из перечисленных возможностей [23, 24].

Охлаждение газа спонтанным световым давлением

В связи с эффектом резонансного светового давления в последние годы наибольшее развитие получило направление исследований, связанное с глубоким охлаждением и пространственной локализацией атомарного газа. Рассмотрим здесь принципиальные стороны соответствующих процессов. Начнем с процесса охлаждения газа спонтанным световым давлением.

В равновесии атомы газа находятся в хаотическом тепловом движении. Вероятность иметь то или иное значение скорости (в единичном интервале скоростей) задается функцией распределения Максвелла. Например, если речь идет об одной из проекций скорости (vx), соответствующее распределение Максвелла есть

График функции W(vx) изображен на рис. 5 (кривая 1).

Пусть теперь на такой газ действует резонансное излучение в виде бегущей (вдоль оси х) монохроматической волны. В соответствии со сказанным выше взаимодействуют с излучением отнюдь не все атомы, а только те, которые обладают скоростью вблизи резонансного значения (56) в интервале (57). После достаточно большого числа циклов поглощения с последующим спонтанным испусканием интервал резонансных скоростей vx опустошается, так как скорость атомов изменяется вследствие светового давления.

Рис. 5. Распределение атомов по скоростям до взаимодействия с излучением (1 – равновесное макселловское распределение) и после (2). Отстройка частоты фиксирована

Атомы группируются в соседнем скоростном интервале, где взаимодействие с излучением практически отсутствует. Если < 0, то этот (соседний) интервал отвечает меньшему значению vx. В итоге функция распределения атомов по скоростям f(vx) в окрестности резко отличается от максвелловского распределения (рис. 5, кривая 2).

Если теперь достаточно медленно изменять (в сторону 0), опустошенная область vx будет увеличиваться, а с левого края от нее, в окрестности с vx ~ /k атомов будет становиться все больше и больше. Здесь можно провести аналогию со сгребанием снега бульдозером, только в нашем случае сгребание происходит в пространстве скоростей. Особо интересен случай, когда атомы имеют ненулевую среднюю скорость (vx0 > vт; модель атомного пучка, рис. 6).

Направим излучение навстречу такому пучку и начнем на него воздействовать, стартуя со значения < k(vт + vx0) и медленно изменяя вплоть до = . В произвольный момент времени все атомы, имевшие до того скорость vx > /k, сосредоточиваются в узком (~ /k) скоростном интервале слева от интервала резонансных скоростей.

После того как примет значение = , прекратим ее изменение. Это будет означать (рис. 6), что, во-первых, атомный пучок остановлен и, во-вторых, распределение атомов по скоростям vx стало существенно уже исходного – произошло эффективное охлаждение по одному из направлений движения.

Рис. 6. Процесс торможения и охлаждения атомного пучка (показаны виды распределения атомов по скоростям в последующие моменты времени)

Возникает естественный вопрос: можно ли похожим способом охладить обычный газ атомов и можно ли это сделать для всех трех направлений движения?

Ответ на оба вопроса положителен. Действительно, рассмотрим равновесный газ атомов с максвелловским распределением по скоростям, а излучение возьмем в виде стоячей волны со стартовым значением < kvт. Как известно, стоячая волна является суперпозицией двух встречных бегущих волн. Для каждой из них существуют свои значения резонансных скоростей (vx = /k и vx = /k; рис. 7), т. е. бегущие компоненты волны независимо друг от друга взаимодействуют с разными группами атомов.

Так как мы установили < 0, то импульсы, передаваемые каждой из волн “своим” атомам, приводят к уменьшению абсолютного значения проекции vx их скорости, т. е. к торможению.

Далее мы можем произвести такую же манипуляцию, что и выше. Будем медленно уменьшать вплоть до = 0 (рис. 7), опустошая скоростные интервалы vx >/k. При = 0 все атомы сосредоточатся в окрестности vx = 0 в интервале vx ~ /k – произойдет эффективное охлаждение по компонентам скорости vx. Степень охлаждения легко оценить, учитывая связь Т = Мvт2/2kБ и вводя эффективную температуру

. (58)

Таким образом,

. (59)

Для характерных значений ~ 108 c1, 0,5 мкм, vт ~ 5 104см/с имеем

.

Рис. 7. Одномерное охлаждение газа атомов (показано последовательное изменение распределения по скоростям с течением времени)

Как видно, это довольно-таки глубокое охлаждение.

Представляется достаточно очевидными и способ трехмерного, т.е. полного, охлаждения газа атомов. Для этого необходимо взять три ортогонально пересекающиеся стоячие световые волны от одного источника и осуществить перестройку так, как описано выше. При этом в области пересечения волн произойдет полное охлаждение газа атомов.

Представленное здесь описание процессов торможения и охлаждения, конечно, cильно идеализировано. При экспериментальной реализации исследователям пришлось столкнуться с препятствиями, связанными и с более тонкой внутренней структурой атомов, и с выбором правильных и выполнимых экспериментальных условий. Тем не менее все эти препятствия были преодолены, и эффекты, главные черты которых обсуждены выше, надежно зарегистрированы.

Вынужденное световое давление и локализация атомов

Мы показали, что спонтанным световым давлением можно сильно охладить газ атомов в области пересечения световых волн. Однако, если не предпринять специальных усилий, они покинут эту область в процессе свободного движения. Представляет интерес каким-то образом задержать их здесь, т.е. речь идет об охлаждении и пространственной локализации холодных атомов. Мы обсудим, как это сделать с помощью того же излучения.

Как оказывается, спонтанное световое давление – не единственная сила, действующая со стороны излучения на атомы. С ростом интенсивности излучения становятся существенными новые виды сил. Обсудим их.

Известно, что потенциальная энергия U электрического диполя (пары связанных разноименных одинаковых по величине зарядов, отстоящих друг от друга на расстоянии а), помещенного в ЭП , есть

U= , = q0а, (60)

где – единичный вектор в направлении от отрицательного заряда к положительному. К тому же мы знаем, что если потенциальная энергия для какого-то тела зависит от координат, то на него действует сила

= U, (61)

где U – градиент потенциальной энергии.

Заметим теперь, что ЭП световой волны способно раскачивать электрон относительно ядра атома (на квантовом языке это и означает вынужденные переходы с одного уровня на другой). Следовательно, в атоме наводится дипольный момент, колеблющийся с частотой (частота вынуждающейся силы):

= , (62)

где – ЭП волны, коэффициент пропорциональности.

Подставим (62) в (60) и получим

U= E2.. (63)

Таким образом, несмотря на то, что поле колеблется с очень большой частотой, существует отличная от нуля средняя потенциальная энергия взаимодействия. Если излучение неоднородно в пространстве, существует и средняя сила типа (61), которую называют стрикционной силой. В связи с оптическим излучением на нее впервые обратил внимание А.Г. Аскарьян (1962). В бегущей волне пространственная неоднородность обусловлена конечным диаметром светового пучка. Если же используется стоячая волна, то возникает более мелкомасштабная периодическая пространственная неоднородность с характерным размером, равным длине волны излучения . Средняя по времени потенциальная энергия атома в стоячей волне приобретает вид, показанный на рис. 8. Мыслима ситуация, когда атом, пролетая мимо одной из потенциальных ям, затормозившись спонтанным излучением, свалится в нее и останется там (на возможность такой локализации атома впервые обратил внимание В.С. Летохов (1968)).

Предположим теперь, что три взаимно ортогональные стоячие волны сфокусированы в одну область пространства (область пересечения).

Рис. 8. Средняя по времени потенциальная энергия атома в стоячей

волне

В этой области интенсивности волн максимальны и для атомов можно осуществить эффективную потенциальную ловушку. Если проделать те манипуляции, которые описаны выше, то можно одновременно охладить атомы и локализовать их в области пересечения световых пучков [25, 26]. При этом возможна ситуация, когда атомы будут локализованы в пучностях или узлах стоячих волн, образуя тем самым трехмерную пространственную решетку с характерным расстоянием между узлами решетки. Нарисованная здесь картина несколько идеализирована. Реально тот факт, что потенциальная энергия осциллирует во времени, приводит к более сложному выражению для силы, чем выражение (61) с потенциалом (63). При строгом подходе сила так называемого вынужденного светового давления может способствовать еще более глубокому охлаждению, чем за счет только спонтанного светового давления. При этом ограничением уже будет энергия отдачи при испускании фотона.

В экспериментах по охлаждению атомов для локализации оказалось удобно использовать дополнительные поля (МП, поле микроволнового излучения). Спонтанным и вынужденным световым давлением осуществляют предварительное охлаждение и пространственную локализацию в приготовленной другими полями ловушке. Затем наступает этап получения ультрахолодных атомов. Для этого меняют параметры ловушки таким образом, чтобы за ее пределы уходили высокоэнергетичные атомы, а оставались ультрахолодные. На этом пути удалось опуститься до температуры в единицы микрокельвинов.

Глубокое охлаждение и локализация атомов представляют не только самостоятельный академический интерес. Ультрахолодные атомы – это новый физический объект, интересный во многих отношениях. Прежде всего он может дать новые возможности для спектроскопии сверхвысокого разрешения (полное отсутствие доплеровского уширения). Физика атомных столкновений здесь также найдет для себя много интересного (столкновения очень медленных частиц). При локализации атомов в узлах стоячих волн получаем специфический объект – газовый кристалл, у которого могут оказаться неожиданные интересные свойства. Локализованные в малых объемах атомы могут начать проявлять квантовый характер движения, а если атомов в одной ловушке набралось достаточно и они хорошо охлаждены, то может произойти процесс так называемой бозе-конденсации, т.е. образуется квантовая жидкость, обладающая свойством сверхтекучести. В 1995 году несколько экспериментальных групп за рубежом заявили о том, что им удалось реализовать процессы бозе-конденсации. К настоящему времени уже существуют убедительные доказательства, что бозе-конденсация действительно реализована.

В исследования механического действия излучения на атомы внесли вклад многие ученые из разных стран. Помимо упомянутых уже Нобелевских лауреатов из зарубежных ученых отметим А. Ашкина, который первым (1970) представил силу резонансного светового давления в виде (55), а также Т. Хэнша и А. Шавлова, предложивших использовать световое давление для охлаждения газа (1975). Значительный вклад внесен и отечественными учеными. Еще в 1968 году В.С. Летоховым предсказана возможность локализации атомов в узлах или пучностях стоячей световой волны. Систематическое развитие теории начато А.П. Казанцевым, который в 1972 году предложил ускорять атомы, захваченные в узлах квазистоячей волны. Значительные результаты в теории получены А.П. Казанцевым с сотрудниками, а также В.С. Летоховым и В.Г. Миногиным. Деформация функции распределения (рис. 5) впервые описана И.В. Красновым и Р.Я. Шапаревым, а экспериментально впервые реализована В.И. Балыкиным (1981) из группы В.С. Летохова. Здесь же впервые осуществлено двухмерное охлаждение (1981). Более подробную информацию о развитии идей и их воплощении можно найти в обзоре [23] и монографии [24].

Хотя выше рассмотрено механическое действие излучения на атомарные объекты, есть смысл упомянуть о таком же действии на макрочастицы малых (микронных) размеров. Для ряда задач, в том числе для управляемого ядерного синтеза, существует потребность ускорить такие частицы до больших энергий. В этом способно помочь лазерное излучение высокой интенсивности. С прямым световым давлением здесь конкурирует сила реактивного движения, возникающая за счет импульса отдачи со стороны продуктов испарения. В итоге ожидается возможность достижения скорости частиц до 108 см/с [25].

Другая интересная возможность – ускорение частиц, поглощающих излучение (но не испаряющихся) в жидкости. В данном случае движущей силой является давление, возникающее вследствие испарения жидкости из-за нагрева той части поверхности частицы, где происходит поглощение излучения. Таким способом удалось [26] разогнать частицы микронного размера до скоростей 106 см/с.

4. Диффузионно-химические явления и фотохимические методы

Фотохимическая реакция. Возбужденный атом или молекула в общем случае имеет повышенную способность вступать в химические реакции по сравнению с атомами или молекулами в основном состоянии, и их можно отделить от последних, выбирая подходящую схему химической реакции. Хотя электронное возбуждение часто бывает в этом отношении более эффективным, в случае молекул может оказаться продуктивным и колебательное возбужение. Ниже приведены два примера, иллюстрирующие изотопически селективную фотохимию [21].

В смеси молекул орто-I2 и пара-I2 с 2-гексаном (Х) молекулы орто-I2 возбуждались линией 514,5 нм аргонового лазера. После часового облучения пучком мощностью 0,2 Вт было обнаружено, что плотность орто-I2 снизилась до 5 %. Этот эффект объяснялся тем, что электронно-возбужденные молекулы орто-I2 могли реагировать с 2-гексаном, тогда как невозбужденные молекулы пара-I2 – не могли:

орто-I2 орто- + X XI2.

В другом примере газовая смесь, содержащая Н3СОН, D3COD и Br2 в пропорции 1:1:1, облучалась лазером на НF непрерывного действия с длиной волны 2,7 мкм. Возбуждалось колебание ОН молекул Н3СОН. Колебательно-возбужденные молекулы Н3СОН затем сильно реагировали с Br, давая в результате 2НBr и Н2СО :

Н3СОН* + Br2 2HBr + H2CO.

В результате после облучения смеси лазером мощностью 90 Вт в течение 60 с отношение концентраций Н3СОН и D3COD снизилось до 1:19. Однако этот результат требует дополнительной проверки.

Химические реакции в описанных примерах были простыми. В результате их получаются стабильные первичные продукты, которые легко можно отделить от исходных молекул. В общем случае, однако, бывает не так. Часто после селективного возбуждения атомов или молекул возникает цепная реакция. В результате неконтролируемых вторичных реакций может произойти перемешивание изотопов.

Одноступенчатая фотопредиссоциация. Унимолекулярная диссоциация является особым классом химических реакций, вызываемых лазерным возбуждением. Если возбуждение является изотопически селективным, то этот процесс можно использовать для разделения изотопов.

Некоторые молекулы имеют резкие ровибронные состояния, накладывающиеся на возбужденное электронное состояние, которое является вырожденным с диссоциационным континуумом другого возбужденного электронного состояния (рис. 9).

Эти состояния носят название предиссоциационных. Они сходны по своей природе с автоионизационными состояниями в ионизационном континууме. Молекула, возбужденная в предиссоциационное состояние, может релаксировать в континуум и диссоциировать. Если резкие предиссоциационные состояния имеют изотопический сдвиг, который можно разрешить в эксперименте, то селективное возбуждение может привести к предиссоциации выделенных изотопических молекул. Продукты диссоциации могут быть стабильными или нестабильными. В последнем случае нужно придумать процесс химической очистки для удаления соединений с выделенным изотопическим составом до того, как произойдет их перемешивание с другими соединениями. Необходимо также предотвратить вторичные химические реакции, которые могут перемещать изотопы. Преиму-ществом метода одноступенчатой предиссоциации является его прос-тота. Для однофотонного селективного возбуждения требуется лишь один лазер сравнительно малой мощности.

Рис. 9. Схематическая диаграмма энергетических уровней молекулы, имеющей предиссоционные состояния, вырожденные с континуумом диссоциирующего электронного состояния

Для примера рассмотрим случай изотопического обогащения дейтерия с помощью фотопредиссоциации формальдегида Н2СО. Этот же процесс можно использовать для обогащения изотопов С и О. При предиссоциации Н2СО преобладает реакция

.

И Н2, и СО являются стабильными молекулами, и их легко можно выделить. При облучении естественной смеси Н2СО и НDCO He – Cd лазером непрерывного действия с длиной волны 325,03 нм был получен фактор обогащения К(D/H), равный 14.

Двухступенчатая фотодиссоциация и фотопредиссоциация

Диссоциация молекул может быть вызвана их возбуждением либо в предиссоциационное состояние, либо в диссоциационный континуум. Для изотопически селективной диссоциации можно воспользоваться двухступенчатой схемой возбуждения: на первом этапе селективно возбуждаются молекулы с данным изотопическим составом, а на втором этапе молекулы дополнительно возбуждаются в диссоциационное или предиссоциационное состояние. Поскольку предиссоциационное состояние также может иметь изотопический сдвиг, то случай двухступенчатой фотодиссоциации в общем случае обладает большей селективностью по сравнению со случаем одноступенчатой фотопредиссоциации, хотя для реализации первой необходимо иметь два перестраиваемых лазера с достаточно большой интенсивностью для ступенчатого возбуждения. Селективное возбуждение может быть либо электронным, либо колебательным. Чаще используется последнее, поскольку для большинства молекул изотопический сдвиг лучше разрешается в колебательных спектрах. В этом случае продукты диссоциации также должны быть удалены прежде, чем вторичные реакции или другие процессы перемещают молекулы с разным изотопическим составом.

В качестве примера приведем первую демонстрацию метода. Смесь молекул 14NH3 и 15NH3 в пропорции 1:1 при давлении 10 20 Торр в присутствии буферного газа при давлении 250 Торр (Хе или Ne) одновременно облучалась импульсным СО2-лазером и УФ-излучением искрового разряда. Излучение СО2-лазера селективно возбуждало колебательную моду 2 молекулы 15NH3 в основном состоянии: (, = 0) (, = 1). Вслед за тем УФ-возбуждение переводило эту молекулу в предиссоциационное состояние (, =0). Получающаяся в результате цепь химических реакций предположи-тельно имела вид

Как видно, во вторичных реакциях не участвуют невозбуж-денные молекулы NH3. Следовательно, эти реакции являются изотопически селективными. Получающиеся в результате молекулы N2 должны быть обогащены изотопом 15N. Действительно, полученный коэффициент обогащения К(15N/14N) в молекулах N2 достигал 2,5 6.

В другом примере импульсный СО2-лазер использовался для селективного возбуждения колебательной моды 3 молекул 11ВСl3 в смеси 10ВСl3 и 11ВСl3. УФ излучение импульсной ксеноновой лампы возбуждало молекулы 11ВСl3* в смеси 10ВСl3 и 11ВСl3. УФ-излучение импульсной ксеноновой лампы возбуждало молекулы 11ВСl3 дальше, в континуум диссоциационного электронного состояния. Продукты диссоциации удалялись при помощи молекул О2. В эксперименте наблюдалось 10 %-ное обогащение изотопа 10В по сравнению с 11В в оставшейся смеси молекул ВСl3. В США рассматривалось использование метода двухступенчатой фотодиссоциации для широкомасштабного разделения изотопов урана.

Многофотонная диссоциация в сильном ИК-поле

Многофотонная диссоциация молекул в сильном ИК-поле подробно будет рассмотрена в подразд. 4. Поскольку переходы через низколежащие дискретные уровни обладают изотопической селективностью, этот процесс также можно использовать для разделения изотопов. Он имеет то преимущество, что для его осуществления требуются только импульсные ИК-лазеры средней мощности. Работы С.Я. Рабиновича с сотрудниками экспериментально продемонстрировали разделение изотопов урана с помощью многофотонной диссоциации молекул UF6 в сильном ИК-поле.

5. Эмиссионные процессы

С феноменологической точки зрения под фотоэлектрическим эффектом понимается явление вырывания электронов с поверхности металла при его освещении, т.е. в результате воздействия ЭМИ в видимой, ИК- и УФ-областях спектра (вырывания электронов с помощью рентгеновского и гамма-излучения также следует назвать фотоэффектом). Естественно, что фотоэффект наблюдается не только в металлах, но и в других твердых телах (полупроводниках, диэлектриках, молекулярных кристаллах и др.), а также и в жидкостях. Однако здесь ограничимся рассмотрением фотоэффекта только для случая твердых металлических тел. Из других типов взаимодействия ЭМП с веществом, родственных в какой-то мере внешнему фотоэффекту, следует еще упомянуть: явление фотоионизации (испускание электронов при освещении газов и паров); явление фотопроводимости (внутренний фотоэффект), т.е. появление электронов проводимости в телах, не проводящих электрический ток (полупроводниках или диэлектриках) при их освещении; фотогальванический эффект (возникновение ЭДС в замкнутом контуре под влиянием освещения, но без внешнего источника тока). Строгого различия между этими явлениями и внешним фотоэффектом нельзя провести в силу их общего физического содержания, но здесь рассмотрим только внешний фотоэффект.

Открытие внешнего фотоэлектрического эффекта принадлежит Г.Герцу [27]. Открытие этого явления (сыгравшего выдающуюся роль в развитии квантовой теории), было сделано Герцем попутно, в его знаменитых опытах по экспериментальному обоснованию электромагнитной теории света. Герцем было обнаружено, что длина электрической искры в разряднике вспомогательного колебательного контура зависела от того, падал ли на нее свет от другой искры, получающейся в разряднике контура, или нет. Было выявлено, что если разрядник вспомогательного контура защищен от света, то длина искры в нем меньше, чем при его освещении. Оказалось также, что этот эффект наблюдается и в УФ-части спектра падающего излучения и что он наблюдается лучше всего, если освещается отрицательный электрод разрядника. Эти результаты опытов Герца послужили началом интенсивного изучения фотоэлектрического эффекта. Среди последующих экспериментальных исследований в первую очередь следует упомянуть работы А.Г. Столетова [28], в которых были впервые вскрыты основные законы фотоэффекта, а также работы Э. Гальвакса (1888) и других исследователей. Р. Ленард (1899, 1900) и С. Томсон (1899) доказали, что при освещении металлов вылетают электроны, открытые ранее в опытах с катодными лучами в разрядных трубках.

При исследовании явления испускания электронов веществом, подвергнутым освещению, необходимо было прежде всего установить связь между характеристиками падающего излучения и характеристиками потока вылетающих фотоэлектронов. Основными характеристиками излучения следует выбрать интенсивность, спектральный состав (частоту) и поляризацию света, а для электронов их число, распределение по скоростям и направлению их испускания. Задачей теории является объяснение закономерных связей между этими величинами и сравнение их с экспериментом.

В результате упомянутых выше опытных исследований, а также и многих других были установлены три основных экспериментальных закона внешнего фотоэффекта:

Сила фотоэлектрического тока j прямо пропорциональна интенсивности I светового потока, вызывающего фотоэффект, при условии неизменности спектрального состава этого потока (закон Столетова).

2. Существует длинноволновая граница (0 или 0) в спектре излучения, начиная с которой (для < 0, или > 0) в данном веществе может иметь место фотоэффект (закон «красной» границы).

3. Энергия фотоэлектронов не зависит от интенсивности света, а максимальная величина этой энергии 0,5(m2)макс линейно связана с частотой падающего света, т.е.

0,5(m2)макс = a + b , (64)

где а и b постоянные, m масса и скорость фотоэлектрона. Известно, что второй и третий законы фотоэффекта не могли быть объяснены на основе классической волновой теории света и привели к очередной «катастрофе» классической физики, не способной объяснить квантовый характер световых явлений. Эйнштейну [29] первому удалось дать теоретическое объяснение этих законов, применив для этой цели планковские представления о квантах света. Работа Эйнштейна по фотоэффекту положила начало современной теории взаимодействия света с веществом. Приняв, что свет частоты может поглощаться и излучаться квантами энергии h, Эйнштейн предположил, что энергия светового кванта, попадающего на металл, целиком поглощается электроном, частично расходуясь при этом на работу вырывания из металла, а в остальном превращаясь в кинетическую энергию выбитого из металла электрона. Таким образом, закон сохранения энергии в данном случае имеет вид

h = + 0,5m2макс,

где минимальная энергия, требующаяся для удаления электрона из металла во внешнее свободное пространство, т.е. так называемая работа выхода, а макс максимальная скорость вылетающих электронов. Из последнего уравнения сразу вытекают второй и третий законы фотоэффекта. А именно для «красной» границы получаем

h0 = , 0 = /h. (65)

Таким образом, минимальная частота 0 определяется работой выхода , а максимальная энергия фотоэлектронов является линейной функцией частоты света, т.е. может быть получена опытным путем (третий закон).

Первый закон Столетова также хорошо объясняется теорией Эйнштейна, ибо число фотоэлектронов растет прямо пропорционально числу фотонов.

Уравнения Эйнштейна были проверены в ряде опытов. Среди них в первую очередь следует упомянуть фундаментальные работы А.Ф. Иоффе (1907) по элементарному фотоэлектрическому эффекту, в которых впервые наблюдался элементарный акт квантового поглощения света, предсказанного Эйнштейном. Важную роль в экспериментальном изучении фотоэффекта сыграли тонкие по экспериментальному искусству работы П. И. Лукирского и С.С. Прилежаева (1928), которые разработали очень точную методику измерений фотоэффекта при помощи сферического конденсатора и произвели тщательное исследование скоростей фотоэлектронов на целом ряде металлов, а также дали прецизионный метод количественного определения постоянной Планка.

Из формулы (65) явствует, что фотоэлектрическая граница определяется работой выхода (которая определяется также условиями на поверхности металла). Таким образом, можно ожидать, что граничная частота 0 в сильной мере зависит от состояния поверхности металла, что полностью подтверждается опытом. Обработка поверхности, наличие адсорбированных газов и т.п. могут сильно менять величину работы выхода, а вместе с ней и величину красной границы, и тем самым делают задачу определения красной границы чистых металлов весьма трудной. На величину 0 может оказывать существенное влияние и температура металла. Опыты с чистыми поверхностями в вакууме показали, что фототок j незначительно меняется с увеличением температуры поверхности для частот, далеких от красной границы, и резко возрастает на частотах, близких к ней, особенно для частот ~ 0 (т.е. температура поверхности эффективно смещает красную границу в область меньших частот, и эта граница перестает быть резкой с ростом температуры). Аналогично температуре действует на фототок ускоряющее ЭП у поверхности фотокатода. Влияние этого поля незначительно для частот , далеких от красной границы ( >> 0), и очень существенно для , близких к 0.

Помимо фотоэлектрической границы для характеристики фотоэффекта имеют существенное значение энергия фотоэлектронов и спектральное распределение фотоэффекта, т.е. зависимость фототока от частоты света. При этом важно определить функцию распределения электронов по скоростям или энергиям , в которую в качестве параметра входит частота света : f(, ).

На рис. 10 в качестве примера приведена кривая распределения энергии фотоэлектронов для алюминия, освещаемого светом длины волны = 0,2536 мкм.

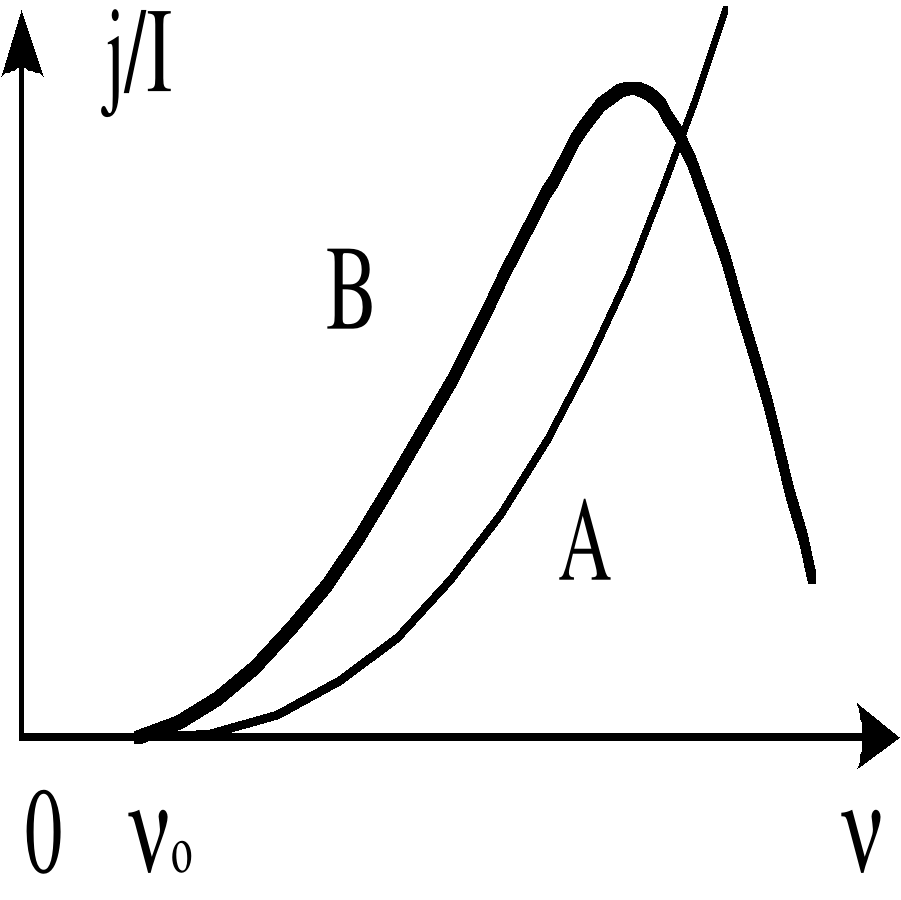
Рис. 10. Кривая распределения Рис. 1 Схематические кривые

фотоэлектронов по энергиям для Al спектрального распределения

фототока

По оси ординат отложено число фотоэлектронов nф (в произвольных единицах), а по оси абсцисс отношение энергии электрона к его максимальной энергии /макс. Эти кривые мало различаются для различных металлов, но могут сильно деформироваться для тонких пленок (толщин d < 1 мкм).

Кривые зависимости фототока от частоты света имеют вид, изображенный на рис. 1 Здесь по оси ординат отложено отношение фототока j к интенсивности света I, вызывающего его (j/I чувствительность фотокатода), а по оси абсцисс частота света . Кривая типа А на рис. 11 соответствует «нормальному» фотоэффекту (нормальная характеристика) и имеет монотонно возрастающий характер с ростом частоты. Кривая В на рис. 11 имеет максимум в той или иной области частот и соответствует «селективному» фотоэффекту [30, 31].

При этом селективность может быть просто спектральной, когда в некоторой области частот имеется максимум на кривой рис. 11 независимо от поляризации света, а может быть и поляризационной, когда этот максимум получается лишь при определенной поляризации падающего на фотокатод света.

Чувствительность фотокатода j/I можно записать и в несколько иной форме, если взять частное от деления фототока на заряд электрона j/e = nф, т.е. число фотоэлектронов, а вместо интенсивности света ее отношение к энергии кванта I/h = nкв, то есть число фотонов данной частоты. Тогда получим чувствительность, выраженную в количестве фотоэлектронов, приходящихся на один поглощенный световой квант (квантовый выход фотоэффекта nф/nкв). Эта величина оказывается очень маленькой. В случае чистых металлов квантовый выход составляет величину порядка 105 103. Эта величина является функцией «расстояния» от красной границы, т.е. разности 0. По экспериментальным данным [32] квантовый выход из максимума спектральной характеристики сложных катодов может достигать величины 0,3 электрона на один поглощенный световой квант.

Рассмотрим основные результаты исследований по квантовомеханической теории фотоэлектрического эффекта в металлах.

6. Основные предпосылки для построения квантовой теории фотоэффекта