ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Контрольная работа

ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

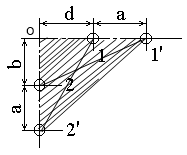
1 Определить взаимную индуктивность между бортовой линией 1-1’ и линией 2-2’ (рис. 1) на метр длины. Диаметр проводов линии 1-1’ 0,6 см, линии 2-2’ - 0,4 см, остальные параметры заданы в таблице.

Таблица 2.4

	№ вар.	a, см	b, см	d, см
Рис. 1	31	2	1	2

Найдем выражение для взаимной индуктивности между 1-1’пользуясь методом участков

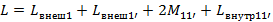
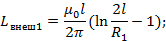
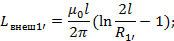
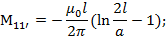
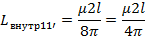
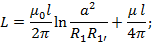
Диаметры проводов 1 и 1’ одинаковы поэтому

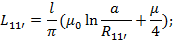
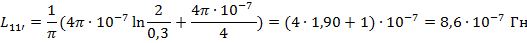
При данная формула, дает при условии точное значение индуктивности

Таким же способом определим взаимную индуктивность между проводами 2 и 2’

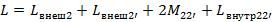
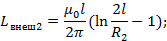
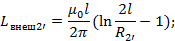
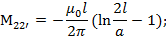
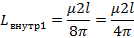
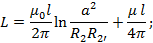
Диаметры проводов 2 и 2’ одинаковы поэтому

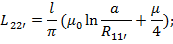
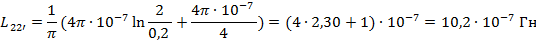
Далее определим взаимную индуктивность между 1-1’ и 2-2’

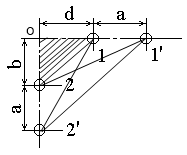
Т.к. длина рассматриваемого участка взаимного влияния во много раз больше всех расстояний между проводами, то воспользуемся расчетом взаимной индуктивности методом участков. Для этого определим расстояния между сечениями проводов взаимного влияния

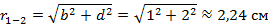
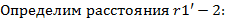
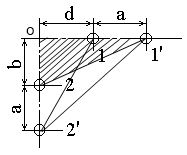
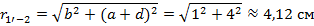
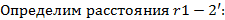
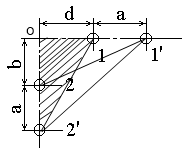
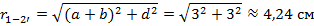
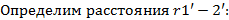
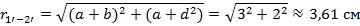
Пользуясь методом участков находим

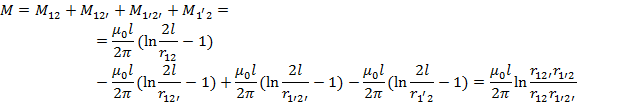
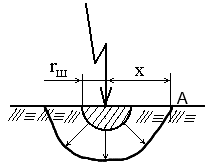
2 Определить закон распределения электрической напряженности и потенциалов в поле растекания зарядов, созданном металлическим полушаровым заземлителем с радиусом rш. Ток замыкания на землю - I, удельная проводимость грунта =10-1 1/Омм (рис. 1).

Таблица 2.5

		№ вар.	rш, м	I, A
Рис. 1		41	0,05	500

Пространство вокруг электрода, в котором наблюдается растекание тока замыкания, представляет собой поле растекания. Если в качестве заземляющего электрода использовать От полусферического заземлителя, как заземляющий электрод ток будет растекаться равномерно и симметрично во все стороны, и плотность его будет убывать по мере удаления от заземлителя, вследствие увеличения сечения слоя земли, через которое растекается ток замыкания.

На расстоянии «х» от центра полусферы плотность тока определяется по формуле:

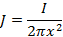
Допустим, что поле растекания тока замыкания можно рассматривать как стационарное электрическое поле, при котором линия плотности тока совпадает с линиями напряженности электрического поля Е. Тогда плотность J тока прямо пропорциональна напряженности электрического поля.

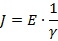
Это выражение позволяет определить потенциал «A» в любой точке поверхности земли, отстоящей от центра заземлителя на расстоянии «х», как падение напряженности на земле на участке от «х» до бесконечности.

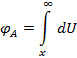
где dU - падение напряжение в отмеченном слое.

Его можно выразить так

Если проинтегрировать это выражение, то получается значение потенциала точки А:

В

Следовательно, наименьший потенциал на поверхности земли будет иметь точка, отстоящая от электрода на расстоянии «х», равном бесконечности.

Наибольший потенциал на поверхности будет иметь точка, отстоящая от полушарового электрода на расстоянии «х», равном наименьшему значению, т.е. rш - радиусу электрода.

Потенциал непосредственно на заземляющем электроде при этом будет равен:

В

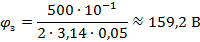
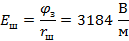
Потенциал на поверхности земли будет меняться по закону

В

А напряженности

представляющие собой уравнение равносторонней гиперболы, т.е. уменьшается от наибольшего значения «З» до нуля по мере удаления от заземлителя. Эквипотенциальные линии на поверхности земли в однородном грунте представляют собой концентрические окружности, центром которых является центр полусферического, стержневого или других форм электродов.

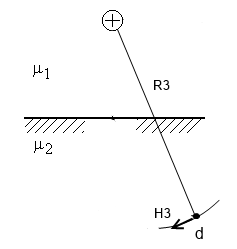
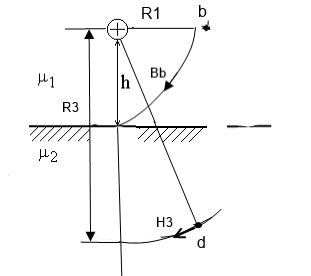
1. Построить картину траектории произвольно выбранной одной силовой линии магнитного поля , созданного проводником с током, находящимся вблизи ферромагнитной среды. Среда, окружающая проводник с током, характеризуется магнитной проницаемостью 1=1, относительная магнитная проницаемость ферромагнитной среды - 2 (рис. 1)

Таблица 2.6

	№ вар.	I, A	h, см	2
Рис. 1	51	50	2	1103

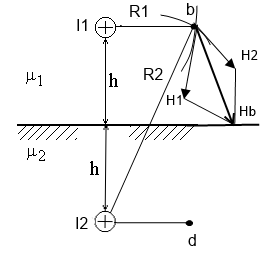
Для определения картины траектории силовой линии магнитного поля воспользуемся методом зеркальных изображений.

Для расчета введем фиктивные токи и . Провод с током поместим зеркально по отношению к проводу с заданным током , а провод с током поместим там, где расположен провод с током

Вычислим токи

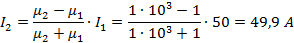
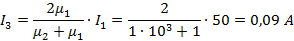
Определим напряженность поля в точке b

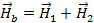
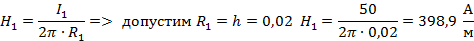
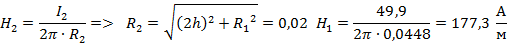
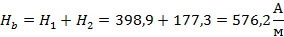
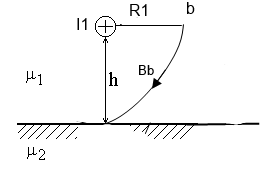
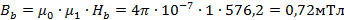
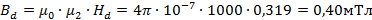
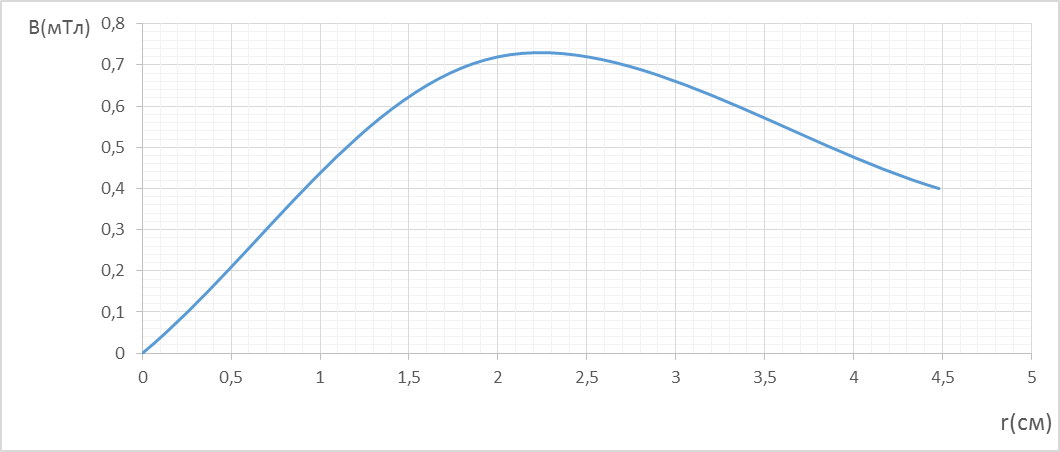
Траектория произвольно выбранной одной силовой линии магнитного поля будет иметь вид:

B(r)=

B(r)=

4. Исследовать электрическое поле и определить емкость и энергию плоского конденсатора с двухслойным диэлектриком (рис. 1). Площадь каждой обкладки - S Приложенное к конденсатору напряжение - U=30 В. Принять =0 при x=d1+d2, то есть на левой пластине, x=0 для левой пластины. Начертить кривые зависимости E(x) и D(x). Относительные диэлектрические проницаемости слоев диэлектрика 1 и 2. Краевым эффектом пренебречь.

Таблица 2.7

	№ вар.	S, см2	d1, мм	d2, мм	1	2
Рис. 1	61	10	5	10	2	1

При условии, что в каждом слое поле будет равномерным, искажающее влияние краев конденсатора учитываться не будет (по условию задачи).

В силу того, что нормальная составляющая вектора непрерывна, имеем

Так как , а , то .

Таким образом, отношение напряженностей обратнопропорционально отношению электрических проницаемостей.

Запишем уравнение связывающая величины и

.

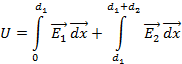
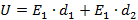
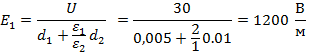
=2400

При выводе формулы для емкости двухслойного плоского конденсатора на границу раздела двух диэлектриков мысленно поместим бесконечно тонкий металлический листок, при условии, что поверхность раздела диэлектриков является эквипотенциальной поверхностью, что оставляет значение потенциала неизменным.

При этих условиях емкость двухслойного конденсатора можно подсчитать, как емкость двух последовательно включенных конденсаторов и

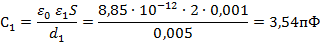
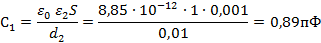
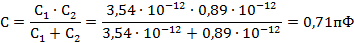
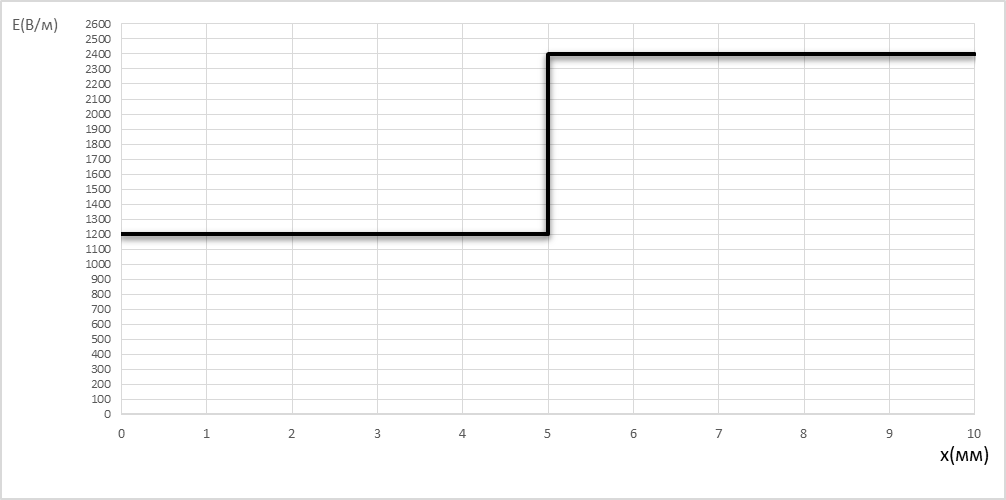
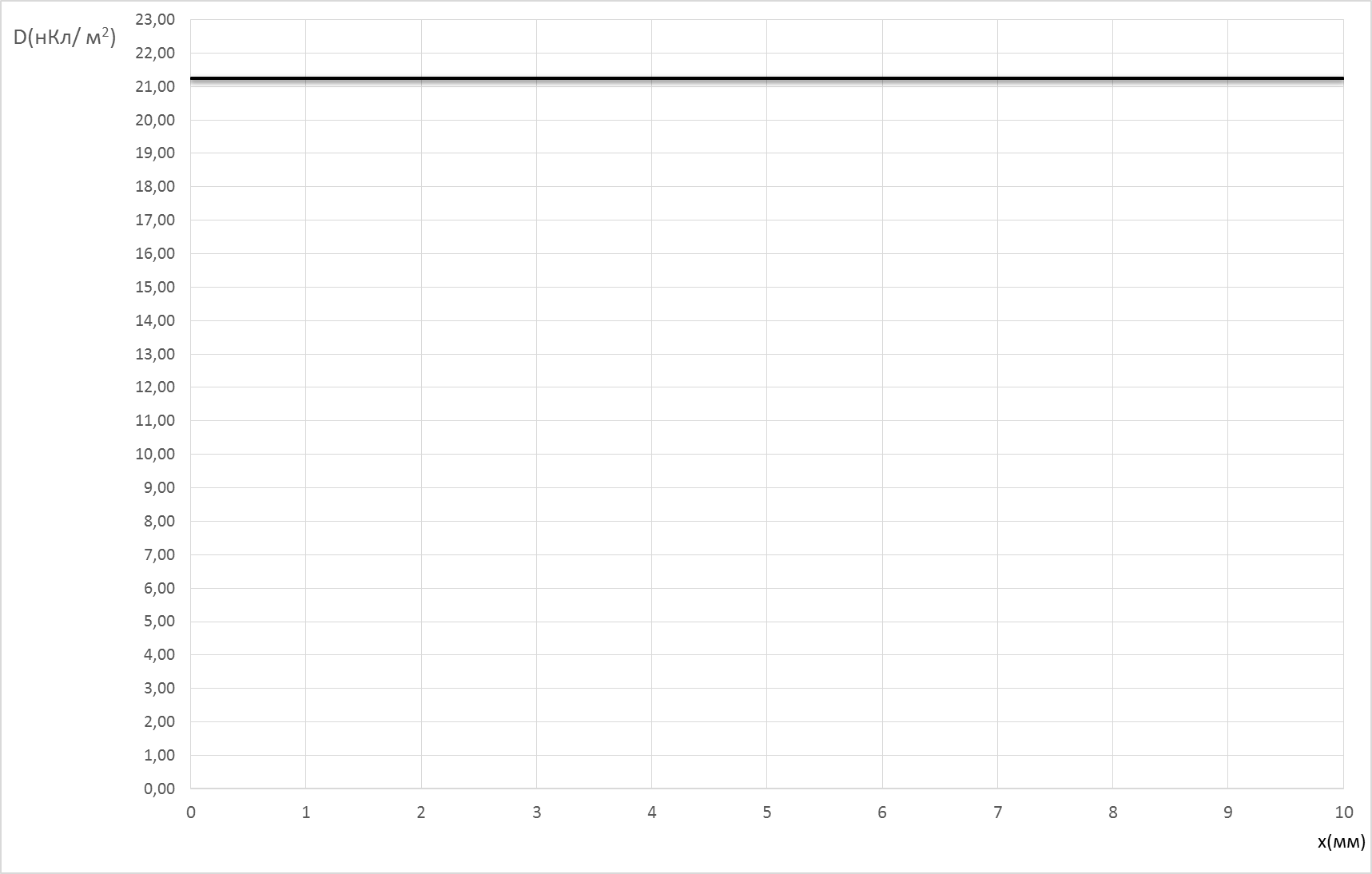
Построим график D(x)

D(x)=

D(x)=

E(x)=

E(x)=

ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ