Общие свойства импульсных систем

Контрольная работа

Общие свойства импульсных систем

Содержание

1 Понятие системы с импульсной модуляцией

2 Информационные возможности импульсных систем

3 Линейные и нелинейные импульсные системы

4 Критерии оценки качества формирования и воспроизведения сигналов с импульсной модуляцией

5 Графическое представление электрических сигналов

6 Амплитудно-частотный и фазово-частотный спектры периодической последовательности прямоугольных импульсов

7 Краткие сведения о разрывных функциях

Литература

1 Понятие системы с импульсной модуляцией (ИМ)

Модуляцией называют процесс изменения физических параметров носителя в определенном соответствии с сообщением. В рассматриваемых нами системах носителями во всех случаях являются колебания тока или напряжения, а при модуляции изменяются параметры этих колебаний.

В импульсных системах колебания имеют форму импульсов – прямоугольных, трапецеидальных, треугольных, колоколообразных и т.д. При внесении информации изменяются те или иные параметры импульсов: амплитуда – амплитудно-импульсная модуляция (АИМ), длительность – широтно-импульсная модуляция (ШИМ), временное расположение – временная-импульсная модуляция (ВИМ), имеющая две разновидности – фазо-импульсную (ФИМ) и частотно-импульсную (ЧИМ) модуляции. Во всех этих системах осуществляется квантование по времени. По этому признаку выделяют класс импульсных систем. Широко применяются комбинации видов модуляции, например, АИМ с ШИМ, ШИМ с ЧИМ и т.д. Если квантование осуществляется не по времени, а по уровню, получаем кодовую модуляцию (КМ). При одновременном квантовании и по уровню и по времени будем иметь импульсно-кодовую модуляцию (ИКМ). ЕЕ еще называют кодовая с тактированием. В системах с КМ и ИКМ важно, что значение выходной величины может принимать только дискретные наперед заданные значения. Это дает возможность обеспечение гарантированной точности представления сигналов в виде импульсов и широко используется в цифровых системах управления. Используется также сочетание кодовой с другими видами импульсной модуляции, например, КМ с ШИМ, КМ с ШИМ и ЧИМ и т.д. Здесь возможны два основных варианта. В первом – базовым является квантование по времени, например, ШИМ, а длительность импульсов задается дискретно в соответствии с КМ. Во втором – базовым является квантование по уровню (КМ), а ШИМ действует в промежутках между уровнями. Такое сочетание в дальнейшем, в силу некоторых особых свойств сигналов названо нами многозонной импульсной модуляцией (МИМ).

2 Информационные возможности импульсных систем

Импульсная система – это совокупность элементов и связей. На рис.1 показана структура разомкнутой импульсной системы в наиболее общем виде.

Структура импульсной системы

Рис.1

ИЭ – импульсный элемент;

М – модулятор;

Х* – импульсный сигнал с модуляцией;

КП – канал передачи (в системах связи);

НЭ – непрерывный элемент или непрерывная часть (фильтр, нагрузка).

Строгое обоснование информационных возможностей импульсных систем дано пока только для линейных систем с АИМ теоремой академика Котельникова В.А. Пусть – непрерывный сигнал (рис.2), – этот же сигнал в дискретные моменты времени, где – период следования импульсов. Вводится функция , фиксирующая импульсы на очень коротком промежутке времени. Общее напряжение всех импульсов на интервале будет равно

, (1)

где ,

,, – коэффициенты.

Пусть наивысшая частота в сигнале равна . Второй член ряда (1) содержит низшую из всех боковых частот, равную . Выделить из первого члена можно в том случае, если эта частота меньше , т.е.

; (2)

, (3)

но – частота амплитудно-модулированных импульсов. Тогда теорема будет формулироваться следующим образом: по импульсам функции при помощи фильтра ли гармонического анализа можно восстановить колебание , если только частота импульсов больше двойной максимальной частоты, входящей в сигнал. Ясно, то на периоде максимальной частоты количество импульсов должно быть больше двух.

Иллюстрация к теореме В.А. Котельникова

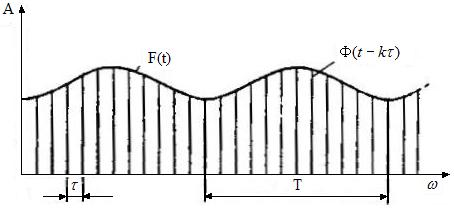
Рис.2

Отметим, что в импульсных системах энергетической электроники указанные предельные возможности реализовать не удается, т.к. силовые фильтры резко отличаются от информационных и различны проблемы демодуляции, т.е. восстановления сигнала из импульсной последовательности. В этих случаях надо «усиливать» неравенство (3), т.е. обеспечивать

. (4)

3 Линейные и нелинейные импульсные системы

Линейной называется импульсная система, в которой линейны все ее элементы по рис.1 – импульсный элемент (ИЭ) с модулятором (М), канал передачи (КП), непрерывная часть (НЧ). Нелинейной – система, у которой хотя бы один из элементов нелинеен.

Определение линейности и нелинейности непрерывной части делятся в теории цепей (курс теоретических основ электротехники). Для выяснения свойств импульсной части (ИЭ;М) введем понятие амплитудной и модуляционной характеристик. Первая из них устанавливает зависимость амплитуды импульсов на выходе модулятора от входного управляющего сигнала , вторая – модулируемого параметра от этого же сигнала. Очевидно, что у АИМ эти две характеристики совпадают, так как модулируемым параметром является амплитуда импульсов. Характеристика представлена на рис.3. Принципиально система с АИМ может иметь линейную модуляционную характеристику и быть линейной, так как с ростом амплитуда импульсов может неограниченно возрастать, однако в реальных системах обязательно наступают технические ограничения, что и показано пунктиром на рис.3.

Модуляционная характеристика системы с АИМ

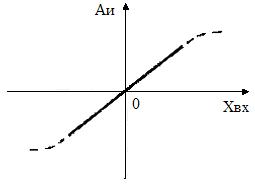
Рис.3

У систем с ШИМ амплитудная и модуляционные характеристики не совпадают (рис.4 и 5), причем обе резко нелинейны. На рис.5 модулируемый параметр – относительная длительность импульсов , где – длительность импульса, – период квантования. Очевидно, что не может быть больше чем .

Амплитудная характеристика с ШИМ

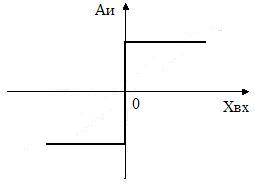
Рис.4

Модуляционная характеристика системы с ШИМ

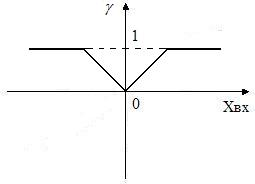
Рис.5

В КМ и ИКМ характеристики совпадают и нелинейны, как это показано на рис.6.

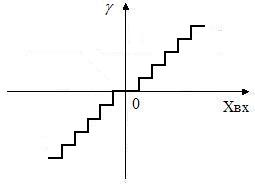
Рис.6

4 Критерии оценки качества формирования и воспроизведения сигналов с импульсной модуляцией

Рассмотрим сущность задач формирования и воспроизведения сигналов с ИМ.

Задача формирования – заданы требования к выходу импульсной системы. Необходимо найти алгоритм, при котором достигается максимальное приближение импульсного выходного сигнала, например, напряжения, к заданному непрерывному. Это приближение может быть достигнуто различными методами ИМ и различными аппаратными средствами. В последнее время используют методы формирования заданного выхода из ортогональных функций Уолша, которые рассматриваются в разделе 4.

Задача воспроизведения (усиления) – задан входной сигнал. Необходимо найти алгоритм, при котором выходной усиленный сигнал максимально (без искажений) приближается к входному.

Критерии оценки качества формирования рассматривались в курсе «Преобразовательная техника». Кратко приведем основные соотношения для типового синусоидального сигнала:

1) коэффициент гармоник

, (5)

где – эффективное значение выходного сигнала;

– эффективное значение первой гармоники выходного сигнала;

2) коэффициент искажения:

; (6)

3) коэффициент нормы:

; (7)

где – среднее по модулю значение выходного сигнала;

4) к.п.д. выделения:

; (7)

где – мощность i-ой гармоники.

В системах воспроизведения теряет свое значение даже в том случае, если мы воспроизводим типовой синусоидальный сигнал, т.к. появляется дефект амплитуды.

Для систем воспроизведения с импульсной модуляцией установим вначале понятие неискажающей системы (НС), структурная схема которой показана на рис.7.

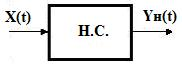
Рис.7

Предварительно отметим, что в разных областях электроники эти критерии различны. Например, в звуковоспроизводящей аппаратуре важна форма спектра. В телевидении, телеметрии, информационно-импульсных системах может изменяться масштаб (k), сдвиг() и постоянная составляющая (a):

. (9)

При наличии энергетического входа (рис.8) в ИМС нельзя менять постоянную составляющую, т.к. она передает энергию. Здесь выражение для выходного сигнала примет вид:

. (10)

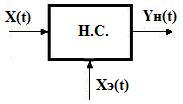
Рис.8

Наиболее жестким является понятие НС в многофазных системах:

, (11)

т.к. изменение сдвига вызовет искажения.

Пусть (12)

тогда, подставляя (12) в (10), получим:

, (13)

где – амплитуда неискаженного сигнала.

В рассматриваемой ИМС

, (14)

где – дефект амплитуды;

– амплитуда первой гармоники выходного сигнала;

– амплитуда k-ой гармоники.

Следовательно, если , то передача первой гармоники производится без искажений.

Для систем воспроизведения введем коэффициент квадратичного отклонения – .

. (15)

С учетом значений для и преобразуем выражение (15):

где , так как

в силу ортогональности функций. Тогда

, (16)

так как , , .

Если нет ограничения на фазу , то можно принять , тогда . Выражение (16) примет вид:

, (17)

так как , то .

Тогда выражение для можно записать только через выходные параметры:

. (18)

Если и , т.е. , то

При оценке качества воспроизведения сигнала в импульсных системах по критерию происходит отображение сигнала в число, и объективно это число говорит о его качестве только в одном случае, когда отсутствуют мешающие компоненты и . Во всех других случаях оценка может считаться объективной только при сопоставлении сигналов, близких по свойствам (по структуре). Для того, чтобы связать оценку сигнала с его структурой в частотной области, было введено понятие частотно зависимого коэффициента среднеквадратичного отклонения :

, (20)

где – абсцисса центра тяжести спектра выходного сигнала.

Определение связано с вычислением моментов n-го порядка:

, (21)

где – огибающая спектра.

В случае вычисления момента первого порядка (n=1) формула (21) приобретает вид:

. (22)

В формуле (22) роль «силы» играет площадь, охваченная огибающей спектра, а является точкой приложения этой силы. Отметим, что для идеальной системы .

5 Графическое представление электрических сигналов

Существует два способа представления электрических сигналов: временной и спектральный.

При временном способе электрический сигнал изображается графиком в прямоугольной системе координат, по ординате которой указывается мгновенное значение напряжения (тока) изображаемого сигнала, а по оси абсцисс – текущее время (рис.9).

Временной способ представления сигнала

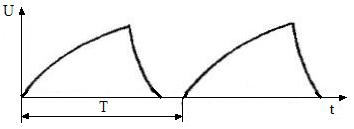
Рис.9

При спектральном способе представления электрический сигнал рассматривается как сумма простых (гармонических) колебаний, каждое из которых имеет свое максимальное значение, частоту и фазу. Эта сумма гармонических составляющих однозначно определяет сигнал (его свойства, форму кривой и т.п.). При спектральном способе гармонические составляющие графически представляют в прямоугольной системе координат в виде вертикальных линий, абсциссы которых определяют частоту гармоник, а высота (ордината) соответствует их максимальным значениям (рис.10).

Спектральный способ представления сигнала

Рис.10

Напомним, что связь сигналов во временной и частотной области устанавливается преобразованиями Фурье. При этом периодический импульсный сигнал с периодом «Т» во временной области представляется дискретным частотным спектром в частотной области по формуле:

, (23)

где – постоянная составляющая;

– амплитуды спектральных составляющих;

– угловая частота следования импульсов.

В свою очередь амплитуды гармоник находятся по известным формулам:

(24)

Непериодический импульсный сигнал имеет непрерывный частотный спектр (спектральную плотность) , который находится с использованием прямого преобразования Фурье:

. (25)

Если известна спектральная плотность , то можно найти сигнал во временной области с использованием обратного преобразования Фурье (интеграла Фурье):

. (26)

6 Амплитудно-частотный и фазо-частотный спектры периодической последовательности прямоугольных импульсов

Для лучшего понимания материала о свойствах спектров модулированных импульсных сигналов, представленных в последующих разделах, рассмотрим способы построения амплитудно-частотного спектра (АЧС) и фазо-частотного спектра (ФЧС) немодулированной последовательности импульсов, а также поведение АЧС при изменении длительности и частоты следования этих импульсов.

Зададим периодическую импульсную последовательность (рис.11):

, (27)

где – амплитуда импульса;

– середина первого импульса, относительно начала координат;

– длительность импульса;

– период следования импульсов.

Периодическая последовательность импульсов

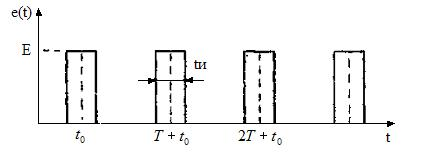
Рис.11

Постоянная составляющая:

, (28)

где – относительная длительность импульсов.

Амплитуды косинусоидальных составляющих:

. (29)

Амплитуды синусоидальных составляющих:

. (30)

Амплитуды гармоник:

. (31)

Фазы гармоник:

. (32)

Выражение для немодулированной последовательности импульсов приобретает вид:

. (33)

Анализ выражения (23) дает следующие выводы:

1. постоянная составляющая пропорциональна ;
2. амплитуды всех гармоник пропорциональны и зависят от
3. распределение амплитуд гармоник по величине подчиняется закону , где ;
4. сдвиг фазы не зависит от , а определяется только значением .

Для определения АЧС выражение (33) запишем в следующем виде:

, (34)

где – частота следования импульсов;

1,2,3,…– номер интервала значений «».

Огибающая АЧС:

, (35)

где .

Огибающая пересекает ось частот при , т.е. при ,,,.

При , ;

при , , , ;

при , , , и т.д.

Переведем огибающую на ось частот :

, тогда при ,

,

,

,

.

Таким образом, для построения АЧС есть все необходимое:

1. угловая частота следования импульсов ;
2. угловые частоты всех других гармоник , где n = 1,2,3,…;
3. закон изменения амплитуд .

Нормируем амплитуды, поделив все в формуле (33) на . Проводим вертикали частот 0, , и т.д. и огибающую. Пересечение их дает амплитуды гармоник (рис.12).

Спектральная характеристика немодулированной

последовательности прямоугольных

импульсов

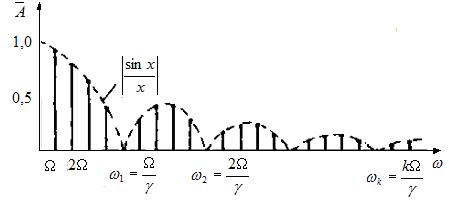
Рис.12

Обычно эффективная полоса частот задается выражением:

.

При построении АЧС необходимо пользоваться следующими положениями:

1. спектральные линии должны быть расположены на равном расстоянии, которое равно ;
2. спектр имеет арочную структуру. Ширина первой полуарки и каждой малой арки равна , т.е. определяется периодом следования и относительной длительностью импульсов ;
3. число спектральных линий под каждой аркой определяется соотношением между длительностью импульсов и частотой их следования и равно , т.к. при кратных амплитуды равны нулю.

Для построения ФЧС воспользуемся выражением:

, (36)

Которое следует из выражения (34) и обозначает сдвиг фазы n – ой гармоники.

Ширина арки равна:

.

Сдвиг фазы на частоте, соответствующей окончанию арки:

.

Получается треугольник (рис.13):

К определению угла наклона ФЧС:

Рис.13

Из рисунка:. Отсюда , т.е. знак определяет наклон огибающей и знак дискретного слагаемого в формуле (36) (см рис.14).

7 Краткие сведения о разрывных функциях

Для аналитического представления импульсных сигналов широко применяют разные функции.

Под разрывными понимают функции, для которых в определенных точках пределы справа и слева от точки не равны друг другу, т.е. имеют в виду функции с разрывами первого рода. Наиболее распространенные из них приведены в табл.1, а графики этих функций представлены на рис.15.

ФЧС при различных значениях

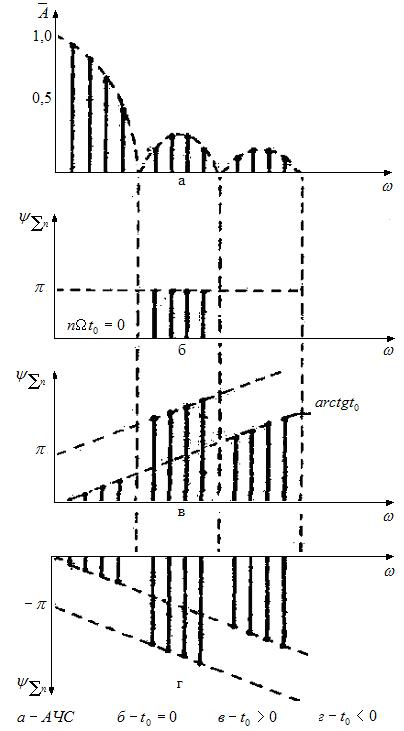
Рис.14

Таблица 1

Наименование функции	График	Аналитическое описание	Обозначение
1. Единичная –“–	рис.15,а рис.15,б		1(x) 1(-x)
3. Модуль	рис.15,в
4. Сигнум(знак х)	рис.15,г
5. Дельта	рис.15,д
6. Антье 7. –“– 8. –“–	рис.15,е рис.15,ж –“–
9. Дробная 10. –“– 11. –“– 1 –“–	рис.15,з рис.15,и рис.15,к рис.15,л
13. Треугольная 14. –“–	рис.15,м рис.15,н
15. Прямоугольный синус 16. –“–	рис.15,о рис.15,п
17. –“– 18. Смещенные функции	рис.15,т рис.15,с

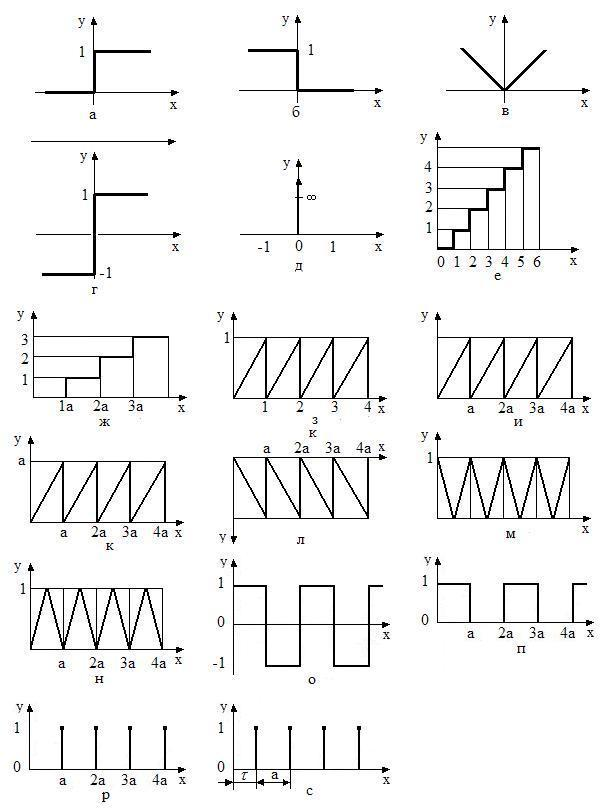
Рис.15

Табл.1 является исходной, для описания сложных сигналов при моделировании электронных импульсных схем, например, с ШИМ, МИМ и т.д.

С помощью рассмотренных разрывных функций можно задавать алгоритмы преобразования сигналов управления и описать импульсный сигнал на выходе модулятора в функции времени.

Литература

1. Барыбин, А.А. Электроника и микроэлектроника. Физико-технологические основы / А.А. Барыбин. - М.: ФИЗМАТЛИТ, 2006. - 424 c.

2. Белов, Н.В. Электротехника и основы электроники: Учебное пособие / Н.В. Белов, Ю.С. Волков. - СПб.: Лань, 2012. - 432 c.

3. Белоусов, В.В. Судовая электроника и электроавтоматика: Учебник / В.В. Белоусов, В.А. Волкогон. - М.: Колос, 2008. - 645 c.

4. Борисенко, В.Е. Наноэлектроника: теория и практика: Учебник / В.Е. Борисенко, А.И. Воробьева, А.Л. Данилюк, Е.А. Уткина. - М.: БИНОМ. ЛЗ, 2013. - 366 c.

5. Вайнштейн, Л.А. Теория дифракции. Электроника СВЧ / Л.А. Вайнштейн. - М.: Радио и связь, 1995. - 600 c.

6. Велстистов, Е. Все о приключениях Электроника: Повести / Е. Велстистов. - СПб.: Азбука-Аттикус, 2013. - 592 c.

7. Велтистов, Е.С. Победитель невозможного: третья книга из цикла о приключениях Электроника / Е.С. Велтистов. - М.: Дет. лит., 2010. - 235 c.

8. Воронков, Э.Н. Твердотельная электроника. Практикум: Учебное пособие для студ. высш. учеб. заведений / Э.Н. Воронков. - М.: ИЦ Академия, 2010. - 128 c.

9. Воронков, Э.Н. Твердотельная электроника: Учебное пособие для студ. высш. учеб. заведений / Э.Н. Воронков, А.М. Гуляев, И.Н. Мирошникова. - М.: ИЦ Академия, 2009. - 320 c.

10. Гальперин, М.В. Электротехника и электроника: Учебник / М.В. Гальперин. - М.: Форум, НИЦ ИНФРА-М, 2013. - 480 c.

11. Голубева, Н.С. Основы радиоэлектроники сверхвысоких частот: Учебное пособие / Н.С. Голубева, В.Н. Митрохин; Под общ. ред. проф. д.т.н. И.Б. Федоров. - М.: МГТУ им. Баумана, 2008. - 488 c.

12. Горохов, П.К. Толковый словарь по радиоэлектронике / П.К. Горохов. - М.: Русский язык, 1993.

13. Гусев, В.Г. Электроника и микропроцессорная техника: Учебник / В.Г. Гусев, Ю.М. Гусев. - М.: КноРус, 2013. - 800 c.

14. Джонс, М.Х. Электроника - практический курс / М.Х. Джонс. - М.: Техносфера, 2013. - 512 c.

15. Евстратов, В.А. Радиоэлектроника прогулочных судов / В.А. Евстратов. - М.: ТрансЛит, 2008. - 128 c.

16. Ермуратский, П.В. Электротехника и электроника / П.В. Ермуратский, Г.П. Лычкина, Ю.Б. Минкин. - М.: ДМК Пресс, 2013. - 416 c.

17. Ефимов, И.Е. Основы микроэлектроники / И.Е. Ефимов, И.Я. Козырь. - М.: Высшая школа, 1983.

18. Жаворонков, М.А. Электротехника и электроника: Учебное пособие для студ. высш. проф. образования / М.А. Жаворонков, А.В. Кузин. - М.: ИЦ Академия, 2013. - 400 c.

19. Иньков, Ю.М. Электротехника и электроника: Учебник для студентов учреждений среднего профессионального образования / Б.И. Петленко, Ю.М. Иньков, А.В. Крашенинников. - М.: ИЦ Академия, 2013. - 368 c.

20. Калашников, В.И. Электроника и микропроцессорная техника: Учебник для студ. учреждений высш. проф. обр. / В.И. Калашников, С.В. Нефедов. - М.: ИЦ Академия, 2012. - 368 c.

21. Кашкаров, А.П. Новейшие технологии в электронике: дома, на даче, в автомобиле / А.П. Кашкаров. - Рн/Д: Феникс, 2013. - 172 c.

22. Колистратов, М.В. Электротехника и электроника: электротехника на оборудовании National Instruments: Лабораторный практикум / М.В. Колистратов, Л.А. Шапошникова; Под ред. Л.А. Шамаро. - М.: ИД МИСиС, 2012. - 79 c.

23. Кузовкин, В.А. Электротехника и электроника: Учебник для бакалавров / В.А. Кузовкин, В.В. Филатов. - М.: Юрайт, 2013. - 431 c.

24. Кучумов, А.И. Электроника и схемотехника: Учебное пособие / А.И. Кучумов. - М.: Гелиос АРВ, 2011. - 336 c.

25. Лапынин, Ю.Г. Контрольные материалы по электротехнике и электронике: Учебное пособие для учреждений среднего профессионального образования / Ю.Г. Лапынин. - М.: ИЦ Академия, 2011. - 128 c.

26. Лачин, В.И. Электроника: Учебное пособие / В.И. Лачин, Н.С. Савелов. - Рн/Д: Феникс, 2010. - 703 c

Общие свойства импульсных систем