ОПТИЧЕСКИЕ И ЭЛЕКТРООПТИЧЕСКИЕ ПРОЦЕССЫ В КВАНТОВЫХ ГЕТЕРОСТРУКТУРАХ

Контрольная работа

Содержание

1. Оптические свойства квантовых ям и сверхрешеток

2. Оптические характеристики квантовых точек и нанокристаллов

3. Электрооптические эффекты в квантовых точках. Квантово-размерный эффект Штарка

4. Электрооптические эффекты в сверхрешетках. Лестницы Штарка и осцилляции Блоха

Литература

1. Оптические свойства квантовых ям и сверхрешеток

Оптические свойства, связанные с межзонными переходами в квантовых ямах, совершенно непохожи на соответствующие характеристики объемных материалов, что легко объяснить особенностями двумерной оптической плотности и тем, что экситонное поглощение в двумерных системах намного сильнее. Значительная разница между трех- и двумерными системами наблюдается и в случае внутризонных переходов. Такие переходы в двумерных системах могут происходить и без участия фононов, за счет электронов (или дырок) в локализованных состояниях ям, а также между локализованными состояниями и непрерывным спектром. Более того, в двумерных системах такие переходы могут специально созданы для излучения света (квантовые каскадные лазеры) или его регистрации (инфракрасные фотодетекторы). На рис. 1 представлена квантовая яма (как в реальном пространстве, так и в пространстве волновых векторов), в которой происходят межзонные переходы из начального состояния в валентной зоне в конечное, расположенное в зоне проводимости. Отметим сразу, что поглощение проявляется при более высоких энергиях, чем в трехмерных системах, поскольку разность энергий между состояниями больше ширины запрещенной зоны полупроводника. Для расчета скоростей перехода можно воспользоваться введенным в главе 2 «золотым правилом» Ферми (2.26) для процессов, происходящих под воздействием зависящего от времени возмущения:

(1)

считая, что возмущение обусловлено взаимодействием фотон - электрон и имеет вид

(2)

где вектор относится к положению электрона в плоскости раздела, т. е.) , а - амплитуда электрического поля падающей световой волны.

Рис. 1.

Матричные элементы для перехода электрона от исходного состояния в валентной зоне в конечное состояние в зоне проводимости определяются уравнением

(3)

Необходимо отметить, что, поскольку введенный выше вектор является планарным, в уравнении 2 можно рассматривать одну из его компонент — или , которые являются координатами электрона в плоскости. Предположим далее, что рассматриваемая кристаллическая структура имеет кубическую (в данном случае квадратную) симметрию, тогда направления хну эквивалентны. В кристаллической двумерной структуре электронные состояния описываются функциями Блоха:

(4)

(5)

где векторы и соответствуют электронам в двумерной системе. Мы пользуемся одинаковыми векторами в обоих уравнениях (4) - (5), поскольку при рассматриваемых переходах сохраняется общий момент, а импульсом фотона можно пренебречь по сравнению с импульсом электрона. Подставляя (4) и (5) в уравнение (3), можно получить выражение для матричного элемента М в виде произведения двух величин

(6)

где

(7)

есть матричный элемент, соответствующий дипольному моменту переходов между блоховскими состояниями в валентной зоне и зоне проводимости, а

(8)

соответствует перекрыванию электронных и дырочных волновых функций в квантовых ямах.

Таким образом, в соответствии с уравнением (6) матричные элементы межзонных переходов распадаются на два сомно сомножителя, для которых могут быть сформулированы следующие условия или правила отбора:

1. Перекрывание электронных и дырочных огибающих функций, определенное уравнением (8) должно быть отлично от нуля. Поэтому в случае прямоугольной ямы бесконечной глубины должно выполняться (из-за ортогональности волновых
функций) правило

(8.9)

где квантовые числа n и относятся к электронным и дырочным квантовым ямам соответственно.

2. Матричные элементы между блоховскими функциями, соответствующие электрическим дипольным переходам и определенные уравнением (7), также должны быть отличны от нуля. Для квантовых ям в структурах AlGaAs/GaAs выражение (9), относящееся к огибающим функциям, на практике может рассматриваться как правило отбора.

На рис. 2 [7] представлен спектр поглощения множественных квантовых ям (MQW) в GaAs/AlAs при температуре 6 К, из которого следует, что поглощение растет с энергией фотонов и в общих чертах соответствует ступенчатой функции плотности состояний для двумерной электронной системы.

Кроме этого, на приведенном графике отчетливо выделяются экситонные пики в начале каждой «ступеньки». В двумерных системах энергия связи экситонов (как и связанное с ними поглощение) очень сильно возрастает вследствие пространственной локализации, в результате чего экситоны регистрируются гораздо легче, чем в трехмерных полупроводниках. Каждый пик на рис. 2 связан с дублетом спин-орбитального взаимодействия, соответствующим характеристикам валентных зон тяжелых и легких дырок в соединениях класса . На рис. 2 можно четко выделить переходы из состояний с числами п = 1, 2, 3 из зон тяжелых (НН) и легких дырок (LH) в электронные состояния.

Рис. 2.

Процесс излучения или поглощения фотонов для внутризонных переходов схематически показан на рис. 3, а. «Свободные» носители в зоне проводимости (или валентной зоне) занимают подзоны, соответствующие уровням каждого электрона (или дырки), расположенных в данной яме. Отметим, что межподзонные переходы происходят только между квантовыми состояниями внутри одной ямы. Дополнительно, межзонные переходы могут происходить между состояниями в квантовых ямах и протяженными электронными состояниями, как показано на рис. 3, б. Исходя из соображений типа предложенных выше для межзонных переходов, можно предложить еще одно правило отбора, связывающее состояния с противоположной четностью (поскольку в рассматриваемом случае матричные элементы должны включать в себя и координаты), что дает условие

(10)

Рис. 3.

В идеальном случае это правило отбора означает, что величина должна равняться нечетному числу, однако уже при интенсивность таких переходов настолько ослабевает, что их уже можно не учитывать формулой (10). Еще одно требование связано с тем, что направление вектора должно быть перпендикулярно к яме, т. е. свет должен быть поляризован вдоль z-направления. Практически это означает, что свет не должен падать вертикально (или, с другой стороны, на поверхности образца должна располагаться какая-либо дифракционная решетка). Оба условия предполагают некоторое ослабление интенсивности используемого светового потока, вследствие чего, естественно, следует стремиться к созданию и использованию MQW с большим числом ям (около сотни).

Изменения, вызываемые электрическим полем в оптических свойствах квантовых ям и сверхрешеток, весьма различаются по своей природе. В настоящее время исследования электрооптических эффектов в сверхрешетках связаны в основном с блоховскими осцилляциями и возможностью излучения в терагерцовом диапазоне. С другой стороны, некоторые оптические свойства сверхрешеток похожи на свойства квантовых ям. В отличие от множественных квантовых ям, сверхрешетки и их оптические особенности уже нашли некоторые интересные применения в оптике, вследствие чего сейчас исследователи проявляют все больший интерес к некоторым смежным вопросам материаловедения, например, к методам выращивания квантовых точек, созданию и «проектированию» материалов с требуемыми энергетическими зонами и т. д.

Из различий в оптических свойствах квантовых ям и сверхрешеток можно выделить следующие, представляющие практический интерес. В сверхрешетках край полосы поглощения сдвинут в голубую сторону спектра из-за расщепления уровней в мини-зоны. Кроме этого, все переходы являются размытыми, что объясняется отличием функции плотности состояний для сверхрешеток от соответствующей, ступенчатой функции для квантовых ям. Вследствие туннелирования электронов через барьеры волновая функция экситонов может простираться сразу на несколько ям внутри сверхрешетки с сильной связью. Таким образом, в сверхрешетках экситоны оказываются значительно менее локализованными и имеют меньшую энергию связи, чем в квантовых ямах. Слабые экситонные особенности проявляются также вблизи переходов из дна мини-зоны дырок в верхнюю часть мини-зоны электронов (экситоны «седловой» точки). На рис. 4 представлен спектр поглощения сверхрешетки в структурах AlGaAs/GaAs, напоминающий спектр для отдельной квантовой ямы. Поведение экситонов на рисунке показано переходами с п = 1, соответствующими переходам от тяжелых и легких дырок в первое электронное состояние.

На графике выделены пики и , относящиеся к упомянутым выше переходам вблизи так называемого седла точки.

Рис. 4.

2. Оптические характеристики квантовых точек и нанокристаллов

Начиная с 90-х годов прошлого века все большее внимание исследователей привлекают технологии так называемой самоорганизации квантовых точек, которые совместимы с существующими методами микроэлектроники и оптоэлектроники. Одна из таких технологий основана на модификации метода Странского - Крастанова , при котором материал выращивается послойно на подложке, с близкой постоянной решетки. При малой (до нескольких процентов) разнице в постоянных решетки сначала осуществляется послойное наращивание, но на некоторой стадии слои начинают расти островками, поскольку при этом минимизируется упругая энергия (режим Странского - Крастанова). При очень большей разнице постоянных решетки такой островковый рост начинается с самого начала процесса (режим Фольмера - Вебера).

Описанные три режима послойного выращивания кристаллических слоев на подложке представлены на рис. 5, где схематически показаны (а) послойный рост, (б) метод Странского - Крастанова и (в) метод Фольмера - Вебера. Наличие определенного режима роста связано не только с различием постоянных решетки подложки и кристалла, но и со значениями поверхностной энергии. Методом Странского - Крастанова выращиваются квантовые точки для лазеров в материалах типа InGaAs/GaAs, однако метод может применяться и в системах SiGe/Si или CdSe/ZnSe. Преимуществом этого метода перед известными литографическими методами является то, что он позволяет получать квантовые точки меньших размеров.

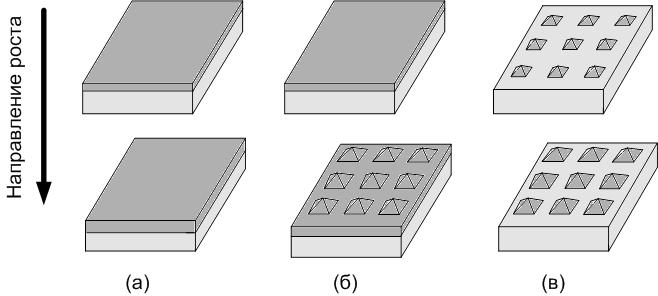
Рис. 5

В квантовых точках (иногда их называют квантовыми ящиками) потенциал ограничивает движение электронов во всех трех пространственных измерениях, естественно имеющих нанометрические размеры, в результате чего энергетические уровни образуют ряд дискретных связанных состояний, несколько напоминающих электронные уровни для изолированного атома. При этом пространственная локализация волновых функций электронов очень сильно влияет на оптические свойства вещества, поэтому мы начнем изложение с перечисления некоторых общих оптических свойств нульмерных ограниченных систем.

1. Уширение запрещенной зоны.

Одной из важнейших особенностей оптических свойств квантовых точек является уширение запрещенной (рис. 1, а). В зависимости от размера R квантовой точки (предполагаем, что она имеет просто сферическую форму) можно рассмотреть несколько ситуаций. Чтобы разделить эти ситуации, сравним радиус квантовой точки R с размерами экситонов, определяемыми соответствующим боровским радиусом :

(11)

где параметр означает приведенную массу экситона. В так называемом режиме «сильной локализации» (область значений ) энергия квантовой локализации превышает энергию кулоновского взаимодействия, вследствие чего можно пренебречь экситонными эффектами, связанными с взаимодействием электронов и дырок. При таком подходе мы можем рассматривать электроны и дырки, расположенные рядом в одних и тех же квантовых точках. Вышесказанное вытекает из того, что кулоновское взаимодействие обратно пропорционально величине R, в то время как ограничивающий потенциал ( энергия) возрастает обратно пропорционально квадрату R. Например, боровский радиус экситона в CdS составляет , вследствие чего все нанокристаллы с размерами меньше ведут себя как квантовые точки. Однако при значениях R, значительно меньших, чем , уже нельзя применять приближение эффективной массы, вследствие чего квантовая точка должна рассматриваться в качестве просто большой молекулы, которую мы должны описывать соответствующими молекулярными орбиталями.

В так называемом режиме «слабой локализации» () огибающие функции практически не изменяются, хотя кинети кинетическая энергия экситонов (связанная с движением центра масс) возрастает, вследствие чего должна уменьшаться энергия связи. Это наблюдается, например, в CdSe при размерах квантовых точек . В кристаллах галидов меди (CuCl, CuBr) размер экситонов настолько мал (~1 нм), что квантовые точки практически всегда существуют в режиме «слабого ограничения».

Наиболее трудными для теоретического описания являются, естественно, системы со средней или промежуточной степенью локализации, для которых мы не можем использовать предложенные выше упрощенные модели.

2. Повышение силы осцилляторов.

Из приведенных выше данных легко заметить некоторую общую закономерность, а именно по мере уменьшения размерности системы электронные состояния становятся все более «концентрированными» по энергии, что и отражают соответствующие функции плотности состояний. В предельном случае (при размерности ) квантовые точки ведут себя подобно атомам, обладающим хорошо выраженными энергетическими уровнями, в результате чего возрастают силы осцилляторов, соответствующих оптическим переходам. Это обстоятельство чрезвычайно важно для создания новых оптоэлектрических устройств, так как концентрация энергетических состояний может быть использована для повышения коэффициентов усиления лазерных устройств. Из тех же общих соображений, по мере уменьшения размерности систем, в них сильнее проявляются электрооптические эффекты, используемые для создания оптоэлектронных модуляторов на квантовых ямах.

3. Оптические переходы.

Выше отмечалось, что межподзонные оптические переходы в двумерных системах разрешены лишь тогда, когда свет распространяется в плоскости квантовой ямы, т. е. электрическое поле фотона направлено перпендикулярно поверхностям раздела. Напротив, квантовые точки способны поглощать падающий свет любого направления вследствие того, что локализация по всем трем оптическим осям означает, что и волновые функции электронов также квантуются по всем трем пространственным координатам.

4. Уширение спектров.

Еще одной важной особенностью оптических характеристик квантовых точек является отсутствие температурной зависимости для ширины спектральных линий, что объясняется просто тем, что в них нет непрерывных областей электронных состояний. Напротив, в одномерных и двумерных системах существуют одно и два направления для непрерывных -состояний соответственно. Разумеется, говоря о дискретности спектров квантовых точек, не следует считать, что они представляют собой совершенно правильные, теоретические -функции, так как некий реальный разброс по ширине линий (~10 мэВ) всегда существует из-за неоднородностей в распределении размеров квантовых точек. При очень высокой однородности размеров квантовых точек ширина линий может быть снижена и до значений < 10 мэВ, однако, с другой стороны, при большом разбросе значений ширина линий может возрасти до 0,1 эВ. Небольшие изменения состава также являются одной из причин уширения запрещенной зоны в системах квантовых точек. Другие причины связаны с примесями, поверхностными или межфазными состояниями и т. п.

Рассмотрев основные особенности оптических свойств квантовых точек (КТ), опишем и некоторые оптические свойства различных систем КТ.

1. Квантовые точки в полупроводниковых соединениях.

Далее приведем лишь некоторые примеры из огромного разнообразия результатов исследований спектров квантовых точек в полупроводниковых соединениях. Наиболее тщательно изучены квантовые точки в нанокристаллах соединений , поскольку именно такие полупроводники могут быть получены достаточно легко и имеют важные технологические применения. Во многих случаях соединения вводятся в качестве легирующих примесей в легированные стекла в процессе выращивания из расплавленной стеклянной массы (при этом обычно введение этих соединений осуществляется для регулирования цвета образующихся стекол за счет образующихся нанокристаллов). На рис. 6 приводятся спектры поглощения квантовых точек CdS () в стекле.

Обращает внимание «синий сдвиг» окраски, связанный с наноразмерными квантовыми эффектами. Используя смеси CdS с другими соединениями того же класса, например с CdSe (), можно покрыть практически весь видимый диапазон.

2. Самоорганизация квантовых точек.

Еще в 1995 г. [15] была обнаружена возможность образования трехмерных островковых структур при выращивании сверхрешеток InAs/GaAs. Было показано, что при наращивании нескольких монослоев (в среднем ~2,5) происходит образование квантовых точек из InAs, что может быть надежно зарегистрировано методами просвечивающей электронной микроскопии высокого разрешения.

Рис. 6.

Линейный спектр фотолюминесценции при этом оказался достаточно широким, благодаря размытости распределения точек по размерам, и пики фотолюминесценции были смещены в сторону меньших энергий из-за того, что точки имеют больший размер, чем периоды сверхрешеток. С этого же времени ученые стали интересоваться процессами создания квантовых точек для использования в лазерах на основе систем типа InGaAs/GaAs. На рис. 8 приведены спектры фотолюминесценции и электролюминесценции для квантовых точек InAs/GaAs, выращенных методами химического осаждения из газовой фазы с использованием металлоорганических соединений (MOCVD), похожими на те, которые используются для получения лазеров на квантовых точках.

При исследовании изолированных квантовых точек InAs/GaAs, удалось зарегистрировать несколько очень важных особенностей изучаемых систем: а) уширение спектральных линий не наблюдается вплоть до 70 К (это является доказательством того, что нанокристаллы, как отмечалось, имеют нулевую размерность); б) ширина отдельный линий не превышает 0,15 мэВ; в) спектроскопическое разрешение метода достаточно высоко, чтобы при относительно небольшом числе молекул в каждой точке (около 2000) регистрировать добавление или исключение даже отдельных молекул InAs.

Рис. 8.

3. Нанокристаллы полупроводников, обладающих запрещенной зоной с непрямыми оптическими переходами.

Начиная с открытия явления сильной люминесценции в кристаллах кремния, исследования кристаллических кластеров Si и пористого кремния представляют особый интерес. Этот интерес связан с тем, что, хотя из физики полупроводников считалось известным, что эффективность излучения света объемными полупроводниками, обладающими запрещенной зоной с непрямыми оптическими переходами, всегда является незначительной, ситуация резко меняется при использовании нанокристаллических образцов. Например, оказалось, что излучение нанокристаллов кремния лежит не в инфракрасном диапазоне (), а видимой области (), что объясняется именно уширением запрещенной зоны из-за квантовых эффектов. Кроме того, эксперименты показали связь эффекта «синего сдвига» линий с уменьшением размера кристаллов. Что касается эффективной люминесценции, то она может объясняться, как обычно, релаксацией закона сохранения волнового вектора (или сохранения момента ) в условиях низкоразмерной локализации.

Сильная люминесценция в видимом диапазоне особенно заметна для пористого кремния (ПК). Образующийся пористый слой формируется из нульмерных и одномерных наноразмерных кристаллов, а наблюдаемый при этом очень широкий спектр эмиссии объясняется квазигауссовским распределением нанокристаллов по размерам. Сначала считали, что наблюдаемое сильное излучение в видимой области связано с образованием разнообразных соединений, на поверхности нанокристаллов в процессе электролитического травления. К числу таких примесей, возникающих в процессе формирования пористого кремния, относили силоксен (Si603H6), гидриды, оксиды и оксигидриды кремния, однако, хотя в некоторых случаях такое объяснение полностью исключить нельзя, в настоящее время считается, что объяснение связано с учетом квантовых эффектов вследствие нанометровых размеров структур. Действительно, такая люминесценция наблюдалась и в пористом кремнии без поверхностных соединений, что неоднократно проверялось с использованием самых современных технологий анализа поверхности, структуры и состава пленок и т. п., таких, как оже-электронная спектроскопия и спектроскопия для химического анализа, спектрометрия резерфордовского обратного рассеяния, инфракрасной фурье-спектроскопии и т. д.

Квантовые эффекты, связанные с размерами структур, наблюдались и в других соединениях кремния, например, в сверхрешетках и квантовых ямах на основе SiGe. Повышенный интерес к гетероструктурам в SiGe объясняется их успешным применением в производстве биполярных транзисторов на гетероструктурах. Были созданы напряженные гетероструктуры в SiGe, использующие различие ширины запрещенной зоны (1,1 эВ в кремнии и 0,74 эВ в германии соответственно), а также соединения SiGe с промежуточными значениями ширины запрещенной зоны.

Интенсивная люминесценция, наблюдаемая в нанокристаллах кремния и сверхрешетках состава кремний - германий, может быть объяснена на основе принципа неопределенности Гейзенберга или концепции расщепления зон Бриллюэна. Предположим, например, что размеры всех нанокристаллов Si в системе не превышают 30 нм. В этой ситуации распределение носителей заряда по импульсам имеет вид, показанный на рис. 10, а, что приводит к повышению вероятности прямых переходов.

В сверхрешетках SiGe мини-зоны и запрещенные мини-зоны формируются на энергетический диаграмме вблизи значения k = 0 (как показано на рис.10, б и объяснено в разделе 5.5), в результате чего сверхрешетки должны вести себя подобно полупроводникам с квазипрямыми оптическими переходами, причем вероятность оптических переходов при этом является достаточно высокой.

3. Электрооптические эффекты в квантовых точках. Квантово-размерный эффект Штарка.

Выше было показано, что внешнее электрическое поле может существенно изменять оптические характеристики рассматриваемых материалов. Такие изменения получили название электрооптических эффектов, и они могут влиять как на величину коэффициента преломления (эффект электропреломления), так и коэффициента поглощения (эффект электропоглощения). Если энергия фотонов не превышает ширины запрещенной зоны, то основным фактором является электропреломление, так как поглощением в этом случае можно пренебречь из-за его малости.

Электрооптические эффекты широко используются во многих оптоэлектронных устройствах для управления светом с помощью внешних электронных схем. Такие устройства являются промежуточными и могут быть отнесены одновременно и к фотонике, и к микроэлектронике.

Вследствие квантовой локализации электронов, высокой энергии связи экситонов и возможности «подгонки» характеристик запрещенной зоны многие полупроводниковые квантовые ямы (и вообще полупроводниковые наноструктуры) часто обладают очень интересными электрооптическими свойствами.

Рис. 10.

Например, перпендикулярное к плоскости ямы электрическое поле, позволяет уменьшить энергию края полосы поглощения («красный сдвиг») и повысить коэффициент преломления материала ниже этого края. В окрестности границ запрещенной зоны эти изменения становятся существенными и очень сильно зависят от энергии фотонов.

Простейшим вариантом регулирования интенсивности светового луча является использование электропоглощения. Из физики твердого тела известно, что внешнее электрическое поле, приложенное к трехмерному образцу полупроводника, уменьшает энергию края поглощения и создает колебания при энергиях выше ширины запрещенной зоны (эффект Франца - Келдыша). Таким образом, для фотонов с энергией чуть ниже края поглощения полупроводник является «прозрачным» в отсутствие внешнего поля, но поглощающим при наложении поля. В объемных полупроводниках этот эффект проявляется слишком слабо для практического использования, однако в квантовых точках пространственная локализация приводит к новым эффектам электропоглощения, намного более сильным, чем в объемных материалах, что позволяет на основе структур с квантовыми ямами создать оптические модуляторы на эффекте электропоглощения. В тех случаях, когда вектор электрического поля параллелен плоскости квантовой ямы, ситуация очень похожа на случай обычного трехмерного полупроводника, поскольку электроны могут свободно двигать в этом направлении, вследствие чего электрооптический эффект напоминает эффект Франца - Келдыша и, подобно последнему, не представляет практического интереса. Значительно более интересная ситуация возникает в системах, где электрическое поле приложено перпендикулярно слоям, когда возникающий эффект подобен эффекту Штарка в атомах (сдвиг энергетических уровней электронов под воздействием поля), вследствие чего это явление называют квантоворазмерным эффектом Штарка (QCSE).

На рис. 11 показаны диаграммы энергетических зон для квантовой ямы до и после наложения постоянного внешнего поля , направленного перпендикулярно слоям структуры [4].

Связанная с таким полем потенциальная электростатическая энергия для электронов «накладывается» на потенциал внутри кристаллического поля, определяемый профилем минимума зоны проводимости.

Рис. 11.

Вследствие этого профиль наклоняется под действием внешнего поля (как показано на рисунке), похожие явления происходят и для дырок. Следствием такого воздействия становится сильная деформация волновых функций электронных состояний и понижение энергии локализации носителей заряда. Понятно, что волновые функции частиц с отрицательным и положительным зарядом (электронов и дырок соответственно) деформируются разным образом: волновые функции электронов смещаются против направления поля, а дырок - в обратном направлении. Понижение энергии квантовой локализации для электронов гетероструктурах и дырок приводит к сдвигу края полосы поглощения квантовых ям в сторону более низких энергий («красный сдвиг»).

На рис. 12 показаны спектры поглощения слоя квантовых ям (толщиной 9,4 нм) в GaAs при различных значениях внешнего электрического поля, направленного перпендикулярно слою.

Рис. 12.

Можно отметить сразу, что, в отличие от объемных кристаллов, экситонные эффекты в слое проявляются при напряженностях поля вплоть до 100 кВ/см. Объяснение этого факта основано на том, что в рассматриваемой системе не происходит ионизация экситонов, так как потенциал ям удерживает электроны и дырки на расстоянии, меньшем толщины слоя. На рисунке показан также «красный сдвиг» границы зоны поглощения и экситонного пика. Для проведения простого расчета мы можем рассмотреть прямоугольную квантовую яму с бесконечным барьером и шириной .

При умеренных значениях напряженности внешнего поля из уравнения Шрёдингера можно легко получить аналитическое выражение для штарковского сдвига , рассматривая прикладываемый потенциал как возмущение второго порядка.

Для основного уровня сдвиг равен

, (12)

где - эффективная масса в направлении перпендикулярном слоям; е — заряд электрона. Отметим, что из уравнения следует очень сильная зависимость величины сдвига от ширины ямы (четвертая степень) и его квадратичная зависимость от напряженности электрического поля, при этом, естественно, не зависит от знака электрического поля (хотя необходимо отметить, что это утверждение справедливо лишь для квантовых ям симметричной формы). Кроме этого, благодаря линейной зависимости от эффективной массы величина сдвига для тяжелых дырок оказывается значительно большей, чем для уровней электронов и легких дырок. Результатом такого воздействия становится то, что вызываемое электрическим полем уменьшение ширины запрещенной зоны квантовой ямы оказывается связанным, главным образом, с вкладом тяжелых дырок. На рис. 13 показана зависимость штарковского сдвига от напряженности приложенного поля для квантовых ям различной ширины в GaAs.

Рис. 13.

Например, для квантовой ямы толщиной в уравнение (12) предсказывает для уровней тяжелых дырок и электронов сдвиги -10 и -2 мэВ соответственно. Методы численного расчета, позволяющие учитывать конечную высоту барьеров и отличие эффективной массы в барьерах, приводят к значениям сдвига -15 и -6 мэВ соответственно. Для фотонов с энергией чуть меньше энергии запрещенной зоны в отсутствие поля можно считать, что яма является прозрачной, однако поглощение света резко повышается с ростом напряженности поля.

Обобщая сказанное, можно отметить, что квантовые ямы представляют большой интерес для прямой модуляции интенсивности пропускаемого света, так как при этом эффективность модуляции оказывается значительно выше, чем в приборах, основанных на объемных полупроводниковых или других электрооптических материалах, применяемых в настоящее время (типа ниобата лития и т. п.).

4. Электрооптические эффекты в сверхрешетках. Лестницы Штарка и осцилляции Блоха

В связанных квантовых ямах приложенное электрическое поле очень сильно влияет на взаимодействие между ямами. Прежде всего, это связано с тем, что электростатическая энергия электронов, находящихся в однородном электрическом поле, линейно растет с расстоянием, что приводит к сдвигу энергетических уровней в соседних ямах на величину, равную , где d расстояние между ямами. Резонанс между двумя такими состояниями в грубом приближении должен быть обратно пропорционален разнице энергий уровней, вследствие чего изменение напряженности поля должно позволять легко осуществлять «подгонку» между состояниями в различных ямах.

При слабой связи между ямами электронное состояние локализуется внутри ямы, так что оптические переходы между электронными и дырочными состояниями внутри одной квантовой ямы могут называться переходами внутри ямы, а переходы между состояниями разным ям - переходами между ямами (рис. 14).

Электрооптические эффекты для переходов внутри ямы во многом напоминают переходы для изолированных квантовых ям. Более сложной выглядит ситуация в случае переходов между ямами, для которых внешнее электрическое поле, как отмечалось, создает сдвиг по энергиям , знак которого определяется направлением поля. Если оно совпадает с направлением от электронных состояний к дырочным, то при переходах должно наблюдаться красное смещение. Кроме того, с ростом напряженности приложенного поля интенсивность переходов внутри ям уменьшается и они постепенно перестают проявляться вообще.

Рис. 14

Использование линейного сдвига в связанных квантовых ямах предлагает богатые возможности «подгонки» переходов при достаточно умеренных значениях внешнего поля [4].

В сверхрешетках наиболее интенсивный экситонный пик соответствует переходу с вершины дырочной мини-зоны на дно электронной мини-зоны, как показано на рис. 15, а. В электрическом поле, направленном нормально к слоям, связь между квантовыми ямами ослабляется, вследствие чего сами мини-зоны расщепляются на ряд эквидистантно расположенных энергетических уровней (расстояние между уровнями при этом составляет , где d - период сверхрешетки). Образующаяся система уровней получила название лестницы Штарка, каждый уровень которой соответствует электронным состояниям, локализованным вблизи разных квантовых ям (рис. 15, б).

Уже при значениях напряженности поля порядка (где и - ширина мини-зоны и постоянная сверхрешетки соответственно) состояния лестницы Штарка становятся полностью локализованными в соответствующей квантовой яме (см. рис. 15, в).

Такой эффект трудно уловить в объемных кристаллах, поскольку ширина зоны в них обычно составляет несколько эВ, вследствие чего для проявления описываемой локализации необходимо воздействовать на кристаллы очень мощными электрическими полями. В сверхрешетках ширина зоны намного меньше, в результате чего эффекты наблюдаются при значительно меньших значениях напряженности поля.

Рис. 15.

Например, в типичной сверхрешетке () на основе ширина электронной мини-зоны составляет лишь около 65 мэВ, так что штарковская локализация состояний достигается при напряженности поля около 115 кВ/см. Ширина мини-зоны тяжелых дырок еще меньше и составляет всего 6 мэВ, так что локализация состояний тяжелых дырок достигается уже при полях порядка 10 кВ/см.

Приведенный спектр поглощения сверхрешетки, как и некоторые другие спектры систем этого типа (например, показанный на рис. 16 спектр фототока, отражает очевидный эффект локализации состояний, вызываемых внешним электрическим полем.

В отсутствие электрического поля на таких спектрах наблюдается один экситонный переход (как отмечалось выше, с вершины дырочной мини-зоны на дно электронной мини-зоны), что соответствует переходам между делокализованными состояниями, как показано на рис. 15, а. В умеренных электрических полях, как показано на рис. 15, б, спектр расщепляется на серию пиков, соответствующих переходам между ямами между различными состояниями лестницы Штарка (рис. 17).Затем, когда напряженность поля достигает значений, при которых происходит локализация Штарка (рис. 15, в), переходы между ямами исчезают, и остается лишь пик, соответствующий переходу внутри ямы.

Рис. 16.

Поскольку уровень этой единственной ямы располагается близко к центру мини-зоны, на краю зоны поглощения сверхрешетки при переходе к полям высокой напряженности наблюдается «синий сдвиг» (от нулевого значения). Такой «синий сдвиг» (резко отличающийся от обычного красного, наблюдаемого для достаточно толстых одиночных ям) равен примерно половине ширины электронной мини-зоны, что уже позволяет создавать на этой основе некоторые электрооптические приборы.

В предыдущем разделе мы рассматривали только статические режимы поведения электронов в условиях существования лестницы Штарка. Однако динамических характеристики также представляют большой интерес для исследований, так как их использование позволяет создавать очень быстрые электромагнитные излучатели, получившие название осцилляторов Блоха.

Излучение с терагерцовой частотой в таких устройствах было впервые зарегистрировано в 1993 г., однако оно было предсказано Эсаки в 1970 году. Рассмотрим эффект воздействия приложенного постоянного электрического поля на электронные состояния в сверхрешетках, как показано на рис. 18.

Рис. 1

Рис. 18.

В отсутствие электрического поля состояния квантовых ям являются полностью связанными, так что электронные состояния в сверхрешетках имеют бесконечную протяженность, а энергетические уровни образуют непрерывный спектр между потолком и дном минизон, как показано на рис. 18, а. В электрическом поле конечной напряженности связь между ямами ослабевает, а сами мини-зоны расщепляются, образуя описанную выше лестницу Штарка для уровней (рис. 18, б).

Пространственную протяженность возникающих состояний можно оценить, рассматривая наличие мини-зон в качестве удобного приближения. Краевые значения таких мини-зон должны «изгибаться» в электрическом поле (из-за наличия в выражении для потенциальной энергии электростатического взаимодействия члена ). В квазиклассическом приближении можно считать, что кинетическая энергия электрона может лежать только в диапазоне энергий мини-зоны, что сразу определяет пространственные ограничения области расположения энергетических уровней данного электрона. Границы этой области определяются теми значениями z, при которых уровни пересекаются с границами мини-зоны. Расстояние между двумя такими точками пересечения равно

(13)

В отсутствие рассеяния любой электронный волновой пакет должен осциллировать от одного конца промежутка до другого. По аналогии с классической задачей о гармоническом осцилляторе частота таких колебаний определяется расстоянием между уровнями, т. е. величиной

где d - период сверхрешетки. Угловая частота при этом называется частотой Блоха, а ее значения могут достигать терагерцового диапазона. Сам факт существования блоховских осцилляции в полупроводниковых сверхрешетках уже подтвержден различными оптическими измерениями.

В заключении отметим, что осцилляции Блоха в сверхрешетках позволяют генерировать микроволновое излучение под воздействием электрического поля. Излучение при этом создается переходами между уровнями, которыми образуют лестницу Штарка. Частота такого излучения лежит в области 1 ТГц, что практически недоступно для существующих полупроводниковых источников микроволнового излучения.

Литература

Национальный исследовательский ядерный ун-т "МИФИ" ; отв. ред. В.В. Шуренков: Всероссийский конкурс научно-исследовательских работ студентов в области нанотехнологий и наноматериалов. - М.: НИЯУ МИФИ, 2009

НИУ БелГУ ; гл. ред. Дятченко: Научные ведомости Белгородского государственного университета. - Белгород: НИУ БелГУ, 2009

НИУ БелГУ ; гл. ред. Л.Я. Дятченко: Научные ведомости Белгородского государственного университета. - Белгород: НИУ БелГУ, 2009

Новиков И.И.: Термодинамика. - СПб.: Лань, 2009

О.С. Габриелян Э.В. Дюльдина, С.П. Клочковский и др. ; Рец.: Каф. общей и теоретической физики Южно-Уральского государственного ун-та и др.: Концепции современного естествознания. - М.: Дрофа, 2009

Олемской А.И.: Синергетика сложных систем. - М.: КРАСАНД, 2009

Пер. с англ. В.А. Осотовой ; Под науч. ред.: Д.В. Тураева, А.Л. Шильникова: Методы качественной теории в нелинейной динамике. - М. ; Ижевск: НИЦ "Регулярная и хаотическая динамика", 2009

под ред. В.Ф. Антонова ; рец.: Ю.А. Владимиров, А.Я. Потапенко: Физика и биофизика. - М.: ГЭОТАР-Медиа, 2009

Под ред.: А.А. Короновского, Д.И. Трубецкова, А.Е. Храмова: Методы нелинейной динамики и теории хаоса в задачах электроники сверхвысоких частот. - М.: ФИЗМАТЛИТ, 2009

Под ред.: А.А. Кураева, Д.И. Трубецкого ; А.В. Аксенчик и др.: Методы нелинейной динамики и теории хаоса в задачах электроники сверхвысоких частот. - М.: ФИЗМАТЛИТ, 2009

Под ред.: Ц.Фукуды, П.Рудольфа, С. Уды ; Пер. с англ. под ред. Б.В. Шульгина: Выращивание кристалловолокон из расплава. - М.: ФИЗМАТЛИТ, 2009

Райзер Ю.П.: Физика газового разряда. - Долгопрудный: Интеллект, 2009

РАН, Институт истории естествознания и техники им. С.И. Вавилова ; отв. ред. Г.М. Идлис ; ред.-сост. Н.В. Вдовиченко ; рец.: Б.М. Болотовский, Ю.С. Владимиров: Исследования по истории физики и механики. 2008. - М.: Физматлит, 2009

РАН, Мин-во образования и науки РФ, Новосибирский гос. ун-т ; отв. ред. Г.В. Поляков: Модельный анализ развития континентальных мантийно-коровых рудообразующих сиситем. - Новосибирск: СО РАН, 2009

Риле Ф.: Стандарты частоты. Принципы и приложения. - М.: ФИЗМАТЛИТ, 2009

Российский фонд фундаментальных исследований ; Под ред. А.М. Желтикова: Сборник научно-популярных статей - победителей конкурса РФФИ 2008 года. - М.: Октопус : Природа, 2009

Симаков Г.: Об унитарной физике. - Ростов н/Д: [Б.И.], 2009

Сковорода А.А.: Магнитные ловушки для удержания плазмы. - М.: ФИЗМАТЛИТ, 2009

Смалюк В.В.: Диагностика пучков заряженных частиц в ускорителях. - Новосибирск: Параллель, 2009

Степанов Е.В.: Диодная лазерная спектроскопия и анализ молекул-биомаркеров. - М.: ФИЗМАТЛИТ, 2009

Сычев В.В.: Сложные термодинамические системы. - М.: МЭИ, 2009

Тарасов Л.В.: Основы квантовой механики. - М.: ЛИБРОКОМ, 2009

Тимофеев А.В.: Резонансные явления в колебаниях плазмы. - М.: ФИЗМАТЛИТ, 2009

ОПТИЧЕСКИЕ И ЭЛЕКТРООПТИЧЕСКИЕ ПРОЦЕССЫ В КВАНТОВЫХ ГЕТЕРОСТРУКТУРАХ