Численное моделирование и экспериментальное исследование средней контактной температуры при плоском шлифовани

Ульяновский государственный технический университет

Кафедра «Технология машиностроения»

Лаборатория Студент

технологии Группа ТМмд-11

машиностроения Дата

ОТЧЕТ

о выполнении лабораторной работы №4

«Численное моделирование и экспериментальное исследование средней контактной температуры при плоском шлифовании»

по дисциплине

«Методы моделирования физических и тепловых процессов механической обработки материалов»

Задание:t = 0,01 … 0,03мм и Vsпр= 10 м/мин.

Работу выполнил: Работу принял:

1. Цель работы.

Получение практических навыков численного моделирования и экспериментального исследования средних контактных температур при различных режимахплоского шлифования.

2. Математические модели и зависимости для расчета

контактных температур

В процессе шлифования материал заготовки диспергируется отдельными (единичными) абразивными зернами (АЗ), расположенными стохастически на рабочей поверхности шлифовального круга (ШК). В результате работы единичных АЗ выделяется теплота. Температуры на поверхностях контакта зерен со стружкой и заготовкой называют локальными. Локальные температуры влияют на изнашивание, затупление и засаливание АЗ, а следовательно, на работоспособность ШК, качество поверхностного слоя материала обработанной детали и производительность процесса шлифования. При схематизации процесса теплообмена, с целью расчета локальных температур принимают во внимание источники теплоты от отдельных зерен ШК (дискретные источники тепловыделения).

При расчете средней контактной температуры в зоне шлифования принимают во внимание суммарное тепловыделение от всех зерен круга, контактирующих в данный момент времени с заготовкой. Схематизируя участвующие в теплообмене объекты, ШК рассматривают как сплошное гетерогенное тело с эквивалентными теплофизическими характеристиками, а источник тепловыделения рассматривают как сплошной. Средние контактные температуры учитывают, в частности, при оценке термоустойчивости связки круга и термических деформаций заготовки.

При решении теплофизических задач зону контакта «шлифовальный круг – заготовка» представляют в виде полосового источника теплоты, перемещающегося по поверхности заготовки.

Для расчета средней контактной температуры в зоне шлифования можно воспользоваться зависимостью, предложенной В. И. Пилинским:

где q – плотность теплового потока в зоне контакта круг – заготовка, Вт/м2; к – длина контакта круга с заготовкой, м; з – коэффициент, характеризующий относительное распределение теплоты между контактирующими при шлифовании объектами (кругом, заготовкой и стружкой) и долю теплоты, поступающей в заготовку; – плотность материала заготовки, кг/м3 ; с – удельная теплоемкость материала заготовки, Дж/(кг·К); а – коэффициент температуропроводности материала заготовки, м2 /с; Vsпр– скорость подачи (заготовки), м/с.

Длина контакта ШК с заготовкой при плоском шлифовании

гдеDк – диаметр круга, м; t – глубина шлифования, м.

Согласно исследованиям Д. Г. Евсеева и А. Н. Сальникова , доля теплового потока, поступающего в заготовку

гдек, – коэффициенты теплопроводности ШК и заготовки соответственно, Вт/(м·К); hф – средний радиус площадки контакта единичного АЗ с заготовкой, м.

Коэффициент, характеризующий относительное распределение теплоты (рис.1), зависит от полуширины теплового источника, которую в случае плоского шлифования можноопределить по следующей зависимости:

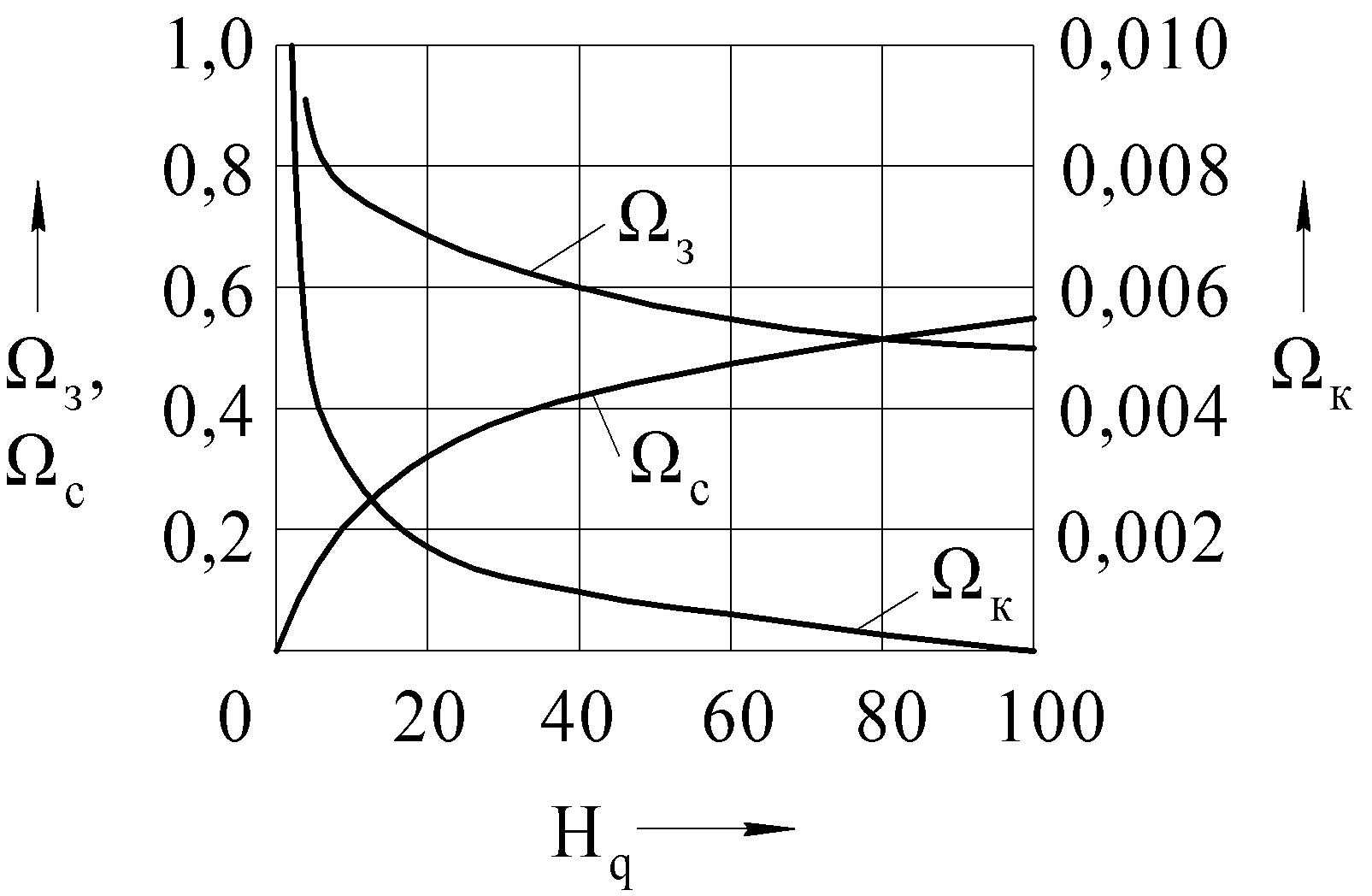
Рис. 1. Распределение тепловых потоков между заготовкой (з), стружкой (с)

и ШК (к) при шлифовании

Учитывая, что часть теплового потока из зоны обработки переходит в СОЖ, можно использовать следующую зависимость для расчета плотности теплового потока в зоне контакта:

гдеPz– касательная составляющая силы шлифования, Н; Vк – рабочая скорость ШК, м/с; Нз– высота круга (размер обрабатываемой поверхности заготовки), м; ФСОЖ – тепловой поток, переходящий в СОЖ (Вт):

гдесж– удельная теплоемкость СОЖ, Дж/(кг·К); x – массовое паросодержание двухфазного потока (СОЖ – пар) на выходе из зоны шлифования; r– удельная теплота парообразования СОЖ, Дж/кг; Тн– температура насыщения СОЖ, К; G1ф – массовый расход СОЖ через зону контакта круга с заготовкой, кг/с.

Для гомогенного стационарного потока с равными скоростями фаз x равно массовому расходу пара, деленному на массовый расход обеих фаз паровоздушной смеси (в случае, когда жидкость полностью испаряется в зоне шлифования, x= 1; если испарение отсутствует, x= 0).

При подаче СОЖ поливом с учетом фазовых превращений:

где ж и жn – плотность СОЖ и ее паров соответственно, кг/м3; n– координата области фазового перехода, м; ж и жп – динамическая вязкость СОЖ и ее паров соответственно, Па·с; G1 – массовый расход СОЖ через зону контакта при отсутствии фазовых превращений, кг/с:

гдеh0 – средняя толщина слоя СОЖ в зоне контакта ШК с заготовкой, м: h0 = 0,125·d0 ; р0 и р01 – давление СОЖ на входе и выходе из контактной зоны, Па; d0 – средневероятный размер АЗ круга, м.

3. Практическая часть.

Исходные данные:

рабочая скорость ШК – 30 м/с; t = 0,01…0,03мм; Vsпр= 10 м/мин;

ШК из электрокорунда белого или нормального зернистости 16 … 40 твердостью СМ1 … СТ1, структуры 6 … 8 на керамической связке;заготовки, имеющие форму прямоугольного параллелепипеда, из конструкционной стали в состоянии поставки;

Решение:

1) При t = 0,01 мм.

Рассчитываемсреднюю толщину слоя СОЖ в зоне контакта ШК с заготовкой h0 = 0,125·d0=0,125

Рассчитываем длину контакта ШК с заготовкой

Определяем массовый расход СОЖ G1 при отсутствии фазовых превращений

Рассчитывают расход СОЖ G1ф с учетом фазовых превращений

Определяют тепловой поток, переходящий в СОЖ

Доля теплового потока, поступающего в заготовку:

= .

Средняя контактная температура в зоне шлифования :

2) При t = 0,02 мм.

Рассчитываем длину контакта ШК с заготовкой

Средняя контактная температура в зоне шлифования :

3) При t = 0,03 мм.

Рассчитываем длину контакта ШК с заготовкой

Средняя контактная температура в зоне шлифования :

По результатам построим график зависимости температуры от t.

Рис. 1. График зависимости средней контактной температуры шлифования от глубины шлифования при Vsпр= 10 м/мин

Вывод: как видно из графика существует прямая связь между температурой и глубиной шлифования. Чем больше глубина, тем больше температура.

Библиографический список

6.1. Евсеев, Д. Г. Физические основы процесса шлифования / Д. Г. Евсеев, А. Н. Сальников. – Саратов : Изд-во Сарат. ун-та, 1978. – 128 с.

6.2. Унянин, А. Н. Повышение эффективности совмещенного шлифования путем рационального применения технологических жидкостей: Дис. … канд. техн. наук: 05.02.08 / Ульян. политехн. ин-т. – Ульяновск, 1986. – 229 с.

6.3. Худобин, Л. В. Минимизация засаливания шлифовальных кругов / Л. В. Худобин, А. Н. Унянин. – Ульяновск :УлГТУ, 2007. – 298 с.

6.4. Марочник сталей и сплавов / А. С. Зубченко, М. М. Колосков, Ю. В. Каширский [и др.]; под общ. ред. А. С. Зубченко. – 2-е изд., доп. и испр. – М. : Машиностроение, 2003. – 784 с.

6.5. Чередниченко, Г. И. Физико-химические и теплофизические свойства смазочных материалов / Г. И. Чередниченко, Г. Б. Фройштетер, М. П. Ступак. – Л. : Химия, 1986. – 224 с.

Численное моделирование и экспериментальное исследование средней контактной температуры при плоском шлифовани