ЛЕМА БЕРНСАЙДА. ЗАДАЧА ПРО НАМИСТА
Вінницький державний педагогічний університет
імені Михайла Коцюбинського
Інститут математики, фізики і технологічної освіти
Кафедра математики і методики навчання математики
Курсова робота на тему:
ЛЕМА БЕРНСАЙДА. ЗАДАЧА ПРО НАМИСТА
Виконав роботу:
Кузема Олександр Олександрович
Студент 3-го курсу
Спеціальності «Математика»
Науковий керівник:
канд. фізико-математичних наук
Панасенко Олексій Борисович
Вінниця 2015
Зміст
Вступ…………………………………………………………………………………3
- Хто ж все таки автор?....................................................................................4
- Група………………………………………………………………………….6
- Твірна функція……………………………………………………………….10
- Циклові індекси групи підстановок………………………………………..11
- Дії групи на множині……………………………………………………….13
- Лема Бернсайда (Коші-Фробеніуса)………………………………………15
- Теорема Рефілдера-Пойа…………………………………………………..17
- Задача про намиста…………………………………………………………21
- Приклади розв’язання комбінаторних задач за допомогою леми Бернсайда……………………………………………………………………22
Висновки…………………………………………………………………………..27
Список використаної літератури………………………………………………….28
Вступ
У житті сучасного суспільства дуже важливу роль відіграє математика. Сьогодні математика знаходить широке застосування при вирішенні найрізноманітніших проблем науки. Однією з найважливіших областей сучасної математики є абстрактна алгебра, в центрі уваги якої знаходяться різні алгебраїчні структури, такі, як групи, підгрупи, напівгрупи, кільця тощо. Одним з фундаментальних розділів сучасної алгебри є теорія груп. Групи, по суті, є один з основних типів алгебраїчних структур. Знадобилася робота кількох поколінь математиків, що зайняла в цілому близько ста років, перш ніж ідея групи викристалізувалася з її сьогоднішньої ясністю.
Теорія груп почала формуватись в якості самостійного розділу математики наприкінці XVIII століття. Протягом перших десятиліть XIX століття вона розвивалася повільно і практично не привертала до себе уваги. Але потім, близько 1830 року, завдяки роботам Е.Галуа і Н.Абеля всього за кілька років вона зробила гігантський стрибок, який зробив глибокий вплив на розвиток всієї математики. З тих пір основні поняття теорії груп стали детально досліджуватися. В даний час теорія груп є однією з найбільш розвинених областей алгебри, що має численні застосування, в тому числі і у інших галузях математики.
Так, теорія груп використовується при розв'язуванні задач комбінаторного характеру. Ця робота і присвячена таким застосуванням теорії груп, зокрема в роботі розглядається відома комбінаторна задача про намиста з узагальненнями.
Найбільший внесок в розв’язанні даної задачі здійснив Вільям Бернсайд завдяки власному твердженню про кількість орбіт в підгрупі симетричної групи, яка зараз відома як лема Бернсайда. Хоча чимало сучасних дослідників схиляються до думки, що він не єдиний автор даної леми.
- Хто все ж таки автор?
Вільям Бернсайд, англ. William Burnside, (1852-1927 рр.) англійський математик-алгебраїст. Член Лондонського Королівського товариства, професор Морського коледжу в Гринвічі. Відомий своїми працями з теорії груп, теорії представлень і характерів груп, вказав критерій розв`язності кінцевих груп. Йому належить також ряд робіт з теорії ймовірності, з аморфними функціями, з теорії хвиль в рідинах та інших.
Центральною частиною роботи Бернсайда була робота в області теорії представлень, де він міг розробити фундамент теорії, доповнюючи і інколи змагаючись з роботою Фробеніуса, який почав працювати в цій області в 1890-х роках. Одна із найвідоміших вкладів в теорію груп – це теорема Бернсайда про те, що кожна кінцева група, порядок яких ділиться менше ніж на три різних простих числа, розв’язна.
У 1897 році була опублікована класична робота Бернсайда «Теорія груп кінцевого порядку», де була опублікована славнозвісна лема. Друге видання (видане в 1911 році) стало стандартом в цій області на багото десятиліть. Головною відмінністю другого видання було включення в неї теорії характерів.
Бернсайд також відомий формулюванням проблеми, що носить його назву: «Чи буде конічною породжена група, в якій кожний елемент має кінчевий порядок, обов’язково кінцевий?».
Проте історики математики знайшли, що він був не перший, хто її відкрив світу: відомому французькому математику Огюстену Луї Коші в 1845 році була відома дана лема.
Огюстен Луї Коші фр. Augustin Louis Cauchy ( 21 серпня 1789 - 23 травня 1857) — французький математик, член Паризької академії наук (1816), Петербурзької академії наук (1831), Лондонського Королівського Товариства.
Автор 800 робіт з арифметики, теорії чисел, алгебри, математичного аналізу, диференціальних рівнянь, і т.д.
Особливо велике значення мають результати, отримані Коші: геометричне представлення комплексної змінної як точки, яка переміщається в площині тим чи іншим шляхом інтегрування (цю думку ще раніш висловили К. Гаус і ін.); вираження аналітичної функції у вигляді інтеграла (інтеграл Коші), та розклад функції в степеневий ряд; розробка теорії лишків і її застосування до різних питань аналізу.
Знайома була вона і Фердинанду Фробеніусу в 1887 році.
Фердинанд Георг Фробеніус нім. Ferdinand Georg Frobenius; (26 жовтня 1849 - 3 серпня 1917) — німецький математик-алгебраїст.
Основні роботи Фробеніуса стосуються теорії груп, зокрема, до теорії представлень.
Він першим довів, що асоціативне, дистрибутивне множення можливе тільки в просторах розмірності один (дійсні числа), два (комплексні числа) і чотири (кватерніони).
Напевно, лема була дуже відома, тому Бернсайд просто-на-просто опустив у своїй книзі імена авторів. У зв’язку з цим, в літературі можна зустріти інші назви цієї леми, наприклад, лема Коші-Фробеніуса або лема Коші-Фробеніус-Бернсайда.
- Група
Поняття множини є одним з найважливіших, фундаментальних понять сучасної математики. Це поняття є первісним. Вона не визначається, а роз’яснюється на конкретних прикладах. Так само як поняття точки і прямої в геометрії. Синонімами слова «множина» можна вважати такі слова, як сукупність, система, клас, збірка, тощо. Говорячи про множину, ми завжди будемо розуміти під цим поняттям певну сукупність деяких об’єктів, розглядаючи її як єдине ціле. Об’єкти, з яких складається множина, називаються елементами цієї множини.
Фундаментальним поняттям для леми Бернсайда є також поняття групи.
Означення 1. Множину називають групою, якщо справджуються такі висловлювання:
1. Задано закон множення (композиції), який впорядкованій парі елементів ставить у відповідність добуток — елемент , який називають добутком на a зліва або добутком a на справа.
2. Справджується сполучний закон множення:
3. Існує ліва одиниця множення (нейтральний елемент) групи, тобто такий елемент групи, множення на який зліва не змінює жоден елемент групи:.
4. Для довільного елемента а групи існує лівий обернений до нього, тобто такий, при якому добуток оберненого елемента на сам елемент дорівнює лівій одиниці множення: .
Групу називають комутативною (абелевою), якщо множення комутативне, тобто добуток не залежить від порядку співмножників: .
Закон асоціативності множення формулюють ще й так: добуток не зале- жить від порядку виконання дії множення (не плутати з порядком співмнож- ників). Саме у такій редакції його потрібно поширити на більшу кількість співмножників, розуміючи добуток як, наприклад, результат виконання дії множення у порядку запису зліва направо: . Множина взаємно однозначних відображень довільної множини в себе є групою щодо суперпозиції, тобто послідовного застосування відображень.
Теорема 1. Для довільної групи справджуються такі висловлювання.
1. Лівий обернений елемент є також правим оберненим елементом, який для кожного елемента групи єдиний: .
2. Ліва одиниця є також правою одиницею, тобто множення на неї справа не змінює жоден елемент групи:.
3. Одиниця множення у групі єдина.
Доведення.
Помножимо зліва рівність на елемент, обернений до і використаємо асоціативність множення. В результаті отримаємо: , тобто лівий обернений елемент є також правим оберненим;
, тобто кожна ліва одиниця є одночасно правою одиницею; • помноживши зліва і справа довільний елемент a групи на його обернені і та по-різному розставляючи дужки, тобто використовуючи асоціативність множення, легко пересвідчитися, що обернений елемент єдиний:;
Обчислюючи добуток (одночасно лівих і правих) одиниць групи, легко пересвідчитися, що одиниця групи єдина:.
Означення 2. Введемо такі поняття:
- Не порожню підмножину групи називають підгрупою групи , якщо:
- добуток двох елементів також належить до;
- елемент, обернений до елемента з також належить до.
2. Нехай — підгрупа групи . Правим класом групи за підгрупою називають множину вигляду де — довільний елемент групи G (аналогічно означають лівий клас суміжності).
3. Підстановкою (перестановкою) називають взаємно однозначне відображення скінченої множини у себе. Не обмежуючи загальності міркувань, надалі будемо розглядати лише множини вигляду — множини всіх перших натуральних чисел.
4. Транспозицією називають підстановку, яка кожному елементу, за виключенням двох, ставить у відповідність цей самий елемент.
5. Множину всіх підстановок на множині при сталому n називають симетричною групою і позначають .
6. Порушенням порядку підстановки на множині {1, 2, ... , n}, що числу ставить у відповідність число при, називають сумісну систему таких двох нерівностей: та.
7. Підстановку називають парною, якщо кількість транспозицій, у добуток яких можна розкласти дану підстановку, є парною.
8. Множину всіх парних підстановок на множині при сталому називають знакозмінною групою і позначають .
9. Циклом довжини називають перестановку, яка певний елемент відображає у деякий елемент , — в , ... , — в, — в за умови, що всі елементи — різні. Такий цикл позначають.
10. Дві групи називають ізоморфними, якщо існує взаємно однозначне відображення f однієї групи в іншу, при якому образ добутку елементів однієї групи є добутком образів співмножників у тому самому порядку:. Таке відображення називають ізоморфізмом відповідних груп.
Зауваження 1. Істинними є такі твердження:
1. Транспозиція, що "міняє місцями" сусідні натуральні числа, змінює кількість порушень порядку на 1.
2. Довільна транспозиція змінює кількість порушень порядку на непарне число.
3. Парність кількості транспозицій у розкладі підстановки не залежить від конкретного подання добутком транспозицій і збігається з парністю кількості порушень порядку.
4. Цикл з непарної довжиною є добутком парної кількості транспозицій.
5. Цикл з парної довжиною є добутком непарної кількості транспозицій.
6. Підстановка є парною тоді й лише тоді, коли її подання добутком циклів без спільних елементів містить парну кількість циклів парної довжини.
Зауваження 2. Довільну підстановку можна подати добутком циклів без спільних елементів.
Зауваження 3. Для довільної скінченої групи множення справа (зліва) на певний елемент задає підстановку на множині елементів цієї групи. Тому довільна скінчена група ізоморфна підгрупі , де — кількість елементів групи .
Зауваження 4. Класи суміжності за однією підгрупою мають однакову кількість елементів, що збігається з кількістю елементів підгрупи.
- Твірна функція
Означення 3. Твірною функцією послідовності називають степеневий ряд такого вигляду:
Надалі такі ряди будемо розглядати формально, тобто не досліджуючи питання збіжності, але використовуючи операції додавання, множення і (почленного) диференціювання твірних функцій. У задачах переліку числа — кількості об'єктів з певними властивостями. Тому твірну функцію називають рядом переліку.
Теорема 2. Якщо при
то при натуральному довільному справджується така рівність:
Доведення.
тобто
Коефіцієнти при лівої та правої частини цієї рівності відповідно дорівнюють звідки випливає формулювання теореми.
- Циклові індекси групи підстановок
Означення 4. Уведемо такі позначення й поняття.
1. Позначимо через кількість усіх циклів довжини, що входять у розклад підстановки a на цикли без спільних елементів. Тут лежить в межах від 1 до — кількості об’єктів множини, на якій діє підстановка.
2. Характеристикою підстановки називають впорядкований набір
3. Цикловим індексом групи підстановок на множині елементів називають многочлен змінних такого вигляду:
Такий многочлен позначають або
Зауваження 5. де додавання здійснюють за всіма можливими характеристиками с елементів групи, — кількість елементів групи з характеристикою .
Наприклад,
Теорема 3. При всіх натуральних справджуються такі рекурентні співвідношення:
Доведення.
Для довільної підстановки позначимо через довжину циклу, що містить -ий елемент. Маємо:
При сталому доданки під знаком першої суми (при прогляданні виразу справа наліво — у порядку обчислення) в останньому виразі ті самі, що й для відповідної суми для . Кратність кожного такого доданка дорівнює кількості циклів довжини l, що містять -ий елемент. Згідно з комбінаторним правилом множення таку кількість можна подати добутком:
Врахувавши множник перед знаком другої суми, отримаємо твердження теореми.
Теорема 4.
Доведення.
Див. твердження попередньої теореми й доведення теореми 2.
- Дії групи на множині
Означення 5. Нехай - група з нейтральним елементом , а -множина. Будемо говорити, Що діє на , якщо задана операція (образ пари позначається просто ), якщо виконуються такі умови:
-
-
Означення 6. Нехай - множина. Множина всіх бієктивних функції з операцією композиції називається симетричною групою на множині і позначається .
Помітимо, що будь-який гомоморфізм задає дію групи на множині за правилом . Навпаки, якщо задано на множині , то можна задати гомоморфізм формулою . Таким чином можна вважати, що дія групи на множині – це гомоморфізм , що і висувається в якості означення дії групи на множині в деякій літературі.
Уведемо тепер деякі поняття пов’язані з дією групи на множині , які використовуються у формулюванні й доведенні леми Бернсайда.
Означення 7. Орбітою елементу під дією називається множина . Кількістю елементів в даній орбіті називається довжина орбіти (в різних орбітах може бути різна кількість елементів).
Будь-які дві орбіти або не перетинаються, або співпадають. Таким чином множина розбивається на диз’юнктивне об’єднання орбіт.
Означення 8. Нерухомими точками елемента називають такі для яких . Множину нерухомих точок елемента позначимо .
Означення 9. Множина елементів групи , що залишають на місці даний елемент називається стабілізатором елемента і позначається через Іншими словами,. Очевидно, що стабілізатор є підгрупою в .
Зауваження 6. Зверніть увагу на те , що кількість пар, для яких можна обчислити двома способами , які вказані в різних частинах наступної рівності :
Остання рівність, не дивлячись на свою очевидність, грає дуже важливу роль при доведенні леми Бернсайда. Інша важлива думка показана в наступній лемі.
Лема1. Довжина орбіти елемента рівна індексу стабілізатора цього елементу. Тому, якщо група - скінченна, то
Доведення.
Індекс підгрупи – це кількість лівих суміжних класів даної підгрупи. Нехай позначає множину лівих суміжних класів. Задамо функцію формулою (очевидно, що права частина не залежить від вибору представника суміжного класу) доведемо, що бієктивна. Сюр’єктивність одразу слідує з означення орбіти. Припустимо, що , тобто . Таким чином бієктивна функція, що відображає на а це можливо лише при умові якщо .
Теорема 5. Для довільного елемента y з орбіти Y групи A справджується така рівність
Доведення.
Подамо групу A об’єднанням правих класів суміжності ajA(y) за підгрупою Позначимо кількість таких класів суміжності через m. Для кожного класу суміжності поставимо у відповідність елемент з орбіти .
1. При різних і різними також є і , бо інакше добуток належить до групи , а тому належить до . Останнє висловлювання суперечить відсутності спільних елементів множин та , тобто розбиттю на класи суміжності. Отже, вказане відображення є відображенням «в» (ін’єкцією).
2. Згідно з означенням орбiти, для довільного елемента орбіти існує елемент групи , при якому. У свою чергу, згідно з розбиттям на праві класи суміжності існують та елемент групи , при яких . В результаті маємо.
Отже, вказане відображення є відображенням «на» (сюр’єкцією). Інакше кажучи, кожний елемент орбіти є образом деякого класу суміжності. Таким чином, доведено існування взаємно однозначного відображення з множини класів суміжності в обіту , тому вони мають однакову кількість елементів. Теорему доведено.
- Лема Бернсайда (Коші-Фробеніуса)
Існують декілька варіантів леми: звичайний, спрощений, ваговий і т.д. Запишемо формулювання леми Бернсайда, використовуючи зазначений вище теоретичний матеріал.
Теорема 6. (спрощений вигляд)
Кількість орбіт групи підстановок дорівнює середньому арифметичному кількості нерухомих точок групи :
, де - кількість вузлів (циклів довжиною 1) в перестановці .
Доведення.
Позначимо через різні орбіти групи A. Для кожного виберемо довільним чином елемент з. Додавши праві та ліві частини рівностей у твердженні попередньої теореми, записаних для для кожного j=1, 2, ... , m, отримаємо таку рівність:
Вже встановлено, що для елементів з однієї орбіти їхні стабілізатори спряжені, а тому мають однакову кількість елементів. Праву частину останньої рівності можна подати таким чином:
Теорема 7. (звичайний вигляд)
Кількість орбіт дії групи на множині рівна:
Доведення.
Позначимо число орбіт через . Кожний елемент лежить в орбіті . Співставимо йому число . Сума цих чисел по всім з даної орбіти очевидно рівна 1. (ми раз складаємо число з самим собою). Тому кількість орбіт можна обчислити за формулою . Підставивши сюди формулу для довжини орбіти, отримаємо . Використовуючи формулу із зауваження1, отримаємо , що й потрібно було довести.
Теорема 8. (ваговий вигляд)
де - вага орбіти (вага будь-якого його представника), - вага елемента.
Перш ніж розв’язати «задачу про намиста» нам потрібно сформулювати та довести теорему Рефілдера-Пойа, на основі якої ґрунтується розв’язання. В свою чергу доведення цієї теореми ґрунтується на основі леми Бернсайда.
- Теорема Рефілдера-Пойа
Означення 10. Нехай:
— група підстановок на множині
— скінчена група підстановок на зліченій множині Y, що містить не менше двох елементів;
— вагова функція, визначена на Y, зі значеннями у множині невід’ємних цілих чисел і така, що при довільному невід’ємному цілому j кількість cj його прообразів скінчена: .
Уведемо такі поняття.
1. Степеневою групою підстановок, яку позначають BA, називають таку групу:
група діє на множині усіх функцій з в
елементом групи є впорядкована пара при ;
на функцію елемент групи діє таким чином:
, .
2. Кажуть, що елемент множини має вагу , якщо.
3. Степеневий ряд змінної , який перераховує елементи множини у порядку зростання їхніх ваг і має такий вигляд:
називають «рядом переліку для фігур».
Вагу функції f з означимо як суму:
Якщо (група, що містить лише тотожне перетворення), то функції, які належать до однієї орбіти степеневої групи, мають одну й ту саму вагу, яку називають вагою орбіти.
Степеневий ряд змінної , який у випадку перераховує кількості орбіт у порядку зростання їхніх ваг і має такий вигляд:
називають «рядом переліку для конфігурацій». Тут — кількість орбіт групи з вагою .
Теорема 9. Ряд переліку конфігурацій отримують підстановкою в
цикловий індекс групи на місце кожної змінної ряду переліку фігур
Доведення.
Позначимо:
• — тотожне перетворення на ;
• — число функцій з вагою , нерухомих відносно підстановки
Обмеживши для кожного дію групи на множину функцій з вагою і
застосувавши обмежену форму леми Бернсайда, маємо:
тому
В останньому виразі ряд � перераховує всі функції, нерухомі відносно підстановки (a; e). Для кожної такої функції при всіх з маємо:
Інакше кажучи, кожна функція, нерухома відносно підстановки стала на циклах, що не перетинаються, підстановки. І навпаки: кожна функція, стала на циклах, що не перетинаються, підстановки, нерухома відносно підстановки . Розглянемо цикл довжини у довільній підстановці. Якщо функція відображає елементи циклу в один з елементів множини , то цей цикл вносить вклад у вагу функції.
При кожному невід’ємному цілому коефіцієнт при у ряді
дорівнює числу способів, якими можна означити функцію f на елементах циклу довжини k таким чином, щоб функція f була нерухомою відносно підстановки (a;e) і її вклад на вибраному циклі у вагу w(f) складав jk.
Ряд перераховує способи визначення функцій, сталих на всіх циклах довжини k підстановки a. Розглянувши всі цикли підстановки a, можемо подати отриманий раніше ряд переліку функцій, сталих на циклах, що не перетинаються, добутком:
Для завершення доведення теореми потрібно поєднати у систему останню рівність, отриману на початку доведення подання ряду та означення 4 циклового індексу.
Повідомлення про цю теорему вперше опублікував Говард Редфілд у 1927 році. На жаль, робота залишилася непоміченою, бо видалася занадто специфічною. Дьйорд Пойа (він же Джордж Поліа) опублікував своє доведення у 1937 році й виявився успішнішим популяризатором. Вже у першій його публікації на цю тему вказано на можливість застосування теореми до переліку хімічних сполук.
- Задача про намиста
Задача.
Знайти кількість намист, що складаються з n бусинок двох кольорів. Намиста, що співпадають при повороті, вважаються однаковими.
Розв’язання
Нехай множина відповідає номерам бусинок в намисті, а - множині можливих кольорів. Вагову функцію . В множині існує один елемент ваги нуль і один ваги один, тобто і .
Звідки слідує, що .
Нехай - множина всіх функцій з в . Будь-яка функція задає деяке намисто, і навпаки, кожне намисто задається деякою функцією з . При цьому вага функції рівна кількості бусинок кольору 1, у відповідному намисті.
На множині діє група поворотів , породжена циклічною перестановкою , яка визначається відношенням еквівалентності на . Тоді намиста співпадають при повороті будуть в точності відповідати еквівалентним функціям, і задача зводиться до підрахунку числа орбіт.
Цикловий індекс групи рівний , де - функція Ейлера, - НСД(); - дільник .
За теоремою Рефілдера-Пойа
Число орбіт ваги ( тобто різноманітних бусинок з кольором 1) дорівнює коефіцієнту при в .
Тому загальне число орбіт (чи намист) дорівнює
.
У випадку для розфарбування намиста з бусинок, за допомогою кольорів, формула набуде такого вигляду:
.
- Приклади розв’язання комбінаторних задач за допомогою леми Бернсайда
Задача
Визначити кількість різних бус із 6 бусин, кожна з яких може бути розфарбована в один з трьох кольорів.
Розв’язання
Уточнимо умову задачі. Під різними бусами розуміють ті, що не можна співставити один з одним за допомогою повороту та осьової симетрії. Занумеруємо місця бусинок від 1 до 6, а кольорами – буквами . Тоді розфарбування – це співставлення конкретного кольору кожному із місць, тобто послідовність , де . Очевидно, що всього існує таких розфарбувань. Зрозуміло, що не всі розфарбування відповідають різним бусам. Наприклад, розфарбування, має колір , а інші – колір , суміщається поворотом з розфарбуванням, у якого друга бусина має колір , а всі інші мають колір.
На множині всіх розфарбувань діє група з поворотом та осьовою симетрією. Операція в цій групі – композиція, тобто послідовне виконання перетворень (композиція повороту і осьової симетрії рівносильна осьовій симетрії відносно іншої осі, а композиція двох симетрій відносно різних осей рівносильна повороту). Операція композиції є асоціативною, а нейтральним елементом є тотожне перетворення, оберненим рухом до осьової симетрії є сама осьова симетрія, а оберненим до повороту – є поворот, тільки в іншу сторону. Позначимо цю групу літерою .
Група діє на множині місць , тобто задано відображення з в симетричну групу . Позначимо через поворот, при якому переходимо на наступне місце (останнє в перше), а через - осьову симетрію відносно осі, що проходить через 6 і 1, 3 і 4. Випишемо перестановки в циклічній формі з , в якій переходить кожен з елементів групи .
|
Елемент
|
|
|
|
|
|
|
|
Перест.
|
|
(123456)
|
(135)(246)
|
(14)(25)(46)
|
(153)(264)
|
(654321)
|
Табл. 1.
|
Елемент
|
|
|
|
|
|
|
|
Перест.
|
(16)(25)(34)
|
(15)(24)
|
(14)(23)(56)
|
(13)(46)
|
(12)(36)(45)
|
(26)(35)
|
Табл. 2.
Далі ми будемо ототожнювати перетворення з відповідними їм перестановками. Тепер легко задати формулу дії елементів групи на множині :
Наприклад, колір другої бусинки після повороту , тобто повороту бус на співпадає з кольором першої бусинки до повороту ( , тому ).
Нагадаємо, що розфарбування, що співпадають один з одним при перетвореннях, що відбуваються у групі , тобто задають однакові буси. В розфарбуваннях однакові буси задають тоді, коли вони лежать в одній орбіті під дією групи . Таким чином, задача полягає в тому, щоб визначити кількість орбіт дії на .
Для того, щоб скористатись лемою Бернсайда, потрібно визначити, скільки елементів множини залишається на місці кожного елементу з групи . Очевидно, що . Так як поворот сусідні елементи один в одного, то у розфарбуванні, не змінюються при цьому повороті, будь-які дві сусідні бусини такого розфарбування мають однаковий колір. Звідси слідує, що всі бусини такого розфарбування мають однаковий колір, .
В загальному ті бусини, елемент групи яких переставляється по циклу мають однаковий колір тоді і тільки тоді, коли елемент групи зберігає розфарбування. Тому кількість кольорів, яку потрібно обрати для отримання розфарбування, що зберігає елемент групи, рівна кількості незалежних циклів в перестановці, відповідаючи даному елементу. Для елементу позначимо це число . Так як за умовою бусини можна розфарбовувати у один з трьох кольорів, то можна обрати способами. Таким чином - це і є кількість розфарбувань, що не змінюються під дією елементу . Отримаємо:
Використовуючи лему Бернсайда, знайдемо кількість бусин:
Відповідь: 56.
Формула Бернсайда може бути використана для обчислення незалежних від поворотів розфарбувань граней куба.
Нехай множина всіх 36 можливих розфарбувань граней куба в три кольори, а - група поворотів куба, що діє на . Два елементи належать до однієї орбіти, якщо один одержується з іншого за допомогою деякого повороту. Тож для обрахунку різних кубів треба обчислити кількість орбіт у множині під дією групи. Для цього визначимо кількість незмінних елементів для кожного з 24 поворотів і використаємо лему Бернсайда.
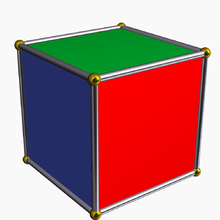
Рис.1 Куб з кольоровими гранями
- одиничний елемент при кому усі 36 елементів залишаються незмінними
- шість поворотів на 90 градусів навколо осей, що з'єднують центри протилежних граней, при кожному 33 елементів залишаються незмінними
- три повороти на 180 градусів навколо осей, що з'єднують центри протилежних граней, при кожному 34 елементів залишаються незмінними
- вісім поворотів на 120 градусів навколо осей, що з'єднують протилежні вершини, при кожному 32 елементів залишаються незмінними
- шість поворотів на 180 градусів навколо осей, що з'єднують центри протилежних ребер, при кожному 33 елементів залишаються незмінними
Тому згідно леми Бернсайда:
Отже, загальна кількість різних з урахуванням поворотів кубів, грані яких розфарбовані в три кольори, рівна 57. Загалом, якщо грані розфарбовані в n кольорів, то справедлива формула:
Висновки
Хоч теорія груп достатньо молода галузь математики, але завдяки титанічним зусиллям багатьох поколінь математиків (Ж-Л. Лагранжа, Е. Галуа, Л. Ейлера, Н. Абеля та ін.) знайшла своє застосування у інших областях «цариці наук». В даній роботі ми розглянули застосування теорії груп при розв’язуванні комбінаторних задач, а точніше при розв’язуванні задачі про знаходження кількості різних намист, що складаються з намистин, що пофарбовані в кольорів.
Опорним фактом для розв’язування задачі «про намиста» є твердження, яке відоме в комбінаториці під назвою «лема Бернсайда». Тому одним із завдань даної роботи було сформулювати та довести це важливе твердження. Виконання цього завдання передбачало використання теоретичного матеріалу з теорії груп, який ми висвітлили в першій половині роботи.
Перш ніж розв’язати задачу про намиста було сформулювано та довено теорему Рефілдера-Пойа, на основі якої ґрунтується розв’язання. В свою чергу доведення цієї теореми ґрунтується на основі леми Бернсайда. Потім, використовуючи теорему Рефілдера-Пойа було успішно розв’язано задачу про намиста. Далі в роботі було продемонстровано декілька прикладів застосування леми Бернсайда при розв’язуванні комбінаторних задач.
За результатами проведеного курсового дослідження на тему «Лема Бернсайда і задача про намиста» можна зробити висновок, що комбінаторні задачі про кількість об'єктів, що не суміщаються один з одним певними перетвореннями, які розв’язуються за допомогою леми Бернсайда, є цікавим важливим застосуванням теорії груп.
ЛЕМА БЕРНСАЙДА. ЗАДАЧА ПРО НАМИСТА