Дидактическая игра как средство развития познавательных способностей младших школьников при обучении математике

ВВЕДЕНИЕ

« Предмет математики настолько серьезен,

что надо не упускать случая, сделать его

занимательным».

Б.Паскаль.

Еще в глубокой древности римляне говорили, что корень учения горек. Зачем учить с горькими слезами тому, чему можно выучиться с улыбкой? Если интересно построить урок, то горький вкус корня учения можно изменить и даже вызвать у детей здоровый аппетит.

Удивление, окрылённость, азарт, любопытство в глазах детей, когда ручонки так и тянуться вверх и невозможно не подпрыгнуть от радости, от сознания, что ты такой умный, сообразительный, - вот что хотелось бы видеть на своих уроках каждому учителю.

Народная мудрость создала дидактическую игру, которая является для ребенка наиболее подходящей формой обучения.

Дидактические игры и занятия способны давать хороший результат лишь в том случае, если преподаватель ясно представляет, какие задачи смогут быть решены в процессе проведения игры и в чем особенности проведения этих занятий в период раннего детства. Психологами доказано, что те знания, которые усваиваются учащимися без интереса, не окрашенные собственным положительным отношением, без эмоций, не становятся полезными, а остаются «мертвым грузом».

Ребенок пишет, читает, отвечает на вопросы, но вся эта работа не затрагивает его мыслей, не вызывает интереса. Ребёнок в данном случае пассивен. Конечно, что-то он усваивает, но пассивное восприятие и усвоение не могут быть опорой прочных знаний. В результате такой учёбы дети запоминают и усваивают материал очень слабо.

Одним из основных предметов в начальной школе является математика. На уроках математики ученики усваивают систему важнейших математических понятий, овладевают умениями и навыками в области счета, письма, речи, без чего невозможно успешное обучение в школе. Велико воспитательное значение математики: она открывает младшим школьникам дидактические игры занимательного характера.

Проблемы методов обучения на сегодняшний день приобретают всё большее значение. Этой проблеме посвящено множество исследований в педагогике и психологии. И это закономерно, т.к. учение – ведущий вид деятельности школьников, в процессе которого решаются главные задачи, поставленные перед школой: подготовить подрастающее поколение к жизни, к активному участию в научно-техническом и социальном процессе. Общеизвестно, что эффективное обучение находится в прямой зависимости от уровня активности учеников в этом процессе.

В настоящее время дидакты пытаются найти наиболее оптимальные и эффективные методы обучения для активизации и развития у учащихся познавательного интереса к содержанию обучения. В связи с этим много вопросов связано с использованием на уроках занимательного материала. И среди них особое значение уделяется дидактическим играм на уроках математики.

Данная работа посвящена изучению применения дидактических игр как средства развития творческих способностей учащихся на уроках математики в начальных классах. Основой развития школьника являются те фундаментальные знания, которые он получает в ходе образовательного процесса. Образование, ориентированное на получение знаний, давно ушло в прошлое. Все изменения в окружающем мире, обществе, быстрый рост объёма информации, разнообразные средства доступа к ней и умение ориентироваться в потоке информации, предъявляют повышенные требования к интеллектуальным качествам личности выпускника, его творческим способностям.

Таким образом, система образования должна способствовать формированию таких новых качеств выпускника, как инициативность, гибкость, мобильность, конструктивность. Будущий выпускник должен уметь не только владеть новыми технологиями и понимать возможности их использования, а также стремиться к самообразованию на протяжении всей жизни; уметь принимать самостоятельные решения и разрешать возникающие проблемы; уметь работать в коллективе и находить выход из сложившихся ситуаций.

Главная цель, предъявляемая к современному образованию – формирование личности, способной решать поставленные задачи в условиях рыночной экономики, максимально быстро находить наиболее оптимальные и эффективные решения возникающей проблемы.

Огромная роль здесь отводится дидактическим играм, способствующих формированию умений решать задачи на основе компетентного выбора альтернативных вариантов. Игра обеспечивает достижение единства эмоционального и рационального в обучении. Игра – один из видов активной деятельности, который в равной степени способствует и приобретению новых знаний и развитию личности. В результате игры на равных в работу включаются как хорошо подготовленные ученики, так и «слабые» учащиеся.

Данная проблема широко рассматривается в работе В.А.Сухомлинского “О воспитании”. В этой книге он знакомит нас со своими мыслями о воспитании детей в семье и школе, в том числе автор пишет об использовании игры: “…Игра – это огромное светлое окно, через которое в духовный мир ребёнка вливается живительный поток представлений, понятий об окружающем мире. Игра – это искра, зажигающая огонёк пытливости и любознательности.”[51]

Продолжая работу Сухомлинского, в своей работе “Психология игры” Эльконин Д.Б. пишет, что игра влияет на развитие психических процессов: “Значение игры не ограничивается тем, что у ребёнка возникают новые по своему содержанию мотивы деятельности и связанные с ними задачи. В игре возникает новая психологическая форма мотивов”.[66] Продолжая работу Эльконина, Амонашвили Ш.А. в своей книге “В школу - с шести лет” описывает опыт обучения шестилетних детей в школах, а также рассматривает проблему использования игры на уроках: “Дидактическая игра, если не делать из неё самоцель, может выполнить свою исключительную роль усиления сложного процесса учения, ускорения развития”[2].

Большой вклад в развитие педагогики Казахстана внесли педагоги – просветители Абай Кунанбаев, Ыбрай Алтынсарин, Чокан Валиханов, Аль-Фараби, Ахмет Байтурсынов и педагоги-новаторы К. Нургалиев, К. Битибаева.

Игра развивает творческие способности ребёнка, формирует навыки, доводит действия до автоматизма и превращает учебник из злейшего врага в друга. В процессе игры ребёнок проявляет индивидуальность, свободу в выборе заданий. Дидактические игры и игровые моменты делают процесс обучения наиболее интересным и занимательным, создают у учащихся бодрое настроение, повышают интерес к изучаемому предмету. В процессе игры дети учатся мыслить самостоятельно, развивается внимание, повышается интерес к знаниям. Дети не замечают, что играя – учатся, т.е. узнают что-то новое, запоминают, пополняют запас понятий, представлений. Благодаря игре у детей развиваются логическое мышление, творческие способности, фантазия.

«Игровая деятельность – это особая сфера человеческой активности, в которой личность не преследует никаких других целей, кроме получения удовольствия от проявления физических и духовных сил» (О. С. Газман). [13]

Учащиеся начальных классов с удовольствием включаются в игровую и творческую деятельность: лепят, рисуют, раскрашивают, изготавливают различные поделки, сочиняют сказки. Но очень важно помнить, что дидактическая игра – это не развлечение и чрезмерное увлечение может нанести вред. И что наряду с решением задач, школа призвана вооружить учащихся знаниями, умениями и навыками.

Общеобразовательная школа направлена на формирование целостной системы универсальных знаний, умений и навыков, а также основы самостоятельной деятельности и личной ответственности обучающихся, то есть ключевые компетентности, определяющие современное качество образования.

Итак, игра воспроизводит стабильное и инновационное в жизненной практике и, значит, является деятельностью, которая создает тренинговую основу развития ребенка. В связи с этим нужно отметить, что игровые формы обучения являются наиболее эффективной технологией усовершенствования образовательного процесса в школе.

Актуальность данного исследования заключается в том, что развитие творческих способностей – одна из важнейших современного образования.

В современной начальной школе происходит активное обновление целей, содержания и методов образования. В «Концепции развития образования в Республике Казахстан до 2015 года» подчеркивается необходимость ориентации образования не только на усвоение определенной суммы знаний, но и на развитие личности, познавательных и созидательных способностей. Общеобразовательная школа должна формировать целостную систему универсальных знаний, умений и навыков, а также самостоятельной деятельности и личной ответственности обучающихся, то есть ключевые компетентности, определяющие современное качество образования» [31].

В Государственном стандарте начального образования особое место отведено деятельностному, практическому содержанию образования, «конкретным способам деятельности, так как развитие личностных качеств учащихся невозможно без приобретения ими опыта разнообразной деятельности: учебно-познавательной, практической, социальной» [17].

В Законе Республики Казахстан «Об образовании» говорится: «общеобразовательные учебные программы начального образования направлены на формирование личности ребенка, развитие его индивидуальных способностей, положительной мотивации и умений в учебной деятельности»[24].

Одним из таких умений является культура поведения для последующего усвоения материала. Во время занятий постепенно формируются некоторая сдержанность, организованность, целенаправленность поведения, достижение результата вызывает чувство радости.

Одной из актуальных проблем казахстанского общества является формирование конкурентоспособной личности, готовой не только творчески мыслить, но и активно влиять на существующую действительность. А как раз игра для ребенка – это сфера его социального творчества, поле его общественного и творческого самовыражения.

Объект исследования – развитие творческих способностей учащихся в образовательном процессе.

Предмет исследования – дидактическая игра как средство развития познавательных способностей младших школьников при обучении математике.

Можно выдвинуть следующую гипотезу: если учитель правильно подберёт формы организации процесса обучения, то данный процесс должен стать интересным, полезным, ученики будут активными, способными самостоятельно решать поставленные перед ними задачи, повысится уровень обучения школьников. Поэтому задачи моей дипломной работы следующие:

• Изучить и проанализировать научно-методическую литературу по данной проблеме;
• Разработать комплекс организационно-педагогических условий применения дидактических игр для развития творческих способностей младших школьников в процессе обучения математике;
• Разработать комплекты дидактических игр на каждый этап урока и апробировать их.
• Определить динамику развития творческих способностей учащихся на уроках математики.

Методологическая и теоретическая основа исследования

При проведении данного исследования мы опирались на труды Л. С. Выготского, Г. Е. Муравьёва, С. Л. Рубинштейна. Теоретическая основа исследования опиралась на работы А. Н. Лука, который определил творческие способности, творческий климат и мотивы творчества как условия успешного развития личности; [34], идеи И.П. Волкова, который утверждал, что каждого ребенка необходимо обучать творчеству; [9], а так же на работы энтузиастов-новаторов – Ш. А. Амонашвили, С. Н. Лысенковой. [3].

При написании курсовой работы были использованы следующие методы психолого-педагогического исследования:

1) теоретический анализ психологической и педагогической литературы по проблеме (изучены работы В. А. Сухомлинского, Д. Б. Эльконина, Ш. А. Амонашвили);

2) анкетирование с целью выявления отношения детей к играм на уроках математики;

3) анкетирование с целью выявления отношения учителей к играм на уроках;

База и методы исследования: Работа проводилась на базе ГУ «Набережная средняя школа» с. Елизаветинка Тарановского района Костанайской области. В исследовании принимали участие 8 учащихся 3-го класса. В ходе работы применялись следующие методы: теоретический анализ научно-методической литературы по исследуемой проблеме, диагностика – анкетирование, тестирование, наблюдение.

Практическая значимость результатов

Предлагаемые в исследовании организационно-педагогические условия применения дидактических игр и разработанный комплект дидактических игр, могут быть использованы педагогами как методический материал при подготовке к урокам с целью развития творческих способностей учащихся на уроках математики.

Структура работы. Работа состоит из введения, двух глав, заключения, списка литературы и приложения. В тексте имеются 14 таблиц и 10 рисунков. Общий объем дипломной работы 67 страниц.

1 Теоретические аспекты применения дидактических игр как средства развития творческих способностей учащихся

1.1 Понятие о формах организации (организационных формах) обучения

Введение в школьную программу начальных классов нетрадиционных методов преподавания имеет целью расширить учебный процесс и, не отрываясь от проблем обучения и воспитания, развить личностные качества ребенка. На сегодняшний день проблема развивающего обучения настольно актуальна, что нет, наверное, ни одного учителя, который бы не задумывался над этим.

Что такое развивающее обучение? В чём его отличие от привычного, родного, которое принято называть «традиционным» и вкладывать в это понятие отрицательный оттенок?

Традиционный процесс обучения - это процесс взаимодействия учителя и учащихся, относящегося к типу профессий «человек – человек», направленный на решение задач образования, воспитания и развития. К основным структурным компонентам, направленным на раскрытие его сущности, относят цели обучения, содержание, деятельность преподавания и учения, характер их взаимодействия, принципы, методы, формы обучения. Через эти общие сущностные характеристики возможно выявление особенностей развивающего обучения. Нельзя утверждать, что идея развивающего обучения это нечто новое, что раньше проблемы развития ребенка в процессе обучения не ставились и не решались. Можно перечислить ряд имен (Л. С. Выготский, Е. Н. Кабанова-Миллер, Н. А. Менчинская, И. С. Якиманская и другие) [11] с которыми связаны проблемы развития личности в процессе обучения. В разные периоды развития общества эта идея выдвигается на передний план или временно «забывается», но никто не снимается, никогда не прекращается её изучение, а главное – практическая реализация в школе.

Если проанализировать ныне сформулированные цели начального образования, то нетрудно заметить, что основной приоритет отдается развитию личности ребенка: «… Обеспечить начальный этап развития личности; выявить и обеспечить развитие способностей; формировать умение и желание учиться, приобрести необходимые умения и навыки учебной деятельности; обучиться чтению, письму, счету; овладеть элементами теоретического мышления, культурой речи и поведения, основами личной гигиены и здорового образа жизни» [19].

Метод обучения выступает как способ обучающей работы учителя и организации учебной работы учащихся по решению таких дидактических задач, как овладение теоретической и мировоззренческо-нравственной стороной изучаемого материала, выработка умений и навыков по применению усвоенных знаний на практике, проверка и оценка знаний учащихся и т.д. Для решения каждой из этих задач используются определенные методы.

Понятие метод обучения характеризует содержательно-процессуальную, или внутреннюю сторону учебного процесса.

Понятие же формы организации обучения, или, как еще говорят, организационной формы обучения, имеет иной смысл.

Латинское слово forma означает наружный вид, внешнее очертание. Следовательно, форма обучения как дидактическая категория обозначает внешнюю сторону организации учебного процесса, которая связана с количеством обучаемых учащихся, временем и местом обучения, а также порядком его осуществления.

Например, учитель может обучать как группу учащихся, то есть заниматься с целым коллективом, так и проводить занятия с одним учеником (индивидуальное обучение). В данном случае форма обучения связана с количественным составом обучаемых. Вместе с тем она может отражать также временную регламентацию учебных занятий. Было, например, время, когда учащиеся занимались с утра и до обеда, но определенного разграничения и перерывов между занятиями не существовало.

Далее, занятия можно проводить как в классе, так и можно осуществлять выход (экскурсию) к изучаемым объектам, что характеризует форму обучения с точки зрения места его проведения. Все это необходимо иметь в виду, осмысливая сущность организационных форм обучения. Однако, будучи внешней стороной организации учебного процесса, форма обучения органически связана со своей внутренней, содержательно-процессуальной стороной. С этой точки зрения одна и та же форма обучения может иметь различную внешнюю модификацию и структуру в зависимости от задач и методов учебной работы.

Например, экскурсия как форма обучения в одном случае может посвящаться изучению нового материала, в другом - проводиться с целью его закрепления, связи теории с практикой. Все это говорит о том, что без глубокого осмысления понятия методов обучения нельзя рассматривать структуру и дидактические основы использования различных форм организации учебных занятий.

1.2 Понятие об игре и её видах

Игра имеет особое важное значение в жизни детей дошкольного и младшего школьного возраста. С. А. Шацкий, высоко оценивая значение игры, писал: “Игра, эта жизненная лаборатория детства, дающая тот аромат, ту атмосферу молодой жизни, без которой эта пора её была бы бесполезна для человечества. В игре, этой специальной обработке жизненного материала, есть самое здоровое ядро разумной школы детства.” [63]

У философов своя точка зрения на это. Они утверждают: “Игра – это особая форма детской жизни, выработанная или созданная обществом для управления развитием детей, в этом смысле она есть особое педагогическое творение”. Щедровицкий Г.П. пишет, что игра есть:

1. особое отношение ребёнка к окружающему миру;

2. особая деятельность ребёнка, которая изменяется и развёртывается как его субъективная деятельность;

3. социально заданный и усвоенный ребёнком вид деятельности;

4. деятельность, в ходе которой происходит усвоение самого разнообразного содержания и развитие психики ребёнка;

5. социально-педагогическая форма организации всей детской жизни. [65

Д. Б. Эльконин даёт такое определение игры: “Человеческая игра – это такая деятельность, в которой воссоздаются социальные отношения между людьми вне условий непосредственно утилитарной деятельности.” [66]

Игра – одно из важнейших средств умственного и нравственного воспитания детей; это средство, снимающее неприятные или запретные для личности школьника переживания.

Игры подразделяются на творческие и игры с правилами. Творческие игры, в свою очередь включают: театральные, сюжетно-ролевые и строительные игры. Игры с правилами – это дидактические, подвижные, музыкальные игры и игры–забавы.

Так какое же значение имеет игра? В процессе игры дети сосредотачиваются, учатся мыслить самостоятельно, у них развивается внимание, стремление к знаниям. И даже самые пассивные из них включаются в игру с огромнейшим желанием, прилагая все усилия для того, чтобы не подвести товарищей по игре.

В дошкольном и младшем школьном возрасте выделяются три класса игр:

1 класс – игры, возникающие по инициативе ребенка – самодеятельные игры.

2 класс – игры, возникающие по инициативе взрослого, внедряющего их с образовательной и воспитательной целью.

3 класс – игры, идущие от исторически сложившихся традиций этноса – народные игры, которые могут возникать как по инициативе взрослого, так и более старших детей [50].

Из раскрытия понятия игры педагогами, психологами различных научных школ можно выделить ряд общих положений:

игра выступает самостоятельным видом развивающей деятельности детей разных возрастов.

игра – свободная форма деятельности детей, в которой осознается, изучается окружающей мир, открывается широкий простор для личного творчества, активности самопознания, самовыражения.

игра – первая ступень деятельности ребенка – дошкольника, изначальная школа его поведения, нормативная и равноправная деятельность младших школьников, подростков, юношества, меняющие свои цели по мере взросления учащихся.

Игра есть практика развития. Дети играют, потому что развиваются, и развиваются потому, что играют.

Игра – свобода самораскрытия, саморазвития с опорой на подсознание, разум и творчество.

Игра – главная сфера общения детей; в ней решаются проблемы межличностных отношений, приобретается опыт взаимоотношений людей [49].

Из всего существующего многообразия различных видов игр именно дидактические игры самым тесным образом связаны с учебно-воспитательным процессом. Поэтому их используют в качестве одного из способов обучения различным предметам в начальной школе, в том числе особое место данные игры занимают на уроках математики.

1. Развитие творческих способностей учащихся в ходе применения дидактических игр на уроках математики: теоретический аспект

Творчество - деятельность, требующая воображения, характеризующаяся своей неповторимостью, оригинальностью. В творчестве рождается что-то новое, неповторимое. Творчество зависит, в первую очередь, от способностей человека, от его характера и темперамента, уровня знаний. Оно неразрывно связано с социальной жизнью.

По мнению Н.Д. Левитов, творчество - это такая деятельность, в результате которой приобретается нечто новое, оригинальное, выражающее индивидуальные склонности, способности и индивидуальный опыт ученика. [33]

По мнению И.П. Волкова: «В мире есть дети, одарённые в какой-либо одной области: музыке, изобразительном искусстве и др. Но это чрезвычайно редкий дар природы, а в общей массе они имеют обыкновенные задатки, т.е. потенциальные способности. Если создать им благоприятные условия, то они могут быть развиты даже до высокого уровня. Но дело в том, что эти таланты проявляются, так сказать, не в один момент, а одни раньше, другие позже», - а значит, поиск и последующее развитие творческих способностей ребят надо вести не один год. Ученику необходимо дать возможность активно проявлять себя в самых разнообразных видах деятельности и творчества. Творчеству надо обучать!». [10] «Творческая деятельность учащихся, — пишет Б.П. Есипов, — не ограничивается лишь приобретением нового, она включает создание нового». [22]

А что-же такое способность? Это, прежде всего, индивидуальные особенности личности, которые являются субъективными условиями успешного осуществления определенного рода деятельности. Способности проявляются в глубине, быстроте, прочности овладения деятельностью и не сводятся к знаниям, умениям и навыкам. [8]

Способность- умение, а также возможность производить какие-нибудь действия. [54].

В каждом ребёнке с момента его рождения уже заложены творческие способности. И для формирования умений творчески работать, требуется постоянный, целенаправленный труд. Благодаря этому, ребёнок сможет достичь определённых результатов, получить багаж знаний и воплотить творческие идеи в действительность. Поэтому все знания и навыки, полученные в процессе учёбы, не должны отрываться от решения творческих задач.

По мнению Л. С. Выготского, основная задача будущей педагогики сформулирована следующим образом. Жизнь в ней «раскрывается как система творчества, постоянного напряжения и преодоления, постоянного комбинирования и создания новых форм поведения. Таким образом, каждая наша мысль, каждое наше движение и переживание является стремлением к созданию новой действительности, прорывом вперёд к чему-то новому». [11].

В психологии существует несколько основных подходов к проблеме творческих способностей. Вот некоторые из них:

1. В.Д. Шадриков определяет творческие способности, как свойство функциональных систем, реализующих отдельные психические функции, которые имеют индивидуальную меру выраженности, проявляющуюся в успешности и качественном своеобразии освоения деятельности [62].

2. С точки зрения Д.Б. Богоявленской, творческие способности являются ситуативно не стимулированной активностью, проявляющейся в стремлении выйти за пределы заданной проблемы. [4].

3. «Задатки детей – это то, на основе чего формируются те или иные творческие способности. Задатки представляют собой то, что дано ребёнку ещё до начала формирования и развития у него соответствующих творческих способностей» - считает Г. Л. Бурменская. Речь идёт о свойствах, появление которых у ребёнка практически не зависит от его обучения и воспитания и которые возникают и развиваются по законам генетики, в процессе созревания организма» [7].

4. Б.М Теплов, в своих работах, под творческими способностями понимал определённые индивидуально-психологические особенности, отличающие одного человека от другого, которые не сводятся к наличному, имеющемуся уже у человека запасу навыков и знаний, а обуславливают лёгкость и быстроту их приобретения [53].

5. В своём философском словаре П.С. Гуревич пишет о том, что творческие способности включают в себя способность творчески воображать, творчески внимать и неординарно мыслить [18].

6. Под содержанием понятия творческой способности доктор философских наук В.К. Лукашевич понимает «совокупность многообразных свойств личности, их органическую взаимосвязь и своеобразную направленность в зависимости от характера поставленных задач».

Для младшего школьного возраста характерны яркость и непосредственность восприятия, лёгкость вхождения в образы. Этот возраст характеризуется лёгким вовлечением детей в любую деятельность, особенно игровую. Для младшего школьника игра имеет исключительное значение: игра для них, это, прежде всего, учёба, труд, серьёзная форма воспитания.

Принцип активности ребёнка в процессе обучения был и остаётся одним из самых основных принципов в дидактике. Под этим предполагается такое качество деятельности, которое характеризуется высоким уровнем мотивации, осознанной потребностью в усвоении знаний, результативностью и соответствием определённым нормам. Такого рода активность сама по себе возникает нечасто. Она является следствием целенаправленных управленческих воздействий и организации педагогической среды, т.е. применением педагогической технологии.

Младший школьный возраст - возраст интенсивного интеллектуального развития. Интеллект определяет развитие всех остальных функций, происходит интеллектуализация всех психических процессов, их осознание и произвольность. Поэтому в данном возрасте в игре развивается:

- мотивационно - потребностная сфера (возникает иерархия мотивов, где социальные мотивы приобретают более важное значение для ребёнка, чем личные);

- появляется познавательный интерес (ребёнок, принимая роль какого-либо персонажа, учитывает особенности его поведения, что помогает в ориентировке во взаимоотношениях между людьми, способствует развитию самооценки и самосознания);

- развивается произвольность поведения (разыгрывается роль, ребёнок стремится приблизиться к образцу, что помогает ребёнку постигать и учитывать нормы и правила поведения)

- развиваются умственные действия.

Изучив все выше изложенные взгляды ученых, за основу своего исследования мы взяли теоретические положения М.Б. Теплова и П.С. Гуревича: «творческие способности – это такие индивидуально-психологические особенности человека (воображение, мышление, память, любознательность, внимание) отличающие одного человека от другого. [18].

Таблица 1

Виды способностей

Элементарные	Способности, связанные с работой органов чувств или с простыми движениями
Сложные	Способности к различным видам деятельности, связанным с человеческой культурой (музыкальные, литературные,..)
Общие	Способности, которые есть у всех людей (умственные, двигательные)
Специальные	Способности, встречающиеся не у всех, в отдельных, специфических видах деятельности
Теоретические	Способности к абстрактно-логическому мышлению, умение ставить и решать теоретические задачи
Практические	Способности к выполнению конкретных действий в реальных условиях
Коммуникативные	Способности общаться между людьми, установление межличностных контактов
Предметные	Способности человека работать с неодушевлёнными предметами

Таблица 2

Творческие способности

Учебные	Творческие
Способность, определяющая успешность обучения, усвоения человеком ЗУН	Способности человека создавать предметы материальной и духовной культуры, производить новые идеи, открывать изобретения, т.е. творчество в различных видах деятельности
	Память	Мышление	Любознательность	Внимание	Воображение

Творческие способности - это все качества человека, собранные воедино. На основе работы Немова Р. С. «Общая психология» я составила таблицу №1 «Виды способностей» и №2 «Творческие способности», которые рассматривают виды способностей и краткое описание способностей. Из данных таблиц можно выделить те теоретические способности, в которые входят рассматриваемые нами творческие способности (таблица №3).[45].

Таблица 3

Виды теоретических способностей и их характеристика

Теоретические способности
Способности к абстрактно-логическому мышлению, умение ставить и решать теоретические задачи
Умственные способности
Умственные способности проявляются в умении человека определить понятия, формулировать и доказывать гипотезы, рассуждать в уме, предлагать и обосновывать теории, объясняющие ту или иную группу явлений
Творческие способности
Память	Мышление	Любознательность	Внимание	Воображение

Наиболее эффективным и результативным периодом развития способностей, выявления одаренности, таланта является детство. Именно этот период жизни человека самый благоприятный, потому что происходит узнавание мира и сначала не произвольно раскрываются некоторые способности, а потом уже и родители, и в школе помогают их развивать.

Способности человека не могут существовать вне конкретной деятельности человека, а формирование их происходит в процессе обучения и воспитания. Творческие способности, в первую очередь, зависят от кругозора человека. Чем шире кругозор, тем легче ему взглянуть на исследуемый вопрос с разных сторон. Дидактические игры, направленные на активизацию и развитие творческих способностей учащихся, позволяют получить личность, которая по всем параметрам отвечает современным требованиям нашего государства.

М.Б. Теплов обнаружил, что если деятельность ребёнка носит творческий, не рутинный характер, то она постоянно заставляет его думать и сама по себе становится достаточно привлекательным делом, как средство проверки и развития способностей. [53].

Творческая деятельность помогает ребёнку почувствовать себя увереннее, получить удовольствие от достигнутых успехов, повышает самооценку.

В таблице №4 описаны виды и характеристики творческих способностей.

Таблица 4

Виды и характеристика творческих способностей

Воображение	Воображение – психический процесс создания образа, предмета, ситуации путём перестройки имеющихся у человека представлений; или воображение - мысленное воспроизведение чего-либо, кого-либо, фантазия. Творческий процесс носит «расходящийся» характер. Творческое воображение – это характер новизны создаваемого им продукта
Мышление	Мышление – процесс опосредованного и обобщённого познания окружающего мира. Мышление проявляется в разных качествах: предметно-действенном, наглядно-образном, абстрактном. Владеет различными мыслительными операциями: сравнение, анализ, синтез, обобщение, конкретизация, абстрагирование.
Любознательность	Любознательность - творческая способность постоянно искать новые пути (способы) мышления, изучать новые вещи и идеи, искать разные возможности решения задач, изучать книги, игры, карты, картины и т. д., чтобы познать как можно больше. Субъект с выраженной любознательностью, чаще всего спрашивает всех и обо всем, ему нравится изучать устройство механических вещей. Сопоставления, сравнения, анализ при решении практических заданий, требуют от учащихся поиска ответов, новых данных, развивает творческие способности.
Память	Память - одна из психических функций и видов умственной деятельности, предназначенная сохранять, накапливать и воспроизводить информацию. Творческая способность длительно хранить информацию о событиях внешнего мира и реакциях организма и многократно использовать её в сфере сознания для организации последующей деятельности

Продолжение таблицы 4

Внимание

Внимание – элемент сознания, которое характеризуется объёмом, распределением, концентрацией, устойчивостью и переключением. Под вниманием понимается творческая способность направлять психическую деятельность, и сосредоточенность её на объекте, имеющем для личности определённую значимость. Творческой способностью является непроизвольное и послепроизвольное внимание, вызванное сознательно поставленной целью и не требующее волевых усилий, оно вызвано творческим отношением к делу

Исходя из вышесказанного, можно отметить, что из основных творческих способностей развиваются следующие творческие умение, благодаря которым возможен процесс познания и развития человека. А именно:

• Умение сворачивать мыслительные операции;
• Умение видеть проблему там, где её не видят другие;
• Умение воспринимать действительность целиком;
• Умение выделить из общего частное;
• Умение применять приобретенные навыки;
• Умение генерировать идеи.

Основная задача дидактической игры на уроке – раскрытие и развитие творческих способностей учащихся. Развитие творческих способностей – это длительный, целенаправленный процесс. Поэтому познавательные задания должны составлять систему, которая позволит формировать и развивать как интеллектуальную, так и творческую деятельность учащихся.

Но не следует также забывать и о том, что творческие способности учащихся – это не знания, умения и навыки, а, в первую очередь, их приобретение, закрепление и использование на практике.

Для более успешной активизации творческой деятельности школьников, педагогу необходимо видеть результативность и продуктивность своей работы. Для этого необходимо следить за динамикой развития творческой деятельности каждого ребенка. Элементы творчества и взаимодействия элементов воспроизведения в деятельности ученика, как и в деятельности зрелого человека, следует различать по двум характерным признакам:

1) по результату (продукту) деятельности;

2) по способу ее протекания (процессу).

Очевидно, что в учебной деятельности элементы творчества учащихся проявляются, прежде всего, в особенностях ее протекания, а именно в умении видеть проблему, находить новые способы решения конкретно-практических и учебных задач в нестандартных ситуациях.Исходя из вышесказанного, можно сказать, что творческие способности есть у каждого ребёнка. И то, насколько они развиты, зависит творческий потенциал каждого человека и общества в целом. Умение педагога развить творческие способности ребёнка, используя дидактические игры, позволит расширить границы проявления их у учащихся.

Вывод: Таким образом, творческая деятельность активизируется в благоприятной атмосфере при доброжелательных оценках со стороны учителей, поощрении оригинальных высказываний. Немаловажную роль при этом играют открытые вопросы, побуждающие школьников к размышлениям, к поиску разнообразных ответов на одни те же вопросы учебного плана. Еще лучше, если самим учащимся позволяется ставить подобные вопросы и отвечать на них.

1.4 Организационно-педагогические условия применения дидактической игры как средства развития творческих способностей учащихся на уроках математики начальной школы

К. Д. Ушинский считал игру свободной деятельностью ребёнка, вносящей в его развитие такой вклад, какой не может сравниваться ни с чем другим. Он писал: «Игра есть свободная деятельность дитяти, и если мы сравним интерес игры, а равно число и разнообразие следов, оставленных ею в душе дитяти, с подобными же влияниями учения первых четырёх – пяти лет, то, конечно, всё преимущество останется на стороне игры». [61]

Известный педагог Е. И. Тихеева высоко ценила дидактическую игру, её роль в ознакомлении детей с предметами, явлениями окружающей жизни. Особое значение она придавала сенсорному воспитанию и обучению родному языку. [54]

Дидактическая игра (игра обучающая) – это вид деятельности, занимаясь которой, дети учатся.[28] Дидактическая игра, как и любая другая игра, представляет собой самостоятельный вид деятельности, которой занимаются дети: она может быть как индивидуальной так и коллективной. Данная игра является ценным средством воспитания действенной активности учащихся, она активизирует психические процессы, вызывает у них живой интерес к процессу познания. В ней охотно дети преодолевают значительные трудности, тренируют свои силы, развивают способности и умения. Она помогает сделать любой учебный материал увлекательным, вызывает у учеников глубокое удовлетворение, создаёт радостное рабочее настроение, облегчает процесс усвоения знаний. В процессе дидактической игры ребёнок наблюдает, сравнивает, сопоставляет, классифицирует предметы по тем или иным признакам, производит доступный ему анализ и синтез, делает обобщения.

Существенный признак дидактической игры – устойчивая структура, которая отличает её от всякой другой деятельности.[29] Структурные компоненты дидактической игры: игровой замысел, игровые действия и правила.

Игровой замысел выражен, как правило, в названии игры. Игровые действия способствуют познавательной активности учащихся, дают им возможности проявить свои способности, применить имеющиеся знания, умения и навыки для достижения целей игры. Правила помогают направлять игровой процесс. Они регулируют поведение детей и их взаимоотношения между собой. Дидактическая игра имеет определённый результат, который является финалом игры, придаёт игре законченность. Она выступает, прежде всего, в форме решения поставленной учебной задачи и даёт школьникам моральное и умственное удовлетворение. Для учителя результат игры всегда является показателем уровня достижений учащихся в освоении знаний или в их применении.

Все структурные элементы дидактической игры взаимосвязаны между собой и отсутствие любого из них разрушает игру.

Дидактическая игра - современный и признанный метод обучения и воспитания, обладающий образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве.

Дидактические игры можно широко использовать как средство обучения, воспитания и развития. Основное обучающее воздействие принадлежит дидактическому материалу, игровым действиям, которые как бы автоматически ведут учебный процесс, направляя активность детей в определенное русло. Дидактическую игру следует отличать от игры вообще и игровой формы занятий, хотя это деление условное.

Природа создала детские игры для всесторонней подготовки к жизни. Поэтому они имеют генетическую связь со всеми видами деятельности человека и выступают как специфически детская форма и познания, и труда, и общения, и искусства, и спорта.

Принято различать два основных типа игр: игры с фиксированными, открытыми правилами и игры со скрытыми правилами. Примером игр первого типа является большинство дидактических, познавательных и подвижных игр, сюда относят также развивающие интеллектуальные, музыкальные, игры-забавы, аттракционы.

Ко второму типу относят сюжетно-ролевые игры. Правила в них существуют неявно. Они – в нормах поведения воспроизводимых героев: доктор сам себе не ставит градусник, пассажир не летает в кабине летчика. [20]

Учебная игра - это обучающая игра, для которой характерно, что игровой процесс сопровождается усвоением игроками содержания обучения. Игра по содержанию, учение по форме. Но она всегда должна оставаться игрой. Связь с содержанием школьного обучения достигается в ней не в результате механического введения учебного материала в ткань уже готовой игры, а путём специального проектирования содержания учебной игры.

Игра, учение и труд являются основными видами деятельности человека. При этом игра готовит ребёнка как к учению, так и к труду, сама являясь одновременно и учением и трудом. Глубоко ошибаются те, кто считает, что игра - лишь забава и развлечение.

Игру можно назвать восьмым чудом света, т.к в ней заложены огромные воспитательные и образовательные возможности. В процессе игр дети приобретают самые различные знания о предметах и явлениях окружающего мира. Игра развивает детскую наблюдательность и способность определять свойства предметов, выявлять их существенные признаки. Таким образом, игры оказывают большое влияние на умственное развитие детей, совершенствуя их мышление, внимание, творческое воображение.

Виды дидактических игр

Игра – это особая осмысленная деятельность, интегрирующая в себе все основные типы человеческой деятельности [преобразовательную, познавательную, ценностно-ориентационную и коммуникативную] и направлена на ориентировку и познание предметной и социальной действительности [50].

Специалисты утверждают, что главные особенности подвижных игр школьников - их соревновательный, творческий, коллективный характер. В них проявляется умение действовать за команду в непрерывно меняющихся условиях.

В нравственном воспитании подвижные игры имеют огромное значение. Они способствуют развитию чувства товарищеской солидарности, взаимопомощи, ответственности за действия друг друга.

Сюжетно-ролевые дидактические игры (иногда их называют сюжетными) также занимают важное место в нравственном воспитании ребенка. Они носят преимущественно коллективный характер, так как отражают существо отношений в обществе. Их подразделяют на ролевые, игры-драматизации, режиссерские. Сюжет могут иметь театрализованные детские праздники, карнавалы, строительно-конструкторские игры и игры с элементами труда.

В этих играх на основе жизненных или художественных впечатлений свободно и самостоятельно воспроизводятся социальные отношения и материальные объекты или разыгрываются фантастические ситуации, не имеющие пока аналога в жизни. Основными компонентами ролевой игры являются: тема, содержание, воображаемая ситуация, сюжет и роль.

В настоящее время появились, и всё чаще активно используются в обучении компьютерные дидактические игры.

Преимущество компьютерных дидактических игр перед другими формами игр заключается в следующем: они наглядно демонстрируют ролевые способы решения игровых задач, например, в динамике представляют результаты совместных действий и общения персонажей, их эмоциональные реакции при успехе и неудаче, что в жизни трудно уловимо. Образцом таких игр могут стать народные сказки и произведения фольклора. В них дети приобретают опыт нравственного поведения в самых разнообразных жизненных условиях. Такие игры помогают избежать штампов и стандартов в оценке поведения разных персонажей в разных ситуациях. Дети усваивают практически средства коммуникации, способы общения и выражения эмоций.

Все компьютерные программы для детей должны быть положительно нравственно направленными, содержать элементы новизны, и ни в коем случае не должны быть агрессивными и жестокими.

Дидактические игры различаются по обучающему содержанию, познавательной деятельности детей, игровым действиям и правилам, организации и взаимоотношения детей. Перечисленные признаки присущи всем играм, но в одних отчетливее выступают одни, в других – иные. В различных сборниках указано более 500 дидактических игр, но четкая классификация игр по видам отсутствует. Можно представить следующие виды дидактических игр:

Игры-путешествия.

Игры-поручения.

Игры-предположения.

Игры-загадки.

Игры-беседы.

Настольно-печатные.

Словесные.

Сюжетно-ролевые.

Предметные.

Игры-упражнения.

Игры-соревнования.

Познавательные.

Игры с правилами.

Коллективные дидактические игры.

Длительные совместные игры со сверстниками. [15]

Теперь более подробно рассмотрим приведенные виды дидактических игр.

В играх с предметами используются игрушки и реальные предметы. Играя с ними, дети учатся сравнивать, устанавливать сходства и различие предметов. При работе с играми, с природным материалом дети закрепляют знания об окружающей природной среде, у них формируются мыслительные процессы (анализ, синтез, классификация).

Настольно-печатные игры разнообразны по видам: парные картинки, различные виды лото, домино. При их использовании разрешаются различные развивающие задачи. Так, например, игра, основанная на подборе картинок по парам. Ученики объединяют картинки не только по внешним признакам, но и по смыслу.

Словесные игры построены на словах и действиях играющих. В этих играх дети учатся, опираясь на имеющиеся представления о предметах, углублять знания о них, так как в этих играх требуется использовать приобретенные знания о новых связях, в новых обстоятельствах. Дети самостоятельно решают разные мыслительные задачи: описывают предметы, выделяя характерные их признаки, отгадывают по описанию, находят признаки, сходства и различия, группируют предметы по различным свойствам, признакам и другое. Для удобства использования словесных игр в педагогическом процессе их условно можно объединить в четыре основные группы:

входят игры, с помощью которых формируют умения выделять существенные признаки предметов, явлений.

составляют игры, используемые для развития умения сравнивать, сопоставлять, давать правильные умозаключения.

игры, с помощью которых развивается умение обобщать и классифицировать предметы по различным признакам, объединены в третьей группе.

В особую, четвертую группу выделены игры на развитие внимания, сообразительности и быстроты мышления [50].

Такая группировка игр подчеркивает их направленность на обучение, познавательную деятельность детей, но не раскрывает в достаточной мере основы дидактической игры - особенностей игровой деятельности детей, игровых задач, игровых действий и правил, организацию жизни детей, руководство воспитателя.

Условно можно выделить несколько типов дидактических игр, сгруппированных по виду деятельности учащихся.

Игры-путешествия.

Игры-поручения.

Игры-предположения.

Игры-загадки.

Игры-беседы (игры-диалоги).

Рисунок 1 Типы дидактических игр по виду деятельности

Игры-путешествия можно сравнить со сказкой, ее развитием, чудесами. Игра-путешествие отражает реальные факты или события, где обычное раскрывается через необычное, простое – через загадочное, трудное – через преодолимое, необходимое – через интересное. Все это происходит в игре, в игровых действиях, становится близким ребенку, радует его. Цель игры-путешествия – усилить впечатление, придать познавательному содержанию чуть-чуть сказочную необычность, обратить внимание детей на то, что находится рядом, но не замечается ими. Игры-путешествия обостряют внимание, наблюдательность, осмысление игровых задач, облегчают преодоление трудностей и достижение успеха.

Игры-путешествия всегда несколько романтичны. Именно это вызывает интерес и активное участие в развитии сюжета игры, обогащение игровых действий, стремление овладеть правилами игры и получить результат: решить задачу, что-то узнать, чему-то научиться.[20] Игры-путешествия иногда неправильно отождествляются с экскурсиями. Существенное различие их заключается в том, что экскурсия – форма обучения и разновидность занятий. Целью экскурсии чаще всего является ознакомление с чем-то, требующим непосредственного наблюдения, сравнения с уже известным. Иногда игру-путешествие отождествляют и с прогулкой. Но прогулка чаще всего имеет оздоровительные цели. Познавательное содержание может быть и на прогулке, но оно является не основным, а сопутствующим.

Роль педагога в игре сложна, требует знаний, готовности ответить на интересующие вопросы детей, играя с ними, вести процесс обучения незаметно.

Игра-путешествие - игра действия, мысли, чувств ребенка, форма удовлетворения его потребностей в знании.

В названии игры, в формулировке игровой задачи должны быть «зовущие слова», которые способны вызвать интерес детей, активную игровую деятельность. В игре-путешествии используются многие способы раскрытия познавательного содержания в сочетании с игровой деятельностью. Это постановка задач, пояснение способов ее решения, иногда разработка маршрутов путешествия, поэтапное решение задач, радость от ее решения, содержательный отдых. В состав игры-путешествия иногда входит песня, загадки, подарки и многое другое.

Игры-поручения имеют те же структурные элементы, что и игры-путешествия, но по содержанию они проще и по продолжительности короче. В основе их лежат действия с предметами, игрушками, словесные поручения. Игровая задача и игровые действия в них основаны на предположении, что-то сделать: «Помоги Буратино расставить знаки в примерах», «Проверь домашнее задание у Незнайки».

Игры-предположения «Что было бы…?» или «Что бы я сделал…», «Как я решил и почему?», и др. Иногда началом такой игры может послужить картинка, задание, задача, проблема и т.п.

Игры-загадки. Возникновение загадок уходит в далекое прошлое. Загадки создавались самим народом, входили в обряды, ритуалы, включались в праздники. Они широко используются для проверки знаний, находчивости. В этом и заключается очевидная педагогическая направленность и популярность загадок как умного развлечения.

В настоящее время загадки, загадывание и отгадывание рассматриваются как вид обучающей игры.

Главным отличительным признаком загадки является замысловатое описание, которое нужно расшифровать (отгадать и доказать). Описание это лаконично и, как правило, оформляется в виде вопроса или заканчивается им. Главной особенностью загадок является логическая задача. Способы построения логических задач различны, но все они активизируют умственную деятельность ребенка.

Детям нравятся игры-загадки. Необходимость сравнивать, припоминать, думать, догадываться – доставляет радость умственного труда. Разгадывание загадок развивает способность к анализу, обобщению, формирует умение рассуждать, делать выводы, умозаключения.

Игры-беседы (диалоги). В основе игры-беседы лежит общение педагога с детьми, детей с педагогом и детей друг с другом. Это общение имеет особый характер игрового обучения и игровой деятельности детей. В игре-беседе учитель часто идет не от себя, а от близкого детям персонажа и тем самым не только сохраняет игровое общение, но и усиливает радость его, желание повторить игру. Однако игра-беседа таит в себе опасность усиления приемов прямого обучения.

Воспитательно-обучающее значение заключено в содержании сюжета – темы игры, в возбуждении интереса к тем или иным аспектам объекта изучения, отраженного в игре. Познавательное содержание игры не лежит «на поверхности», его нужно найти, добыть – сделать открытие и в результате что-то узнать.

Ценность игры-беседы заключается в том, что она предъявляет требования к активизации эмоционально-мыслительных процессов: единства слова, действия, мысли и воображения детей. Игра-беседа воспитывает умение слушать и слышать вопросы учителя, вопросы и ответы детей, умение сосредоточивать внимание на содержании разговора, дополнять сказанное, высказывать суждение.

Все это характеризует активный поиск решения поставленной игрой задачи. Немалое значение имеет умение участвовать в беседе, что характеризует уровень воспитанности.

Основным средством игры-беседы является слово, словесный образ, вступительный рассказ о чем-то. Результатом игры является удовольствие, полученное детьми. [63]

Перечисленными типами игр не исчерпывается, конечно, весь спектр возможных игровых методик. Однако на практике наиболее часто применяются указанные игры, как в «чистом» виде, так и в сочетании с другими видами игр: подвижными, сюжетно-ролевыми и др. (Приложение 1)

Роль педагога в игре очень сложная, требующая знания, готовность ответить на вопросы детей, играя с ними, вести процесс обучения незаметно.

Дидактическая игра - явление сложное, но в ней явно обнаруживается структура, т.е. основные элементы, характеризующие игру как форму обучения и игровую деятельность одновременно. Один из главных составляющих элементов игры - дидактическая задача, которая определяется целью обучающего и воспитательного воздействия. Познавательное содержание берётся из школьной программы. Наличие дидактической задачи или нескольких задач подчеркивает обучающий характер игры, направленность обучающего содержания на процессы познавательной деятельности детей. Дидактическая задача определяется учителем и отражает его обучающую деятельность.

Главным составляющим элементом игры является игровая задача, осуществляемая детьми в игровой деятельности. Две задачи - дидактическая и игровая - отражают взаимосвязь обучения и игры. В отличие от прямой постановки дидактической задачи на занятиях в дидактической игре она осуществляется через игровую задачу, определяет игровые действия, становится задачей самого ребенка, возбуждает желание и потребность решить ее, активизирует игровые действия.

Правила игры – это один из составляющих элементов дидактической игры.

Их содержание и направленность обусловлены общими задачами формирования личности ребенка и коллектива детей, познавательным содержанием, игровыми задачами и игровыми действиями в их развитии и обогащении. В дидактической игре правила являются заданными. Используя правила, педагог управляет игрой, процессами познавательной деятельности, поведением детей [28].

В основу любой игровой методики, проводимой на занятиях, должны входить следующие принципы:

• Актуальность дидактического материала (актуальные формулировки математических задач, наглядные пособия и др.) собственно помогает детям воспринимать задания как игру, чувствовать заинтересованность в получении верного результата, стремиться к лучшему из возможных решений.
• Коллективность позволяет сплотить детский коллектив в единую группу, в единый организм, способный решить задачи более высокого уровня, нежели доступные одному ребенку, и зачастую – более сложные.
• Соревновательность создает у учащегося или группы учащихся стремление выполнить задание быстрее и качественнее конкурента, что позволяет сократить время на выполнение задания с одной стороны, и добиться реально приемлемого результата с другой. Классическим примером указанных выше принципов могут служить практически любые командные игры: «Что? Где? Когда?» (одна половина задает вопросы – другая отвечает на них).

На основе вышеизложенных принципов можно выдвинуть следующие рекомендации к проводимым на занятиях дидактическим играм:

• Каждая игра должна содержать элемент новизны.
• Нельзя навязывать детям игру, которая кажется полезной, игра – дело добровольное. Ребята должны иметь возможность отказаться от игры, если она им не нравится, и выбрать другую игру.
• Игра – не урок. Игровой прием, включающий детей в новую тему, элемент соревнования, загадка, путешествие в сказку и многое другое,… - это не только методическое богатство учителя, но и общая, богатая впечатлениями работа детей на занятии.
• Эмоциональное состояние учителя должно соответствовать той деятельности, в которой он участвует. В отличие от всех других методических средств игра требует особого состояния от того, кто ее проводит. Необходимо не только уметь проводить, но и играть вместе с детьми.
• Игра – средство диагностики. Ребенок раскрывается в игре во всех своих лучших и не лучших качествах.

В последнее время всё чаще стали использовать нетрадиционные формы уроков. В игре ученик свободно получает различные сведения и знания. В игровой форме ученику легче усвоить самый трудный материал. Известный французский учёный Луи де Бройль утверждал, что все игры, даже самые простые, имеют много общих элементов с работой учёного. [40]

Во-первых, сначала привлекает трудность, поставленная задача, которую нужно преодолеть, и, во-вторых, радость от того, что ты преодолел это препятствие, сделал какое-то открытие. Поэтому всех людей, независимо от возраста, привлекает игра.

Дидактические игры направлены на развитие познавательных процессов, которые являются творческими способностями (внимание, память, восприятие, воображение, наблюдательность, сообразительность и другое), закрепление знаний, умений и навыков, полученных на уроке.

Каждый учитель стремится к тому, чтобы его уроки были интересными, запоминающимися, увлекательными. И именно дидактическая игра является одной из уникальных форм, которая позволяет сделать более увлекательной и интересной не только работу учеников на творческо-поисковом уровне, но и ежедневные шаги по изучению материала.

Впервые термин «дидактические игры», как специально создаваемые или приспособленные для целей обучения игры, ввели Фридрих Фребель [37] и Мария Монтесори. [43] Игры, предложенные ими, были предназначены для детей дошкольного возраста. Но со временем они начали принимать форму игровых приёмов в обучении и таким образом вошли в школу.

Ценность дидактических игр заключается не только в том, чтобы дать учащимся знания, но и научить их использовать эти знания в разнообразной деятельности.

Ребёнок будет развиваться тогда, когда он сможет открывать, творить, рассуждать, спорить. На уроке дидактические игры выполняют несколько функций. (рисунок 2)

Рисунок 2 Функции дидактических игр

Дидактическая игра преследует три цели: воспитательную, учебно-развлекательную и игровую. В наш век дети всё больше времени проводят перед экранами телевизоров и компьютерами, попадая в зависимость компьютерной реальности, на деле оставаясь одинокими. Альтернативой компьютеру и телевизору должно быть что-то интересное. Игра – лучший способ развивать творческие способности ребёнка, подготовить его к жизни, к общению с людьми и окружающим миром.

Дидактические игры различаются по содержанию, познавательной деятельности детей, игровым правилам и действиям, организации и взаимоотношениям детей. Все эти признаки присущи всем играм, но в одних играх они проявляются более, а в других – менее отчётливее.

Давайте рассмотрим психолого-педагогические особенности применения дидактических игр на уроках математики в начальной школе.

Во-первых, во время игры учитель должен создать в классе атмосферу доверия, вселить уверенность в собственных силах и достижения поставленных целей в учащихся. А залогом всего этого будет доброжелательность, тактичность учителя, похвала и поощрение ученика.

Во-вторых, предлагая игру, необходимо хорошо продумать все детали и подготовиться к ней тщательно (наглядность, доступность).

В-третьих, учитель должен быть внимателен к тому, насколько ученики подготовлены к игре (творческие игры, где учащиеся будут более самостоятельны).

В-четвёртых, следует обратить внимание и на состав команды для игры. В каждой группе должен быть лидер и участники разного уровня подготовки.

В-пятых, распределяя роль ведущего, обращать внимание и на более слабых учеников, давая им возможность проявить себя в качестве лидера.

Не следует также приучать детей к тому, что на каждом уроке они будут работать с новыми сказочными героями или играть в новые игры. Следует последовательно переходить от уроков, насыщенных игровыми ситуациями к урокам, где игра будет поощрением за работу на уроке или использоваться для активизации внимания. Например, шутки-минутки, игры путешествия в страну чисел, страну знаний и т.д.

Правила игры имеют обучающий, организационный, формирующий характер, и чаще всего они разнообразно сочетаются между собой. Обучающие правила помогают раскрывать перед детьми, что и как нужно делать, они соотносятся с игровыми действиями, раскрывают способ их действий. Правила организуют познавательную деятельность детей: что-то рассмотреть, подумать, сравнить, найти способ решения поставленной игрой задачи.

Организующие правила определяют порядок, последовательность игровых действий и взаимоотношений детей. В игре формируются игровые отношения и реальные отношения между детьми. Отношения в игре определяются ролевыми отношениями. Правила игры и должны быть направлены на воспитание положительных игровых отношений и реальных в их взаимосвязи.Соблюдение правил в ходе игры вызывает необходимость проявления усилий, овладения способами общения в игре и вне игры и формирования не только знаний, но и разнообразных чувств, накопления добрых эмоций и усвоения традиций [48].

Таким образом, применяя дидактические игры на уроках математики реализуются идеи совместного творчества, сотрудничества, соревнования, воспитания через коллектив, дети приобщаются к ответственности каждого за учёбу и дисциплину в классе, а также развиваются творческие способности.

Перед педагогом, использующим дидактические игры, ставятся следующие задачи: целенаправленно развивать у детей подвижность и гибкость мышления, настойчиво стимулировать процессы переключения, поисковой активности; учить детей рассуждать, логически мыслить, не заучивать всё, а пытаться самим делать выводы, находить пути решения из сложившихся ситуаций, получать удовольствие от полученного результата в от обучения в целом.

Работа по развитию творческих способностей в начальной школе состоит из нескольких этапов:

1) подготовительный (элементы творчества в обычной деятельности, например, игры): используется в 1 - 2-х классах;

2) исследовательский (творчество в изучении языка, например, составление словарей): проходит во 2 - 3-х классах;

самовыражение через деятельность (например, написание сочинений): применяется в 3 - 4-х классах. [26] Чтобы любой урок (факультатив, занятие) был направлен на развитие творческих способностей учащихся и реализовал их, учителю необходимо при его проведении ориентироваться на следующие принципы. [27] (таблица №5).

Таблица 5

Принципы проведения урока, направленного на развитие

творческих способностей

1	Принцип «субъекта»	Учитель должен пользоваться современными педагогическими развивающими технологиями, ориентированными на развитие способностей учащегося, быть субъектом образовательной деятельности процесса своего развития в целом: и телесного, и эмоционального, и интеллектуального, и личностного, и духовно-нравственного.
2	Принцип «принятия другого»	Согласно данному принципу учитель должен изначально принимать ученика как индивидуальность, имеющую право быть личностью со своими, уже сложившимися особенностями. Это означает, что отношение ученик-учитель уже не может строиться по логике объективно-субъектного взаимодействия.
3	Принцип проектирования	Этот принцип направлен на раскрытие творческих способностей учащихся.
4	Принцип сотрудничества	Для развития творческих способностей у учащихся, учителю необходимо обращать внимание на способность учащихся быстро схватывать смысл принципов, понятий, логических построений; потребность и способность длительно сосредотачиваться на заинтересовавших ребёнка сторонах проблемы и стремление разобраться в них; способность подмечать, рассуждать и выдвигать объяснения, в том числе необычные: повышенную молчаливость или же, напротив, повышенную потребность в постоянном высказывании и отстаивании своего мнения.

В ходе данной работы был определён следующий комплекс условий, необходимых для развития творческих способностей посредством дидактических игр:

1. Организационно-педагогические.
2. Психолого-педагогические
3. Методические.

К организационно-педагогическим условиям можно отнести: организацию совместных действий взрослых и детей. Это значит, что процесс обучения должен основываться на системном анализе образовательного процесса и осуществляться в тесной связи науки и практики. Выбор учебно-методического комплекса, учитывающий применение дидактических игр для развития творческих способностей на уроках математики.

К психолого-педагогическим условиям можно отнести: диагностику психологических особенностей ребёнка; изучение интересов и потребностей учащихся, их творческих способностей; использование различных способов мотивации деятельности учащихся.

К методическим условиям относятся: использование в образовательном процессе дидактических игр и разработка комплектов дидактических игр.

Учитывая все организационно-педагогические условия и теоретический материал, мы составили таблицу, в которой, классифицируя все дидактические игры, разбили их на комплекты для различных этапов урока (Таблица 6). Такая группировка подчёркивает направленность дидактических игр на обучение, стимулирует познавательную деятельность учащихся и развивает их творческие способности.

Дидактические игры должны иметь место на протяжении всей работы, и прежде всего, на уроке. В начале урока цель игры заключается в следующем – организовать и заинтересовать детей, стимулировать их активность. Середина урока – решение задачи усвоения темы. Конец урока – игра может носить поисковый характер. Но на каждом этапе урока игра должна соответствовать следующим требованиям: доступность, увлекательность, интерес. Дидактическая игра входит в целостный педагогический процесс и тесно взаимосвязана с другими формами обучения и воспитания детей.

Таблица 6

Комплекты дидактических игр

Этап урока	Классификация игр	Примеры
Организационный этап. Проверка домашнего задания.	Игры, направленные на формирование и совершенствование навыков устного счёта.	Рассказ-небылица. Определи слово. Игра-цепочка. Расшифруй слово.
Этап актуализации опорных знаний.	Игры, направленные на актуализацию теоретических знаний.	Что лишнее? Крестики-нолики.
Этап мотивации (определение совместной цели деятельности)	Игры, направленные на составление задач по рисункам, таблицам, символическим записям.	Счастливый случай. «Черный» ящик.

Продолжение таблицы 6

Изучение нового материала	Игры по формированию вычислительных навыков и умений	Лови ошибку. Ролевая игра. Игра-путешествие.
Контроль и самопроверка	Контрольно-обобщающие игры	Кто хочет стать отличником. Заморочки из бочки.
Подведение итогов. Рефлексия. Домашнее задание.	Игры, направленные на самостоятельное переложение изученного материала в творческий продукт (сказки, стихотворные правила, сочинения, ребусы, кроссворды)	Головоломки. Кроссворды. Сочинялки.

Вывод

В ходе анализа были рассмотрены теоретические аспекты творческих способностей, виды дидактических игр при обучении математике в начальной школе. В результате чего было установлено следующее: дидактические игры развивают творческие способности учащихся. И развивать творческие способности на уроках математики возможно при реализации комплекса организационно-педагогических условий применения комплекта дидактических игр.

2 Реализация дидактических игр как средства развития творческих способностей учащихся на уроках математики

2.1 Экспериментальная работа по апробации комплекса условий применения дидактической игры, для развития творческих способностей учащихся на уроках математики начальной школы

В первой части теоретически была обоснована важность проблемы развития творческих способностей, и если предположить, что применяя дидактические игры на различных этапах урока, можно развить их у учащихся. Исходя из вышесказанного, мною было проведено исследование, в результате которого проведена диагностика, позволяющая выявить, что применение дидактических игр на уроках математики влияет на уровень развития творческих способностей.

Практической базой исследования является ГУ «Набережная средняя школа» села Елизаветинка Тарановского района Костанайской области. На протяжении двух четвертей велась опытно-экспериментальная работа по изучению влияния дидактических игр на развитие творческих способностей школьников при изучении математики в начальной школе. Наблюдения проводились с сентября 2012 года по март 2013 года на учениках 3-го класса ГУ «Набережная средняя школа». Суть эксперимента заключалась в следующем: апробировать комплекты дидактических игр и определить их влияние на развитие творческих способностей школьников на уроках математики в начальной школе.

Основными этапами опытно-экспериментальной работы были:

Констатирующий этап

• Изучение учащихся класса (диагностика личности учащегося, диагностика мотивационной и когнитивной сферы, диагностика исходного уровня творческих способностей).

Формирующий этап

• Выбор УМК, составление рабочей программы с учётом поставленных задач: Реализация комплекта дидактических игр. Выбор оптимальных методов, форм и средств к уроку
• Промежуточная диагностика отдельных параметров развития творческих способностей.
• Коррекция организации процесса применения комплекта дидактических игр на уроке математики.

Завершающий этап

• Завершающая диагностика отдельных параметров развития творческих способностей.
• Разработка методических рекомендаций по применению комплекта дидактических игр.

Констатирующий этап эксперимента предполагал изучение учащихся класса, раскрытие исходного уровня их творческих способностей Совместно с психологом школы была проведена диагностика личности учащихся 3 класса, которая показала исходные индивидуально-психологические качества личности

• по доминанте функциональной асимметрии полушарий головного мозга,

• по каналам восприятия (аудиал, визуал, кинестетик),

• по уровню отдельных параметров развития творческих способностей.

(Приложение 2).

В дальнейшей работе это может сыграть огромную роль как в планировании и организации работы со всем классом, так и с отдельными ребятами. В исследуемом классе 8 учеников, из них 5 девочек и 3 мальчика. Класс разделён на 3 группы: сильные дети, дети средних возможностей и слабые. Большинство ребят по своему темпераменту сангвиники и меланхолики. (рисунок 3)

Рисунок 3 Тип темперамента 3 класса

Как видно из рисунка 4 мотивационная сфера так же резко отличается, есть дети с высокой степенью мотивации 60%, а остальные с низкой степенью мотивации, как правило, это слабоуспевающие, недобросовестно относящиеся к выполнению заданий учащиеся. Это создает определенные трудности в работе с классом. Вот тут-то на помощь и приходят дидактические игры. Они помогают создавать ситуацию успеха и повышать мотивацию слабоуспевающих детей.

Рисунок 4 Уровень мотивационной сферы

Скорость реакции у некоторых ребят (25%) быстрая, у части ребят (45%) средняя, и у остальных (30%) - низкая. Это говорит о том, что в классе есть медлительные дети, которые не могут быстро дать ответ на поставленный вопрос - требуется время на осмысление. Такие ученики с трудом переключаются с одного вида деятельности на другой. Им требуется переходный этап. В качестве таких переходных этапов - «мостиков» можно использовать дидактические игры как средство активизации.

При первичной диагностике уровня творческих способностей учащихся 3 класса было обнаружено следующее: память, мышление, любознательность развиты на среднем уровне, а такой критерий, как: воображение оказался менее развитым. (рисунок 5). Исходя из этого, я пришла к выводу, что при планировании отдельных этапов урока работу следует организовывать таким образом, чтобы активизировать процесс обучения в нужном русле. А значит, необходимо учитывать индивидуальные особенности учащихся, использовать различные дидактические приёмы.

Рисунок 5 Уровень творческих способностей учащихся 3 класса

В начальной школе у детей, как правило, развито наглядно-образное мышление. Изучив особенности детей, необходимо достаточно глубоко анализировать схему предполагаемого урока. Все дети разные. В классе есть и кинестетики и аудиалы и визуалы. Поэтому, кинестетику и аудиалу бесполезно что-либо предъявлять в виде схем или чертежей, хотя для визуала эта методика подойдёт намного лучше, чем другие. Кинестетики легко справятся со сбором различных моделей, макетов. Для них очень занимательны исследования, эксперименты. Для аудиала увлекательным будет сочинение какой-либо сказки или рассказа, работа в паре, диалог, ролевая игра. Всё это поможет лучшему развитию творческих способностей учащихся.

Игра имеет ценность только в том случае, когда она способствует лучшему пониманию математического смысла вопроса, уточнению и формированию математических знаний учащихся. Дидактические игры и игровые упражнения побуждают общение между учениками и преподавателем, отдельными учениками, поскольку в процессе проведения этих игр взаимоотношения между детьми начинают носить более непринуждённый и эмоциональный характер.

2.2 Исследование отношения детей и учителей к дидактическим играм на уроках математики

Одним из методов психолого-педагогического исследования было анкетирование учителей и учащихся с целью выявления их отношения к играм на уроках математики. В результате в ГУ «Набережная средняя школа» было проведено анкетирование учителей и учащихся. В анкетировании приняло участие 7 учителей. В процессе опроса были выявлены следующие данные:

Вопрос №1: «Какое место занимает игра в развитии личности ребёнка» 71% опрошенных учителей считает "самое главное", 29% – "не самое главное". (рисунок 6)

главное	не самое главное	второстепенное	никакого места не занимает	не задумывался над этим	не знаю
5	71%	2	29%	-	-	-	-	-	-	-	-

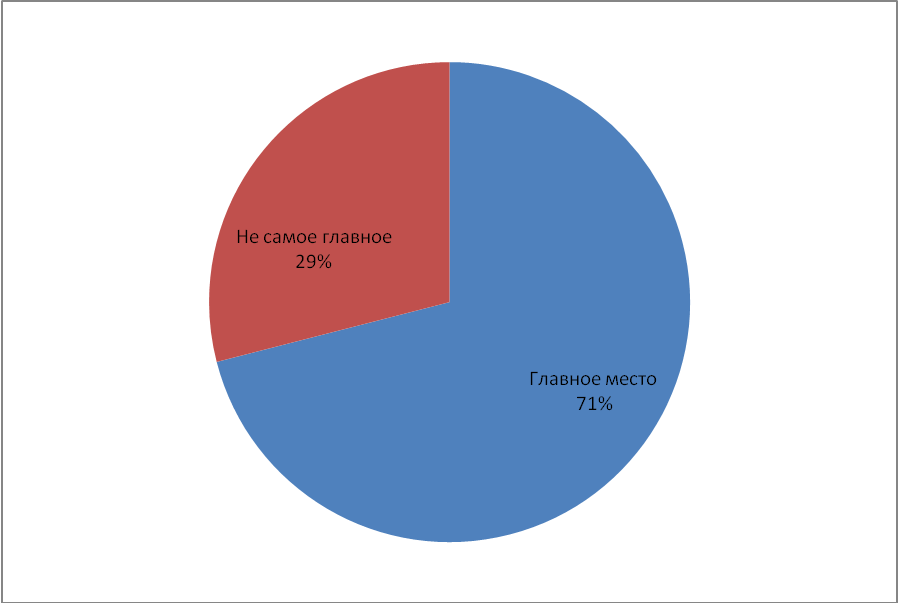
Рисунок 6 Место игры в развитии личности ребёнка

Вопрос №2: "Вы в своей педагогической практике много времени отводите дидактической игре в учебном процессе?" 71% учителей ответило "очень много", а 29% – не очень много, но достаточно.

много	не очень много	только на уроках математики	сегодня это никому не нужно	не задумывался над этим	не знаю
5	71%	2	29%	-	-	-	-	-	-	-	-

По мнению основной массы опрошенных учителей (5 чел. – 71%), главной трудностью в проведении дидактической игры является отсутствие в школе необходимых условий. И лишь 29% учителей не имеют трудностей в проведении дидактических игр. По этому вопросу можно составить следующую таблицу.

Отсутствие в школе необходимых условий	Равнодушие детей	Не задумывались над этим	Не знаю	Нет
4	57%	-	-	1	14%	-	-	2	29%

Вывод: учителя положительно относятся к дидактической игре и активно используют её в своей педагогической деятельности, несмотря на объективные трудности в проведении, и не считают игру пустой тратой времени.

В ГУ «Набережная средняя школа» также были проанкетированы учащиеся начальных классов. В опросе приняло участие 26 учеников из четырёх классов по произвольному выбору. В таблице указаны те ответы, которые выбрали ученики.

Таблица 7

Отношение к играм на уроках

Вопрос	Варианты ответов
Какие уроки ты больше всего любишь?	Люблю все уроки	С использованием схем, таблиц, картин	С использование различных игр	Главное, чтобы на уроке было интересно
	9	5	7	5
Если бы ты был учителем, чего больше было бы у тебя на уроке:	Работы с учебником	Таблиц, схем, картин	Различных игр	Самостоятельных работ
	5	2	15	4
Как часто на уроках в вашем классе бывают игры	Очень часто	Часто	Не очень часто
	10	8	8
Как ты относишься к игре на уроках?	Очень хочу участвовать
	26
Как ты думаешь, какая польза от игры на уроке?	Очень большая	Большая	Не очень большая	Небольшая
	11	10	3	2

На первой неделе обучения с классом была проведена анкета на тему «Как вы относитесь к учебе по разным предметам» (анкета взята из книги «Управление образовательными системами»).

Каждому ученику был выдан бланк анкеты в виде небольшой таблицы. (Таблица №8)

Таблица 8

Твоё отношение к учёбе

№	Отношение	Предметы
		Математика	Русский язык	Литература
1.	На уроке иногда бывает интересно.
2.	Учу, потому что надо учиться.
3.	Получаю удовольствие, работая на уроке, всегда интересно, узнаю много нового.
4.	С нетерпением жду урока и стремлюсь узнать больше, чем требует учитель.

В таблице внесены три основных предмета для того, чтобы проследить, как изменились результаты после проведения дидактических игр только по математике.

Ребятам нужно было поставить знак «+» по каждому предмету в той строчке, которая лучше характеризует его отношение к предмету. Номера вариантов ответов соответствуют 4 уровням познавательной деятельности.

1. проявляет ситуативный интерес;
2. учит по необходимости;
3. интересуется предметом;
4. проявляет повышенную познавательную активность.

Результаты анкетирования были занесены в сводную ведомость и обработаны. Итоги занесены в таблицу, высчитан процент от общего количества учеников (количество учеников в классе – 8).

Таблица 9

Результаты анкетирования в первую неделю обучения в 3 классе

(в начале экспериментальной работы)

Ф.И. ученика

математика

русский язык

литература

1

2

3

4

1

2

3

4

1

2

3

4

Аскарова Адель

+

+

+

Астафьева Ольга

+

+

+

Балгабаева Айжан

+

+

+

Жузбеков Ильдар

+

+

+

Кламм Алина

+

+

+

Нуржанов Нуржан

+

+

+

Парижжанова Айдана

+

+

+

Погорелов Данил

+

+

+

Таблица 10

Уровни сформированности познавательной активности учащихся

(в процентах)

№	Уровень	Предметы
		Математика	Русский язык	Чтение
1.	Проявляет ситуативный интерес	0 учеников	0 учеников	0 учеников
2.	Учит по необходимости	4 ученика 50%	4 ученика 50%	4 ученика 50%
3.	Интересуется предметом	1 ученик 12,5%	2 ученика 25%	2 ученика 25%
4.	Проявляет повышенную познавательную активность.	3 ученика 37.5%	2 ученика 25%	2 ученика 25%

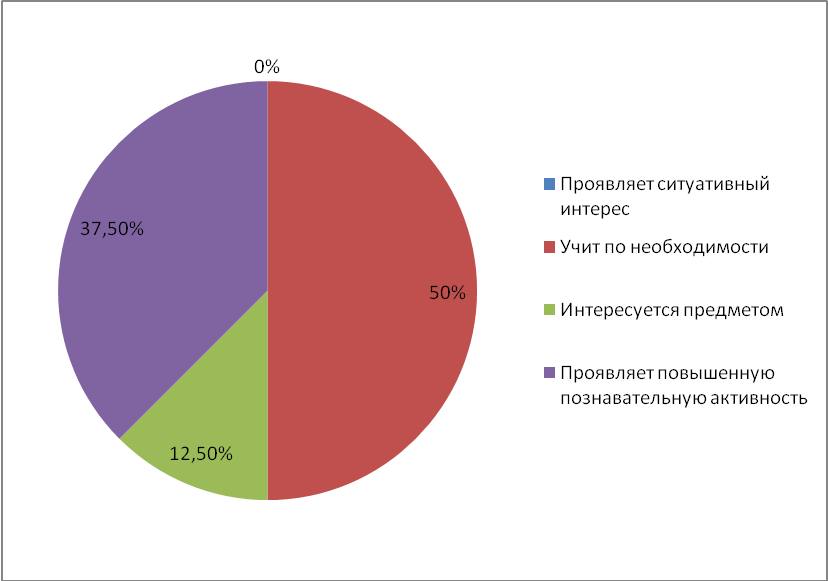
Рисунок 7 Математика в процентном соотношении

На первом этапе такую оценку нельзя назвать ещё объективной. Анализ уровня сформированности познавательной активности подтвердил актуальность проблемы и необходимость подбора дидактических игр с целью развития творческих способностей учащихся на уроках математики. Из всего этого можно сделать вывод: учащимся начальной школы нравятся все уроки, положительно относятся к использованию игры на уроках. Если бы учащиеся были учителями, то более 50% использовали бы на своих уроках игры. И практически основная масса детей считает, что игра на уроках приносит большую пользу и с удовольствием в них участвуют. Таким образом, необходимо в каждый урок включать игровые моменты, но не в качестве разрядки обстановки, а с целью активизации знаний детей, развития психических процессов.

2.3 Особенности использования дидактических игр при объяснении нового материала

Практика показывает, что увлекательный материал применяется на разных этапах усвоения знаний: на этапах объяснения нового материала, его закрепления, повторения, контроля. Применение дидактических игр оправдано только тогда, когда они тесно связаны с темой урока, целостно сочетаются с учебным материалом, соответствующим дидактическим целям урока. [32]В практике начальной школы имеется большой опыт использования игр на этапе повторения и закрепления изученного материала, и крайне редко применяются игры для получения новых знаний.

При объяснении нового материала целесообразно использовать такие игры, которые содержат необходимые признаки изучаемой темы. Также в ней должны быть заложены практические действия детей с группами предметов или рисунков.

При изучении раздела “Нумерация чисел первого десятка” применяются, прежде всего, такие игры, с помощью которых дети осознают приёмы образования каждого последующего и предыдущего числа.

На этом этапе можно применить игру “Составим поезд”.

Дидактическая цель: ознакомить детей с приёмом образования чисел путём прибавления единицы к предыдущему числу и вычитания единицы из последующего числа.

Содержание игры: учитель вызывает к доске поочерёдно учеников. Каждый из них выполняет роль вагона, называет свой номер. Например, первый вызванный ученик говорит: “Я первый вагон”. Второй ученик, выполняя роль второго вагона, цепляется к первому вагону (кладёт руку на плечо ученика, стоящего впереди). Называет свой порядковый номер, остальные составляют пример: “Один да один, получится два”. Затем цепляется третий вагон, и все дети по сигналу составляют пример на сложение: “Два да один – это три”. Потом вагоны (ученики) отцепляются по одному. А класс составляет примеры вида: “Три без одного – это два. Два без одного – это один”.

На основе использования игры “Составим поезд” учащимся предлагают считать число вагонов слева направо и справа налево и подводят их к выводу: считать числа можно в одном направлении, но при этом важно не пропустить ни одного предмета и не сосчитать его дважды.

Также при знакомстве детей с приёмом образования чисел можно использовать игру “Живой уголок”.

Дидактическая цель: ознакомление детей с приёмом образования чисел при одновременном закреплении пространственной ориентации, понятий “больше”, “меньше”.

Средства обучения: изучение животных.

Содержание игры: учитель говорит: “В нашем живом уголке живут кролики: серый и белый, кролики грызут морковь. Сколько кроликов грызут морковь? (два, ответ фиксируется показом цифры 2). Назовите, какие кролики грызут морковь? (серый и белый). К ним прибежал ещё один кролик. Что изменилось? (кроликов стало больше) Сколько кроликов теперь едят морковь? (три, ответ фиксируется показом цифры 3) Перечисли их (один белый и ещё один белый, и ещё один серый, всего три). Каких кроликов больше, белых или серых? (белых) Почему их больше? (их два, а два это один и один). Почему 2>1? (два идёт при счёте после числа 1).

Аналогично можно рассматривать образование последующих чисел.

При изучении нумерации в пределах десяти необходимо довести до понимания детей, что последнее названное при счёте число обозначает общее количество всей группы предметов.

С этой целью следует проводить игры “Лучший счётчик”, “Хлопки”. С помощью этих игр дети устанавливают соответствие между числом и цифрой.

“Лучший счётчик”

Содержание игры: учитель на магнитной доске по секторам соответственно размещает от 1 до 10 рисунков. Открывая каждый сектор поочерёдно, учитель предлагает детям сосчитать число рисунков и показать нужную цифру. Сосчитавший первый называется лучшим счётчиком. Затем учитель показывает цифры вразбивку, а ученики – соответствующее число рисунков в секторах круга. В итоге игры учитель открывает 2 сектора, предлагает сравнить число рисунков в них и определить, где предметов меньше и на сколько.

“Хлопки”

Содержание игры: учитель на магнитной доске размещает по секторам от 1 до 10 рисунков. Открывая по очереди сектор за сектором, предлагает сосчитать число рисунков и по его сигналу похлопать столько же раз, сколько открыто рисунков, и показать нужную цифру. (учитель задаёт ритм хлопков).

Изучая числа первого десятка, важно сравнивать каждое предыдущее число с последующим и наоборот. Для этого предназначены игры “Лучший счётчик”, “Число и цифру знаю я”.

«Число и цифру знаю я»

Содержание игры: учитель на магнитной доске поочередно открывает сектор за сектором, дети считают число цифр в каждом из них и показывают учителю соответствующую карточку с цифрой, а затем сравнивают число цифр в двух соседних секторах магнитного моделеграфа.

Работа над составом числа начинается в разделе “Нумерация чисел первого десятка”. Состав чисел от одного до пяти дети в этот период должны знать на память, состав чисел 6-10 можно рассматривать на наглядной основе, на следующем этапе дети знакомятся с составом чисел на основе сложения по памяти. На третьем этапе дети воспроизводят состав чисел на основе выявленной закономерности: числа, стоящие на одинаковых местах (слева и справа) в числовом ряду, составляет в сумме последнее число в этом ряду.

В этот период большую помощь учащимся в изучении состава чисел окажет игра “Числа, бегущие навстречу друг другу”

«Числа, бегущие навстречу друг другу»

Дидактическая цель: знакомство с составом числа 10.

Содержание игры: учитель предлагает детям записать в тетрадь числа от 1 до 10 по порядку и дугами показать два числа, которые бегут навстречу друг другу, образуя в сумме число 10. Затем просит записать примеры на сложение с этими числами. Например:

0 1 2 3 4 5 6 7 8 9 10

0 + 10 = 10 10 + 0 = 10

1 + 9 = 10 9 + 1 =10

Учитель спрашивает: “Что интересного вы заметили при составлении примеров? Дети отвечают, что числа, стоящие на одинаковых местах справа и слева в числовом ряду, составляют в сумме число 10”.

При изучении нумерации чисел в пределах 20 можно выделить 4 этапа:

1. Образование чисел путём прибавления единицы к предыдущему числу и вычитание единицы из последующего числа. Игра “Составим поезд”.

2. Образование чисел из десятков и единиц. Здесь можно предложить игру “Математическая эстафета”.

3. Анализ состава чисел в пределах 20.

4. Письменная нумерация чисел в пределах 20.

“Математическая эстафета”

Дидактическая цель: ознакомление с образованием чисел из десятка и единиц.

Средства обучения: 10 кругов и 10 треугольников из приложенных к учебнику математики для подготовительного класса.

Содержание игры: учитель делит класс на 3 команды по рядам и проводит игру-соревнование. Первый ученик из первой команды иллюстрирует число с помощью кругов и треугольников, второй из этой же команды называет цифрой обозначенное число, третий – его состав, четвёртый показывает число на карточках.

Аналогичные упражнения выполняют из второй и третьей команд. Победит та команда, которая не допустит ни одной ошибки или допустит меньшее их число.

При изучении нумерации чисел в пределах 100 задача состоит в том, чтобы научить считать и записывать числа.

Установлению связи между устной и письменной нумерацией поможет известная игра “Молчанка”.

«Молчанка».

Содержание игры: учитель иллюстрирует на абаке или карточках двузначные числа, а учащиеся обозначают их с помощью разрезных цифр и показывают их молча учителю или записывают в тетради.

2.4 Особенности использования дидактических игр при закреплении нового материала

На уроках закрепления нового материала важно использовать игры на воспроизведение свойств, действий, вычислительных приёмов и т.д. В этом случае применение средств наглядности следует ограничить и направить внимание на проговаривание вслух правил, свойств, вычислительных приёмов. При закрепление материала форма проведения игры может быть разнообразной: коллективной, групповой и индивидуальной. Целесообразно проводить игры в группах и в виде соревнования.

Для проведения соревнования учитель в таблице на доске звёздочками отмечает дружную работу команд в течение урока. Если активность и заинтересованность детей какой-либо команды ослабевает (например, из-за того, что команда набрала меньшее число очков), то учитель должен спросить такого ученика из этой команды, который сможет правильно ответить и заработает звезду.

В конце урока учитель, вместе с детьми подводя итоги соревнования, обращает внимание на дружную работу участников команд. Это способствует формированию чувства коллективизма, сплочению. Необходимо отнестись с большим тактом к детям, которые допустили какие-либо ошибки. Ошибки учащихся необходимо анализировать не в ходе игры, а в конце, чтобы не нарушать общего впечатления от игры.

Для закрепления устной нумерации в пределах 100 используется игра “Цепочка”, при проведении которой дети каждого ряда (команды) на основе иллюстративного материала образуют числа в пределах 100, соревнуясь друг с другом.

Для закрепления состава чисел можно предложить следующие игры: “Арифметический лабиринт”, “Угадай-ка!”, Эстафета”. Смысл этих игр заключается в том, что дети проговаривают все случаи состава числа 10 и выигрывает тот, кто назовёт наибольшее число комбинаций. Можно провести игру в виде соревнования по рядам. Также здесь можно предложить игру “Контролёры”.

«Контролёры».

Дидактическая цель: закрепление знания состава чисел первого десятка.

Содержание игры: учитель распределяет детей на две команды. Два контролёра у доски следят за правильностью ответов: один – первой команды, второй - другой команды. По сигналу учителя ученики первой команды делают несколько ритмических наклонов вправо, влево и считают про себя. По сигналу учителя они называют хором число наклонов первой команды до заданного числа и ведут счёт про себя (например 6 – прибавил 1, 7 – прибавил 2, 8 – прибавил 3). Затем они называют число выполненных наклонов. По числу наклонов, выполненных учениками 1 и 2 группы и называется состав числа. Учитель говорит: “Восемь – это…”, ученики продолжают: “Пять и четыре”. Контролёры показывают зелёные круги в правой руке, если согласны с ответом, красные – если нет. В случае ошибки упражнение повторяется. Потом учитель предлагает детям второй команды по сигналу сделать несколько приседаний, а ученики первой команды дополняют приседания до заданного числа. Называется состав числа. Аналогично анализируется состав чисел на основе хлопков.

Данная игра не только систематизирует знания учеников, но и несёт элементы физической разгрузки, т.к. использует физкультурные упражнения.

При закреплении состава десятичного состава двузначных чисел используются игры “Сколько палочек в другой руке?”, “Хлопки”.

“Сколько палочек в другой руке?”

Дидактическая цель: закрепление знания десятичного состава двузначного числа.

Средства обучения: набор отдельных палочек и пучков палочек.

Содержание игры: вызванный ученик берёт пучок палочек в одну руку, а отдельные палочки – в другую руку и показывает их классу. Дети угадывают их количество и показывают карточку с соответствующим числом.

Затем задание усложняется: надо угадать, сколько отдельных палочек в руке, если в другой – пучок, и составить пример на сложение. Например, ученик взял 15 палочек, положив пучок из 10 палочек в правую руку и 5 отдельных палочек в левую. Дети составляют пример на сложение 10+5=15.

“Хлопки”

Цель игры: закрепление знания десятичного состава двузначного числа.

Средства обучения: набор определённых палочек и пучков палочек.

Содержание игры: учитель вызывает двух детей к доске. Ученик, стоящий справа, обозначает единицы, а стоящий справа – десятки. Учитель называет двузначное число, правый ученик хлопками обозначает число единиц в этом числе, а левый – число десятков. Все остальные ученики выполняют роль контролёров. Они сигналят, если десятичный состав числа показан учениками неверно.

Как уже упоминалось в п.2 при изучении нумерации чисел в пределах 20 выделяют 4 этапа. Один из этапов – это письменная нумерация чисел в пределах 20. Здесь можно предложить игру “Стук-стук”.

«Стук-стук».

Дидактическая цель: закрепление знаний по нумерации чисел в пределах 20.

Средства обучения: на доске изображена таблица с двумя разрядами:

Десятки	Единицы

Содержание игры: учитель молча стучит указкой один раз в разряде десятков и несколько раз в разряде единиц. Дети внимательно слушают и показывают учителю соответствующее число на карточке с цифрами.

Для закрепления навыков счёта можно предложить игру “Слушай и считай”.

«Слушай и считай».

Содержание игры: у каждого из учеников набор карточек с числами от 1 до 10. У учителя палочка, которой он ударяет по какому-либо предмету, издающему громкий звук, определённое число раз. Все учащиеся должны немедленно поднять и показать карточку с числом, соответствующим количеству ударов.

Можно условиться, что играющие, услышав удары, должны поднять карточку с числом, недостающим, например, до десяти (ударов было три, поднять карточку с числом 7). Затем устанавливается другое правило: показать надо не число, соответствующее числу ударов, а два соседних числа – меньшее и большее. Можно предложить и другой вариант игры: учитель сначала ударит палочкой по одному предмету 8 раз, а по другому – 3 раза. Это значит, что учащиеся должны от восьми отнять три и показать карточку с числом 5. Игра требует тишины и внимания, поэтому можно предложить ребятам, прислушиваясь к числу ударов, закрывать глаза.

В теме “Нумерация чисел первой сотни” для усвоения порядка следования чисел при счёте, порядковых и количественных отношений между смежными числами можно использовать игры “Считай дальше с любого числа”, “Назови соседей числа”, “Кто быстрей сосчитает? ”.

“Считай дальше с любого числа”

Эта игра поможет избавиться от ошибки, когда ученик называет число с переходом через круглый десяток, например, 67, 68, 69, 70 (а не шестьдесят десять).

“Назови соседей числа”

Эта игра даёт возможность каждое число первой сотни рассматривать не изолированно, а в связи с предыдущим и последующим числом.

Средства обучения: мяч или два мяча – большой и маленький (или разного цвета).

Содержание игры: учитель бросает мяч то одному, то другому участнику игры, а те, возвращая мяч, отвечают на вопрос учителя. Бросая мяч, учитель называет какое-либо число, например двадцать один, играющий должен назвать смежные числа – 20 и 22 (обязательно сначала меньшее, потом большее).

Возможен и другой, более сложный вариант игры. Возвращая мяч, играющий должен сначала отнять от названного учителем числа единицу, потом прибавить к нему полученную разность.

Например, учитель назвал число 11, а играющий должен назвать числа

10 (11-1=10) и 21 (11+10=21).

Эту игру можно провести и с двумя мячами: большим и маленьким (или разного цвета). Когда учитель бросает большой мяч, то отвечающий должен, к примеру, прибавить 9 и вернуть мяч обратно, а когда маленький – то отнять 3. Здесь дети не только считают, но и развивают внимание, чтобы не перепутать действия.

2.5 Особенности использования дидактических игр на этапе обобщения знаний

На этапе обобщения знаний целесообразно проводить уроки в форме путешествия в сказочную страну или условной экскурсии в лес с элементами игры.

При обобщении темы “Нумерация чисел в пределах 20” можно предложить следующую ситуацию. Класс отправляется на луг ловить бабочек. Начинается игра “Поймай бабочку”.

«Поймай бабочку»

Дидактическая цель: обобщение знаний о разрядном составе числа.

Содержание игры: на доску вывешивается иллюстрация с изображением луга и макеты бабочек. На каждой бабочке написан разрядный состав чисел до 20. У каждого ребёнка бабочка из картона жёлтого цвета, на обратной стороне которой записаны числа. Один из вызванных к доске учеников ловит бабочку, прикреплённую на ниточке, на которой указан разрядный состав числа, остальные ученики поднимают (ловят) тех бабочек, на которых написаны числа, соответствующие разрядному составу.

Потом все отправляются в магазин, (проголодались на прогулке). Далее проходит игра “В магазин”.

«В магазин»

Дидактическая цель: обобщение знаний учащихся о составе числа.

Содержание игры: вывешивается два плаката: один с рисунками монет, другой с изображением предмета и его ценой (хлеб – цена, батон, булочка, рогалик и т.п.). Дети подходят к плакатам, показывают хлеб, и расплачиваются за покупку набором из существующих монет.

Также при обобщении знаний по теме “Нумерация чисел в пределах 100” можно использовать следующие игры: «Войди в ворота», «Если вместе, если дружно».

“Войди в ворота”

Дидактическая цель: обобщение знаний о составе числа.

Содержание игры: дети берут карточки с числами 0, 1, 2, … , 10. Два ученика образуют ворота (оба поднимают вверх сцепленные руки), в свободных руках они держат карточки с цифрами. В результате образуется несколько пар детей и один лишний. Он входит в ворота, выбирает ученика с такой карточкой, чтобы их числа в сумме составили число 10. Оба ученика проходят назад. Оставшийся без пары ученик также входит в ворота и подбирает пару себе. Все дети сидевшие за столами, следят за правильностью подбора пар.

“Если вместе, если дружно”. Особенность этой игры – соревнования – эстафетный характер заданий, когда от вклада каждого, от чёткости и взаимодействия зависит общий результат.

Дидактическая цель: развитие логического мышления и воображения, проверка элементарных математических навыков.

Ход игры: учитель объявляет, что урок пройдёт в виде игры под девизом “Если вместе, если дружно”. Класс делится на две команды. Обе команды носят имена великих математиков прошлого: “Пифагоры”, “Архимеды” (желательны эмблемы). Учитель предупреждает, что соревнования будут эстафетными, поэтому будьте готовы проявить взаимопонимание и взаимовыручку.

Эстафета №1 “Очень длинный пример”

На доске написаны примеры. Каждый ученик из команды подбегает к доске по очереди, решает один пример и передаёт эстафету следующему. Кто быстрее и правильнее решит весь пример?

Эстафета №2 “Собери робота”

Участники команд берут из корзин геометрические фигуры (круги, треугольники, квадраты и т.п.) и крепят их на доске так, чтобы получилась фигура, напоминающая робота. У кого робот получится лучше?

Эстафета №3 “Каждому по примеру”

Количество примеров на доске соответствует числу участников команды. Участники команд по очереди подбегают к доске и решают по одному примеру (на выбор). Побеждает команда, которая быстро и без ошибок решит все примеры.

Эстафета №4: “Найди цифру”

На доске два плаката, где в беспорядке прикреплены цифры от 1 до 30. Участники команд по очереди снимают цифры по порядку и составляют числовой ряд. Побеждает команда, первая и правильно построившая полный числовой ряд.

На формирующем этапе. При разработке конспекта урока я обращалась к полученному ранее комплекту дидактических игр, учитывая выявленные организационно-педагогические условия.

Дидактические игры очень многообразны. Среди них есть игры, направленные на развитие творческих способностей, совершенствование и тренировки памяти, мышления, воображения, любознательности. Они помогают лучше усвоить и закрепить материал, полученный на уроке, побуждают живой интерес к изучаемому предмету.

Я хочу остановиться на каждом этапе урока.

Организационный этап: Начало урока – очень важный этап. И, как правило, успех урока зависит от умелой организации. На этом этапе наиболее эффективны такие дидактические игры, как «Расшифруй слово»; «Игра – цепочка»; «Расшифруй пароль» и другие, которые направлены на формирование и совершенствование навыков устного счёта, внимания, анализа и выявления проблем. (Приложение 3, 4)

Например: «Шифровальщики».

Данную игру использую на уроках математики при устном счёте. На доске записываю задания и зашифрованные буквами алфавита ответы. Выполнив задания правильно, ученики открывают слово и узнают тему урока или зашифрованное слово, связанное с данной темой.

Тема урока «Решение уравнений. Составление равенств и неравенств».

«Шифровальщик»

164 – 8 = а 160 + 40 = у 90 – 2 = н 102 + 18 = с

26 + 7 = в 58 + 9 = е 100 – 5 = и 48 + 9 = р

52 – 3 = т

200	57	156	33	88	67	88	95	67
У	Р	А	В	Н	Е	Н	И	Е

57	156	33	67	88	120	49	33	156
Р	А	В	Е	Н	С	Т	В	А

Следующий этап – этап актуализации опорных знаний.

На данном этапе рационально применять такие игры, которые направлены на актуализацию теоретических знаний: Что лишнее? Математический аукцион; Поле чудес; Крестики – нолики и другие. Это могут быть задания – загадки: «Что лишнее?», «Что вы видите?», «Не собьюсь» и другие. Эти дидактические игры развивают воображение, творческое мышление, внимательность, память, любознательность. Такую работу можно организовывать как в парах, так и индивидуально.

Например, на уроке математики в 3 классе при закреплении таблицы умножения и деления на 3 я использую такую дидактическую игру как «Бег на короткие дистанции» или «Не собьюсь».

«Бег на короткие дистанции» или «Не собьюсь».

Проверка знания таблицы умножения на 3. Ученики называют все числа от 1 до 30, но вместо чисел, делящихся на 3, говорят фразу “Не собьюсь”.

1, 2, не собьюсь, 4, 5, не собьюсь, 7, 8, не собьюсь и т.д.

При устном счёте использую такие задания, как «Шифровальщик».

Расположить карточки так, чтобы произведение возрастало.

7·8	7·4	9·6	6·6	9·8
Ч	У	А	Д	А

7·6	8·3	8·6	8·7	9·6
С	У	П	Х	Е

Ответ: После решения и расположения карточек с результатами в порядке возрастания должны получиться два слова “УДАЧА” и “УСПЕХ”. (Приложение 5)

Следующий этап - этап мотивации (определение совместной цели деятельности).

Для данного этапа следует подбирать дидактические игры, направленные на составление задач по рисункам, таблицам, символическим записям. ( Шляпная дискуссия; Невод; Дурная голова; Чёрный ящик; Счастливый случай).

С помощью данных игр ученикам предоставляется возможность самим обозначить круг вопросов, требующих актуализации. На данном этапе развивается память, любознательность, ученики становятся более уверенными в своих силах. Рассуждая вслух, обсуждая, анализируя, ученики учатся высказывать свои мысли, отстаивать свою точку зрения. В обсуждения включаются как сильные, так и слабые учащиеся. Этот приём позволяет создавать ситуацию успеха на уроке.

Например, при закреплении пройденного материала урок можно построить по принципу ученик – учитель. Где сильные ученики могут проверять знания у слабых учащихся, выступая в роли учителя. В результате чего ученики сами выдвигают задачи урока, развиваются творческие способности, память, внимание, любознательность, культура речи, смелость рассуждений. В качестве дидактических игр подойдут такие игры, как: «Найди ошибку», «Самый внимательный» и т.д. На карточках написаны слова, в которых Буратино допустил ошибки. Он пропустил гласные буквы. Какие слова написаны?

Рзнсть, мнс, смм, чсл, квдрт, здч, тргльнк, прмгльник.

(Ответы: разность, минус, сумма, число, квадрат, задача, треугольник, прямоугольник).

В этап изучения нового материала можно включить дидактические игры по формированию вычислительных навыков. Это: «Мозговая атака», «Сюжетные задачи», «Лови ошибку», игра-путешествие. (Приложение 6) Использование дидактических игр эффективно тогда, когда оно тесно связано с темой урока, соответствует дидактическим целям урока, сочетается с учебным материалом. При изучении нового материала целесообразно использовать такие дидактические игры, которые содержат существенные признаки изучаемого материала, данной темы.

Большую роль в процессе изучения темы урока играют сюжетные задачи. Сюжетная задача описывает реальную или близкую к реальности ситуацию на неформально-математическом языке. Решение задач, как правило, всегда сложный момент в преподавании математике. Для улучшения ситуации уместно включать игровые моменты или дидактические игры, основанные на сказочных сюжетах.

Например, вспомнить и назвать сказки, в названиях которых есть числа. («Три поросёнка», «Волк и семеро козлят», «Белоснежка и семь гномов», «Сказка о мёртвой царевне и семи богатырях»).

Следующее задание - Сказочные герои вам предлагают решить задачу.

Задача 1. Три поросёнка собрали яблоки. Наф-Наф собрал 10кг, Ниф-Ниф собрал в 2 раза больше, а Нуф-Нуф собрал столько, сколько Наф-Наф и Ниф-Ниф собрали вместе. Сколько яблок собрали поросята вместе? (Ответ: 60кг).

В качестве домашнего задания можно предложить составить задачи по другим сказкам.

Следующий этап – этап контроля и самопроверки. Для данного этапа можно использовать такие игры, как «Эстафета», таблицы тренажёры, «Кто хочет стать отличником» и другие. (Приложение 7)

Контроль на уроке должен быть всесторонним и осуществляться дифференцированно: со стороны учителя, взаимопроверка, самоконтроль. Можно использовать карточки-тренажёры, тестовые задания. Работа может выполняться как индивидуально, так и в парах или микрогруппах.

Эстафета 1 «Самый быстрый и внимательный».

Каждому ученику раздаются одинаковые карточки. По сигналу учителя начинается работа. Реши примеры, связанные между собой. Если ученики при подсчете допустили ошибку, то последующие примеры они решить не смогут, а значит, они должны будут вернуться и найти допущенную ошибку. Такие задания развивают самоконтроль, внимание.

Эстафета 2 «Цепочка».

Решение примеров по-цепочке. На доске записывается пример в несколько действий и ученики по очереди выходят к доске и записывают результат действия. Кто быстрее и правильнее решит пример?

Эстафета 3 «Каждому по примеру».

Количество примеров на доске соответствует числу участников команды. Участники команд по очереди подбегают к доске и решают по одному примеру (на выбор). Побеждает та команда, которая быстро и без ошибок решит все примеры.

Этап рефлексии. Подведение итогов.

Для данного этапа лучше всего подходят игры, направленные на самостоятельное формулирование условий и требований задачи, закодированные в данных схемах или знаках. ( Не зевай; Чайнворд; Укрась ёлочку и т.д.) (Приложение 8, 9)

Рефлексия в конце урока или на промежуточных этапах должна присутствовать обязательно. Именно на этом этапе предоставляется возможность оценить урок вместе с ребятами точки зрения поставленных задач. Здесь присутствует анализ учителя, учеников и самоанализ. Делаются акценты на трудовых успехах или неудачах, затрагиваются аспекты развития и пр.

Подача домашнего задания

Для данного этапа урока можно использовать дидактические игры, направленные, на самостоятельное переложение изученного материала, в творческий продукт (сказки, стихотворные правила, сочинения, ребусы и кроссворды).

Творческие способности можно развивать и на основе домашних заданий. Огромный развивающий эффект на уроках математики в начальной школе имеют математические сказки, которые развивают фантазию, воображение. Ученики 3-4 классов с увлечением выполняют такие задания.

Известный учёный – педагог А. И. Маркушевич говорил, что человек, не воспитывающийся на сказках, труднее воспринимает мир идеальных стремлений, что благодаря сказкам ребёнок начинает отличать реальное от необычного, что нельзя развить, минуя стихию сказки, не только воображение, но и первые навыки творческого мышления.

Сказки вносят в процесс обучения юмор, фантазию, творчество, выдумку.

Развитие творческих способностей процесс сложный и многогранный, который возлагает на учителя огромную ответственность. Процесс отслеживания развития творческих способностей занимает много времени, и целесообразнее такую работу вести совместно с психологом.

Ежедневное общение с учениками и наблюдение за ними позволят сделать определённые выводы и внесение некоторых корректировок, а специальные диагностики позволят определить уровень развития творческих способностей.

При повторной диагностике можно заметить положительную динамику уровня развития творческих способностей по определённым критериям. Дидактические игры, направленные на развитие таких способностей как: мышление, память, любознательность, воображение помогли добиться следующих результатов. (рисунок 6).

Рисунок 8 Уровень творческих способностей учащихся

Завершающий этап предполагал итогово-обобщающий анализ данных. Проведя диагностику, можно увидеть следующее – уровень творческих способностей учащихся заметно вырос. У учеников появилось желание и умение творческого преобразования учебного материала. Дети стали более активно принимать участие в НОУ, различных международных и республиканских конкурсах, таких как: «А бота», «Кенгуру», «Русский медвежонок».

На завершающем этапе мною, совместно с психологом школы использовались следующие методики:

Модифицированные креативные тесты Вильямса.

САР – это набор тестов, состоящих из двух методик для детей: Теста дивергентного (творческого) мышления и Теста творческих личностных характеристик.

САР был разработан первоначально для отбора одарённых и талантливых детей в школы, работавшие по федеральным, государственным и местным программам развития творческих способностей. В настоящее время САР доступен для измерения творческого потенциала всех детей. Эти методики могут быть использованы учителями, заинтересованными в выявлении и развитии различных способностей детей, а не только в традиционной оценке академических достижений и тестировании интеллекта.

Тестовые методики предназначены для школьников в возрасте от 8 до 17 лет (со 2 по 11 класс). Тест определения творческих способностей – опросник, состоит из 50 пунктов, помогающих выяснить, насколько любознательными, наделёнными воображением, умеющими разбираться в сложных идеях и способными на риск считают себя дети. На заполнение опросника творческих характеристик личности отводится 20 – 30 минут.

В настоящее время, применяя данные тесты, можно получить возможность отслеживания и оценки познавательных и личностных качеств ученика. САР делает более доступной объективную оценку большинства исследуемых факторов, относящихся к творческим способностям человека, по Модели Вильямса. [57] Этот набор тестов предназначен для эффективного, практичного и экономичного метода оценки четырёх когнитивно-дивергентных и четырёх личностно-дивергентных факторов этой модели.

Тест «Запомни и расставь точки», измеряющий объем внимания (Тестирование детей. Автор-составитель Богомолов В., Ростов-на-Дону, «Феникс», 2003). (Приложение 10) К окончанию формирующего эксперимента, целью которого было применение дидактических игр как средства развития творческих способностей учащихся, наблюдая за детьми, было отмечено, что дети активнее стали работать на уроке, проявляют живой интерес к математике, с удовольствием посещают эти уроки.

Цель дальнейшей работы – провести тестирование познавательной активности учащихся и определить динамику развития.

2.6 Динамика развития познавательной активности учащихся 3 класса

После формирующего эксперимента был проведён замер учения, как одного из основных компонентов активной деятельности учащегося.

Таблица 11

Уровни отношений учащихся 3 класса ГУ «Набережная средняя школа», после применения различных дидактических игр как средств активизации познавательной деятельности на уроках математики.

Ф.И. ученика

математика

русский язык

литература

1

2

3

4

1

2

3

4

1

2

3

4

Аскарова Адель

+

+

+

Астафьева Ольга

+

+

+

Балгабаева Айжан

+

+

+

Жузбеков Ильдар

+

+

+

Кламм Алина

+

+

+

Нуржанов Нуржан

+

+

+

Парижжанова Айдана

+

+

+

Погорелов Данил

+

+

+

Таблица 12

Результаты опроса

№	Уровень	Предметы
		Математика	Русский язык	Чтение
1	Проявляет ситуативный интерес	0 учеников 0%	0 учеников 0%	0 учеников 0%
2	Учит по необходимости	1 ученик 12,5%	2 ученика 25%	3 ученика 37.5%
3	Интересуется предметом	3 ученика 37.5%	3 ученика 37.5%	3 ученика 37.5%
4	Проявляет повышенную познавательную активность	4 ученика 50%	3 ученика 37.5%	2 ученика 25%

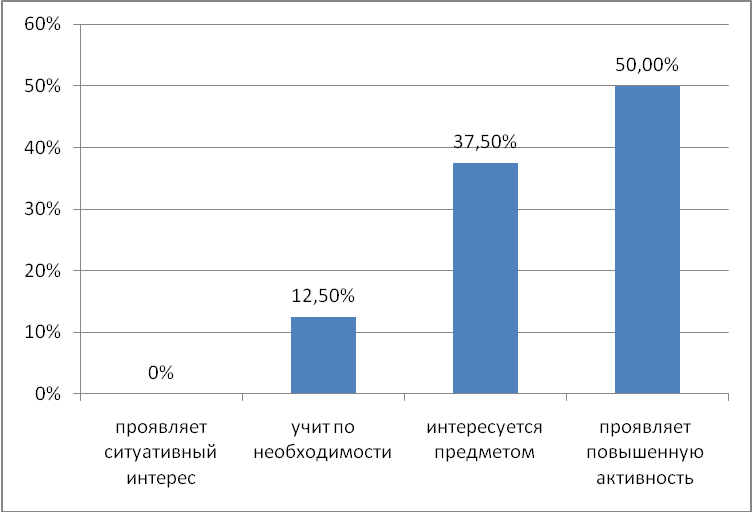
Рисунок 9 Математика в процентном отношении

Затем результаты были сравнены и занесены в таблицу.

Таблица 13

Сравнительные результаты анкетирования до и после проведения экспериментальной работы (процентах)

№	Уровень	Предметы
		Математика	Русский язык	Чтение
		до	после	до	после	до	после
1	Проявляет ситуативный интерес	0%	0%	0%	0%	0%	0%
2	Учит по необходимости	50%	12,5%	50%	25%	50%	37,5%
3	Интересуется предметом	12,5%	37,5%	25%	37,5%	25%	37.5%
4	Проявляет повышенную познавательную активность	37,5%	50%	25%	37.5%	25%	25%

Результаты формирующего эксперимента показали, что проведённая работа дала положительные результаты по развитию творческих способностей учащихся. Их качество повысилось с 37.5% до 62,5% (рисунок 10)

Рисунок 10 Динамика развития творческих способностей учащихся 3 класса ГУ «Набережная средняя школа» (в процентном соотношении)

Вывод: Из сравнительных данных хорошо видно, что результаты повторной анкеты изменились значительно по математике и изменились в лучшую сторону, так как повысился процент интересующихся предметом и снизился процент обучающихся по необходимости. Таким образом, результаты опытной работы свидетельствуют об эффективности проведенной работы. Из этого можно сделать вывод, что правильная, интересная организация учебных занятий по математике повышает интерес к предмету.

В результате уровень творческих способностей учащихся вырос, что подтвердило правильность сделанной нами гипотезы: что развитие творческих способностей учащихся основной школы на уроках математики возможно при реализации комплекса организационно-педагогических условий применения дидактической игры.

2.7 Практические рекомендации по применению комплекса дидактических игр для развития творческих способностей учащихся

Традиционно задача развития творческих способностей учащихся решается применением дидактических средств активизации учения, таких как: умелое использование учебника, проблемное обучение, самостоятельная работа, дидактические игры, занимательные задания, карточки, фокусы, кроссворды и ребусы, стихи, ритмические игры, поощрения.

Однако следует больше использовать так называемую «внутреннюю занимательность» - это появление необычных, нестандартных ситуаций с уже знакомыми детям понятиями, возникновение новых «почему» там, где, казалось бы, всё ясно и понятно (но только на первый взгляд).

Это, наконец, проникновение в методику элементов игровой деятельности, которая, естественно присуща ребёнку. Чему можно заинтересовать ребёнка, сделать учение более интересным? Прежде всего, учителю необходимо проявить творчество.

Проведение исследования выявило необходимость в сборе и классификации тестов, при помощи которых можно отследить уровень и изменение творческих способностей.

Для этого нужно:

1. Проанализировать литературу по психологии и отобрать необходимый материал.

Этот материал должен отвечать таким критериям:

• Текст должен быть понятен испытуемым
• Подходить по возрасту
• Легко обрабатываться

После того, как данный тестовый материал собран, нужно выделить его в отдельную папку.

1. Проанализировать специальную дидактическую литературу. Выделить

организационно-педагогические условия роста творческих способностей при применении дидактических игр на уроках математики:

• Методологические подходы и принципы организации совместных действий взрослых и детей.

• Создание системы мониторинга эффективности развития творческих способностей, посредством применения дидактических игр при изучении математики.
• Выбор УМК и составление рабочей программы учителя, учитывающей применение дидактических игр, для развития творческих способностей на уроке, элективном курсе, кружке и т.д.

3. Рассмотреть психолого-педагогические особенности применения дидактических игр на уроке математики:

• Атмосфера доверия, уверенности учащихся в собственных силах и достижимости поставленных целей. Доброжелательность, тактичность учителя, поощрение и одобрение действий учащихся.
• Игра должна быть хорошо продумана и подготовлена
• Учитель должен проверить подготовку учащиеся к игре.
• Подобрать состав команд для игры. Они подбираются так, чтобы в каждой были участники разного уровня и при этом в каждой группе должен быть лидер.

1. Рассмотреть основы применения дидактических игр по этапам урока.
2. Составить комплекты дидактических игр для каждого из этапов урока математики.

Таблица 14

Виды дидактических игр на разных этапах урока

Этап урока	Классификация игр	Примеры
Организационный этап проверка домашнего задания	Игры, направленные на формирование и совершенствование навыков устного счета.	Рассказ-небылица; Определи слово; Игра - цепочка; Иностранец, Расшифруй пароль
Этап актуализации опорных знаний	Игры, направленные на актуализацию теоретических знаний	Что лишнее? математический аукцион Домино Крестики – нолики
Этап мотивации (определение совместной цели деятельности)	Игры, направленные на составление задач по рисункам, таблицам, символическим записям.	Шляпная дискуссия Невод Чёрный ящик Счастливый случай
Изучение нового материала	Игры по формированию вычислительных навыков и умений	Мозговая атака Лови ошибку Ролевая игра Игра – путешествие

Продолжение таблицы 14

Контроль и самопроверка	Контрольно-обобщающие игры.	Заморочки Кто хочет стать отличником Эрудит Перекрёстный поединок
Подведение итогов рефлексия Подача домашнего задания	Игры, направленные, на самостоятельное переложение изученного материала в творческий продукт (сказки, стихотворные правила, сочинения, ребусы и кроссворды)	Превращения Сочинялка Головоломка Кроссворд Враки

1. Организовать процесс мониторинга изменений творческих способностей и подобрать упражнения для развития данных творческих способностей.

Например: Упражнения на развитие творческих способностей.

Развитие воображения:

1. Величина, количество, цифра, счет, номер.

Слово – буква.

Натуральное число - ?

1. Координата, начало, единичный отрезок, направление, шкала

Мороженое – порция.

Координатный луч - ?

1. Разность, умножение, произведение, деление, частное.

Слагаемое – сумма.

Множитель - ?

1. Шкала, сантиметр, прямая, длина, деления.

Весы – масса.

Линейка - ?

1. Минуты, секунды, время, стрелки, цифры.

Термометр – температура.

Циферблат - ?

Умение классифицировать:

1. Даны числа:

12, 0, 15, 1, 8, 5, 2, 3, 44.

Распределите их по следующим признакам:

• Однозначные числа
• Натуральные числа в порядке возрастания
• Целые числа
• Цифры

1. В каждом из четырех данных ниже списков подчеркните лишнее слово.
   • Отрезок, прямая, луч, треугольник, фигура, квадрат.
   • Сантиметр, миллиметр, дециметр, длина, метр.
   • Тонна, центнер, масса, грамм, пуд.
   • Треугольник, прямоугольник, многоугольник, квадрат, пятиугольник.

1. Дан ряд чисел. Укажите, по какому правилу составлен ряд чисел, и продолжите его еще на три числа в соответствии с этим правилом.

1, 2, 4, 5, 7, 8, 10, …

1. Из данных ниже дробей укажите лишнюю:

а)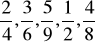

б)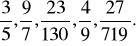

Развитие внимания.

1. Найти ошибку.

а) 3,2 + 8,=4,0; б) 16,6 – 5,16,1; в) 21,7 – 3 =21,4;

г) 29 + 7,1 = 100; д) 25,16 + 0,4 = 25,56;

е) 0,1 – 0,034 = 0,035.

Развитие творческого мышления:

1. Что общего в этих фигурах и в чем их различие?

а) б)

1. В чем сходство и в чем различие геометрических фигур?

1. Какая их фигур лишняя и чем она отличается.

Развитие воображения.

Задачи со спичками.

Переложите две спички так, чтобы корова смотрела в обратную сторону.

1. Задачи, побуждающие к выбору неверного способа решения.

• Тройка лошадей проскакала 15 км. Сколько километров проскакала каждая лошадь?
• У палки 2 конца. Если один из них отпилить, сколько концов получится?
• У куба 8 вершин, если одну из них отпилить, сколько вершин будет?
• Шесть рыбаков съедят 6 судаков за 6 дней. Сколько судаков съедят 12 рыбаков за 12 дней?

1. Задачи, вводящие в заблуждение из – за неоднозначности словесных оборотов, буквенных и числовых выражение.

• Чему равно: 2 в квадрате? 3 в квадрате? 5 в квадрате? Угол в квадрате?
• Как можно истолковать равенства: 8 + 9 =5, 3 – 5 =10.
• На листке бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить его в полтора раза?

Упражнение «Золушка»

Как бы вам не было трудно, во время веселой вечеринки или в дружеской компании целый час (лучше два, а еще лучше три) постарайтесь сидеть в стороне, молча наблюдая за всем происходящим. При этом вас, конечно, будут просить принять самое активное участие в общем веселье, но сошлитесь на потерю «золотой туфельки» и останьтесь в стороне.

При этом постарайтесь понаблюдать за присутствующими. Как они себя ведут? Что делают? Как говорят? Не узнаете ли вы себя в некоторых из них? Если «да», то может быть что-то захочется изменить и в себе?

Упражнение «Полный порядок»

Возьмите себе за правило – периодически приводить в порядок свои вещи, книги, учебники, свои записи. Для начала наведите элементарный порядок у себя на столе. Определите каждому предмету конкретное место и в дальнейшем постарайтесь класть его именно туда.«Навести порядок в своих мыслях» вы можете с помощью дневника или еженедельника, в котором следует записывать основные дела на предстоящий день и вечером проверять, все ли вы выполнили из того, что было намечено. Стремитесь выполнять все намеченные дела.

Упражнение «Риск – дело благородное»

Как правило, вы долго и серьезно обдумываете любое более или менее важное решение. Наверное, это разумно, но позвольте себе иногда безрассудные поступки, рискните, и самое главное – не жалейте и не расстраивайтесь, если вы не получите нужный результат. Ведь жизнь так увлекательна и интересна.

Возьмите себе за правило, хотя бы один раз в день (неделю) совершать рискованный поступок (пусть совсем маленький, но обязательно).

Упражнение «Оратор»

Во время бесед и разговоров со своими друзьями сознательно стремитесь быть Оратором (именно с большой буквы). Для этого вам нужно говорить громко, четко, используя различные ораторские приемы, чтобы привлечь внимание собеседников. Не забудьте, что ваша речь должна быть понятна собеседнику (время от времени спрашивайте у него: «Ты понимаешь о чем я говорю?»).

Упражнение «Массовик – затейник»

В дружеской компании или на вечеринке не сидите в стороне, в очередной раз обдумывая свои мысли, а попробуйте сыграть роль массовика – затейника. Предложите всем участникам вечеринки какую-нибудь игру или другое интересное занятие. Важно не просто предложить интересную игру, но и организовать ее проведение, привлечь как можно больше людей.

Безусловно, вам сначала это будет очень трудно, но первый же успех окрылит вас и вы почувствуете радость от общения с людьми.

Упражнение «Найди себя»

Вам нужно поверить в свои силы и знания, в свои способности и талант. Поверьте, что на свете нет неталантливых людей. У каждого человека есть задатки таланта, его нужно только обнаружить. Для того чтобы это произошло, ищите свой талант, начинайте различные дела, пробуйте себя в разных сферах деятельности. И вы обязательно найдете свой талант, свое место, Себя.

Упражнение «Пойми себя»

Если вы захотите – вы добьетесь успеха, только для этого вам нужно глубже понять себя, разобраться в том, что вас особенно привлекает, найти ту сферу деятельности, в которой вы сможете максимально проявить свой талант. Чаще задавайте себе вопрос: «Мое ли это дело?»

29 очков и более. У вас значительный творческий потенциал. Если вы на деле сможете применить ваши способности, то добьетесь больших успехов.

Упражнение «Сохрани свой талант»

Вам повезло, так как вы уже знаете, в чем ваш талант и где вы можете проявить свои способности. Но перед вами трудная задача – сохранить и развить то, что вы имеете. Поэтому постоянно совершенствуйте свою память, приобретайте новые знания, творите и выдумывайте новое.

Выполнив все необходимые условия и рекомендации применения дидактических игр на различных этапах урока математики можно быть уверенным, что динамика роста творческих способностей учащихся будет положительной.

Вывод

В период обучения большое место в жизни и обучении занимают игры. В них ребенок учится подчинять свое поведение правилам, формируется внимание, умение сосредоточиться. То есть развиваются личностные качества и способности ребенка, которые важны для успешного обучения.

Чтобы сформировать у младших школьников умение складывать и вычитать числа в пределах 10 необходимо целенаправленная активизация их учебной деятельности. Способом такой активизации является дидактическая игра. Подбор игр должен осуществляться с учетом возрастных особенностей детей, уровнем их подготовленности и в соответствии с целями и задачами урока. Игры можно использовать на разных этапах урока, эффективны уроки-путешествия. Выделяют также условия формирования познавательного интереса, а именно: максимальная опора на активную мыслительную деятельность учащихся, ведение учебного процесса на оптимальном уровне развития учащихся, положительный эмоциональный тонус учебного процесса, благоприятное общение в учебном процессе.

Познавательный интерес к математике формируется и развивается в процессе учения. Главная цель учителя заключается в том, чтобы заинтересовать учащихся своим предметом. А успешно осуществлять данную цель можно не только на уроках, но и во внеклассной работе по математике.

В основе любой игровой методики, проводимой на занятиях и внеклассных мероприятиях, должны лежать следующие принципы:

- актуальность дидактического материала;

- коллективность;

- соревновательность.

ЗАКЛЮЧЕНИЕ

Настоящее исследование посвящено изучению применения дидактических игр как средства развития творческих способностей учащихся на уроках математики. На современном этапе становления образования основой развития школьника являются фундаментальные знания, которые он получает в ходе образовательного процесса. Образование, ориентированное только на получение знаний, ушло в прошлое. Для государства важны такие новые качества выпускника, как инициативность, мобильность, гибкость, динамизм и конструктивность. Будущий выпускник должен обладать стремлением к самообразованию на протяжении всей жизни; владеть новыми технологиями и понимать возможности их использования; уметь принимать самостоятельные решения, адаптироваться в социальной и профессиональной сфере; разрешать проблемы и работать в команде; быть готовым к стрессовым ситуациям и уметь быстро из них выходить. Решающее значение для адаптации человека к сложным реалиям современного общества имеет не только объем накопленных знаний, но их системность и умение применять знания в практической деятельности. Это требует определённого стиля мышления, способного увидеть новые связи между вещами и создать новое, как в материальной, так и в духовной сфере.

Методологическую основу исследования составили работы Д.Б. Богоявленской; Л.С. Выготского, С.Л. Рубинштейна, Б.М.Теплова, Г.Е.Муравьева, С.П.Гуревича, Э.П. Торренса. Теоретической базой данного исследования являются работы А.Н. Лука, который определил творческие способности, творческий климат и мотивы творчества как условия успешного развития личности; [4]. Идеи И.П. Волкова, который утверждал, что каждого ребенка необходимо обучать творчеству; [10], а так же на работы энтузиастов-новаторов – Ш. А. Амонашвили, С. Н. Лысенковой. [37, 26]

Проведенное исследование было посвящено изучению развития творческих способностей учащихся на уроках математики в условиях применения дидактических игр. В ходе анализа мы рассмотрели теоретические аспекты творческих способностей, виды и классификацию дидактических игр при обучении математики. Установили, что дидактические игры развивают творческие способности и сделали предположение о том, что развитие творческих способностей учащихся основной школы на уроках математики возможно при реализации комплекса организационно-педагогических условий применения комплекта дидактических игр. В нашей работе мы проанализировали научную литературу, в которой исследуется сущность и структура понятия «творческих способностей». Раскрыли понятия «игра », «дидактическая игра», «способности», «творчество», «творческие способности», а так же исследовали психологические аспекты развития творческих способностей.

Мы выявили организационно-педагогические условия применения дидактической игры, а именно

• Методологические подходы и принципы организации совместных действий взрослых и детей.
• Создание системы мониторинга эффективности развития творческих способностей, посредством применения дидактических игр при изучении математики.
• Выбор УМК и составление рабочей программы учителя, учитывающей применение дидактических игр, для развития творческих способностей на уроке.

Эти условия подразумевали разработку комплекта дидактических игр, классифицированных для конкретного этапа урока математики на основной ступени обучения, на основе организационно-педагогических условий составили комплект дидактических игр, спроецировали его результаты на учебный процесс. Мы рассмотрели виды дидактических игр и изучили методику организации игр на уроках математики.

На основе изученных данных составили комплект дидактических игр классифицированных по этапам урока математики.

Следующим этапом мы провели эмпирическую проверку предположения. По составленному комплекту. Была организована опытно- экспериментальная работа по развитию творческих способностей учащихся основной школы на уроках математики при реализации комплекса организационно-педагогических условий применения комплекта дидактических игр.

Диагностика на завершающем этапе показала, что выполнив все необходимые условия и рекомендации применения дидактических игр на различных этапах урока математики можно быть уверенным, что динамика роста творческих способностей учащихся будет положительной.

По результатам исследования и проведенных диагностик мы сделали выводы, что развитие творческих способностей учащихся основной школы на уроках математики происходит при реализации комплекса организационно-педагогических условий применения комплекта дидактических игр на различных этапах урока математики.

Таким образом в исследовании были решены все поставленные вопросы, гипотеза нашла свое подтверждение, цель исследования была достигнута.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Аванесов В. С. Ошибочные цели – плачевные результаты

// Статья журнал «Педагогические измерения» №4 2009г.-33с.

2. Амонашвили Ш. А. В школу – с шести лет. М., 1986 стр.160

3. Амонашвилли Ш.А. Здравствуйте дети: Пособие для учителя// Ш.Н. Амонашвилли - Москва: Издательский центр «Академия», 1990 .-98с.

4. Богоявленская Д.Б. . Психология творческих способностей: Монография. – Самара: Издательский дом «Федоров», 2009. – 416 с.

5. Большая педагогическая энциклопедия в 4 томах. Том3 /гл. редактор И.А. Каиров, Ф.Н. Петров, А.И.Богомолов и др. Москва: Советская энциклопедия, 1964.-783-787с.

6. Букатов М.Б. Секреты дидактических игр: Психология. Методика. Дисциплина // М.Б. Букатов-Москва: Сфера, 2009.-203с.

7. Бурменская Г. Л. Хрестоматия по детской психологии// Под ред. Г. В. Бурменской – Москва: - Издательский центр «Академия», 2005.-308с.

8. Википедия //ru.Wikipedia.org.wiki.критерий

9. Волков И. П. Учим творчеству. М., Просвещение, 1986

10. Волков И.П. Учим творчеству // И.П.Волков. Москва:- Издательский центр «Академия», 2005.-308с.

11. Выгодский Л.С. Проблема возраста // Выготский Л.С. Игра и её роль в психическом развитии. Москва: 1960.-224с.

12. Выготский Л.С. Вопросы детской (возрастной) психологии [текст] \ Л.С. Выготский Собр. соч.- М., 1984

13. Газман О.С., Харитонова Н.Е. В школу с игрой. – М.: Просвещение, 1991.- 96с.

14. Газман О.С. Неклассическое воспитание.// Редактор-составитель А. Н. Тубельский От авторитарной педагогики к педагогике свободы. Москва: МИРОС, 2002.-56с.

15. Газман О. С. Каникулы: Игра, воспитание. –М., 1988 с. 6-12

16. Гальперин П.Я. . Актуальные проблемы возрастной психологии // Ж-л «Вопросы психологии» , 1966, №4, или : 4 лекции, 2000

17. Государственный стандарт начального образования. Познание мира. 2-4. Классы.- Алматы, 2004.- 59 с.

18. Гуревич П.С. Философский словарь// Москва: « Республика», 2001. — 719с.

19. Давыдов В. В. Проблемы развивающего обучения: опыт теоретического и экспериментального психологического исследования. – М., Педагогика, 1986.

20. Данилов, И.К. Об игровых моментах на уроках математики // Математика в школе. – 2005.- №1.- 98с.

21. Днепров Э. Д. Ушинский и современность. М., 2008.

22. Есипов Б.П. Самостоятельные работы учащихся на уроке. М., 1961.

23. Жикалкина Т.К. Система игр на уроках математики в 1 и 2 классах. М., 1996 стр.46

24. Закон Республики Казахстан «Об образовании» // Казахстанская правда. – 2007.- 15 августа.- С.9-11.

25. Зверев А.О. Игры на уроках математики//Зверев А.О. Волгоград: Учитель, 2008.-99с.

26. Ильин Е. П. Психология творчества, креативности, одаренности: моногр. - СПб., Питер, 2008. - С.210.

27. «Начальная школа плюс До и После» журнал. Москва, 8.02 стр. 68 - 69

28. Карпова Е.В. Дидактические игры в начальный период обучения. – Ярославль, 1997 - 423 с.

29. Коваленко В.Г. Дидактические игры на уроках математики. – М., 1990

30. Козлова Е.Г. Сказки и подсказки: задачи для математического кружка// Е. Г. Козлова - Москва: МЦНМО,2008-165с.

31. Концепция развития образования в Республике Казахстан до 2015 года // 24 февраля 2004 года - С.3-5.

32. Кушнерук Е.Н. Занимательность на уроках математики в начальных классах.

33. Левитов Н.Д. Детская и педагогическая психология. М., 1960.

34. Лук А. И. Мышление и творчество// А. И. Лук. Москва: Политиздат, 1976.-45с.

35. Лук А. Н. Психология творчества// А. Н Лук. Москва: Наука, 1978

36. Лысенкова С.Н. Жизнь моя – моя школа, или право на творчество// С.Н Лысенкова. – Москва,1995.-47с.

37. Математика. 2-4 классы/ Н.В.Барышникова.- Волгоград: Учитель, 2009. 154с.

38. Математика. 2-4 классы: игровые технологии на уроках.-2-е из. // И. Б. Ремчукова. - Волгоград: Учитель, 2008.-99с.

39. Математика. Издательский дом «Первое Сентября» № 39 2002

40. Математика в стихах: задачи, сказки, рифмованные правила. 5-11 классы//О.В. Панишева.- Волгоград: Учитель, 2009. 219с.

41. Математика в школе № 3 2011, Беркалиев Т.Н. Инновации и качество современного образования »/ научно-методическое пособие для педагогов инновационных школ/ Т.Н Беркалиев.

42. Математические игры: 2-4 классы. - Москва: Вако, 2010.-208с.

43. Монтесори М. Руководство к моему методу.//М.Монтессори.- Москва: 1916.-78с.

44. Муравьева Г.Е. Игровые технологии// Г.Е.Муравьева.- Волгоград: Учитель, 2009. 29с

45. Немов Р.С. Общая психология: краткий курс//Немов Р.С.- СПБ: Питер, 2008-199с.

46. Платонов К.К. Краткий словарь системы психологических понятий//учебное пособие. - Москва: Высшая школа,-1984.-174с.

47. Попова В.И. Игра помогает учиться. //Начальная школа №2, 1987 стр.39

48. Психолого-педагогические особенности проведения дидактических игр. Под. ред. Акшиной А., Акшиной Т., Жарковой Т. – М., 1990.- 540 с.

49. Рахимжанова М.К., Мукашева А.Д. Игра в педагогическом процессе // 12-летнее образование. - 2008.- №2.- С.75-77.

50. Степкина И.А. Дидактическая игра как средство развития творческих способностей младших школьников // Начальная школа Казахстана.-2007.- №6.- С.13-18.

51. Сухомлинский В.А. О воспитании. М., 1985 стр.93

52. Сухомлинский В.А. Сердце отдаю детям // Сухомлинский В.А.- Москва: МИРОС, 2002.-56с

53. Теплов Б.М. Проблемы индивидуальных различий// Теплов Б.М. Москва: Наука, 1965.-302с.

54. Тихеева Е.И. Развитие речи детей (раннего и дошкольного возраста) –– М.: Просвещение, 1981

55. Толковый словарь русского языка. 4-е издание, дополнительное, - Москва: Азбуковник,1999-757с.

56. Туник Е. Е. Модифицированные креативные тесты Вильямса. Санкт-Петербург, 2003

57. Туник Е.Е. Практикум по психодиагностике//Е.Е. Туник - Санкт–Петербург: издательство «РЕЧЬ», 2003г.-304с.

58. Универсальный словарь русского языка. Санкт-Петербург, 2009

59. Учебно-практическое пособие. /В.К. Лукашевич, В.М. Белокурский, И.П. Мамыкин, Е.З. Волчек, Е.А. Криштапович; Под общ. ред. В.К. Лукашевича – Мн.: БГЭУ, 2000. – с.

60. Философия: Учеб. для вузов / П. С. Гуревич. — Москва: Проект, 2003. — 348 с.

61. Хрипкова А. Г. "Мудрость воспитания", Москва, "Педагогика", 1989.

62. Шадриков В.Д. Психология деятельности и способности человека.// В.Д. Шадриков Психол. журнал – 1983. - № 5.

63. Шацкий С.Т. Педагогические сочинения в 4-х т. – М., 1959

64. Шмаков, С.А. Культура – досуг – ребенок. – М.: Просвещение, 1994. – 381с.

65. Щедровицкий Г.П. Методические замечания к педагогическим исследованиям игры. // Психология и педагогика игры дошкольников. Под.ред.Запорожца М.,1996 с.24

66. Эльконин Д.Б. Психология игры. М., 1978 стр.57, 277

67. http://shgpi.edu.ru/biblioteka/

Приложение 1

Типы дидактических игр и их характеристики

	Типы дидактических игр	Характеристика дидактических игр
1	Сюжетно-ролевые дидактические игры (иногда их называют сюжетными)	Занимают особое место в развитии творческих способностей. Они носят преимущественно коллективный характер, ибо отражают существо отношений в обществе. Подразделяют их на ролевые, игры-драматизации, режиссёрские. В данном виде дидактических игр как никогда ярко выражаются творческие способности детей. В этих играх на основе жизненных или художественных впечатлений свободно и самостоятельно воспроизводятся социальные отношения и материальные объекты или разыгрываются фантастические ситуации, не имеющие пока аналога в жизни. Основные компоненты ролевой игры - тема, содержание, воображаемая ситуация, сюжет и роль.
2	Компьютерные дидактические игры	Наглядно демонстрируют ролевые способы решения игровых задач, например, в динамике представляют результаты совместных действий и общения персонажей, их эмоциональные реакции при успехе и неудаче, что в жизни трудноуловимо. Такие игры помогают избежать штампов и стандартов в оценке поведения разных персонажей в разных ситуациях, что опять же развивает творческое воображение. Дети усваивают практически средства коммуникации, способы общения и выражения эмоций
3	Игры-путешествия	Имеют сходство со сказкой, ее развитием, чудесами. Игра-путешествие отражает реальные факты или события, но обычное раскрывает через необычное, простое - через загадочное, трудное - через преодолимое, необходимое - через интересное. Все это происходит в игре, в игровых действиях, становится близким ребёнку, радует его. Цель игры-путешествия - усилить впечатление, придать познавательному содержанию чуть-чуть сказочную необычность, обратить внимание детей на то, что находится рядом, но не замечается ими. Игры-путешествия обостряют внимание, наблюдательность, осмысление игровых задач, облегчают преодоление трудностей и достижение успеха, развивают логическое мышление и творческие способности.
4	Игры-поручения	Имеют те же структурные элементы, что и игры-путешествия, но по содержанию они проще и по продолжительности короче. В основе их лежат действия с предметами, словесные поручения. Игровая задача и игровые действия в них основаны на предложении что-то сделать: «Помоги расставить правильно знаки», «Проверь домашнее задание», «Составь алгоритм»
5	Игры-предположе- ния	«Что было бы..?» или «Что бы я сделал...», «Кем бы хотел быть и почему?», «Кого бы выбрал в друзья?» и др. Иногда началом такой игры может послужить картинка. На развитие творческих способностей работает дидактическое содержание игры, оно заключается в том, что перед детьми ставится задача и создаётся ситуация, требующая осмысления последующего действия. Дети высказывают предположения, констатирующие или обобщённо-доказательные. Эти игры требуют умения соотнести знания с обстоятельствами, установления причинных связей. В них содержится и соревновательный элемент: «Кто быстрее сообразит?».
6	Игры-загадки	Возникновение загадок уходит в далёкое прошлое. Загадки создавались самим народом, входили в обряды, ритуалы, включались в праздники. Они использовались для проверки знаний, находчивости. В этом и заключается очевидная педагогическая направленность и популярность загадок как умного развлечения и средства развития творческих способностей.
7	Игры-беседы (диалоги, дискуссии).	В основе игры-беседы лежит общение педагога с детьми, детей с педагогом и детей друг с другом. Это общение имеет особый характер игрового обучения и игровой деятельности детей. В игре-беседе учитель часто идёт не от себя, а от близкого детям персонажа и тем самым не только сохраняет игровое общение, но и усиливает радость его, желание повторить игру. Ценность игры-беседы заключается в том, что она предъявляет требования к активизации эмоционально-мыслительных процессов: единства слова, действия, мысли и воображения детей. Игра-беседа воспитывает умение слушать и слышать вопросы учителя, вопросы и ответы детей, умение сосредоточивать внимание на содержании разговора, дополнять сказанное, высказывать суждение. Все это характеризует активный поиск решения поставленной игрой задачи.
8	Игры-состязания	В данной игре победа обеспечивается в основном за счёт скорости выполнения вычислений, преобразований, но без ущерба качеству выполнения задания, такие игры полезны для выработки автоматизма действий. Одним из видов игры состязания является игра-олимпиада. Победа обеспечивается, главным образом, за счёт качества решений задач повышенной трудности или доказательства сложных теорем
9	Анализ конкретных ситуаций	В основе метода лежит коллективное решение обучающимися проблемной задачи. Задача может быть технической, социальной, управленческой. Она может требовать нахождения конкретного решения или определения совокупности действий, которые приведут к выходу из критической ситуации. Такие задачи, в отличие от традиционных учебных задач, будучи построены на реальном материале, могут не иметь однозначного решения, и могут содержать избыточную информацию или ее недостаток, то есть носят творческий, проблемный характер. В большинстве случаев проблемные, творческие задачи используются не только в составе методов активного обучения, но и как самостоятельное средство активизации мыслительной деятельности учащихся как средство развития творческих способностей
10	Игровое проектиро- вание	В соответствии с названием под игровым проектированием понимают конструирование, проектирование, разработку технологии производства работ или деятельности, проводимое в игровой форме. Выделяют следующие характерные признаки метода: Наличие сложной творческой задачи; Групповая работа; Имитация заседания научно-технического совета, на котором авторы проекта публично его защищают.
	МОЗГОВАЯ АТАКА (мозговой штурм, мозговой обмолот)	Мозговая атака – это групповое нахождение новых альтернативных вариантов решения проблемной ситуации. Мозговая атака была предложена А. Осборном в конце 30-х годов как метод, направленный на активизацию творческой мысли. Для этого применяются средства, снижающие критичность и самокритичность человека с целью повышения уверенности в себе и проявляющие на этой основе механизмы творческого акта. Стимулирование творческой активности достигается посредством четырёх правил: - исключается критика, что позволяет высказывать любую мысль без боязни признания ее плохой; -поощряется необузданное ассоциирование: чем более «дикой» покажется идея, тем лучше; -количество предложенных идей должно быть как можно большим; -разрешается «улучшать» идеи, комбинируя и видоизменяя их
	Деловая игра	Деловая игра представляет собой последовательность учебных действий в процессе решения поставленной задачи. Это – модель взаимодействия людей в процессе достижения экономических, производственных или политических целей. Деловая игра позволяет создавать такие ситуации, в ходе которых играющему необходимо найти правильную линию поведения, оптимальное решение проблемы. В процессе игры вырабатывается умение мыслить системно, продуктивно; пробуждается стремление к поиску новых идей; развиваются творческие способности. Таким образом, дело не сводится лишь к механическому использованию программного материала, ребята подходят к проблеме творчески.

Приложение 2

Проявление творческой активности и творческих способностей

учащихся 3 класса

1.Желание выполнять творческие задания:

а). С большим желанием;

б). Не проявляет особого желания;

в). Отказывается выполнять.

2. Включение в творческую деятельность:

а). Всегда включается;

б). Редко принимает участие;

в). Никогда.

3. Творческий подход к выполнению творческих заданий:

а). Высокий уровень (проявляет самостоятельность, оригинальность);

б). Средний уровень (выполняя задания ученику требуется небольшая помощь учителя),

в). Низкий уровень (работа строится под руководством учителя).

4. Уровень проявления креативности в выполняемых заданиях:

а). Высокий уровень (работа отличается оригинальностью, нестандартным подходом)

б). Средний уровень (в задании прослеживается участие воображения ребенка);

в). Низкий уровень (задание выполнено на репродуктивном уровне).

Полученные результаты мы представили в таблице. В графе итог сделали выводы об уровне проявления творческих способностей: ВУ – высокий уровень, СУ – средний, НУ – низкий уровень.

№ п/п

Ф. И. ученика

Показатели проявления творческих способностей

Итог

1

2

3

4

а

б

в

а

б

в

а

б

в

а

б

в

1

Адель

+

+

+

+

ВУ

2

Ольга

+

+

+

+

СУ

3

Айжан

+

+

+

+

СУ

4

Ильдар

+

+

+

+

СУ

5

Алина

+

+

+

+

СУ

6

Нуржан

+

+

+

+

НУ

7

Айдана

+

+

+

+

СУ

8

Данил

+

+

+

+

НУ

Обобщая данные наблюдений, можно отметить, что у 75 % детей прослеживается большое желание к выполнению любых творческих заданий. 25 % ребят не проявляют особого желания к выполнению подобных заданий.

Так же мы наблюдали по показателям: часто ли включаются учащиеся в творческую деятельность. Здесь мы видим, что 38 %учеников всегда с большим желанием включаются в любую творческую деятельность. Эти дети принимают участие в творческих играх, в проигрывании ситуаций и т.д. 50 % ребят иногда включаются в данную деятельность, а иногда у них не возникает подобного желания. И всего 12 % всегда отказываются от участия в творческой коллективной работе.

Мы вынесли такой показатель, как творческий подход к выполняемым заданиям. 12% школьников всегда проявляли самостоятельность, неординарность, творчество при выполнении различных заданий. Средний уровень проявления креативности прослеживался у 50% учащихся. Низкий уровень у 38% ребят.

Анализ продуктов творческой деятельности детей: рисунки, поделки, позволил нам выявить степень креативности детей. 12 % учащихся имеют высокий уровень креативности; у 38 % детей наблюдается средний уровень; 50 % - выполняют творческие задания на низком уровне.

В итоге всего 12 % учащихся имеют высокий уровень проявления творческих способностей, 63% имеют средний уровень и 25% - низкий уровень.

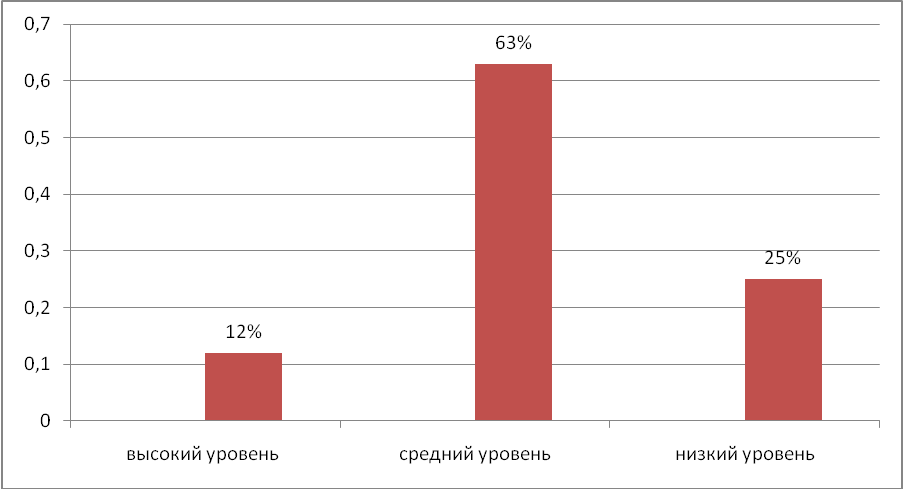
Приложение 3

Математический лабиринт

Для прохождения задания потребуется вооружиться ручкой или карандашом, с помощью которых ребенок проложит путь.

Путь начинается от цифры 5, затем к этой цифре ребенок прибавляет 5, получается 10, затем 10+5=15, 15+5=20 и т.д.

Помоги Пингвинчику найти шарики

Помоги Рексу пройти к мячу

Приложение 4

Игра «Цепочка»

Выполните вычисления:

358 кг 120 г – 65 кг 237 г 12 км 670 м + 28 км 380 м

26 см 76 м – 9 см 87 м 45 кг 97 г + 25 кг 61 г

«Математический лабиринт»

Помоги лягушонку, стремящемуся к знаниям, добраться в школу через лабиринт с числовыми выражениями. При этом значения выражений должны составить отрезок натурального ряда.

Такие игры на этапе ознакомления, повторения и закрепления изученного материала выполняют функцию формирования в процессе игры общеучебных умений и навыков, а так же психологических образований, крайне необходимых для активизации учебного процесса.

Приложение 5

УРОК МАТЕМАТИКИ (3 КЛАСС)

Тема: Приемы письменного вычитания в пределах 1000.

Цели: 1) познакомить с приемами письменного вычитания, развивать умение решать задачи, уравнения;

2)развивать вычислительные навыки, умение рассуждать

3)воспитывать организованность, собранность.

ХОД УРОКА

I. Оргмомент

Долгожданный дан звонок,

Начинается урок.

Вычитанье, вычитанье!

Вычитанье как понять?

Это значит что-то надо

У чего-нибудь отнять

Важные трехзначные

Числа встали в ряд.

И такие числа

Мы будем вычитать.

II. Устный счет

а) 271 125 229

184 155 116

Если поставим знаки сложения, получим числовые выражения.

Удобным способом найдите значения.

б) Игра « Шифровальщик».

Расшифруй слово.

Запиши ответы в порядке убывания и расшифруй название героя.

Ответ:

290 + 10 = – к	710 + 90 = – е
50 + 450 = – а	860 + 40 = – н
170 + 30 = – а	360 + 40 = – й
80 + 520 = – н	70 + 630 = – з
900	800	700	600	500	400	300	200
Н	Е	З	н	а	й	к	а

На скамейку сели малыши: Дюймовочка занимает 1см.. Незнайка 6см, а Доктор Пилюлькин – 8см.Уместятся ли они все, если длина скамейки 2дм?

II. Постановка учебной задачи.

Что общего в примерах?

-81 -70

63 25

28 55

Д.-Действие вычитания.

У. Решите.

Д.В вычислениях ошибки.

У. Какие?

Д. В первом примере ответ 18, а во втором- 45.

У. Почему ошибки?

Д. Точки над десятками не поставили и забыли, что брали по десятку.

У.Решите эти примеры верно. (называют ответы)

У. Назовите тему урока. Какова цель?

Д.Вычитание многозначных чисел. Цель: научиться вычитать без ошибок.

IV. Введение новых знаний.

У. Откройте учебник на странице 60.Прочитайте объяснение.

На доске закрепляется «карточка- помогайка»- алгоритм вычитания.

1.Пишу…….. 2.Вычитаю единицы…… 3.Вычитаю десятки…….. 4.Вычитаю сотни…… 5.Читаю ответ……..

У.Объясните, как из числа 637 вычесть 273. (Объясняет ученик)

У.Объясните решение примеров на с. 60, 1.(Дети объясняют).

У.Задание 2. У доски 2 примера с объяснением, последние 2 выполняют самостоятельно. (проверка)

Физминутка:

Шли по крыше три кота,

Три кота Василия.( ходьба)

Поднимали три хвоста

Прямо в небо синее (поднимание рук)

Посмотрели вверх и вниз.(приседание)

И сказали три кота:

- Красота, красота! (хлопки в ладоши)

V. Домашнее задание.

У. Какая тема была на уроке?

У.Запишем д/ задание.Учебник: с.60,п. 3.

VI. Закрепление.

У. Прочитайте задачу 6.

Дети читают вслух, составляют схему.

У. Кто готов начертить на доске?

На ?

? 56

120

- Можем ли мы сразу ответить на вопрос задачи? ( Нет.)

- Что для этого необходимо знать? (Сколько книг выдали и сколько осталось)

- Знаем сколько выдали? (Нет)

- Что известно? (Что было 120, а осталось 56.)

- Как? (Вычитанием)

- Почему такой выбор действия? (Потому что 120 состоит из того, что осталось и выдали)

- Сейчас мы можем ответить на вопрос задачи? (Да)

- Какое выполним действие? (Вычитание.)

Решение записывают самостоятельно.

120 – 56 = 64 (кн.) – выдали

64 – 56 = 8 (кн.);

(120 – 56) – 56 = 8 (кн.)

VII. Сам. работа. (учебник стр. 60 примеры 3)

VIII. Итог. С какой темой познакомились на уроке?

Приложение 6

Урок математики в 3 классе.

Тема: Письменное сложение трёхзначных чисел. Закрепление.

Игра – путешествие.

Цель: Закрепить умение детей складывать в столбик трехзначные числа, знание нумерации чисел в пределах 1000, умение решать уравнение.

Оборудование: Карта полушарий, острова, фигурки персонажей – жителей островов, компьютер.

1. Сегодня мы с вами отправимся в гости к Робинзону Крузо. Путешествие далекое, интересное, но опасное, поэтому с собой мы берем самых смелых, дружных, сообразительных и находчивых математиков. Есть среди вас такие? Это мы сейчас проверим, когда выполним 3 задания.

1. Назовите число, в котором

8 сотен 3 дес. 6 ед.(836)

5 ед. 7 дес. 3 сотни (375)

6 сотен 8 дес.(680)

4 сотни 3 ед.(403)

1. Что можете сказать об этих числах?

105 260 37 376 812

Почему оно лишнее?

1. Каждый ряд назвал свои суммы на билетах(посчитали)

Проходим на корабль по рядам.

Располагайтесь поудобнее, любуйтесь морем, свежим воздухом дышите.

Итак, в путь!

2. Впереди остров Обезьян. Хозяйка острова тоже приготовила задание. (Задачи на экране) Прочитайте 2 задачи про себя.

С одного дерева собрали 213 бананов, с другого – на 96 меньше. А с третьего на 119 больше. Сколько всего бананов собрали?

- В один ящик уложили 125 бананов, в другой на 51 банан больше, а в третий столько, сколько в 1 и 2 вместе. Сколько бананов в третьем ящике? Вслух прочитать только ту задачу, которая решается в 2 действиях, похожих на Гошины примеры.

Самостоятельно, кроткая запись.

I – 125 шт. III-?

II - ? на 51 б.

1)125

+ 51

176(шт) бананов во 2-ом ящике

2)125

+ 176

301(шт)

Ответ: в третьем ящике 301 банан.

3. А теперь плывем на Остров Слонов. Маленький слоненок давно ждет гостей. Он учится в школе зверей, решил примеры, которые задали домой, но не уверен, правильно ли. Помогите слоненку. Решите примеры в тетради.

438

+ 25

688

265

+ 351

516

523

+ 284

807

Попрощаемся с нашим новым другом и в путь. Ой, что это?

4. Необитаемый остров. Караул! Наш корабль захватили дикари. Пока не выполним их задание, они не выпустят корабль.

Решим уравнение в тетради.

Х•5=200-50 х-260=270/9

Ура! Мы на свободе! Скорее на корабль. Нас ждет Робинзон! Но что это? На палубе вода! Кто – то из дикарей успел пробить наш корабль. Ищите пробоины!

32/4-2=16(6)

18+(29-20)/3=9(21)

45+75/25*4-20=53(37)

Почему неверные ответы? Дикари не знают о порядке действий. Повторили правила о порядке действий. Пробоины найдены, ответы исправлены. Поплыли дальше.

5. А вот и сам Робинзон Крузо. Мы добрались до цели. Как вы повзрослели! И, наверное, стали еще сообразительнее. Молодцы! Вы настоящие путешественники: смелые, находчивые, сообразительные, знающие. А теперь в обратный путь! Обратное плавание прошло без происшествий. Путешествие закончилось! Ура! Мы дома.

Приложение 7

Урок математики в 3 классе «Путешествие в сказочное царство Лукоморье»

(Урок закрепления)

Тема: «Деление и умножение двузначных чисел»

Цели и задачи:

Образовательные:

усвоение полученных знаний, умений и навыков при делении и умножении двузначных чисел в системе;

развитие умения переносить навыки в сходные и новые условия;

отработать умения представлять двузначное число в виде суммы разрядных и удобных слагаемых;

Развивающие:

развивать наблюдательность и умение рассуждать;

развивать математические способности, логическое мышление, внимание и интерес к предмету через игру;

Воспитательные:

воспитывать навыки самоконтроля и самопроверки.

Оборудование: учебник, рабочие тетради; карточки с математическими заданиями (№1, №2, №3), карточки с д/з (дифференцированное задание); опорные схемы; карточки с числами и буквами; геометрические фигуры; фонограмма Н.Н.Римского-Корсакова «Полёт шмеля», сказки; портрет А.С.Пушкина; фигуры сказочных персонажей ( царь Салтан, князь Гвидон, царевна Лебедь, Балда, мёртвая Царевна, королевич Елисей).

Тип урока: Обобщение и систематизация знаний.

Урок разработан в форме игры-путешествия.

На уроке были использованы следующие методы обучения: словесный, наглядный, практический.

Формы обучения: коллективная, самостоятельная, индивидуальная.

В ходе урока использовались разноуровневые задания, самоконтроль и самооценка знаний учащихся. А так же:

- отрабатываются вычислительные навыки умножения и деления чисел;

- решения задач, уравнений;

- развиваются внимание, память, логическое мышление;

- воспитывается интерес к математике

- прививается умение работать в коллективе.

Ход урока:

І. Организационный момент

Придумано кем-то просто и мудро

При встрече здороваться: «Доброе утро!»

Доброе утро солнцу и птицам!

Доброе утро улыбчивым лицам!

И каждый становится добрым, доверчивым,

И доброе утро длится до вечера.

Я желаю, чтобы доброе и солнечное настроение сопровождало вас в течение всего урока.

II. Сообщение темы и целей урока.

Сегодня на уроке мы отправимся в сказочное царство Лукоморье, в гости к славному царю Салтану. Сегодня мы в гостях у сказки. А может быть сказка у нас.

Ведь где считают дружно,

Решают умело,

Там сказке можно появиться смело.

Ребята, кто из вас уже догадался, герои каких сказок придут к нам на урок и кто их автор?

Правильно. У нас в гостях герои из сказок А.С.Пушкина/вывешиваю портрет/.

А знаете ли вы, что сказке о царе Салтане уже 180 лет?!

Лукоморье - царство не простое, а математическое. Чтобы туда попасть, нужно исполнить царя указ.

УКАЗ

Повелеваю в моем математическом Лукоморье ученикам 3 класса исполнять мои желания:

знать таблицу умножения;

уметь делить и умножать двузначные числа;

решать задачи;

уметь работать с геометрическими фигурами;

а также вам пригодятся знания русского языка и литературы.

У мудрого царя есть ещё условия. Он привык за работу платить из царской казны.

Если был ответ прекрасный,-

Ты жетон получишь красный.

Если твой ответ похуже –

Жёлтый цвет тобой заслужен,

Если плох твой был ответ –

Не получишь ты монет.

III. Устный счёт.

Чтобы пропустить нас в Лукоморье царь устроит вам испытание.

Царь не долго собирался –

В класс к ребятам он примчался.

Думу думает при сём:

Новым станет кто царём?

Самый умный кто и смелый,

Самый быстрый и умелый,

Тот взойдёт на царский трон,

Коронован будет он.

Подсказал тут звездочёт:

-Проверь, как знают устный счёт.

У нас в гостях золотая рыбка. Как называется эта сказка?

Она приплыла к нам не одна, а со своими подругами и предложила игру «Математическая рыбалка».

Выходите, ловите рыбку, читайте пример, отвечайте /на карточках примеры табличного умножения /.

/в ходе урока учитель раздаёт отвечающим жетоны соответствующего цвета/

Ребята, я предлагаю вам отпустить рыбок в синее море, пусть гуляют себе на просторе. Но прежде чем отпустить - попросите у них чего нибудь.

Моё желание: прошу у золотой рыбки, чтобы вы на уроке быстро и правильно считали, хорошо работали.

/отпускаем рыбок/

IV. Работа по теме урока.

Актуализация опорных знаний.

• Мы пропущены в Лукоморье.

При повторении таблицы умножения, какие числа у вас получались?/ двузначные/

Вспомните, как умножают двузначное число? /заменяем его суммой разрядных слагаемых/.

Как выполнить проверку? /умножение можно проверить делением: произведение разделить на множитель, или умножением, переставив множители/.

Как делить двузначные числа? /заменить суммой разрядных или удобных слагаемых; путём подбора частного/

Как проверить деление? /деление проверяем умножением: частное умножить на делитель, или делением: делимое разделить на частное/

• Математический диктант. Запишите только ответы.

Найди произведение 20 и 4;

Найди частное 55 и 5:

Делимое 70, делитель 5, частное?;

Увеличь 30 в 3 раза;

Во сколько раз 90 больше 45?

Черномор построил 33 богатыря в ряды по 11 человек.

Сколько рядов получилось?

/На доске карточки: 11, 90, 80, 2, 14, 3./

Перед вами карточки с числами. Надо поставить их в том порядке, как у вас записаны ответы в тетради./ученик выходит к доске и располагает карточки:80, 11, 14, 90, 2, 3 /

А теперь перевернём их обратной стороной.

На доске появляется слово: Г В И Д О Н. /звучит аудиозапись диалога Князя и Лебеди/

Герой, какой сказки пришёл в гости?

Скажите, в кого превратился Гвидон в третий раз?

Самостоятельная работа.

Кто успел решить все примеры?

Какие примеры решали подбором?

Как выполнить проверку?

Физкультминутка.

/звучит музыка Н.Н.Римского-Корсакова «Полёт шмеля», дети выполняют под неё движения/

Лебеди летят, крыльями машут.

Проснулись над водой, машут головой.

Прямо и гордо умеют держаться,

Тихо, бесшумно на воду садятся.

• Оборотила царевна Лебедь князя Гвидона шмелем, и полетел он вслед за кораблём. Но чтобы ему попасть на корабль вовремя, вам надо решить задачу.

/задача на карточке №1 /

Шмель пролетел 36 м за 18 с.Сколько метров он пролетал за одну секунду, если известно, что он движется равномерно? /

Прочитайте, что утверждается в задаче?

Что требуется узнать?

Как сделать краткую запись?

18 с – 36 м

1 с - ? м

Повторите задачу по краткой записи.

Решение запишите самостоятельно.

Проверим решение задачи. / 36 : 18=2(м) – за 1 с /

Запишите ответ.

• Ребята, такую величину позднее мы будем называть скоростью, с ней вы познакомитесь в 4 классе, а более подробно об этом вы будете говорить на уроках физики.

• Сегодня у нас в гостях ещё один пушкинский герой. Вы узнали его? / Балда /

Из какой он сказки?

Балда принёс с собой свой рабочий чемоданчик. Давайте посмотрим, какие у него там инструменты.

Доставайте фигуру, называйте её и читайте название инструмента.

• Чтобы узнать название последнего инструмента, необходимо выполнить задание, записанное на карточке №2.

/Начерти прямоугольник со сторонами 4 см и 2 см. Найди периметр. /

Прочитайте задание про себя.

У кого есть вопросы?

Выполнив задание, вы получите число, которое найдёте на доске и прочитаете под ним название последнего инструмента.

На доске:

42 12 36

дрель клещи отвёртка

Так какой инструмент был у Балды?/ клещи /

Объясните, как вы узнали это /способы /.

• Работа с геометрическими фигурами.

Как назвать эти фигуры, одним словом?

Какие 3 фигуры можно объединить в одну группу?

Какие 2 фигуры можно объединить в одну группу? По каким признакам?

Что вы можете сказать о квадрате и о четырёхугольнике?

• Словарная работа /связь с русским языком /.

Посмотрите на слова, которые обозначают название инструментов.

Что вы можете сказать об этих словах? /назвать грамматические признаки, сделать вывод – им. сущ. /

Найдите лишнее слово? По какому признаку? /лишнее – клещи (мн. ч); все остальные словарные слова /

Физкультминутка.

/звучит пени птиц /

Шагая по царству,

Устали немножко.

Сейчас отдохнём

И обратно в дорожку.

Из-за парты тихо встали

И по царству зашагали.

Мы шагаем, мы шагаем,

Голову не опускаем,

Дышим ровно, глубоко.

Раз – подняться, потянуться,

Два – согнуться, разогнуться,

Три – присесть,

Четыре – встать,

Пять – руками помахать,

Шесть – за парту тихо сесть.

V. Закрепление опорных знаний.

• Работа в парах по карточке №3.

28:2= 33:3= 76:19= 99:11= 44:22=

28*2= 33*3= 75:25= 46:2= 72:4=

72:3= 80:4+72=

72:12= 100 – 60:2=

• Из математического муравейника, выбрать свой ответ и поставить в ряд.

Расположите числа в порядке возрастания.

2 3 4 6 9 11 14 18 23 24 56 70 92 99

Сосчитайте сколько здесь чисел?

Покажите одну вторую часть от количества этих чисел.

А теперь переверните эти карточки.

м ё р т в а я ц а р е в н а

• Следующая наша гостья, это Царевна, которая оказалась мёртвой, после того как откусила кусочек отравленного ядом яблока. Как называлась эта сказка А.С.Пушкина?

Но мы не можем закончить так печально наш урок. Вы помните, что Царевну искал её жених королевич Елисей. Мы должны помочь ему поскорее оживить его невесту. Для этого нам надо разорвать цепи, на которых качался хрустальный гроб.

• Решить уравнения с объяснением у доски.

25 + k = 38 b * 9 = 54

x – 20 = 46 y : 8 = 9

Царевна спасена.

VI. Итог урока. Рефлексия.

Наше путешествие подошло к концу. Умея делить и умножать двузначные числа, вы сможете быстро решать примеры и задачи, в которых требуется увеличить или уменьшить число в несколько раз, а главное, проверять самих себя.

Давайте ещё раз назовём героев сказок А.С.Пушкина, которые помогали нам работать на уроке. / выставить всех /

• Оценка работы учеников. /подсчёт жетонов /

Так скажу: ни дать ни взять –

Вам оценка нынче «пять»!

Царь портрет свой подарил

И раскрасить разрешил.

/сюрприз – математическая раскраска/

• Домашнее задание.

Вы преодолели пока недолгий, но трудный путь и получили в награду знания. Храните этот клад знаний и пополняйте на каждом уроке. И помните: знания – это самое ценное богатство. Повторив приёмы деления и умножения двузначного числа, вы заработали свой приз. Он находится в трёх волшебных сундучках.

В первом сундучке – задания для тех, кто хорошо запомнил все приёмы.

Во втором сундучке – задания для тех, кто тему понял, но объяснить другому не может.

В третьем сундучке – задания для тех, кто ещё затрудняется решать без подсказки.

• Оценка урока.

У вас на парте лежат сердечки.

Кому урок не понравился – пусть сердечко останется лежать на парте.

Кому урок не очень понравился – поднимите сердечко на высоту согнутой руки.

А кому урок понравился – поднимите руку с сердечком высоко вверх.

Окончен урок, и выполнен план.

Спасибо, ребята, огромное вам!

За то, что упорно и дружно трудились,

За то, что царю, все вы так пригодились!

/запись в дневники домашнего задания, выставление оценок/

Приложение 8

Тест на тему: «Числа от 1 до 1000. Нумерация»

Задание 1: Отметь знаком (+) выражение, значение которых содержат 43 десятка.

1. 430 – 1
2. 443 – 40
3. 450 – 20
4. 348 – 3
5. 439 + 1
6. 434 – 400
7. 400 + 30
8. 500 – 70
9. 590 – 190
10. 300 + 130

Задание 2: Отметь знаком (+) выражение, значение которых содержат 52 десятка.

1. 520 – 20
2. 540 – 20
3. 522 – 2
4. 450 + 50
5. 520 + 4
6. 520 + 40
7. 570 – 70
8. 620 – 20
9. 730 – 210
10. 500 + 23

Приложение 9

Проверочная работа

Запиши цифрами числа:

четыреста двадцать три
триста пятьдесят один
восемьсот
четыреста шестьдесят
триста восемь
семьсот шестьдесят семь
двести три

Запиши число, в котором:

3 сот., 5 дес. и 4 ед.
7 сот. и 2 дес.
45 дес.
9 сот. и 15 ед.
7 сот. и 1 ед.
8 сот.
3 сот. 5 дес. и 8 ед.

3.Увеличь в 10 раз:

54
94
27
37
44
58
12

4.Уменьши в 10 раз:

460
380
940
200
470
500
280

5. Составь и запиши все возможные трёхзначные числа, используя цифры 5, 3, 0 так, чтобы цифры в записи числа не повторялись.

Приложение 10

Тест “Запомни и расставь точки”

С помощью данной методики оценивается объем внимания ребенка 4-6 лет.

Для этого используется стимульный материал, изображенный на рисунке. Лист с точками предварительно разрезается на 8 малых квадратов, которые затем складываются в стопку таким образом, чтобы вверху оказался квадрат с двумя точками, а внизу - квадрат с девятью точками (все остальные идут сверху вниз по порядку с последовательно увеличивающимся на них числом точек).

Перед началом эксперимента ребенок получает следующую инструкцию:

"Сейчас мы поиграем с тобой в игру на внимание. Я буду тебе одну за другой показывать карточки, на которых нарисованы точки, а потом ты сам будешь рисовать эти точки в пустых клеточках в тех местах, где ты видел эти точки на карточках"

Далее ребенку последовательно, на 1-2 сек, показывается каждая из восьми карточек с точками сверху вниз в стопке по очереди и после каждой очередной карточки предлагается воспроизвести увиденные точки в пустой карточке за 15 сек. Это время дается ребенку для того, чтобы он смог вспомнить, где находились увиденные точки, и отметить их в пустой карточке.

Оценка результатов теста

Объемом внимания ребенка считается максимальное число точек, которое ребенок смог правильно воспроизвести на любой из карточек (выбирается та из карточек, на которой было воспроизведено безошибочно самое большое количество точек).

Результаты эксперимента оцениваются в баллах следующим образом:

10 баллов - ребенок правильно за отведенное время воспроизвел на карточке 6 и более точек

8-9 баллов - ребенок безошибочно воспроизвел на карточке от 4 до 5 точек

6-7 баллов - ребенок правильно восстановил по памяти от 3 до 4 точек.

4-5 баллов - ребенок правильно воспроизвел от 2 до 3 точек.

0-3 балла - ребенок смог правильно воспроизвести на одной карточке не более одной точки.

Выводы об уровне объема внимания

10 баллов - очень высокий.

8-9 баллов - высокий

6-7 баллов - средний

4-5 балла - низкий

0-3 балла - очень низкий.

PAGE \* MERGEFORMAT 69

Дидактическая игра как средство развития познавательных способностей младших школьников при обучении математике