Методика преподавания раздела математического анализа «Предел функции в точке, на бесконечности, слева и справа, бесконечный предел

PAGE \* MERGEFORMAT 1

факультет математики и информатики

специальность: математика; информатика

кафедра математики и МПМ

ДИПЛОМНАЯ РАБОТА

«Методика преподавания раздела математического анализа «Предел функции в точке, на бесконечности, слева и справа, бесконечный предел»

ОГЛАВЛЕНИЕ

Введение 4

§1. Психолого-педагогические аспекты образования в высей школе 6

§2. Тематическое планирование по лекционному материалу 14

§3. Методические рекомендации по проведению лекционных занятий 17

§4. Конспект фондовых лекций 23

§4.1. Определение предела функции по Гейне 23

§4.2. Определение предела функции в точке по Коши или на 26

§4.3. Эквивалентность двух определений предела функции в точке 28

§4.4. Односторонние пределы 30

§4.5. Предел функции на бесконечности. Предел функции при

34

§4.6. Горизонтальные асимптоты 36

§4.7. Бесконечный предел функции 37

§4.8.Вертикальные асимптоты 38

§4.9. Свойства функции, имеющей предел в точке 39

§4.10. Свойства пределов функции 41

§4.11. Переход к пределам функций в неравенстве 42

§4.12. Теорема о пределе сжатой переменной (или теорема о пределе промежуточной функции) 44

§4.13. Предел суммы, произведение и частного функций, имеющих пре- дел в точке 45

§4.14. Предел сложной функции 46

§5. Тематическое планирование по практическим занятиям 48

§6. Методические рекомендации по проведению практических занятий 55

§7. Конспект практических занятий

§7.1. Практическое занятие №9 59

§7.2. Практическое занятие №10 66

§7.3. Практическое занятие №11 76

§7.4. Практическое занятие №12 86

§8. Электронное пособие по теме «Предел функции в точке, на бесконечности, слева и справа, бесконечный предел» и методические реко- мендации по его использованию 95

Заключение 101

Литература 103

Приложение 1 106

Приложение 2 111

Введение

В настоящее время учебный процесс в высшей школе стал более сложным по своим задачам, интенсивности и содержанию. Объем знаний, необходимых современному специалисту, возрастает, в то время как срок обучения в вузе ограничен несколькими годами. Поэтому необходимо интенсифицировать учебный процесс за счет обновления всех его сторон – содержания, форм, методов, и внедрения новейших педагогических и информационных технологий. Реформа Российского математического образования высшей школы заключается в том, что к традиционно изучаемым курсам в математике добавляются новые. Это ведет к сокращению аудиторных часов, предназначенных для изучения базовых дисциплин математического блока , в том числе математического анализа.

Потребности современного образования ставят перед методикой преподавания математики новые задачи. Особенно остро встает вопрос о методике изучения математического анализа в вузе. Несмотря на то, что число публикаций по всему курсу математического анализа все возрастает, ощущается острая нехватка обобщающих материалов по отдельным вопросам и разделам математики, где делалась бы попытка систематизировать уже полученные результаты. Изучение и анализ соответствующей литературы показали, что ни один источник не может представить целостной системы теории предела функции.

Поэтому теоретические и практические исследования по данной теме являются актуальными и обусловлены потребностями вузов педагогической специальности.

Итак, объектом исследования выпускной квалификационной работы является процесс организации учебной деятельности при преподавании дисциплины “Математический анализ” в педагогическом вузе.

В качестве предмета исследования выступает методика преподавания раздела математического анализа “ Предел функции в точке, на бесконеч- ности, слева и справа, бесконечный предел ” в вузе педагогическом вузе.

Цель исследования данной работы можно сформулировать так: разработка методики преподавания предела функции в высшей школе и электронного пособия по данной теме.

Реализация поставленной цели потребовала решения ряда конкретных задач, а именно:

обосновать и разработать содержание и методику преподавания темы «Предел функции в точке, на бесконечности, слева и справа, бесконечный предел» в педагогическом вузе с учетом возрастных особенностей студентов;

создать электронное пособие по данной теме для студентов I курса физико-математических факультетов педагогических вузов, которое включает в себя: электронный конспект фондовых лекций, демонст- рационный материал, электронный конспект практических занятий, тест .

Для достижения цели и выполнения поставленных задач были привлечены следующие методы: анализ, систематизация и обобщение психолого-педагогической, математической и методической литературы, учебных пособий и периодических изданий, работ по истории математики, учебных программ, периодических изданий, изучение опыта преподавателей вуза.

Практическая значимость исследования определяется тем, что в нем разработаны и проверены:

учебные материалы для изучения темы «Предел функции в точке , на бесконечности, слева и справа, бесконечный предел» в высшем учебном заве- дении педагогической направленности;

учебно-методическое электронное пособие по данной теме, которое включает в себя: электронный конспект фондовых лекций, демонстрацион-ный материал, электронный конспект практических занятий, тест ;

методические рекомендации для преподавателей вузов педагоги- ческого профиля по организации процесса обучения соответствующего раз- дела математического анализа.

§1. Психолого-педагогические аспекты образования в высшей школе

В настоящее время нет, пожалуй, более спорной проблемы в педагогике и психологии высшей школы, чем проблема воспитания студентов. “Надо ли воспитывать взрослых людей?”, “Стоит ли и корректно ли это делать?” Ответ на эти вопросы зависит от того, как понимать воспитание. Если его понимать как воздействие на личность с целью формирования нужных воспитателю, вузу, обществу качеств, то ответ может быть только отрицательным. Если как создание условий для саморазвития личности в ходе вузовского обучения, то ответ должен быть однозначно положительным.

Зачем нужен преподаватель в вузе, только ли как носитель и «передатчик» информации? Но как раз в этом качестве он значительно уступает многим другим источникам информации, таким, например, как книги и компьютеры. Вуз служит не только и может быть не столько для передачи специальных знаний, сколько для развития и воспроизведения особого культурного слоя, важнейшим элементом которого является и сам специалист. Специалиста как представителя определенной культуры характеризует не только специфический набор знаний и умений, но и определенное мировоззрение, жизненные установки и ценности, особенности профессионального поведения и т.п. Поэтому он не только передает студенту знания и профессиональные умения, а приобщает его к определенной культуре, и чтобы эта культура развивалась и воспроизводилась, необходимы живые люди, живое человеческое общение [24].

Воспитывать — это в значительной степени означает строить систему взаимоотношений между людьми. В современной педагогике (и еще
более явно в психологии) начинает преобладать подход к воспитанию не как к целенаправленному формированию личности, в соответствии с выбранным идеалом, а как к созданию условий для саморазвития личности.

Положения гуманистической психологии запрещают любые прямые воздействия на личность, какие бы цели (воспитательные или терапевтические) они не преследовали. Мы не имеем также права заранее решать за человека, каким ему быть, ибо каждый имеет право и должен сам прожить свою жизнь, не перекладывая на других ответственность за тот выбор, за те решения, которые ему приходится принимать. Уникальность и неповторимость каждой личности составляют богатство всего общества, и всякое искусственное ограничение свободного проявления и развития личности подрывает ее творческие потенции.

Сам способ существования личности есть постоянный выход за пределы самой себя, стремление к росту и развитию, направление которого воспитатель не может предугадать заранее и он не имеет права принимать сколько-нибудь ответственные решения за воспитуемого, какими бы само собой разумеющимися эти решения не казались ему. Самый главный прием воспитания — это принятие человека таким, какой он есть, без прямых оценок и наставлений. Только в этом случае будет сохраняться у воспитателя контакт с воспитуемым, что является естественным условием плодотворного взаимодействия обоих участников воспитательного процесса.

Означает ли это, что воспитатель должен занимать пассивную позицию в отношении тех выборов и принципиальных решений, которые принимает его воспитанник? Разумеется, нет. Главная задача воспитателя — раскрыть перед воспитуемым широкое поле выборов, которое часто не открывается самим ребенком, подростком, юношей из-за его ограниченного жизненного опыта, недостатка знаний и неосвоенности всего богатства культуры. Раскрывая такое поле выборов, воспитатель не должен, да и не может скрыть своего оценочного отношения к тому или иному выбору. Следует избегать только слишком однозначных и директивных способов выражения этих оценок, всегда сохраняя за воспитанником право на самостоятельное принятие решения, в противном случае ответственность за любые последствия принятых решений он с себя снимет и переложит на воспитателя [21].

Другое принципиальное требование к организации процесса воспитания состоит в неизменно уважительном отношении к личности воспитуемого как полноценного и равноправного партнера любой совместной деятельности. Идея равенства, партнерства и взаимного уважения друг к другу лежит в основе так называемой педагогики сотрудничества, принципы которой совершенно неоспоримы в вузовском обучении. Как утверждают многие крупные ученые и педагоги, основатели больших научных школ, наибольший учебный и воспитательный эффект достигается в таких ситуациях, когда учитель и ученик вместе решают задачу, ответ на которую не знает ни тот ни другой. В этом случае феномен партнерства и сотрудничества выражен максимально.

Другая важнейшая задача воспитания — помощь воспитуемому в выработке индивидуального стиля жизни, индивидуального стиля деятельности и общения. Для решения такой задачи преподавателю необходимо владеть некоторыми навыками и методиками психодиагностики, а также вооружить студентов приемами самопознания. Важнейшее значение имеет знание психологических и психофизиологических особенностей студентов, определяемых их социальным статусом, возрастом и характером основной деятельности.

Свою способность знать и понимать студентов, адекватно оценивать их личностные качества и состояния, преподаватели справедливо считают одним из важнейших профессиональных качеств и ставят ее на второе место после знания предмета, который они преподают. Но преподаватели, как правило, прикладывают очень мало усилий, чтобы повысить свою подготовку в этой области, хотя постоянно стремятся обновить и пополнить свои специальные (предметные) знания [24].

Часто преподаватели руководствуются индифферентными представлениями о студентах как об устройствах по переработке информации, которые слушают лекции, читают учебники, выполняют задания и, когда это требуется, демонстрируют эти знания на зачетах и экзаменах. Иногда это приводит к безличным и неадекватным требованиям, с которыми студенты просто не могут справиться. Для того, чтобы при построении программы учесть возможности и потребности студентов, нужно хорошо их знать. Успешная учебная деятельность студента зависит не только от степени владения приемами интеллектуальной деятельности; она обусловлена также личностными параметрами учебной деятельности — устойчивой системой отношений студента к окружающему миру и к самому себе.

На какие же вопросы следует обращать внимание в связи с необходимостью учета возрастных особенностей и индивидуальных различий студентов в воспитательно-образовательном процессе вуза? Современные студенты — это прежде всего молодые люди в возрасте 18 - 25 лет. Этот возраст определяется как поздняя юность или ранняя зрелость. Отсутствие единого термина уже говорит о сложности, неоднозначности психологических характеристик этого периода жизни. Очень важно иметь в виду, что человек непрерывно эволюционирует как единое целое, так что ни одну сторону его жизни нельзя понять в отрыве от других сторон. Возьмем, например, такой, казалось бы не имеющий отношения к педагогической ситуации параметр, как физическое развитие молодых людей. Студенческий возраст характеризуется наивысшим уровнем таких показателей, как мышечная сила, быстрота реакции, моторная ловкость, скоростная выносливость и др. Как принято говорить - это возраст физического совершенства человека. Большинство спортивных рекордов установлено именно в этом возрасте. Однако, как свидетельствуют данные Всемирной организации здравоохранения, именно студенты характеризуются худшими показателями физиологических функций в своей возрастной группе. Они лидируют по числу больных гипертонией, тахикардией, диабетом, нервно-психическими нарушениями. Причины этого, как показывают исследования, кроются в том, что в процессе вузовского обучения студенты испытывают сильное психическое напряжение, часто разрушительное для здоровья [24].

Преподаватель должен учитывать, что эти нагрузки особенно велики в периоды контроля и оценивания. Но именно здесь часто совершается одна из грубейших педагогических ошибок: негативную оценку результатов усвоения учебной программы преподаватель переносит на оценку личности студента в целом, давая студенту знать с помощью мимики, жестов, а то и в словесной форме, что он неумен, ленив, безответствен и т.п. Заставляя студента переживать негативные эмоции, преподаватель оказывает прямое влияние на физическое состояние и здоровье студента.

Учеба в вузе требует больших затрат времени и энергии, что обуславливает некоторую задержку социального становления студентов по сравнению с другими группами молодежи. Этот факт часто порождает у преподавателей ошибочное представление о студентах как социально незрелых личностях, нуждающихся в постоянной опеке, снисходительном отношении. Сам того не осознавая преподаватель в этом случае как бы ставит планку, ограничивает уровень, до которого студент, по его представлению, может развить свои личные качества, в данном случае ответственность, инициативность, самостоятельность. Воспитуемый (в данном случае студент) неосознанно воспринимает такую программу и, что особенно огорчительно, внутренне принимает ее. Человеку свойственно легко адаптироваться к заниженным требованиям: в этих условиях способности студента не только не развиваются, но и часто деградируют.

Отношение же педагога к студенту как к социально зрелой личности, напротив, как бы отодвигает планку, раскрывает новые горизонты, тем самым не ограничивая возможности развития личности, а усиливая их своей верой, внутренней поддержкой [24].

Как правило, именно в студенческом возрасте достигают максимума в своем развитии не только физические, но и психологические свойства и высшие психические функции: восприятие, внимание, память, мышление, речь, эмоции и чувства. Этот факт позволил Б.Г. Ананьеву сделать вывод о том, что данный период жизни максимально благоприятен для обучения и профессиональной подготовки. В этот период происходит активное формирование индивидуального стиля деятельности. Преобладающее значение в познавательной деятельности начинает приобретать абстрактное мышление, формируется обобщенная картина мира, устанавливаются глубинные взаимосвязи между различными областями изучаемой реальности.

Если преподаватель не развивает именно эти способности, у студента может закрепиться навык полумеханического запоминания изучаемого материала, что ведет к росту показной эрудиции, но тормозит развитие интеллекта. Результаты специальных обследований показывают, что у большинства студентов уровень развития таких интеллектуальных операций, как сравнение, классификация, определение весьма невысок. Преподавателю зачастую приходится прилагать большие усилия, чтобы преодолеть школярское отношение к учебе: ориентацию только на результат интеллектуальной деятельности и равнодушие к самому процессу движения мысли.

Лишь немного более половины студентов повышают показатели интеллектуального развития от первого курса к пятому, и как правило такое повышение наблюдается у слабых и средних студентов, а лучшие студенты часто уходят из вуза с тем же уровнем интеллектуальных способностей, с которым пришли.

Важнейшая способность, которую должен приобрести студент в вузе, - это собственно способность учиться, которая радикальным образом скажется на его профессиональном становлении, ибо определяет его возможности в послевузовском непрерывном образовании. Научиться учиться важнее, чем усвоить конкретный набор знаний, которые в наше время быстро устаревают. Еще важнее способность самостоятельного добывания знаний, основанная на творческом мышлении.

Особенно бурно в период вузовского обучения идет развитие специальных способностей. Студент впервые сталкивается со многими видами деятельности, являющимися компонентами его будущей профессии, поэтому на старших курсах необходимо уделять особое внимание диалоговым формам общения со студентами, в частности, в процессе выполнения ими курсовых и дипломного проектов, прохождения практик и т.п.

Передача «личностного знания» возможна, как правило, только в диаде «учитель-ученик» [24].

Эмоциональная сфера в студенческом возрасте приходит к некоторому уравновешенному состоянию, «успокаиваясь» после своего бурного развития и брожения в подростковый период. Но определенные отголоски прошедших «бурь» иногда дают себя знать, особенно у студентов с задержками личностного развития, т.е. страдающих инфантилизмом. Часто может наблюдаться гипертрофированная и несколько абстрактная неудовлетворенность жизнью, собой и другими людьми. При неадекватном педагогическом воздействии такие состояния могут стать причиной деструктивных тенденций в поведении. Но при обращении энергии этого эмоционального состояния на решение сложной и значимой для студента задачи неудовлетворенность может стать стимулом к конструктивной и плодотворной работе.

Выраженный и часто подчеркнутый рационализм в обращении преподавателей со студентами негативно сказывается на развитии их эмоциональной сферы в целом. Поэтому преподавателю необходимо сознательно следить за тем, не переходит ли опасную черту почти неизбежный дисбаланс рационального и эмоционального в стиле его общения со студентами. В этом случае без некоторой, пусть порой даже искусственно добавляемой, эмоциональной теплоты, эффективность его работы со студентами может сильно снизиться даже при ее очень высоком содержательном уровне. Без принятия таких мер у преподавателя самого могут возникнуть эмоциональные перегрузки, еще более усиливающие трудности нахождения верного эмоционального тона в общении со студентами.

Самая главная особенность юношеского возраста (включая и позднюю юность) состоит в осознании человеком своей индивидуальности, неповторимости, в становлении самосознания и формировании «образа Я». Образ «Я», — это социальная установка, отношение личности к себе, включающее три взаимосвязанных компонента: познавательный, эмоциональный и поведенческий. За последние десятилетия произошел сдвиг пика становления самосознания с возраста 17-19 лет на 23-25 лет. Становление самосознания актуализирует проявление важнейших и часто противоречивых потребностей юношеского возраста — в общении, уединении, в достижениях и др. [21].

Потребность в достижении, если она не находит своего удовлетворения в основной для студента учебной деятельности, закономерно смещается на другие сферы жизни — в спорт, бизнес, общественную деятельность, хобби, или в сферу интимных отношений. Но человек обязательно должен найти для себя область успешного самоутверждения, в противном случае ему грозит уход в болезнь, невротизация или уход в криминальную жизнь.

И здесь ответственна роль преподавателя как первого эксперта, дающего студенту «обратную связь» о результатах его исследовательской работы. Своими оценками он может неосторожно убить у студента всякую надежду и, соответственно, желание утверждаться на ниве науки и подтолкнуть его к выбору других сфер жизни для самоутверждения и удовлетворения потребности в достижении.

Благоприятное положение студента в окружающей его среде содействует нормальному развитию его личности. Не должно быть существенного расхождения между самооценкой и оценкой, получаемой студентом от значимых для него людей (референтной группы), к которым обязательно должен относиться и преподаватель. В этом случае он может помочь студенту в преодолении неблагоприятного соотношения самооценки, ожидаемой оценки и оценки, исходящей от референтной группы. Это можно сделать целенаправленно, организовав такую педагогическую ситуацию, чтобы студент предстал перед значимыми для него «другими» в выгодном свете и получил положительную оценку, что приведет к повышению ожидаемой оценки, улучшит его психологическое состояние и сделает более благоприятной позицию личности в целом.

Заключая разговор об условиях успешной воспитательной работы, следует напомнить изложенные в начале параграфа общие положения о сущности воспитания как о создании благоприятных условий для самовоспитания человека путем раскрытия перед ним поля возможных выборов и их последствий, при том, что окончательное решение всегда должен принимать сам воспитуемый. Важнейшим условием внимания студента к тому, что раскрывает перед ним преподаватель выступает безусловное принятие студента преподавателем и признания за ним права на любой выбор без того, чтобы быть отвергнутым [24].

§2. Тематическое планирование по лекционному материалу

Согласно учебной программе раздел «Предел функции» изучается на физико-математических факультетах педагогических вузов на первом курсе в первом семестре. Распределение часов представлено в следующих таблицах:

1.Тематический план по разделу «Предел функции» курса «Математический анализ» факультета математики и информатики по спе- циальности «Математика» с дополнительной специальностью «Инфор -матика».

ТЕМА	КОЛИЧЕСТВО ЛЕКЦИЙ
1. Предел функции по Гейне и по Ко- ши. Примеры. Эквивалентность двух определений. Односторонние пределы. Предел функции на бесконечности. Бес- конечный предел. Горизонтальные и вертикальные асимптоты.	ЛЕКЦИЯ №1
2. Свойства функции, имеющей пре- дел в точке. Свойства пределов функции. Переход к пределам в неравенствах, пре- дел сжатой переменной, предел суммы, произведения и частного.	ЛЕКЦИЯ №2
3. Предел сложной функции. Дока- зательство неравенства . Первый замечательный предел. Теорема о необходимом и достаточном условии существовании предела функции в точке.	ЛЕКЦИЯ №3
4. Второй замечательный предел. Вычисление пределов. Сравнение беско -нечно малых функций. Эквивалентность бесконечно малых функций. Порядок бесконечно малых.	ЛЕКЦИЯ №4
Всего лекций	4

2.Тематический план по разделу «Предел функции» курса «Математика» факультета математики и информатики по специальности «Информатика» с дополнительной специальностью «Математика».

ТЕМА	КОЛИЧЕСТВО ЛЕКЦИЙ
1. Предел функции по Гейне и по Ко- ши. Примеры. Эквивалентность двух опре- делений. Односторонние пределы. Предел функции на бесконечности. Бесконечный предел. Горизонтальные и вертикальные асимптоты.	ЛЕКЦИЯ №1
2. Свойства функции, имеющей предел в точке. Свойства пределов функции. Пере ход к пределам в неравенствах, предел сжатой переменной, предел суммы, произ- ведения и частного.	ЛЕКЦИЯ №2
3. Предел сложной функции. Доказа- тельство неравенства . Первый замечательный предел. Теорема о необходимом и достаточном условии существовании предела функции в точке.	ЛЕКЦИЯ №3
4. Второй замечательный предел. Вы -числение пределов. Сравнение бесконечно малых функций. Эквивалентность беско- нечно малых функций. Порядок беско- нечно малых.	ЛЕКЦИЯ №4
Всего лекций	4

Основными учебниками для изучения данной темы в педагогическом вузе являются учебные пособия Фихтенгольца Г. М. «Курс дифференциального и интегрального исчисления», Фихтенгольца Г. М. «Основы математического анализа», Кудрявцева Л. Д. «Курс математического анализа». Помимо этих учебников можно пользоваться другими пособиями, указанными в литературе.

Вопросы, которые необходимо рассмотреть по обязательной программе разбиты так, чтобы:

1. лекции по объёму приблизительно были равны;
2. чтобы не нарушалась целостность лекции, т.е. не терялась её основная мысль.

По этой же структуре разработаны и фондовые лекции по исследуемой теме [17].

§3. Методические рекомендации по проведению лекционных занятий

Среди разнообразных методов и средств совершенствования процесса обучения в высшей школе, интенсификации и повышения эффективности учебной деятельности важное место отводится умелому и рациональному использованию технических средств обучения (ТСО).

Меры, которые были приняты для улучшения подготовки специалистов с высшим образованием, научно-технический прогресс, бурное развитие вычислительной техники – всё это способствовало развитию интереса к использованию ТСО [21].

ТСО – это совокупность технических устройств и дидактических материалов, используемых в учебном процессе в качестве средства повышения эффективности обучения. Ни отдельное устройство, ни дидактический материал, взятые сами по себе, не могут выступать как технические средства обучения, становятся таковыми в результате их “соединения”.

На лекционных занятиях целесообразно использовать технические средства предъявления информации (ТСПИ). К таким ТСПИ относятся следующие технические устройства: графопроектор, видеопроектор, учебное телевидение (телевизор, компьютер), ПО ЭВМ.

Вся вышеперечисленная аппаратура составляет материально-техническую базу факультета математики и информатики СГПИ и является доступной для преподавателей факультета.

Но не только свободный доступ к данным средствам обучения обуславливает их использование в учебном процессе. Каждое из них имеет свои технические характеристики, позволяющие с разной степенью эффективности предъявлять информацию. Преимущества и недостатки графопроектора и видеопроектора были выявлены преподавателями вуза при проведении лекций в течение длительного срока. Их опыт, описанный ниже, может быть использован при подготовке и проведении лекций по изучению предела функции.

Идея использовать ПО ЭВМ как средство предъявления информации при подключении к нему телевидения появилась совсем недавно в связи с бурным развитием научно-технического прогресса. Поэтому его эффективность необходимо было подтвердить экспериментально. В связи с этим с помощью данных средств обучения были проведены лекции по изучению предела функции, в ходе которых установлены преимущества и недостатки использования новых технологий.

Рассмотрим полученные характеристики каждого из данных средств обучения.

Графопроекторы (или кодоскопы) имеют важные достоинства с ди- дактической точки зрения. Они компактны, просты в обращении, обладают очень большим световым потоком (около 2000 лм), что позволяет демонстрировать изображение в освещённой комнате без существенного снижения контраста. Размеры кадрового окна обычно 2424 см. Дидактический материал чаще всего готовится заранее в виде отдельных листов прозрачной плёнки – фолий с нанесёнными надписями и рисунками. По мере надобности фолии накладываются на кадровое окно и изображение проецируется на экран.

Фолии можно накладывать одна на другую, чем создаётся возможность последовательно “выстраивать” окончательную картину из частичных изображений, в том числе окрашенных в разные цвета. Используются также фолии с подвижными элементами, что позволяет демонстрировать разнообразные динамические процессы. Необходимый для учебных занятий материал можно готовить заранее или выполнять в ходе занятий на непрерывной ленте с постепенной перемоткой ленты с подающей кассеты на приёмную. При создании фолий могут возникнуть трудности в подборе пары «плёнка – пишущие приспособления» (карандаши). При отсутствии фломастеров, специально приспособленных для работы с графопректором, лучшие результаты достигаются, когда применяется гидрофильная (например, триацетатная) плёнка и тушь (в том числе цветная), которая наносится с помощью плакатных перьев, трубочек, рапидографа. При использовании фломастеров типа “projector pen” можно получить сочные рисунки и надписи на любой плёнке.

Опыт показывает, что преподаватели очень охотно работают с графопроекторами, поскольку они всё время обращены лицом к учащимся, не теряют контакта с ними и ведут занятия в освещённой аудитории, что благоприятно сказывается на учебной деятельности [21].

Видеопроектор – это аппарат динамической проекции, который обеспечивает проекцию на экран видеоизображения, записанного на носитель информации, как в аналоговой, так и в цифровой форме. Видеопроекторы различных моделей имеют разнообразные технические и эксплуатационные характеристики. Они производятся различными фирмами, имеющими мировую известность: Philips, InFocuS, Toshiba, Hitachi и т.д.

Видеопроекторы, являясь современными мультимедийными аппаратами, обеспечивают идеальное качество изображения в любом видеоформате (NTSC/PAL/SECAM). Для видеопроекторов разработаны специальные лампы с повышенной светоотдачей. При создаваемом световом потоке до 3500 лм, лампа может работать до 1000 часов без потери яркости. Несмотря на то, что лампа обеспечивается принудительным охлаждением, вентилятор работает практически бесшумно, что удовлетворяет санитарно-гигиеническим нормам при использовании ТСО.

Универсальность использования видеопроектора на лекциях также обеспечивается ещё и тем, что размер изображения на экране может варьиро- ваться от 1,0 м 1,5 м до 3,5 м 6,0 м.

Настройки видеопроектора можно изменять с помощью пульта дистан- ционного управления.

Видеопроектор InFocuS LP 290, имеющийся в наличии материальной базы института, обеспечивает возможность проецирования на экран динамического и статического изображения, подаваемого на его вход как в аналоговой, так и в цифровой форме с видеовыхода телевизора, видеомагнитофона или компьютера [23].

Очевидные преимущества видеопроектора – яркость изображения, бесшумность работы, варьирование изображения на экране, возможность хранить информацию на различных носителях (видеокассета, дискета, диск) – делают его настоящей находкой для преподавателя и одним из наиболее эффективных средств обучения.

Как показывает эксперимент, по качеству обучения с видеопроектором может сравниться комплекс, состоящий из ПО ЭВМ и подключённых к ней телевизоров.

На лекционный курс по теме «Предел функции в точке, на бесконечности, слева и справа, бесконечный предел» отводится 8 часов. Поэтому необходимо внедрять информационные технологии (электронный учебник) и средства ТСО (мультимедийный проектор, графопроектор) для более продуктивной работы. В связи с этим и был создан электронный конспект фондовых лекций. Разработанная методика проведения лекционных занятий была апробирована на первом курсе факультета математики и информатики СГПИ в 2003-2004 учебных годах.

Апробационные лекции проводились в аудитории № 28 корпуса М СГПИ. Аудитория рассчитана на 120 человек, на лекции присутствовало 112 студентов. Для визуализации лекций в таких условиях оказалось достаточно двух телевизоров. Поэтому комплекс ТСО включал в себя два телевизора Samsung с диагональю 72 см, подключённых к компьютеру P–III в комплектности с дисководом и CD-ROM-ом.

Для осуществления апробации проводилась подготовка: за несколько дней до лекции проверялась исправность и рабочее состояние аппаратуры, демонстрация лекции на экране, корректировался масштаб текста, проверялся сам материал фондовых лекций. Перед началом лекции подключалась аппаратура и активизировалась дискета; проверялась видимость текста на экранах телевизоров из разных мест в аудитории и в соответствии с этим определялось максимальное расположение телевизоров по отношению к зрителям, подбиралось нужное освещение.

По окончании лекции производилось завершение работы компьютера и отключение всей аппаратуры.

Подключение телевизоров к компьютеру позволяет выводить на экраны телевизоров изображение с экрана дисплея. Таким образом, информация, предъявляемая на лекциях, может храниться на дискетах и дисках. Это создаёт большие преимущества компьютеру перед другими средствами обучения – огромная информационная ёмкость видеодиска, высокое качество воспроизведения на экране телевизоров, возможность организации управления выводом нужных кадров, малое время поиска кадров [21].

В ходе апробации были выявлены и другие достоинства использования данного комплекса ТСПИ при проведении лекций: преподаватель видит лекции перед собой на экране дисплея компьютера и с помощью мышки или клавиатуры может передвигаться вверх и вниз страницы с нужным темпом; преподаватель обращён лицом к аудитории – поддерживается контакт со студентами, появляется возможность подробных комментариев, а также постоянного контроля дисциплины; студенты, не успевающие записывать лекцию со слов преподавателя, могут переписывать лекционный материал с экранов телевизоров, не переспрашивая и не отвлекая вопросами преподавателя от хода его мыслей – тем самым экономится время (до 50 %), которое может быть использовано для контроля знаний; студенты, пропустившие лекции по уважительной причине, могут попросить преподавателя скопировать нужные лекции на их дискеты и затем распечатать их; хорошая освещённость аудитории также создаёт благоприятные условия для обучения.

Апробация прошла успешно – удалось избежать «накладок».

Таким образом, при хорошей подготовке использование в лекции даже простых технических средств предъявления информации может существенно повысить её привлекательность для студентов, дидактическую эффективность, а также снизить нагрузку на голосовой аппарат преподавателя.

§4. Конспект фондовых лекций

В ходе составления лекционного материала были проанализированы различные учебники для студентов вузов, а именно:

• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т. 2.- СПб: «Лань», 1997. – 800 с.
• Виленкин Н. Я. и др. Математический анализ: Интегральное исчисление. М.: Просвещение, 1988. – 192 с.
• Фихтенгольц Г. М. Основы математического анализа. Т.2. – СПб: Лань, 1999.- 395с.
• Бохан К. А. и др. Курс математического анализа. Т. 1. – М.: Просвещение, 1965. – 435 с.
• Кудрявцев Л. Д. Курс математического анализа. Т. 1. – М.: Высш. шк., 1970. – 592 с.

В силу сложности и абстрактности изложения теоретического материала в вышеперечисленных книгах, он был систематизирован в соответствии с учебной программой курса математического анализа.

§4.1. Определение предела функции по Гейне

Генрих Эдуард Гейне – немецкий математик (1821-1881)

1.Пусть дана функция , определённая на некотором множестве . И пусть точка или . Возьмём из множества последовательность точек на отличных от при :

, сходящуюся к , т.е. .

Т.о. — последовательность значений аргумента х. Значения функции в точках этой последовательности также образуют числовую последовательность: ., т.е. .

Теперь можно поставить вопрос о существовании предела функции в точке .

Определение по Гейне( на языке «последовательностей»). Число называется пределом функции в точке , если для любой сходящейся к последовательности значений аргумента х, соответст -вующая последовательность значений функции сходится числу .

Символически это записывается так: или .

Из определения следует, что функция , определенная на множестве Х, имеет предел, равный , т.е. , если

а) — сходящаяся к последовательность значений аргумента; причем , , .

б) а сходящаяся к последовательность значений функции , т. е.

.

Примеры. 1). Функция . Доказать, что эта функция имеет в каждой точке числовой прямой предел равный .

Доказательство

1. Если , сходящаяся к последовательность значений аргумента, то последовательность значений функции будет иметь вид:

или

2. Значит, предел последовательности значений функции имеет тот же предел :.

3. На основании определения предела функции в точке по Гейне функция будет иметь тот же предел в точке : .

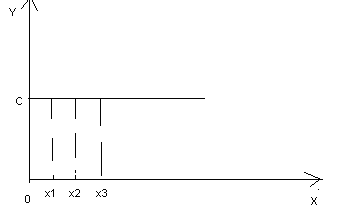
Рис.1.

4. Так как точка выбиралась произвольно, то функция будет иметь в любой точке числовой прямой, предел, равный С. Ч.т.д.

2). Функция . Доказать, что в каждой точке числовой прямой эта функция имеет предел, равный , т.е. .

Доказательство

Провести самостоятельно.

1. Пусть последовательность значений аргумента, сходящаяся к имеет вид:

, и .

2. Тогда последовательность значений функции будет иметь вид: или ,… .

3. То есть последовательности и тождественны.

4. Значит, последовательность значений функции имеет тот же предел:

5. Поэтому на основании определения предела функции в точке по Гейне функция будет , то есть .

6. Так как точка выбиралась произвольно, то функция в любой точке числовой прямой будет иметь предел равный [26]. Ч.т.д.

3). Функция Дирихле не имеет предела ни в одной точке числовой прямой.

Доказательство

1. Так для последовательности рациональных значений аргумента, сходящуюся к , соответствующая последовательность значений функции имеет предел , равный 1.

2. А для последовательности иррациональных значений аргумента, сходящихся к , соответствующая последовательность значений функции будет иметь предел , равный 0.

3. Следовательно, предела не имеет. Ч.т.д.

§4.2. Определение предела функции в точке по Коши или на языке «»

Огюстен Луи Коши –французский математик (1789-1857).

Определение (по Коши или на языке«»). Число называется пределом функции в точке , если

С помощью символов определение можно записать так:

.

Замечание. Неравенство можно записать так:

.

Геометрический смысл предела функции в точке

1. Дан график функции .
2. Неравенство означает , что отстоит от не далее, чем на , т. е. или « говорят» принадлежит проколотой - окрестности точки оси Ох: .
3. Неравенство означает , что значения функции не выходят за интервал оси Оy, то есть значения функции принадлежат - окрестности точки оси Оy : .

4. Если выполняется равенство , то точка графика функции должна находиться в полосе шириной , ограниченной прямыми , , дл всех значений х , удаленных от точки не дальше , чем на .

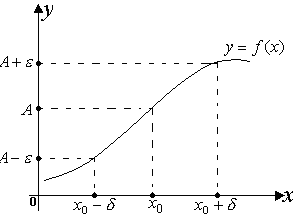
Рис.2.

§4.3. Эквивалентность двух определений предела функции в точке

Теорема. Первое и второе определение предела функции в данной точке эквивалентны.

Доказательство

1. 1. Пусть число – предел функции в точке согласно определения по Гейне. Требуется доказать, что число будет являться пределом функции в точке на основании определения по Коши.

2. Доказательство проведём методом от противного, то есть, предположим, что число не является пределом функции согласно определения по Коши.

3. Это значит, что не можно указать такое , что из неравенства следовало бы неравенство . То есть, существует такое , для которого какое бы мы не взяли, найдётся хоть одна точка , что вслед за неравенством будет выполняться неравенство .

4. Возьмём в качестве последовательно такие числа:

5. Тогда

а) для найдётся такое ;

б) для найдётся такое ;

в) для найдётся такое ;

…………………………………………………………………………

для найдётся такое .

…………………………………………………………………………

6. В результате получим последовательность значений аргумента . Причём, эта последовательность сходится к при .

7. Согласно определению предела последовательности в точке по Гейне, соответсвующая последовательность значений функции должна сходиться к числу , т. е., . (1)

8. На основании определения предела последовательности выражение (1) можно переписать по-другому:

. (2)

9. Сравним неравенства (1) и (2). Получим противоречие. Значит, наше предположение о том, что число не является пределом функции в точке на основании определения по Коши неверно.

II. 1. Пусть – предел функции в точке согласно определения по Коши. Требуется доказать, что является пределом функции в той же точке в соответствии с определением предела функции по Гейне.

2. Согласно определения предела функции в точке по Коши:

.

3. Возьмём последовательность точек из множества , на котором определена функция . Пусть эта последовательность сходится к . Пусть .

4. В соответствии с определением предела последовательности для данного значения , соответствующего некоторому , будет .

5. Последнее неравенство выполнимо благодаря определению по Коши , т. е. . Это равносильно тому, что последовательность значений функции сходится к при .

6. Таким образом, для произвольной последовательности значений аргумента сходящейся к при , , соответствующая последо- вательность значений функции сходится к .

7. Поэтому на основании определения по Гейне функция сходится к при . Ч.т.д.

Замечание 1. Итак, установлена эквивалентность обоих определений предела функции в точке. Можно использовать любое из них в зависимости от того, какое более удобно при решении той или иной задачи.

2. Оба определения сами по себе еще не дают способа отыскания предела данной функции в точке. С их помощью иногда можно установить, будет ли то или иное число пределом функции, или можно убедиться, что данная функция вовсе не имеет предела.

§4.4. Односторонние пределы