Анализ электрической цепи системы управления

ЗАДАНИЕ

Для электрической цепи, соответствующей номеру варианта необходимо выполнить следующие задания (указаны в содержании):

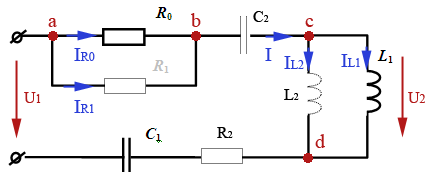
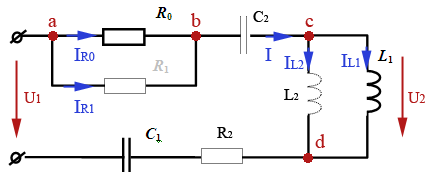
Рис. 1. Электрическая схема системы управления

Таблица 1

Номер варианта задания	Номер рисунка	Параметры электрической схемы
		R1	R2	R3	L1	L2	C1	C2
		Ом	мГн	мкФ
12	2	300	900	240	5000	15000	1,12	0,2

1. Провести анализ электрической цепи системы управления. Обозначить узлы схемы и токи ветвей, указать входной и выходной сигналы;
2. Определить передаточную функцию четырехполюсника;
3. Определить и представить графически амплитудно-частотную (АЧХ) и фазо-частотную (ФЧХ) характеристики;
4. По полученному дифференциальному уравнению построить структурную схему системы управления;
5. Определить реакцию исследуемой системы на единичное ступенчатое воздействие при нулевых начальных условиях:

Определить устойчивость системы управления, используя критерий устойчивости Михайлова решение представить графически.

Содержание

Наименование пункта	Стр.
1.	Анализ электрической цепи: обозначение узлов, токов; определение входного и выходного сигналов	3
2.	Определение передаточной характеристики четырехполюсника	4
3.	Определение АЧХ и ФЧХ	4
4.	Построение структурной схемы системы управления	5
5.	Определение реакции исследуемой системы на единичное ступенчатое воздействие при нулевых начальных условиях	7
6.	Определение устойчивости системы управления (критерий устойчивости Михайлова)	8

1. Анализ электрической цепи: обозначение узлов, токов;

определение входного и выходного сигналов

Составим модель объекта:

Сопротивления реактивных элементов:

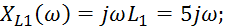
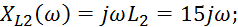
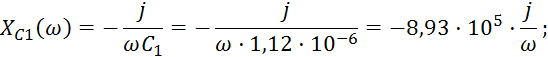
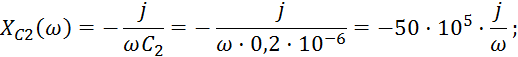
Эквивалентное сопротивление параллельно включенных индуктивностей:

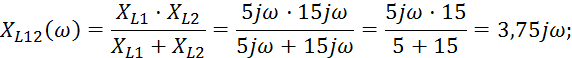
Эквивалентное сопротивление параллельно включенных сопротивлений:

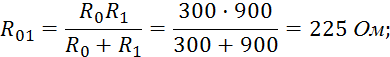
Входное сопротивление цепи:

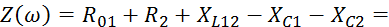
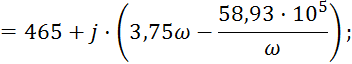
Ток в цепи:

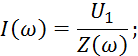
Напряжение на выходе цепи:

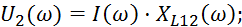
2. Определение передаточной характеристики четырёхполюсника

Определим передаточную характеристику:

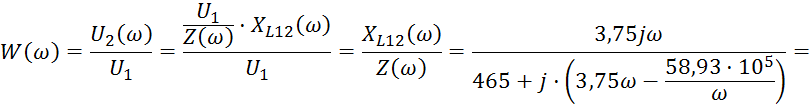
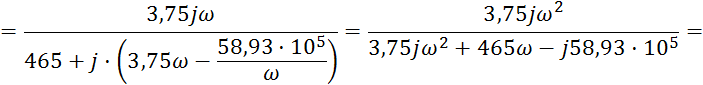
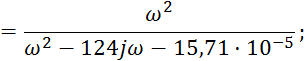
3. Определение АЧХ И ФЧХ

Амплитудно-частотная характеристика (АЧХ) цепи — модуль передаточной функции.

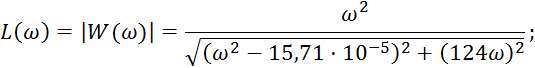
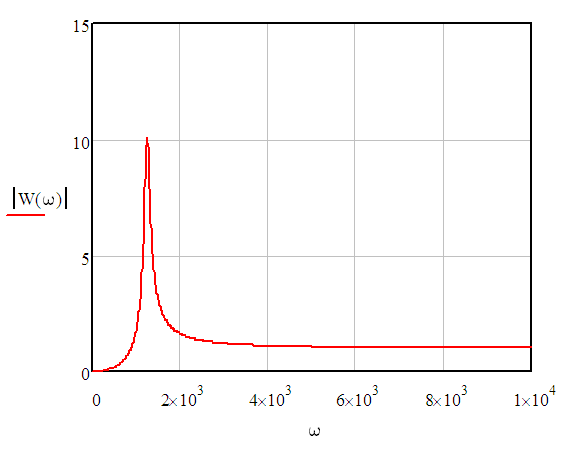
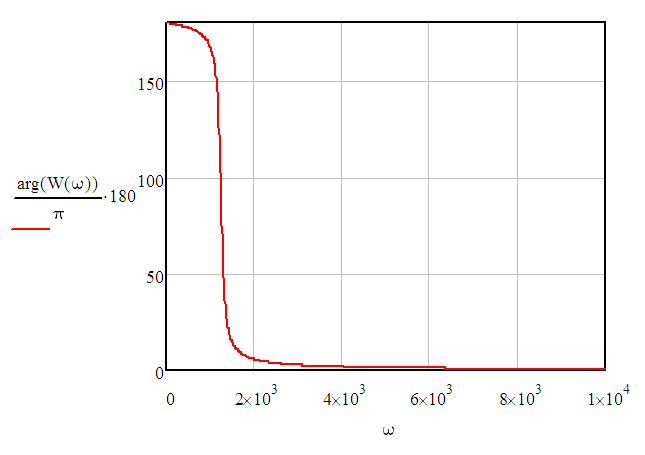
Фазо-частотная характеристика (ФЧХ) цепи — аргумент передаточной функции.

Для ФЧХ цепи необходимо разделить передаточную функцию на действительную и мнимую часть, умножим на комплексно-сопряженное к знаменателю выражение:

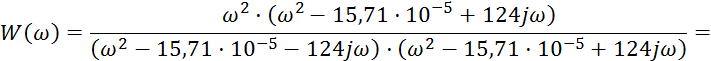
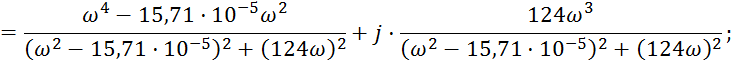
4. Построение структурной схемы системы управления

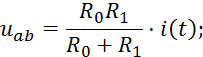
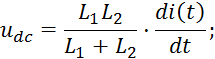
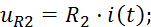
Определим передаточную функцию четырехполюсника в области изображений, выразив входное и выходное напряжение цепи через ток:

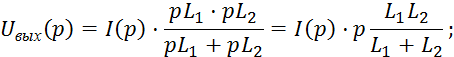
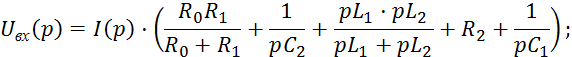
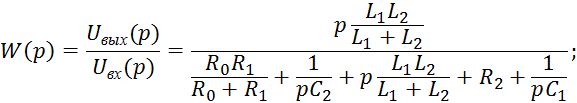
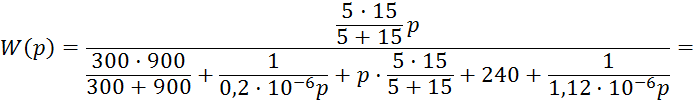
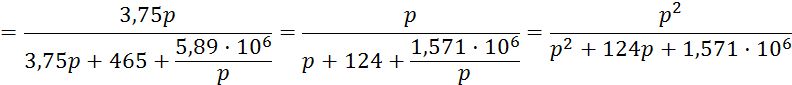
Данное выражение сопоставимо с полученным ранее выражением для частотной функции исследуемого четырехполюсника пи выполнении замены сомножителя j на оператор p.

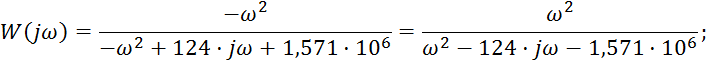
Структурная схема четырехполюсника:

Структурная схема исследуемого четырехполюсника может быть представлена в виде двух последовательно соединенных блоков:

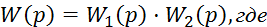
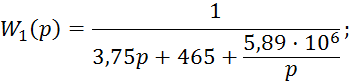
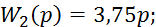
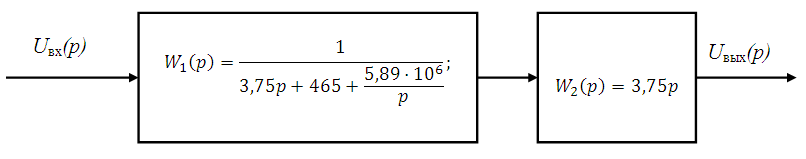
5. Определение реакции исследуемой системы на единичное ступенчатое воздействие при нулевых начальных условиях

Передаточная характеристика исследуемого четырехполюсника:

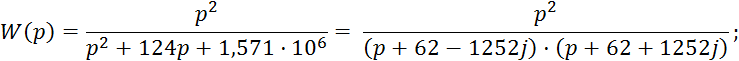
При единичном ступенчатом воздействии Uвх=1/p выходное напряжение равно:

Воспользуемся теоремой разложения для перехода в область времени:

, где

M(p) — числитель передаточной характеристики;

— производная от выражения, стоящего в знаменателе знаменатель передаточной характеристики;

N(p) — знаменатель передаточной характеристики;

pk – k-й корень производной от полинома N(p).

Производная от полинома знаменателя:

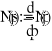
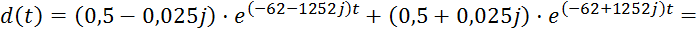
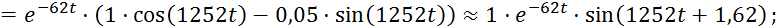
Графическая иллюстрация:

6. Определение устойчивости системы управления (критерий устойчивости Михайлова)

Определим передаточную функцию замкнутой системы:

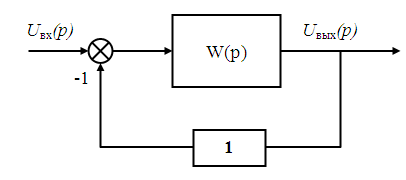
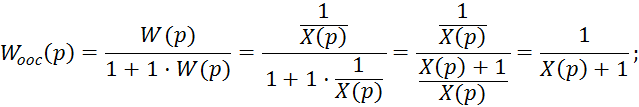
Запишем характеристический полином:

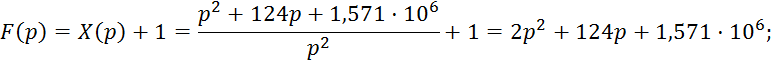
Перейдем к функции частоты:

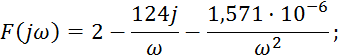
Построим годограф Михайлова

Критерий устойчивости по Михайлову:

Чтобы система автоматического управления была устойчивой, необходимо и достаточно, чтобы вектор кривой Михайлова при изменении от 0 до повернулся, нигде не обращаясь в нуль, вокруг начала координат против часовой стрелки на

угол , где n — порядок характеристического уравнения. Заметим, что для устойчивых систем кривая Михайлова начинается при = 0 на вещественной положительной полуоси.

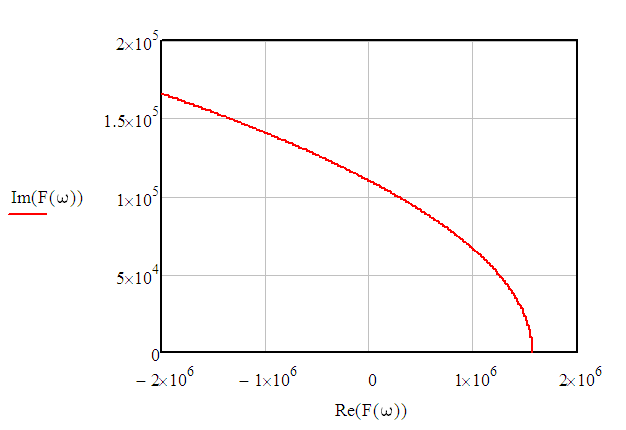
Im(F(w)) – мнимая составляющая полинома F(w)

Re(F(w)) – мнимая составляющая полинома F(w)

В данном случае, на основании критерия устойчивости Михайлова, можно утверждать, что исследуемая система является устойчивой – годограф начинается на положительной действительной полуоси и уходит в бесконечность во втором квадранте, что соответствует второй степени полинома.

Зарегистрирована

Дата

Подпись

Кафедра “Электротехника”

Контрольная работа 1.2

Основы теории управления

Волгоградский государственный технический университет

2

3

4

5

Замечания

6

1

4

5

6

3

1

2

Рейтинговая оценка