Написание программы построения вероятностного автомата
ВВЕДЕНИЕ
Вычислительные системы существуют уже не один десяток лет. Целью их создания являлась возможность заменить человека, сделать за него трудоемкую работу, требующую сложных вычислений. С развитием теории больших систем, усиленное изучение функционирования биологических структур, исследование надежности систем, состоящих из большого числа элементов, поиски методов управления объектами, для которых неизвестна достаточно точная математическая модель их функционирования, привели к возникновению и интенсивному развитию специального раздела теоретической кибернетики — теории вероятностных автоматов. Эта теория опирается, с одной стороны, на мощные методы и результаты теории конечных детерминированных автоматов, а с другой стороны, широко использует идеи и методы теории статистических решений и теории игр. Теория вероятностных автоматов еще не получила какого–либо окончательного завершения и терминологического оформления. Различные исследователи, работающие в этой области, используют различную терминологию, что существенно усложняет выработку единой точки зрения. Кроме того, как и в теории детерминированных автоматов, в теории вероятностных автоматов можно наметить два направления, различных по своим задачам и методам: абстрактная теория вероятностных автоматов занимается проблемами эквивалентности автоматов, представимостью тех или иных событий в вероятностных автоматах, алгебраическими задачами, связанными с моделями такого типа; структурная теория исследует другой круг проблем, в который входят задачи анализа работы имеющихся устройств, разработка методов синтеза вероятностных устройств, исследование их поведения в реальных средах, решение задач структурной надежности и т. д,
Актуальность. В последнее время одними из актуальных становятся задачи связанные с объектами или комплексами объектов, действующих в недетерминированных средах. Актуальность обуславливается развитием технологий, усложнением объектов, а также стремлением автоматизировать процессы, ранее производимые с помощью человека
Целью дипломной работы является: написание программы построения вероятностного автомата
Задачи, решаемые в дипломной работе, для достижения поставленной цели:
- исследование вероятностных автоматов;
- исследование классификации вероятностных автоматов;
- выбор представления вероятностных автоматов;
- выбор подходящей среды разработки программы;
- разработка программного обеспечения.
1 СИСТЕМА ЦИФРОВЫХ АВТОМАТОВ
1.1 Основные понятия и определения
В компьютере обрабатывается числовая информация, представленная в двоичной системе счисления, то имеется информация представлена в облике композиции нулей и единиц. Потому работу хоть какой схемы ЭВМ разрешено рассматривать как многофункциональный преобразователь с огромным количеством входов и выходов. При данном прибытие на входы некой очередности входных сигналов, состоящих из 0 и 1, вызывает появление на выходах полностью определенной последовательности выходных сигналов, также состоящей из нулей и единиц.
Все схемы ЭВМ можно поделить на 2 класса: Класс логических или комбинационных схем, класс конечных автоматов.
В логических и комбинационных схемах смысл выходных сигналов в эпизод времени t несомненно ориентируется значениями входных сигналов в момент времени t1t.
Технические вопросы синтеза комбинационных схем находят решение с помощью аппарата математической логики. При этом употребляется исключительно обычная часть математической логики, а конкретно, алгебра логики либо Булева алгебра. Главным понятием в алгебре логики, на котором базируется ее приложение к синтезу КС, считается понятие Булевой либо переключательной функции.
В вычислительной технике в основном употребляется схемы 2-ух классов: комбинационные схемы и цифровые автоматы. Характерной особенностью комбинационных схем считается наличие жесткой функциональной зависимости между выходным сигналом и входным: y(t)=f(х(t)). При этом при отсутствии входных сигналов выходные сигналы еще отсутствуют, поскольку эти схемы не имеют памяти. В отличии комбинационных схем схемы второго класса содержат в своем составе элементы памяти (запоминающие элементы). Данные схемы именуются цифровыми автоматами либо просто автоматами.
Автомат – дискретный преобразователь информации способный воспринимать разные состояния, переходить перед действием входных сигналов из 1-го состояния в иное и выдавать выходные сигналы. Если множество состояний автомата, а так же большого количества входных и выходных сигналов конечны, то автомат именуется конечным автоматом. Понятие состояния введено во взаимосвязи с тем, что часто появляется необходимость в описании поведения систем, выходные сигналы каких находятся в зависимости не только от состояния входов в этот момент времени, однако и от некоторых предысторий, то есть от сигналов, которые поступали на входы системы раньше. Состояния как раз и соответствуют некой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входов в этот момент времени. [1]
Кодирование информации. Информацию, поступающую на вход автомата, а так же выходную информацию принято кодировать конечной совокупностью знаков. Эту совокупность именуют алфавитом, отдельные символы, образующие алфавит – буквами, а любые упорядоченные последовательности букв данного алфавита – словами в данном алфавите.
К примеру: в алфавите Х=(х1, х2), состоящем из двух букв, словами будут: х1, х2, х1х1, х1х2, х2х1,х2х2, х1х1х1 и т.д.
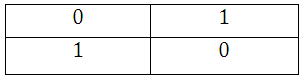
Математической моделью реального конечного автомата считается абстрактный автомат, который имеет один входной канал и один выходной канал (таблица 1).
Таблица 1.
Математическая модель автомата

Автомат работает в дискретные моменты времени, интервал, между которыми Т именуется тактом. При этом в любой дискретный момент времени на вход автомата поступает 1 буква входного алфавита, автомат переходит из 1-го состояния в другое и выдается 1 буква выходного алфавита. В зависимости от того, как задается продолжительность такта Т, различают автоматы синхронного действия (T=соnst) и асинхронного действия (Tсоnst).
Автомат действует следующим образом: в любой момент времени t он располагаться в определенном состоянии а(t) из множества А вероятных состояний. При этом в начальный момент времени t=0 он всегда находится в состоянии а(t=0)=а0. В момент времени t автомат принимает входной сигнал х(t), выдает выходной сигналу y(t)=l[а(t), х(t)] и переходит в последующее положение а(t+1)=d[а(t), х(t)]. Иными словами абстрактный автомат каждой паре символов а(t) и х(t) ставит в однозначное соотношение пару символов а(t+1) и y(t). Эти автоматы именуют детерминированными. На преобразование информации в детерминированных автоматах наложены условия.
Условия преображения информации в детерминированных автоматах.
Любое входное слово, длинною l букв, преобразуется в выходное слово той же длины.
Если каждый раз перед подачей входных сигналов автомат располагаться в одном и том же состоянии, то при совпадении в 2-ух входных словах первых l1 букв, в выходных словах 1-ые l1 букв также совпадут.
Работа таких автоматов описывается уже матрицей переходов d, элементами которой считаются вероятности переходов из 1-го состояния в иное.
1.2 Классификация автоматов
Используемые на практике автоматы принято делить на 2 класса – это автоматы Мили и автоматы Мура, названные так по имени американских экспертов, которые в первый раз начали их изучать. Функционирование автоматов строго подчиняется конкретным законам законы – функционирования автоматов. Законы функционирования автоматов описываются системами уравнений. Рассмотрим каждый из автоматов подробней.
Законы функционирования автомата Мили описываются последующей системой уравнений, представленные в таблице 2.
Таблица 2.
Автомат Мили
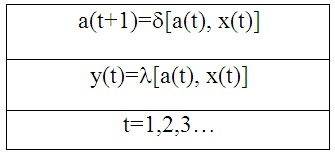
Функциональная схема автомата Мили представлена на рисунке 1.
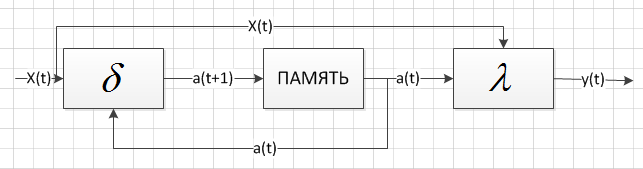
Рисунок 1. Схема автомата Мили
Характерной особенностью автоматов Мили считается то, что их выходные сигналы находятся в зависимости, как от состояния автомата, так и от значения входного сигнала.
Законы функционирования автомата Мура описываются последующей системой уравнений, представленные в таблице 3.
Таблица 3.
Автомат Мура
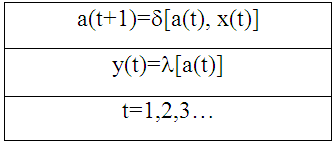
Функциональная схема автомата Мили представлена на рисунке 2.
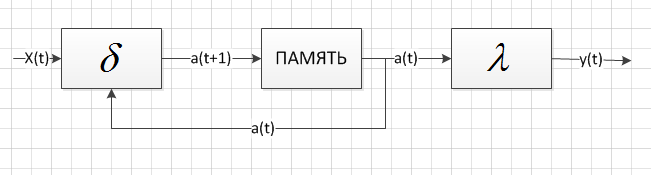
Рисунок 2. Схема автомата Мура
- Способы задания автоматов
Чтобы задать конечный автомат S, нужно описать все элементы множества S={А, Х, Y, d, l}. То есть нужно описать входной, выходной алфавиты и алфавит состояний, а также функции переходов d и выходов l. При этом среди большого количества А={а0,а1,…, аn} нужно отметить начальное состояния а0, в котором автомат располагаться в момент времени t=0. Существует некоторое количество способов задания работы автомата, однако наиболее часто используются табличный и графический.
Табличный способ. При табличном способе задания автомат Мили описывается 2-мя таблицами: таблицей переходов и таблицей выходов (таблицы 4,5).
Таблица 4.
Таблица переходов
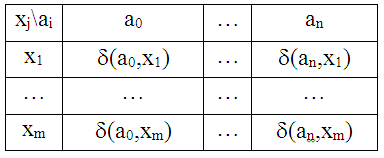
Таблица 5.
Таблица выходов

Строки данных таблиц соответствуют входным сигналам х(t), а столбцы – состояниям. На пересечении столбца аi и строки хj в таблице переходов ставится состояние аs=d[аi, хj], в которые автомат перейдет из состояния аi под действием сигнала хj; а в таблице выходов – соответствующий данному переходу выходной сигнал yg=l[аi,хj]. Время от времени автомат Мили задают совмещенной таблицей переходов и выходов, она в некоторых вариантах более удобна (таблица 6).
Таблица 6.
Совмещенная таблица переходов и выходов автомата Мили

Задание таблиц переходов и выходов вполне описывает работу конечного автомата, поскольку задаются не только сами функции переходов и выходов, но еще и все 3 алфавита: входной, выходной и алфавит состояний. Так как в автомате Мура выходной сигнал однозначно определяется состоянием автомата, то для его задания требуется лишь 1 таблица, которая именуется отмеченной таблицей переходов автомата Мура (таблица 7).
Таблица 7.
Отмеченная таблица переходов автомата Мура

Примеры табличного задания автоматов Мили и Мура (таблицы 8,9).
Таблица 8.
Автомат Мура
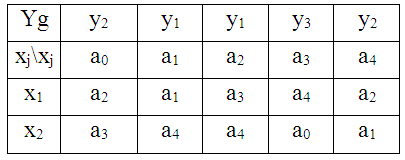
Таблица 9.
Автомат Мили

По этим таблицам можно найти реакцию автомата на любое входное слово: для автомата Мура в таблице 10, для автомата Мили в таблице 11.
Таблица 10.
Реакция автомата Мура
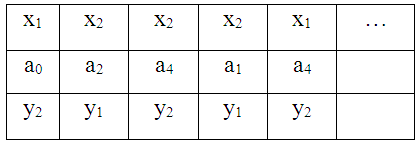
Таблица 11.
Реакция автомата Мили
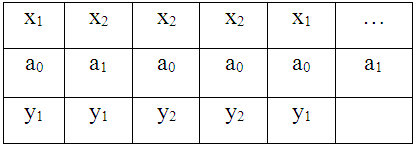
Графический способ. При графическом способе задание автомата осуществляется с помощью графа. Граф для автоматов Мили и Мура представлен на рисунке 3 и 4 соответственно.
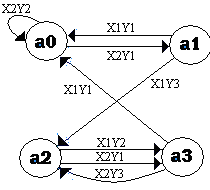
Рисунок 3. Граф для автомата Мили
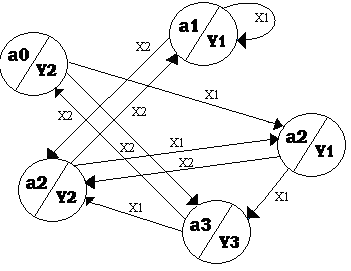
Рисунок 4. Граф для автомата Мура
Данный способ базируется на применении ориентированных связных графов. Вершины графов соответствуют состояниям автомата, а дуги – переходам между ними. 2 вершины графа аi и аs объединяются дугой, направленной от аi к аs, если в автомате имеется переход из аi в аs, то есть аs=d(аi, хj).
1.4 Другие виды автоматов
Частичные автоматы. В инженерной практике нередко встречаются автоматы, на входы которых некоторые последовательности сигналов ни разу не подаются. Эти последовательности станем именовать запрещенными входными словами данного автомата, а сам автомат – частичным автоматом. У частичного автомата функции переходов и выходов определены не на всех парах аi, хj. На месте неопределенных состояний и выходных сигналов ставится прочерк. При синтезе традиционно производят до определение частичного автомата, чтоб его схемная осуществление вышла как можно легче. Пример переходов и выходов частичного автомата представлен в таблице 12.
Таблица 12.
Таблица переходов и выходов частичного автомата Мили

Элементарные автоматы. В настоящее время в вычислительной технике, как правило, употребляются элементарные автоматы, имеющие следующие особенности:
1) Элементарные автоматы считаются автоматами Мура с 2-мя внутренними состояниями;
2) Автомат выдает 2 различных выходных сигнала, соответственных двум его внутренним состояниям. В предстоящем состояния автомата и его выходные сигналы будем обозначать одной буквой Q и кодировать цифрами 0 и 1;
Элементарные автоматы имеют все шансы иметь в общем случае некоторое количество физических входов, на любой из которых могут подаваться сигналы, закодированные цифрами 0 и 1.
В качестве элементарных автоматов в вычислительной технике используются, в основном, триггеры разных типов (рисунок 5). Здесь рассмотрены некоторые из них.
Рисунок 5. Элементарный автомат
Т–триггером называют автомат Мура с двумя устойчивыми состояниями и одним входом Т, который изменяет свое состояние на противоположное всякий раз, когда на вход Т поступает входной единичный сигнал (таблица 13).
Таблица 13.
Таблица переходов Т– триггера

Кроме того, любое состояние автомата отмечено отличным от остальных выходным сигналом. На практике наиболее комфортно за место указанных таблиц переходов воспользоваться так именуемыми матрицами переходов элементарных автоматов (таблица 14).
Таблица 14.
Матрица переходов
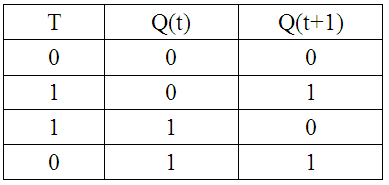
Матрица переходов описывает значения сигналов на входах элементарного автомата, обеспечивающие любой их 4 вероятных переходов. Здесь Q(t) и Q(t+1) – состояния автомата в моменты времени t и t+1 соответственно. Так как Т–триггер владеет один вход, а количество вероятных переходов одинаково четырем, то матрица переходов имеет 4 строки.
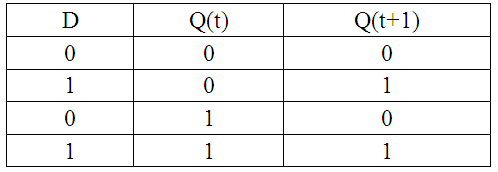
D–триггером (триггером задержки) именуют элементарный автомат Мура с 2-мя устойчивыми состояниями и одним входом D таким, что Q(t+1)=D(t). Название D–триггера проистекает от английского слова «dеlаy» – задержка.
Матрица переходов для D–триггера представлена в таблице 15.
Таблица 15.
Матрица переходов D–триггера
Обозначения асинхронного и синхронного D–триггеров представлено на рисунке 6:
Рисунок 6. Асинхронный и синхронный D–триггеры
Схема перехода состояний D–триггера представлена на рисунке 7.
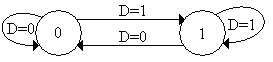
Рисунок 7. Граф D–триггера
RS–триггером именуют автомат Мура с 2-мяустойчивыми состояниями, имеющий 2 входа R и S такие, что при S=1 и R=0 триггер воспринимает состояния 1, а при R=1 и S=0 состояние 0. В соответствие с состоянием, принимаемым триггером, вход S называет единичным входом, а вход R нулевым (таблица 16).
Таблица 16.
Матрица переходов RS–триггера
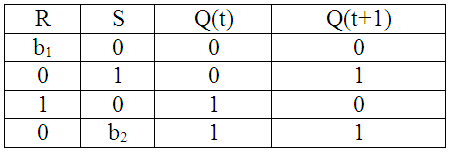
Комбинация сигналов R=1 и S=1 считается запрещенной и поэтому переход в триггере при таких значениях входных сигналов не определен. Переход триггера из 0 в 0 вероятен при 2-ух комбинациях входных сигналов: R=0, S=0 и R=1, S=0. Поэтому в первой строке матрицы переходов RS триггера в столбце R поставлена переменная b1, которая имеет возможность воспринимать 2 значения 0 v 1.
Автоматы, которые имеют все шансы переходить из 1-го состояния в иное под действием нескольких комбинаций входных сигналов, именуются автоматами с лишней системой переходов. Избыточность можно применять в процессе синтеза для упрощения схемы, придавая переменным b1 и b2 эти значения, которые разрешают минимизировать количество элементов. Поэтому, если схемы 2-ух элементарных автоматов равноценны по сложности, то предпочтение отдают автомату, имеющему огромную избыточность системы переходов.
JK–триггером именуют автомат Мура с 2-мя устойчивыми состояниями и 2-мя входами J и K, который при условии J*K=1 исполняет инверсию предыдущего состояния (т.е. при J*K=1, Q(t+1)= Q(t)), а в других вариантах работают в соответствии с таблицей истинности RS триггера, при этом вход J эквивалентен входу S, а вход K – входу R. Данный триггер уже не имеет запрещенной комбинации входных сигналов и его таблица истинности, то имеется зависимость Q(t+1)=f[J, K, Q(t)] имеет вид (таблица 17).
Таблица 17.
Таблица истинности JK–триггера
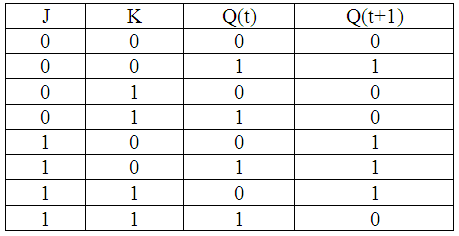
По таблице истинности JK–триггера можно построить матрицу переходов (таблица 18).
Таблица 18.
Матрица переходов JK–триггера
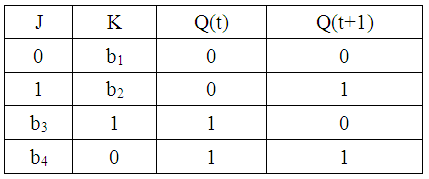
В интегральной схемотехнике используются лишь синхронные JK триггера, которые при С=0 сохраняют свое состояние, а при С=1 действуют как асинхронные JK триггера.
Универсальный триггер. Триггер JK относится к уровню универсальных триггеров, так как на его основе путем легкой внешней коммутации разрешено построить RS–, D– и T– триггера. RS–триггер получается из триггера JK простым наложением ограничения на комбинацию входных сигналов J=K=1, так как данная комбинация считается запрещенной для RS триггера.
Вероятностные автоматы с e-переходами. В теории нередко рассматривается автоматы, именуемые автоматами с e-пере-ходами (с эпсилон - переходами). Эпсилон-переходом именуется переход между состояниями, который может существовать выполнен в отсутствии входного сигнала. Эти переходы классифицируются символом e. Внедрение эпсилон-переходов позволяет просто объединять некоторое количество автоматов в один.
Пускай требуется построить граф автомата, который должен распознавать двоичные, десятичные и шестнадцатеричные количества в обычном формате ассемблера. Автомат должен распознавать строчки, удовлетворяющие 1 из следующих критерий:
I строка состоит из одной или более цифр (0 – 9) и может заканчиваться символом «D» (например «1367» или «2345D»);
строка состоит из одного или более символов «0» или «1» и заканчивается символом «B» (например «01011B»);
строка состоит из одной или более десятичной цифр или символов от « А » до «F» и заканчивается символом «H» (например «9AD4H»).
Граф такого автомата представлен на рисунке 8.
В теории автоматов доказывается, что хоть какой вероятностный автомат имеет возможность быть заменен эквивалентным детерминированным (обычным) автоматом.
Вероятностные автоматы используются в тех вариантах, когда методика вероятностного автомата легче, чем методика эквивалентного детерминированного автомата. Вероятностные автоматы могут использоваться при моделировании умственной деятельности человека, к примеру при машинном переводе с 1-го языка на иной, в частности, при разработке трансляторов.
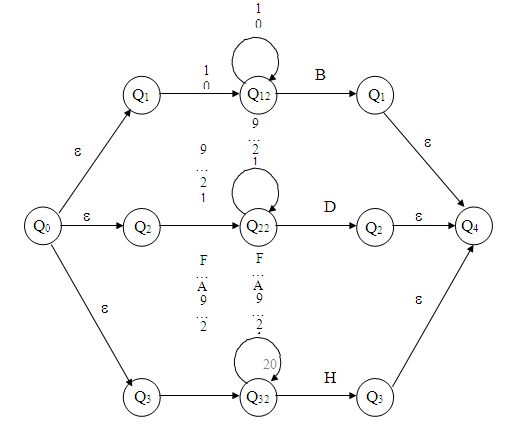
Рисунок 8. Граф эквивалентного детерминированного автомата имеет меньше состояний, но более сложную систему переходов.
1.5 Структурная схема конечного автомата
В структурной теории автомат предполагают в виде композиции 2-ух частей: запоминающей части, состоящей из частей памяти, и комбинационной доли, состоящей из логических элементов (рисунок 9).
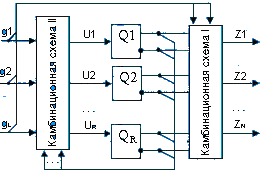
Рисунок 9. Логическая схема конечного автомата
Комбинационная схема основывается на логических элементах, образующих функционально полную систему, а память – на элементарных автоматах, владеющих полной системой переходов и выходов.
Любое состояние абстрактного автомата аi, где i={0, n}, кодируется в структурных автоматах комплектом состояний частей памяти Qi,
r={1, R}. Так как в качестве элементов памяти употребляются обычные триггера, то любое состояние можно закодировать двоичным числом аi = Q1а1Q2а2... Qrаr. Здесь аi={0, 1}, а Q – состояние автомата (таблица 19).
Таблица 19.
Матрица переходов JK–триггера
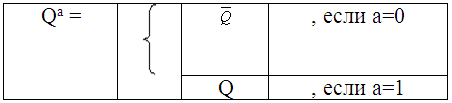
Общее число необходимых элементов памяти можно определить из следующего неравенства
где (n+1) – число состояний.
Логарифмируя это неравенство получим:
где ]С[ – значит, что нужно взять ближайшее целое число, большее или равное С.
В отличии от абстрактного автомата, имеющего один входной и один выходной каналы, на которые поступают сигналы во входном Х={х1,х2,...,хm} и выходном Y={y1, y2,..., yk} алфавитах, структурный автомат владеет L входных и N выходных каналов. Любой входной хj и выходной yj сигналы абстрактного автомата имеют все шансы существовать закодированы двоичным комплектом состояний входных и выходных каналов структурного автомата.
Очевидно, количество каналов L и N можно определить по формулам (4,5), подобным формуле для определения R.
Изменение состояния частей памяти происходит под действием сигналов U=(U1,U2,...,Ur), поступающих на их входы. Данные сигналы создаются комбинационной схемой II и именуются сигналами побуждения элементарных автоматов. На вход комбинационной схемы II, не считая входного сигнала хj, по цепи обратной взаимосвязи поступают сигналы Q=(Q1, Q2, ..., QR), именуемые функцией обратной взаимосвязи от памяти автомата к комбинационной схеме. Комбинационная схема I работает для формирования выходного сигнала yg, при этом в случае автомата Мили на вход данной схемы поступает входной сигнал хj, а в случае автомата Мура – сигнал хj, не поступает, так как yg не зависит от хj,.
Табличный метод структурного синтеза конечных автоматов. Структурный синтез конечных автоматов заключается в выборе типов элементарных автоматов, в составлении функции возбуждения всякого элементарного автомата и функций кодированных выходов заданного автомата.
Рассмотрим примеры синтеза, которые разрешают сформулировать совместный алгоритм структурного синтеза конечных автоматов. В качестве элементарных автоматов будем применять JK–триггера, а в качестве логических частей – элементы И, ИЛИ, НЕ. Итак, имеем А={а0,а1,а2}; Х={х1,х2}; Y={y1, y2, y3}. Здесь n=2, n+1=3; m=2, k=3.
Пусть нужно синтезировать автомата Мили, данный совмещенной таблицей переходов и выходов (таблица 20).
Таблица 20.
Таблица переходов и выходов автомата Мили
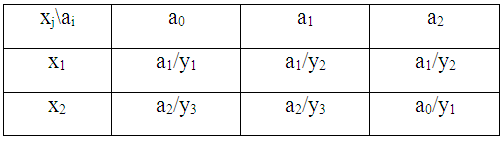
Перейдем от абстрактного автомата к структурному, для чего определим численность частей памяти R и количество входных L и выходных N каналов. По формуле 1, 2, 3 получим следующую таблицу (таблица 21).
Таблица 21.
Параметры абстрактного автомата
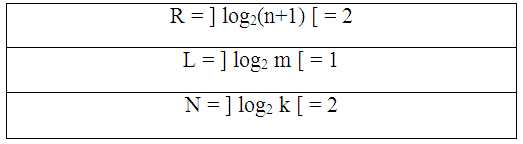
Таким образом, нужно иметь 2 элементарных автомата Q1 и Q2 (так как R=2), один входной канал О1 и два выходных канала Z1 и Z2.
Закодируем состояния автомата, входные и выходные сигналы совокупностью двоичных сигналов (таблица 22).
Таблица 22.
Таблица кодирования
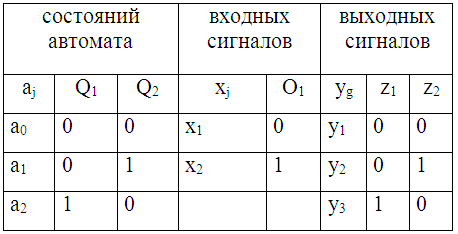
Так как автомат имеет 3 состояния, то комбинация состояний элементарных автоматов 11 не употребляется и считается запрещенной (автомат в это состояние никогда не попадет). Тут и в дальнейшем станем применять естественное кодирование, когда наборы значений двоичных переменных расписываются в порядке возрастания их номеров. С учетом кодирования перерисуем совмещенную таблицу переходов и выходов абстрактного автомата (таблица 23).
Таблица 23.
Совмещенная таблица переходов и выходов
В таблицах кодировки выходные каналы Z1 и Z2 именуются физическими выходами автомата.
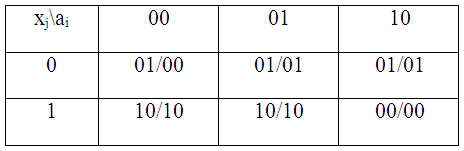
Пользуясь таблицами кодировки, разрешено на основе заданных переходов и выходов построить кодированные таблицы переходов и выходов. Кодированная таблица переходов определяет зависимость состояний Qi(t+1)элементарных автоматов в момент времени (t+1) от значения входного сигнала и внутренних состояний автоматов в предыдущий момент времени t.
Кодированная таблица переходов и выходов (совмещенная) имеет следующий вид (таблица 24):
Таблица 24.
Кодированная таблица переходов и выходов
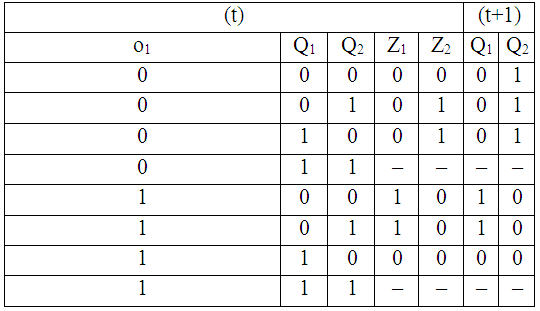
Главная задача, решаемая в процессе структурного синтеза – построение таблицы функций побуждения элементарных автоматов, которая описывает значения сигналов на входах элементарных автоматов, нужные для обеспечения переходов автомата из 1-го состояния в иное. При построении данной таблицы используется матрица переходов подобранных элементарных автоматов, в нашем случае JK–триггера (таблица 25).
Таблица 25.
Матрица переходов JK–триггера
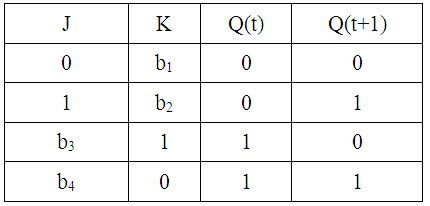
С помощью матрицы переходов заполняются столбцы таблицы функций возбуждения. В строках данной таблицы записываются значения J и K, обеспечивающие подходящий переход.
Так как функции возбуждения J(t) и K(t)определенны в тот же момент времени, что и их аргументы Q1(t), Q2(t) и О1(t), то данные функции считаются переключательными. В итоге мы получим систему переключательных функций Z1(t), Z2(t), J1(t), K1(t), J2(t) и K2(t) данных в виде таблиц их истинности.
Следующий шаг – синтез комбинационной доли конечных автоматов. На данном шаге по приобретенным переключательным функциям синтезируются комбинационные схемы. Обычно полученную систему ПФ минимизируют вместе. Но совместная минимизация всех ПФ представляет собой достаточно трудоемкую и долгую операцию, применимую, в общем случае, при применении машины. В итоге минимизации мы получим следующую схему конечного автомата (рисунок 10).
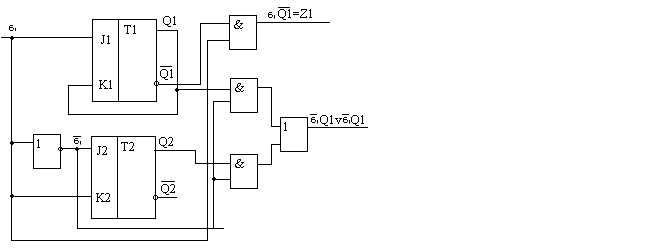
Рисунок 10. Схема конечного автомата
Функциональные схемы, получаемые в итоге структурного синтеза, в дальнейшем на шаге инженерной доработки подвергаются изменениям. Данные конфигурации связаны с тем, что прибавляются специальные цепи, нужные для работы разработанной схемы в составе остальных схем ЭВМ. К примеру, в схеме регистра сдвига информации прибавляется цепь «установка в 0». Остальные конфигурации связаны с особенностью физического представления информации в ЭВМ, с особенностями логических элементов и с техническими особенностями конечных автоматов.
1.6 Вероятностные автоматы
Детерминированные автоматы S мы задавали совокупностью из 5 объектов: S(А, Х, Y, d, l), где А={а0,а1,а2,...,аM}– множество внутренних состояний автомата, Х={х1, х2,…, хF} – множество входных сигналов (входной алфавит), хi – буква входного алфавита, Y={y1, y2,…, yG} – множество выходных сигналов (выходной алфавит),
d – функция переходов, обеспечивающая однозначный переход автомата в положение аs из состояния аm под действием входного сигнала хf, то есть аs=d [аm, хf],
l – функция выходов, характеризующая однозначное значение выходного сигнала yg в зависимости от состояния автомата аm и входного сигнала хf, т.е. yg =l[аm , хf].
В работе Поспелова Д.А. «Вероятностные автоматы» рассмотрена наиболее общую модель автомата, а конкретно: зная состояние автомата аm и входной сигнал хf, мы не можем с вероятностью, равной 1 сказать, в каком состоянии окажется автомат в последующий момент времени, а также какой выходной сигнал он в этом случае вырабатывает. [2]
Законы распределения задаются в виде следующих таблиц (таблица 26, 27).
Таблица 26.
Матрица переходов состояний
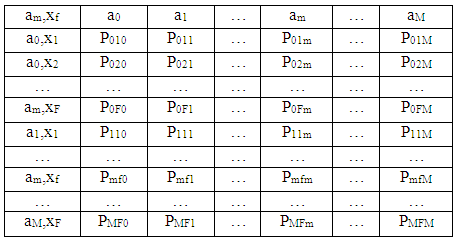
То есть в каждом случае имеем закон распределения, заданный в виде гистограмм.
Разумеется, так как автомат непременно перейдет в одно из состояний, то
где , .
Таблица 27.
Матрица появления выходных сигналов
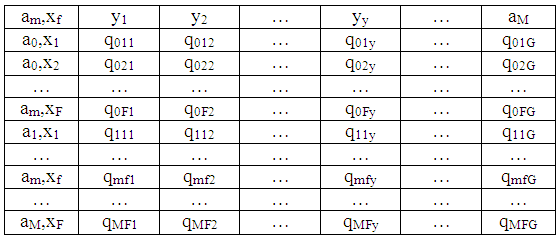
Автоматы, в которых зная состояние автомата аm и входной сигнал хf, мы можем указать только вероятности перехода в новое состояние и вероятности появления выходных сигналов, т.е. законы распределения, именуются вероятностными автоматами (ВА).
По аналогии с детерминированными автоматами, Можно найти вероятностными автоматами Мили и Мура. Вероятностные автоматы, у которых вероятности появления выходных сигналов (закон распределения) находятся в зависимости только от состояний автомата, но не находятся в зависимости от входных сигналов, именуются ВА Мура. Если же вероятности появления выходных сигналов (закон распределения) находятся в зависимости как от состояний автомата, так и от входных сигналов, имеем автомат Мили.
Рассмотрим некие частные случаи вероятностных автоматов. Имеет возможность существовать, что выходные сигналы автомата ориентируются детерминировано, а переходы автомата – случайно. Эти автоматы именуются Y – детерминированными вероятностными автоматами. Ежели состояния определяются детерминировано, то владеем А – детерминированный вероятностный автомат.
Разумеется, разрешено рассмотреть общий случай, когда данные законы распределения находятся в зависимости от времени. Эти автоматы именуются ВА с переменной структурой. ВА с переменной структурой в любой фиксированный такт работы считается неким обычным ВА, однако в период между тактами ВА имеет возможность изменять свои матрицы переходных вероятностей или таблицы выходных вероятностей, либо и то и другое совместно.
Часто при построении ВА изменение вероятностей создают по некоторому закону, при этом закон находится в зависимости от истории функционирования автомата (т.е. находится в зависимости от входных сигналов, поданных на него и от выходных сигналов, т.е. реакции автомата). Эти ВА с переменной структуройименуются автоматами компенсирующего типа. Их исследованию и уделяется основное внимание.
В данном случае можно сказать, что ВА действует в некоторой среде, в которую он выдает выходные сигналы и из которой он приобретает входные (рисунок 11).
Рисунок 11. Схема вероятностного автомата
Входные сигналы условно можно поделить на поощрения («нештрафы») и наказания («штрафы»). При данном в зависимости от выходного сигнала на вход подается поощрение либо штраф. Если в зависимости от данных сигналов поменятьвероятности перехода автомата из 1-го состояния в иное, то оказывается, что с течением времени автомат перестраивается таковым образом, будто он начинает с большой вероятностью получать сигналы поощрения, т.е. он в некотором смысле адаптируется к той среде, в которой он располагаться.
Неувязка организации целесообразного поведения автомата в случайной среде тесно связана со способом конфигурациивероятностей перехода автомата. Может быть, модифицирование возможностей перехода автомата по строкам и по столбцам.
Рассмотрим У–детерминированный вероятностный автомат. Пускай автомат в некий момент времени t располагаться в состоянии аm, выдал соответственный данному состоянию выходной сигнал yg и получил на вход сигнал поощрения. Тогда возможность рmm перехода из состоянии аm в состояние аm растут на некую величину, а все другие вероятности в строке уменьшаются на /М. Если же автомат получает сигнал штрафа, то возможность рmm перехода из состоянии аm в состояние аm убавляются на некую величину , а все другие вероятности в строке на растут на /М, чтобы сумма вероятностей осталась равной 1.
Возможен и иной принцип конфигурации вероятностей, при котором проистекает учет предыстории поведения автомата. Если автомат в момент времени t перешел из состояния аm в состояние ак и в момент времени t+1 получил сигнал «штраф», то вероятность рmк заменяется на рmк, где коэффициент более 0 и меньше 1, а все другие вероятности в строчке меняются на значение . Если же получил сигнал «нештраф», то вероятность рmк величину , а все другие убавляются на значение .
Можно поменять вероятности в матрице перехода не только по строкам, однако и по столбцам. К примеру, вероятен последующий алгоритм. Если в момент времени t под воздействием входного сигнала хf автомат перешел в положение аm и в момент времени t+1 получил сигнал «штраф», то самостоятельно от того, из какого состояния он перешел, все составляющие m–го столбца в матрице переходов заменяются на (рmm–) или рmm, а все другие вероятности меняются подобно тому, как это происходило при изменении возможностей по строчкам.
Основы организации подходящего поведения автомата в случайной среде тесно соединены со способом конфигурации возможностей перехода автомата. Может быть, модифицирование вероятностей перехода автомата по строчкам и по столбцам.
Подобные автоматы уже обретают использование при управлении в сложных системах и предоставляют более значительный результат там, где ранее действовали детерминированные автоматы.
Рассмотрим пример, который приводит Д.А. Поспелов – регулировка перемещения через автомобильный перекресток. Традиционно (мы с вами постоянно встречаемся именно с таким светофором) задают твёрдый режим переключения светофоров, при котором продолжительность включенных сигналов (красного и зеленого) – многократны. Но, как показывает практика работы таких светофоров, решение задачи получается неэффективным, так как предполагается, что потоки автомашин постоянные, стационарные.
Можно установить детекторы на перекрестке, которые бы подсчитывали количество автомашин, возникающее в данном направлении при красном свете светофора. Пускай на перекрестке стоит ВА компенсирующего типа, который имеет 2 состояния: подключен красный свет вдоль главного направления и подключен зеленый свет. Любому состоянию однозначно подходит выходной сигнал, т.е. автомат У–детерминированный. С датчиков поступают сигналы штрафа и нештрафа (рисунок 12).
Рисунок 12. Схема перекрестка
Матрица переходов выглядит следующим образом (таблица 28).
Таблица 28.
Матрица переходов

Пускай в начале все эти вероятности равны 0,5 и на главном направлении накопилось П1 машин, а на другом – П2. На вход автомата поступает сигнал = П1 – П2. Пусть > 0, т.е. на главном направленности больше автомашин. Тогда если автомат в момент времени t располагался в состоянии зеленом, перешел в положение зеленый и получил сигнал нештраф, то возможность рзз (t+1) возрастает, а возможность рзк (t+1) миниатюризируется.
Тем самым возрастает возможность состояния зеленое вдоль главного направления, т.е. автомат подстраивается под ситуацию. Заметим, что если потоки одинаковы, то хорошей считается последующая матрица переходов (таблица 29).
Таблица 29.
Матрица переходов