Оптимальное решение двойственной задачи
Оптимальное решение двойственной задачи
Прямая и двойственная задачи так тесно взаимосвязаны, что оптимальное решение одной задачи можно получить непосредственно (без дополнительных вычислений) из симплекс-таблицы, представляющей оптимальное решение другой. Покажем два метода получения этого результата.
Соотношения между прямой и двойственной задачами
Метод 1

Элементы в вектор-строке исходных коэффициентов целевой функции должны быть перечислены в таком порядке, в каком базисные переменные перечислены в столбце "Базис" в симплекс-таблице.
Метод 2
Оптимальное решение двойственной задачи можно получить из следующего уравнения.
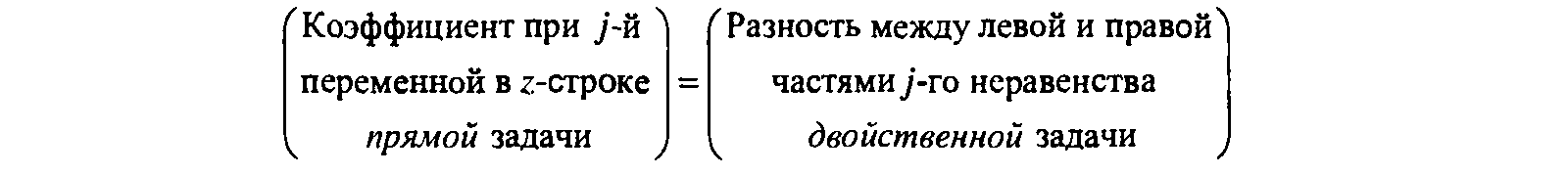
Поскольку двойственной к двойственной задаче будет прямая задача (проверьте!), эти методы симметричны относительно прямой и двойственной задач. Их можно использовать для определения оптимального решения одной задачи непосредственно из симплекс-таблицы, содержащей оптимальное решение другой. Данное обстоятельство обусловливает возможность проведения вычислений именно по той задаче (прямой или двойственной), которая требует меньших вычислительных ресурсов (меньший объем вычислений имеет задача с меньшим количеством ограничений). После нахождения оптимального решения решаемой задачи оптимальное решение обратной задачи определяется одним из описанных методов.
Метод 3.
Заметим, что базисные переменные в оптимальной симплекс-таблице
в столбце "Базис" записаны в таком порядке, что сначала идет х2, а затем х,. Поэтому в вектор-строке первоначальных коэффициентов целевой функции коэффициенты этих двух переменных должны идти в том же порядке:(вектор коэффициентов) = (коэффициент при х2, коэффициент при *,) = A2,5). Оптимальное решение двойственной задачи вычисляется так:

Метод 4.
Поскольку двойственная задача имеет две переменные, необходимо два уравнения, чтобы найти их значения. Сначала посмотрим, как ограничения двойственной задачи связаны с переменными хА и R, составляющими первоначальный базис прямой задачи.
Переменная xt: у1 0
Переменная R: у2 -М.
Из симплекс-таблицы с оптимальным решением имеем
коэффициент в г-строке при х4 = 29/5
коэффициент в г-строке при R = -2/5 + М.
Теперь, следуя методу 4, получаем систему уравнений
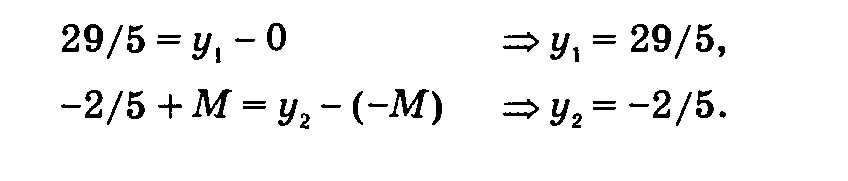
Соотношения между прямой и двойственной задачами
Отметим, что каждое уравнение включает только одну неизвестную, поэтому решение двойственной задачи существует всегда и находится легко. Так бывает всегда, когда ограничения двойственной задачи связаны с начальными базисными переменными. Конечно же, ничего не мешает использовать другие переменные при построении уравнений, необходимых для определения значений переменных двойственной задачи. Например, ограничения, ассоциируемые с переменными х1 и *,, порождают следующие уравнения (проверьте!):
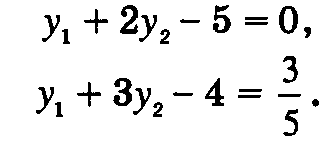
Решение этой системы уравнений также приводит к оптимальным значениям двойственной задачи у, = 29/5 и у2 = -2/5. Однако эти уравнения уже не так просты, как уравнения, ассоциируемые с переменными x4 и R. (Убедитесь самостоятельно, что уравнения, ассоциированные с любыми двумя переменными из множества x1, х2, х3, x4, R, дают одни и те же значения переменных двойственной задачи.)
1. Вычисление значений в столбцах ограничений симплекс-таблицы (как левой, так и правой частей ограничений).
2. Вычисление значений в 2-строке.
Вычисление значений в столбцах ограничений. На произвольной симплекс- итерации значения коэффициентов в столбцах левой и правой частей ограничений вычисляются по следующей формуле 1.

Вычисление значений z-строки. На произвольной симплекс-итерации значения коэффициентов в z-строке вычисляются по следующей формуле 2.
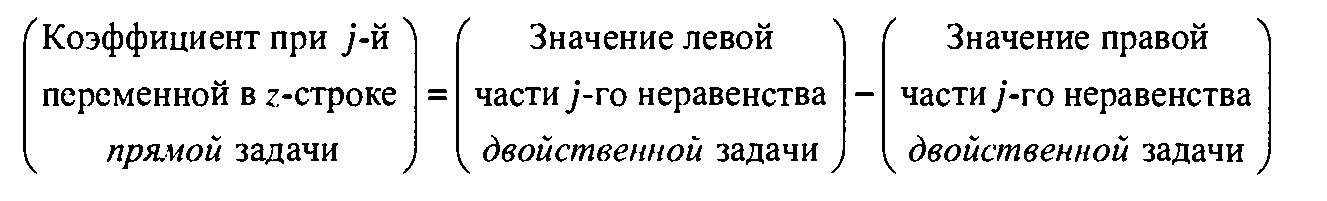
Экономическая интерпретация двойственности
Строгое равенство здесь достигается только тогда, когда решения прямой и двойственной задач оптимальны.
Рассмотрим сначала вариант оптимума, т.е. когда z = w. Исходя из представления прямой задачи как модели распределения ресурсов, можно считать, что величина z соответствует величине дохода (в долларах3). Поскольку b1- общее доступное количество ресурса i, равенство z = w можно переписать следующим образом.
Доход(долл.)= (количество ресурса i) x (доход(долл.) на единицу ресурса i).
Это означает, что переменная y1 двойственной задачи должна представлять стоимость единицы ресурса i. В литературе по исследованию операций переменные y1 двойственной задачи часто называют двойственными ценами. Кроме того, иногда их именуют теневыми ценами и симплексными мультипликаторами.
Аналогично для любой пары допустимых решений прямой и двойственной задач неравенство z < w можно интерпретировать следующим образом:
доход < общая стоимость ресурсов.
Это соотношение показывает, что до тех пор, пока суммарный доход от всех видов деятельности строго меньше суммарной стоимости всех используемых ресурсов, решение как прямой, так и двойственной задачи не может быть опти-
мальным. Оптимум (максимальный доход) может быть достигнут только тогда, когда все потребляемые ресурсы использованы полностью. Если модель ЛП рассматривать более обще как модель некой системы, имеющую "вход" и "выход", то потребляемые ресурсы характеризуют "вход" этой системы, а получаемый доход— ее "выход". Система будет находиться в нестабильном (неоптимальном) состоянии, пока вход превышает выход. Устойчивое состояние системы характеризуется равенством входа и выхода.
Экономическая интерпретация двойственности
a) Сформулируйте задачу линейного программирования и с помощью про- граммы TORA найдите ее оптимальное решение.
b) Основываясь на двойственных ценах, приведенных программой TORA, определите возможное увеличение ежедневного фонда времени по каждой
технологической операции.
c) Выгодно ли компании выполнение требования заданного минимального уровня производства? Обоснуйте ответ, основываясь на величинах двойственных цен.
d) Возможно ли увеличение на 10% временного фонда операции пайки с со- хранением величины ее вклада в суммарный доход, определяемый текущей двойственной ценой?
Задача
Компания производит кожаные чехлы и сумки. На производство одного чехла требуется 8 м2 кожи и 12 часов рабочего времени, на производство сумки 2 м2 кожи и 5 часов рабочего времени. Текущие еженедельные ресурсы производства ограничены 1200 м2 кожи и 1850 часами рабочего времени.
Компания продает чехлы и сумки по цене 350 и 120 долл. соответственно.
Определите для этой компании схему производства, максимизирующую чистую прибыль. Допустим, компания желает расширить свое производство.
Какова максимальная цена, по которой компании имеет смысл закупать дополнительную кожу? А какова допустимая максимальная цена дополнительных трудовых ресурсов?
Экономическая интерпретация ограничений двойственной задачи
Для интерпретации ограничений двойственной задачи используем формулу 2 из раздела. В соответствии с этим соотношением на любой итерации решения прямой задачи справедливо равенство
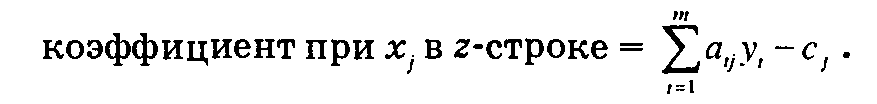
Условие оптимальности симплекс-метода в задаче максимизации говорит о том, что j-й вид деятельности (переменная xf), не представленный в текущем базисном решении, можно ввести в базис для увеличения дохода только тогда, когда коэффициент при Xj в z-строке (равный 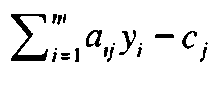 ) будет неотрицательным. В рамках предлагаемой экономической интерпретации это означает, что j-й вид деятельности должен быть представлен в базисном решении, если выполняется следующее неравенство.
) будет неотрицательным. В рамках предлагаемой экономической интерпретации это означает, что j-й вид деятельности должен быть представлен в базисном решении, если выполняется следующее неравенство.
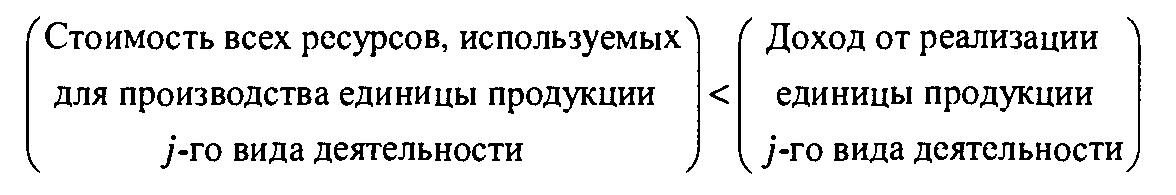
Таким образом, условие оптимальности (в задаче максимизации) говорит о том, что деятельность любого вида следует наращивать до тех пор, пока доход от нее превышает возможные издержки. Приведем стандартные определения, используемые в литературе по линейному программированию. Введем обозначение 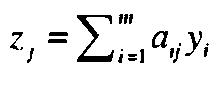 Величина zj представляет суммарную стоимость ресурсов, используемых на производство единицы продукции j-го вида деятельности. Величина zj - сj равна коэффициенту при хj в z-строке симплекс-таблицы и часто называется приведенной стоимостью (приведенными издержками)
Величина zj представляет суммарную стоимость ресурсов, используемых на производство единицы продукции j-го вида деятельности. Величина zj - сj равна коэффициенту при хj в z-строке симплекс-таблицы и часто называется приведенной стоимостью (приведенными издержками)
j-го вида деятельности. В некоторых случаях разности 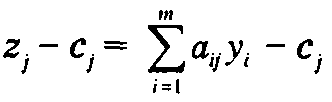 используются непосредственно для вычисления коэффициентов в z-строке симплекс-таблицы (вместо метода Гаусса-Жордана). Такие вычисления используются в модифицированном симплекс-методе.162 страница!!!!
используются непосредственно для вычисления коэффициентов в z-строке симплекс-таблицы (вместо метода Гаусса-Жордана). Такие вычисления используются в модифицированном симплекс-методе.162 страница!!!!
Прямая и двойственная задачи.
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции
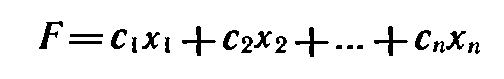 (1)
(1)
при условиях
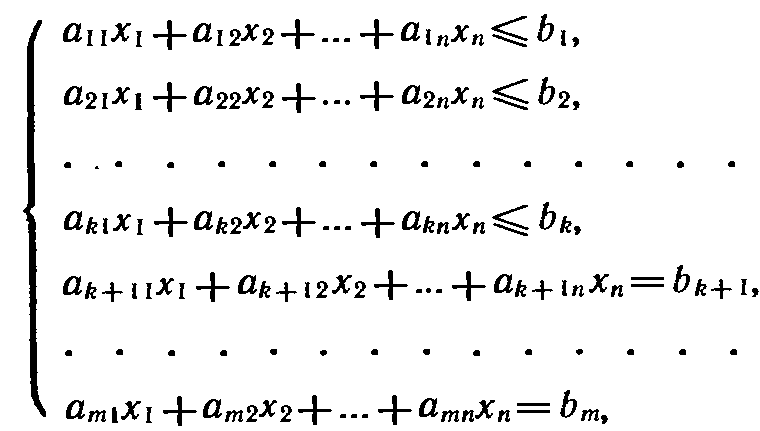 (2)
(2)
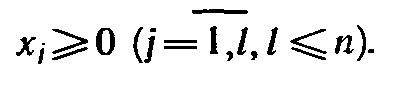 (3)
(3)
Задача, состоящая в нахождении минимального значения функции
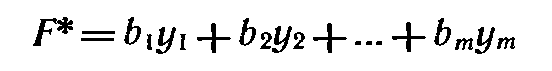 (4)
(4)
при условиях
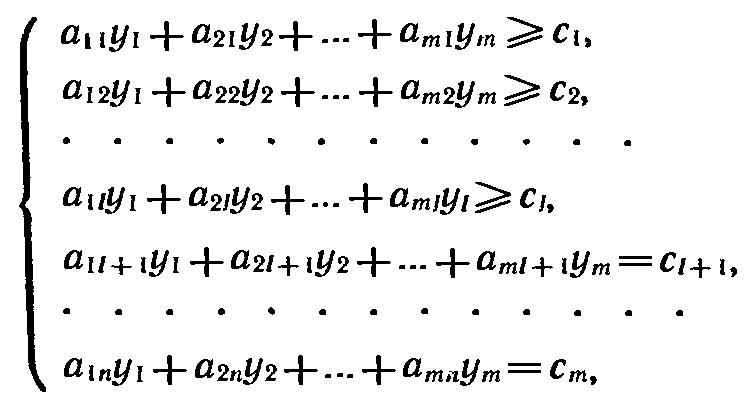 (5)
(5)
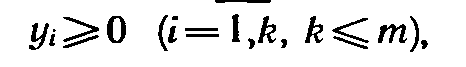 (6)
(6)
называется двойственной по отношению к задаче (1) (3). Задачи (1) –(3) и (4) (6) образуют пару задач, называемуювлинейномпрограммировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам:
- Целевая функция исходной задачи (1)(3) задается на максимум, а целевая функция двойственной (4) (6) на минимум.
- Матрица:
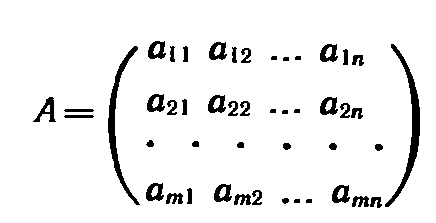 (7)
(7)
составленная из коэффициентов при неизвестных в системе ограничений (2) исходной задачи (1) (3), и аналогичная матрица
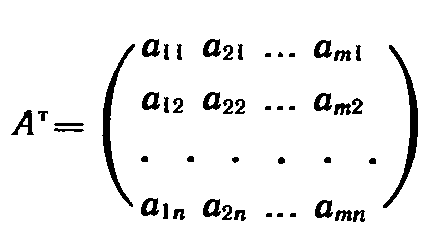 (8)
(8)
В двойственной задаче (4) (6) получаются друг из друга транспонированием (т. е. заменой строк столбцами, а столбцов строками).
3. Число переменных в двойственной задаче (4) (6) равно числу соотношений в системе (2) исходной задачи (1) (3), а число ограничений в системе (5) двойственной задачи числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (4) двойственной задачи (4) (6) являются свободные члены в системе (2) исходной задачи (1) (3), а правыми частями в соотношениях системы E4) двойственной задачи коэффициенты при неизвестных в целевой функции E0) исходной задачи.
5. Если переменная Xj исходной задачи (1) (3) может принимать только лишь положительные значения, то е условие в системе (5) двойственной задачи (4) (6) является неравенством вида «^». Если же переменная Xj может принимать как положительные, так и отрицательные значения, то j-e соотношение в системе (5) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (2) исходной задачи (1) (3) и переменными двойственной задачи (4) (6). Если t-e соотношение в системе (2) исходной задачи является неравенством, то t-я переменная двойственной задачи уО. В противном случае переменная у1 может принимать как положительные, так и отрицательные значения. Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (2) прямой задачи и соотношения (5) двойственной задачи являются неравенствами вида «». Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Составить двойственную задачу по отношению к задаче, состоящей в максимизации функции
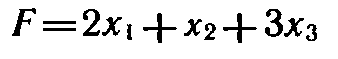 (9)
(9)
при условиях:
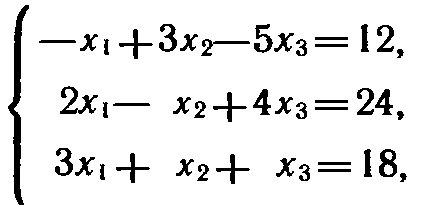 (10)
(10)
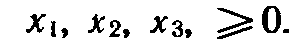 (11)
(11)
Для данной задачи
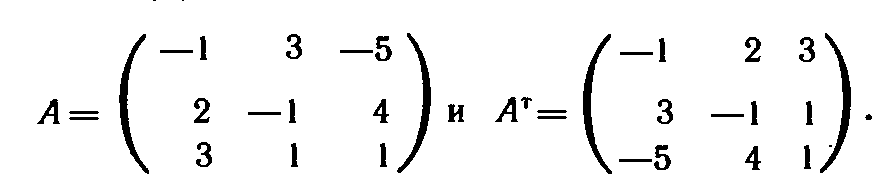
Число переменных в двойственной задаче равно числу уравнений в системе (10), т. е. равно трем. Коэффициентами в целевой функции двойственной задачи являются свободные члены системы уравнений (10), т.е. числа 12, 24, 18. Целевая функция исходной задачи (9) (11) исследуется на максимум, а система условий (10) содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные).Так как все три
переменные исходной задачи (9) — (11) принимают только лишь неотрицательные значения, то в системе условий двойственной задачи должны быть три неравенства вида «». Следовательно, для задачи (9)(11) двойственная задача такова:
найти минимум функции F*= l2yl+24y2+18y3 при условиях
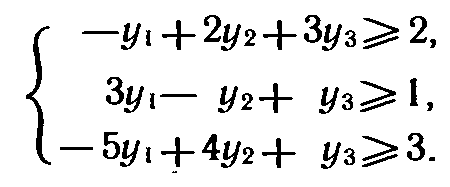
Для задачи, состоящей в максимизации функции
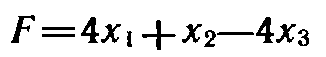
при условиях
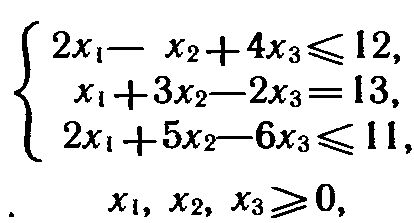
сформулировать двойственную задачу.
Решение. Для данной задачи
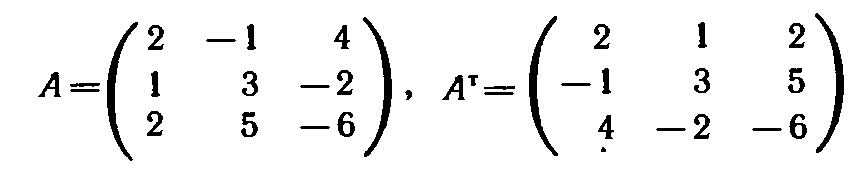
В соответствии с общими правилами задача, двойственная по отношению к данной, формулируется следуюш,нм образом: найти минимум функции F*=12у1 + 13у2+11уз при условиях
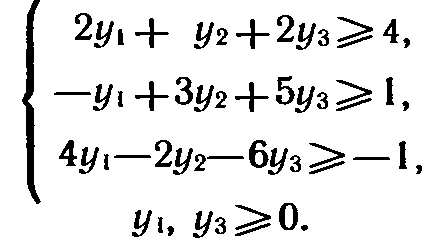
Связь между решениями прямой и двойственной задач.
Рассмотрим пару двойственных задач, образованную основной задачей линейного программирования и двойственной к ней.Исходная задача: найти максимум функции
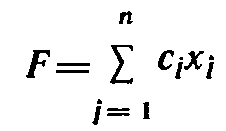 (12)
(12)
при условиях:
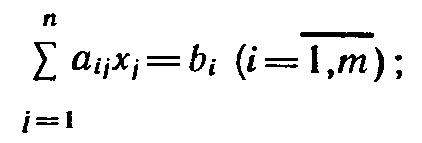 (13)
(13)
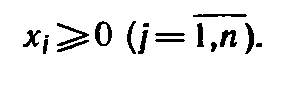 (14)
(14)
Двойственная задача: найти минимум функции
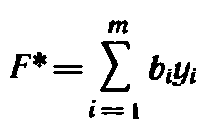 (15)
(15)
при условиях
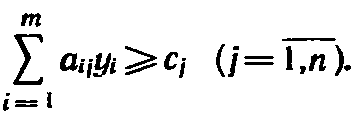 (16)
(16)
Каждая из задач двойственной пары (12) (15) и (14), (16) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач тем самым находится решение и другой задачи.
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1. Если X некоторый план исходной задачи (12) (15), aY произвольный план двойственной задачи (15), (16), то значение целевой функции исходной задачи при плане X всегда не превосходит значения целевой функции двойственной задачи при плане Y, т. е. 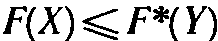
Лемма 1.2. Если 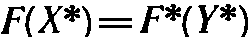 для некоторых планов X* и У* задач F1) — F3) и (15), (16), то X* — оптимальный план исходной задачи, а Y* — оптимальный план двойственной задачи.
для некоторых планов X* и У* задач F1) — F3) и (15), (16), то X* — оптимальный план исходной задачи, а Y* — оптимальный план двойственной задачи.
Теорема (первая теорема двойственности). Если одна из пары двойственных задач (12) (14) или (15), (16) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е. 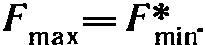
Если же целевая функция одной из пары двойственных задач не ограничена [для исходной (12) (14) сверху, для двойственной (15), (16) — снизу], то другая задача вообще не имеет планов.
Теорема (вторая теорема двойственности).
План 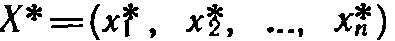 задачи (12) (14) и план Y*
задачи (12) (14) и план Y* 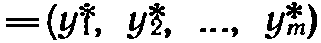 задачи (15), (16) являются оптимальными планами этих задач тогда и только тогда, когда для любого
задачи (15), (16) являются оптимальными планами этих задач тогда и только тогда, когда для любого
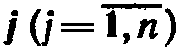 выполняется равенство
выполняется равенство
Геометрическая интерпретация двойственных задач. Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию задачи линейного программирования, можно легко найти решение данной пары задач. При этом имеет место один из следующих трех взаимно исключающих друг друга случаев: I) обе задачи имеют планы; 2) планы имеет только одна задача; 3) для каждой задачи двойственной пары множество планов пусто.
Для задачи, состоящей в определении максимального значения функции
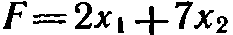
при условиях
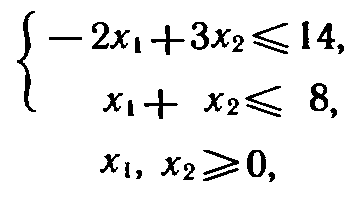
составить двойственную задачу и найти решение обеих задач.
Решение. Двойственной задачей по отношению к исходной является задача, состоящая в определении минимального значения функции
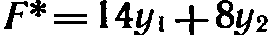
при условиях
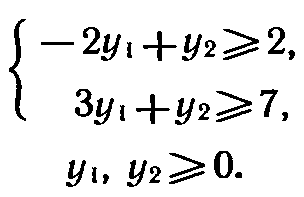
Как в исходной, так и в двойственной задаче число неизвестных равно двум. Следовательно, их решение можно найти, используя геометрическую интерпретацию задачи линейного программирования.
Максимальное значение целевая функция исходной задачи принимает в точке В. Следовательно, 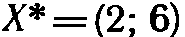 является оптимальным планом, при котором Fmax =46.
является оптимальным планом, при котором Fmax =46.
Минимальное значение целевая функция двойственной задачи принимает в точке E Значит, У* = (1; 4) является оптимальным планом двойственной задачи, при котором Fmax= 46. Таким образом, значения целевых функций исходной и двойственной задач при их оптимальных планах равны между собой.
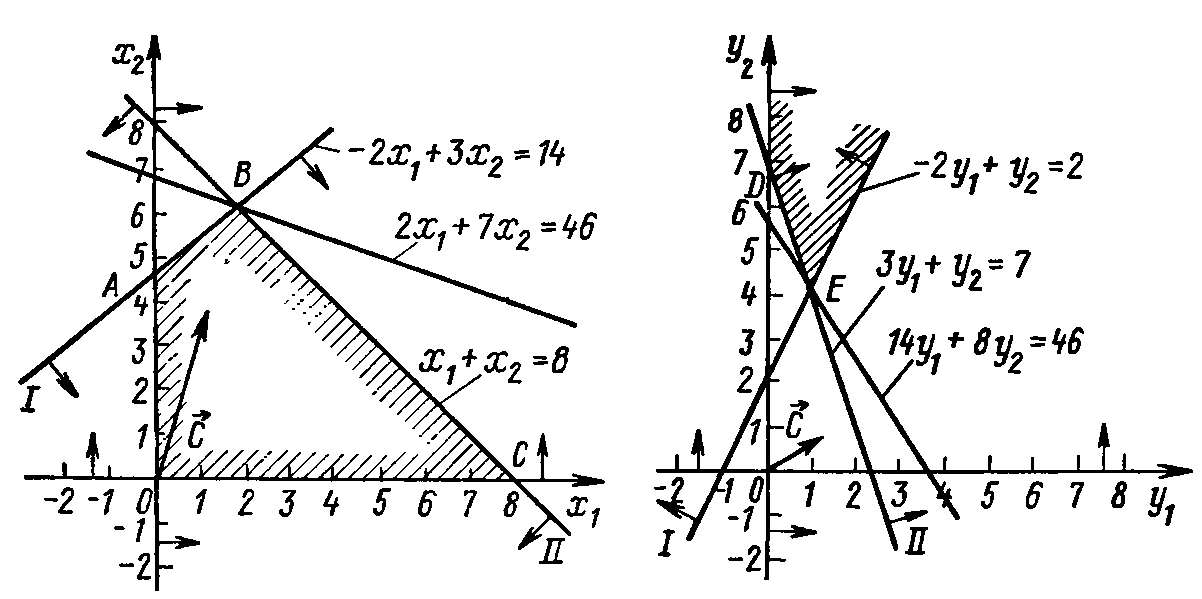 (1) (2)
(1) (2)
Из рис. 1 видно, что при всяком плане исходной задачи значение целевой функции не больше 46. Одновременно, как видно из рис. 1 значение целевой функции двойственной задачи при любом ее плане не меньше 46. Таким образом, при любом плане исходной задачи значение целевой функции не превосходит значения целевой функции двойственной задачи прн ее произвольном плане.
Найти решение двойственной пары задач.
Исходная задача:
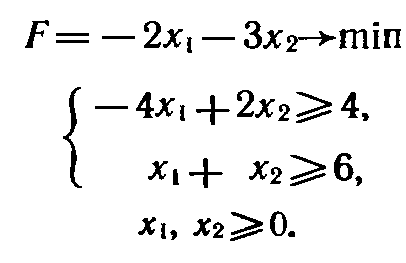
Двойственная задача:
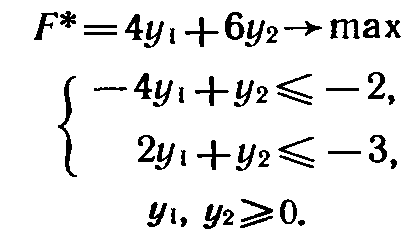
Решение. Как исходная, так и двойственная задача содержат по две переменные. Поэтому нх решение находим, используя геометрическую интерпретацию задачи линейного программирования (рис. 3 и 4). Из рис. 3 видно, что исходная задача не имеет оптимального плана из-за иеограниченности снизу ее целевой функции на множестве допустимых решений.
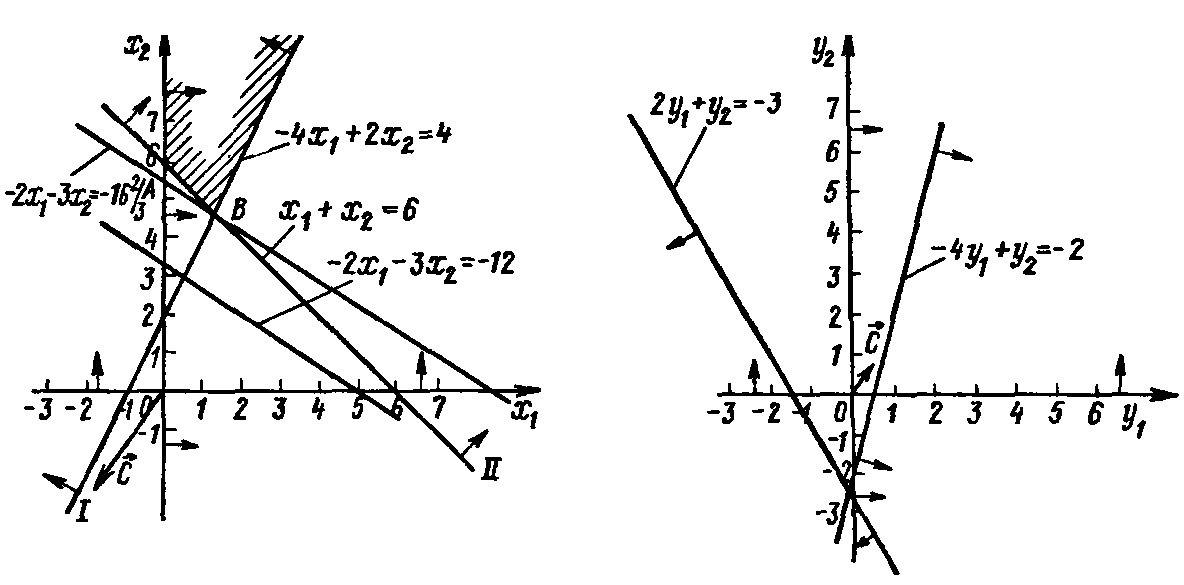 (3) (4)
(3) (4)
Из рис. 1.17 следует, что двойственная задача не имеет планов, поскольку многоугольник решений ее пуст. ЭтС означает, что если исходная задача двонствеинон пары не имеет оптимального плана из-за неограниченности на множестве допустимых решений ее целевой функции, то двойственная задача также не имеет планов. Нахождение решения двойственных задач. Рассмотрим пару двойственных задач — основную задачу линейного программирования (12)(14) и двойственную к ней задачу (15), (16).
Предположим, что с помощью симплексного метода найден оптимальный план X* задачи (12) — (14) и этот план определяется базисом, образованным векторами 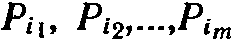 .
.
Обозначим через 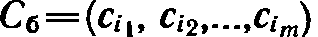 вектор-строку, составленную из коэффициентов при неизвестных в целевой функции (12) задачи (12) — (14), а через Р-1- матрицу, обратную матрице Р, составленной из компонент векторов
вектор-строку, составленную из коэффициентов при неизвестных в целевой функции (12) задачи (12) — (14), а через Р-1- матрицу, обратную матрице Р, составленной из компонент векторов 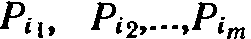 базиса.
базиса.
Тогда имеет место следующее утверждение.
Теорема. Если основная задача линейного программирования имеет оптимальный план X*, то У* = СбР-1 является оптимальным планом двойственной задачи.
Таким образом, если найти симплексным методом оптимальный план задачи (12) — (14), то, используя последнюю симплекс- таблицу, можно определить Сб и Р-1 и с помощью соотношения Y*=Cб и Р-1 найти оптимальный план двойственной задачи (15), (16).
В том случае, когда среди векторовP1, Р2…Рn, составленных из коэффициентов при неизвестных в системе уравнений (13), имеется m единичных, указанную матрицу Р~' образуют числа первых m строк последней симплекс-таблицы, стоящие в столбцах данных векторов. Тогда нет необходимости определять оптимальный план двойственной задачи умножением Сб на Р-1 поскольку компоненты этого плана совпадают с соответствующими элементами (m+1)-й строки столбцов единичных векторов, если данный коэффициент Cj = 0, и равны сумме соответствующего элемента этой строки и Cj, если с0. Сказанное выше имеет место и для симметричной пары двойственных задач. При этом так как система ограничений исходной задачи содержит неравенства вида «^», то компоненты оптимального плана двойственной задачи совпадают с соответствующими числами (m+1)-й строки последней симплекс-таблицы решения исходной задачи. Указанные числа стоят в столбцах векторов, соответствующих дополнительным переменным.
Сказанное выше имеет место и для симметричной пары двойственных задач. При этом так как система ограничений исходной задачи содержит неравенства вида «»,то компоненты оптимального плана двойственной задачи совпадают с соответствующими числами (m+1)-й строки последней симплекс-таблицы решения исходной задачи. Указанные числа стоят в столбцах векторов, соответствующих дополнительным переменным.
Для задачи, состоящей в определении максимального значения функции
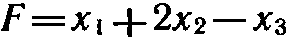 при условиях
при условиях
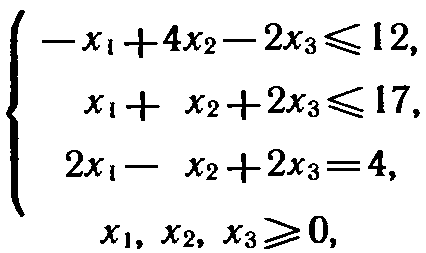
составить двойственную задачу и найти ее решение.
Решение. Двойственная задача по отношению к исходной состоит в нахождении минимума функции 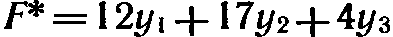 при условиях
при условиях

Вычисление симплекс-таблиц
В этом разделе будет показано, как на основе исходных данных задачи вычисляется симплекс-таблица и как вычисляется обратная матрица на каждой итерации. С учетом структуры симплекс-таблиц, все эти вычисления можно разбить на две группы.
Соотношения между прямой и двойственной задачами
1. Вычисление значений в столбцах ограничений симплекс-таблицы (как ле- вой, так и правой частей ограничений).
2. Вычисление значений в 2-строке. Вычисление значений в столбцах ограничений. На произвольной симплекситерации значения коэффициентов в столбцах левой и правой частей ограничений вычисляются по следующей формуле 1.

Вычисление значений z-строки. На произвольной симплекс-итерации значения коэффициентов в z-строке вычисляются по следующей формуле 2.

Отметим, что формула 2 такая же, какая используется в методе 2 для определения оптимального решения двойственной задачи.
На основе задачи покажем, как использовать формулы 1 и 2. Из оптимальной симплекс-таблицы этой задачи получаем
обратная матрица =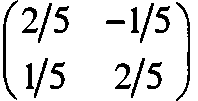
С помощью формулы 1 вычислим коэффициенты в столбцах ограничений оптимальной симплекс-таблицы.
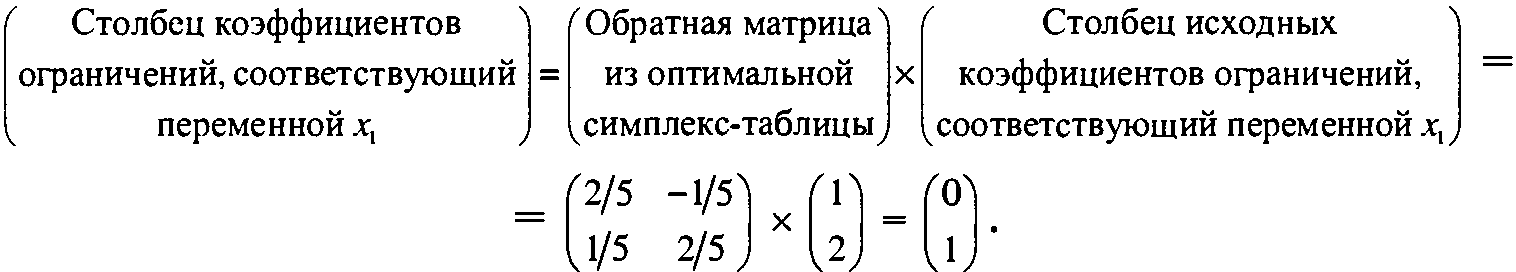
Аналогично вычисляются другие столбцы коэффициентов ограничений.
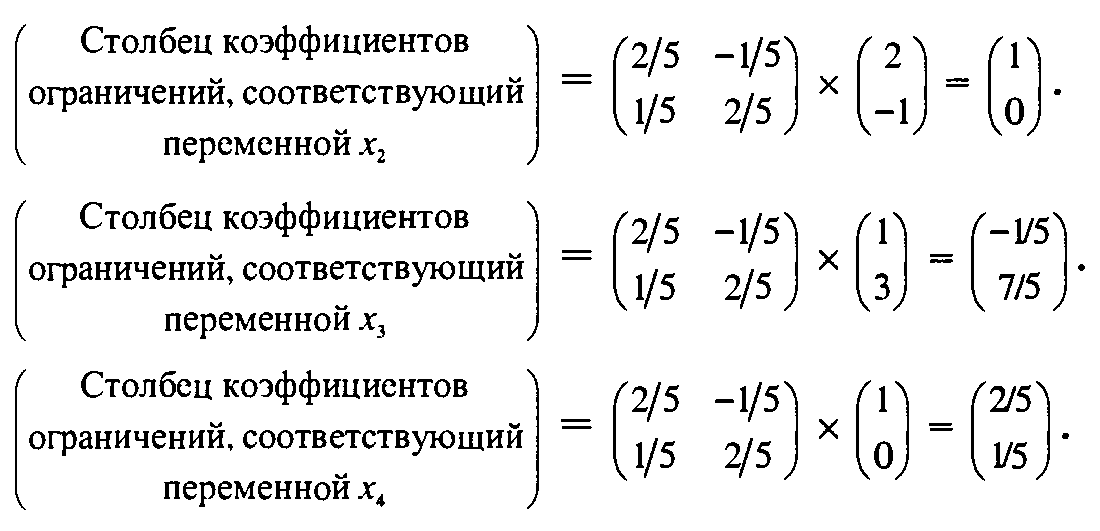
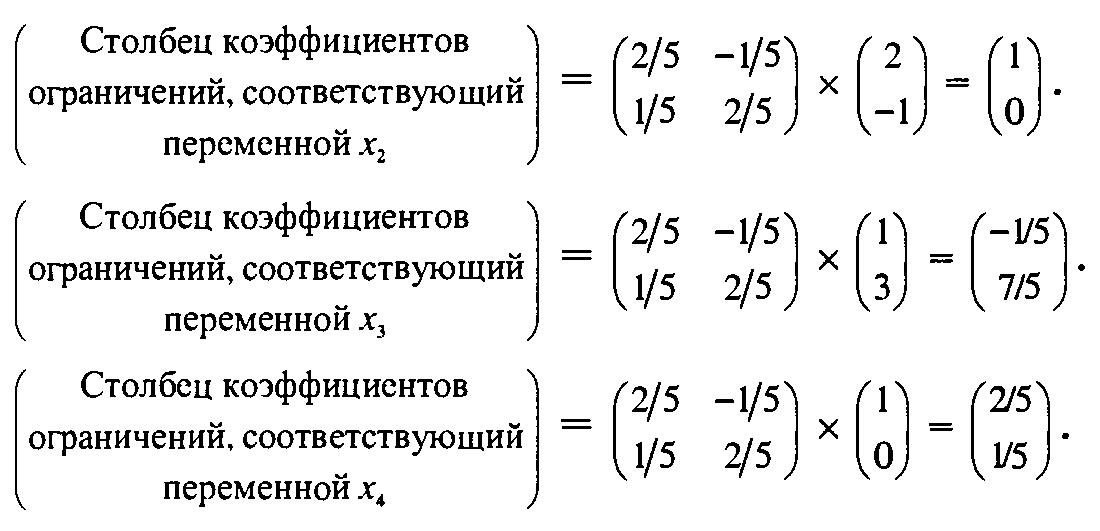
Теперь применим формулу 2 для вычисления коэффициентов в г-строке. Оптимальные значения двойственных переменных (у1, у2) = 29/5, -2/5) вычислены двумя различными методами. Эти значения используются для вычисления коэффициентов в z-строке.
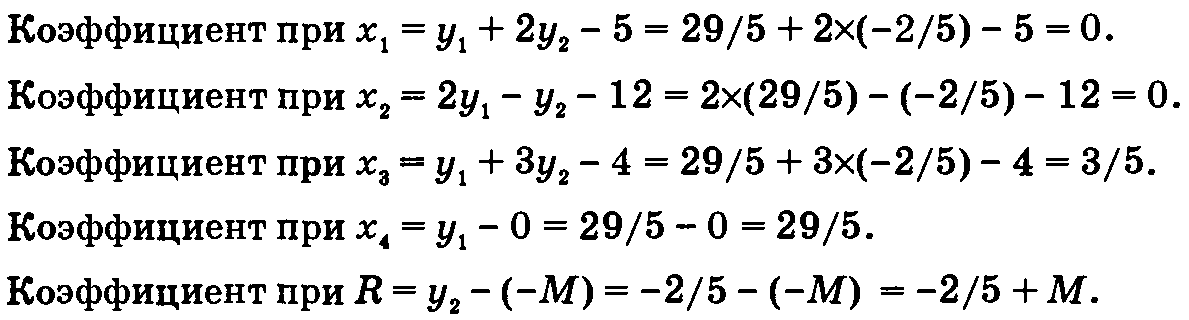
Важно отметить, что формулы 1 и 2 можно применять на любой симплекс- итерации как к прямой, так и к двойственной задаче.
ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ДВОЙСТВЕННОСТИ
Задачу линейного программирования можно рассматривать как модель распределения ограниченных ресурсов, в которой целевая функция, отображающая прибыль или доход от производственной деятельности, подлежит максимизации. Если рассматривать задачу ЛП с этой точки зрения, соответствующая ей двойственная задача получает интересную экономическую интерпретацию. Чтобы формализовать рассматриваемый вопрос, приведем еще раз общее представление прямой и двойственной задач, причем прямая задача будет играть роль модели распределения ресурсов. Исходя из модели распределения ресурсов, прямая задача отображает п видов экономической (производственной) деятельности и возможности получения т ресурсов. В прямой задаче коэффициент с} представляет собой прибыль на единицу продукции j-го вида экономической деятельности, причем на единицу продукции этого вида деятельности расходуется ац единиц ресурса ai, максимальные запасы которого ограничены величиной bt.

.
Экономическая интерпретация переменных двойственной задачи
Соотношение устанавливает, что для любой пары допустимых решений прямой и двойственной задач значения (конечные) их целевых функций удовлетворяют неравенству
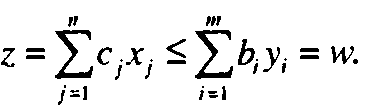
Строгое равенство здесь достигается только тогда, когда решения прямой и двойственной задач оптимальны.
Рассмотрим сначала вариант оптимума, т.е. когда 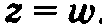 Исходя из представления прямой задачи как модели распределения ресурсов, можно считать, что величина z соответствует величине дохода (в долларах3). Поскольку i— общее доступное количество ресурса i, равенство z = w можно переписать следующим образом.
Исходя из представления прямой задачи как модели распределения ресурсов, можно считать, что величина z соответствует величине дохода (в долларах3). Поскольку i— общее доступное количество ресурса i, равенство z = w можно переписать следующим образом.
Доход (долл.) = (количество ресурса i) x (доход (долл.) на единицу ресурса i).Это означает, что переменная yt двойственной задачи должна представлять стоимость единицы ресурса i. (Данное понятие уже вводилось в разделе 2.3.3, исходя из графического представления задачи Л П.) В литературе по исследованию операций переменные yt двойственной задачи часто называют двойственными ценами. Кроме того, иногда их именуют теневыми ценами и симплексными мультипликаторами. Аналогично для любой пары допустимых решений прямой и двойственной задач неравенство zw можно интерпретировать следующим образом:
доход < общая стоимость ресурсов.
Это соотношение показывает, что до тех пор, пока суммарный доход от всех видов деятельности строго меньше суммарной стоимости всех используемых ресурсов, решение как прямой, так и двойственной задачи не может быть оптимальным. Оптимум (максимальный доход) может быть достигнут только тогда, когда все потребляемые ресурсы использованы полностью. Если модель ЛП рассматривать более обще как модель некой системы, имеющую "вход" и "выход", то потребляемые ресурсы характеризуют "вход" этой системы, а получаемый доход ее "выход". Система будет находиться в нестабильном (неоптимальном) состоянии, пока вход превышает выход. Устойчивое состояние системы характеризуется равенством входа и выхода.
Приведем формулировки прямой и двойственной задач, описывающие модель производства компании Reddy Mikks

Напомним вкратце, что в этой модели описывается производство двух видов краски (для внутренних и наружных работ) на основе двух видов сырья Ml и М2 (ресурсы 1 и 2) с учетом рыночных условий, выражаемых третьим и четвертым ограничениями. Зада- ча состоит в определении объемов производства красок каждого вида (в тоннах), при которых будет получен максимальный доход (в тыс. долл.).
Оптимальное решение двойственной задачи показывает, что стоимость единицы первого ресурса (сырье Ml) составляет у1 = 0,75 (или 750 долл. за тонну), а второго (сырье М2) — у2 = 0,5 (или 500 долл. за тонну). Графически по- казали, что приведенные значения стоимостей справедливы, если значение первого ресурса не выходит из интервала B0, 36), а второго — из интервала D, 6,67) Таким образом, расход сырья Ml может возрасти с 24 до 36 тонн, что приведет к соответствующему увеличению дохода
на величину12 х 750 = 9000 долл. Аналогично количество вто- рого ресурса (сырье М2) можно увеличить с 6 до 6,67 тонн с увеличением дохода на величину 0,67 х 500 = 335 долл. Но еще раз напомним, что подобные расчеты при- менимы только тогда, когда увеличение числа используемых ресурсов не выходит за приведенные выше интервалы значений. Конечно, это не означает, что количе- ство используемых ресурсов в принципе не может выходить за указанные пределы. Однако приведенные выше стоимости ресурсов определены только для ситуации, когда количество этих ресурсов не выходит за указанные пределы.
Для третьего и четвертого ресурсов двойственные цены (оптимальное решение двойственной задачи) равны нулю. Это указывает на то, что данные ресурсы неде- фицитны. Поэтому их стоимость равна нулю.
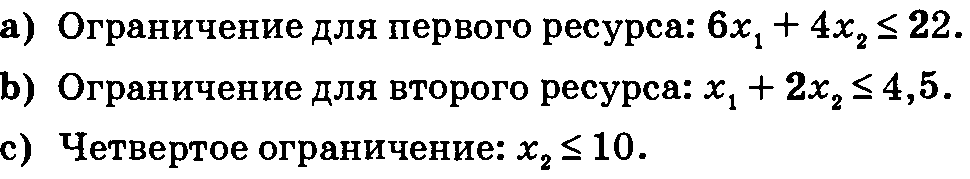
Электротехническая компания NWAC производит четыре типа кабеля для оборонного ведомства. Каждый тип кабеля подвергается четырем последова- тельным операциям: разделка, пайка, оплетка и проверка. В следующей таб- лице приведены данные, характеризующие производство кабелей.
a) Сформулируйте задачу линейного программирования и с помощью про-граммы TORA найдите ее оптимальное решение.
b) Основываясь на двойственных ценах, приведенных программой TORA, определите возможное увеличение ежедневного фонда времени по каждой технологической операции.
c) Выгодно ли компании выполнение требования заданного минимального уровня производства? Обоснуйте ответ, основываясь на величинах двой- ственных цен.
d) Возможно ли увеличение на 10% временного фонда операции пайки с со- хранением величины ее вклада в суммарный доход, определяемый текущей двойственной ценой?
Компания производит кожаные чехлы и сумки. На производство одного чех-ла требуется 8 м2 кожи и 12 часов рабочего времени, на производство сумки — 2 м2 кожи и 5 часов рабочего времени. Текущие еженедельные ресурсы производства ограничены 1200 м2 кожи и 1850 часами рабочего времени. Компания продает чехлы и сумки по цене 350 и 120 долл. соответственно. Определите для этой компании схему производства, максимизирующую чис-тую прибыль. Допустим, компания желает расширить свое производство. Какова максимальная цена, по которой компании имеет смысл закупать до-полнительную кожу? А какова допустимая максимальная цена дополни-тельных трудовых ресурсов?
Экономическая интерпретация ограничений двойственной задачи
Для интерпретации ограничений двойственной задачи используем формулу2. В соответствии с этим соотношением на любой итерации решения прямой задачи справедливо равенство
коэффициент при xj в z-строке = 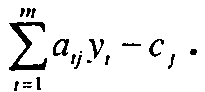
Условие оптимальности симплекс-метода в задаче максимизации говорит о том, что j-й вид деятельности (переменная xj), не представленный в текущем базисном решении, можно ввести в базис для увеличения дохода только тогда, когда коэффициент при Xj в z-строке 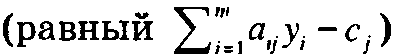 будет неотрицательным. В рамках предлагаемой экономической интерпретации это означает, что j-й вид деятельности должен быть представлен в базисном решении, если выполняется следующее неравенство.
будет неотрицательным. В рамках предлагаемой экономической интерпретации это означает, что j-й вид деятельности должен быть представлен в базисном решении, если выполняется следующее неравенство.
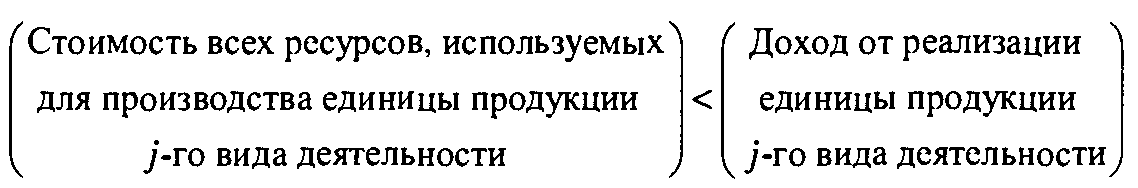
Таким образом, условие оптимальности (в задаче максимизации) говорит о том, что деятельность любого вида следует наращивать до тех пор, пока доход от нее превышает возможные издержки.
Приведем стандартные определения, используемые в литературе по линейному программированию. Введем обозначение 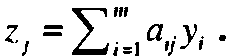
Величина zjпредставляет суммарную стоимость ресурсов, используемых на производство единицы продукции j-го вида деятельности. Величина zj- сj равна коэффициенту при в z-строке симплекс таблицы и часто называется приведенной стоимостью (приведенными издержками) j-го вида деятельности. В некоторых случаях разности 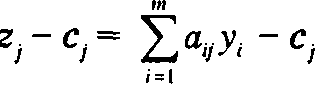 используются непосредственно для вычисления коэффициентов в z-строке симплекс таблицы (вместо метода Гаусса-Жордана). Такие вычисления используются в модифицированном симплекс-методе.
используются непосредственно для вычисления коэффициентов в z-строке симплекс таблицы (вместо метода Гаусса-Жордана). Такие вычисления используются в модифицированном симплекс-методе.
значения целевой функции, пока не будет достигнута точка оптимума. Такой алгоритм иногда называют прямым симплекс-методом. В этом разделе рассмотрим две другие разновидности симплекс-метода: двойственный симплекс-метод и обобщенный симплекс-метод. В двойственном симплекс- методе решение задачи ЛП начинается с недопустимого, но лучшего, чем оптимальное, решения. Последовательные итерации этого метода приближают решение к области допустимости без нарушения оптимальности (точнее, "супероптимальности") промежуточных решений. Когда будет достигнута область допустимых решений, процесс вычислений заканчивается, так как последнее решение будет оптимальным. В обобщенном симплекс-методе комбинируются элементы прямого и двойст- венного методов. Начальное решение в этом методе будет и неоптимальным, и недопустимым. На последующих итерациях базисные решения могут быть как допустимыми, так и недопустимыми. На последней итерации решение должно быть и оптимальным, и допустимым (если, конечно, такое решение существует). Эти три алгоритма — прямой, двойственный и обобщенный — дают основу для проведения анализа чувствительности.
Двойственный симплекс-метод
Так же, как и в прямом симплекс-методе, основная проблема двойственного симплекс-метода состоит в том, чтобы на каждой итерации получить "правильное" базисное решение. Для реализации двойственного симплекс- метода разработаны следующие два условия, выполнение которых гарантирует оптимальность последовательных промежуточных решений и приближение их к области допустимых решений. Двойственное условие допустимости. В качестве исключаемой переменной хг выбирается базисная переменная, имеющая наибольшее по абсолютной величине отрицательное значение. Если таких переменных несколько, то выбор произволен. Если все базисные переменные неотрицательные, процесс вычислений заканчивается. Двойственное условие оптимальности. Вводимая в базис переменная определяется как переменная, на которой достигается следующий минимум:
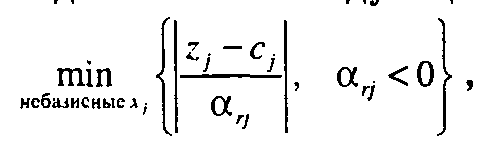
где z1 – c1 — коэффициент в z-строке симплекс-таблицы, соответствующий переменной xj aj — отрицательный коэффициент из симплекс-таблицы, расположен- ный на пересечении ведущей строки (соответствующей исключаемой переменной хг) и столбца, соответствующего небазисной переменной хг При наличии несколь- ких альтернативных переменных выбор делается произвольно. Отметим, что двойственное условие оптимальности гарантирует достижение оптимального решения.
Чтобы существовало начальное оптимальное ("супероптимальное") и недопустимое решение, необходимо выполнение двух условий.
1. Целевая функция должна удовлетворять условию оптимальности обычного
симплекс-метода .
2. Все ограничения должны быть неравенствами типа "".
Второе условие можно удовлетворить простым умножением на -1 неравенств типа "". Если есть ограничения в виде равенств, то эти равенства заменяются на два не- равенства. Например, равенство х1 + х2 = 2 эквивалентно двум неравенствам
Разновидности симплекс-метода
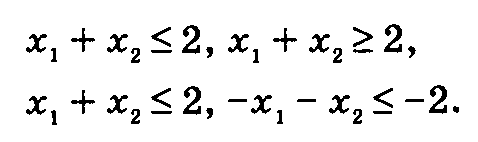
После преобразования всех ограничений в виде неравенств типа "<" начальное недопустимое решение возможно тогда и только тогда, когда по крайней мере в одном неравенстве правая часть будет строго отрицательной. В противном случае двойственный симплекс-метод не применяется, поскольку возможное начальное решение уже оптимально и допустимо.
Дана следующая задача ЛП.
Минимизировать z = Зх1 + 2х2
при ограничениях
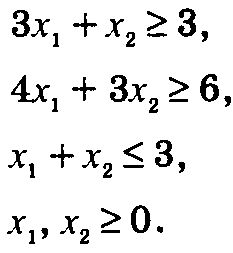
Сначала первых два неравенства умножаются на -1, чтобы привести их к неравенствам типа "". Начальная симплекс-таблица этой задачи имеет следующий вид.

Поскольку Zj - Cj 0 для всех у1 = 1, ..., 5, начальное базисное решение
(х3 = -3, х4 = -6, х5 = 3) является оптимальным и недопустимым. Двойственное условие допустимости указывает на переменную х4 (= -6) как на исключаемую из базиса. Теперь применим двойственное условие оптимальности для определения вводимой переменной. Для этого используем следующую таблицу.
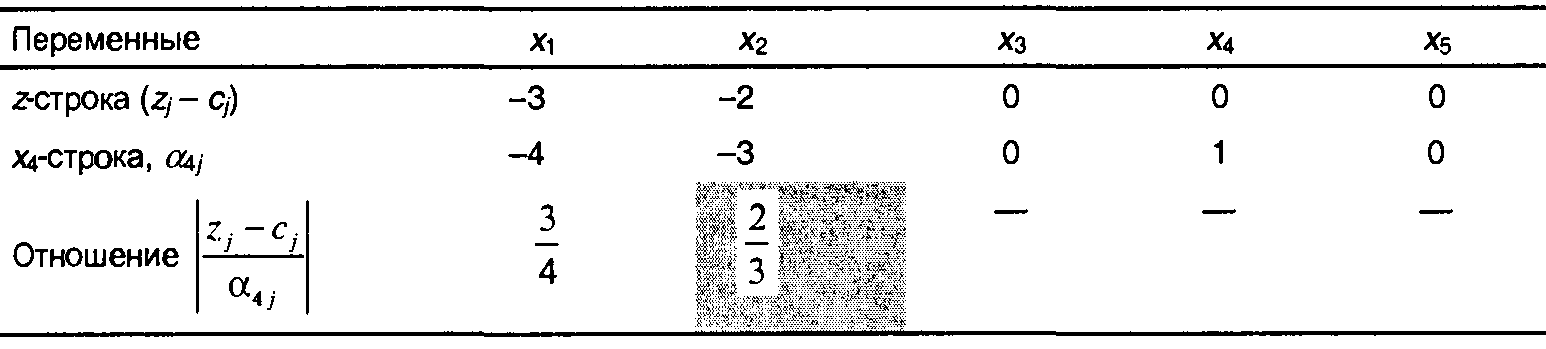
Приведенные отношения показывают, что вводимой переменной будет х2. Отметим, что переменные xi будут кандидатами на включение в базисное решение только тогда, когда коэффициент atj будет строго отрицательным. По этому критерию переменные х3, х4 и х5 не рассматриваются как кандидаты на включение в базис.
Следующая таблица получена с помощью известных операций над строками, применяемых в прямом симплекс-методе.
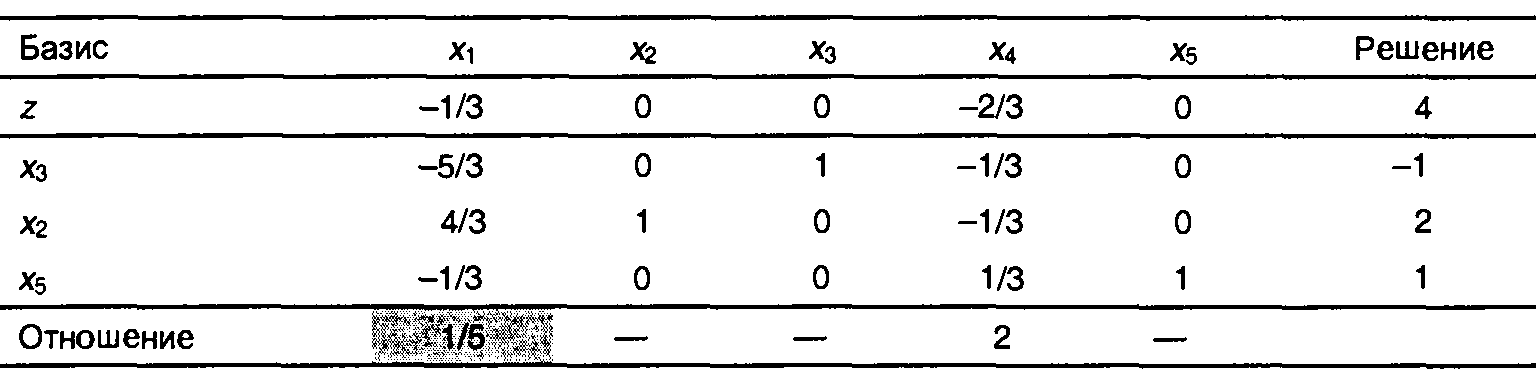
Последняя таблица показывает, что из базиса исключается переменная х3 и вводится x1,. В результате получаем следующую симплекс-таблицу.
Оптимальное решение двойственной задачи