Производство мебели не только существенно отличается от остальных производственных процессов но и оснащен.
- Аналитический обзор
Мебельное производство — сфера деятельности человека, направленная на производство мебели. Производство мебели не только существенно отличается от остальных производственных процессов, но и оснащено оборудованием, предназначенным для выполнения узкоспециальных технологических операций [1].
Деревообрабатывающие станки – специальное оборудование, предназначенное для обработки дерева. Сфера применения:
- промышленное изготовление древесных полуфабрикатов: плит, фанеры, бруса и других изделий;
- производство деталей для машиностроительной, мебельной, судостроительной отраслей;
- производство товаров общего потребления: дверей, окон, паркета, лыж, инструментов и др.
Классификация и требования к такому оборудованию отражены в ГОСТ на деревообрабатывающие станки. Отечественная нормативная база насчитывает более 80 стандартов.
Общепринятая классификация подразделяет станки на:
- общего назначения, которые задействованы во многих сферах производства и хозяйствования, это фрезерные, долбежные, шлифовальные, токарные, сверлильные, круглопильные и другие;
- специального назначения, такое оборудование предназначено для выполнения узконаправленных работ в определенном производстве.
По видам выполняемых работ выделяют: дереворежущие, сборочные, гнутарные, отделочные для нанесения клея, фрезерно-копировальныс, форматно-раскроечные, мебельный пресс, сверлильно – присадочные, фрезерные станки с ЧПУ, калибровально-шлифовальные.
Наиболее востребованы дереворежущие станки. На таких станках различными дереворежущими инструментами с обрабатываемого древесного материала методом резания отделяется стружка с целью получения заготовок, деталей или изделий с заданной формой, размерами и шероховатостью обработанных поверхностей. Резание древесины выполняется различными методами: пилением, фрезерованием, строганием, сверлением, долблением, точением, лущением и шлифованием. Стружка может быть либо отходом производства, либо продукцией (например, шпон при лущении и строгании, тонкая дощечка при безопилочном резании). Бесстружечное резание происходит при раскалывании (дровокольный станок либо дровоколы), разрезании шпона (ножницы), вырезании штампами (шпонопочиночные станки), дроблении (дробильные и рубительные станки).
Пиление – это процесс деления древесины пилой на объемные недеформированные части путём превращения в стружку объёма древесины между этими частями. Различают пиление пилами рамными, ленточными и дисковыми.
Выделяют следующие станки для процесса пиления: ленточные пильные станки (ЛПС), дисковые пильные станки, бревнопильные станки, многопильные станки. Ленточная установка предназначена для продольной распиловки круглого леса на доску, шпалу, брус, шпон. Они делятся на два больших класса. Лесопильные рамы общего назначения. Производятся для установки в специальных лесопильных цехах. Такие рамы оборудованы четырёхвальцовым механизмом подачи. Лесопильные установки делят на первый и второй род. Рамы специального назначения: горизонтальные рамы – перемещение пильной рамки происходит в горизонтальном направлении (подходят для распила брёвен ценных пород и для выпиливания ванчесов в фанерном производстве); коротышевые рамы – более надёжное закрепление бревна (благодаря восьмивальцовому механизму подачи); тарные рамы – используются в производстве тарных досок (незначительное количество отходов); передвижные рамы – подходят для временных цехов (возможна транспортировка без демонтажа).
Форматно – раскроечные станки являются одним из самых распространённых видов оборудования в мебельных цехах и используются для раскроя листовых материалов. С их помощью раскраивают мебельные щиты как в продольном и поперечном направлении, так и под определённым углом. Форматно ��– раскроечные станки могут быть вертикального и горизонтального типа, что определяется позиционированием на рабочем столе раскраиваемой заготовки. Операция распила ДСП осуществляется посредством дисковой пилы. Плоскость дисковых пил на некоторых моделях может менять позицию от 90 до 45 градусов по отношению к плоскости рабочего стола.
Гнутарные обеспечивают нужную форму древесины за счет осуществления изгиба, при этом структурные связи материала не нарушаются.
Сборочные выполняют соединение деталей в узлы и изделия методом склеивания, соединения гвоздями, скобами, нагелями, шурупами и др.
Мебельный пресс предназначен для облицовки термопластичной пленкой и шпоном плоских поверхностей мебельных щитов и панелей из ДСП, МДФ (англ. Medium Density Fiberboard, MDF – древесноволокнистой плиты средней плотности), ДВП (Древесноволокнистая плита) и фанеры. Существуют модификации мебельных прессов, посредством которых изготавливаются клееные мебельные щиты из массива.
Фрезерно – копировальные станки рассчитаны на проведение различных фрезерных операций с ручной подачей; для выбора пазов, проушин и шипов в длинных и коротких деталях посредством специальной шипорезной каретки; для фрезерования фасонных деталей в соответствии с имеющимся шаблоном.
Сверлильно – присадочные станки являются незаменимым оборудованием при сверлении отверстий всех типов в плоскостях и торцах.
Фрезерные станки с ЧПУ – наиболее востребованное оборудование в цехах мебельных производств. Предназначено для фрезеровальных, гравировальных и сверлильных операций. Посредством концевых фрез и в полном соответствии с программой, на станки с ЧПУ заготовки из дерева, пластика и МДФ превращаются в сложные декоративные элементы, филенчатые вставки и другие мебельные аксессуары любой степени сложности.
Калибровально – шлифовальные станки являются оборудованием для финишной отделки заготовок из массива и мебельных щитов. Белое шлифование заготовок и щитов осуществляется с помощью специальных шлифовальных лент, имеющих разную степень зернистости.
Отделочные станки выполняют нанесение на изделие (преимущественно ДСП) или заготовку защитного или декоративного покрытия. Нанесение осуществляется с помощью вальцев или струйным обливом. Клей наносится вальцами, роликовыми механизмами, щеточками, дисками, впрыскиванием. Кромко-облицовочные станки предназначены для отделки края мебельных щитов специальным кромочным материалом из шпона, меламина или ПВХ. Для облицовки прямолинейных, криволинейных и скошенных кромок требуются различные модификации оборудования.
1.1 Материал для производства
Древесно – стружечная плита (официальная аббревиатура – ДСтП, неофициально – ДСП) – листовой композиционный материал, изготовленный путем горячего прессования древесных частиц, преимущественно стружки, смешанных со связующим неминерального происхождения с введением при необходимости специальных добавок (6 – 18% от массы стружек) на одно – и много этажных периодических прессах (0,2–5 МПа, 100–140 °С) или в непрерывных ленточных, гусеничных либо экструзионных агрегатах.
Материал имеет следующие свойства: плотность –0,5–1,0 г/см3, набухание в воде –5 – 30 %, предел прочности при растяжении – не менее 0,2–0,5 МПа, предел прочности при изгибе не менее – 10–25 МПа, влажность –5–12 %. В таблице 1 приведены сортаменты плит.
Таблица 1 - Номинальные размеры плит и их отклонения
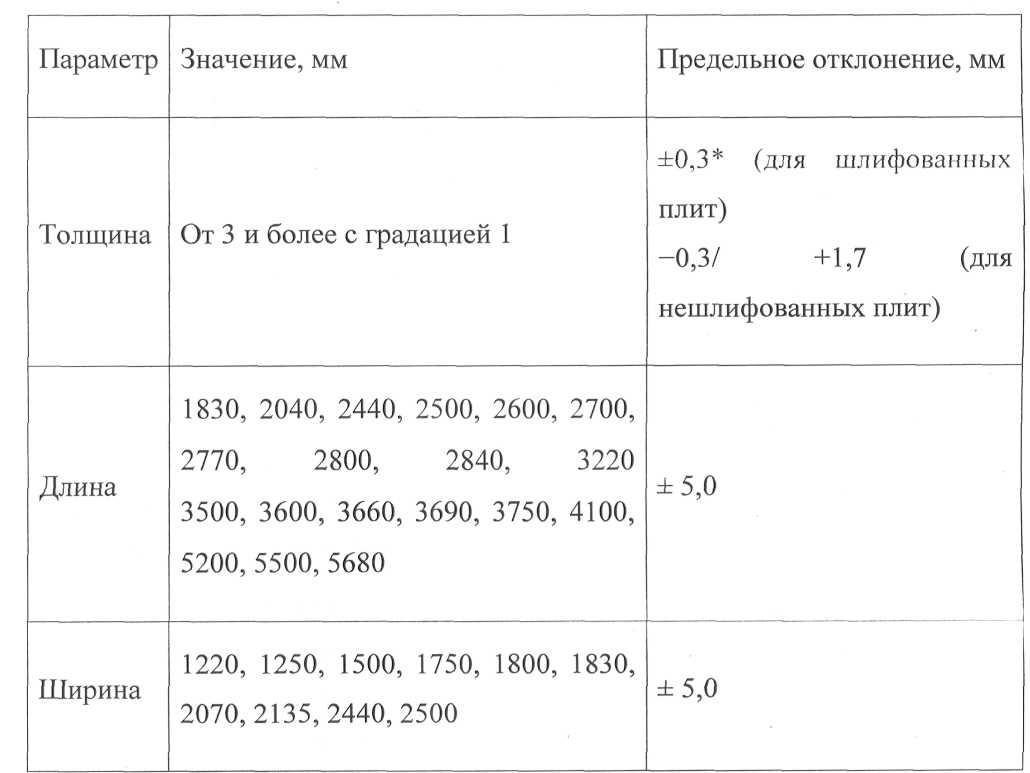
*Как в пределах одной плиты, так в партии плит. Примечания:
- допускается выпускать плиты размерами меньше номинальных на 200 мм с градацией 25 мм в количестве не более 5 % партии;
- по согласованию изготовителя с потребителем допускается выпускать плиты форматов, не установленных в настоящей таблице.
Недостатки:
- материал плохо удерживает гвозди и шурупы, особенно при повторном закручивании;
- материал экологически небезопасен: связующие смолы, которые применяются при его производстве, выделяют вредный для человека формальдегид. Поэтому немаловажным параметром плит является предельно-допустимая концентрация вредных веществ на удельный объём, определяемый санитарными нормами. В России довольно часто производители выпускают низкосортную, дешевую плиту, выделение формальдегида из которых значительно превышает ПДК (до 40 раз) и хуже, чем у плит класса Е1 (в Е1 до 8 раз больше формальдегида чем в рекомендациях ГОСТ). За рубежом плиты такого класса уже не выпускают, а производят лишь сверхбезопасные плиты класса «Super E».
Е1 отличается большей экологической чистотой, показатель эмиссии формальдегида у неё заметно ниже. А вот Е2 запрещается использовать в производстве детской мебели.
ДСП применяются для изготовления корпусной, мягкой и другой мебели, строительных элементов, вагонов и в производстве тары. Плиты могут быть облицованы шпоном, бумагой, полимерными пленками, пластиком.
1.2 Классификация ДСП
Конструкция: по количеству слоев ДСтП подразделяется на 1-слойный, 3-слойный и многослойный.
Марка: в зависимости от показателей прочности на изгиб, деформацию, водостойкость, подверженность короблению и деформации ДСтП делится на 2 марки: П-А и П-Б.
Сорт: в зависимости от критериев внешнего вида плиты (трещины, сколы, окрашивание, пятна, выступы и углубления). Плиты ДСтП делятся на 1 сорт (дефекты не приемлемы кроме минимальных), 2 сорт (допустимы крупные дефекты поверхности) и без сорта (кардинальные дефекты поверхности, используется в строительстве).
Наружный слой: выделяются плиты с мелкоструктурной поверхностью (возможна облицовка полимерными материалами), обычной (применяется облицовка шпоном) и крупнозернистой (используется в строительстве).
Уровень обработки поверхности: выделяется шлифованная и нешлифованная ДСтП.
Класс эмиссии формальдегида: по содержанию в 100 г сухой плиты ДСтП свободного формальдегида выделяются классы Е1 (менее 10 мг), Е2 (от 10 до 30 мг).
Водостойкость: кроме того, что плита марки П-А обладает лучшими водостойкими свойствами (22 % деформации против 33 % у П-Б при погружении в воду на сутки), выделяется отдельный вид водостойкой ДСтП, предназначенной для производства мебели и специфических строительных работ.
Огнестойкость: при введении в состав ДСтП антипиренов плита приобретает огнестойкие характеристики. Сейчас на территории РФ производство данного вида ДСтП не ведется.
Плотность: по плотности ДСтП делится на плиту малой плотности (менее 550 кг/м3), средней (550—750 кг/м3) и высокой (более 750 кг/м3).
По способу прессования: плоское или экструзионное прессование.
1.3 Разновидности ДСП
Ламинированная ДСП (неофициальное, часто используемое сокращение – ЛДСП) – древесно – стружечная плита, произведённая на основе высококачественной ДСП, облицованная при повышенном давлении и температуре стойкой меламиновой пленкой и иногда (у дорогих сортов ЛДСП) покрытая специальным лаком, устойчивым к влаге и механическим повреждениям. Ламинирование обеспечивает хороший внешний вид, высокие потребительские качества и повышает физико-механические свойства. Ламинированная ДСП не требует дальнейшей отделки и широко применяется для производства мебели.
Экструзионная ДСП. Древесные частицы в таких плитах расположены преимущественно перпендикулярно плоскости плиты, в результате чего эти плиты обладают низкой прочностью при изгибе перпендикулярно плоскости. В России производство экструзионных плит практически отсутствует. ДСП экструзионного способа прессования делятся на трубчатые, полосовые, звукоизоляционные и противопожарные. Плиты существенно различаются по плотности, размеру, весу и стоимости. В частности, трубчатые экструзионные плиты используются при производстве межкомнатных дверей, так как имеют высокую звукоизоляцию.
Древесно-стружечные плиты появились в 1940-х годах в США (англ. Chipboard) для временной мебели американских беженцев. В настоящее время является широко распространенным конструкционным материалом для производства мебели, применяется в строительстве и др. Годовое производство ДСП в мире в 1978 году составляло 45 миллионов м3.
Соответствие оборудования требованиям ГОСТ на деревообрабатывающие станки подтверждается испытаниями. Их периодичность и методы проведения регламентированы нормативно – техническими документами. Обязательными в нашей стране за рубежом являются испытания на безопасность.
1.4 Обзор оборудования
Brandt Optimat KDF 660 GC односторонний кромко-облицовочный станок в правостороннем исполнении для работы на клее расплаве. Быстросменная оклеивающая часть для работы на клее расплаве в гранулах. Переработка гранулированного полиуретанового клея расплава возможна при условии непременного соблюдения предписаний и рекомендаций производителей клея. Запас клея находится под клеевым роликом.
Нанесение клея на деталь с помощью клеевого ролика, вращающегося в направлении или против направления подачи и не требующего установки на толщину заготовки. Электронная регулировка температуры в клеевом бачке, с автоматическим снижением температуры в клеевом бачке при остановке работы. Инфракрасный излучатель для предварительного прогрева кромки заготовки.
Автоматический магазин для рулонного и полосового кромочного материала, вкл. устройство для резки рулона и тарелку для рулонного кромочного материала диаметром 800 мм, исполнение с усиленным ножом для деления кромок ПВХ, макс. 3 х 45 мм.
Стандартное оснащение устройством контроля расстояния между заготовками и устройством контроля положения кромочного материала.
Тяжелая зона прижима с главным прижимным роликом с пневматическим приводом и тремя дожимными роликами без привода.
Центрально регулируемый механизм верхнего, и центральная автоматическая смазка цепного транспортера. Пульт управления на входе в станок. Система управления BRANDT с цветной графической оболочкой обслуживания, для простого и удобного программирования и обслуживания.
Технические особенности:
- поворотный пульт на входе в станок;
- пленочная клавиатура с повышенным сроком службы
- плоский экран с цветной графикой
- промышленный персональный компьютер с компактным флеш - диском в качестве запоминающего устройства
- функциональные кнопки для агрегатов со светодиодными индикаторами состояния
- поддержка руководства для оператора с цветной пиктограммой
- переключение в режиме online для использования различных иностранных языков
- индикация важнейших истинных и заданных состояний станка
- указание статуса в прямом тексте
- простой выбор и изменение путевых точек
- возможность простого перемещения по осям (при наличии соответствующей агрегатной оснастки)
- помощь в режиме online в прямом тексте посредствам вызываемого в любой момент окна
- анализ производственных данных для учета рабочего времени, длины кромки и количества заготовок в виде ежедневных и общих значений
- индикация временных интервалов проведения обслуживания и инспекций
- возможность сохранения программ обработки
- возможность сохранения программ обработки на дискету.
Электрическое оснащение модульной системой управления для упрощения сервиса.
Модем для дистанционной диагностики станка через открытую телефонную сеть. При этом к станку должна быть подведена телефонная линия (обеспечивается заказчиком). По истечении гарантийного срока дистанционная диагностика осуществляется по отдельному контракту.
Допустимая температура окружающей среды: мин. 5 / макс. 35 градусов Цельсия. При колебаниях напряжения в сети более чем на /- 10 % на месте эксплуатации необходима установка стабилизатора напряжения.
На рисунках 1 и 2 показаны трехмерное изображение станка и его основных узлов.
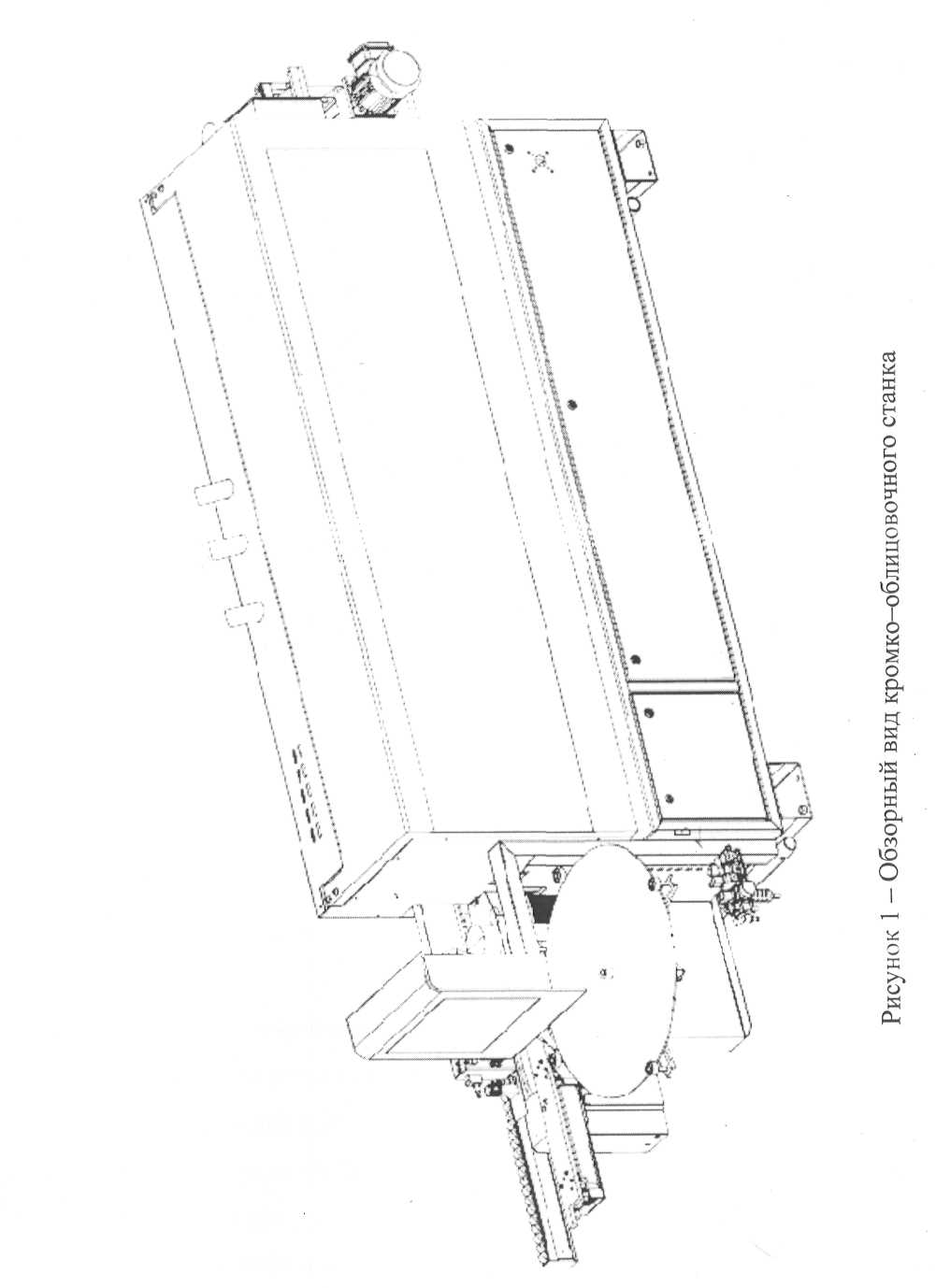
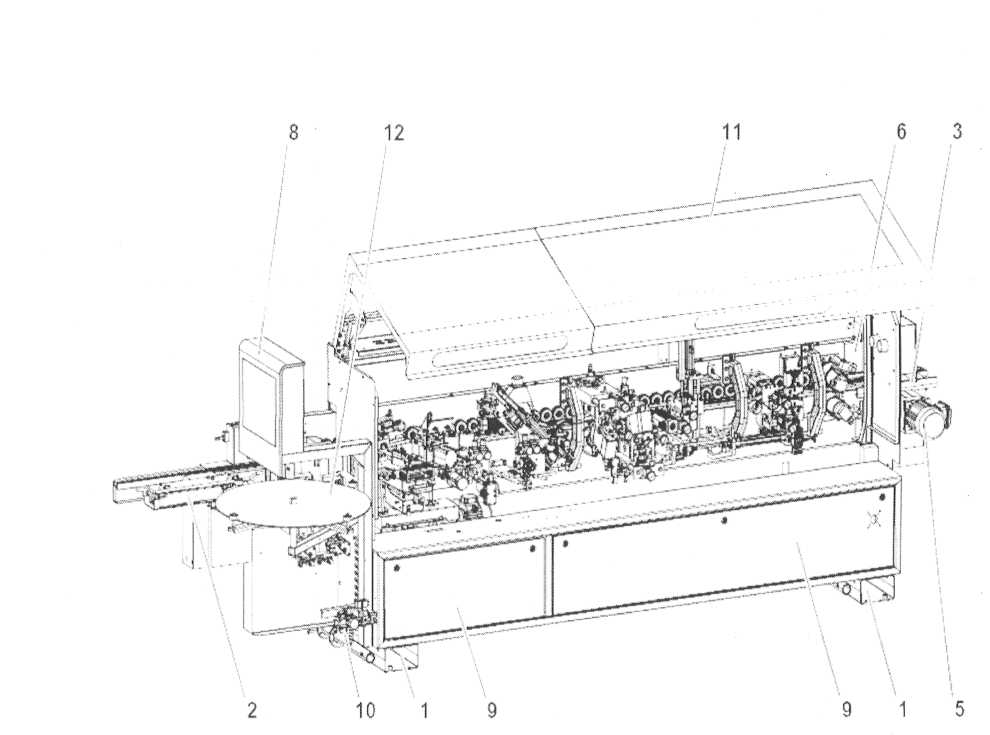
Рисунок 2 - Основные узлы станка
- Держатель
- Входная линейка
- Выходная линейка
- Цепной транспортер с транспортировочной цепью
- Привод
- Верхнее прижимное устройство
- Основа для заготовок
- Пульт управления
- Шкаф электроприборов
- Пневматика
- Звукоизоляционный кожух
- Тарелка для рулона
Основной проблемой, которая была обозначена на предприятии, при обработке изделий из ДСП является подача материала.
2 Технологическая часть
Совершенствование раскроя на отрезном оборудовании заключается в минимизации отходов материала, при разрезке на заготовки деталей мебели. Базовый представитель мебели — стол офисный.
2.1 Применение линейного программирования
Оптимизация раскроя одномерного материала сводится к решению задачи линейного программирования (ЛП). Исходные данные: значения L и некоторого перечня длин [1], а также требуемое число (партии) [N] заготовок.
Рассмотрим конкретный пример раскроя листов на полосы: L= 1000мм, [1]=380,290,180мм. Требуемое число заготовок соответственно: [N] = 15, 10, 20 шт.
Оценочная функция – число листов, расходуемое на выполнение всего заказа [2]. На рисунке 3 показан пример группового раскроя листа.
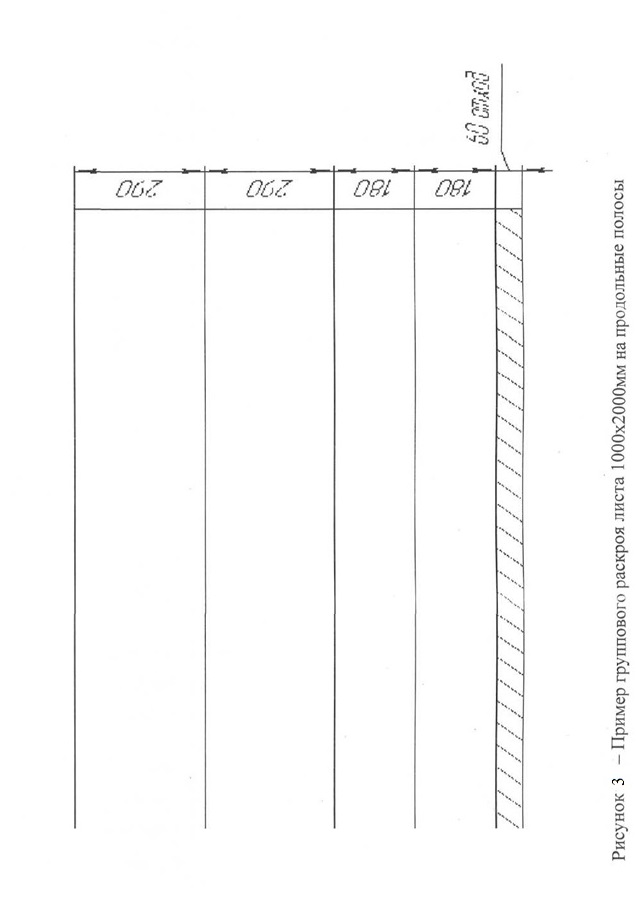
Различные планы разрезки одного листа (таблица 2) составлены в результате полного рассмотрения вариантов по принципу убывания числа заготовок в одном плане, начиная с более длинных. Данный приоритет сохраняется при доукомплектовании плана заготовками меньшей длины, пока отход не оказывается меньше lmin, в данном примере это 13 = 180 мм.
Таблица 2 – Варианты раскроя листа по размеру 1000 мм на полосы шириной l1, l2, l3
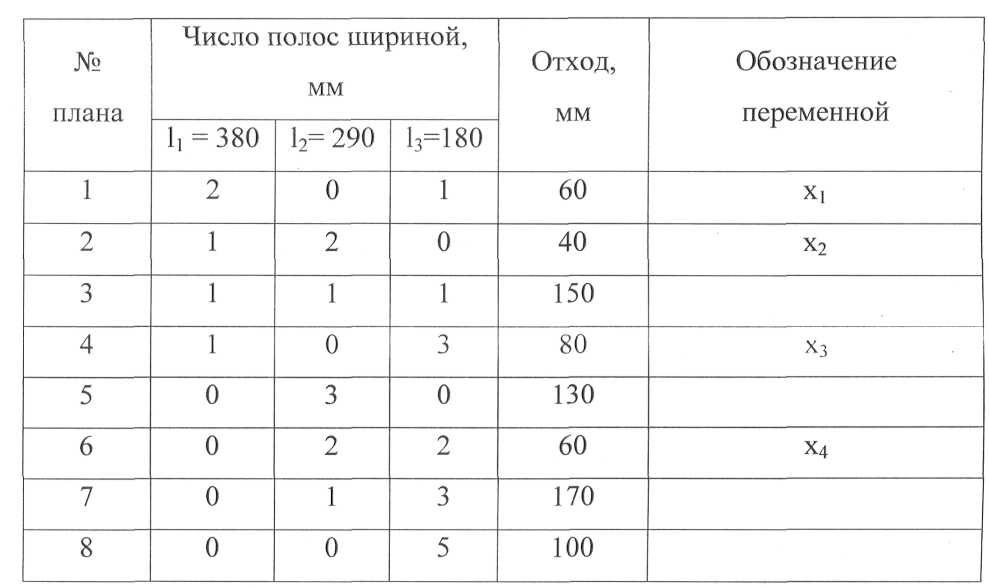
Размер отхода в соответствующей графе таблицы 3 рассчитан без учета припуска на разрезку, поскольку операция выполняется на ножницах. Например, согласно плану 6 (см. рисунок 3), размер отхода 60 = L- 2/2-2/3.
Планы 5, 8 относятся к примитивным, они содержат заготовки одной длины соответственно 11, 12 и сравнительно просты в реализации, но в данном примере неэкономичны по причине большого отхода. Исключим их при постановке задачи ЛП, равно как и заведомо неприемлемые по тому же показателю отходов комбинированные планы 3, 7. Остальным поставлены в
соответствие переменные (см. таблицы 2). Каждая переменная х, обозначает число листов, для разрезки которых будет применен соответствующий план.
Необходимо найти значения переменных, обеспечивающие минимум оценочной функции:
Z=x1+x2+x3+x4; (1)
То есть общего числа израсходованных листов. Система уравнений ограничений учитывает требуемые числа заготовок [N]:
2x1+x2+x3=15;
2x2+2x4 =10; (2)
x1+3x2+2x4=20;
Коэффициентами при неизвестных являются числа заготовок в соответствующих столбцах таблицы 2. Например, первое уравнение (1) ограничивает число заготовок длиной l1= 380 (15 шт.). Коэффициенты содержатся в планах, которым соответствуют переменные х1, х2, х3. Первый план содержит две таких заготовки, остальные — по одной. Эти числа и являются коэффициентами в выражении 2x1+ x2+ х3 (см. (2)). Значения х1, х2, х3 должны быть такими, чтобы данная сумма равнялась 15. Аналогично составлены и другие ограничения. Уравнения (1), (2) линейны (отсюда и термин — линейное программирование), в зависимости от общего числа переменных n они описывают прямые (n = 2), плоскости (n = 3) или гиперплоскости (n > 3). Система ограничений (2) определяет границы так называемой области допустимых решений (ОДР): многоугольника, многогранника или гипермногогранника в n-мерном пространстве. Минимум оценочной функции можно найти простым перебором вариантов решения, поочередно подставляя координаты вершин ОДР, т.е. соответствующие значения переменных в уравнение оценочной функции. Существуют методы, ускоряющие решение задачи. Применим один из них — так называемый симплекс-метод Дж. Данцига, используя преобразование таблиц с разрешающим элементом. Преобразование начинают с таблицы 3, приведенной ниже, которая содержит уравнения (1), записанные в виде
0=2x1+x2+x3-15;
0=2x2+2x4 -10; (3)
0=x1+3x2+2x4-20.
Таблица 3 - Матричное преобразование линейных уравнений
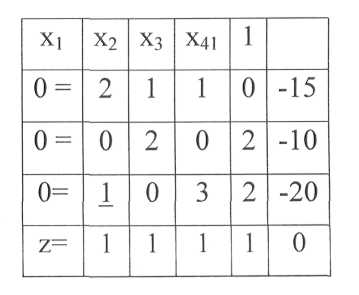
Подчеркнутый элемент выбран в качестве разрешающего, его роль сформулирована ниже. Выбор разрешающего элемента на данном этапе преобразований определяется необходимостью избавиться от отрицательных чисел в правом столбце. Для этого находим минимальное отношение элементов, которые принадлежат одной строке и содержат в качестве числителя отрицательное число правого столбца. В данном случае таковым является отношение —20/1, оно меньше других подобных, например —10/2. Знаменатель найденного отношения становится разрешающим элементом (подчеркнут в таблице 5); содержащие его строка и столбец также называются разрешающими. Разрешающий элемент должен быть отличным от нуля. Алгоритм преобразования таблиц представим состоящим из трех этапов. На первом этапе заготавливают форму новой таблицы, у которой, по сравнению предыдущей, меняют местами символы, находящиеся вверху разрешающего столбца и слева от разрешающей строки. В данном случае это приведет к перемещению символа х1. из столбца в строку, а также к замене 0-строки на 0-столбец. Последний не будет включен в новую таблицу, как не имеющий значения, поскольку все его числа становятся коэффициентами при нуле.
На втором этапе разрешающий столбец остается без изменений, числа разрешающей строки, кроме разрешающего элемента, записывают в новую таблицу с обратными знаками. Остальные элементы таблицы (разумеется, кроме левого столбца и верхней строки, где располагаются переменные) пересчитывают по правилу прямоугольника и затем переносят в новую таблицу. Проиллюстрируем это правило с помощью представления фрагмента преобразуемой таблицы в общем виде (см. таблица 4).
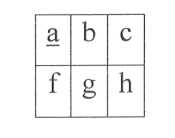
Таблица 4 - Правило прямоугольника
Формулы новых значений пересчитываемых элементов:
g = ag-bf , h = ah-cf. (4)
Правая часть формулы содержит произведения чисел, расположенных на концах диагоналей воображаемого прямоугольника. Произведение разрешающего и пересчитываемого элементов записано первым. На третьем этапе алгоритма элементы заполняемой таблицы делятся на разрешающий элемент, а сам он заменяется обратной величиной и в таком виде входит в новую таблицу. В итоге новые значения чисел преобразуемой таблицы оказываются следующими:
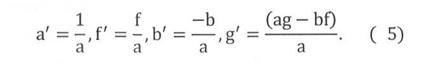
Изложенные правила относятся к общему случаю преобразования таблиц, когда их размерность остается неизменной. В случае замены 0-строки на 0-столбец последний не подлежит переносу в новую таблицу, а попросту аннулируется. Также оказывается излишним третий этап алгоритма, если разрешающий элемент таблицы равен единице. После преобразования таблица 3 приобретает иной вид (таблица 5).
Таблица 5 — Преобразование таблицы 3

Разрешающий элемент таблицы 3 определен по тому же принципу, что и предыдущий. На эту роль имеются два равноценных претендента в столбцах х2 и х4. После преобразования таблицы 3 в таблицу 4 еще одна 0-строка заменяется 0-столбцом, изымаемым из обращения.
Таблица 6 — Преобразование таблицы 5
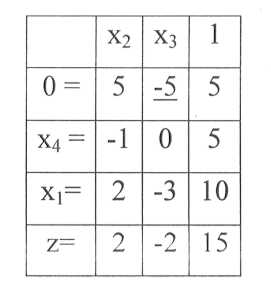
Отсутствие отрицательных чисел в правом столбце является признаком выхода на условно допустимое решение задачи. Приравнивают к нулю переменные, расположенные в верхней строке (х2= О, х3 = 0), и получают: х1 = 10, х4 = 5, т. е. 10 листов подлежат разрезке по плану 1 и пять листов по плану 6 (см. таблица 2). Перечисленные листы содержат 20 длинных, 10 средних и 20 коротких заготовок, что превышает заказанную партию (15, 10, 20) на пять длинных заготовок. На это указывает и формальный признак – наличие хотя бы одного отрицательного числа в Z-строке. В столбцах, содержащих такие числа, должны быть и другие отрицательные элементы. Каждый из них рассматривают в качестве знаменателя отношения, числитель которого — крайний правый элемент той же строки. В данном примере имеем два подобных отношения: 5/-5, 10/-3. Разрешающим элементом должен быть знаменатель наибольшего из этих отношений (подчеркнут в таблица 6). Результат очередного преобразования, имеющего целью избавиться от отрицательных чисел в Z-строке, представлен в таблице 7.
Таблица 7 - Преобразование таблицы 8

Полученная таблица содержит искомое решение задачи, на что указывает отсутствие отрицательных чисел в Z-строке и правом столбце. Присваиваем нулевые значения переменным, оставшимся в верхней строке (в данном случае х2), остальные переменные равны соответствующим числам правого столбца: х1= 7, х3 = 1, х4 = 5. Искомый минимум целевой функции Z= 13 также присутствует в таблице. Для проверки полученного решения обратимся к таблица 2. По плану 1 будет раскроено семь листов (х1 = 7), это дает 14 полос длиной l1= 380 мм и семь полос длиной 13 = 180 мм. План 2 не нашел применения, хотя и характеризуется наименьшим отходом. По плану 4 (х3= 1) получаем недостающую полосу длиной l1 = 380 мм и 3 полосы длиной 13 = 180 мм; по плану 6 (х4=5) соответственно по 10 полос длиной 12= 290 мм и 13 = 180 мм. Рассмотренный пример довольно прост, и найденное решение (xi = 7, х3 = 1, х4 = 5.) не является единственным. Такое же значение Zmin = 13 можно получить при другом плане раскроя, применив так называемый метод проб и ошибок. Здравый смысл подсказывает, что для получения 10 полос длиной 12 = 290 мм целесообразно раскроить пять листов по плану 2 с минимальным отходом. Тогда для доукомплектования партии полос длиной li= 380 мм необходимо раскроить пять листов по плану 1, а недостающие 15 полос длиной 13 — 180 мм можно получить по плану 8. Однако в реальных ситуациях, когда номенклатура заготовок исчисляется десятками или сотнями, более эффективно применение математических методов. По сравнению с планами, которые можно назвать рациональными, достигается экономия порядка нескольких процентов расхода металла. В абсолютном выражении она может выразиться в тоннах и более.
Из восьми возможных планов раскроя (см. табл. 4) в уравнениях задачи ЛП фигурировали четыре, выбранных с учетом величины отхода, а также требуемого числа заготовок ([N] = 15, 10, 20). Эти числа согласуются с соотношениями чисел различных заготовок, содержащихся в выбранных планах раскроя. При других исходных данных размерность задачи (число неизвестных) может быть увеличена. Например, при [N] = 15, 10, 100 нельзя обойтись без плана 8, так как любой другой план не обеспечит требуемого отношения числа коротких заготовок к длинным и средним. На основе рассмотренного симплекс-метода созданы компьютерные программы, однако размерность задач, решаемых в условиях многономенклатурного производства, может быть настолько большой, что строгие подходы к оптимизации раскроя трудно реализовать даже с помощью ЭВМ. В таких случаях применяют эвристические методы и алгоритмы, они обеспечивают проектирование планов, по крайней мере, близких к оптимальным, за
приемлемое время. Сказанное относится прежде всего к задачам, постановка которых усложнена дополнительными условиями. Чаще всего это условие Lmax > L > Lmin означает возможность выбора размера исходного материала из некоторого множества значений. Например, листы их холоднокатаной стали в зависимости от толщины имеют ширину 500...2300 мм и длину 1000...6000 мм. Всего стандартом предусмотрено более 300 типоразмеров. Для конкретной толщины число типоразмеров намного меньше, тем не менее варьирование хотя бы несколькими значениями L существенно расширяет область поиска оптимального решения. Также возможны предпосылки для варьирования размерами заготовок. Если имеется в виду ширина полос, отрезаемых от листа и используемых в дальнейшем для вырубки деталей в штампе, то размер li, во многих случаях зависит от технологического процесса изготовления указанных деталей, параметры которого могут быть изменены с целью экономичного раскроя листов. В работе дана постановка задачи раскроя плетей, состоящих из труб, сваренных встык. Речь идет о производстве теплообменников большой длины (порядка нескольких десятков метров). Расположение сварных стыков теплообменника регламентируется в довольно широких пределах. Важно только, чтобы они находились на достаточном удалении от изогнутых участков. Приведен пример решения подобной задачи на одном из котельных заводов. Трубы длиной 9191 мм, поставляемые металлургической промышленностью по специальному заказу, сваривают в непрерывную плеть, а затем отрезают от нее заготовки секций змеевика. Длина комплекта заготовок составляет величину того же порядка, что и длина исходной трубы; расположенные на заготовках сварные швы плети не должны оказаться в зоне последующей гибки. Варьируя очередностью отрезки заготовок различных секций, удается выдержать все ограничения и исключить отходы труб, не считая стружки, образующейся в процессе резки. Наиболее сложной является оптимизация раскроя рулонного материала на ленты, широко используемые в листоштамповочном производстве. Кроме размеров L и [1] (в данном случае
это значения ширины рулона и лент) необходимо учитывать различную длину последних. Она зависит от потребных значений длины различных лент, которые могут составлять от нескольких десятков до нескольких сотен метров в расчете на месячную программу выпуска продукции. Чтобы свести задачу к одномерной, назначают некоторую единичную длину лент, приемлемую в техническом отношении, например 10 м. Число [N] лент, соответствующее перечню их ширины [1], подсчитывают, разделив требуемые длины на единичную и округлив результаты. Получают исходные данные для решения задачи одномерного раскроя, однако из-за округленных [N] после раскроя образуется избыток одних лент и возможен недостаток других. Поэтому проектирование раскроя рулона для следующей программы выпуска той же продукции выполняют заново, откорректировав значения потребной длины лент. Листы и длинномерный прокат разрезают последовательно, отделяя с помощью ножниц, пильных и других станков заготовки одну за другой. В отличие от них рулоны разрезают на ленты одновременно по всей ширине, на которой располагают набор дисковых ножей. Расстояния между соседними парами ножей соответствуют значениям ширины лент, отрезаемых в соответствии с реализуемым планом раскроя. Смена плана требует трудоемкой переустановки дисковых ножей. Вместо постоянной корректировки планов раскроя рулонов на ленты возможно использование избытка одной ленты для покрытия дефицита другой при условии, что ширина первой 1; ненамного больше, чем ширина второй lj. В результате такой замены образуется дополнительный отход материала, площадь которого равна произведению разности lj—lj на длину покрываемого дефицита j-й ленты. Минимизация отходов такого рода на заданном множестве лент также сводится к решению задачи ЛП.
2.2 Решение систем уравнений
Автоматизированные рабочие места технологов целесообразно оснащать специальными компьютерными программами проектирования оптимального раскроя, в том числе одномерного. Относительно простые задачи можно решать универсальными средствами, включая ручной счет, как это было сделано выше и предстоит сделать в примере со следующими исходными данными: L= 1000 мм, [1] = 370, 300, 230 мм.
В таблице 10 представлены все возможные планы раскроя листа по размеру 1000 мм на полосы шириной 1Ь 12, Ь-
Таблица 10 - Планы раскроя листа заданного размера
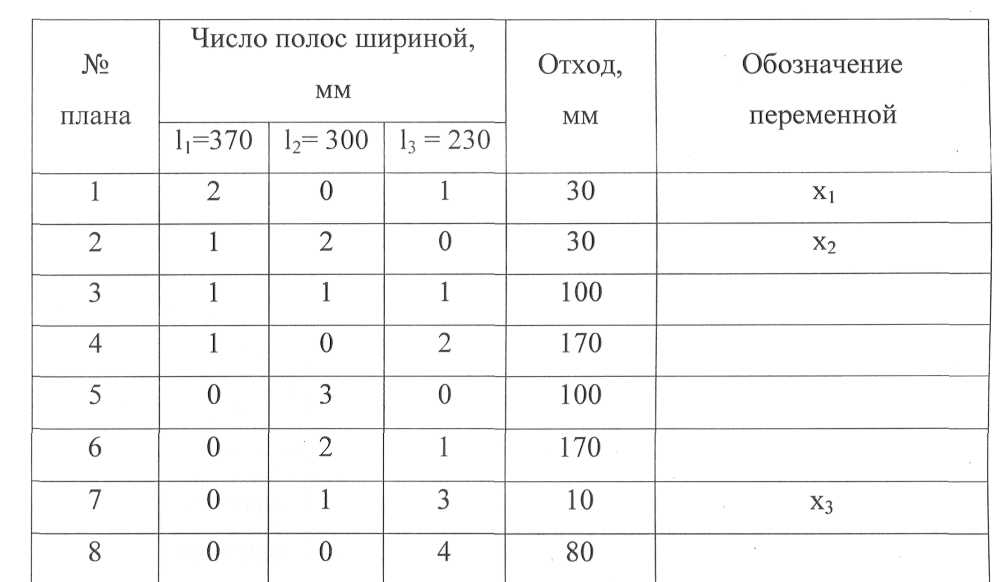
Ограничим число переменных задачи тремя, получив таким образом замкнутую систему уравнений ограничений, число которых равно числу переменных; необходимые числа заготовок записаны символами Ni(lj = 370мм), N2(l2= 300 мм), N3(l3 = 230 мм):
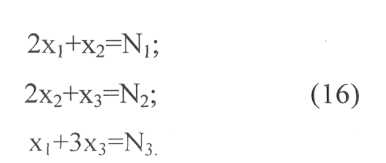
Сокращая до минимума (в данном случае до трех) число переменных, исходили из того, что три соответствующих плана существенно экономичнее остальных (см. табл. 10). Однако такой подход не всегда является оправданным, как это будет показано в конце данного параграфа. Система (16) при заданных значениях Nb N2, N3 имеет единственное решение. Запишем его в общем виде с учетом того, что значения переменных не могут быть отрицательными:
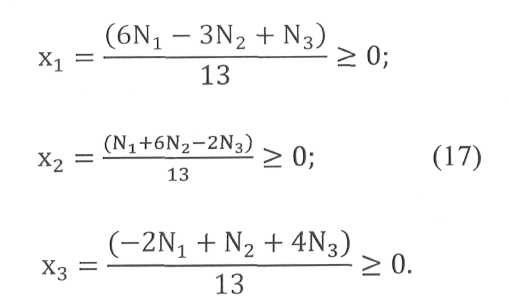
Область допустимых решений системы вида (17) ограничена в пространстве координат Nb N2, N3. Иначе говоря, соотношения между Nb N2, N3 не могут быть абсолютно произвольными. Например, при N^ N: из второго и третьего уравнений системы (16) следует: 3,5Nj >N3 > 0,25Nb. Область допустимых значений Nb N2, N3 для данного примера можно представить геометрически (рис. 2). Она ограничена тремя плоскостями, образующими бесконечную трехгранную призму с вершиной в начале координат и ребрами, расположенными в координатных плоскостях.
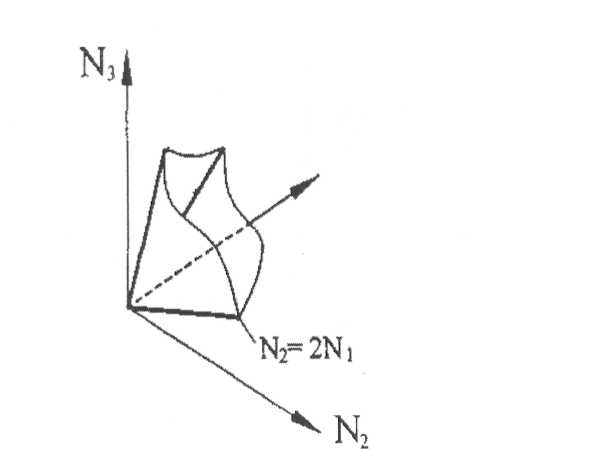
Рисунок 11- Область допустимых решений системы неравенств (17)
Уравнения ребер (рис. 11) получены из соотношений числа различных заготовок в планах раскроя (см. табл. 10). Если принять N]= 0, то окажется, что из трех переменных отлична от нуля только х3, поскольку соответствующий ей план не содержит широких заготовок. Соотношение числа других заготовок в этом плане 3:1, следовательно, в координатной плоскости N]= 0 уравнение ребра ОДР: N3= 3N2. Аналогично получаем уравнения ребер: N1= 2 N2 при N2 = 0 и N2 = 2N|, при N3 = 0.
Если в результате решения системы уравнений, подобной (16), хотя бы одна переменная окажется отрицательной, значит, заданные значения Nb N2, N3.находятся за пределами ОДР системы неравенств (17). В таком случае необходимо увеличить число переменных добавлением других возможных планов раскроя листа к отобранным ранее. Например, в систему уравнений (16) при N1= N2 и N3= 4N1 cледует добавить переменную х4, поставив ее в соответствие плану 8:
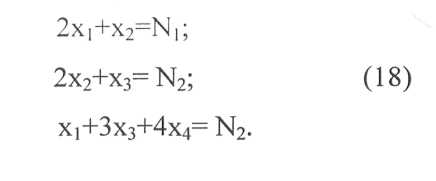
Детерминированное решение становится невозможным, поэтому вводим оценочную функцию и получаем рассмотренную ранее задачу ЛП.
2.3 Получение целочисленных решений
Одна из проблем оптимизации раскроя связана с получением нецелочисленных решений, что противоречит физическому смыслу переменных хi . Если округлять их произвольным образом до целых чисел, можно получить далеко не лучший план раскроя. Строгий метод исключения нецелочисленных значений xi предложенный Р. Гомори, предусматривает ввод дополнительных ограничений в систему уравнений (16) и постепенный выход на лучшее целочисленное решение. Компьютерные программы решения задач ЛП могут автоматически корректировать разрешающую систему уравнений. Соответствующий алгоритм разделяет исходную область допустимых решений на подобласти, исключая определенные части ОДР.
Например, при получении значения xi = 5,72 вводятся дополнительные ограничения: хi < 5 и xi > 6, после чего задача решается повторно. Последовательное применение подобных итераций позволяет избавиться от всех нецелочисленных значений переменных, однако полученные числа заготовок могут отличаться от заданных в большую сторону.
2.4 Графический метод
Задача с двумя переменными имеет наглядную геометрическую интерпретацию, проиллюстрируем ее простым примером:
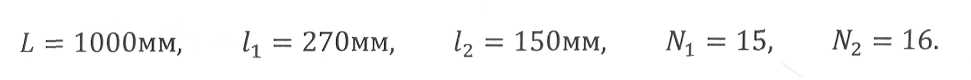
В таблице 11, представлены возможные варианты раскроя листа по размеру 1000 мм на полосы шириной 11, 12, из которых отбираем наиболее экономичные - планы 1, 2.
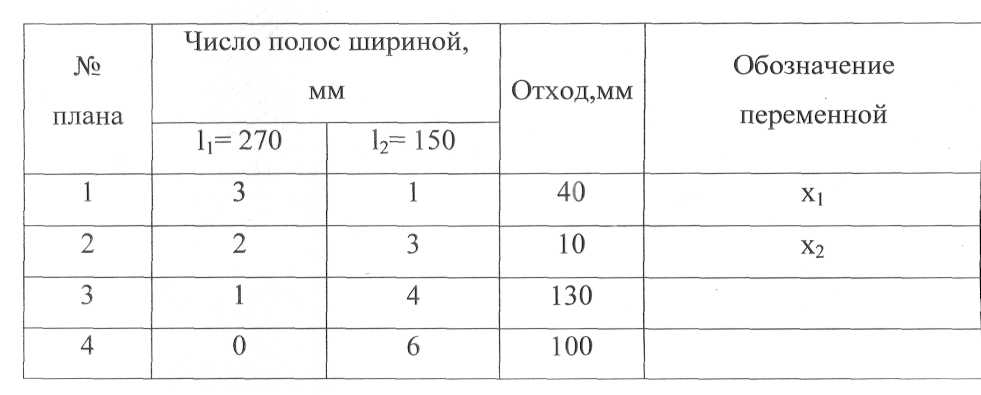
Таблица 11 - Возможные варианты раскроя листа заданного размера
Имея два уравнения
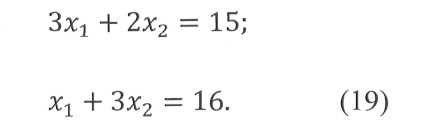
с двумя неизвестными, вычисляем: x1 = 1,86; х2= 4,71 (с точностью до сотых). Общее число раскраиваемых листов Z = x1 + х2 = 6,57. Найденные значения x1 и х2 с практической точки зрения абсурдны. Так, из 1,86 листа, разрезанного по плану 1, получается 5,64 широкой полосы (1= 270 мм) и 1,86 узкой, недостающие 9,36 широкой полосы и 14,14 узкой содержатся в 4,71 листа, разрезанного по плану 2. В ряде случаев подобные решения можно откорректировать, не меняя их по существу. В данном примере принимают x1= 2; х2 = 4, получая из этих шести листов 14 широких и 14 узких полос. Остальные две узкие и одну широкую полосы отрезают от седьмого листа, ширина остатка (430 мм) вполне допускает его дальнейшее использование.
Для иллюстрации метода Р. Гомори перейдем от ограничений, записанных в виде уравнений (19), к соответствующим неравенствам:
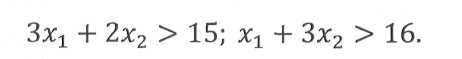

Рисунок 12 - Область допустимых решений:
а - при ограничениях (4); б - с дополнительными ограничениями (5);
в - с дополнительными ограничениями (6)
Им соответствует ОДР, заштрихованная на рисунке 12, а. Приведенному выше нецелочисленному решению задачи соответствуют координаты точки пересечения прямых (19). Исключим из ОДР эту точку и ее окрестности вводом дополнительных ограничений:

На рисунке 12, б заштрихована измененная ОДР, оптимальное решение может принадлежать любой из ее вершин. Одна имеет целочисленные координаты x1= 1; х2 = 6), координаты другой: x1= 2; х2 = 4,66. Исключаем из ОДР нецелочисленную координату х2 с помощью дополнительных ограничений по х2, аналогичных:

Координаты всех вершин полученной ОДР отвечают требованию целочисленности (см. рис. 12, в). В принципе, могло потребоваться более двух корректировок ОДР, однако число их всегда конечно независимо от числа переменных. Двум из трех вершин ОДР на рис. 12, в соответствуют минимальные целочисленные значения Z = x1+х2 = 7, но различные значения переменных соответствуют различным комплектам полос (N]= 15, N2 = 19) и (N1 = 16, N2 =17). Сравнивая эти решения, с полученным ранее нецелочисленным Z = 6,57, с округлением в меньшую сторону до 6, исходят из чисто практических предпочтений в пользу любого из них.
2.5 Применение метода преобразования таблиц
Для решения задачи с тремя переменными используем метод преобразования таблиц с разрешающим элементом, рассмотренный в п. 3.1, и данные таблицы 4, подготовленные для проектирования раскроя листов по размеру L= 1000 мм на полосы: [1] = 380, 290, 180 мм. Требуемые числа полос [N] =10, 12, 20 мм отличаются от приведенных в п. 3.1; соответственно откорректируем систему уравнений ограничений (2):
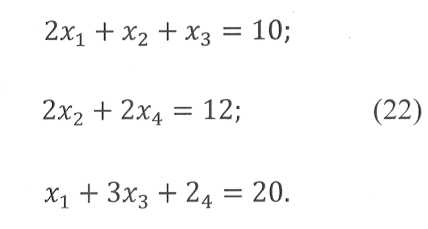
Оценочная функция — число листов, расходуемое на выполнение всего заказа, описывается уравнением (11). Занесем уравнения (22) и (11) в табл. 12, в табл. 12—14 показаны этапы преобразований и конечный результат.
Таблица 12 – Матричное преобразование линейных уравнений
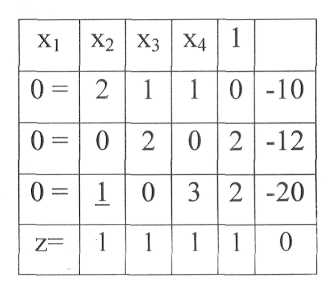
Таблица 13 -Преобразование таблицы 12
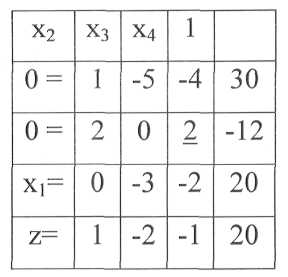
Таблица 14 - Преобразование таблицы 13
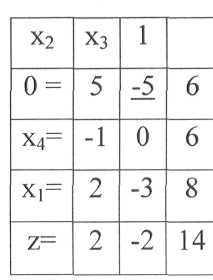
Таблица 14 - Преобразование таблицы 15

Исключим нецелочисленное значение х3 = 1,2 с помощью дополнительных ограничений:

Введем вспомогательные переменные y1> О, у2> О, у3> 0, у4>0, связав их с уравнениями (22) и дополнительным ограничением х3< 1:
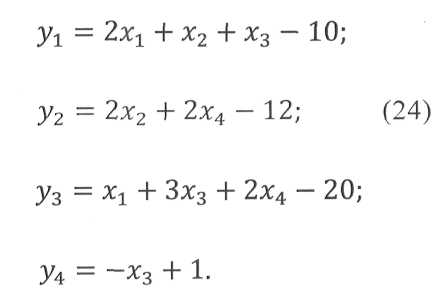
Нулевые значения у1 у2, у3 соответствуют заданным числам полос: 10, 12, 20; положительные — завышенным. Возможное завышение числа полос связано с переходом от нецелочисленного решения к целочисленному. Ниже приведены табл. 15, адекватная системе уравнений (24), и ее преобразования; разрешающие элементы подчеркнуты.
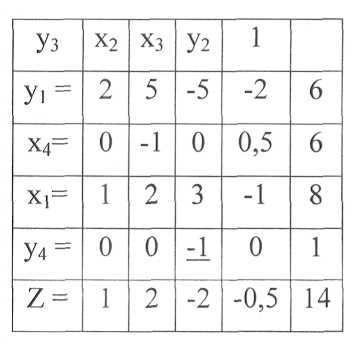
Разрешающие элементы таблиц 15, 16 выбраны в соответствии с правилом избавления от отрицательных чисел в правом столбце, что является признаком допустимого решения. Первое допустимое решение содержится в таблице15: у3=О, х2= 0, х3 =0, у2= 0, y1= 6, х4=6, x1=8, у4=1, Z = 14. Здесь, как и в п. 3.1, переменные верхней строки таблицы приравнены к нулю, при этом переменные левого столбца равны числам правого столбца. Согласно этим значениям переменных восемь листов раскраиваются по плану 1 и шесть – по плану 6. Планы приведены ранее в таблице 4 (им соответствуют
переменные x1 и х4). При х4 =6, х,= 8 получается шесть лишних заготовок длиной 380 мм, на что указывает значение у1= 6 (см. табл. 17).
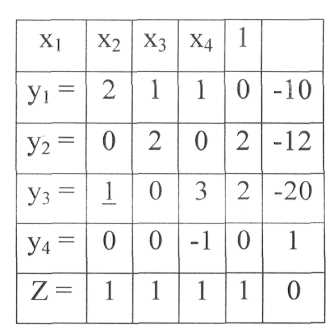
Таблица 16- Преобразование таблицы 15
Таблица 15 - Матричное преобразование линейных уравнений
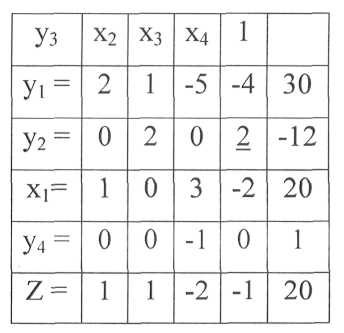
Таблица 17- Преобразование таблицы 16
3.6 Оптимизация раскроя листа древесно-стружечной плиты (ДСП)
В качестве раскраиваемого материала в данном случае будет выступать лист древесно-стружечной плиты (ДСП) размером 2770х2440мм. Пусть заготовка имеет длину L = 2770мм , и ширину 1 = 2440мм . При разрезке листа на заготовки одного размера возможны значительные отходы из-за некратности L по отношению к 1. Для сокращения отходов в условиях многономенклатурного производства применим групповой раскрой, при котором лист разрезают на заготовки различной длины из заданной номенклатуры. В нашем случае разделение материала происходит в направлении двух размеров листа и считается двумерным.
3.6.1 Применение линейного программирования
Оптимизация раскроя двумерного материала сводится к решению задачи линейного программирования (ЛП). Теоретическая задача по раскрою материала была рассмотрена в разделах 3.1 - 3.5, поэтому приступим к решению практической задачи, поставленной на предприятии. Исходные данные: значения L и / известны, а также требуемое число (партии) [N] столов.
Рассмотрим конкретный пример раскроя листов на комплектующие: крышка (S]= 1100х680мм2), ножка (S2= 710х560мм2), панель задняя (S3—970х80мм ). Требуемое число заготовок соответственно: [N] = 100, 200, 100 шт. Пропил материала составляет 4мм. Оценочная функция — число листов, расходуемое на выполнение всего заказа.
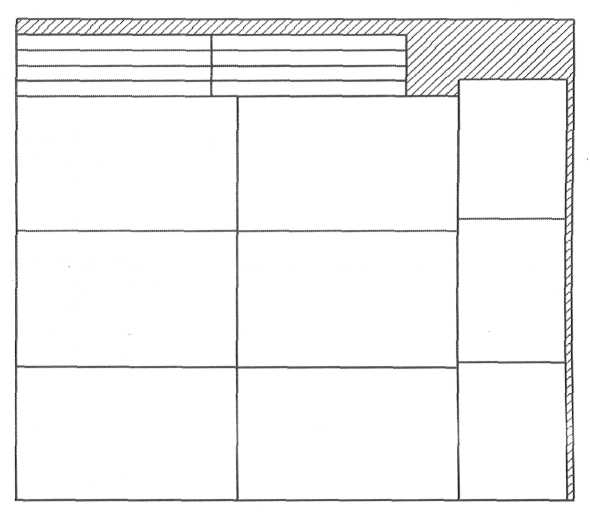
Рисунок 13 - План раскроя №1
Разместим заготовки таким образом, что их число, расположенное на листе будет рациональным (Sотхода=4998мм2). При размещении заготовок следует учитывать ширину пропила. Чем большее количество заготовок будет размещено на листе, тем больше будет ширина пропила. Из первого плана получаем, что: крышек - 6 штук, ножек - 3 штуки, панелей задних - 8 штук.
Рисунок 14 - План раскроя №2
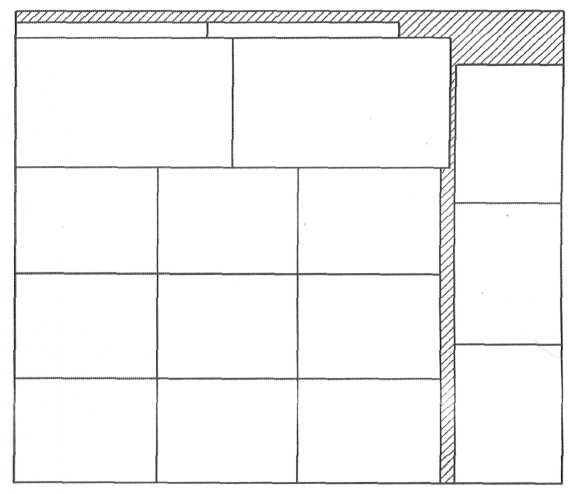
При втором варианте расположения заготовок (Sотхода=4220мм ). Количество крышек - 2 штук, ножек - 12 штуки, панелей задних - 2 штук.
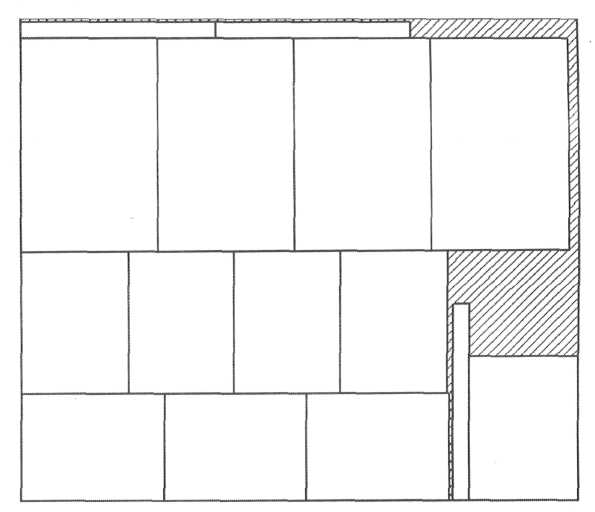
Рисунок 15 - План раскроя №3
В третьем варианте расположения заготовок (Sотхода=5165мм2 ). Количество крышек - 4 штук, ножек - 8 штуки, панелей задних - 3 штук. Дальнейшие варианты расположения комплектующих стола нас не устраивают, т.к. они не соответствуют рациональному расходу материала. План №4: крышек 2 шт., ножек 10 шт., панелей задних 4 шт. (Sотхода:=9816мм2). План №5: крышек - 3 шт., ножек - 9 шт., панелей задних -1 шт. (Sотхода =l 1428мм2). Ниже приведена таблица 18.
Таблица 18 - Варианты раскроя листа ДСП заданного размера
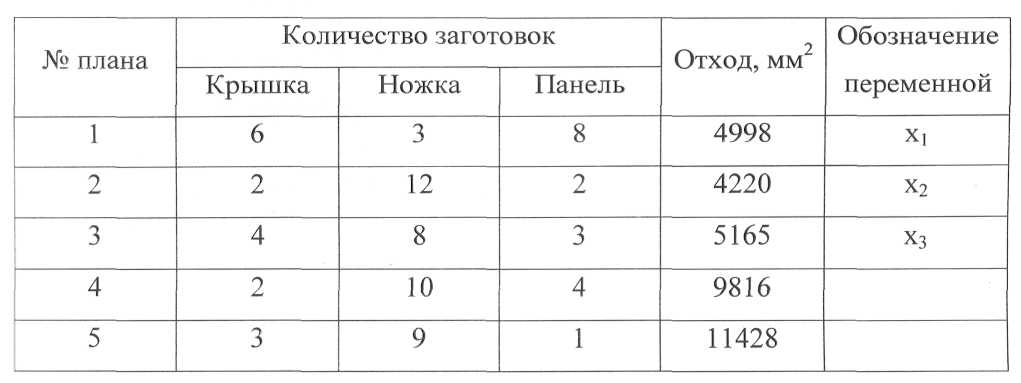
Найдем значения переменных, обеспечивающих минимум оценочной функции:
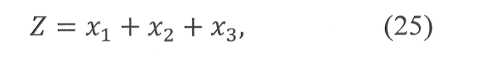
Т.е. из общего числа израсходованных листов. Система уравнений ограничений учитывает требуемые количества заготовок N:
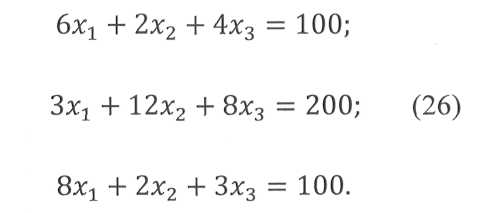
Коэффициентами при неизвестных являются числа заготовок в соответствующих столбцах таблицы. Уравнения (25), (26) линейны, в зависимости от общего числа переменных п они описывают прямые (п = 2), плоскости (n = 3) или гиперплоскости (n > 3). Система ограничений (2) определяет границы так называемой области допустимых решений (ОДР): многоугольника, многогранника или гипермногогранника в n-мерном пространстве. Минимум оценочной функции можно найти простым перебором вариантов решения, поочередно подставляя координаты вершин ОДР, т.е. соответствующие значения переменных в уравнение оценочной
функции. Существуют методы, ускоряющие решение задачи. Применим один из них - - симплекс-метод Дж. Данцига, используя преобразование таблиц с разрешающим элементом. Преобразование начинают с табл. 18, приведенной ниже, которая содержит уравнения (26), записанные в виде:
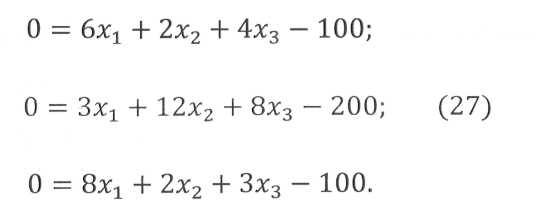
Уравнения (27) представлены в таблицу 18.
Таблица 18 - Матричное преобразование линейных уравнений
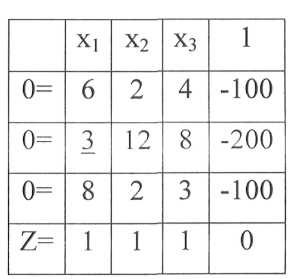
Подчеркнутый элемент выбран в качестве разрешающего, его роль сформулирована в п. 3.1 .На втором этапе разрешающий столбец остается без изменений, числа разрешающей строки, кроме разрешающего элемента, записывают в новую таблицу с обратными знаками. Остальные элементы таблицы (разумеется, кроме левого столбца и верхней строки, где располагаются переменные) пересчитывают по правилу прямоугольника и затем переносят в новую таблицу. Правило проиллюстрировано в п. 3.1 (см. табл. 6).
На следующем этапе алгоритма элементы заполняемой таблицы делятся на разрешающий элемент, а сам он заменяется обратной величиной и
в таком виде входит в новую таблицу В итоге новые значения чисел преобразуемой таблицы оказываются следующими:
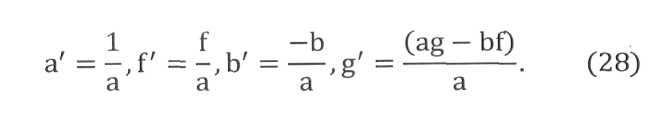
Изложенные правила относятся к общему случаю преобразования таблиц, когда их размерность остается неизменной. В случае замены 0-строки на 0-столбец последний не подлежит переносу в новую таблицу, а попросту аннулируется. Также оказывается излишним третий этап алгоритма, если разрешающий элемент таблицы равен единице. После преобразования таблица 18 приобретает иной вид (табл. 19).
Таблица 19 - Преобразование таблицы 18
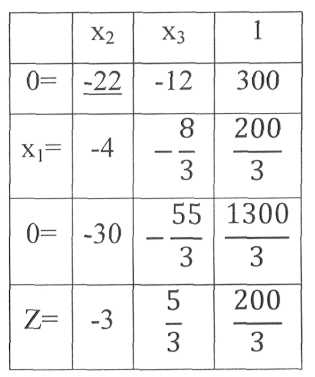
Пересчитываем таблицу 19. Выбираем разрешающий элемент, в данном случае им будет -22 (подчеркнут в таблице 19). С учетом разрешающего элемента необходимо избавиться от отрицательных значений в строке Z, число -3.
Таблица 20 -Преобразование таблицы 19

В получившейся таблице 20, нас интересуют следующие значения. Во-первых, в строке Z нет отрицательных чисел - это говорит о том, что первый этап мы пересчитали без ошибок и достигли поставленной цели (избавиться от отрицательных значений строки Z). Во-вторых, для самопроверки необходимо проверить, соблюдение первоначального условия поставленной задачи, а именно: Z=x1+x2+x3. Итак, делаем проверку:
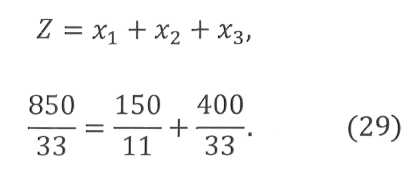
Тождество 29 выполняется, значит, решение верное. Однако, дробных значений, очевидно, быть не может (1,5 крышки или 1,2 ножки). Поэтому для избавления от дробных значений необходимо увеличить минимальную изначальную партию со 100 до 3300 столов.
Получаем,
x1 =400,х2 =450
Крышки: 6 * 400 + 2 * 450 = 3300 (шт.), Ножки: 3 * 400 + 12 * 450 = 6600(шт.);
Панели: 8 * 400 + 2 * 450 = 4100(шт.),
Имеем, задел панелей 4100 — 3300 = 800 (шт.).
Задел панелей в 800 штук, говорит нам о том, что в следующей партии необходимо будет сделать поправку. В таком случае получаем для второй партии:
Крышки: 6 * 400 + 2 * 450 = 3300 (шт.), Ножки: 3 * 400 + 12 * 450 = 6600(шт.), Панели: 4 * 400 + 2 * 450 = 2500(шт.). Необходимо будет уменьшить количество раскроя панелей в 2 раза.
3.6.2 Операции раскроя листов по выбранным планам
Для раскроя листа, на который был намечен план распила заготовок, оператору распиловочного станка необходимо знать, с какой операции начать выполнять распиливание, чтобы рационально отделить из заданного материала необходимые для сборки заготовки, при этом, не испортив, сам материал.
Использование в мебельном производстве различных типов древесно�стружечных плит вынуждает фирмы, занимающиеся изготовлением мебели, обзаводиться специальным оборудованием для распила (или раскройки) листов ДСП. Таким оборудованием является распиловочный станок для ДСП.
Основными составными частями распиловочного станка являются:
поперечный (горизонтальный) стол для установки плиты;
шариковая или роликовая каретка для перемещения плиты вдоль
пильного механизма;
пильный механизм, состоящий из одного или двух режущих узлов;
режущий узел, оснащенный основной и подрезной пилами.
Каждая деталь распиловочного станка имеет строго определенное предназначение. Пильный узел практически у всех модификаций станков имеет возможность изменения угла наклона до 45 градусов, что повышает качество резки. Основная пила глубоко раскраивает лист ДСП, а подрезная -точным движением дорезает нижний край, защищая от повреждений и сколов ламинированную или шпонированную поверхность плиты.
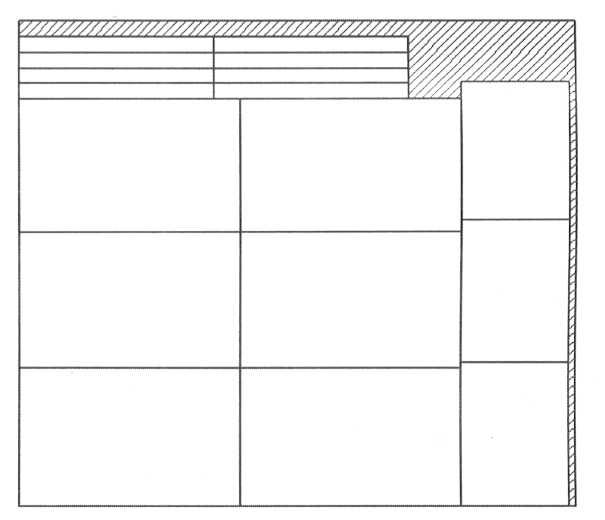
Рисунок 16 — Операции плана раскроя № 1
Обозначим операции для раскроя листа по плану № 1.
1) Отделение кромки листа. Первичная операция, которая необходима для определения границ распиливания на заготовки.
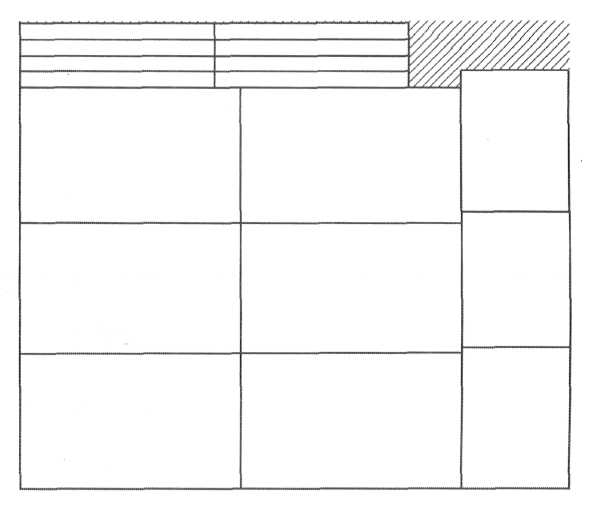
Рисунок 17 - Операции раскроя
2) Отделение ножек (Зшт.)

Рисунок 18 - Операции раскроя
3) Отделение крышек (6шт.)

Рисунок 19- Операции раскроя

4) Отделение оставшейся части отхода от панелей
Рисунок 20 — Операции раскроя
5) Распиливание на единичные образцы, массивных заготовок: крышек - 6шт., ножек - Зшт., панелей - 8шт.
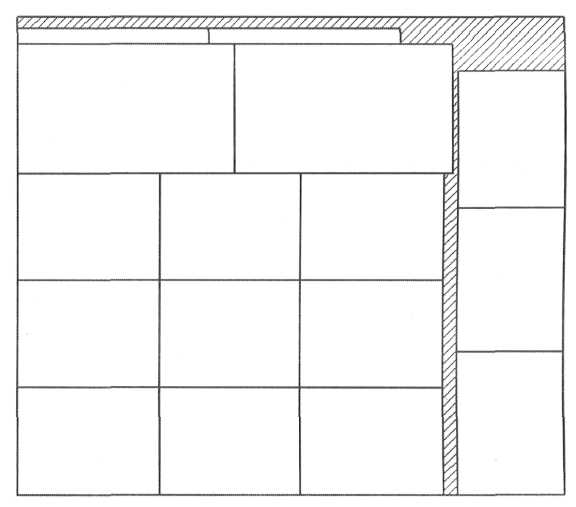
Рисунок 21 - Операции плана раскроя №2
Обозначим операции для раскроя листа по плану №2.
1) Отделение кромки листа
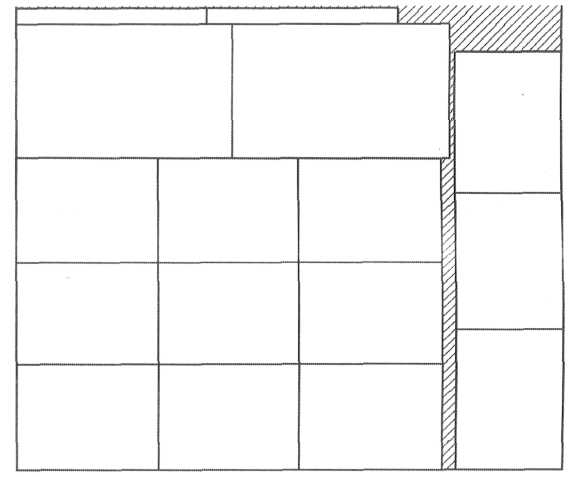
Рисунок 22 — Операции раскроя
2) Отделение ножек от основной площади листа, с последующей операцией отделения части отхода от основной площади ножек.

Рисунок 23 - Операции раскроя
3) Отделение панелей, с последующим отделением части отхода

Рисунок 24 - Операции раскроя

4) Отделение части крышек
Рисунок 25 - Операции раскроя
5) Отделение оставшейся части отхода от ножек

Рисунок 26 - Операции раскроя
6) Распиливание на единичные образцы, массивных заготовок: крышек - 2шт., ножек - 12шт., панелей - 2шт.
В данном разделе была решена задача по оптимизации раскроя листа ДСП заданных размеров. Проведены расчеты с применением симплекс метода Дж. Данцига. В ходе расчетов выяснилось, что третий избранный план раскроя можно не применять в производственном процессе. Описаны операции по раскрою массивного листа на заготовки указанных размеров.
Производство мебели не только существенно отличается от остальных производственных процессов но и оснащен.