Рассчт конструкции одноэтажного промышленного здания с мостовыми кранам
Содержание
1 Выбор несущих конструкций каркаса здания 5
1.1 Компоновка поперечной рамы 5
1.2 Устройство связей 8
2 Сбор нагрузок на раму 10
2.1 Постоянная нагрузка 10
2.1.1 Нагрузка от веса покрытия 10
2.1.2 Постоянные нагрузки от подкрановой балки 10
2.1.3 Постоянная нагрузка от веса продольной стены и остекления 11
2.1.4 Постоянная нагрузка от собственного веса колонны 11
2.2 Временная нагрузка 12
2.2.1 Снеговая нагрузка 12
2.2.2 Вертикальное давление кранов 12
2.2.3 Горизонтальное действие кранов 13
2.2.4 Ветровая нагрузка 13
3 Статический расчет рамы 14
3.1 Определение расчетных величин и коэффициентов 15
3.2 Усилия в колоннах рамы от постоянной нагрузки 16
3.3 Усилия в колоннах рамы от снеговой нагрузки 18
3.4 Усилия в колоннах рамы от ветровой нагрузки 21
3.4.1 Ветер слева 21
3.4.2 Ветер справа 24
3.5 Усилие в колоннах рамы от крановой нагрузки 26
3.5.1 Максимальный изгибающий момент на колонне ряда А, минимальный на колонне ряда Б 26
3.5.2 Максимальный изгибающий момент на колонне ряда Б, минимальный на колонне ряда А 30
3.5.3 Четыре крана с максимальным изгибающим моментом на колонне ряда Б 33
3.5.4 Горизонтальная сила приложена к колонне ряда А 36
3.5.5 Горизонтальная сила приложена к колонне ряда Б 38
3.6 Таблица нагрузок и расчетных усилий 40
4 Расчет колонны 43
4.1 Расчет надкрановой части 43
4.1.1 Комбинация нагрузок для надкрановой части колонны 43
4.1.2 Выбор материалов и определение расчетных характеристик 44
4.1.3 Расчет надкрановой части 45
4.2 Расчет подкрановой части 51
4.2.1 Комбинация нагрузок для подкрановой части колонны 51
4.2.2 Выбор материалов и определение расчетных характеристик 51
4.2.3 Расчет подкрановой части 52
4.3 Расчет промежуточной распорки 60
4.4 Расчет колонны в стадии транспортировки 62
4.5 Расчет по образованию трещин нормальных к продольной оси элемента в
процессе транспортировки 64
4.6 Расчет колонны в стадии монтажа 65
5 Расчет ребристой плиты покрытия 66
5.1 Сбор нагрузок на панель покрытия 67
5.2 Определение внутренних усилий в сечениях элементов от внешней нагрузки 68
5.3 Расчет полки панели на местный изгиб 69
5.4 Расчетная прочность по нормальному сечению в середине пролета 70
5.5 Расчет поперечного ребра 71
5.6 Расчет продольного ребра по нормальным сечениям 73
5.7 Определение геометрических характеристик приведенного сечения 74
5.8 Определение потерь предварительного напряжения в арматуре и усилия
предварительного обжатия 76
5.9 Расчет прочности продольного ребра по наклонным сечениям 77
5.10 Расчет по трещиностойкости 79
5.10.1 Расчет по образованию трещин, нормальных к продольной оси
элемента 79
5.10.2 Расчет по раскрытии трещин нормальных к продольной оси элемента 79
5.10.3 Расчет по образованию трещин, наклонных к продольной оси элемента 81
5.11 Расчет по деформациям при отсутствии трещин в растянутой зоне 82
6 Расчет панели в стадии изготовления, транспортировки и монтажа 84
6.1 Расчет панели на усилия, возникающие в стадии транспортировки и монтажа 84
6.2 Расчет панели на усилия, возникающие в стадии изготовления 85
Список литературы 87
Задание: Рассчитать конструкции одноэтажного промышленного здания с мостовыми кранами.
Данные:
- Пролет здания: первый - 24 м; второй - 24 м.
- Шаг рам - 6 м.
- Высота до низа несущей конструкции покрытия – 16,8 м.
- Грузоподъемность кранов: 15 т и 10 т.
- Место строительства - Новгород.
- Класс бетона колонн - В20.
- Класс арматуры колонн – А-300.
- Класс арматуры плиты перекрытия – А-600.
- Класс бетона фермы - В30.
1 Выбор несущих конструкций каркаса здания
1.1 Компоновка поперечной рамы
Плиты покрытия ребристые 2ПГ-5: L=5960мм, В=2980мм, Н=300мм, марка бетона 30, масса плиты 2,47 т.
Рисунок 1 - Плита перекрытия
Несущие конструкции покрытия - железобетонные фермы пролетом 24 м (т, бетон класса В40).
Рисунок 2 - Ферма пролетом 24 м
Стены навесные из керамзитобетона:
- ПС-60-18-30-6: L=5980мм, В=300мм, Н=1785мм, расход арматуры 48,5 кг, масса панели 4,8 т,
- ПС-60-12-30-6: L=5980мм, В=300мм, Н=1185мм, расход арматуры 35,1 кг, масса панели 3,2 т.
Рисунок 3 - Навесные стеновые панели из керамзитобетона
Подкрановая балка двутаврового сечения пролетом 6 м под краны грузоподъемностью до 30 т: L=5980мм, вf/=650мм, Н=1000мм, т=5400кг.
Рисунок 4 - Подкрановая балка
Мостовые краны грузоподъемностью 15т и 10т, среднего режима работы, с параметрами приведенными в таблице 1.
Таблица 1 - Основные параметры мостовых кранов (ГОСТ 6711-70)
|
Грузоподъемность, т |
Размеры, мм |
Максимальное давление колеса, kH |
Масса, т |
Тип кранового рельса |
Высота рельса, мм |
|||||
|
Главный крюк |
Вспомогательный крюк |
НК |
В1 |
В2 |
К |
тележки |
крана с тележкой |
|||
|
15 |
- |
2300 |
260 |
6300 |
4400 |
185 |
5,3 |
31 |
КР-70 |
120 |
|
10 |
- |
1900 |
260 |
6300 |
4400 |
145 |
4 |
27 |
КР-70 |
120 |
Колонны двухветвевые сквозного сечения:
Высота надкрановой части
,
где - высота крана;
- высота подкрановой балки;
- величина, которая дается на прогиб стропильной фермы для безопасного продвижения крана, мм;
Примем мм.
Высота подкрановой части до уровня пола
,
где - высота от нулевой отметки до низа несущей конструкции покрытия;
Глубина заделки колонны в стакане фундамента
,
Полная высота колонны:
Рисунок 5 – Колонны
Рисунок 6 - Схема поперечной рамы
1.2 Устройство связей
Рисунок 7 - Вертикальные связи
Рисунок 8 - Горизонтальные связи по нижнему поясу ферм.
1 - вертикальные связевые фермы; 2 - распорки по верху колонн; 3 - вертикальные связи по колоннам; 4 - ферма; 5 - подкрановая балка.
Система связей предназначена для обеспечения жесткости покрытия, восприятие тормозных усилий мостовых кранов, восприятие ветровых нагрузок действующих на торец здания. Система связей работает совместно с основными элементами каркаса и повышает пространственную жесткость здания.
Сопряжение между плитами покрытия и колоннами осуществляется через фермы, которые обладают малой жесткостью, значит необходимо устройство связей.
Вертикальные связевые фермы, установленные в крайних пролетах здания между колоннами, выполняются из стальных уголков и связываются распорками из стальных уголков по верху колонн. Решетка вертикальных связевых ферм проектируется как крестовая система.
Вертикальные связи между колоннами выполняются из стальных уголков и привариваются к стальным закладным деталям колонн.
Горизонтальные связи по нижнему поясу ферм выполняются из стальных уголков, образующих вместе с нижним поясом крайней фермы связевую ферму с крестовой решеткой.
В устройстве связей по верхнему поясу ферм нет необходимости, т.к. роль связей выполняют панели покрытия.
2 Сбор нагрузок на раму
2.1 Постоянная нагрузка
2.1.1 Нагрузка от веса покрытия
Таблица 2 - Нагрузка от веса покрытия
|
Наименование |
Нормативная нагрузка qf, kН/м2 |
Коэффициент надежности по нагрузке f |
Расчетная нагрузка q, kH/м2 |
|
Бикрост =0,008 м, =0,4 кН/м3 |
0,0032 |
1,2 |
0,0038 |
|
Цементно-песчаная стяжка =0,02 м, =20 кН/м3 |
0,4 |
1,3 |
0,52 |
|
Утеплитель пенополистирол =0,05 м, =10 кН/м3 |
0,5 |
1,2 |
0,6 |
|
Обмазочная пароизоляция битумом =0,002 м, =13 кН/м3 |
0,026 |
1,2 |
0,03 |
|
Плита перекрытия |
1,37 |
1,1 |
1,5 |
|
Стропильная ферма |
1,03 |
1,1 |
1,13 |
|
Связи покрытия |
0,05 |
1,05 |
0,0525 |
|
Итого: |
3,38 |
3,84 |
Погонная расчетная нагрузка от веса покрытия, передающаяся на колонну
,
,
Расчетное давление на колонну от веса покрытия
,
2.1.2 Постоянные нагрузки от подкрановой балки
,
2.1.3 Постоянная нагрузка от веса продольной стены и остекления
Рисунок 9 – Действие постоянных нагрузок от веса продольной стены и остекления
Нагрузка от веса стены и остекления прикладывается к колонне на отметках: +4,800; +10,200.
Нагрузка от стеновой панели: кН/м2.
Нагрузка от остекления: кН/м2.
Вес цокольной панели и нижнего остекления передается на фундаментную балку.
2.1.4 Постоянная нагрузка от собственного веса колонны
Объем бетона верхней и нижней части колонны
Вес верхней и нижней части колонны
,
,
2.2 Временная нагрузка
2.2.1 Снеговая нагрузка
Новгород находится в IV снеговом районе, в котором расчетная снеговая нагрузка составляет kН/м2.
Полное расчетное значение снеговой нагрузки на горизонтальную проекцию покрытия
Нормативное значение снеговой нагрузки
Давление на колонну от снеговой нагрузки
,
2.2.2 Вертикальное давление кранов
Рисунок 10 - Линии влияния опорных реакций подкрановой балки
Наибольшее нормативное значение вертикальной нагрузки
,
,
где кд – коэффициент динамичности учитывает режим работы крана;
nc – коэффициент сочетания;
Наибольшее расчетное давление на колонну
,
Наименьшее нормативное значение вертикальной нагрузки
,
Наименьшее расчетное давление на колонну
,
2.2.3 Горизонтальное действие кранов
Нормативное значение горизонтальной силы, передаваемой на поперечную раму
,
где f- коэффициент трения при торможении тележки;
nm/- число тормозных колес тележки;
nm- общее число колес тележки.
Расчетная сила поперечного торможения
,
2.2.4 Ветровая нагрузка
Нормативный скоростной напор ветра в данном районе (IV) для открытой местности: kПа.
Коэффициент, учитывающий изменение ветрового давления по высоте, тип местности В: , .
Тогда:
,
,
Аэродинамический коэффициент с наветренной стороны: , с заветренной :с3=-0,6.
Полная высота проектируемого цеха мм.
Полной высоте цеха соответствует напор:
,
Уровню низа стропильной фермы соответствует напор:
,
Для упрощения расчета определим среднее значение ординат в пределах высоты цеха: kН/м2; выше отметки +16,800: kН/м2.
Подставим ветровую нагрузку в виде двух составляющих:
1) равномерно распределенную по высоте колонны ;
2) сосредоточенная нагрузка на уровне пояса ригеля, заменяющая равномерно распределенную на вышерасположенных участках здания :
,
где - площадь участка покрытия:
- площадь участка стены:
С заветренной стороны
Рисунок 11 - Эпюры ветровой нагрузки
3 Статический расчет рамы
Расчетная схема рамы находится на рисунке 12.
Рисунок 12 - Расчетная схема рамы
3.1 Определение расчетных величин и коэффициентов
Моменты инерции для двухветвевой колонны крайнего ряда:
Реакция верха колонны крайнего ряда от единичного перемещения
Моменты инерции для двухветвевой колонны среднего ряда:
Реакция верха колонны от единичного перемещения
Суммарная реакция
3.2 Усилия в колоннах рамы от постоянной нагрузки
Рисунок 13 – К определению усилий в колонах от постоянной нагрузки
Нагрузка от веса покрытия GП действует на колонну с эксцентриситетом (рисунок 13)
Нагрузка от веса стеновой панели G1 действует на колонну с эксцентриситетом
Нагрузка от веса подкрановой балки GП.Б. действует на колонну с эксцентриситетом
Нагрузка от веса верхней части колонны GК.В. действует на колонну с эксцентриситетом
Момент, действующий в сечении 1 колонны
Момент, действующий в сечении 3 колонны
Реакция верхнего конца колонны ряда А на рисунке 14.
Рисунок 14 – Реакция верхнего конца колонны ряда А
Реакция колонны ряда В
Реакция колонны ряда Б
Т.к. колонна ряда Б загружена центрально, то ее реакция
.
Суммарная реакция верха колонны от заданной нагрузки в основной системе
Тогда горизонтальное перемещение верха колонны
.
Упругая реакция колонны ряда А
Изгибающие моменты в колонне ряда А
kHм,
Поперечные силы в колонне ряда А
kH.
Продольные силы в колонне ряда А
kH,
Эпюры изгибающих моментов, продольных и поперечных сил на рисунке 15
Рисунок 15 - Эпюры изгибающих моментов, продольных и поперечных сил
в колонне ряда А от постоянной нагрузки
3.3 Усилия в колоннах рамы от снеговой нагрузки
Рисунок 16 – К определению усилий в колонах от снеговой нагрузки
Нагрузка от снега FСН в сечении 1 передается на колонну аналогично постоянной нагрузке от покрытия с эксцентриситетом (рисунок 16):
м.
В сечении 3 в связи с изменением сечения колонны усилие FСН будет приложено с эксцентриситетом
Момент, действующий в сечении 1 колонны
Момент, действующий в сечении 3 колонны:
Реакция верхнего конца колонны ряда А на рисунке 17
Рисунок 17 – Реакция верхнего конца колонны ряда А
,
Реакция колонны ряда В
Реакция колонны ряда Б
Т.к. колонна ряда Б загружена центрально, то ее реакция
.
Суммарная реакция верха колонны от заданной нагрузки в основной системе:
.
Тогда горизонтальное перемещение верха колонны
.
Упругая реакция колонны ряда А
Изгибающие моменты в колонне ряда А
kHм,
Поперечные силы в колонне ряда А
kH.
Продольные силы в колонне ряда А
kH.
Эпюры изгибающих моментов, продольных и поперечных сил на рисунке 18.
Рисунок 18 - Суммарные эпюры от снеговой нагрузки
3.4 Усилия в колоннах рамы от ветровой нагрузки
3.4.1 Ветер слева
Рисунок 19 - Расчетная схема при расчете на ветровую нагрузку (ветер слева)
Реакция верхнего конца колонны ряда А (рисунок 20).
Рисунок 20 – Реакция верхнего конца колонны ряда А
Реакция верхнего конца колонны ряда Б (рисунок 21).
Рисунок 21 – Реакция верхнего конца колонны ряда Б
Реакция верхнего конца колонны ряда В (рисунок 22)
Рисунок 22 – Реакция верхнего конца колонны ряда В
С учетом реакции от сосредоточенной ветровой нагрузки, суммарная реакция связи в основной системе
Горизонтальное перемещение верха колонны
Упругая реакция колонны ряда А
Упругая реакция колонны ряда Б
Упругая реакция колонны ряда В
Изгибающие моменты в колонне ряда А
,
Поперечные силы в колонне ряда А
Продольные силы в колонне ряда А
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда А (рисунок23)
Рисунок 23 – Эпюры изгибающих моментов, продольных и поперечных сил
в колонне ряда А от ветровой нагрузки (ветер слева)
Изгибающие моменты в колонне ряда Б
,
Поперечные силы в колонне ряда Б
kH.
Продольные силы в колонне ряда Б
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда Б (рисунок 24)
Рисунок 24 - Эпюры изгибающих моментов, продольных и поперечных сил
в колонне ряда Б от ветровой нагрузки (ветер слева)
Изгибающие моменты в колонне ряда В
,
Поперечные силы в колонне ряда В
Продольные силы в колонне ряда В
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда В (рисунок 25)
Рисунок 25 - Эпюры изгибающих моментов, продольных и поперечных сил
в колонне ряда Б от ветровой нагрузки (ветер слева)
3.4.2 Ветер справа
Рисунок 26 - Расчетная схема при расчете на ветровую нагрузку (ветер справа)
Эпюры изгибающих моментов, продольных и поперечных сил аналогичны эпюрам ветровой нагрузки направленные слева но имеют противоположный знак.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда А (рисунок 27)
Рисунок 27 - Эпюры изгибающих моментов, продольных и поперечных сил
в колонне ряда А от ветровой нагрузки (ветер справа)
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда Б (рисунок 28)
Рисунок 28 - Эпюры изгибающих моментов, продольных и поперечных сил
в колонне ряда Б от ветровой нагрузки (ветер справа)
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда В (рисунок 29)
Рисунок 29 - Эпюры изгибающих моментов, продольных и поперечных сил
в колонне ряда В от ветровой нагрузки (ветер справа)
3.5 Усилие в колоннах рамы от крановой нагрузки
При расчете рамы на крановые нагрузки необходимо рассмотреть два вида загружения:
1. максимальный изгибающий момент на колонне одного ряда и минимальный на колонне другого ряда;
2. горизонтальная сила у колонны одного ряда.
3.5.1 Максимальный изгибающий момент на колонне ряда А, минимальный на колонне ряда Б
Рисунок 30 – К определению усилий в колонах от крановой нагрузки,
максимальный изгибающий момент на колонне ряда А
Сила Dmax приложена к колонне ряда А с эксцентриситетом
м.
Изгибающий момент в сечении 3
Сила Dmin приложена к колонне ряда Б с эксцентриситетом
м.
Изгибающий момент в сечении 3:
Реакция верхнего конца колонны ряда А, ряда Б, ряда В (рисунок 31).
Рисунок 31 – Реакция верхнего конца колонны ряда А, ряда Б, ряда В
.
Суммарная реакция в основной системе
Горизонтальное перемещение верха колонны:
Упругая реакция колонны ряда А, ряда Б, ряда В
Изгибающие моменты в колонне ряда А:
,
Поперечные силы в колонне ряда А:
kH.
Продольные силы в колонне ряда А:
,
kH.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда А (рисунок 32)
Рисунок 32 - Эпюры изгибающих моментов, продольных и поперечных сил в
колонне ряда А от крановой нагрузки с max моментом на колонне ряда А
Изгибающие моменты в колонне ряда Б:
,
Поперечные силы в колонне ряда Б:
kH.
Продольные силы в колонне ряда Б:
,
kH.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда Б (рисунок 33)
Рисунок 33 - Эпюры изгибающих моментов, продольных и поперечных сил в
колонне ряда Б от крановой нагрузки с max моментом на колонне ряда А
Изгибающие моменты в колонне ряда В:
,
Поперечные силы в колонне ряда В:
kH.
Продольные силы в колонне ряда В:
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда В (рисунок 34)
Рисунок 34 - Эпюры изгибающих моментов, продольных и поперечных сил в
колонне ряда В от крановой нагрузки с max моментом на колонне ряда А
3.5.2 Максимальный изгибающий момент на колонне ряда Б, минимальный на колонне ряда А
Рисунок 35 – К определению усилий в колонах от крановой нагрузки,
максимальный изгибающий момент на колонне ряда Б
Сила Dmin приложена к колонне ряда А с эксцентриситетом:
м.
Изгибающий момент в сечении 3
Сила Dmax приложена к колонне ряда Б с эксцентриситетом
м.
Изгибающий момент в сечении 3:
Реакция верхнего конца колонны ряда А, ряда Б, ряда В
.
Суммарная реакция в основной системе
Горизонтальное перемещение верха колонны
Упругая реакция колонны ряда А, ряда Б, ряда В
Изгибающие моменты в колонне ряда А:
,
Поперечные силы в колонне ряда А:
kH.
Продольные силы в колонне ряда А:
,
kH.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда А (рисунок 36)
Рисунок 36 - Эпюры изгибающих моментов, продольных и поперечных сил в
колонне ряда А от крановой нагрузки с max моментом на колонне ряда Б
Изгибающие моменты в колонне ряда Б:
,
Поперечные силы в колонне ряда Б:
kH.
Продольные силы в колонне ряда Б:
,
kH.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда Б (рисунок 37)
Рисунок 37 - Эпюры изгибающих моментов, продольных и поперечных сил в
колонне ряда Б от крановой нагрузки с max моментом на колонне ряда Б
Изгибающие моменты в колонне ряда В:
;
Поперечные силы в колонне ряда В:
kH.
Продольные силы в колонне ряда В:
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда В:
Рисунок 38 - Эпюры изгибающих моментов, продольных и поперечных сил в
колонне ряда В от крановой нагрузки с max моментом на колонне ряда Б
3.5.3 Четыре крана с максимальным изгибающим моментом на колонне ряда Б
Рисунок 39 - Расчетная схема при расчете на крановую нагрузку
от 4 кранов с максимальным изгибающим моментом на колонне ряда Б
Моменты в сечениях средней колонны будут равны 0, т.к. крановые нагрузки приложены симметрично. В крайних колоннах сила Dmin приложена с эксцентриситетом
м.
Изгибающий момент в сечении 3 колонн ряда А и В
kHм.
Реакция верхнего конца колонны ряда А
Реакция верхнего конца колонны ряда Б
.
Реакция верхнего конца колонны ряда В
kH.
Суммарная реакция в основной системе:
kH.
Горизонтальное перемещение верха колонны:
.
Упругая реакция колонны ряда А:
Упругая реакция колонны ряда Б:
.
Упругая реакция колонны ряда В:
kH.
Изгибающие моменты в колонне ряда А:
;
.
Поперечные силы в колонне ряда А:
kH.
Продольные силы в колонне ряда А:
kH.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда А (рисунок 40)
Рисунок 40 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда А от крановой нагрузки 4 кранов с максимальным изгибающим
моментом на колонне ряда Б
Изгибающие моменты в колонне ряда Б:
.
Поперечные силы в колонне ряда Б:
.
Продольные силы в колонне ряда Б:
,
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда Б (рисунок 41)
Рисунок 41 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда Б от крановой нагрузки 4 кранов с максимальным изгибающим
моментом на колонне ряда Б
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда В аналогично в колонне ряда А, но с противоположным знаком (рисунок 42).
Рисунок 42 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда В от крановой нагрузки 4 кранов с максимальным изгибающим
моментом на колонне ряда Б
3.5.4 Горизонтальная сила приложена к колонне ряда А
Рисунок 43 - Расчетная схема от горизонтальной крановой нагрузки,
приложенной к колонне ряда А
Горизонтальная сила торможения крана T приложена к колонне на высоте м от верха колонны (рисунок 43).
Реакция верхнего конца колонны ряда А:
Реакция верхнего конца колонны ряда Б:
Реакция верхнего конца колонны ряда В:
.
Суммарная реакция в основной системе:
kH.
Горизонтальное перемещение верха колонны:
Упругая реакция колонны ряда А, ряда Б, ряда В
Изгибающие моменты в колонне ряда А:
,
Поперечные силы в колонне ряда А:
kH;
Продольные силы в колонне ряда А:
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда А (рисунок 44)
Рисунок 44 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда А от действия горизонтальной крановой нагрузки, приложенной к колонне ряда А
Изгибающие моменты в колонне ряда Б:
,
.
Поперечные силы в колонне ряда Б:
kH.
Продольные силы в колонне ряда Б:
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда Б
Рисунок 45 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда Б от действия горизонтальной крановой нагрузки, приложенной к колонне ряда А
Изгибающие моменты в колонне ряда В:
,
Поперечные силы в колонне ряда В:
kH.
Продольные силы в колонне ряда В:
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда В (рисунок 46)
Рисунок 46 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда В от действия горизонтальной крановой нагрузки, приложенной к колонне ряда А
3.5.5 Горизонтальная сила приложена к колонне ряда Б
Рисунок 47 - Расчетная схема от горизонтальной крановой нагрузки,
приложенной к колонне ряда Б
Реакция верхнего конца колонны ряда А:
.
Реакция верхнего конца колонны ряда Б:
Реакция верхнего конца колонны ряда В:
Суммарная реакция в основной системе:
kH.
Горизонтальное перемещение верха колонны:
Упругая реакция колонны ряда А, ряда Б, ряда В
kH.
Изгибающие моменты в колонне ряда А и В:
,
Поперечные силы в колонне ряда А и В:
kH.
Продольные силы в колонне ряда А и В:
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда А и В (рисунок48)
Рисунок 48 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда А и В от действия горизонтальной крановой нагрузки,
приложенной к колонне ряда Б
Изгибающие моменты в колонне ряда Б:
,
Поперечные силы в колонне ряда Б:
kH;
Продольные силы в колонне ряда Б:
.
Эпюры изгибающих моментов, продольных и поперечных сил на колонне ряда Б (рисунок49)
Рисунок 49 - Эпюры изгибающих моментов, продольных, поперечных сил в колонне
ряда Б от действия горизонтальной крановой нагрузки, приложенной к колонне ряда Б
3.6 Таблица нагрузок и расчетных усилий
При составлении таблицы расчетных усилий в соответствии с [1] и нормами на проектирование железобетонных конструкций рассмотрим 2 группы основанных сочетаний нагрузок.
В первой группе основных сочетаний учитывают постоянную нагрузку, временную длительно действующую и 1 временную кратковременную, взятые с коэффициентом сочетания =1.
Во второй группе основных сочетаний учитывают постоянную нагрузку и все временные нагрузки (не менее 2) в их наиболее не выгодном сочетании, взятые с коэффициентом сочетания =0,9. При этом нагрузки от вертикального и горизонтального воздействия кранов рассматривается как одна кратковременная нагрузка.
Комбинация нагрузок и расчетных усилий в сечениях колонны ряда А приводится в таблице 3.
4 Расчет колонны
4.1 Расчет надкрановой части
4.1.1 Комбинация нагрузок для надкрановой части колонны
Рисунок 50 – Колонна ряда А
Для надкрановой части колонны из таблицы усилий выписываем комбинации нагрузок
1) Mmax=59,78 kHм; Nсоотв.=426,96 kH;
2) Mmin=-46,77 kHм; Nсоотв.=488,83 kH;
3) Мсоотв.=4,26 kHм; Nmax=652,99 kH.
Расчет ведем на две комбинации нагрузок: 1 и 3, та как в расчет комбинации вошла снеговая нагрузка, то находим длительную часть силовых факторов, умножая изгибающий момент и продольную силу снеговой нагрузки на коэффициент =0,6.
1) Mmax=59,78 kHм;
kHм;
kH;
kH.
2) Мсоотв.=4,26 kHм;
kHм;
Nmax=652,99 kH;
kH.
Для обеих комбинаций нагрузок коэффициент условия работы бетона .
4.1.2 Выбор материалов и определение расчетных характеристик
Бетон марки В20 с расчетными характеристиками: kН/м2; ; ; ;
Арматура класса А300 с расчетными характеристиками: ; .
Определим расчетные размеры (рисунок 51)
Рисунок 51 - Схема расчетных размеров надкрановой части колонны
Сечение надкрановой части колонны bxh=50x60 см. Примем ширину защитного слоя а=4см, тогда полезная высота сечения h0=56 см, расчетная длина надкрановой части колонны из плоскости рамы
4.1.3 Расчет надкрановой части
Расчет выполняем в табличной форме (таблица 4).
Таблица 4 - Расчет надкрановой части колонны
|
Поз. |
Расчетная формула |
Номер комбинации |
|
|
1 |
3 |
||
|
1 |
2 |
3 |
4 |
|
1 |
Расчетные усилия |
||
|
kНм |
59,78 (50,6) |
4,26 (-5,6) |
|
|
kН |
426,96 (361,3) |
652,99 (587,3) |
|
|
2 |
Эксцентриситет продольной силы, м , |
||
|
3 |
Расчетная длина надкрановой части колонны в плоскости рамы, м |
||
|
4 |
Гибкость колонны, см , где I - радиус инерции сечения необходим учет влияния прогиба на прочность элемента |
||
|
5 |
Момент инерции сечения, см4 |
||
Продолжение таблицы 4
|
1 |
2 |
3 |
4 |
|
6 |
Момент относительно оси, проходящей через центр наиболее растянутого или наименее сжатого стержня арматуры от действия постоянных и длительных нагрузок, кН·м , |
||
|
7 |
Момент относительно оси, проходящей через центр наиболее растянутого или наименее сжатого стержня арматуры от действия полной нагрузки, кН·м , |
||
|
8 |
Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента , где =1 для тяжелого бетона |
||
|
9 |
Коэффициенты е и е min при условии е е min 1,5 |
||
|
10 |
Коэффициент армирования |
||
Продолжение таблицы 4
|
1 |
2 |
3 |
4 |
|
11 |
Первоначально примем минимальный процент армирования % Таким образом, минимальный коэффициент армирования . Тогда момент инерции сечения арматуры, вычисленный относительно центра тяжести бетонного сечения: |
||
|
12 |
Жесткость железобетонного элемента , где Eb , Es – модуль упругости бетона и арматуры J, Js – момент инерции площадей сечения бетона и продольной арматуры |
||
|
13 |
Условная критическая сила, кН |
||
|
14 |
Коэффициент, учитывающий влияние прогиба на значение эксцентриситета продольного усиления , |
||
|
15 |
Расчетный эксцентриситет, м , |
||
Продолжение таблицы 4
|
1 |
2 |
3 |
4 |
|
16 |
Случайный эксцентриситет приложения действия силы, м , По максимальному значению примем см. Тогда полный эксцентриситет: , |
||
|
17 |
Величина максимально допустимой относительной высоты сжатой зоны при , см , где - относительная деформация растянутой арматуры при напряжениях Rs , - относительная деформация сжатого бетона при напряжениях Rb , |
||
|
18 |
Предположим, что имеем случай больших эксцентриситетов, и , тогда высота сжатой зоны, см , |
||
Продолжение таблицы 4
|
1 |
2 |
3 |
4 |
|
19 |
Относительная высота сжатой зоны, см , Предположение оправдано, в обоих случаях имеем случай больших эксцентриситетов. |
||
|
20 |
В сечении могут возникать как сжатая, так и растянутая арматура. Площадь сечения сжатой арматуры, см2 , , |
||
|
21 |
Сжатой арматуры по расчету не требуется, поэтому примем : Примем 316 А300 с см2. |
||
|
22 |
Площадь растянутой арматуры |
Продолжение таблицы 4
|
1 |
2 |
3 |
4 |
|
23 |
Для обоих сочетаний растянутой арматуры по расчету не требуется, примем , по сортаменту примем 316 А300 с см2 Диаметр поперечной арматуры примем из условия свариваемости 4 В-500. Конструктивно примем 214 А300. Шаг поперечной арматуры: мм Примем мммм Рисунок 52 - Поперечное сечение верхней части колонны |
||
|
24 |
Проверим необходимость расчета сечения колонны из плоскости изгиба рамы. Радиус инерции: Расчетная длина колонны из плоскости рамы: м. Гибкость: Условие выполняется, расчет сечения из плоскости рамы не нужен. |
4.2 Расчет подкрановой части
4.2.1 Комбинация нагрузок для подкрановой части колонны.
Для подкрановой части из таблицы усилий выписываем комбинации нагрузок.
1) Mmax=145,4 kHм; Nсоотв.=771,86 kH; Q=43,53;
2) Mmin=-353,6 kHм; Nсоотв.=771,86 kH;
3) Мсоотв.=-85,2 kHм; Nmax=1308,18 kH.
Расчет ведем на две комбинации нагрузок: 2 и 3.
Т.к. в расчет комбинации вошла снеговая нагрузка, то находим длительную часть силовых факторов, умножая изгибающий момент и продольную силу снеговой нагрузки на коэффициент =0,6. Также в расчетную комбинацию вошла крановая нагрузка, значит, при определении длительной части силовых факторов умножим изгибающий момент и продольную силу кроновой нагрузки на коэффициент =0,5.
kHм;
kHм;
kH;
kH.
Для первой комбинации b2=1, для второй комбинации коэффициент условия работы бетона .
4.2.2 Выбор материалов и определение расчетных характеристик
Бетон марки В20 с расчетными характеристиками: kН/м2; ; ; ;
Арматура класса А300 с расчетными характеристиками: ; .
Определим расчетные размеры (рисунок 53)
Рисунок 53 - Схема расчетных размеров нижней части колонны
Расстояние между осями распорок S=3000 мм, высота сечения распорки 500мм.
Расчетная длина подкрановой части колонны
Расчетная длина подкрановой части колонны из плоскости рамы
4.2.3 Расчет подкрановой части
Расчет выполняется в табличной форме (таблица 5)
Таблица 5 - Расчет подкрановой части колонны
|
Поз. |
Расчетная формула |
Номер комбинации |
|
|
1 |
3 |
||
|
1 |
2 |
3 |
4 |
|
1 |
Расчетные усилия |
||
|
kНм |
-353,6 (-353,6) |
-85,2 (-95,83) |
|
|
kН |
771,86 (771,86) |
1308,18 (1056,44) |
|
|
2 |
Эксцентриситет продольной силы, м , |
||
|
3 |
Расчетная длина надкрановой части колонны в плоскости рамы, м м. |
||
|
4 |
Приведенная гибкость сечения , где - приведенный радиус инерции двухветвевой колонны в плоскости изгиба: , |
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
необходим учет влияния прогиба на прочность элемента |
|||
|
5 |
Момент инерции сечения: |
||
|
6 |
Момент относительно оси, проходящей через центр наиболее растянутого или наименее сжатого стержня арматуры от действия постоянных и длительных нагрузок, кН·м , |
||
|
7 |
То же от действия полной нагрузки, кН·м |
||
|
8 |
Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента: Для тяжелого бетона |
||
|
9 |
Коэффициенты е и е min при условии е е min 1,5 |
||
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
10 |
Коэффициент армирования , |
||
|
11 |
Первоначально примем минимальный процент армирования % Таким образом, минимальный коэффициент армирования: . Тогда момент инерции сечения арматуры, вычисленный относительно центра тяжести бетонного сечения: |
||
|
12 |
Жесткость железобетонного элемента , |
||
|
13 |
Условная критическая сила, кН |
||
|
14 |
Коэффициент, учитывающий влияние прогиба на значение эксцентриситета продольного усиления |
||
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
15 |
Продольное усилие в ветвях колонны, кН |
||
|
16 |
Изгибающий момент ветвей, кН·м |
||
|
17 |
Эксцентриситет продольной силы, м , |
||
|
18 |
Случайный эксцентриситет приложения действия силы, см По максимальному значению примем см. Т.к. см, то полный эксцентриситет, см , |
||
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
19 |
Величина максимально допустимой относительной высоты сжатой зоны при , , см , |
||
|
20 |
Предположим, что имеем случай больших эксцентриситетов, т.е. , тогда высота сжатой зоны, см |
||
|
21 |
Относительная высота сжатой зоны, см , Предположение оправдано, имеем случай больших эксцентриситетов. |
||
|
22 |
В сечении может возникать как сжатая, так и растянутая арматура. Площадь сечения сжатой арматуры, см2 |
||
|
23 |
Для обоих сочетаний сжатой арматуры по расчету не требуется, поэтому примем Примем 214 А300 с см2. |
||
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
24 |
Площадь растянутой арматуры, см2 , , Т.к. , то для обоих сочетаний растянутой арматуры по расчету не требуется, поэтому примем . Примем 214 А300 с см2 (рисунок 54) |
||
|
Рисунок 54 - Поперечное сечение нижней части колонны Диаметр поперечной арматуры примем из условия свариваемости 4 В-500. Шаг поперечной арматуры: мм Примем мммм |
|||
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
25 |
Проверим необходимость расчета сечения колонны из плоскости изгиба рамы. Радиус инерции: Расчетная длина колонны из плоскости рамы: м. Гибкость: Необходим расчет подкрановой части из плоскости рамы, так как , то необходим учет влияния прогиба на прочность элемента. |
||
|
26 |
Случайный эксцентриситет приложения действия силы, см По максимальному значению примем см. Полный эксцентриситет, м |
||
|
27 |
Момент относительно оси, проходящей через центр наиболее растянутого или наименее сжатого стержня арматуры от действия постоянных и длительных нагрузок, кН·м , |
||
|
28 |
Момент относительно оси, проходящей через центр наиболее растянутого или наименее сжатого стержня арматуры от действия полной нагрузки, кН·м |
||
|
29 |
Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента: |
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
30 |
Коэффициенты и при условии 1,5 |
||
|
31 |
Момент инерции ветви, см4 |
||
|
32 |
Момент инерции сечения арматуры, см4 |
||
|
33 |
Жесткость железобетонного элемента , |
||
|
34 |
Условная критическая сила, кН |
||
Продолжение таблицы 5
|
1 |
2 |
3 |
4 |
|
35 |
Коэффициент, учитывающий влияние прогиба на значение эксцентриситета продольного усиления: |
||
|
36 |
Окончательный полный эксцентриситет, см |
||
|
37 |
Предположим, что имеем случай больших эксцентриситетов, т.е. , тогда высота сжатой зоны, см |
||
|
38 |
Относительная высота сжатой зоны, см смсм, случай больших эксцентриситетов смсм случай малых эксцентриситетов. |
||
|
39 |
Площадь сечения арматуры Принятого количества арматуры достаточно. |
||
4.3 Расчет промежуточной распорки
Рисунок 55 - Схема сечения промежуточной распорки колонны
Сечение распорки см (рисунок 55). Примем высоту защитного слоя см, тогда расчетная высота сечения см.
Изгибающий момент в распорке:
Эпюра изгибающих моментов в распорке двузначная, поэтому в сечении возникает растянутая и сжатая арматура. Примем:
Примем 316 А300 с As см2 (рисунок 56).
Поперечная сила в распорке:
Проверим необходимость расчета распорки по наклонным сечениям:
,
Условие выполняется, прочность наклонных сечений обеспечена прочностью бетона.
Поперечную арматуру принимаем конструктивно, исходя из условия свариваемости, 4 В-500 с шагом:
Примем мм.
Рисунок 56 - Поперечное сечение распорки
4.4 Расчет колонны в стадии транспортировки
Рисунок 57 - Расчетная схема колонны в стадии транспортировки
Собственный вес колонны
,
При транспортировании конструкции коэффициент динамичности .
Нагрузка от собственного веса колонны:
Примем l1 м
Тогда:
Проверим прочность опорного и пролетного сечения в процессе транспортировки:
Сечение 1-1 (рисунок 58):
Рисунок 58 - Сечение 1-1
Относительная высота сжатой зоны:
,
Условие выполняется, прочность сечения обеспечена.
Сечение 2-2 (рисунок 59):
Рисунок 59 - Сечение 2-2
Относительная высота сжатой зоны:
Условие не выполняется, прочность сечения не обеспечена.
Увеличиваем диаметр арматуры, примем 616 А300 с AS, диаметр поперечной арматуры примем из условия свариваемости 4 В500 (рисунок 60).
Рисунок 60 – Сечение 2-2
Таким образом, колонна выдерживает нагрузку, возникающую в процессе транспортировки.
4.5 Расчет по образованию трещин нормальных к продольной оси элемента в процессе транспортировки
Расчет сводится к проверке условия:
Для сечение 1-1 момент внешних сил:
kH·м.
Момент, воспринимаемый сечением нормальным к продольной оси элемента:
,
где - момент сопротивления приведенного сечения для крайнего растянутого волокна:
Сечение 2-2:
kH·м.
Момент, воспринимаемый сечением нормальным к продольной оси элемента:
, где
см3;
kH·мkH·м.
Условия выполняются, трещины в процессе транспортировки не возникают.
4.6 Расчет колонны в стадии монтажа
Рисунок 61 - Расчетная схема колонны в стадии монтажа
При монтаже конструкции коэффициент динамичности .
Нагрузка от собственного веса колонны:
Изгибающие моменты на опоре и в пролете:
Сечение 1-1:
kH·мkH·м.
Сечение2-2:
kH·мkH·м.
Условия выполняются, колонна выдерживает нагрузку возникающую в процессе монтажа.
5 Расчет ребристой плиты покрытия
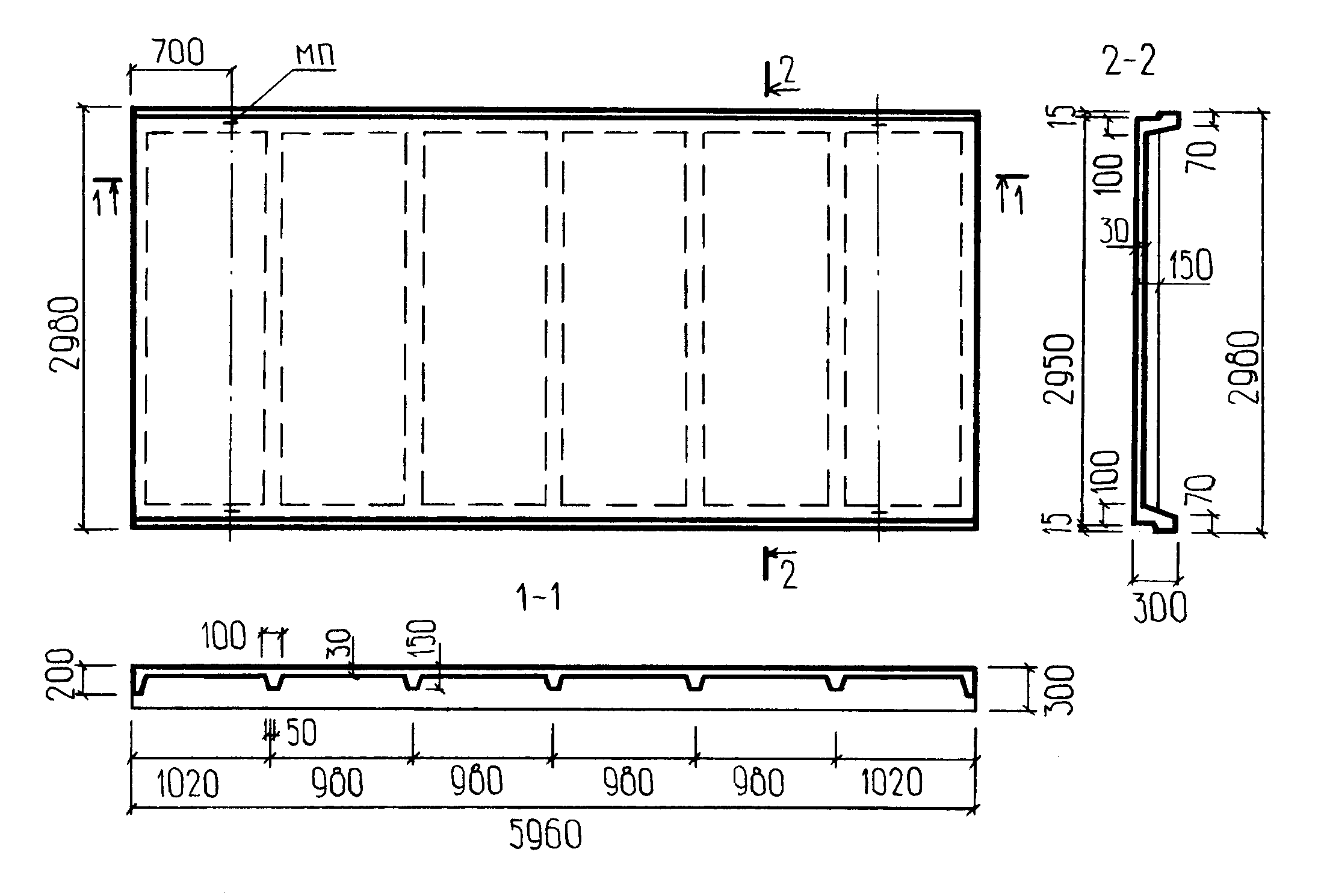
Рисунок 62 – Плита покрытия
Необходимо рассчитать ребристую панель покрытия размером 6х3 м. Бетон класса В30:
kН/см2,
kН/см2,
kН/см2,
kН/см2,
kН/см2.
Для ускорения твердения бетона панель подвергают тепловой обработке при атмосферном давлении вместе с формой. Для армирования продольных ребер панели принята предварительно напряженная арматура класса А600, натягиваемая механическим способом на упоры:
kН/см2,
kН/см2,
Для обеспечения прочности наклонных сечений в ребра устанавливаем каркасы из арматуры класса А240:
kН/см2,
kН/см2.
Полку панели армируем сварными сетками из холоднотянутой проволоки класса В500 с kН/см2.
5.1 Сбор нагрузок на панель покрытия
Сбор постоянной нагрузки на 1 м2 панели покрытия приводится в таблице 6.
Таблица 6 - Постоянная нагрузка на 1 м2 панели покрытия
|
Поз. |
Наименование |
Нормативная нагрузка qf, kН/м2 |
Коэффициент надежности по нагрузке f |
Расчетная нагрузка q, kH/м2 |
|
1 |
Бикрост =0,008 м, =0,4 кН/м3 |
0,0032 |
1,2 |
0,0038 |
|
2 |
Цементно-песчаная стяжка =0,02 м, =20 кН/м3 |
0,4 |
1,3 |
0,52 |
|
3 |
Утеплитель пенополистирол =0,05 м, =10 кН/м3 |
0,5 |
1,2 |
0,6 |
|
4 |
Обмазочная пароизоляция битумом =0,002 м, =13 кН/м3 |
0,026 |
1,2 |
0,03 |
|
Итого: |
0,93 |
1,15 |
Временная снеговая нагрузка в соответствии с пунктом 2.2.1:
Нормативная снеговая нагрузка:
kH/м2.
Расчетная снеговая нагрузка:
kH/м2.
5.2 Определение внутренних усилий в сечениях элементов от внешней нагрузки
Рисунок 63 – Эпюра от внешней нагрузки
Примем глубину опирания панели покрытия 100 мм (рисунок 63) тогда расчетная длина панели
,
Погонная нормативная нагрузка и расчетная нагрузка с учетом коэффициента надежности по назначению:
Нормативная постоянная нагрузка:
Расчетная постоянная нагрузка:
Расчетная длительная нагрузка:
.
Полная нормативная нагрузка:
Полная расчетная нагрузка:
Момент от расчетных нагрузок:
Момент от постоянных и длительных нагрузок:
Момент от полных нормативных нагрузок:
Момент от собственного веса панели:
Момент от кратковременных нагрузок:
Максимальная расчетная поперечная сила:
Поперечная сила от нормативных постоянных нагрузок:
Поперечная сила от нормативных постоянных и длительных нагрузок:
kH.
Поперечная сила от полных нормативных нагрузок:
5.3 Расчет полки панели на местный изгиб
При наличии часто расположенных поперечных ребер и соотношение сторон опорного контура полка плиты испытывает преимущественный местный изгиб и рассчитывается как балочная (рисунок 64). Расчетная полоса шириной 1 м вырезается в рабочем направлении и рассматривается как многопролетная статически не определимая балка, рабочая продольная арматура сеток рассчитывается на момент М2.
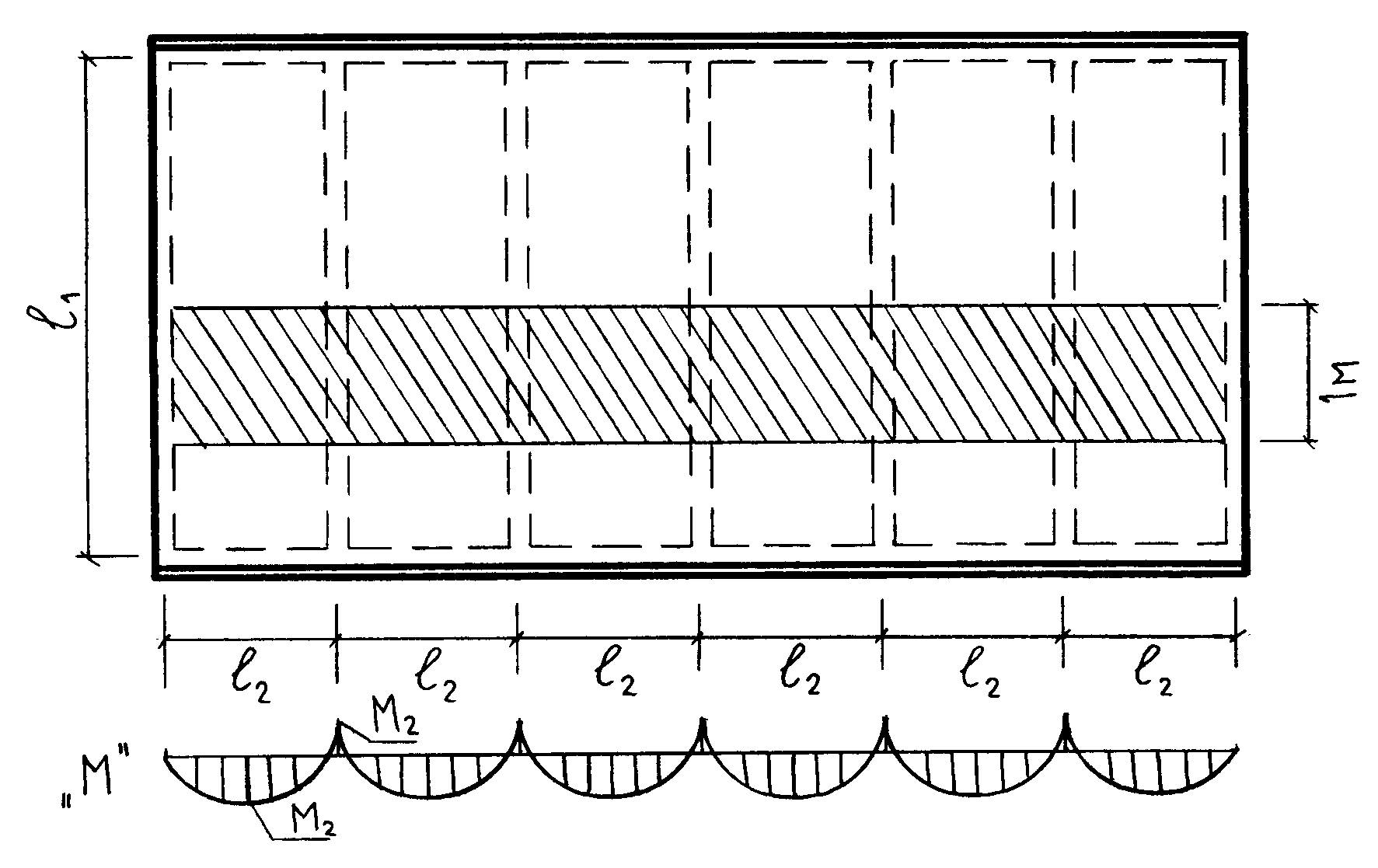
Рисунок 64 – Расчетная схема
Размеры полки в свету между ребрами:
Соотношение сторон:
.
Плита рассчитывается как защемленная по двум длинным сторонам.
Собственный вес полки:
Полная нагрузка на полку:
Изгибающий момент для полосы плиты шириной 1 м:
5.4 Расчетная прочность по нормальному сечению в середине пролета
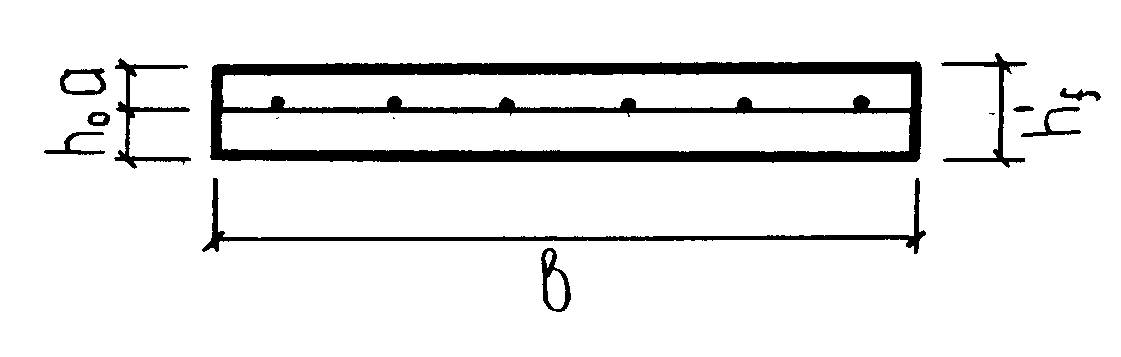
Рисунок 65 - Схема сечения средней части пролета
Ширина расчетного сечения: см.
Высота: см.
Расчетная высота сечения: см.
Определим площадь арматуры в середине пролета.
Коэффициент
Граничная относительная высота сжатой зоны бетона:
,
где - относительная деформация арматуры растянутой зоны:
где - предварительное напряжение в арматуры,
;
- относительная деформация сжатого бетона,
;
Относительная высота сжатой зоны бетона:
,
Требуемая площадь арматуры:
,
Примем сварную сетку из арматуры класса В500 с шагом стержней s=300 мм. Примем 34 В500 с As см2.
5.5 Расчет поперечного ребра
Поперечные ребра панели рассматриваются как балки таврового сечения, закрепленные в продольных ребрах. С учетом развития пластических деформаций изгибающие моменты определяют в пролете и на опоре:
.
Нагрузка на поперечное ребро для балочных плит собирается с прямоугольной грузовой площади (рисунок 66)
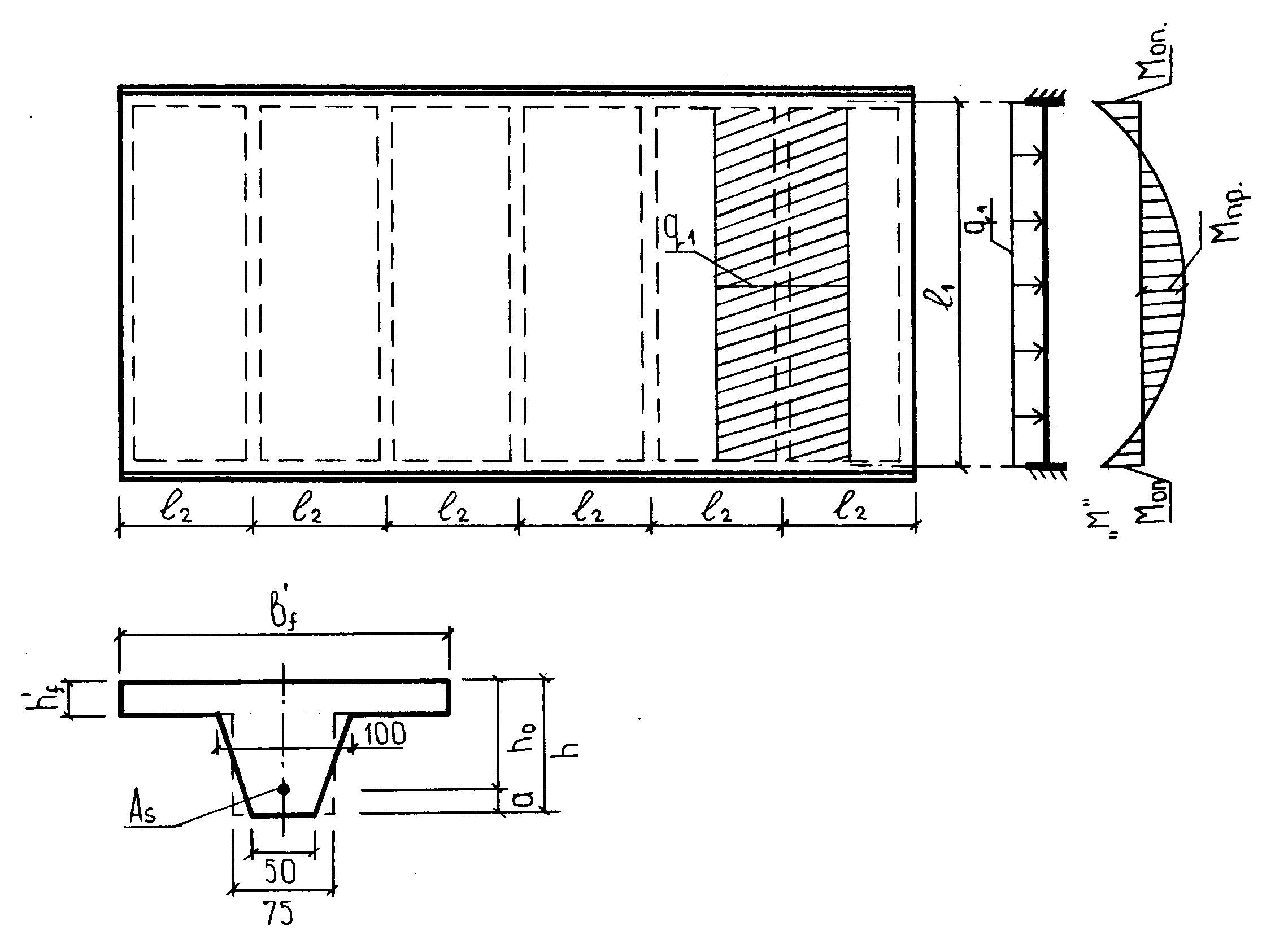
Рисунок 66 – К расчету поперечного ребра
Конструируем расчетное сечение поперечного ребра:
Средняя толщина поперечного ребра:
Расчетное сечение поперечного ребра:
Нагрузка на поперечное ребро собирается с прямоугольной грузовой площади, ее наибольшая интенсивность:
,
Нагрузка от собственного веса ребра:
Полная расчетная нагрузка:
С учетом развития пластических деформаций определим моменты в пролете и на опоре по равномоментной схеме:
Определим площадь сечения рабочей арматуры.
Предположим, что имеем первый случай работы сечения, т.е .
Граничная относительная высота сжатой зоны бетона:
,
Относительная высота сжатой зоны бетона:
,
Высота сжатой зоны:
,
Предположение оправдано, имеем первый случай работы сечения.
Требуемая площадь арматуры:
Примем каркас Кр-1 с рабочей арматурой 10 А240 с см2. Поперечные стержни примем из условия свариваемости из арматуры 3 В500.
Шаг поперечных стержней принимаем из конструктивных соображений:
На концевых участках каркаса длиной :
мм.
Примем мм.
В средней части каркаса:
мм.
Примем мм.
5.6 Расчет продольного ребра по нормальным сечениям
Продольные ребра являются основными несущими сечениями панелей. Поперечное сечение панели может быть приведено к тавровому профилю. Расчет по прочности нормальных сечений производят по общим правилам расчета тавровых сечений в зависимости от положения тавровой оси. В процессе расчета подбирается площадь сечения продольной напрягаемой арматуры. Приведенное сечение имеет тавровую форму с параметры (рисунок 67):
- ширина полки (ширина панели по верху): см;
- толщина полки: см;
- т.к. ширина продольных ребер понизу - 7см, то ширина ребра: см;
- примем толщину защитного слоя см, тогда расчетная высота сечения:
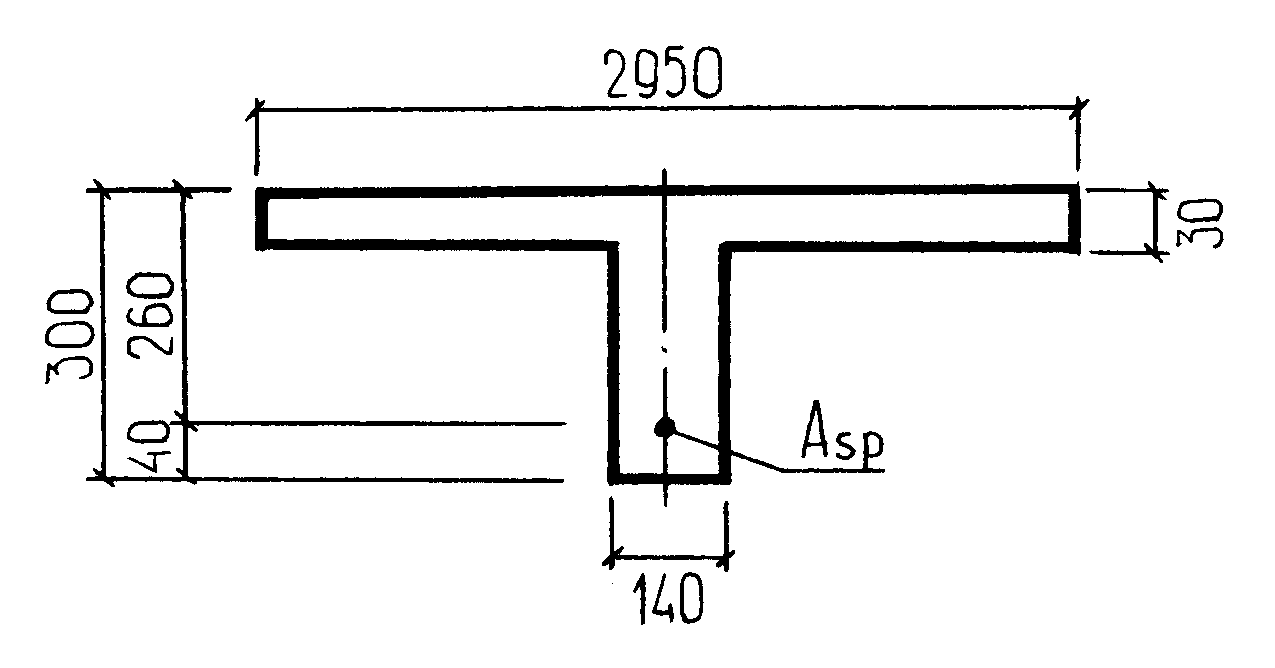
Рисунок 67 – К расчету продольного ребра
Продольные ребра армируем механическим способом натяжения.
Определим граничную относительную высоту сжатой зоны бетона:
,
Предположим, что имеем первый случай работы таврового сечения, т.е .
Относительная высота сжатой зоны бетона:
,
Высота сжатой зоны:
,
Предположение оправдано, имеем первый случай работы сечения.
Коэффициент условия работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести:
,
для арматуры А600 , тогда
.
Примем
Тогда, площадь сечения предварительно напряженной арматуры:
Примем 216 А600 с см2.
5.7 Определение геометрических характеристик приведенного сечения
Для определения напряжения в сечениях предварительно напряженных железобетонных элементов до образования трещин (стадия I), рассматривают приведенное бетонное сечение, в котором площадь сечения арматуры заменяют площадью сечения бетона (рисунок 68). Исходя из равенства деформаций арматуры и бетона, приведение выполняют через коэффициент, равный отношению модулей упругости двух материалов:
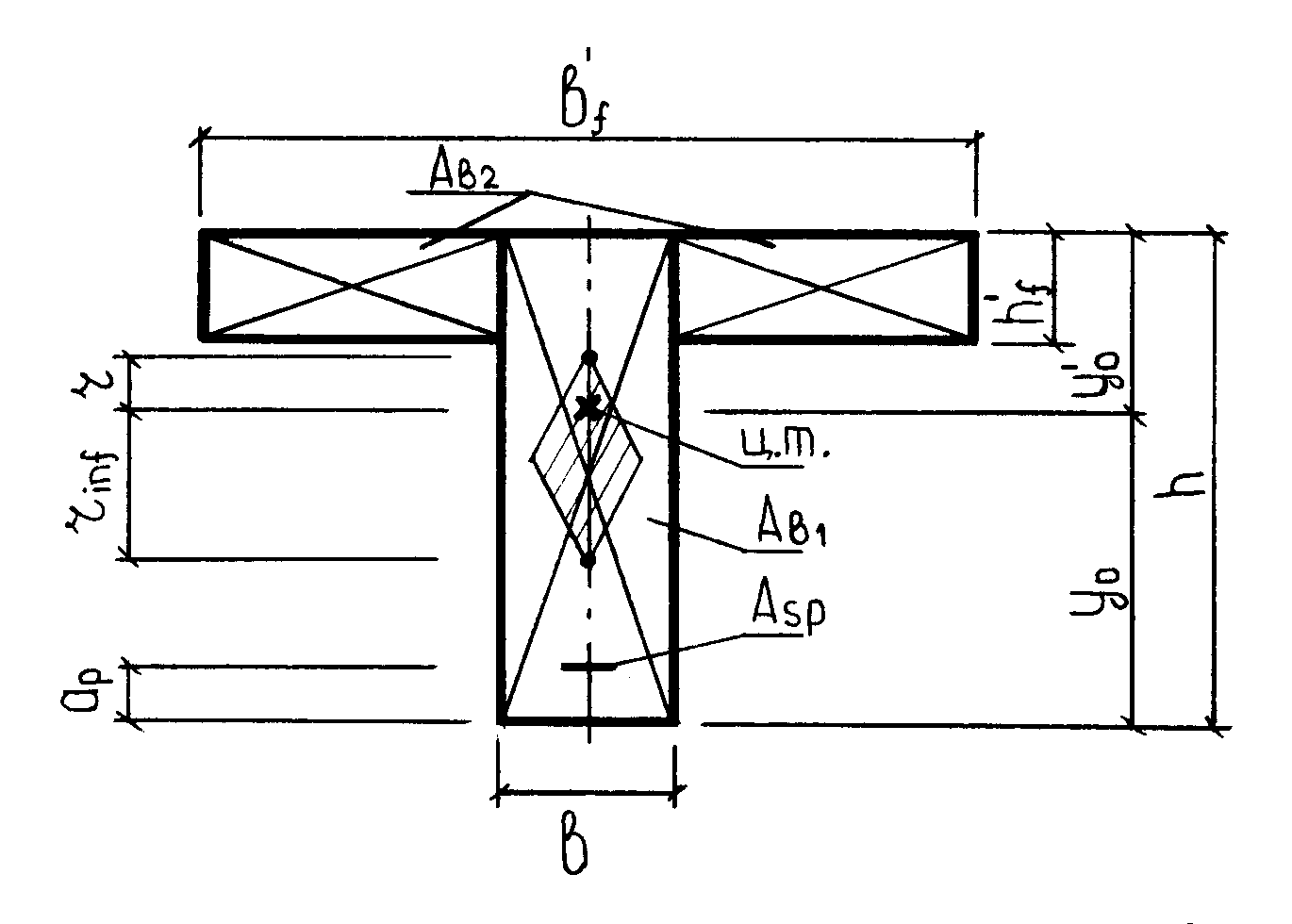
Рисунок 68 – Ядро приведенного сечения
Площадь приведенного сечения составит:
,
где - площадь сечения бетона:
Статический момент приведенного сечения относительно оси I-I, проходящей по нижней грани сечения:
,
где - площадь части сечения;
- расстояние от центра тяжести i-той части сечения до оси I-I;
Расстояние от центра тяжести приведенного сечения до наиболее растянутой грани (до оси I-I):
Расстояние от центра тяжести приведенного сечения до наиболее сжатой грани (до оси II-II):
Момент инерции приведенного сечения относительно оси, проходящей через центр тяжести данного сечения:
,
- момент инерции i-той части сечения относительно оси, проходящей через центр тяжести этой части сечения;
Момент сопротивления относительно оси I-I:
Момент сопротивления приведенного сечения относительно оси II-II:
Определим коэффициент:
где - максимальное напряжение в сжатом бетоне от внешней нагрузки и усилия предварительного обжатия:
,
где Р2 - усилие предварительного обжатия:
- эксцентриситет приложения усилия предварительного обжатия относительно центра тяжести приведенного сечения:
Примем .
Расстояние от центра тяжести приведенного сечения до верхней границы ядра сечения:
Расстояние от центра тяжести приведенного сечения до нижней границы ядра сечения:
Упругопластический момент сопротивления приведенного сечения относительно растянутой и сжатой грани элемента:
,
,
где - коэффициенты, учитывающие влияние неупругих деформаций бетона растянутой (сжатой) зоны, в зависимости от формы сечения; для прямоугольных и тавровых сечений с полкой в сжатой зоне:
;
5.8 Определение потерь предварительного напряжения в арматуре и усилия предварительного обжатия
А Первые потери:
1. Потери от релаксации напряжений в арматуре при механическом способе напряжения:
2. Потери от температурного перепада:
,
где - разность между температурой нагреваемой арматуры и неподвижных упоров, воспринимающих усилия натяжения, при отсутствии точных данных принимают:
;
3. Потери от деформации стальной формы при механическом способе натяжения:
где n – число стержней, натягиваемых одновременно,
l – сближение упоров по линиям действия усилия натяжения арматуры,
l – расстояние между наружными гранями упоров
4. Потери от деформации анкеров натяжных устройств:
где l – обжатие анкеров или смещение стержня в зажимах анкеров,
Примем l мм
Б Вторые потери.
5. Потери от усадки бетона:
6. Потери от ползучести бетона:
,
Усилия обжатия после первых потерь
,
где - предварительное напряжение в j-той группе стержней напрягаемой арматуры с учетом первых потерь:
Полные значения первых и вторых потерь:
МПа.
Усилие в напрягаемой арматуре с учетом полных потерь:
,
где - предварительное напряжение в j-той группе стержней напрягаемой арматуры с учетом полных потерь:
5.9 Расчет прочности продольного ребра по наклонным сечениям
Для оценки прочности наклонных сечений проверяют условие:
где Q - поперечная сила в вершине наклонного сечения от действия полных расчетных нагрузок;
Условие не выполняется, прочность наклонных сечений не достаточна. Необходим расчет элемента по наклонным сечениям: на действие поперечной силы по наклонной трещине; на действие поперечной силы по наклонной полосе между трещинами.
Проверим обеспечение прочности на действие поперечной силы по наклонной трещине из условия:
Qb - поперечное усилие, воспринимаемое бетонным сечением:
,
b2 - коэффициент, учитывающий влияние вида бетона, принимаемый ;
c - длина проекции наиболее опасного наклонного сечения на продольную ось элемента:
Должно выполняться условие:
;
Прочность бетона не обеспечивает прочность наклонных сечений арматуры, то поперечная арматура для каркаса Кр-2 устанавливаем по расчету. Определяем поперечные усилия воспринимаемые стержнями поперечной арматуры.
,
где qs - погонное усилие в поперечных стержнях:
,
где - площадь сечения поперечных стержней:
,
где n – количество поперечных стержней
f – площадь сечения одного поперечного стержня первоначально принимаемое из конструктивных соображений
6 А240 с см2. Количество поперечных стержней в сечении, нормальном к продольной оси элемента, пересекающих наклонное сечение примем шт. Конструктивно шаг примем мм.
Условие выполняется, прочность по наклонной трещине обеспечена
Проверим обеспечение прочности на действие поперечной силы по наклонной полосе между трещинами из условия:
где 1 – коэффициент учитывающий влияние поперечных стержней
,
где – коэффициент армирования для поперечных стержней
Условие выполняется, прочность по наклонным сечениям обеспечена.
5.10 Расчет по трещиностойкости
Трещиностойкость элементов проверяют расчетом в сечениях, нормальных к продольной оси, а при наличии поперечных сил - и в сечениях, наклонных к продольной оси элемента.
5.10.1 Расчет по образованию трещин, нормальных к продольной оси элемента
Расчет сводится к проверке условия:
MR - момент внешних сил, способствующих раскрытию трещин;
Mcrc - момент внутренних усилий, воспринимаемый сечением, нормальным к продольной оси элемента перед образованием трещин:
,
где Mrp- момент усилия обжатия бетона предварительно напряженной арматурой в стадии эксплуатации:
Момент усилия обжатия бетона предварительно напряженной арматурой в стадии изготовления:
Момент внутренних усилий в стадии эксплуатации:
Условие не выполняется, трещиностойкость в стадии эксплуатации не обеспечена..
Момент внутренних усилий в стадии изготовления:
Момент внутренних усилий в стадии обжатия:
;
Условия выполняется, трещиностойкость в стадии обжатия обеспечена.
5.10.2 Расчет по раскрытии трещин нормальных к продольной оси элемента
Расчет сводится к проверке условия
,
где acrc,ult – предельно допустимая ширина раскрытия трещин обеспечивающая сохранения арматуры принимаемая в соответствии с п. 4.3.1.3 [2]
acrc – ширина раскрытия трещин нормальных к продольной оси элемента
где s – напряжение в продольной растянутой арматуре от соответствующей внешней нагрузки,
где М=МRi – изгибающий момент от внешней нагрузки,
NP – усилие предварительного обжатия,
z – расстояние от центра тяжести арматуры, расположенной в растянутой зоне сечения до точки приложения равнодействующей усилий в сжатой зоне элемента,
,
eSP – расстояние от центра тяжести той же арматуры до точки приложения усилия NP,
см.
ls – базовое расстояние между смежными нормальными трещинами,
где Abt – площадь сечения растянутого бетона при ее высоте <0,5·h см2
1 – коэффициент продолжительности действия нагрузки,
1=1,4 при продолжительном действии нагрузки,
1=1 при не продолжительном действии нагрузки,
2 – коэффициент учитывающий профиль продольной арматуры,
2=0,8 для гладкой арматуры,
3 – коэффициент учитывающий характер нагружения,
3=1 для изгибающих и внецентренно сжатых элементов,
3=1,2 для растянутых элементов
s – коэффициент учитывающий не равномерное распределение относительно деформации растянутой арматуры между трещинами,
s =1,
Приращение напряжений от непродолжительного действия нагрузок
Приращение напряжений от продолжительного действия нагрузок
Ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок,
Ширина продолжительного раскрытия трещин
,
Ширина раскрытия трещин от непродолжительного действия постоянной и временной (длительной и кратковременной) нагрузок,
Ширина раскрытия трещин от непродолжительного действия постоянных и временных длительнодействующих нагрузок,
Ширина не продолжительногораскрытия трещин,
,
Условия выполняются, ширина раскрытия трещин не превышает предельнодопустимой величины.
5.10.3 Расчет по образованию трещин, наклонных к продольной оси элемента
Трещиностойкость наклонного сечения может считаться обеспеченной, если выполняется условие:
,
где - главные растягивающие напряжения в бетоне:
,
где - нормальное напряжение в бетоне на площадке, перпендикулярной продольной оси элемента, от внешней нагрузки и усилия предварительного обжатия
,
где MX - изгибающий момент от внешней нагрузки
- нормальное напряжение в бетоне на площадке, параллельной продольной оси элемента, от местного действия опорных реакций, сосредоточенных сил и распределенной нагрузки, а также от усилия предварительного обжатия поперечной арматуры:
при :
,
при :
,
т.к. смсм, то:
- касательное напряжение в бетоне от внешней нагрузки и усилия предварительного обжатия отогнутой арматурой:
,
где S - приведенный статический момент части сечения, расположенной выше рассматриваемого уровня, относительно оси, проходящей через центр тяжести сечения:
- коэффициент условия работы бетона:
,
где - главные сжимающие напряжения:
В - класс бетона по прочности на сжатие, МПа
- коэффициент, принимаемый: для тяжелого бетона - ;
причем:
,
,
т.к. , примем .
Проверим условия:
,
,
Условия выполняется, трещиностойкость наклонных сечений обеспечена..
5.11 Расчет по деформациям при отсутствии трещин в растянутой зоне
Расчет сводится к проверке условия:
,
где fult - предельно допустимый прогиб элемента;
f- прогиб элемента:
где - коэффициент, зависящий от расчетной схемы и вида нагрузки; для свободно опертой балки:
- полная кривизна для участка без трещин в растянутой зоне:
,
где - кривизна от непродолжительного действия полных нагрузок:
;
- кривизна от непродолжительного действия постоянных и временных длительных нагрузок:
,
где NP – усилие предварительного обжатия
- изгибная жесткость приведенного поперечного сечения элемента от непродолжительного действия нагрузок:
,
где Eb1 - модуль деформации сжатого бетона; при непродолжительном действии нагрузки:
,
- момент инерции приведенного сечения элемента:
,
где - момент инерции сжатой зоны бетона относительно центра тяжести приведенного сечения:
- момент инерции площади сечения растянутой арматуры относительно центра тяжести приведенного поперечного сечения элемента:
- коэффициент приведения арматуры к бетону; для растянутой арматуры:
,
где - приведенный модуль деформации бетона:
,
где - относительные деформации; при непродолжительном действии нагрузки:
,
- приведенный модуль деформации растянутой арматуры:
,
где - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами:
,
Условие выполняется, жесткость обеспечена.
6 Расчет панели в стадии изготовления, транспортировки и монтажа
6.1 Расчет панели на усилия, возникающие в стадии транспортировки и монтажа
Составим расчетную схема плиты с учетом того, что монтажные петли расположены на расстоянии 0,7 м от торцов, рисунок 69.
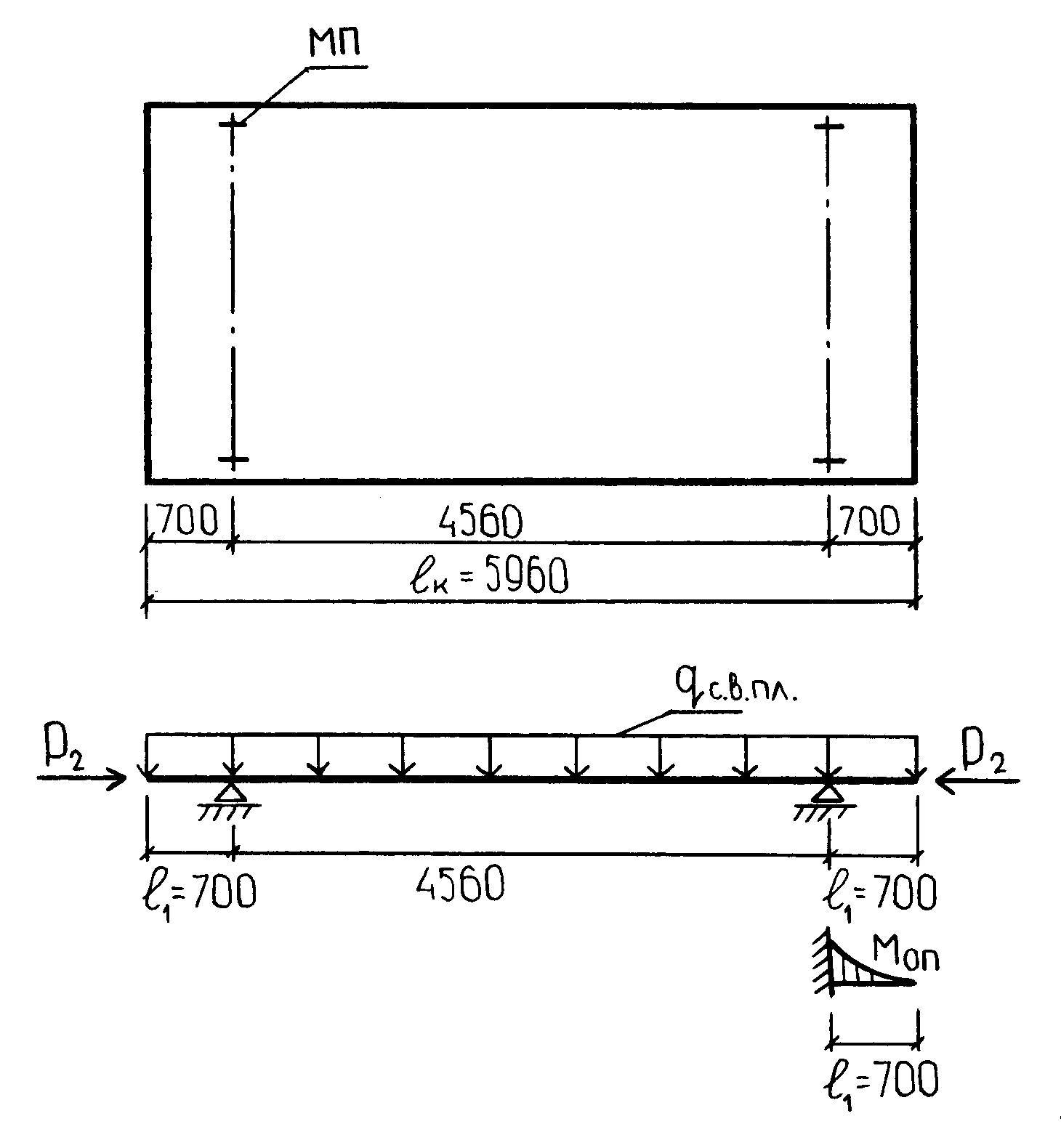
Рисунок 69 – Расчетная схема
Коэффициент динамичности .
Собственный вес плиты: kH.
Нагрузка от собственного веса плиты с учетом коэффициента динамичности:
Расчетный момент в опорном сечении с учетом коэффициента динамичности:
Проверим достаточность сечения арматуры верхней зоны при
,
см2
Условие выполняется, площадь сечения арматуры достаточна.
Расчет монтажных петель производим с учетом возможного перекоса плиты при подъеме и передачи ее веса на две петли.
Усилие на каждую петлю:
Площадь сечения стержня из арматуры класса А240:
Примем 12 А240 c см2.
6.2 Расчет панели на усилия, возникающие в стадии изготовления
Усилия обжатия панели вводим как внешнюю сжимающую внецентренно приложенную нагрузку, обжимающую сечение панели при достижении бетоном 70% проектной прочности, тогда расчетное сопротивление бетона:
,
Эксцентриситет продольной силы относительно центра тяжести арматуры:
.
По наибольшему значению примем случайный эксцентриситет приложения силы:
;
примем см.
Момент от собственного веса плиты без учета коэффициента динамичности:
Толщина защитного слоя верхней арматуры:
,
Для зоны, наиболее удаленной от напрягаемой арматуры, расчетная высота сечения:
,
Определим требуемую площадь сечения арматуры в верхней зоне:
Коэффициент:
,
Величина относительной высоты сжатой зоны:
,
Принимаем
Определим случай работы сечения, внецентренно сжатого усилием обжатия, проверкой условия:
,
Условие выполняется, сечение рассматриваем как прямоугольное шириной .
Определим требуемую площадь арматуры в верхней зоне:
см2.
Условие выполняется, принятой арматуры для армирования полки плиты достаточно.
Произведем проверку верхней зоны по образованию трещин из условия:
,
где - момент, воспринимаемый опорным сечением перед образованием трещин:
Условие выполняется, трещины в опорном сечении в стадии изготовления не образуются.
Список литературы
1. СниП 2.01.07-85*(2004). Нагрузки и воздействия.
2. СП 52-102-2004. Предварительно напряженные железобетонные конструкции.
3. СП 52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры.
4. ГОСТ 5781-82. Сталь горячекатаная для армирования железобетонных конструкций. Технические условия.
5. ГОСТ 6727-80. Проволока из низколегированной стали холоднотянутая для армирования железобетонных конструкций. Технические условия.
6. ГОСТ 19903-74. Прокат листовой горячекатаный. Сортамент.
7. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелого бетона (к СП 52-102-2004)
8. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: общий курс. – М: Стройиздат. 1991. – 767с.
9. Бондаренко В.М. Железобетонные и каменные конструкции. М.: Высшая школа, 2004.
- ГОСТ 2.105-95 (2002) ЕСКД. Общие требования к текстовым документам.
Рассчт конструкции одноэтажного промышленного здания с мостовыми кранам