Цифровые (двоичные) компараторы
?4
3.4. Цифровые (двоичные) компараторы
Лекция 1.7
Цифровые (двоичные) компараторы
Цифровой (двоичный) компаратор (устройство сравнения) [от англ. compare – сравнивать] – это КЦУ, определяющее отношения между двумя двоичными словами.
За основные отношения, через которые можно выразить все осталь�ные, обычно берут два – “равно” (=) и “больше” (>), хотя также можно рассматривать и пару “равно” (=) и “меньше” (<).
Определим функции, вырабатываемые компараторами, следующим образом: они принимают единичное значение (истинны), если соблюдается условие, указанное в индексе обозначения функции F. Например, функция FA=B = 1, если А = В и принимает нулевое значение при А В.
Приняв в качестве основных отношения “равно” (=) и “больше” (>), для всех остальных отношений можно записать:
;
;
;
Эти отношения используются как логические условия в микропрограммах, в устройствах контроля и диагностики ЭВМ и т. д.
В сериях цифровых элементов обычно имеются компараторы с тремя выхо�дами: “равно”, “больше” и “меньше” (рис. 3.11). Для краткости записей в обозначении выходных функций компаратора указывается только слово А.
Соотношения входных и выходных сигналов (таблица истинности) компаратора представлены в табл. 3.11.
Таблица 3.11
|
Сравниваемые данные
|
Входы наращивания
|
Выходы
|
|
A3, B3
|
A2, B2
|
A1, B1
|
A0, B0
|
I(A>B)
|
I(A<B)
|
I(A=B)
|
A>B
|
A<B
|
A=B
|
|
A3>B3
|
|
|
|
|
|
|
1
|
0
|
0
|
|
A3<B3
|
|
|
|
|
|
|
0
|
1
|
0
|
|
A3=B3
|
A2>B2
|
|
|
|
|
|
1
|
0
|
0
|
|
A3=B3
|
A2<B2
|
|
|
|
|
|
0
|
1
|
0
|
|
– » –
|
A2=B2
|
A1>B1
|
|
|
|
|
1
|
0
|
0
|
|
– » –
|
A2=B2
|
A1<B1
|
|
|
|
|
0
|
1
|
0
|
|
– » –
|
– » –
|
A1=B1
|
A0>B0
|
|
|
|
1
|
0
|
0
|
|
– » –
|
– » –
|
A1=B1
|
A0<B0
|
|
|
|
0
|
1
|
0
|
|
– » –
|
– » –
|
– » –
|
A0=B0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
– » –
|
– » –
|
– » –
|
A0=B0
|
0
|
0
|
1
|
0
|
0
|
1
|
|
– » –
|
– » –
|
– » –
|
– » –
|
1
|
0
|
0
|
1
|
0
|
0
|
|
– » –
|
– » –
|
– » –
|
– » –
|
0
|
1
|
0
|
0
|
1
|
0
|
|
– » –
|
– » –
|
– » –
|
– » –
|
1
|
1
|
0
|
0
|
0
|
1
|
|
– » –
|
– » –
|
– » –
|
– » –
|
1
|
1
|
1
|
1
|
1
|
1
|
Три последние строки таблицы отражают режим наращивания каскадов, который может быть последовательным или параллельным. При последовательном наращивании выходы A>B, A<B, A=B от схемы, анализирующей младшие разряды, следует присоединить к одноименным входам последующего каскада. Этим способом с помощью двух 4-разрядных компараторов можно сравнить два восьмиразрядных слова. Нетрудно подсчитать число каскадов для любой большей длины слова. Однако каждый последовательный каскад добавит время задержки распространения сигнала 15 нс.
Для правильной работы последовательного многокаскадного компаратора на входы I(A>B), I(A<B) следует подать напряжение высокого уровня, а на вход I(A=B) – низкого.
Устройства сравнения на равенство строятся на основе поразрядных опера�ций над одноимёнными разрядами обоих слов.
Слова равны, если равны все их одноимённые разряды, т. е. если в обоих нули или единицы. Признак равенства i-ых разрядов можно вычислить так:
или
.
Признак неравенства разрядов
.
Признак равенства двух слов A и B в целом
.
Схема компаратора на равенство в базисе И-НЕ показана на рис. 3.12, а.

а б
Рис. 3.12. Схемы компараторов на равенство
Схема проверки на равенство без парафазных входов (рис. 3.12, б) основана на выражениях для ri , преобразованных следующим образом:
Построение компаратора на “больше” для одноразрядных слов (табл. 3.12) требует реализации функции запрета по b: .
Таблица 3.12
|
a
|
b
|
Fa>b
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
1
|
|
1
|
1
|
0
|
Функцию FA>B для многоразрядных слов проще всего получить на основе следующих рассуждений. Пусть нужно срав�нить двухразрядные слова A=a1a0 и B=b1b0 . Если старшие разряды a1 и b1 не равны, то результат известен независимо от младших разрядов: при a1 = 1 и b1 = 0 имеем А > В, а при a1 = 0 и b1 = 1 имеем А < В. Если же a1 = b1 , то результат ещё неизвестен, и требуется анализ младших разрядов по тому же алгоритму. Поэтому для двухразрядных слов можно записать
.
Подобный же подход справедлив и для слов любой разрядности – к анализу следующего разряда нужно переходить только при равенстве предыдущих. Таким образом, для общего случая n-разрядных слов имеем
(3.11)
Правильно рассуждая, мы получили правильный результат. Однако цель ми�нимизации формул при этом не ставилась и на самом деле выражения для FA>B не минимальны. В минимальном варианте признаки равенства ri можно заменить более простыми функциями , которые равны ri для всех комбинаций, кроме ai = 1 и bi = 0, но это соответствует условию , которое уже проверялось в предыдущем слагаемом уравнения (3.11). Однако для построения компарато�ра с тремя выходами (“равно”, “больше” и “меньше”) полученный нами вариант (3.11) остаётся предпочтительным, поскольку функции ri всё равно нужны для срав�нения на “равно”, и для операций сравнения на “больше” они могут быть взяты в готовом виде.
Пример реализации компаратора с тремя выходами для двухразрядных слов приведён на рис. 3.13.
Выработка признака A > B в этой схеме производится по соотношению (штрихом отмечены функции с выходов младшей группы):
.
Компараторы для слов большой разрядности получают наращиванием раз�мерности путём использования нескольких ИС компараторов. Принцип на�ращивания хорошо иллюстрируется на том же рис. 3.13.
Примером гибкости цифровой схемотехники может служить возможность построения компаратора на равенство с помощью последовательного соеди�нения демультиплексора и мультиплексора, как показано на рис. 3.14. В ра�боте такого компаратора легко разобраться, если вспомнить, как функционируют входящие в него блоки.
Пример 3.11. Построить на ЛЭ схему сравнения на равенство двух 8-разрядных чисел.
Особенность данной задачи состоит в том, что для её решения практически невозможно построить таблицу: число строк в ней будет 2(8+8) =
= 216 =65536. Подобные задачи решают иначе – методом декомпозиции задачи – разбиения её на более мелкие подзадачи. В нашем случае: два числа равны, если попарно равны их одноименные разряды. Структурная схема такого компаратора показана на рис. 3.15, а.
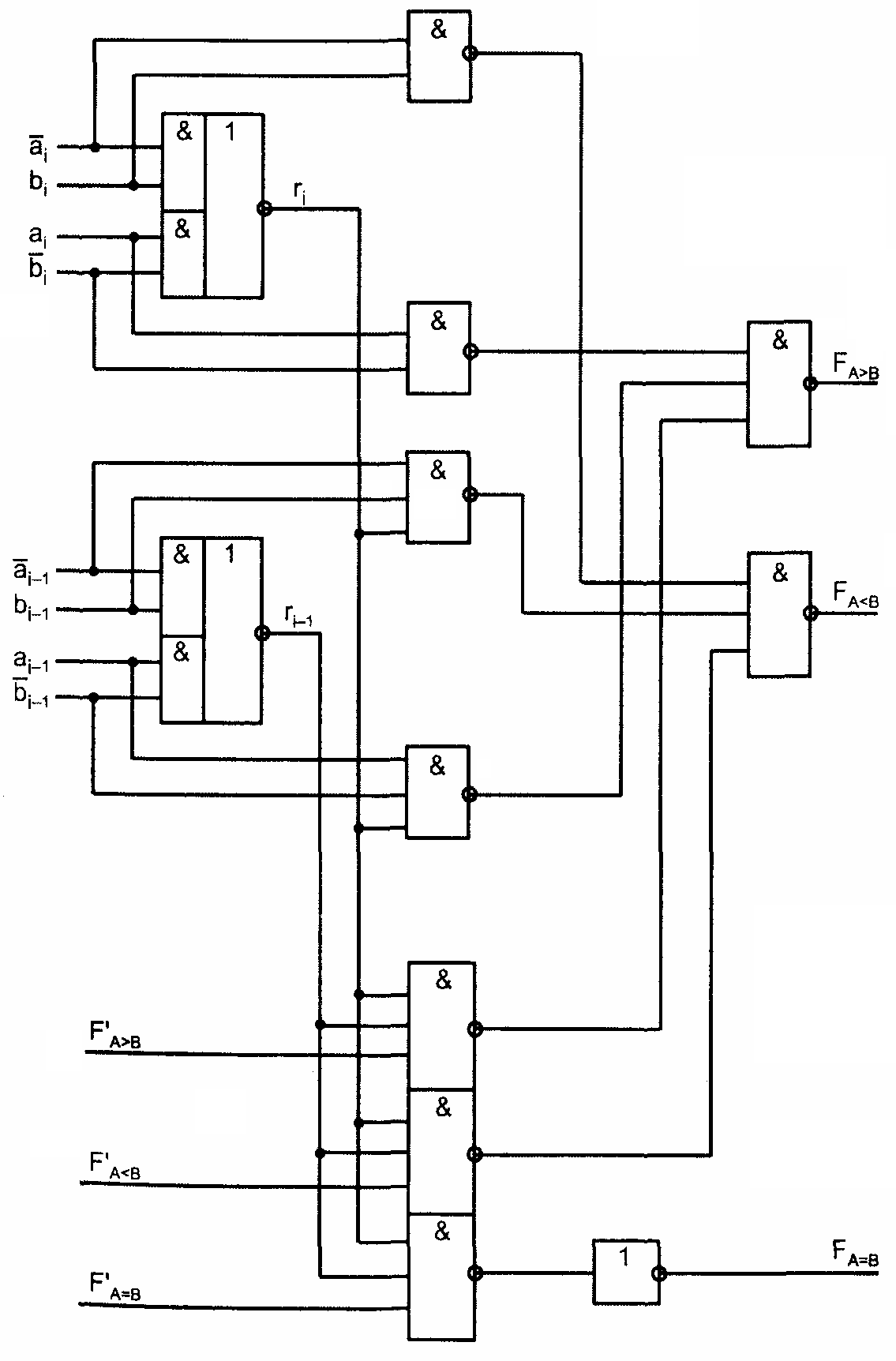
Рис. 3.13. Пример построения компаратора
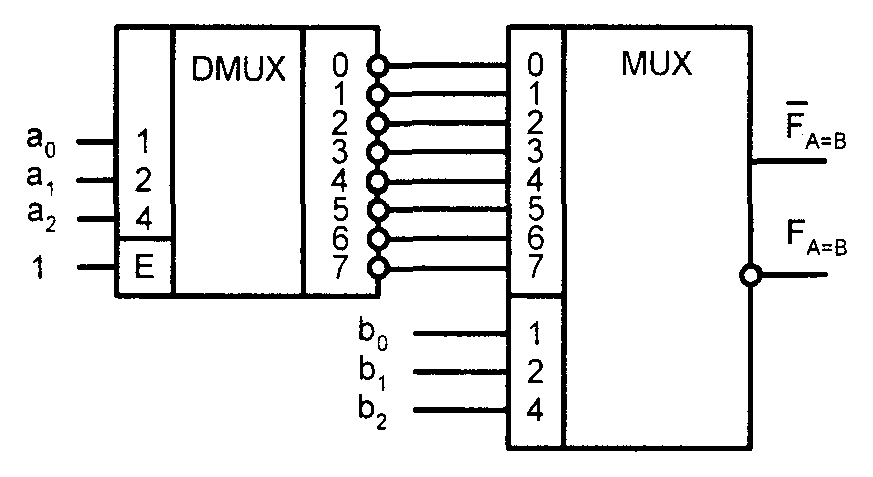
Рис. 3.14. Реализация компаратора на равенство
с помощью дешифратора-демультиплексора и мультиплексора
Известно, что функция равенства двух аргументов – это инверсия их суммы по модулю 2. Чтобы исключить из проектируемой схемы 8 инверторов воспользуемся соотношением:
.
Решение данной задачи показано на рис. 3.15, б. Оно учитывает, что в семействах ЛЭ нет элемента 8ИЛИ-НЕ, а есть только 4ИЛИ-НЕ.
Рис. 3.15. Узел сравнения на равенство 8-разрядных слов
Отечественной промышленностью выпускаются компараторы ТТЛ 555СП1, 531СП1 и КМОП 561ИП2.
Микросхема К555СП1 (рис. 3.16) является 4-разрядным компаратором. Он имеет три выхода: “A>B”, “A<B”, “А=В”, и в зависимости от соотношения чисел А и В активный уровень появляется на одном из этих выходов. Входы “>”, ”<”, ”=” служат для подключения выходов компаратора нижнего уровня, сравнивающего младшие разряды слов большей битности, при наращивании разрядности компараторов.
Схема параллельного компаратора для двух двадцатичетырехразрядных слов представлена на рис. 3.17.
Здесь младший (нижний в схеме) компаратор СП1 используется как четырёхразрядный, четыре старших как пятиразрядные, т. к. входы I(A>B), I(A<B) служат пятой парой разрядных входов, т. е. А4 и В4 соответственно. На входы I(A=B) старших компараторов подано напряжение нулевого уровня.
Таким способом и однозначную микросхему СП1 можно использовать как пятиразрядный компаратор.
В КМОП серии компаратор 561ИП2 имеет несколько отличных режимов работы: например при всех низших уровнях входных сигналов I(A>B), I(A=B), I(A<B) выходные A>B, A=B, A<B также низкие (у 555СП1 – высокие), т. е. для анализа работы компаратора надо использовать другую таблицу.
Схема последовательного соединения ИП2 для сравнения двенадцатиразрядных слов представлены на рис. 3.18.