Кинематическая пара
Лекция N2
Каким бы не был механизм машины он всегда состоит только из звеньев и кинематических пар.
Условия связи, налагаемые в механизмах на подвижные звенья, в теории машин и механизмов Принято называть кинематическими парами.
Кинематической парой называется подвижное соединение двух со�прикасающихся звеньев, обеспечивающее их определенное относительное движение.
В табл. 2.1 приведены названия, рисунки, условные обозначения наи�более распространенных на практике кинематических пар, а также про�изведена их классификация.
Звенья при объединении их в кинематическую пару могут соприка�саться между собой по поверхностям, линиям и точкам.
Элементами кинематической пары называют совокупность Поверх�ностей, линий или точек, по которым происходит подвижное соединение двух звеньев и которые образуют кинематическую Пару. В зависимости от вида контакта элементов кинематических пар различают высшие и низшие кинематические пары.
Кинематические пары, образованные элементами в виде линии или точки,называются высшими.
Кинематические пары, образованные элементами в виде поверхно�стей, называются низшими.
Чтобы пара существовала, элементы входящих в нее звеньев должны находиться в постоянном контакте, Т.е. быть замкнутыми. Замыкание ки�нематических пар может быть геометрически или силовым, Например, с помощью собственной массы, пружин и т.п..
Прочность, износостойкость и Долговечность кинематических пар зависят от их вида и конструктивного исполнения. Низшие пары более износостойкие, чем высшие. Это объясняется тем, что в низших Парах контакт элементов пар происходит по поверхности, а следовательно, при одинаковой нагрузке в ней возникают меньшие удельные давления, чем в высшей. Износ, при прочих равных условиях, Пропорционален удель�ному давлению, а поэтому низшие Пары изнашиваются Медленнее, Чем высшие. Поэтому с целью уменьшения износа в машинах предпочти�тельнее использование низших пар, однако часто применение высших ки�нематических пар позволяет значительно упростить структурные схемы машин, что снижает их Габариты и упрощает конструкцию. Поэтому правильный выбор кинематических пар является сложной инженерной за�дачей.
Кинематические Пары разделяют также по числу степеней свободы (подвижности), которые она предоставляет соединенным посредством ее звеньям, или по числу условий связей (класс пары), налагаемых парой на относительное движение соединяемых звеньев. При использовании такой классификации разработчики машин получают сведений о возможных от�носительных движениях звеньев и о характере взаимодействия силовых факторов между элементами пары.
Свободное звено, находящееся в общем случае в М - мерном про�странстве, Допускающем П видов простейших движений, обладает числом степеней свобода! (Н) или W - подвижно.
Так, если звено находится в трехмерном пространстве, допус�кающем шесть видов Простейших движений - три вращательных и три по�ступательных вокруг и вдоль осей X, V, Z, то говорят, что оно обладает шестью степенями свободы или имеет шесть обобщенных координат, или шестиподвижно. Если звено находится в двухмерном пространстве, до�пускающем три вида простейших движений - одно вращательное вокруг Z и два поступательных вдоль осей X и Y, то говорят, что оно имеет три степени свободы, или три обобщенные координаты, или оно трехподвижно и т. д..
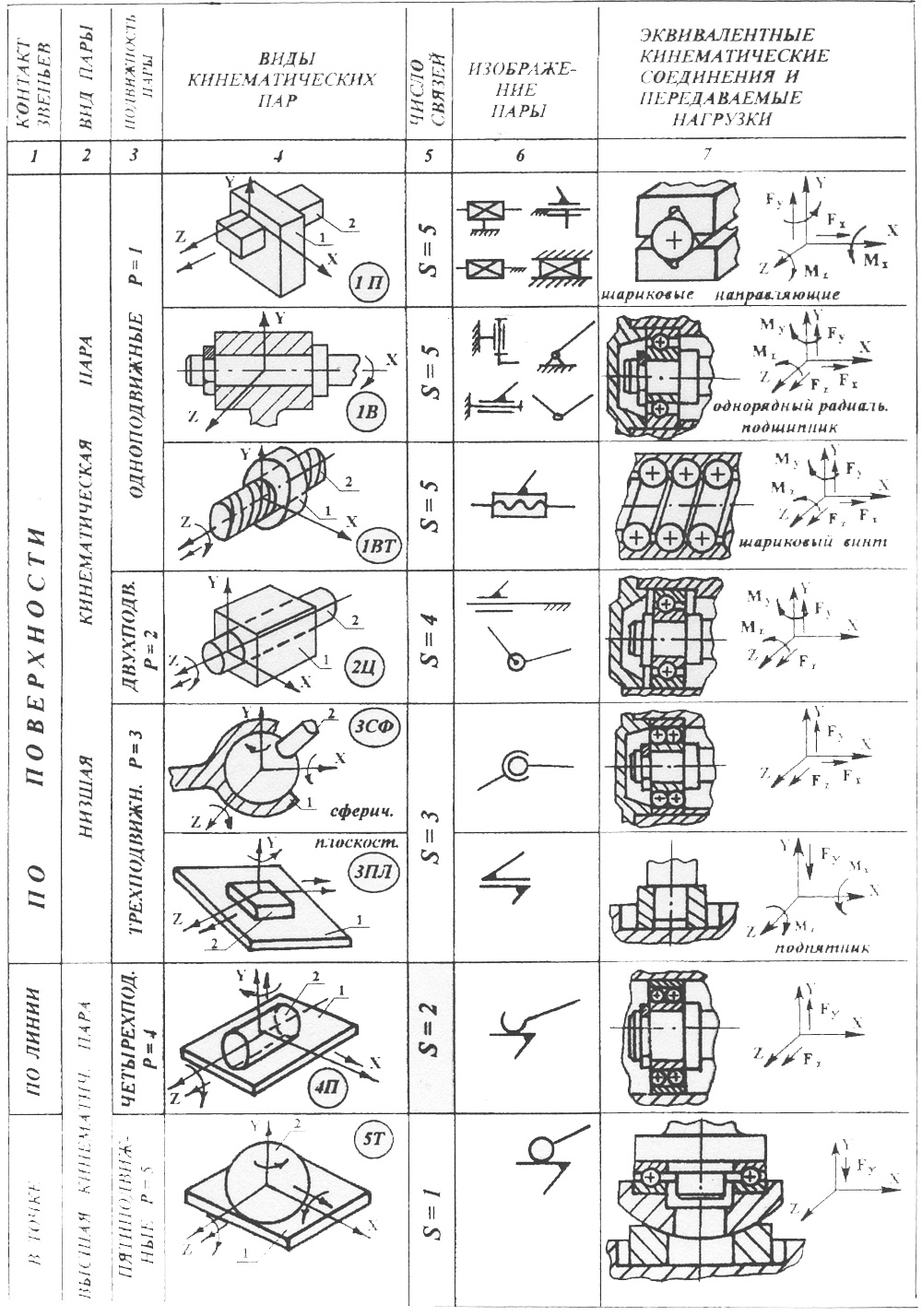
Таблица 2.1
При объединении звеньев с помощью кинематических пар они ли�шаются степеней свободы. Значит, кинематические пары налагают на сое�диняемые ими звенья связи числом S.
В зависимости от числа степеней свободы, которым обладают в от�носительном движении звенья, объединенные в кинематическую пару, определяют подвижность пары (W=Н). Если Н - число степеней свободы звеньев кинематической пары в относительном движении, to подвижность пары определится следующим образом:
где П - подвижность пространства, в котором .существует рассматривае�мая пара; S - число налагаемых парой связей.
Следует заметить, что подвижность пары W, определенная по (2.1), зависит не от вида пространства, в котором она реализуется, а только от конструкции.
Например, вращательная (поступательная) (см, табл. 2.1) пара как в шести-, так и в трехподвижном пространстве, все равно останется одноподвижной, в первом случае на нее будет наложено 5 связей, а во втором случае - 2 связи, и, значит, будем иметь, соответственно:
для шестиподвижного пространства:
для трехподвижного пространства:
Как видим, подвижность кинематических пар не зависит от характе�ристик пространства, что является преимуществом данной классифика�ции. Напротив, часто встречающееся деление кинематических пар на классы страдает тем, что класс пары зависит от Характеристик про�странства, а значит, одна и та же пара в разных пространствах имеет раз�ный класс. Это неудобно для практических целей, значит, такая Классифи�кация кинематических пар нерациональна, поэтому ее лучше не применять.
Можно подобрать такую форму элементов пары, чтобы при одном независимом простейшем движений возникало второе - зависимое (производное). Примером такой кинематической пары является винтовая (табл. 2.1). В этой паре вращательное движение винта (гайки) вызывает поступательное его (ее) перемещение вдоль оси. Такую пару следует от�нести к одноподвижной, Так как в ней реализуется всего одно независимое простейшее Движение.
Кинематические соединения.
Кинематические пары, приведенные в табл. 2.1, просты и компактны. Они реализуют практически все, необходимые при создании механизмов простейшие относительные перемещения звеньев. Однако при создании машин и механизмов они применяются редко. Это обусловлено тем, что в точках соприкосновения звеньев, образующих пару, обычно возникают большие силы Трения. Это приводит к значительному износу элементов пары, а значит, к ее разрушению. Поэтому простейшую двухзвенную ки�нематическую цепь кинематической пары часто заменяют более длинны�ми кинематическими цепями, Которые в совокупности реализуют то же самое относительное движение звеньев, что и заменяемая кинематическая пара.
Кинематическая цепь, предназначенная для замены кинематической пары, называется кинематическим соединением.
Приведем примеры кинематических цепей, для наиболее распро�страненных на практике вращательной, поступательной, винтовой, сфе�рической и плоскость-плоскость кинематических пар.
Из табл. 2.1 видно, что простейшим аналогом вращательной кине�матической пары является подшипник с телами качения. Аналогично, ро�ликовые направляющие заменяют поступательную пару и т.д.
Кинематические соединения удобнее и надежнее в эксплуатации, вы�держивают значительно большие силы (моменты) и позволяют механиз�мам работать при высоких относительных скоростях звеньев.
Основные виды механизмов.
Механизм Можно рассматривать как частный случай кинематической цепи, у которой, как минимум, одно звено обращено в стойку, а движение остальных звеньев определено заданным движением входных звеньев.
Отличительными особенностями кинематической цепи, представ�ляющей механизм, являются подвижность и определенность движения ее звеньев относительно стойки.
Механизм может иметь несколько входных и одно выходное звено, в этом случае он называется суммирующим механизмом, и, наоборот, одно входное и несколько выходных, тогда он называется дифференцирующим механизмом.
По назначению Механизмы разделяются на направляющие и передаточные.
Передаточным механизмом называется устройство, предназначенное для воспроизведения заданной функциональной зависимости между пере�мещениями входного и выходного звеньев.
Направляющим механизмом называют механизм, у которого траек�тория определенной точки звена, образующего кинематические пары только с подвижными звеньями, совпадает с заданной кривой.
Рассмотрим основные виды механизмов, нашедших широкое приме�нение в технике.
Механизмы, звенья которых образуют только низшие кинема�тические пары, называют шарнирно-рычажными. Эти механизмы нашли широкое применение благодаря тому, что они долговечны, надежны и просты в эксплуатации. Основным представителем таких Механизмов яв�ляется шарнирный четырехзвенник (рис.2.1).
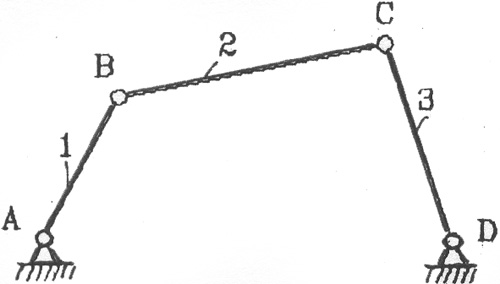
Названия механизмов обычно определяются по названиям их вход�ного и выходного звеньев или харак�терного звена, входящего в их сос�тав.
В зависимости от законов дви�жения входного и выходного звеньев этот механизм может называться кривошипно-коромысловым, двой�ным кривошипным, двойным коромысловым, коромыслово-кривошипным.
Шарнирный четырехзвенник применяется в станкостроении, прибо�ростроении, а также в сельскохозяйственных, пищевых, снегоуборочных и других машинах.
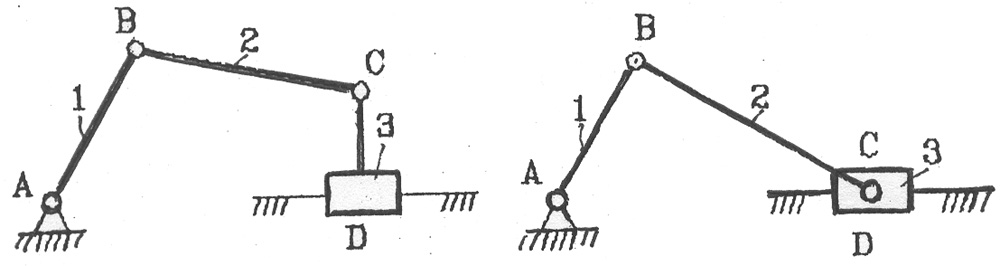
Если заменить в шарнирном четырехзвеннике вращательную пару, например D, на поступательную, то получим широко известный кривошипно-ползунный механизм (рис. 2.2).
Рис. 2.2. Различные виды кривошипно-ползунных механизмов:
1 – кривошип 2 - шатун; 3 - ползун
Кривошипно-ползунный (ползунно-кривошипный) механизм нашел широкое применение в компрессорах, насосах, двигателях внутреннего сгорания и других машинах.
Заменив в шарнирном четырехзвеннике вращательную пару С на по�ступательную, получим кулисный механизм (рис. 2.3).
На pиc.2.3, в кулисный механизм получен из шарнирного четырехзвенника путем замены в нем вращательных пар С и О на поступательные.
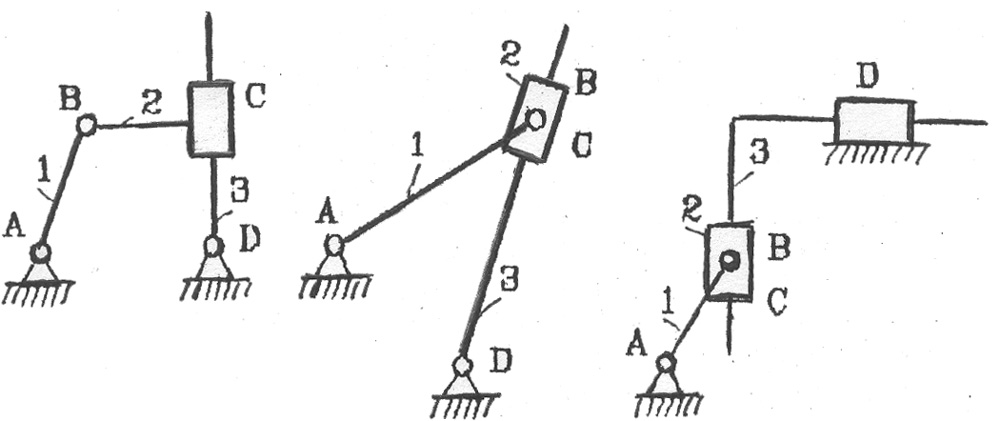
Кулисные механизмы нашли широкое применение в строгальных станках благодаря присущему им свойству асимметрии рабочего и хо�лостого хода. Обычно у них длительный рабочий ход и быстрый, обеспечивающий возврат резца в исходное положение холостой ход.
Рис. 2.3. Различные виды кулисных механизмов:
1 – кривошип; 2 – камень; 3 – кулиса.
Большое применение шарнирно-рычажные механизмы нашли в робототехнике (рис. 2.4).
Особенностью этих механизмов является то, что они обладают большим числом степеней свободы, а значит, имеют много приводов. Со�гласованная работа приводов входных звеньев обеспечивает перемещение схвата по ра�циональной траектории и в заданное место окружающего пространства.
Широкое применение в технике получили кулачковые механизмы. При помощи кулачковых меха�низмов конструктивно Наиболее просто можно Получить практически лю�бое движение ведомого звена по заданному закону,
В настоящее время существует большое число разновидностей ку�лачковых механизмов, некоторые из которых представлены на рис. 2.5.
Необходимый закон движения выходного звена кулачкового меха�низма достигается за счет придания входному звену (кулачку) соответ�ствующей формы. Кулачок может совершать вращательное (рис. 2.5, а, б), поступательное (рис. 2.5, в, г) или сложное движение. Выходное звено, если оно совершает поступательное движение (рис.2.5, а, в), называют толкателем, а если качательное (рис. 2.5, г) - коромыслом. Для сниже�ния потерь на трение в высшей кинематической паре В применяют до�полнительное звено-ролик (рис. 2.5, г).
Кулачковые механизмы применяются как в рабочих машинах, так и в разного рода командоаппаратах.
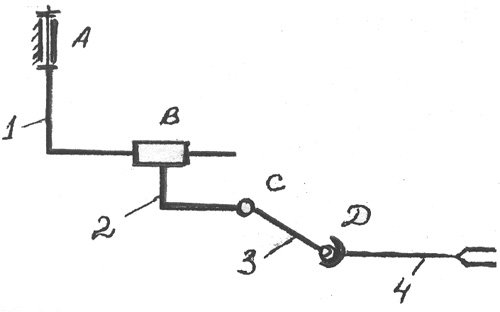
Очень часто в металлорежущих станках, прессах, различных прибо�рах и измерительных устройствах применяются винтовые механизмы, простейший из которых представлен на рис. 2.6:
Рис. 2.6 Винтовой механизм:
1 - винт ; 2 - гайка; А, В, С - кинематические пары
Винтовые механизмы обычно применяются там, где необходимо пре�образовать вращательное движение в взаимозависимое поступательное или наоборот. Взаимозависимость движений устанавливается правиль�ным подбором геометрических параметров винтовой пары В.
Клиновые механизмы (рис.2.7) применяются в различного вида за�жимных устройствах и приспособлениях, в которых требуется создать большое усилие на выходе при ограниченных силах, действующих на вхо�де. Отличительной особенностью этих механизмов являются простота и надежность конструкции.
Механизмы, в которых передача движения между соприкасающимися телами осуществляется за счет сил трения, называются фрикционными. Простейшие трехзвенные фрикционные механизмы представлены на рис. 2.8
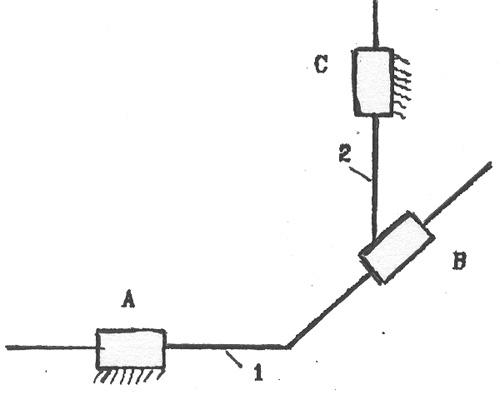
Рис. 2.7 Клиновый механизм:
1, 2 - звенья; Л, В, С - кинематические пиры.
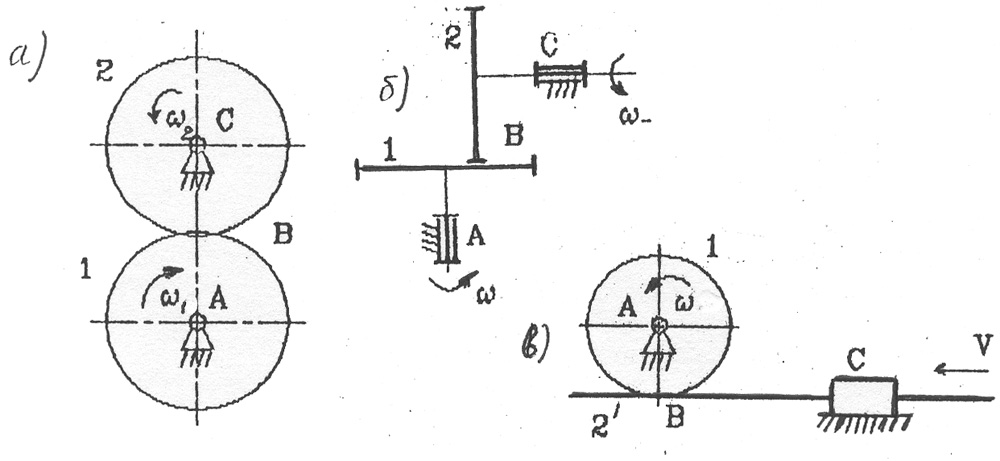
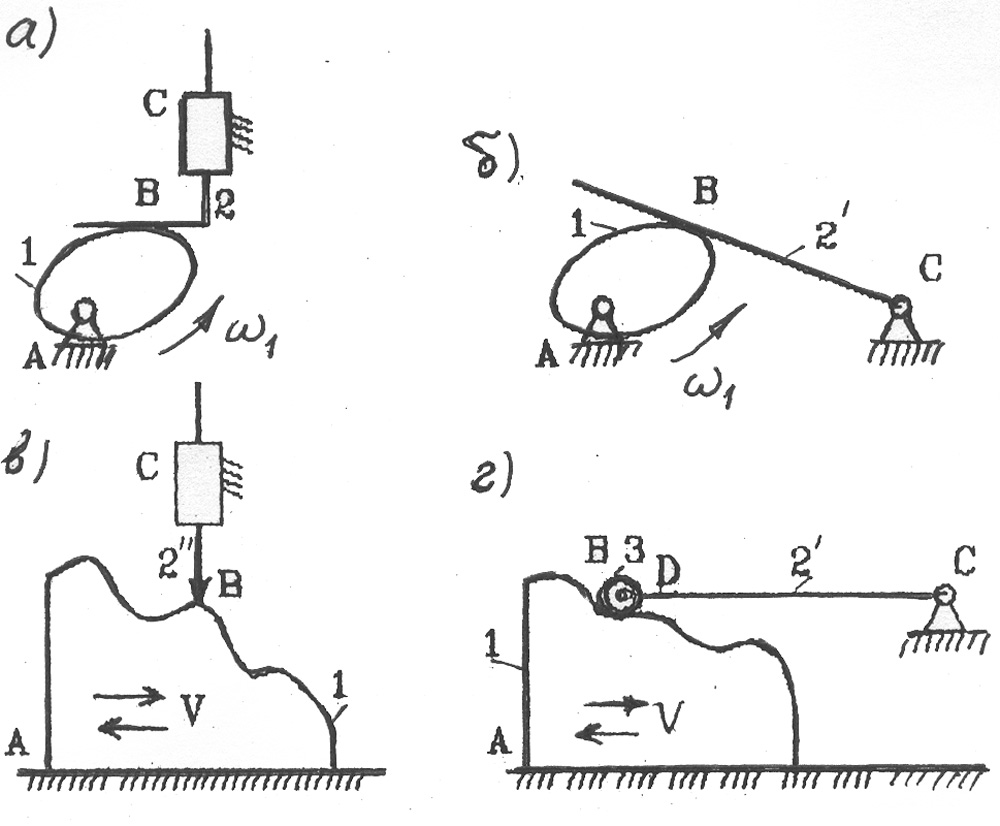
Рис. 2.8 Фрикционные механизмы:
а - фрикционный механизм с параллельными осями; б - фрикционный механизм с пересекающимися» осями; в - реечный фрикционный меха�низм; 1 - входной ролик (колесо);
2 – выходной ролик (колесо); 2'- рейка
Вследствие того что звенья 1 и 2 прижиты друг к другу, по линии ка�сания между ними возникает сила трения, которая увлекает за собой ведо�мое звено 2.
Широкое применение фрикционные передачи получили в приборах, лентопротяжных механизмах, вариаторах (механизмах с плавной регули�ровкой числа оборотов).
Для передачи вращательного движения по заданному закону между валами с параллельными, пересекающимися и перекрещивающимися ося�ми применяются различного вида зубчатые механизмы. При помощи зубчатых колес можно осуществлять передачу движения как между валами с неподвижными осями, так и с перемещающимися в пространстве.
Зубчатые механизмы применяют для изменения частоты и направ�ления вращения выходного звена, суммирования или разделения движе�ний.

На рис. 2.9 показаны основные представители зубчатых передач с неподвижными осями.
Рис 2.9. Зубчатые передачи с неподвижными осями:
а - цилиндрическая; б - коническая; в - торцовая; г - реечная;
1 - шестерня; 2 - зубчатое колесо; 2 * рейка
Меньшее из двух зацепляющихся зубчатых колес называют шестер�ней, а большее - зубчатым колесом.
Рейка является частным случаем зубчатого колеса у которого радиус кривизны равен бесконечности.
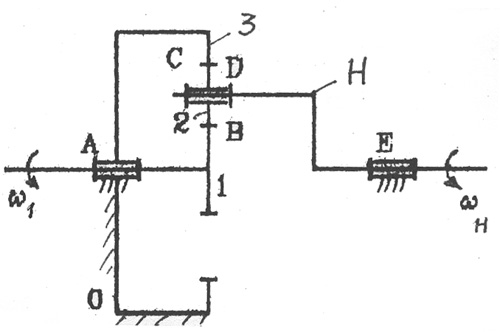
Если в зубчатой передаче имеются зубчатые колесе с подвижными осями, то их называют планетарными (рис. 2.10):
Планетарные зубчатые передачи но сравнению с передачами с непо�движными осями позволяют передавать большие мощности и переда�точные числа при меньшем числе зубчатых колес. Они также широко применяются при создании суммирующих и дифференциальных механиз�мов.
Передача движений между перекрещивающимися осями осуществля�ется с помощью червячной передачи (рис. 2.11).
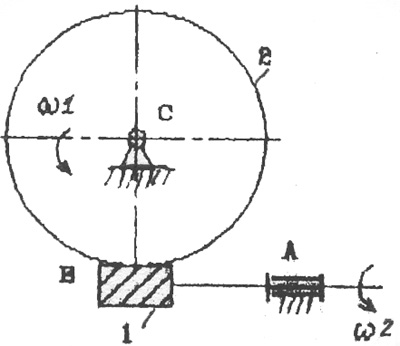
Червячная передача получается из передачи винт-гайка путем продольной разрезки гайки и ее двукратного сворачивания во взаимно перпендикулярных плос�костях. Червячная передача обладает свой�ством самоторможения и позволяет в одной ступени реализовывать большие переда�точные отношения.
Рис. 2.11. Червячная передача:
1 - червяк, 2 - червячное колесо.
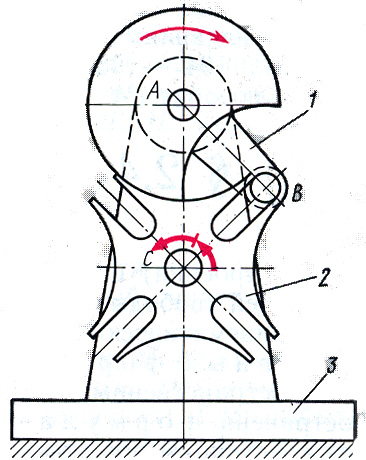
К зубчатым механизмам прерывисто�го движения относятся также механизм мальтийского креста. На рис. З-Л'2. показан механизм четырех лопастного "мальтийского креста".
Механизм "мальтийского креста" преобразует непрерывное вращения ведущего эвена - кривошипа 1 с цевкой 3 в прерывис�тое вращение "креста" 2, Цевка 3 без удара входит в радиальный паз "креста" 2 и пово�рачивает его на угол , где z -число пазов.
Для осуществления движения только в одном направлении применяют храповые ме�ханизмы. На рис.2,13 показан храповый ме�ханизм, состоящий из коромысла 1, храпо�вого колеса 3 н собачек 3 и 4.
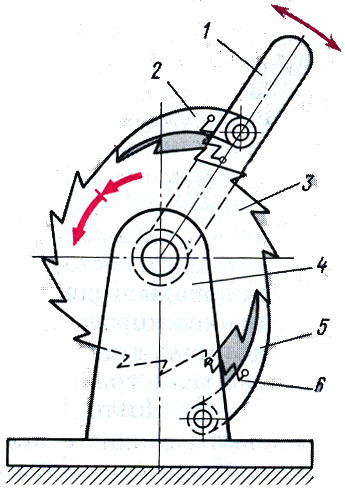
При качаниях коромысла 1 качающаяся собачка 3 сообщает вращение храповому ко�лесу 2 только при движении коромысла про�тив часовой стрелки. Для удержания колеса 2 от самопроизвольного поворота па часовой стрелке при движении коромысла против хода часов служит стопорная собачка 4.
Мальтийские и храповые механизмы широко применяются в станках и приборах,
Если необходимо передать на относительно большое расстояние механическую энергию из одной точки пространства а другую, то приме�няют механизмы с гибкими звеньями.
В качестве гибких звеньев, передающих движение от одного эвена механизма к другому, используются ремни, канаты, цепи, нити, ленты, шарики и т.п.,
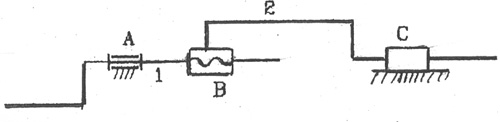
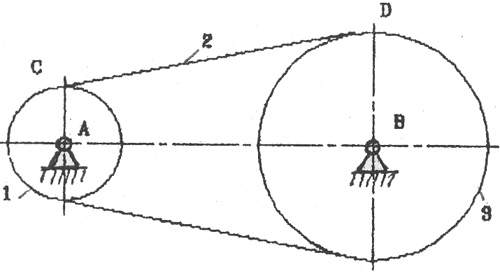
На рис. 2.14 приведена структурная схема простейшего механизма с гибким звеном.
Передачи с гибкими звеньями широко при�меняются в машиностроении, приборостроении и в других отраслях промышленности.
Выше были рассмотрены наиболее типичные простейшие механизмы. механизмов приводятся и специальной Литературе, па-свидетельствах и справочниках, например таких, как [7, 9, 14].
Структурные формулы механизмов.
Существуют общие закономерности в структуре (строении) самых различных механизмов, связывающие число степеней свободы W механизма с числом звеньев и числом и видом его кинематических пар. Эти закономерности носят название структурных формул механизмов.
Для пространственных механизмов в настоящее время наиболее распространена формула Малышева, вывод которой произ�водится следующим образом.
Пусть в механизме, имеющем m звеньев (включая, стойку), - число одно-, двух-, трех-, четырех- и пятиподвижных пар. Число подвижных звеньев обозначим . Если бы все подвижные звенья были свободными телами, общее число степеней свободы было бы равно 6n. Однако каждая одноподвижная пара V класса накладывает на относительное движение звеньев, образующих пару, 5 связей, каждая двухподвижная пара IV класса - 4 связи и т. д. Следовательно, общее число степеней свободы, равное шести, будет уменьшено на величину
где - подвижность кинематической пары, - число пар, подвижность которых равна i. В общее число наложенных связей может войти некоторое число q избыточных (повторных) связей, которые дублируют другие связи, не уменьшая подвиж�ности механизма, а только обращая его в статически неопредели�мую систему [12]. Поэтому число степеней свободы пространствен�ного механизма, равное числу степеней свободы его подвижной кинематической цепи относительно стойки, определяется по следую�щей формуле Малышева:
или в краткой записи
(2.2)
при механизм – статически определимая система, при - статически неопределимая система.
В общем случае решение уравнения (2.2) - трудная задача, поскольку неизвестны W и q; имеющиеся способы решений сложны и не рассматриваются в данной лекции. Однако в частном случае, если W, равное числу обобщенных координат механизма, найдено из геометрических соображений, из этой формулы можно найти число избыточных связей (см. Решетов Л. Н. Конструирование рациональных механизмов. М., 1972)
(2.3)
и решить вопрос о статической определимости механизма; или же, зная, что механизм статически определимый, найти (или прове�рить) W.
Важно заметить, что в структурные формулы не входят размеры звеньев, поэтому при структурном анализе механизмов можно предполагать их любыми (в некоторых пределах). Если избыточных связей нет (), сборка механизма происходит без деформиро�вания звеньев, последние как бы самоустанавливаются; поэтому такие механизмы называют самоустанавливающимися [12] . Если избыточные связи есть (), то сборка механизма и движение его звеньев становятся возможными только при деформировании последних.
Для плоских механизмов без избыточных связей структурная формула носит имя П. Л. Чебышева, впервые предложив�шего её в 1869 году для рычажных механизмов с вращательными парами и одной степенью свободы. В настоящее время формула Чебышева распространяется на любые плоские механизмы и выво�дится с учетом избыточных связей следующим образом
Пусть в плоском механизме, имеющем т звеньев (включая стойку), -число подвижных звеньев, - число низших пар и - число высших пар. Если бы все подвижные звенья были свободными телами, совершающими плоское движение, общее число степеней свободы было бы равно Зn. Однако каждая низшая пара накладывает на относительное движение звеньев, образующих пару, две связи, оставляя одну степень свободы, а каждая высшая пара накладывает одну связь, оставляя 2 степени свободы.
В число наложенных связей может войти некоторое число избыточных (повторных) связей, устранение которых не увеличива�ет подвижности механизма. Следовательно, число степеней свободы плоского механизма, т. е. число степеней свободы его подвижной кинематической цепи относительно стойки, определяется по следую�щей формуле Чебышева:
(2.4)
Если известно, отсюда можно найти число избыточных связей
(2.5)
Индекс «п» напоминает о том, что речь идет об идеально плос�ком механизме, или точнее о его плоской схеме, поскольку за счет неточностей изготовления плоский механизм в какой-то мере явля�ется пространственным.
По формулам (2.2)-(2.5) проводят структурный анализ имею�щихся механизмов и синтез структурных схем новых механизмов.
Структурный анализ и синтез механизмов.
Влияние избыточных связей на работоспособность и надежность машин.
Как было сказано выше, при произволь�ных (в некоторых пределах) размерах звеньев механизм с избыточ�ными связями () нельзя собрать без деформирования звеньев. Поэтому такие механизмы требуют повышенной точности изготовле�ния, в противном случае в процессе сборки звенья механизма деформируются, что вызывает нагружение кинематических пар и звеньев значительными дополнительными силами (сверх тех основ�ных внешних сил, для передачи которых механизм предназначен). При недостаточной точности изготовления механизма с избыточны�ми связями трение в кинематических парах может сильно увеличить�ся и привести к заклиниванию звеньев, поэтому с этой точки зрения избыточные связи в механизмах нежелательны.
Что касается избыточных связей в кинематических цепях меха�низма, то при конструировании машин их следует стремиться устранять или же оставлять минимальное количество, если полное их устранение оказывается невыгодным из-за усложнения конструкции или по каким-либо другим соображениям. В общем случае оптимальное решение следует искать, учитывая наличие необходимого технологического оборудования, стоимость изготовле�ния, требуемые ресурс работы и надежность машины. Следователь�но, это весьма сложная задача для каждого конкретного случая.
Методику определения и устранения избыточных связей в кинематических цепях механизмов рассмотрим на примерах.
Пусть плоский четырехзвенный механизм с четырьмя одноподвижными вращательными парами ( рис. 2.15, а) за счет неточностей изготовления (например, вследствие непараллельности осей A и D) оказался пространственным. Сборка кинематических цепей 4, 3, 2 и отдельно 4, 1 не вызывается трудностей, а точки B, B’ можно расположить на оси х. Однако собрать вращательную пару В, образованную звеньями 1 и 2, можно будет, лишь совместив системы координат Bxyz и B’x’y’z’, для чего потребуется линейное перемещение (деформация) точки B’ звена 2 вдоль оси х и угловые деформации звена 2 вокруг осей х и z (показаны стрелками). Это означает наличие в механизме трёх избыточных связей, что подтверждается и по формуле (2.3): . Что бы данный пространственный механизм был статически определимый, нужна его другая структурная схема, например изображённая на рис. 2.15, б, где Сборка такого механизма произойдёт без натягов, поскольку совмещение точек В и В’ будет возможно за счёт перемещения точки С в цилиндрической паре.
Возможен вариант механизма (рис. 2.15, в) с двумя сферическими парами (); в этом случае, помимо основной подвижности механизма появляется местная подвижность - возможность вращения шатуна 2 вокруг своей оси ВС; эта подвижность не влияет на основной закон движения механизма и может быть даже полезна с точки зрения выравнивания износа шарниров: шатун 2 может при работе механизма поворачиваться вокруг своей оси за счёт динамических нагрузок. Формула Малышева подтверждает, что такой механизм будет статически определимым:
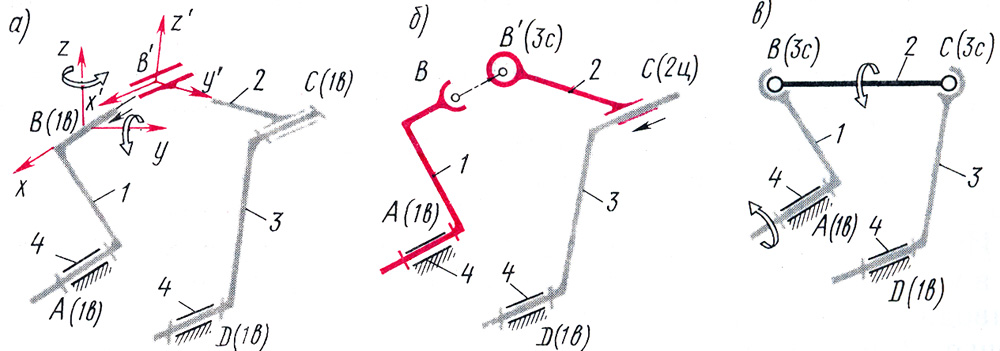
Рис. 2.15
Наиболее простой и эффективный способ устранения избыточ�ных связей в механизмах приборов - применение высшей пары с точечным контактом взамен звена с двумя низшими парами; сте�пень подвижности плоского механизма в этом случае не меняется, поскольку, по формуле Чебышева (при ):
На рис. 2.16, а,б,в дан пример устранения избыточных связей в кулачковом механизме с поступательно движущимся роликовым толкателем. Механизм (рис. 2.16, а) - четырехзвенный (); кроме основной подвижности (вращение кулачка 1) имеется мест�ная подвижность (независимое вращение круглого цилиндрического ролика 3 вокруг своей оси); следовательно, . Плоская схема избыточных связей не имеет (механизм собирается без натягов, ). Если вследствие неточностей изготов-ления механизм считать пространственным, то при линейном контакте ролика 3 с кулачком 1 по формуле Малышева при получим , но при определенном условии. Кинематическая пара цилиндр - цилиндр (рис. 2.16, 6) при невозможности относительного поворота звеньев 1, 3 вокруг оси z была бы трехподвижной парой. Если же такой поворот вследствие неточности изготовления имеет место, но мал, и практи�чески сохраняется линейный контакт (при нагружении пятно кон�такта по форме близко к прямоугольнику), то данная 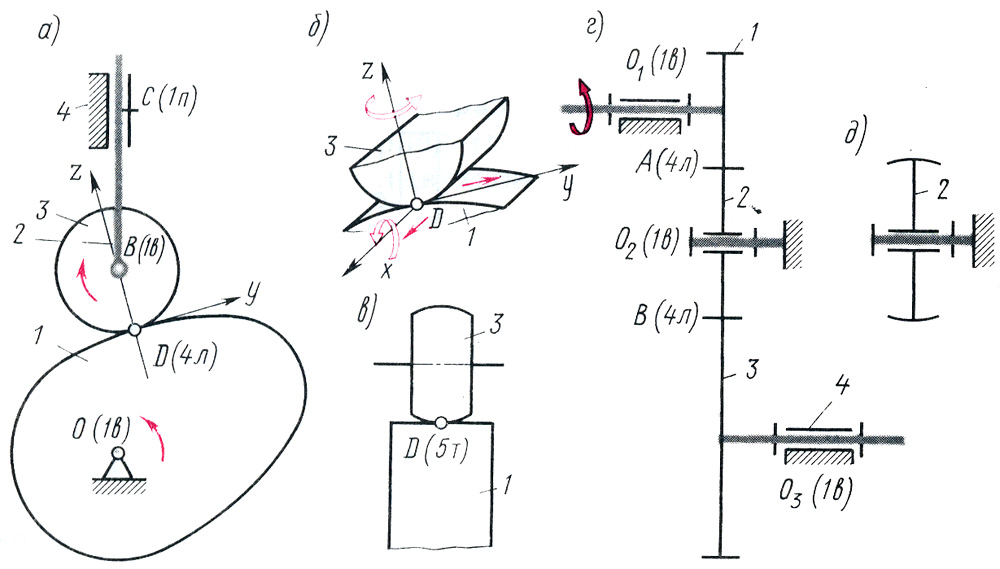
кинемати�ческая пара будет четырехподвижной, следовательно, и
Рис.2.17
Снижая класс высшей пары путем применения бочкообразного ролика (пятиподвижная пара с точечным контактом, рис. 2.16, в), получим при и - меха�низм статически определимый. Однако при этом следует помнить, что линейный контакт звеньев, хотя и требует при повышен�ной точности изготовления, позволяет передать большие нагрузки, чем точечный контакт.
На рис.2.16, г, д дан другой пример устранения избыточных связей в зубчатой четырехзвенной передаче (, контакт зубьев колес 1, 2 и 2, 3 - линейный). В этом слу�чае, по формуле Чебышева, - плоская схема избыточных связей не имеет; по формуле Малышева, - механизм статически неопреде�лимый, следовательно, потребуется высокая точность изготовления, в частности для обеспечения параллельности геометрических осей всех трех колес.
Заменяя зубья промежуточного колеса 2 на бочкообразные (рис. 2.16, д), получим статически определимый механизм.
Кинематическая пара