Структурный синтез механизмов

Лекция N3

Структурный синтез механизмов.

Проектирование механизма по заданным входным и выходным условиям называется синтезом.

Синтез механизмов является самым ответственным этапом при создании будущей машины. Синтез представляет собой сложную задачу, которая обычно имеет многовариантное решение. Поэтому для выбора наиболее подходящего из получившихся решений необходимо производить дополнительный их анализ.

Неоднозначность решений при синтезе происходит из-за того, что:

• во-первых, на этапе разработки технического задания на создание нового механизма (машины) обычно невозможно правильно и однозначно сформулировать требования, предъявляемые к ним;

• во-вторых, одни и те же условия могут быть воспроизведены как несколькими различными по структуре механизмами, так и одним и тем же механизмом, но имеющим различные размеры звеньев.

Традиционно синтез механизмов [23,15] проводят в два этапа:

1) определяют структуру будущего механизма (структурный синтез);

2) по заданным кинематическим или динамическим свойствам определяют размеры его звеньев (параметрический синтез).

В последние годы также начинает активно развиваться структурно-параметрический синтез механизмов [15,5], при котором одновременно определяются и структура механизма, и размеры его звеньев.

Задачей структурного синтеза является разработка структурной схемы будущего механизма по заданной подвижности, с учётом желаемых структурных, кинематических и динамических свойств.

Результаты структурного синтеза механизмов обычно многовариантны. Это связано с тем, что, используя одни и те же кинематические пары, но по-разному их расставив, можно получить различные по структуре механизмы. Поэтому окончательный выбор рациональной структурной схемы будущей машины выполняется с учетом:

• кинематических и динамических свойств той или иной схемы;

• технологичности и надежности звеньев и кинематических пар, в нее входящих;

• условий сборки и эксплуатации и других условий.

Научные основы структурного синтеза механизмов разрабатываются более ста лет. Первые основополагающие работы в этом направлении были сделаны П.Л. Чебышевым и Л.В. Ассуром. Однако анализ научной литературы [2,3,4,8,11,12,15,*], посвященной структурному синтезу машин и механизмов, позволяет сделать вывод, что этот раздел теории машин и механизмов является еще слабо разработанным.

В настоящее время традиционно выбор структуры вновь проектируемой машины ведут либо интуитивно, опираясь на опыт и квалификацию разработчиков, либо путем наслоения структурных групп [2,3,5,8,11]. Эти подходы обычно позволяют найти приемлемое решение. Однако такое решение не всегда рационально, поскольку невозможно проанализировать все варианты.

Структурный синтез простых и сложных механизмов с помощью структурных групп.

Наиболее распространенным методом создания механизмов с замкнутыми кинематическими цепями в настоящее время является метод присоединения к элементарным механизмам структурных групп или групп Accypa. Этот метод образования механизмов впервые был предложен Л.В. Ассуром для так называемых плоских замкнутых цепей, заканчивающихся -во всех направлениях поводками с вращательными или поступательными кинематическими парами.

Кинематические цепи, обладающие нулевой подвижностью относительно внешних кинематических пар и не распадающиеся на более простые цепи, удовлетворяющие этому условию, получили название структурных групп или групп Ассура.

Структурную формулу любого простого или сложного механизма. образованного с помощью структурных групп, можно представить следующим образом:

(3.1)

где W - подвижность синтезируемого механизма; - подвижность элементарного механизма; - подвижность структурной группы; m - число элементарных первичных механизмов; n - число присоединяемых структурных групп; i=1, 2, ... m; j =1, 2, ... n.

Так как подвижность присоединяемых (ой) структурных(ой) групп(ы) равна нулю, то , а значит, (3.1) эквивалентно выражению:

(3.2)

Анализ (3.2) показывает, что присоединяемые к элементарномк механизму структурные группы не влияют на подвижность простого или сложного механизма. Они только изменяют его структуру и законы движения звеньев.

Число подвижных контуров К, количество кинематических пар и количество звеньев n, входящих в структурную группу, можно установить с помощью структурных формул:

(3.3)

(3.4)

где - общее число кинематических пар в механизме, П – подвижность пространства.

Для механизмов существующих в шестиподвижном пространстве (П=6), которые в технической литературе принято называть пространственные выражение (3.3) примет вид хорошо известной формулы Сомолова-Мальшева:

Для механизмов, существующих в трёхподвижном пространстве (плоских механизмов) П=3, выражение (3.3) примет вид формулы П.Л. Чебышева:

Так как по определению подвижность структурных групп равна нулю, то (3.3) для структурных групп примет следующий вид:

(3.3`)

Формулы (3.3) и (3.4) описывают любую структурную группу Ассура.

Распишем, например, (3.3) для одно-, двух-, ... , шестиподвижных пространств. В результате получим следующие условия существования структурных групп в различных пространствах:

(3.5)

(3.6)

(3.7)

(3.8)

(3.9)

(3.10)

Из (3.5) следует, что в одноподвижном пространстве структурные группы существовать не могут, а это означает, что в одноподвижном пространстве механизмы не могут иметь замкнутых кинематических цепей, т.е. в таком пространстве могут существовать только механизмы с незамкнутыми кинематическими цепями.

Из (3.6) следует, что простейшей структурной группой (структурной единицей) является монада, которая состоит из одного звена и двух кинематических пар. На рис. 3.1 приведена в качестве примера структурная единица (монада), существующая в двухподвижном пространстве, которая используется для образования клинового механизма.

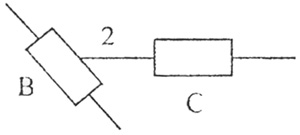
В соответствии с (3.6) эта монада имет одно звено 2 и две внешние кинематические пары С и В, которыми она затем присоединяется к стойке и звену 1 элементарного механизма. В результате этого образуется клиновой механизм.

На рис.3.2, а представлена монада, существующая в трехподвижном пространстве, на основе которой созданы зубчатые и кулачковые механизмы. В соответствии с (3.7) эта монада должна иметь одно звено, одну одноподвижную и одну двухподвижную кинематические пары.

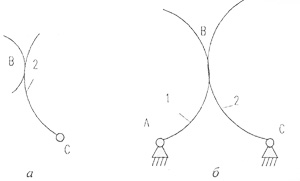
Рис. 3.2. Структурная единица и механизм, существующие и трехподвижном пространстве:

А - структурная единица; б - механизм; А,С - вращательная кинематическая пара; В - высшая двухподвижная кинематическая пара; 1 - звено элементарного механизма; 2 - структурная единица.

Присоединив эту монаду к элементарному механизму, получим простой механизм (рис. 3.2, 6), который является аналогом зубчатого и кулачкового механизмов.

Структурная группа, существующая в трехподвижном пространстве и имеющая только одноподвижные кинематичесие пары, в соответствии с (3.7) должна состоять из двух звеньев и трёх одноподвижных кинематических пар. Эта группа носит название диады Сильвестера или двухповодковой группы и приведена на рис. 3.3, а.

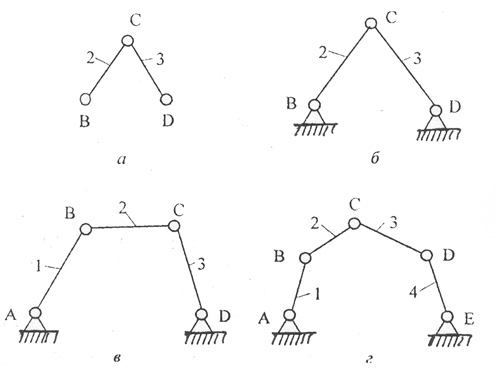
Рис. 3.3. Двухповодковая структурная группа и простые механизмы на её основе:

а - диада Сильвестера; б - статически определимая ферма, в - одноподвижный четырехзвенник;

г - двухподвижный пятизвенник; 1, 2 ... 4 ~ подвижные звенья; А, В ... Е - кинематические пары

Если двухповодковую группу связать шарнирами В и D со стойкой, то получим элементарную статически определимую ферму (рис.3.3, 6).

Присоединив эту двухповодковую структурную группу к одному неподвижному и одному или двум подвижным звеньям 1 и 4 элементарных механизмов, получим простой механизм с одной (рис.3.3, в) или двумя (рис.3.3, г) степенями свободы.

Синтез структурных групп с помощью структурных формул

Анализ (3.6),...,(3.10) показывает, что, задаваясь различными кинематическими парами и звеньями для каждого пространства, можно синтезировать множество структурных групп.

Рассмотрим синтез структурных групп с помощью структурных формул на примере наиболее распространенных в технике механизмов, которые существуют в трехмерном (М=3) трехподвижном (П=3) пространстве, допускающем два поступательных перемещения вдоль осей X и Y и одно вращательное вокруг оси Z.

Структурная формула групп Ассура для механизмов, существующих в трехподвижном пространстве, имеет вид (3.7)

Уравнение (3.7) для структурных групп в трехподвижном пространстве, можно переписать в виде:

(3.11)

Решив (3.11) относительно числа одноподвижных кинематических пар, получим

(3.12)

Равенство (3.12) устанавливает связь между ч иск кинематических пар и подвижных звеньев, входящих в структуру* группу. Так как число звеньев и кинематических пар в группе Ассура может быть только целым числом, условию (3.12) могут удовлетворять следующие сочетания чисел звеньев и кинематических пар

n	2	4	6	8	…
P1	3	6	9	12	…

Первое из этих соответствий между подвижными звеньями и кинематическими звеньями реализуется в рассмотренной диаде Сильвестера (рис. 3.3, а).

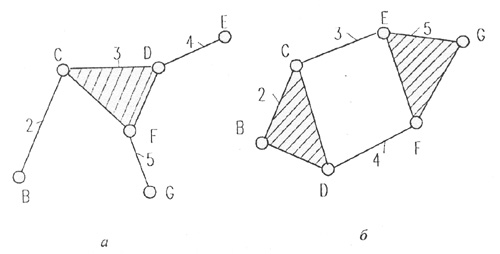
Второе сочетание чисел звеньев (n=4) и кинематических пар () позволяет реализовать две различные структурные группы. Эти группы приведены на рис. 3.4.

Рис. 3.4. Структурные группы, содержащие чегыре подвижных звена

и шесть кинематических пар:

а - структурная группа стремя внешними кинематическими пирами;

б - структурная группа с двумя внешними книсмш нческими парами.

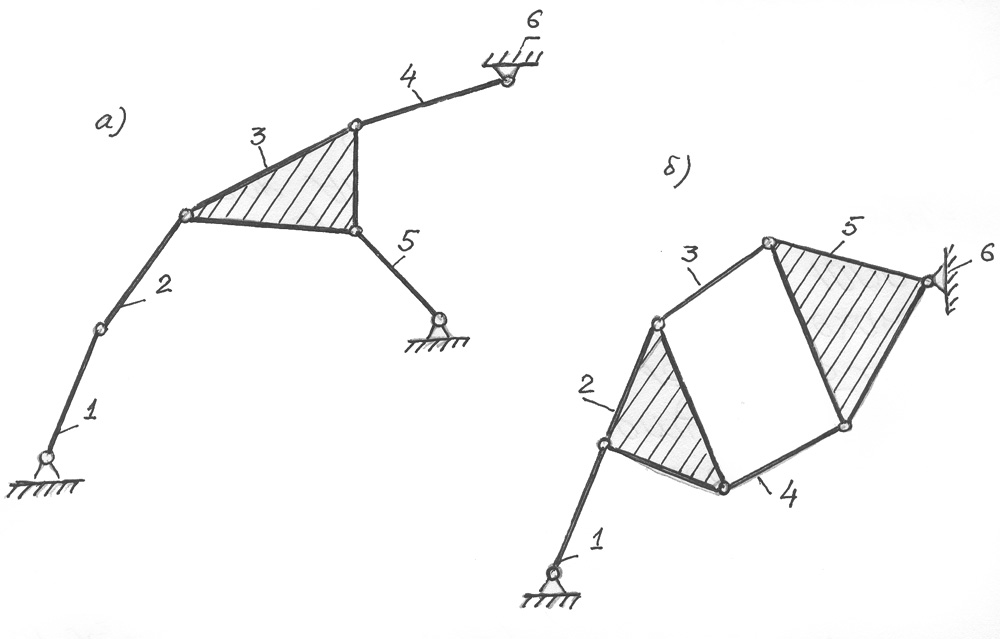
Присоединение структурных групп, изображенных на рис.3.4, а,б, к элементарным механизмам и стойке приводит к образованию следующих простых механизмов (рис.3.5).

Рис.3.5

Заметим, что в механизме (рис.3.5, а) в зависимости от выбора начального звена можно выделить две или одну структурные группы. Действительно, если в качестве начального звена выбрать звено 1, то структурная группа будет иметь вид, изображенный на рис. 3.4, а. Однако если за начальное звено взять, например, звено 5, то в механизме (рис.3.5) можно выделить две двухповодковые структурные группы (диады Сильвестера).

Классификация структурных групп.

Анализ (3.6),..., (3.10) показывает, что в машинах и механизмах имеется большое количество разнообразных структурных групп. Это усложняет их анализ и синтез. С целью упрощения изучения и анализа группы Ассура пытаются классифицировать.

В настоящее время нет единой классификации всех структурных групп. Наиболее полно проклассифицированы только группы Accура, существующие в трехмерном трёхподвижном пространстве, допускающем два независимых поступательных движения вдоль осей Х и Y и одно вращательное вокруг оси Z. Отметим, что в современном машиностроении именно механизмы, существующие в трехмерном трехподвижном пространстве, нашли самое широкое распространение на практике. Потому в данной лекции рассмотрим структурную классификацию структурных групп и так называемых плоских механизмов.

Напомним, что механизмы с высшими парами можно привести к механизмам с низшими кинематическими парами. В настоящее время признано, что лучшей классификацией механизмов с низшими кинематическими парами, которые существуют в трехмерном трехподвижном пространстве, является структурная классификация Ассура-Артоболевского [3]. Достоинством этой классификации является то, что с ее помощью не только упрощаются структурный анализ и синтез механизмов, но и она увязывается с методами кинематического, силового и динамического исследования механизмов.

Каждый рычажный механизм рассматривается как система, состоящая из элементарного первичного механизма, который в классификации Ассура-Артоболевского назван механизмом 1 класса, и соединенных с ним и между собой структурных групп.

Все механизмы и структурные группы, в них входящие, делятся на классы, а класс механизма в целом определяется высшим классом структурной группы, которая в него входит.

Элементарные механизмы условно отнесены к механизмам 1 класса.

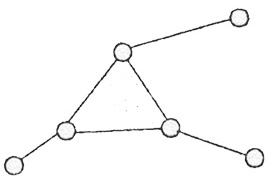
Класс структурной группы определяется числом кинематических пар, входящих в замкнутый контур, образованный внутренними кинематическими парами.

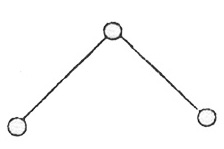
При этом двухповодковая структурная группа (рис.3.3, а), не имеющая замкнутого контура, отнесена ко второму классу (см. табл. 3.1)

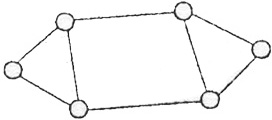
Порядок группы определяется числом внешних кинематических пар.

Так как на практике наибольшее применение нашла двухповодковая группа, то, в зависимости от места размещения на ней вращательных и поступательных кинематических пар, эта группа разделяется еще и по видам (рис.3.11).

N п/п	Структурная схема	Класс группы	Порядок группы	Вид группы
1		II	2	I
2		III	3	-
3		IV	2	-

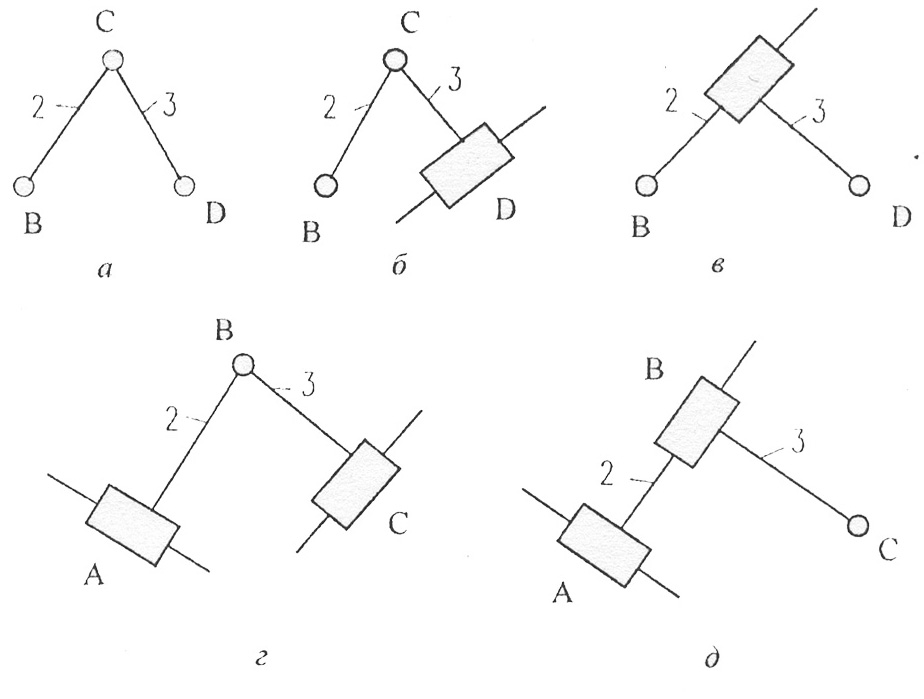
Рис. 3.11 Виды двухповодковых структурных групп:

а – диада 1 вида; б – диада 2 вида; в – диада 3 вида; г – диада 4 вида; д – диада 5 вида

К первому виду отнесена диада, у которой все кинематические пары - вращательные (рис. 3.11, а). Диада, у которой одна из внешних кинематических пар является поступательной, отнесена ко второму виду (рис. 3.11, 6). Диада, у которой внутренняя пара поступательная, относится к третьему виду (рис. 3.11, в). Двухповодковая группа, у которой две внешние кинематические пары поступательные, отнесена к четвертому виду (рис. 3.11, г). И, наконец, группа, у которой одна внешняя и внутренняя пары - поступательные, отнесена к пятому виду (рис. 3.11, д).

Казалось бы, что идя по пути последовательной замены в диаде Сильвестера вращательных кинематических пар поступательными, можно заменить все три вращательные пары на поступательные. Однако этого делать нельзя, так как в этом случае получим не структурную группу, а клиновой, который, конечно же, не является структурной группой и даже существует в другом по подвижности пространстве.

При проектировании механизмов без избыточных связей чаще всего применяется метод наслоения групп, предложенный Л.В. Ассуром. При этом механизм образуется из первичного механизма (обычно кривошип со стойкой) и присоединённых к нему групп нулевой подвижности. Что бы избежать избыточных связей, необходимо, что бы они отсутствовали как в первичном механизме так и в присоединяемых группах. При структурном синтезе механизма без избыточных связей с W=1 (в частном случае) необходимо соблюдать правила:

Замкнутая кинематическая цепь механизма с W=1 и одним контуром без избыточных связей (q=0) должна иметь такой набор кинематических пар, что бы сумма их подвижностей была равна семи (7) для пространственного механизма и четырём (4) для плоского.
Последующие присоединяемые группы звеньев, образующий после присоединения замкнутый контур, должны иметь в своём составе набор кинематических пар, сумма подвижностей которого равна 6 для пространственного механизма и 3 для плоского.

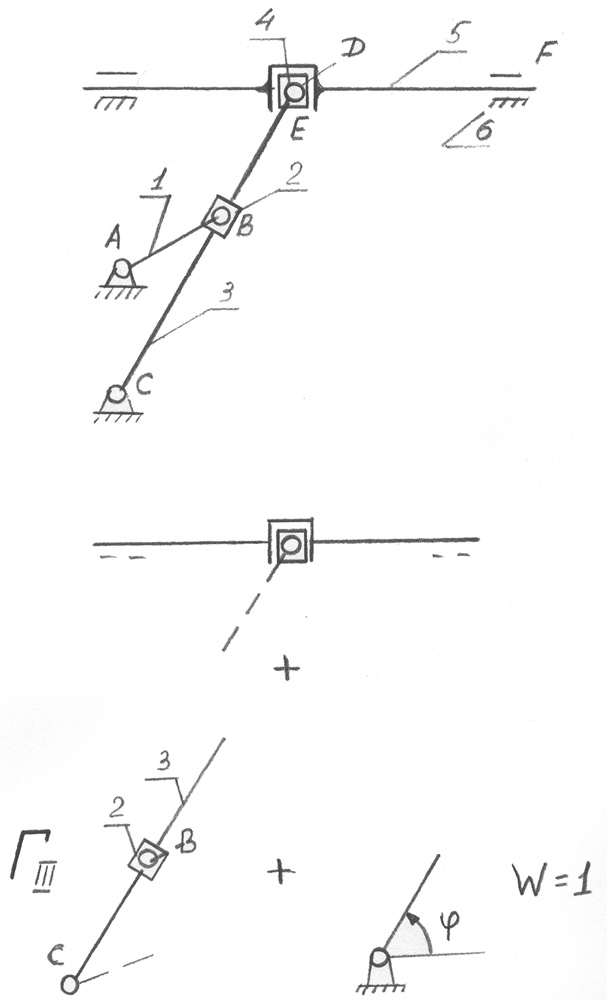
Давайте разберем несколько примеров структурного анализа.

Дано:

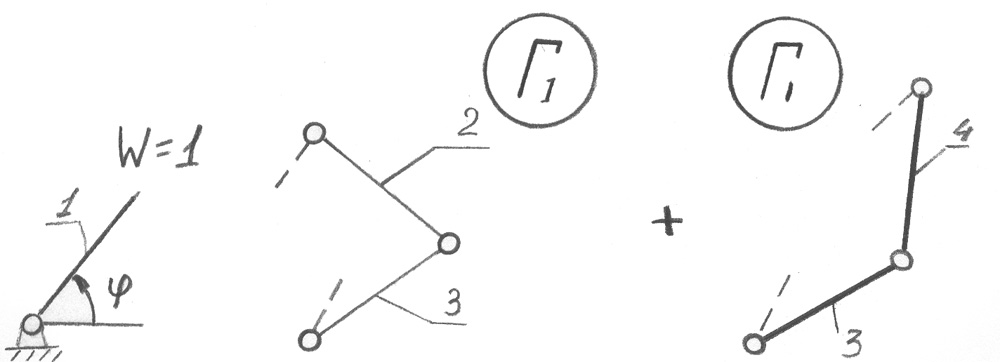
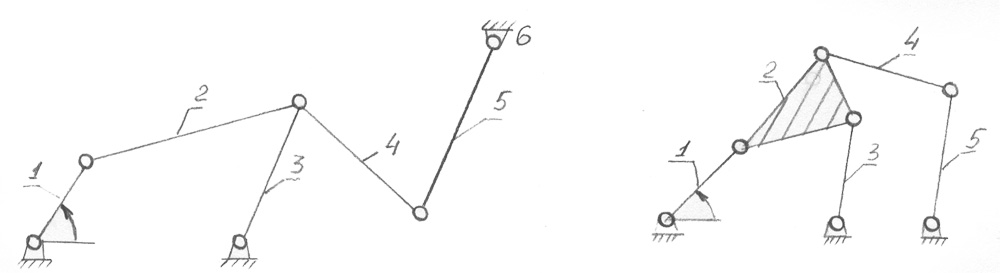
2. Дано:

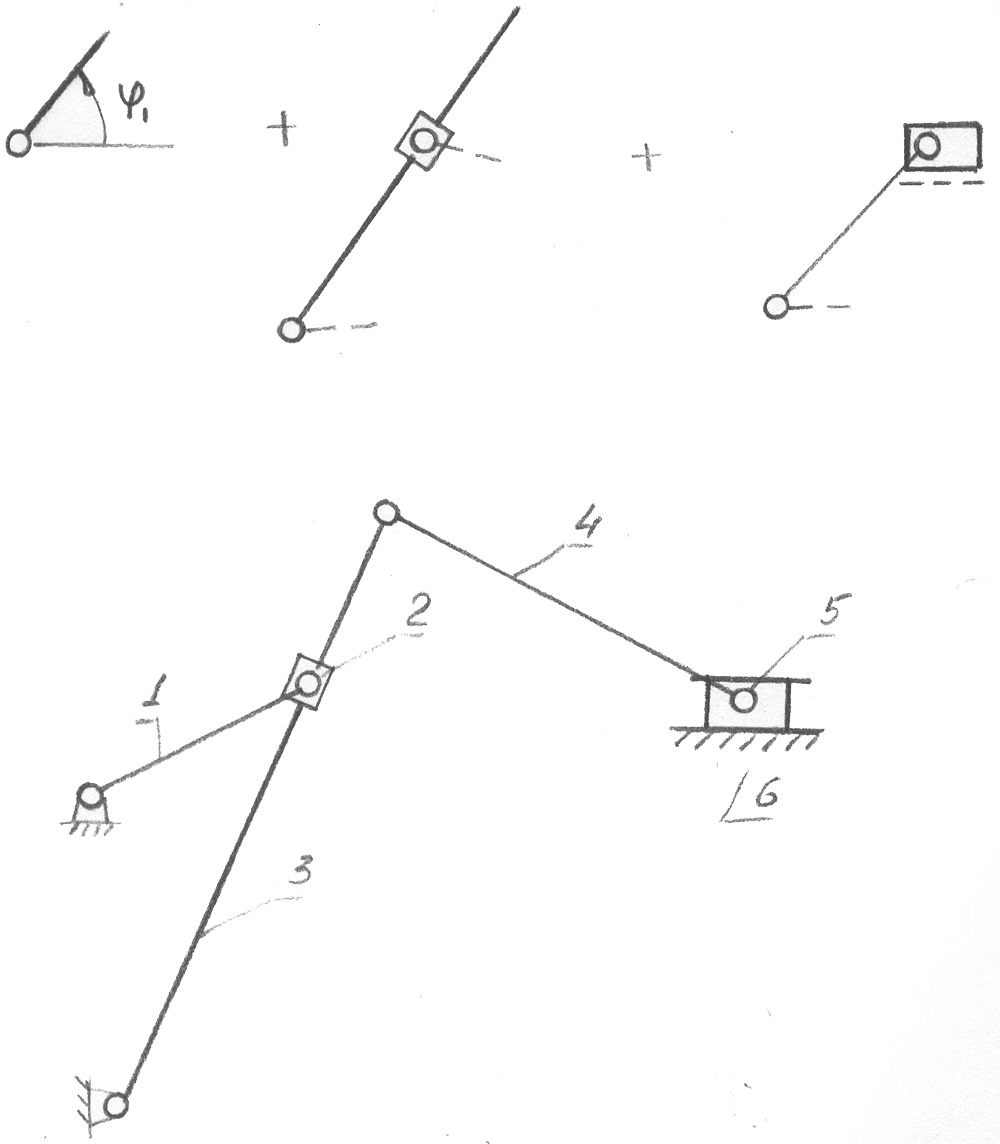
Структурный анализ – задача обратная синтезу. Структурный анализ заданного механизма следует производить путём расчленения его на структурные группы и первичные механизмы в порядке обратном образованию механизма.

От структурной схемы механизма при этом отделяют по одной все структурные группы таким образом, что бы оставшаяся цепь продолжала быть механизмом. После снятия всех групп далжны остаться первичные механизмы, количество которых определяет число степеней свободы механизма

3. Дано: Поперечно-строгальный станок.

Структурный синтез механизмов