Основной принцип МНК: Сумма квадратов ошибки модели должна быть минимальной
Министерство образования и науки рф
филиал федерального Государственного бюджетного образовательного учреждения высшего
профессионального образования
Уфимского государственного нефтяного
технического университета в г.октябрьском
Кафедра ИТМЕН
ПРАКТИЧЕСКАЯ РАБОТА
по дисциплине “Математические методы обработки результатов экспериментов”
|
Выполнил: студент группы БГРз 12-10 |
Кирюков Е. М. |
|
Проверил: |
Усман Ф.К. |
ОКТЯБРЬСКИЙ 2014
Практическая работа №2
Метод наименьших квадратов
Основной принцип МНК: Сумма квадратов ошибки модели должна быть минимальной.
Условие задачи :
Изучается зависимость средней ожидаемой продолжительности жизни от нескольких факторов по данным за 1955 г. С этой целью по 14-ти странам были получены данные по нескольким факторам, влияющим на продолжительность жизни, (таблица 1).
Таблица 1
|
Название страны |
y |
x1 |
x2 |
|
Мозамбик |
47 |
3 |
2,6 |
|
Бурунди |
49 |
2,3 |
2,6 |
|
Чад |
48 |
2,6 |
2,5 |
|
Непал |
55 |
4,3 |
2,5 |
|
Буркина -Фасо |
49 |
2,9 |
2,8 |
|
Мадагаскар |
52 |
2,4 |
3,1 |
|
Бангладеш |
58 |
5,1 |
1,6 |
|
Гаити |
57 |
3,4 |
2 |
|
Мали |
50 |
2 |
2,9 |
|
Нигерия |
53 |
4,5 |
2,9 |
|
Кения |
58 |
5,1 |
2,7 |
|
Того |
56 |
4,2 |
3 |
|
Индия |
62 |
5,2 |
1,8 |
Решение:
- Изучим влияние фактора х1 на среднюю ожидаемую продолжительность жизни по методу наименьших квадратов.
Для определения формы функциональной зависимости между переменными у и х1 построим диаграмму рассеяния.
На основании диаграммы рассеяния можно сделать вывод о позитивной зависимости продолжительности жизни от фактора х1 (т.е. у будет расти с ростом х1). Наиболее подходящая форма функциональной зависимости — линейная.
Требуется найти уравнение прямой y=ax+b, наилучшим образом согласующейся с опытными точками.
Для этого составим и решим систему уравнений:
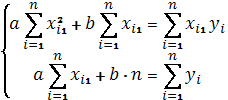
Построим таблицу 2 с данными для решения системы уравнений.
Таблица 2
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
xi |
3 |
2,3 |
2,6 |
4,3 |
2,9 |
2,4 |
5,1 |
3,4 |
2 |
4,5 |
5,1 |
4,2 |
5,2 |
6,5 |
53,5 |
|
yi |
47 |
49 |
48 |
55 |
49 |
52 |
58 |
57 |
50 |
53 |
58 |
56 |
62 |
50 |
744 |
|
xi2 |
9 |
5,29 |
6,76 |
18,49 |
8,41 |
5,76 |
26,01 |
11,56 |
4 |
20,25 |
26,01 |
17,64 |
27,04 |
42,25 |
228,47 |
|
xiyi |
141 |
112,7 |
124,8 |
236,5 |
142,1 |
124,8 |
295,8 |
193,8 |
100 |
238,5 |
295,8 |
235,2 |
322,4 |
325 |
2888,4 |
Получим и решим систему уравнений:
228,47a + 53.5 b = 2888,4
53.5a + 14b=744
228,47a + 53.5 b = 2888,4
6.287b= 288.828
a=1,883864062
b=45,94381
Итак, а=1,883864062 b=45,94381
Таким образом y = 1,8838x+45,94381
Следовательно, при увеличении показателя фактора х1 на единицу при прочих равных условиях средняя ожидаемая продолжительность жизни в среднем увеличивается на 1,8838 единиц.
Графически такая зависимость имеет вид:
- Изучим влияние фактора х2 на среднюю ожидаемую продолжительность жизни по методу наименьших квадратов.
На основании диаграммы рассеяния можно сделать вывод о зависимости валового дохода от стоимости оборотных средств (т.е. у будет уменьшаться с ростом х2). Наиболее подходящая форма функциональной зависимости — линейная.
Требуется найти уравнение прямой y=ax+b, наилучшим образом согласующейся с опытными точками.
Для этого составим и решим систему уравнений:
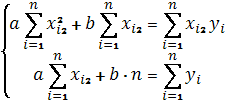
Построим таблицу с данными для решения системы уравнений.
Таблица 3
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
xi |
2,6 |
2,6 |
2,5 |
2,5 |
2,8 |
3,1 |
1,6 |
2 |
2,9 |
2,9 |
2,7 |
3 |
1,8 |
2,9 |
35,9 |
|
yi |
47 |
49 |
48 |
55 |
49 |
52 |
58 |
57 |
50 |
53 |
58 |
56 |
62 |
50 |
744 |
|
xi2 |
6,76 |
6,76 |
6,25 |
6,25 |
7,84 |
9,61 |
2,56 |
4 |
8,41 |
8,41 |
7,29 |
9 |
3,24 |
8,41 |
94,79 |
|
xiyi |
122,2 |
127,4 |
120 |
137,5 |
137,2 |
161,2 |
92,8 |
114 |
145 |
153,7 |
156,6 |
168 |
111,6 |
145 |
1892,2 |
Получим и решим систему уравнений:
94,79 a + 35.9b = 1892.2
35.9 a + 14 b = 744
94,79 a + 35.9b = 1892.2
94.79a +35.9 b = 1892.2
94,79 a + 35.9b = 1892.2
-1.06545b = -722501
a= - 5.7202
b= 67.811
Итак, а= - 5.7202 b= 67.811
Таким образом y= - 5.7202x + 67.811
Следовательно, при увеличении фактора х2 на единицу при прочих равных условиях ожидаемая продолжительность жизни в среднем уменьшается на 5,7202 единиц.
Графически зависимость имеет вид:
- Рассмотрим влияние факторов х1 и х2 на среднюю ожидаемую продолжительность жизни.
На основании диаграммы рассеяния можно сделать вывод о позитивной зависимости продолжительности жизни от стоимости фактора х1 и о негативной зависимости продолжительности жизни от фактора х 2(т.е. у будет расти с ростом х1 и у будет убывать с ростом х2 ). Форма функциональной зависимости — линейная.
В целом необходимо определить параметры двухфакторной эконометрической модели- y=ах1+bx2+c ,наилучшим образом согласующейся с опытными точками.
Оценим параметры линейной двухфакторной эконометрической модели с помощью метода наименьших квадратов. Для этого составим и решим систему уравнений:
Собранные данные представлены в таблице 4:
Таблица 4

|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
xi1 |
3 |
2,3 |
2,6 |
4,3 |
2,9 |
2,4 |
5,1 |
3,4 |
2 |
4,5 |
5,1 |
4,2 |
5,2 |
6,5 |
53,5 |
|
xi2 |
2,6 |
2,6 |
2,5 |
2,5 |
2,8 |
3,1 |
1,6 |
2 |
2,9 |
2,9 |
2,7 |
3 |
1,8 |
2,9 |
35,9 |
|
yi |
47 |
49 |
48 |
55 |
49 |
52 |
58 |
57 |
50 |
53 |
58 |
56 |
62 |
50 |
744 |
|
xi1 xi2 |
7,8 |
5,98 |
6,5 |
10,75 |
8,12 |
7,44 |
8,16 |
6,8 |
5,8 |
13,05 |
13,77 |
12,6 |
9,36 |
18,85 |
134,98 |
|
xi12 |
9 |
5,29 |
6,76 |
18,49 |
8,41 |
5,76 |
26,01 |
11,56 |
4 |
20,25 |
26,01 |
17,64 |
27,04 |
42,25 |
228,47 |
|
xi22 |
6,76 |
6,76 |
6,25 |
6,25 |
7,84 |
9,61 |
2,56 |
4 |
8,41 |
8,41 |
7,29 |
9 |
3,24 |
8,41 |
94,79 |
|
yi xi1 |
141 |
112,7 |
124,8 |
236,5 |
142,1 |
124,8 |
295,8 |
193,8 |
100 |
238,5 |
295,8 |
235,2 |
322,4 |
325 |
2888,4 |
|
yi xi2 |
122,2 |
127,4 |
120 |
137,5 |
137,2 |
161,2 |
92,8 |
114 |
145 |
153,7 |
156,6 |
168 |
111,6 |
145 |
1892,2 |
Получим систему уравнений:
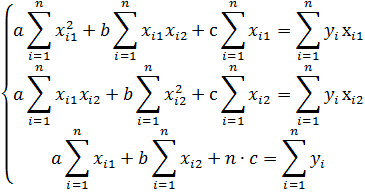
228.47a + 134.98b + 53.5c = 2888.4
134.98a + 94.79b + 35.9c = 1892.2
53.5a + 35.9b + 14c = 744
228.47a + 134.98b + 53.5c = 2888.4
25.464b -7.2651c = - 314,377700
-18.33b -6.2865c = -288,827664
228.47a + 134.98b + 53.5c = 2888.4
25.464b -7.2651c = - 314,377700
1,46811c = 86,859049
228.47a + 134.98b + 53.5*59,16393 = 2888.4
25.464b -7.2651*59,16393 = - 314,377700
c = 59,16393
228.47a + 134.98*(-4,53409) + 53.5*59,16393 = 2888.4
b = -4,53409
c = 59,16393
a = 1,4668944
b = -4,53409
c = 59,16393
Итак, а = 1,4668944 b = -4,53409 c= -59,16393
Таким образом y= 1,4668944x1 - 4,53409 x2 - 59,16393
Вывод: Данная функциональная зависимость позволяет примерно прогнозировать зависимость средней продолжительности жизни от нескольких факторов (х1 и х2)
Коэффициент a= 1,4668944 показывает, что при прочих равных условиях с увеличением влияния фактора х1 на единицу средняя продолжительность жизни увеличится в среднем на 1,4668944 единиц.
Коэффициент b= -4,53409 показывает, что при прочих равных условиях с увеличением влияния фактора х2 на единицу средняя продолжительность жизни уменьшится в на 4,53409 единиц.
Пример:
МНК может применяться и в повседневной жизни. в медицине он служит показателем зависимости артериального давления человека от окружающих параметров, то есть от тех же самых факторов. В зависимости от температуры, влажности воздуха, атмосферного давления и времени суток состояние человека может изменяться. Все данные заносятся в таблицы, подобные тем, что представлены выше в соответствии с изменяющимися факторами. Проанализировав данные наблюдатель может проследить за тенденцией изменения здоровья и понять, что именно влияет на человека.
PAGE \* MERGEFORMAT1
Основной принцип МНК: Сумма квадратов ошибки модели должна быть минимальной