Подрезание и заострение зуба

Лекция 15.

Подрезание и заострение зуба.

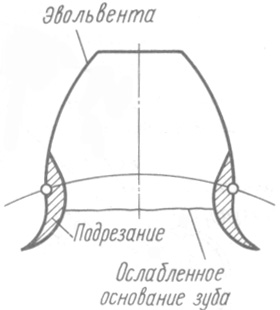
Согласно свойствам эвольвентного зацепления (см. лекцию 14) прямолинейная, т. е. эвольвентная, часть ИПК и эвольвентная часть профиля зуба колеса располагаются касательно друг к другу только на линии станочного зацепления, начинающейся в точке N. Левее этой точки прямолинейный участок ИП не касается эвольвентного профиля зуба колеса, а пересекает его. Так как ИПК физически представляет собой тот след, который режущая кромка инструмента оставляет на материале изготавливаемого колеса, то указанное пересечение приводит к подрезанию зуба колеса у его основания (рис. 15.1) Подрезание уменьшает эвольвентную часть профиля зуба колеса и ослабляет зуб в его опасном сечении.

Подрезание не происходит, когда граница Вl', активной части линии станочного зацепления располагается правее точки N (см. рис. 14.6, a), т. е. когда выполняется условие:

P0N P0Bl’ (15.1)

Используя условие (15.1), определим минимальное число зубьев колеса, при котором они не будут подрезаны. Из P0ON (см. рис. 14.6, а) следует, что P0N = P0O*sin , а из P0FBl’, что P0 Bl’ = P0F/sin

Подставляя величины P0N и P0Bl’ в условие (15.1) и решая относительно z, имеем:

z 2(ha* - x)/sin2 (15.2)

Если x = 0, то из этого выражения получается минимальное число зубьев колеса без смещения, которые не будут подрезаны реечным инструментом

zmin = 2ha*/ sin2 (15.3)

При проектировании колес без смещения число зубьев необходимо брать равным пли больше zmin. В случае стандартного инструмента (ha* = 1,0; = 20o) zmin 17.

Для косозубых колес уравнение (15.3) приобретает вид:

zmin = 2ha* cos()/sin2

Следовательно, косозубые колеса менее подвержены подрезанию зубьев, поскольку t > , а cos < 1. В лекции 14 было указано, что для уменьшения габаритов зубчатых передач колеса следует проектировать с малым числом зубьев. Однако при z < 17, чтобы не произошло подрезания, колеса должны быть изготовлены со смещением инструмента. Выясним, каково же то минимальное смещение, при котором не получается подрезания зубьев. Оно определяется также из выражения (15.1), на основании которого, используя (15.2), можно записать, что

Подставляя сюда значение sin2 из (15.3) и решая относительно х, имеем:

(15.4)

а, переходя к минимальному значению xmin, получим формулу

(15.5)

Из зависимости (15.5) следует, что зубчатое колесо, имеющее z > zmin, можно нарезать с положительным, нулевым и даже с отрицательным смещением, поскольку для такого колеса xmin < 0. Для зубчатого колеса, у которого z = zmin, можно взять положительное или нулевое смещение, а для колеса, у которого z < zmin - только положительное смещение.

Если увеличивать коэффициент смещения, то толщина зуба sa у вершины будет уменьшаться. При некотором коэффициенте смещения, называемом максимальным (xmin), наступает заострение зуба (sa = 0). Опасность заострения особенно велика у колес с малым числом зубьев (меньше 15).

Для предотвращения излома вершины заостренного зуба коэффициент смещения назначают так, чтобы толщина sa была бы не меньше 0,2m (sa > 0,2m). Толщину зуба sa при проектировании определяют по уравнению, положив ry = ra и y = a ; согласно уравнению (14.2) cosa = rb/ra.

Эвольвентная зубчатая передача.

Элементы эвольвентной зубчатой передачи. На рис. 15.2 показана зубчатая передача внешнего зацепления w (угол зацепления), полюс зацепления P, межосевое расстояние аw, начальные окружности радиусами rw1 и rw2. Эти элементы были рассмотрены ранее (в лекции 13) при знакомстве со свойствами эвольвентного зацепления.

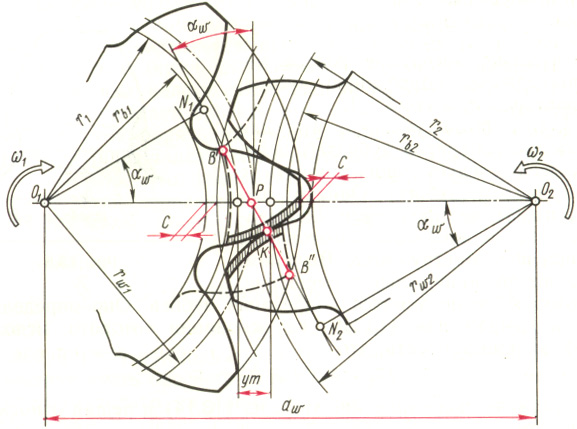
В точках В’ и B’’ линия зацепления пересекается окружностями вершин зубьев колес; в точке В’ сопряженные профили входят в зацепление, а в точке B’’ - выходят из зацепления. Процесс взаимодействия главных поверхностей сопряженных зубьев происходит на участке В’B’’ линии зацепления; эта часть линии зацепления называется активной линией зацепления. Зубчатая передача должна быть спроектирована так, чтобы участок В’B’’ укладывался в пределах линии зацепления N1N2. Если точки В’ и B’’ выйдут за эти пределы, то в зубчатой передаче произойдет заклинивание.

При заданном направлении вращения только одна сторона зуба будет передавать и воспринимать усилие; ее называют рабочей стороной (профилем) зуба. В зацеплении участвуют активные профили зубьев, расположенные на рабочих сторонах зубьев, которые соответствуют активной линии зацепления. На рис. 15.2 активные профили заштрихованы.

Между окружностью вершин одного колеса и окружностью впадин другого имеется расстояние, которое называется радиальным зазором. На рис. 15.2 радиальный зазор отмечен буквой С его величина выражается произведением коэффициента с* на модуль, т.е С = с*m, где с* = 0,25.

Уравнения эвольвентной зубчатой передачи.

При составлении уравнений для определения угла зацепления w и межосевого расстояния aw следует иметь в виду, что номинальные значения этих величин подсчитывают при условии, что зубья одного колеса входят во впадины другого плотно, без бокового зазора. Учтя это, а также то, что начальные окружности катятся друг по другу без скольжения, запишем sw1 = ew2 и sw2 = ew1, где sw1 и sw2 - толщина зубьев, а ew1 и ew2 - ширина впадин по начальным окружностям колес зубчатой передачи.

Поскольку начальные окружности перекатываются без скольжения, то шаги pw1 и pw2 пo этим окружностям равны друг другу: pw1 = pw2 = pw.

Шаг pw = sw1 + ew1, или, поскольку sw2 = ew1 :

pw = sw1 + sw2 (15.6)

С другой стороны, шаг по начальной окружности :

Учитывая уравнения (14.2), (14.3) и (14.6), выразим толщину зубьев sw1 и sw2 по формуле (14.6) и подставим в (15.6). Проделав несложные преобразования, получим уравнение для определения угла зацепления :

invw = inv + 2xtg/z (15.7)

где x = x1 + x2, z = z1 + z2. После подсчета инволюты угла зацепления по уравнению (15.7) сам угол w следует определить по таблице инволютной функции.

Межосевое расстояние зубчатой передачи:

аw = rw1 + rw2

Учитывая зависимость (14.6), можно записать:

поэтому межосевое расстояние

(15.8)

Межосевое расстояние может быть выражено также следующим образом (рис. 15.2):

аw = r1 + r2 +ym (15.9)

где ym - расстояние между делительными окружностями. Оно называется воспринимаемым смещением, а величина у - коэффициентом воспринимаемого смещения.

Приравнивая (15.8) и (15.9) и учитывая (14.3), получим формулу для определения коэффициента воспринимаемого смещения:

(15.10)

При расчете косозубых передач применяют те же формулы, что и при расчете прямозубых, но вместо параметров m и берут m/cos и t а произведения xtg и уm сохраняют без изменения.

Определим уравнительное смещение зубчатой передачи. При геометрическом проектировании передачи должны бить выполнены два условия: 1) зубья колес должны зацепляться друг с другом теоретически без бокового зазора; 2) между окружностями вершин и впадин зубчатых колес должен быть стандартный радиальный зазор c = c*m = 0,25m.

Выполнение первого условия обеспечивается тем, что межосевое расстояние выражается через воспринимаемое смещение по формуле (15.9). Второе условие требует, чтобы:

aw = ra1 + с*m + rf2 (15.11)

Совместное решение уравнений (15.9) и (15.11) дает:

r1 + ym + r2 = ra1 + C + rf2

или

r1 + ym + r2 = ra1 + C + ra2 - h

Подставляя в это равенство формулы для ra1, ra1 и h из лекции 14 после преобразования придем к выражению:

ym = x1m - ym + x2m

откуда получим у - коэффициент уравнительного смещения, упомянутый ранее

у = x - y (15.12)

Итак, уравнительное смещение ym (cм. схему станочного зацепления) вводится для получения зубчатой передачи без бокового зазора и со стандартной величиной радиального зазора.

Если зубчатая передача составлена из колес без смещений (x1 = 0, x2 = 0, x = 0, x = x1 + x2 = 0), то, согласно уравнениям (15.7), (15.10), (15.12) и (15.9) такая передача будет характеризоваться следующими параметрами: угол зацепления w = = 20°, коэффициент воспринимаемого смещения y = 0, коэффициент уравнительного смещении y = 0, межосевое расстояние aw = r1 + r2 = m(z1 + z2)/2, т.е. равно сумме радиусов делительных окружностей. При указанных условиях радиусы начальных окружностей rw1 = mz1/2 = r1, rw2 = mz2/2 = r2 т.е. начальные окружности колес совпадают с их делительными окружностями.

Особенности эвольвентной передачи внутреннего зацепления. На рис. 15.3 изображена передача внутреннего зацепления. Меньшее колесо (шестерня), обозначенное номером 1, имеет внешние зубья; большее колесо, именуемое просто колесом и обозначенное номером 2. имеет внутренние зубья. Инструментом для изготовления колес с внутренними зубьями способом сгибания является не реечный

инструмент, а долбяк (инструментальное колесо), число зубьев и основные размеры которого стандартизованы. При изготовлении колес долбяком может произойти не только подрезание и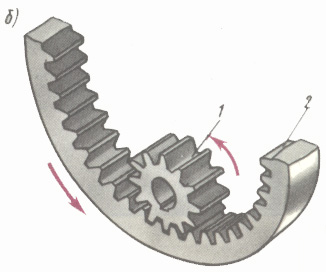

заострение зубьев, но и срезание их у вершины. Предотвращение этого явления должно быть учтено при проектировании передачи внутреннего зацепления.

При внутреннем зацеплении, в отличии от внешнего, эвольвентные профили Э1 и Э2 пересекаются на участке N1N2. Кроме того, при внутреннем зацеплении может иметь место еще один вид пересечения эвольвент, если числа зубьев шестерни (z1) и колеса (z2) близки друг к другу.

В правильно спроектированной передаче внутреннего зацепления должны отсутствовать оба вида пересечения эвольвентных профилей. Это значит, что активная часть линии внутреннего зацепления должна целиком находиться вне отрезка N1N2. Кроме того, числа зубьев z1 и z2 должны подчиняться определенным ограничениям.

Для передачи, составленной из колес без смещений, нарезаемых стандартным долбяком, необходимо иметь z1 20, z2 85, а разность z1 - z2 8. Если передачу составить из колес со смещениями. то z'i и 22—2i можно существенно уменьшить и сократить тем самым размеры всей передачи.

Качественные показатели зубчатой передачи.

Выбор расчетных коэффициентов смещения.

Рассмотрим качественные показатели, которые дают возможность оценить передачу в отношении плавности и бесшумности зацепления, возможного износа и прочности зубьев, а также сравнить ряд передач по тем же показателям. Такая оценка важна для рационального назначения расчетных коэффициентов смещения при проектировании зубчатых передач.

Коэффициент пере-крытия учитывает непрерыв-ность и плавность зацепления в передаче. Такие качества передачи обеспечиваются перекрытием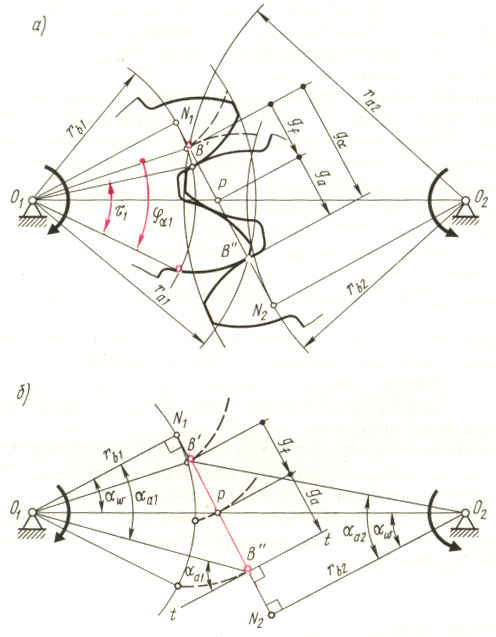

работы одной пары зубьев работой другой пары. Для этого каждая последующая пара зубьев должна войти в зацепление еще до того, как предшествующая пара выйдет из зацепления. О величине перекрытия судят по коэффициенту перекрытия, который выражают отношением угла торцового перекрытия к угловому шагу. Угол торцового перекрытия - это угол

поворота колеса от положения зубьев при входе в зацепление, когда они касаются в точке В’, до положения зубьев при выходе из зацепления, когда они касаются в точке B'' (рис. 15.4, a). Следовательно, коэффициент перекрытия прямозубой передачи

(15.13)

Здесь 1 = 2/z1 - угловой шаг; = g/rb1, где g = gf + ga - длина активной линии зацепления. Она складывается из длин дополюсной gf и заполюсной ga частей активной линии зацепления (рис. 15.4):

gf = rb2(tga2 - tgw) (15.14)

ga = rb1(tga1 - tgw) (15.15)

Подстановка (15.14) и (15.15) в (15.13) с учетом (14.5) дает формулу для определения коэффициента перекрытия прямозубой передачи:

(15.16)

Если при расчете по формуле (15.16) получится < 1, то в этом случае непрерывности процесса зацепления зубьев не будет: одна пара зубьев успеет выйти из зацепления еще до того, как следующая пара зубьев войдет в него. Поэтому минимально допустимым значением является 1,05 которое обеспечивает непрерывность процесса зацепления с 5%-ным запасом.

Важно отметить, что коэффициент перекрытия уменьшается при увеличении коэффициентов смещения x1 и x2. Поэтому при проектировании передачи коэффициенты смещения надо назначать так, чтобы не получился бы меньше 1,05.

Продолжительность зацепления одной пары зубьев в косозубой передаче ( 0) больше, чем в прямозубой ( = 0). Поэтому и коэффициент перекрытия косозубой передачи больше и подсчитывается по формуле

= + (15.17)

В этой сумме слагаемое определяется по формуле (15.16). Второе слагаемое = b/px. Здесь b = m - ширина зубчатого колеса, - коэффициент ширины зубчатого колеса, назначаемый из условий прочности и износостойкости зуба, px = m/sin - осевой шаг косого зуба. Подставив b и px в выражение для получим:

= sin/ (15.18)

Как непосредственно следует из уравнений (15.17) и (15.18), коэффициент перекрытия косозубой передачи ( 0) больше коэффициента перекрытия прямозубой ( = 0), что является достоинством косозубой передачи.

Коэффициент скольжения учитывает влияние геометрических и кинематических факторов на величину проскальзывания профилей в процессе зацепления. Наличие скольжения при одновременном нажатии одного профиля на другой приводит к износу профилей. Коэффициенты скольжения выражаются формулами:

1 = ск/K1-K; 2 = ск/K2-K

где ск - скорость скольжения; K1-K и K2-K - скорости перемещения точек контакта по профилям зубьев первого и второго колеса.

За время одного оборота колеса с меньшим числом зубьев z1 второе колесо не завершает полный оборот. Следовательно, его зубья в u12 раз реже вступают в контакт, чем зубья первою колеса, и поэтому меньше изнашиваются. Для того чтобы сравнивать интенсивность износа зубьев по коэффициентам скольжения, разделим 2 на u12 = 1/2 = z1/z2 :

1 = ск/K1-K; 2 = ск/(K2.K u12)

Расчетные формулы для 1 и 2 имеют такой вид:

(15.19)

где lK - величина алгебраическая, выражающая расстояние от полюса зацепления Р до текущего положения точки К контакта пары зубьев (см. рис. 15.2); lP1 и lP2 - абсолютные значения длин отрезков РN1 и РN2.

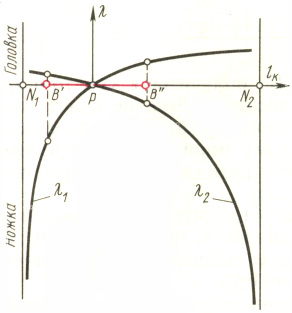
В процессе зацепления точка контакта К зубьев движется вдоль линии зацепления от положения В' (вход зубьев в зацепление) до положения В" (выход зубьев из зацепления). Отсюда следует, что расстояние lK изменяется от значения (-В'P) до нуля и затем от нуля до значения (+В"P). Поэтому, как вытекает из формул (15.19), коэффициенты скольжения 1 и 2 также изменяются в процессе зацепления. Наибольшее значение 1 приобретает в положении и В' , а 2 - в положении B" (рис. 15.5).

Коэффициенты скольжения 1 и 2 зависят от коэффициентов смещения x1 и x2 . Воздействуя на x1 и x2, конструктор получает значения коэффициентов 1 и 2, отвечающие условиям эксплуатации.

Коэффициент удельного давления учитывает влияние геометрии зубьев (радиусов кривизны их профилей) на величину контактных напряжений, возникающих в местах соприкосновения зубьев. При чрезмерном нагружении контактные напряжения могут быть столь значительны, что вызовут выкрашивание материала на рабочей поверхности зубьев.

Контактные напряжения определяются по формуле Герца:

где Q - сила взаимодействия зубьев; b - ширина зубчатых колес; E = 2E1E2/( E1 + E2) - приведенный модуль упругости их материалов; - приведенный радиус кривизны эвольвентных профилей в точке контакта, посредством которою определяется влияние геометрии зуба на контактные напряжения.

Для текущего момента зацепления зубьев (см. рис. 15.2)

или, согласно свойствам эвольвентных профилей:

Коэффициентом удельного давления называется отношение:

(15.20)

Коэффициент - величина безразмерная, не зависящая от модуля m, так как пропорционален модулю.

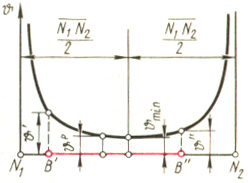
Поскольку точка К контакта зубьев движется вдоль линии зацепления, расстояние N1K увеличивается, а расстояние N2K уменьшается (см. рис. 15.2) Поэтому, как следует из уравнения (15.20), коэффициент удельного давления изменяется в процессе зацепления. График этого изменения представлен на рис. (15.6)

Подставив коэффициент в формулу Герца, получим:

Коэффициент удельного давления уменьшается при увеличении коэффициентов смещения х1 и х2. Поэтому конструктор может снижать контактные напряжения, назначая коэффициенты смещения х1 и х2 так, чтобы коэффициент имел возможно меньшее значение.

Выбор расчетных коэффициентов смещения для передач внешнего зацепления. При назначении коэффициентов смещения х1 и х2 для любой передачи должны быть выполнены следующие три условия: 1) отсутствие подрезания; 2) отсутствие заострения; 3) непрерывность зацепления. Первое условие применительно к шестерне выполняется, если её коэффициент смещения х1 превосходит свой минимальный уровень хmin1. Второе и третье условия ограничивают коэффициент смещения х1 шестерни верхними пределами х’max1 и х’’max1. Эти пределы неодинаковы, и для расчета зубчатой передачи важен тот xmax1, который имеет меньшее значение. Таким образом, коэффициент смещения х1 шестерни надо назначать так, чтобы соблюдалось соотношение хmin1 х1 хmax1. To же самое следует сказать и о коэффициенте смещения х2 колеса, хmin2 х2 хmax2.

Внутри указанных пределов коэффициенты смещения х1 и х2 надо назначать так, чтобы зависящие от них качественные показатели передачи, характеризующие ее свойства (плавность хода, износостойкость, прочность), имели бы оптимальные значения. При этом надо учитывать конкретные условия работы передачи: быстроходность, характер нагрузки, наличие или отсутствие закрытой масляной ванны, материалы шестерни и колеса и вид их термообработки и др.

Контрольные вопросы к лекции N15:

1. Запишите условия отсутствия подрезания в станочном зацеплении.
2. Что такое ? Выведите формулу для определения .
3. Что такое ? Выведите формулу для .
4. Выведите формулу для определения угла зацепления эвольвентной передачи внешнего зацепления.
5. Какая эвольвентная передача называется передачей без смещения?
6. По каким признакам классифицируют зубчатые передачи?
7. Перечислите основные качественные показатели цилиндрической эвольвентной передачи?
8. Что такое коэффициент торцевого перекрытия? Выведите формулу для .
9. Как записывается формула для коэффициента осевого перекрытия?

Подрезание и заострение зуба