Сумматоры
Лекция 18
Сумматоры
1. Определение и классификация сумматоров
Сумматоры – это КЦУ, выполняющие арифметическое (в противоположность логическому) сложение и вычитание чисел. Они имеют самостоятельное значение и являются также ядром схем арифметико-логических устройств (АЛУ), реализующих ряд разнообразных операций и являющихся непременной частью всех про�цессоров.
Аппаратная сложность и быстродействие сумматора являются очень важны�ми параметрами и поэтому разработано множество вариантов сумматоров, которые имеют разветвлённую классификацию. Выделяя главные варианты, остановимся на следующих типах сумматоров:
1) одноразрядный сумматор;
2) сумматор для последовательных операндов;
3) сумматор для параллельных операндов с последовательным переносом;
4) сумматор для параллельных операндов с параллельным переносом;
5) сумматор с последовательным распространением переноса по цепочке замкнутых ключей;
6) сумматор групповой структуры с цепным переносом;
7) сумматор групповой структуры с параллельным межгрупповым переносом;
8) сумматор с условным переносом;
9) накапливающий сумматор.
Наряду с сумматорами могут быть реализованы вычитатели, однако это поч�ти никогда не делается, поскольку вычитание выполняется посредством сложения с применением дополнительных либо обратных кодов.
2. Одноразрядный сумматор
Одноразрядный сумматор имеет три входа (два слагаемых и перенос из предыдущего разряда) и два выхода (суммы и переноса в следующий разряд).
Таблица истинности одноразрядного сумматора имеет вид, представленный в табл. 1.
Таблица 1
|
ai
|
bi
|
ci–1
|
ci
|
si
|
|
|
0
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
1
|
1
|
|
0
|
1
|
1
|
1
|
0
|
0
|
|
1
|
0
|
0
|
0
|
1
|
1
|
|
1
|
0
|
1
|
1
|
0
|
0
|
|
1
|
1
|
0
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
1
|
0
|
Как видно из таблицы, совокупность сигналов ci и si по сути является двухзначной суммой трёх чисел ai, bi и ci–1 .
Аналитические выражения функций суммы S (от англ. sum) и переноса С (от англ. Carry) имеют вид
; .
В базисе Шеффера функции si и ci выражаются следующим образом:
; .
Непосредственное воспроизведение полученных формул на элементах двух�ступенчатой логики И-ИЛИ-НЕ приводит к применению элемента 2-2-2И-ИЛИ-НЕ для выработки сигнала переноса и элемента 3-3-3-3И-ИЛИ-НЕ для сигнала суммы . Такое решение используется в некоторых сериях микросхем, но более популярно решение, приводящее к некоторому сокра�щению аппаратной сложности схемы при сохранении минимальной задерж�ки по цепи переноса. Идея этого решения состоит в использовании полу�ченного уже значения в качестве вспомогательного аргумента при вычислении .
Из табл. 1 видно, что во всех её строчках, кроме первой и последней, si = . Чтобы сделать формулу справедливой также в первой и последней строчках, нужно убрать единицу в строчке нулевых входных величин и до�бавить единицу в строчку единичных входных величин, что приводит к со�отношению
.
Схема сумматора, построенного по этому соотношению, показана на рис. 1, а.
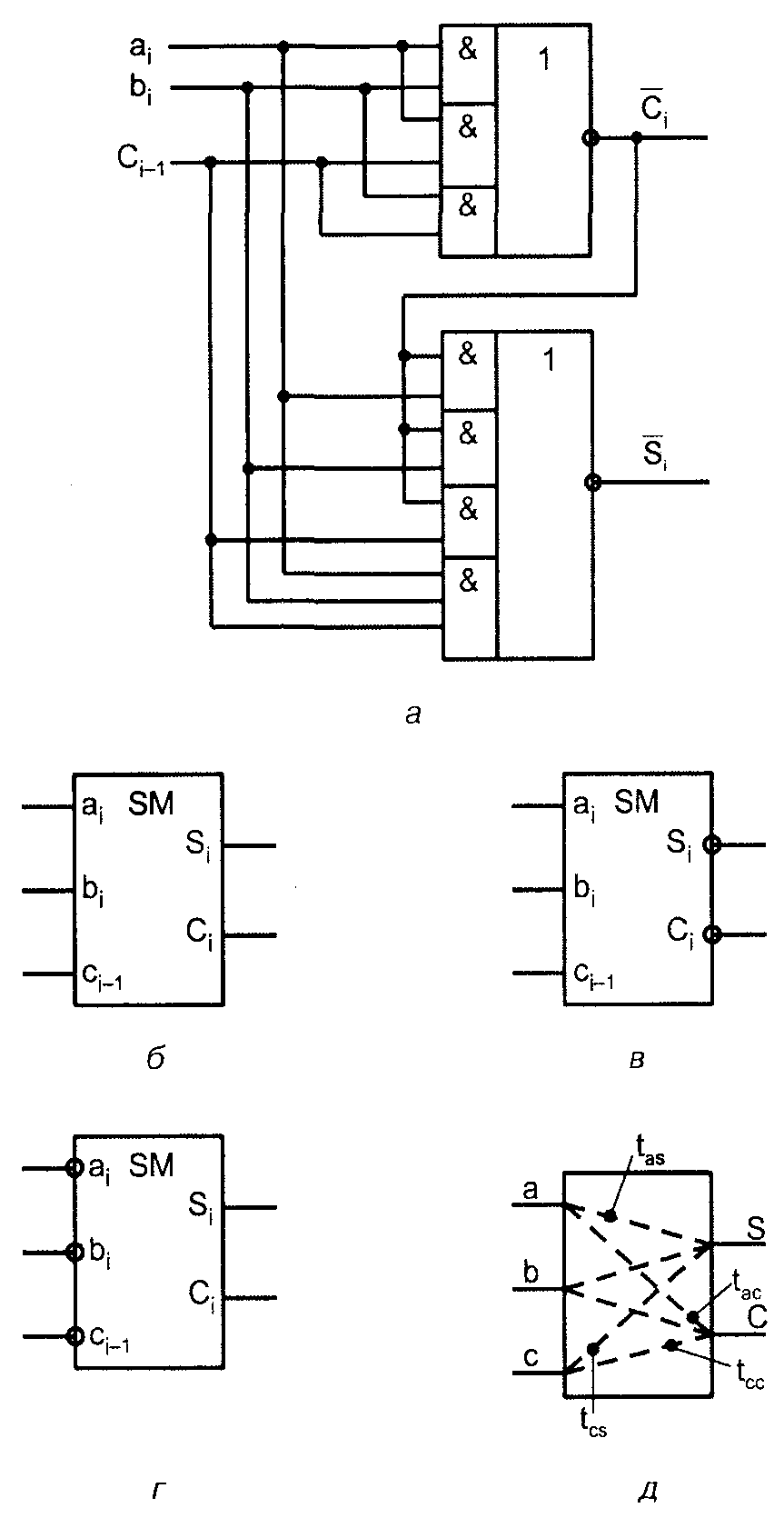
Рис. 1. Схема (а), условные обозначения (б, в, г) и пути распространения сигналов одноразрядного сумматора (д)
Можно привести ещё одно выражение для si , в котором происходит инвертирование на первой и последней комбинациях:
.
Это выражение, хотя и красиво с идейной точки зрения, но немного сложнее в реализации, чем приведённое выше соотношение.
Из табл. 1 видно, что и функция суммы, и функция переноса обладают свойством самодвойственности: при инвертировании всех аргументов ин�вертируется и значение функции, т. е.
, .
Условное обозначение одноразрядного сумматора показано на рис. 1, б. Для варианта с выработкой инвертированных значений суммы и переноса на основании свойства самодвойственности можно пользоваться двумя ва�риантами обозначений для одной и той же схемы (рис. 1, в, г).
Быстродействие одноразрядного сумматора оценивается задержками по шести трактам распространения сигналов: от первого слагаемого до выхода суммы, от первого слагаемого до выхода переноса, от второго слагаемого до тех же выходов и от входа переноса до выхода переноса, от входа переноса до выхода суммы (рис. 1, д). Так как тракты от обоих слагаемых обычно одинаковы, то остаются четыре задержки, отмеченные надписями tas , tac , tcc и tcs на рис. 1, д.
На рис. 2 показана схема сумматора, входящая в библиотеку схемных ре�шений семейства программируемых СБИС фирмы Altera.
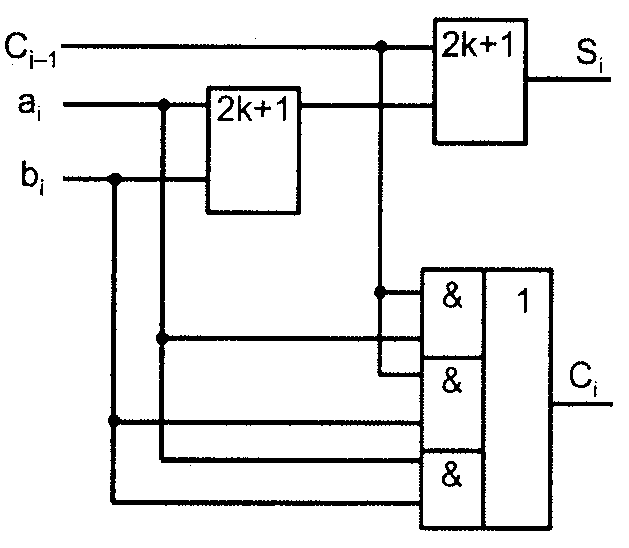
Рис. 2. Схема одноразрядного сумматора из библиотеки схемных решений
для СБИС фирмы Altera
3. Последовательный сумматор
Сумматор для последовательных операндов содержит всего один одноразряд�ный сумматор, обрабатывающий поочерёдно разряд за разрядом, начиная с младшего. Сложив младшие разряды, одноразрядный сумматор вырабатывает сумму для младшего разряда результата и перенос, который запоминается на один такт.
В следующем такте складываются вновь поступившие разряды слагаемых a1 и b1 с переносом из младшего разряда и т. д. Схема сумматора последователь�ных операндов (рис. 3, а), помимо сумматора, содержит сдвигающие реги�стры слагаемых и суммы, а также триггер запоминания переноса. Регистры и триггер тактируются синхроимпульсами СИ.
На рис. 3, б показана временная диаграмма, соответствующая операции сложения двух операндов 101 + 110 = 1011 или в десятичном выражении 5 + 6= 11.
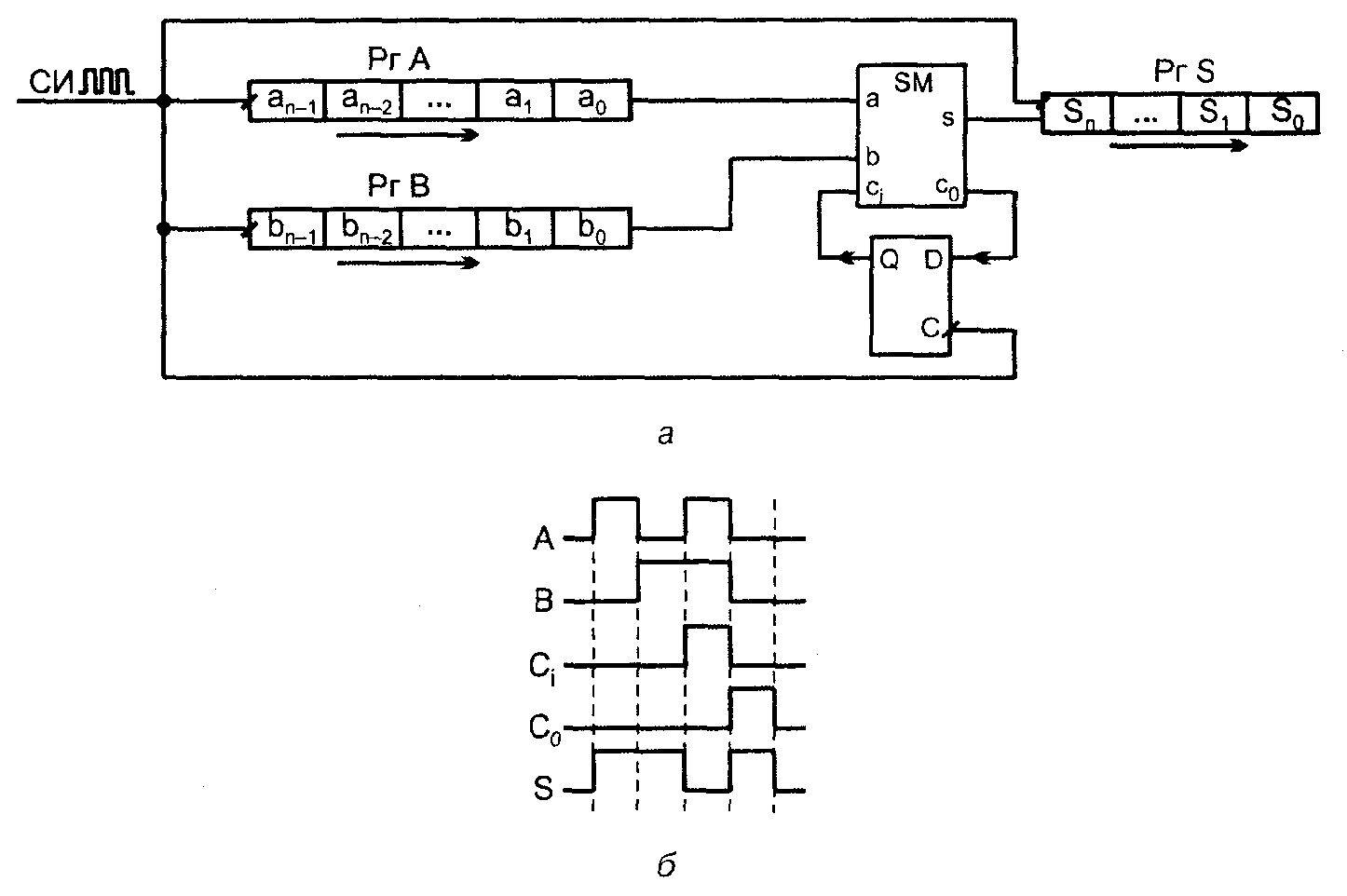
Рис. 3. Схема сумматора для последовательных операндов (а) и её временная диаграмма (б)
4. Параллельный сумматор с последовательным переносом
Сумматор для параллельных операндов с последовательным переносом строится как цепочка одноразрядных, соединённых последовательно по це�пям переноса. Для схемы с одноразрядными сумматорами, вырабатываю�щими инверсии суммы и переноса, такая цепочка имеет вид, приведенный на рис. 4, поскольку функции суммы и переноса самодвойственны. Там, где в разряд сумматора должны подаваться инверсные аргументы, в их ли�ниях имеются инверторы, а там, где вырабатывается инверсная сумма, ин�вертор включен в выходную цепь. Важно, что инверторы не входят в цепь передачи переноса – они при этом не замедляют работу сумматора в целом.
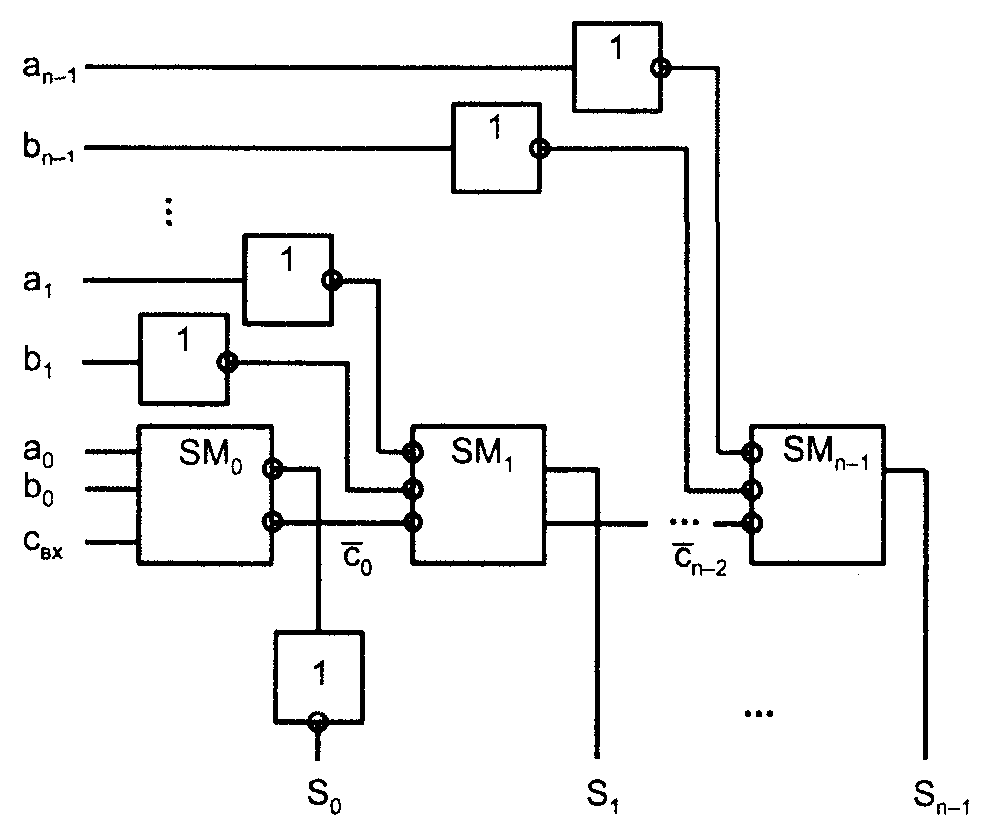
Рис. 4. Схема сумматора с последовательным переносом
Длительность суммирования для этой схемы в наихудшем случае распро�странения переноса по всей цепочке разрядов составит
tsum = tac + (n – 2)tcc + tcs ,
где n – разрядность сумматора.
Как и в других схемах с последовательным распространением сигналов от разряда к разряду, здесь время суммирования практически пропорциональ�но разрядности сумматора.
Если одноразрядные сумматоры выполнены по схеме (см. рис. 1, а), то время суммирования для многоразрядного сумматора составит
tsum = (n + l)tЛР ,
где tЛР – задержка элемента И-ИЛИ-НЕ, обозначенная индексом ЛР, по�скольку именно эти буквы входят в маркировку элементов данного типа. Если одноразрядные сумматоры выполнены по схеме (см. рис. 2), то
tsum = ntЛР .
5. Параллельный сумматор с параллельным переносом
Сумматоры для параллельных операндов с параллельным переносом разра�ботаны для получения максимального быстродействия.
Подход к решению этой задачи требует пояснений. Дело в том, что рассмат�риваемые сумматоры – комбинационные схемы, и вырабатываемые ими функции могут быть представлены в нормальных формах, например, в ДНФ, что приводит к двухъярусной реализации при наличии парафазных аргументов и к трёхъярусной при однофазных аргументах. Таким образом, предельное быстродействие оценивается 2-3 элементарными задержками. Однако реальные схемы таких пределов не достигают, т. к. построение сум�маторов многоразрядных слов на основе нормальных форм дало бы неприемлемо громоздкие схемы. Реальные схемы имеют модульную структуру, т. е. состоят из подсхем (разрядных схем), что резко упрощает их, но не даёт предельно возможного быстродействия.
Сумматоры с параллельным переносом не имеют последовательного распро�странения переноса вдоль разрядной сетки. Во всех разрядах результаты вы�рабатываются одновременно, параллельно во времени. Сигналы переноса для данного разряда формируются специальными схемами, на входы которых поступают все переменные, необходимые для выработки переноса, т. е. те, от которых зависит его наличие или отсутствие. Ясно, что это внешний входной перенос cвх (если он есть) и значения всех разрядов слагаемых, младших относительно данного. Одноразрядные сумматоры, имеющиеся в разрядных схемах, здесь упрощены, т. к. от них выход переноса не требуется, достаточно одного выхода суммы (рис. 5). Обозначение CR происходит от слова carry (перенос).
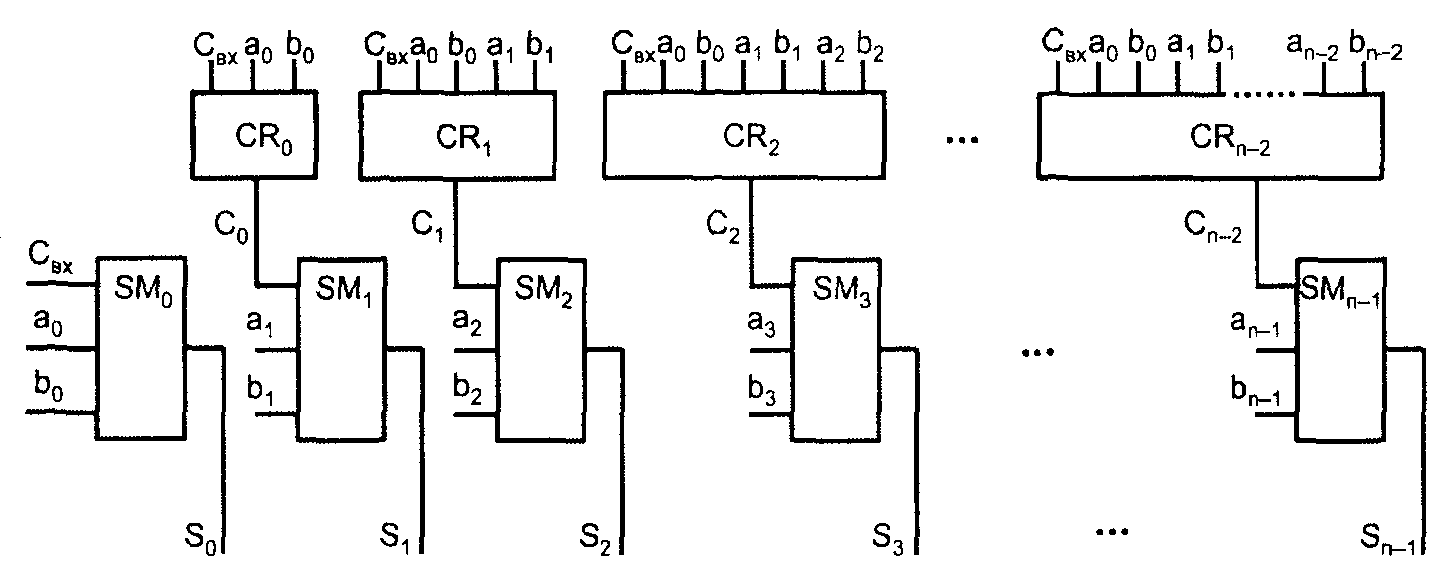
Рис. 5. Структура сумматора с параллельным переносом
Для перехода от идеи построения схемы к её конкретному виду удобно вве�сти две вспомогательные функции: генерации и прозрачности.
Функция генерации принимает единичное значение, если перенос на выходе данного разряда появляется независимо от наличия или отсутствия входного переноса. Очевидно, что эта функция gi = aibi .
Функция прозрачности (транзита) принимает единичное значение, если пе�ренос на выходе данного разряда появляется только при наличии входного переноса. Эта функция 0i = ai + bi . Строго говоря, , но т. к. при ai = bi = 1, т. е. в ситуации, где между функциями ИЛИ и “исклю�чающее ИЛИ” проявляется разница, перенос всё равно формируется из-за gi = 1, допустимо заменить функцию прозрачности на дизъюнкцию.
Теперь выражение для сигнала переноса можно записать в виде ci = gi + ci–10i . На основе полученного выражения выведем функции переноса C для нуле�вого, первого и второго разрядов с последующим их обобщением.
Перенос на выходе младшего разряда c0 = g0 + cвх00 , согласно чему он либо генерируется самим разрядом (g0 = 1), либо пропускается через него (00 = 1 и cвх = 1).
Аналогичным образом для переноса c1 на выходе следующего разряда спра�ведливо соотношение c1 = g1 + c001 .
Подставив в это соотношение выражение для c0 , получим
c1 = g1 + g001 + cвх0100 .
Для следующего разряда произведем те же действия
c2 = g2 + c102 = g2 + g102 + g00201 + cвх020100 .
Выведённые формулы имеют ясный физический смысл – перенос на выхо�де разряда сгенерируется в нём или придёт от предыдущих разрядов при прозрачности тех, через которые он распространяется.
Для произвольного разряда с номером i можно записать
ci = gi + gi–10i + gi–20i0i–1 + … + cвх0i0i–1…00 .
Функции переноса имеют нормальную дизъюнктивную форму и могут быть реализованы элементами И-ИЛИ (либо И-ИЛИ-НЕ, для , если это свой�ственно данной схемотехнике). Однако у этих элементов недостаточное чис�ло входов по И, требуемое для построения многоразрядного сумматора. По�этому предпочтительна схема на элементах И-НЕ (у стандартных элементов имеется до восьми входов по И). Перевод полученных выражений в базис И-НЕ даёт выражения
;
;
.
Схема сумматора (рис. 6) соответствует полученным выражениям.
Исходя из схемы, можно видеть, что время суммирования складывается из времени формирования функций прозрачности (одна задержка элемента И-НЕ, которую обозначим tЛА), времени формирования функций переноса (2tЛА) и задержки упрощённых одноразрядных сумматоров (tЛР), что в ре�зультате даёт tsum = (4...5)tЛА .
Длительность суммирования, полученная из рассмотрения логической схе�мы сумматора, не зависит от его разрядности, что является характерным признаком структур с параллельными переносами вообще, и не только сум�маторов. Однако фактически это не совсем так, поскольку с ростом разряд�ности сумматора увеличивается нагрузка элементов схемы, что увеличивает их задержки. В частности, коэффициент разветвления элементов, вырабатывающих функции прозрачности, равен n2/4, т. е. квадратично зави�сит от разрядности сумматора. Поэтому рост разрядности замедляет процесс суммирования.
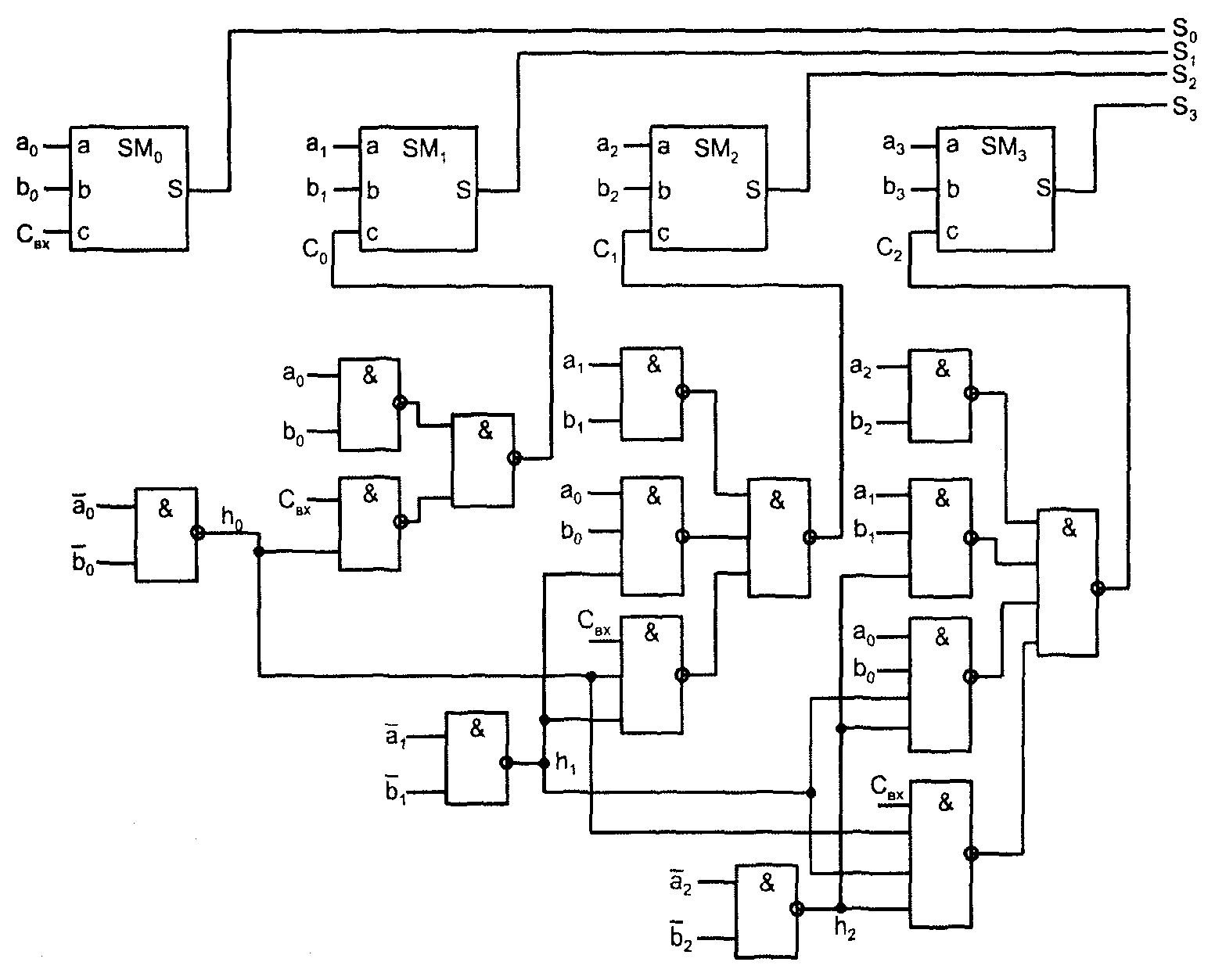
Рис. 6. Вариант схемы сумматора с параллельным переносом
Диапазон разрядностей, в которых проявляются достоинства сумматоров с параллельным переносом, невелик. До n = 3...4 преимущества имеют более простые схемы сумматоров с последовательным переносом, после n = 8 по�являются перегруженные элементы и элементы с большим числом входов, что замедляет работу сумматора, требует введения развязывающих элементов с их задержками и т. п.
6. Сумматор с передачей сигнала переноса по цепочке замкнутых ключей
Среди компромиссных вариантов сумматоров, занимающих промежуточное положение между сумматорами с последовательным и параллельным переносами, имеется интересный вариант, который в первом приближении оценивается как обладающий простотой сумматора с последовательным переносом при быстродействии, близком к быстродейст�вию сумматора с параллельным переносом.
Предложенный подход предусматривает разделение задачи вычисления сиг�налов переноса на два этапа. На первом этапе для всех разрядов (парал�лельно во времени) задаются условия вычисления переносов, на втором происходит простая передача информации по образованной на первом этапе цепи.
При вычислении сигнала переноса ci возможны два случая: ai = bi или ai bi . В первом случае перенос от предыдущего разряда не имеет значения (не влияет на сигнал переноса из данного разряда) и его можно исключить из рассмотрения. Действительно, при ai = bi = 0 перенос ci = 0, а при ai = bi = 1 перенос ci = 1. Следовательно, в качестве переноса может ис�пользоваться значение любого операнда (ai или bi). Примем, что ci = ai . Во втором случае сигнал переноса из данного разряда совпадает с сигналом пе�реноса в данный разряд, т. е. ci = ci–1 .
В обоих случаях после установления факта равенства или неравенства опе�рандов дальнейших переключений элементов не требуется, происходит только передача информации по цепи, заготовленной на предыдущем этапе, что может происходить достаточно быстро.
Схема разряда описанного сумматора (рис. 2.31) содержит ключ, управ�ляемый от элемента сложения по модулю 2 операндов aj и bj, который вы�являет равенство или неравенство этих операндов. В зависимости от вы�ходного сигнала этого элемента выходному переносу присваиваются значения aj или Q. Этот же элемент используется для вычисления совме�стно со вторым элементом сложения по модулю 2 значения суммы дан�ного разряда по формуле: S, = aj XOR bj XOR Q.i, где XOR (от англ. exclusive OR) – обозначение операции "исключающее ИЛИ" (синоним операции сложения по модулю 2).
Автор описанного метода построения сумматора проверил его работу при реализации схемы на элементах ТТЛ. Результат оказался эффективным. На�пример, для сумматоров с 2, 4 и 8 разрядами время сложения практически не зависело от разрядности, как это свойственно структурам с параллель�ным переносом. По скорости четырехразрядный сумматор выиграл у вари�анта с последовательным переносом в 2 раза, а восьмиразрядный сумматор в 3,5 раза. Естественно, рассматриваемая структура может быть реализована в Рамках любой схемотехнологии, в том числе и на наиболее популярной схе-Мотехнологии КМОП. Эффективность метода будет зависеть от задержки сигнала при его распространении через цепочку, состоящую из последова�тельного соединения замкнутых ключей, и в зависимости от параметров этих ключей будет меняться.
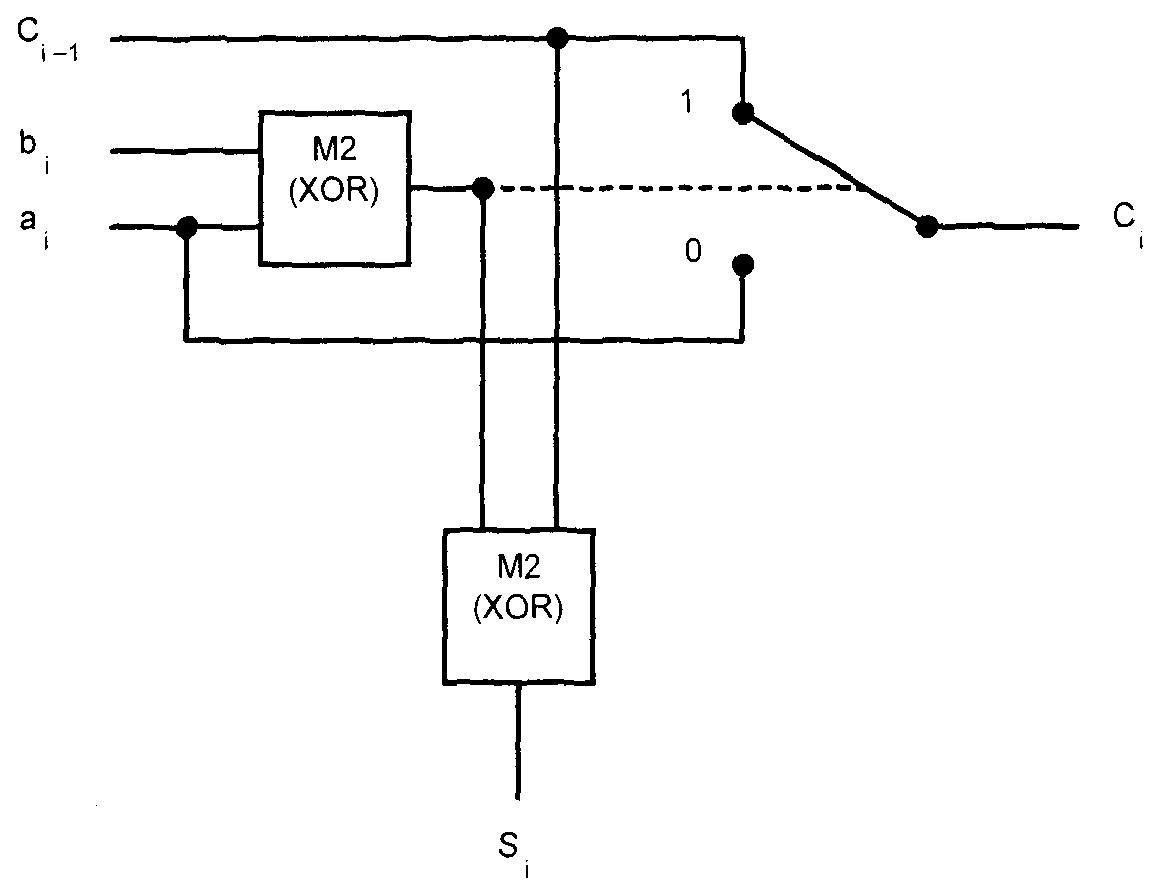
Рис. 7. Схема разряда сумматора с передачей сигнала переноса
по цепочке замкнутых ключей
Сумматор с условным переносом
Сумматор с условным переносом – давно известная структура, которая со временем вышла из широкого применения, но сейчас возродилась в новей�ших СБИС программируемой логики. Эта структура улучшает быстродейст�вие сумматоров с последовательным переносом. В СБИС программируемой логики, начиная с семейства микросхем FLEX 8000 фирмы Altera, была реа�лизована цепь последовательных переносов с малыми задержками (1 нс на разряд, впоследствии задержка переноса была снижена до 0,2 нс на разряд). Это возродило интерес к структурам с последовательным переносом и, со�ответственно, к методам улучшения их быстродействия.
Идея построения сумматора с условным переносом такова. Имея сумматор с n разрядами, делят его на две равные группы с разрядностями n/2. Старшую группу дублируют, так что в схему входят три сумматора с разрядностью n/2. На одном суммируются младшие поля операндов Амл и Вмл . На втором – старшие поля операндов Аст и Вст при условии Свх = 1, в третьем – старшие же поля операндов при условии Свх = 0. После получения результата в младшем сумматоре становится известным фактическое значение переноса в старший сумматор, и из двух заготовленных заранее результатов выбирается тот, ко�торый нужен в данном случае. Цепь последовательного переноса здесь как бы укорачивается вдвое, т. к. обе половины сумматора работают параллель�но во времени (рис. 10).
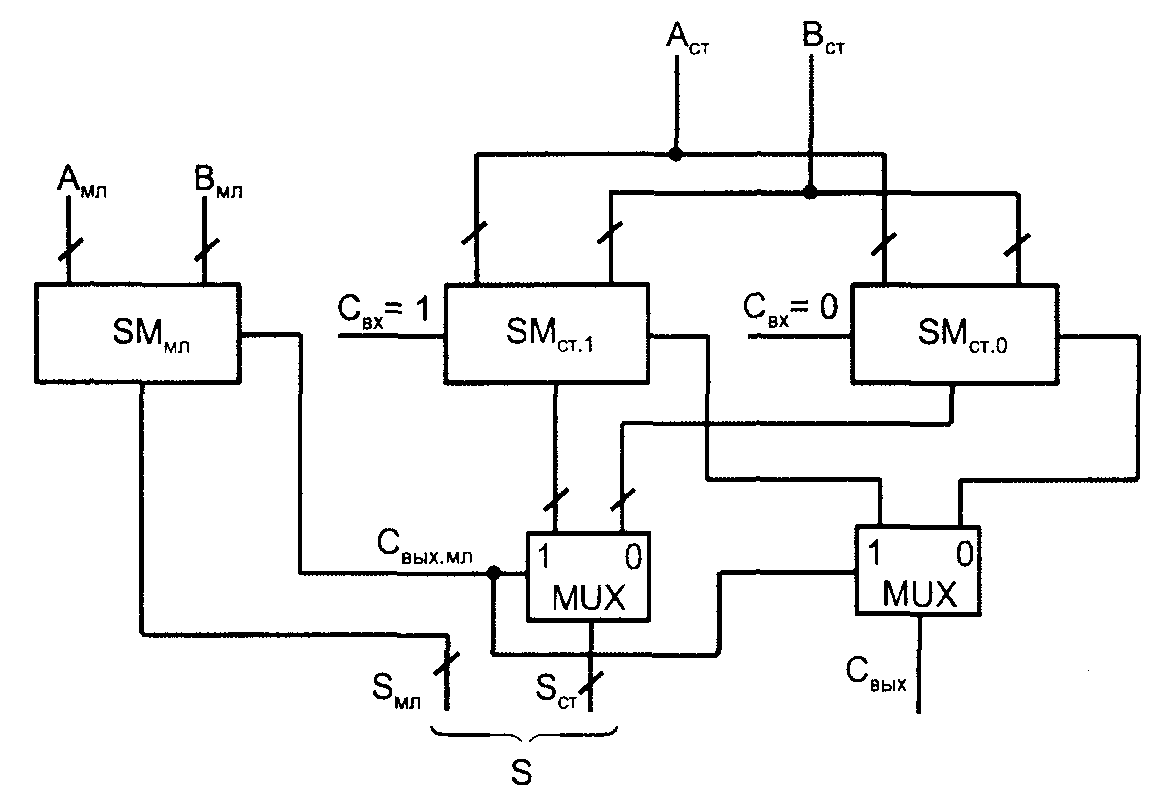
Рис. 10. Схема сумматора с условным переносом
Накапливающий сумматор
Накапливающий сумматор обычно представляет собою сочетание комбинацион�ного сумматора и регистра, работающее по формуле S := S + А, согласно которой к содержимому сумматора добавляется очередное слагаемое, и результат заме�щает старое значение суммы. Структура накапливающего сумматора показана на рис. 11. Очередное прибавление слагаемого тактируется синхроимпульсами СИ. Учитывая особенности функционирования, накапливающие сумматоры назы�вают иногда аккумуляторами.
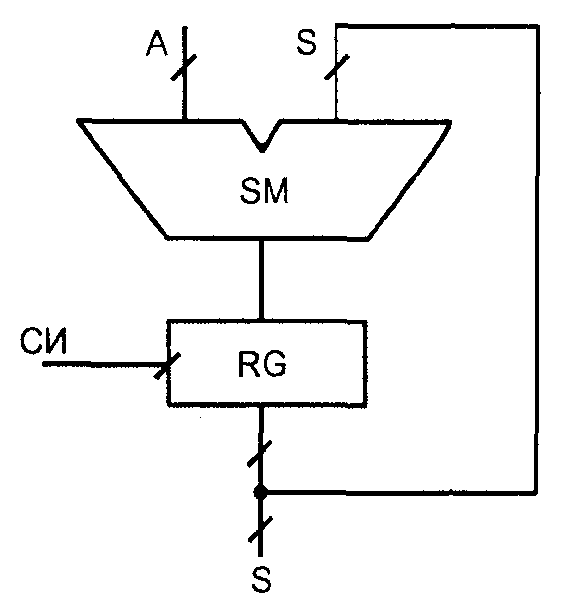
Рис. 11. Структура накапливающего сумматора
В сериях элементов имеются одноразрядные сумматоры, в том числе с до�полнительной входной логикой, двухразрядные и четырехразрядные. При�мером стандартных ИС сумматоров могут служить микросхемы ИМЗ серии К555, содержащие четырехразрядный сумматор с последовательным перено�сом и блок переноса (рис. 2.36), которые непосредственно пригодны для составления из них группового сумматора с цепным переносом.
Микросхемы четырехразрядных сумматоров можно также объединять в групповую структуру с межгрупповым параллельным переносом с помощью специальных блоков ускоренного переноса.
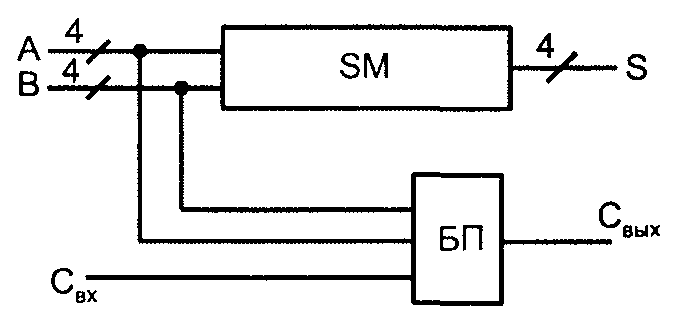
Рис. 12. Структура микросхемы К555ИМ3
В некоторых сериях элементов сумматоры отсутствуют. Причиной этого обычно является наличие арифметико-логического устройства (АЛУ), для которого режим суммирования есть один из возможных режимов.
Арифметико-логические устройства
1. Арифметико-логические устройства и блоки ускоренного переноса
Арифметико-логические устройства (АЛУ) [ALU = Arithmetic-Logic Unit] предназначены для вы�полнения ряда действий над двоичными словами. Основой АЛУ служит сумматор, схема которого дополнена логикой, расширяющей функциональные возможности АЛУ и обеспечивающей его перестройку с одной операции на другую.
Обычно АЛУ четырёхразрядны и для наращивания разрядности объединя�ются с формированием последовательных или параллельных переносов. Логические возможности АЛУ разных технологий (ТТЛШ, КМОП, ЭСЛ) сходны. В силу самодвойственности выполняемых операций условное обо�значение и таблица истинности АЛУ встречаются в двух вариантах, отли�чающихся взаимно инверсными значениями переменных.
АЛУ (рис. 1) имеет входы операндов А и В, входы выбора операций S, вход переноса и вход М (Mode – режим), сигнал которого задаёт тип выпол�няемых операций: логические (М = 1) или арифметико-логические (М = 0). Результат операции вырабатывается на выходах F, выходы G и Н дают функции генерации и прозрачности, используемые для организаций параллельных переносов при наращивании размерности АЛУ. Сигнал – выходной перенос, а выход А = В – это выход сравнения на равенст�во с открытым коллектором.
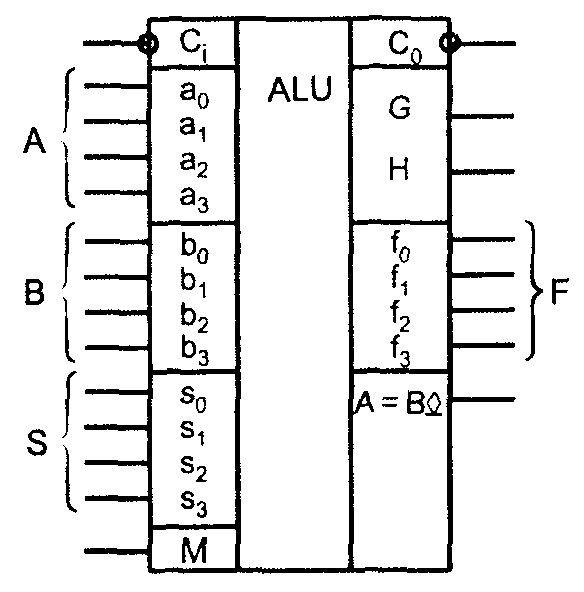
Рис. 1. Условное обозначение АЛУ
Перечень выполняемых АЛУ операций дан в табл. 1. Для краткости дво�ичные числа S3S2S1S0 представлены их десятичными эквивалентами. Под по�лужирными обозначениями 1 и 0 следует понимать наборы 1111 и 0000, входной перенос поступает в младший разряд слова, т. е. равен 000Ci . Логи�ческие операции поразрядные, т. е. операция над словами А * В означает, что ai * bi при отсутствии взаимовлияния разрядов. При арифметических операциях учитываются межразрядные переносы.
16 логических операций позволяют воспроизводить все функции двух пере�менных. В логико-арифметических операциях встречаются и логические, и арифметические операции одновременно.
Запись типа следует понимать так: вначале поразрядно выпол�няются операции инвертирования (), логического сложения () и умножения (АВ), а затем полученные указанным образом два четырёхразряд�ных числа складываются арифметически.
Таблица 1
|
S
|
Логические функции (М = 1)
|
Арифметико-логические функции (М = 0)
|
|
0
1
2
3
|
0
|
A + Ci
+ Ci
+ Ci
1 + Ci
|
|
4
5
6
7
|
|
А + + Ci
+ AB + Ci
А + + Ci
+ 1 + Ci
|
|
8
9
10
11
|
В
АВ
|
А + АВ + Ci
А + В + Ci
+ AB + Ci
АВ + 1 + Ci
|
|
12
13
14
15
|
1
А
|
А + А + Ci
+ A + Ci
+ A + Ci
А + 1 + Ci
|
При операциях над словами большой размерности АЛУ соединяются друг с другом с организацией последовательных (рис. 2, а) или параллельных (рис. 2, б) переносов. В последнем случае совместно с АЛУ применяют микросхемы – блоки ускоренного переноса (CRU = CaRry Unit), получающие от отдельных АЛУ функции генерации и прозрачности, а также входной пе�ренос и вырабатывающие сигналы переноса.
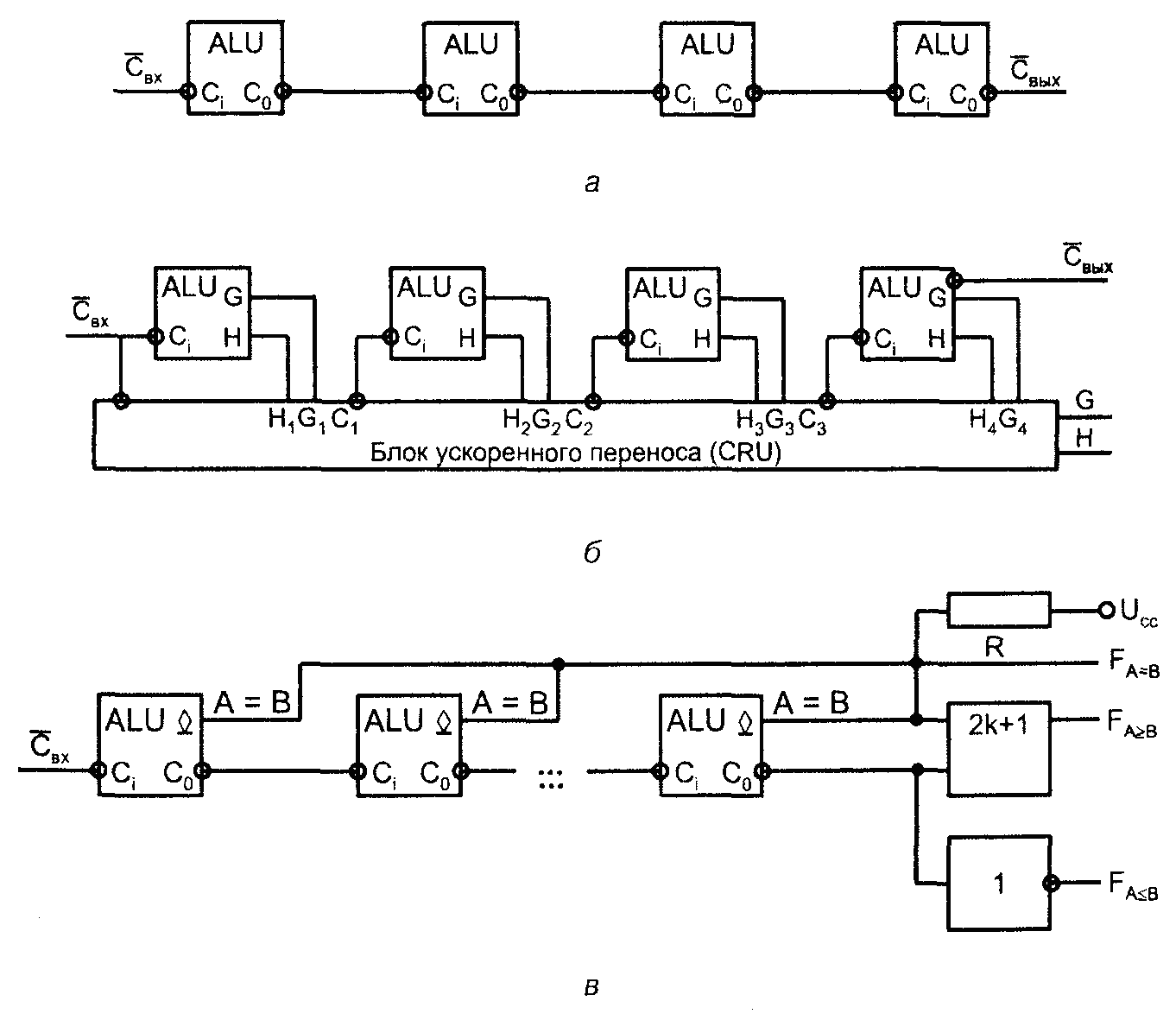
Рис. 2. Схемы наращивания АЛУ при последовательном (а) и параллельном (б) переносах и реализация функций компаратора для группы АЛУ (в)
Блок CRU вырабатывает также функции генерации и прозрачности для всей группы обслуживаемых им АЛУ, что при необходимости позволяет органи�зовать параллельный перенос на следующем уровне (между несколькими группами из четырёх АЛУ).
На рис. 2, в показаны способы выработки сигналов сравнения слов для группы АЛУ. Выход сравнения на равенство выполняется по схеме монтаж�ной логики для выходов типа ОК (общий коллектор). Комбинируя сигнал равенства слов с сиг�налом переноса на выходе группы при работе АЛУ в режиме вычитания, легко получить функции Fab и Fab . Если А < В, то при вычитании возни�кает заём из старшего разряда и Fab = 1. Если заём отсутствует (А > В), то получим Fab = 1.
2. Матричные умножители
Микросхемы множительных устройств появились в 1980-х г.г., когда достиг�нутый уровень интеграции позволил разместить на одном кристалле доста�точно большое количество логических элементов.
Структура матричных умножителей тесно связана со структурой математи�ческих выражений, описывающих операцию умножения.
Пусть имеются два целых двоичных числа без знаков Аm = аm–1...а0 (множимое) и Bn = bn...b0 (множитель). Их перемножение выполняется по известной схеме “умножения столбиком”. Если числа четырёхразрядные, т. е. m = n = 4, то
а3 а2 а1 а0
b3 b2 b1 b0
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
a3b0 a2b0 a1b0 a0b0
+ a3b1 a2b1 a1b1 a0b1
+ a3b2 a2b2 a1b2 a0b2
+ a3b3 a2b3 a1b3 a0b3
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
p7 p6 p5 p4 p3 p2 p1 p0
Произведение выражается числом Pm+n = pm+n–1 pm+n–1… p0 .
Члены вида aibj , где i = 0...(m – 1) и j = 0...(n�–1) вырабатываются парал�лельно во времени конъюнкторами. Их сложение в столбцах, которое мож�но выполнять разными способами, составляет основную операцию для ум�ножителя и определяет почти целиком время перемножения.
Матричные перемножители могут быть просто множительными блоками (МБ) или множительно-суммирующими блоками (МСБ), последние обеспечивают удоб�ство наращивания размерности умножителя.
МСБ реализует операцию Р = Аm Вn + Сm + Dn , т. е. добавляет к произ�ведению два слагаемых: одно разрядности т, совпадающей с разрядностью множимого, другое разрядности n, совпадающей с разрядностью множителя.
Множительно-суммирующие блоки
Множительно-суммирующий блок (МСБ) для четырёхразрядных операн�дов без набора конъюнкторов, вырабатывающих члены вида aibj , показан на рис. 3, а, где для одноразрядного сумматора принято обозначение (рис. 3, б).
Для построения МСБ чисел равной разрядности потребовалось n2 конъюнк�торов и n2 одноразрядных сумматоров.
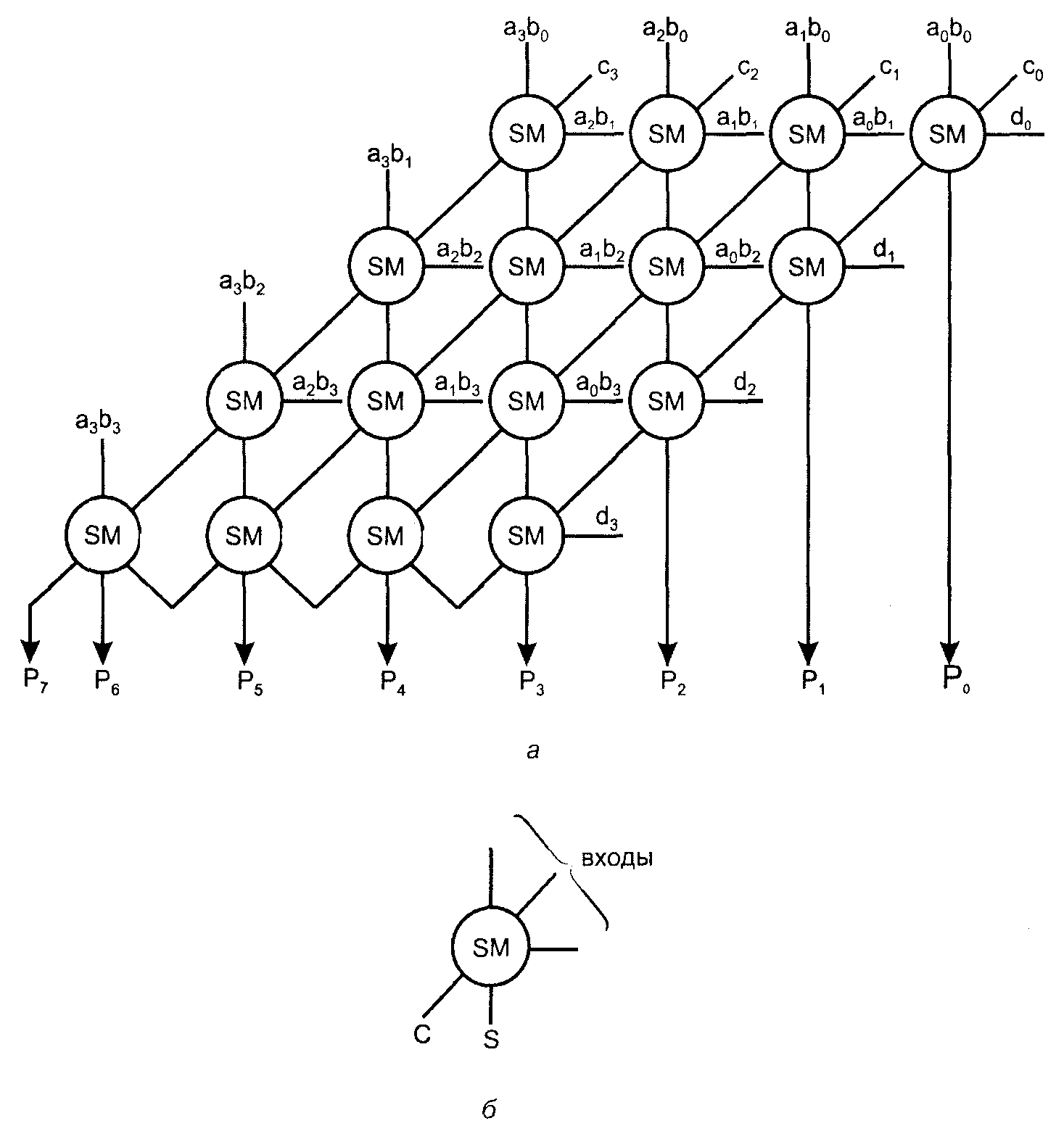
Рис. 3. Схема множительно-суммирующего блока для четырёхразрядных
сомножителей (а), обозначение одноразрядного сумматора для данной схемы (б)
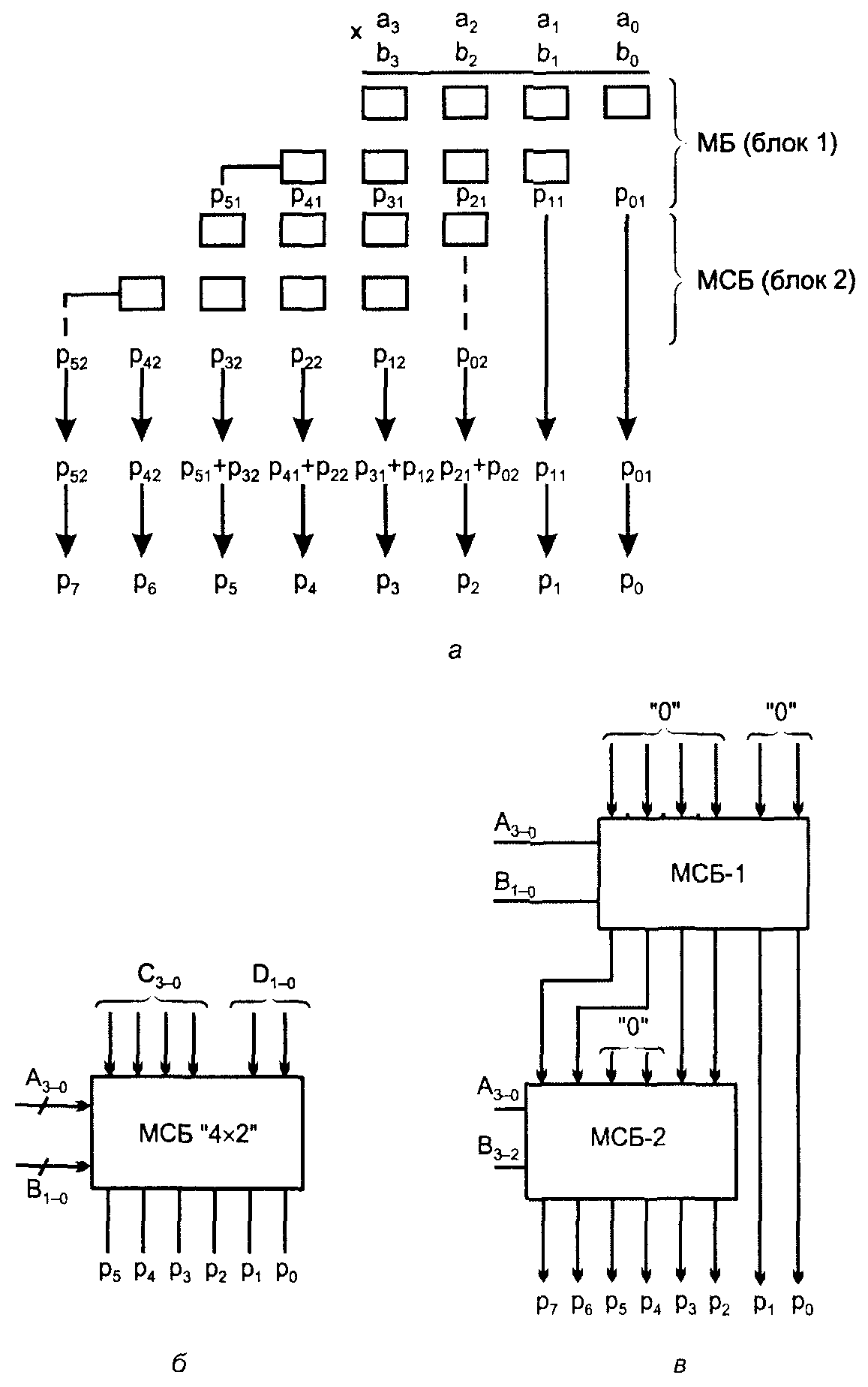
Рис. 4. К пояснению принципа наращивания размерности множительных устройств (а),
условное обозначение множительно-суммирующего блока (б) и схема умножителя
“4 4”, построенная на множительно-суммирующих блоках “4 2” (в)
Максимальная длительность умножения – сумма задержек сигналов в конъюнкторах для выработки членов aibj и задержки в наиболее длинной цепочке передачи сигнала в матрице одноразрядных сумматоров, равной 2n – 1 (m + n – 1 в общем случае). Таким образом, tMPL = tк + (2n – l)tSM , где tк – задержка конъюнктора.
Схема множительного блока отличается от схемы МСБ тем, что в ней отсут�ствуют сумматоры правой диагонали, т. к. при Сm = 0 и Dn = 0 они не тре�буются.
Построение умножителей большей размерности из умножителей меньшей размерности на основе МБ требует введения дополнительных схем, называе�мых “деревьями Уоллеса”, которые имеются в некоторых зарубежных сериях. При использовании МСБ дополнительные схемы не требуются. Принцип на�ращивания размерности умножителя иллюстрируется на рис. 4, а на при�мере построения MPL “4 4” из МСБ “4 2”. На поле частичных произве�дений выделены зоны, воспроизведение которых возможно на блоках размерности 42 (это две первые и две последние строки).
Перемножение в пределах зон даёт частичные произведения
p1 = p51 p41 p31 p21 p11 p01 и р2 = р52 р42 р32 р22 р12 р02 . Для получения конечного значения произведения эти частичные произведения нужно сложить с учё�том их взаимного положения (сдвига одного относительно другого).
Схема, реализующая указанный принцип, изображена на рис. 4, в. В ней использовано условное обозначение МСБ (рис. 4, б). Для общности оба блока размерности 42 показаны как МСБ, хотя первый может быть про�сто множительным блоком, т. к. для него слагаемые С и D имеют нулевое значение.
Схемы ускоренного умножения
Для ускорения умножения разработан ряд алгоритмов, большой вклад в эти разработки внёс Э. Бут (Е. Boot). Рассмотрим процесс умножения по так называемому модифицированному алгоритму Бута (умножение сразу на два разряда).
Из изложенного ранее видно, что основную задержку в процесс выработки произведения вносит суммирование частичных произведений. Уменьшение их числа сократило бы время суммирования. К этому приводит алгоритм, основанный на следующих рассуждениях.
Пусть требуется вычислить произведение
Р = А В = А (bn–12n–1 + bn–22n–2 + ... + b020). (2.1)
Непосредственное воспроизведение соотношения (2.1) связано с выработ�кой частичных произведений вида Abi2i (i = 0...n–1). Число таких произве�дений равно разрядности множителя n.
Выражение (2.1) можно видоизменить с помощью соотношения
bi2i = bi2i+1 – 2bi2i–1, (2.2)
справедливость которого очевидна.
Это соотношение позволяет разреживать последовательность (спектр) сте�пеней в сумме частичных произведений. Можно, например, исключить чёт�ные степени, как показано на рис. 5, а.
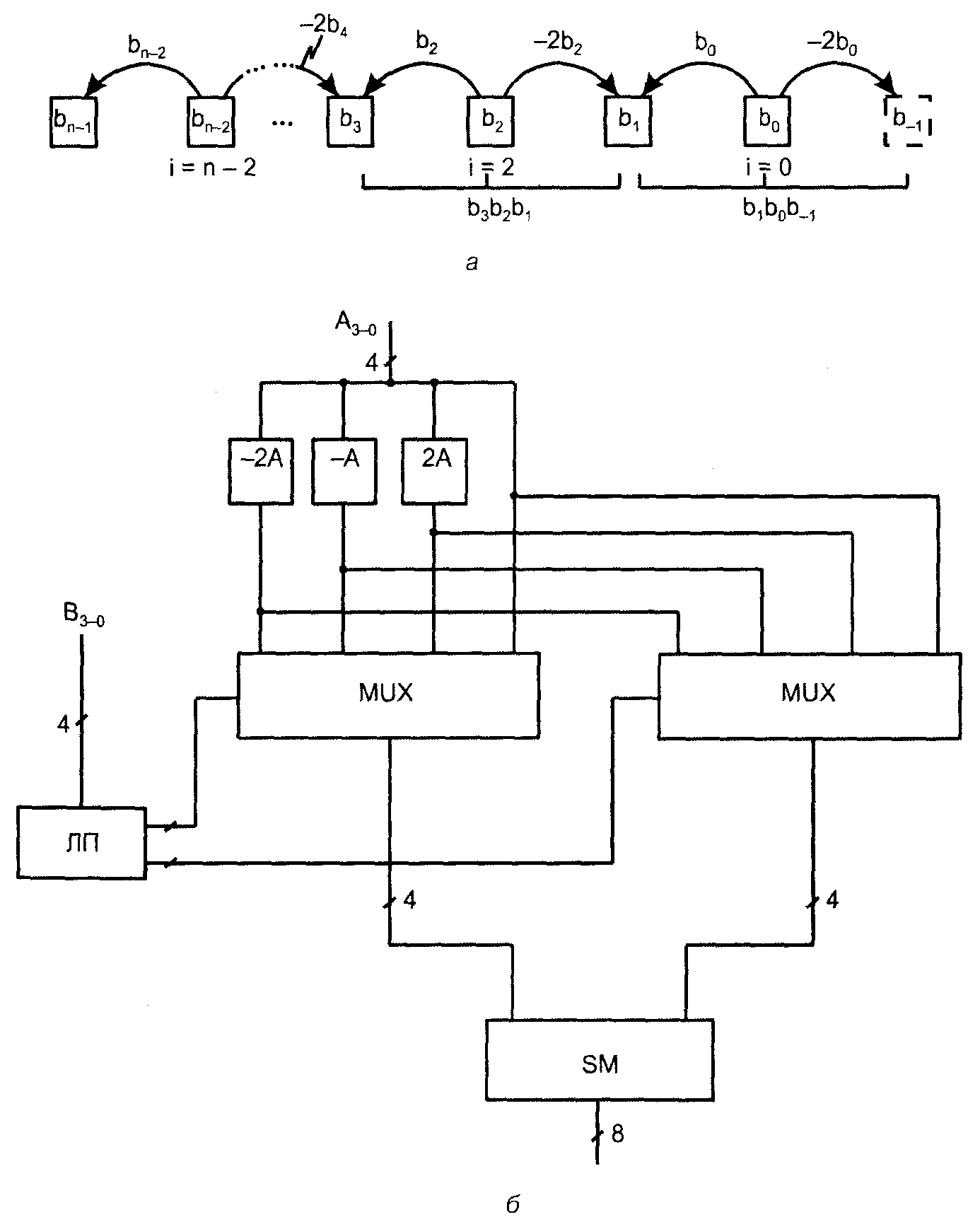
Рис. 5. К пояснению принципа быстрого умножения “сразу на два разряда” (а)
и схема быстрого умножения (б)
Исключение чётных (или нечётных) степеней не только изменяет значения оставшихся частичных произведений, но и сокращает их число примерно вдвое, что, в конечном счёте ускоряет выработку произведения. Для того чтобы “разнести по соседям” член со степенью 20, расширим разрядную сет�ку, введя слагаемое b–12–1 (нулевой разряд с номером –1).
Оставшиеся частичные произведения имеют вид
Ri = A(–2bi+1 + bi + bi–1)2i.
Так как число частичных произведений уменьшилось примерно вдвое, при применении этого алгоритма говорят об умножении сразу на два разряда.
Для всех возможных сочетаний bi+1 , bi, bi+1 можно составить таблицу (табл. 2) частичных произведений.
Таблица 2
|
b|+i
|
ь,
|
bi_i
|
Значение скобки
|
Ri/2'
|
Операция для получения R|/2'
|
|
0
|
0
|
0
|
0
|
0
|
Заменить А нулем
|
|
0
|
0
|
1
|
1
|
А
|
Скопировать А
|
|
0
|
1
|
0
|
1
|
А
|
Скопировать А
|
|
0
|
1
|
1
|
2
|
2А
|
Сдвинуть А влево
|
|
1
|
0
|
0
|
-2
|
-2А
|
Сдвинуть А влево и преобразо�вать в дополнительный код
|
|
1
|
0
|
1
|
-1
|
-А
|
Преобразовать А в дополнитель�ный код
|
|
1
|
1
|
0
|
-1
|
-А
|
Преобразовать А в дополнитель�ный код
|
|
1
|
1
|
1
|
0
|
0
|
Заменить А нулем
|
Пример
Пусть требуется умножить \0\Ъ2 на ОИЪ, т. е. 10x7. При разреживании час�тичных произведений оставим только нечётные, как показано на рис. 2.41, а. Расширив разрядную сетку множителя, имеем В = b4b3b2bibob_ib-2 = 0011100.
Первому частичному произведению соответствует тройка bob_ib^2 = 100. Из табл. 2.14 получаем, что этой тройке соответствует частичное произведение – -2А 2" = -А, для получения которого требуется перевести А в дополнительный код. Сама величина А в пределах разрядной сетки произведения должна быть записана как 00001010, ее обратный код 11110101 и дополнительный код 11110110.
Второму частичному произведению соответствует тройка b2bibo = 111, следо�вательно, второе частичное произведение равно нулю (табл. 2.14).
Третьему частичному произведению соответствует тройка ЬдЬзЬг = 001, следо�вательно, оно имеет вид А 23 = 01010000.
У 38
Глава 2
Для получения результата заданного умножения требуется сложить частичные произведения:
11110110
01010000
01000110 = 26 + 22 + 21 = 64 + 4 + 2 = 70.
Схема, реализующая алгоритм быстрого умножения сразу на два разряда, показана на рис. 2.41, б.
Множимое А поступает в этой схеме на ряд преобразователей, заготавли�вающих все возможные варианты частичных произведений (-2А, -А, 2А), кроме самого А и нуля, которые не требуют схемной реализации. Множи�тель В поступает на логический преобразователь ЛП, который анализирует тройки разрядов, декодирует их и дает мультиплексорам MUX сигналы вы�бора того или иного варианта частичных произведений. Окончательный ре�зультат получается суммированием частичных произведений с учетом их взаимного сдвига в разрядной сетке. Размерность умножителя 4x4.
Приведенные ранее примеры множительных устройств касались операций с прямыми кодами. В этом случае умножение знакопеременных чисел сведется только к выработке знакового разряда как суммы по модулю 2 знаковых раз�рядов сомножителей. Если же числа представлены не прямыми кодами со знаковыми разрядами, а, например, дополнительными кодами, то, имея рас�смотренные ранее умножители, можно дополнить их преобразователями до�полнительного кода в прямые на входах и преобразователем прямого кода в дополнительный на выходе или использовать схемы, непосредственно реали�зующие алгоритмы умножения дополнительных кодов (см., например, [37]).
Разработке матричных умножителей уделяют внимание многие фирмы. В оте�чественных сериях МИС/СИС имеются умножители малой размерности (2 х 2, 4 х 4, 4 х 2 и др.). В сериях БИС размерности умножителей значительно боль�ше. В серии 1802, например, имеются умножители 8x8, 12x12, 16x16 (ВРЗ, ВР4 и ВР5 соответственно). В схемотехнике ЭСЛ выполнен умножитель 1800ВР1 (8 х 8 за 17 не). Зарубежные фирмы разработали умножители (фирмы BIT, Hitachi и др.) размерностями 16x16 и более с временами умножения 3...5 не. Несколько лет назад предприятие "Интеграл" (г. Минск) выпустило ум�ножитель КА1843ВР1 размерностью 32x32 со временем умножения 250 нс в корпусе с 172 выводами.
§ 2.11. Быстрые сдвигатели
Сдвиги слов в разрядной сетке – типовая операция, используемая при вы�числениях с представлением чисел с плавающей точкой, умножениях чисел на константу и в других случаях. Среди самых распространенных узлов
цифровых устройств (регистров) имеются сдвигающие, но с их помощью сдвиг на несколько разрядов можно реализовать только как результат не�скольких одноразрядных, а это занимает много времени. Поэтому были раз�работаны так называемые быстрые сдвигатели, которые перемещают слово сразу на несколько разрядов в соответствии с указанным значением сдвига.
Схемотехника быстрых сдвигателей насчитывает ряд вариантов, из которых основными являются сдвигатели, управляемые кодом "1 из N" (Barrel Shifters) и сдвигатели, управляемые двоичным кодом (Logarithmic Shifters).
Сдвигатель, управляемый кодом "1 из N"
Структура этого варианта показана на рис. 2.42, б с обозначением ключевых транзисторов согласно рис. 2.42, а. Ключевые транзисторы (Pass transistors) для наглядности представления структуры изображены кружками, причем по прямой линии расположены выводы истока и стока (т. е. в эту линию включен управляемый ключ), а боковой вывод связан с затвором, и на него подается управляющее напряжение. Обозначение управляющего напряже�ния, замыкающего ключ, записывается в кружке в сокращенном виде. Если ключ замыкается сигналом "Сдвиг N", т. е. при команде сдвига на N разря�дов, то в кружке ставится символ N.
Основа схемы сдвигателя – матрица ключевых транзисторов, управляемых кодами "1 из N" согласно табл. 2.15 (сдвиги производятся в сторону разря�дов с меньшими номерами).
Таблица 2.15
|
Операция
|
Сигналы управления
|
|
|
Сдвиг 0
|
Сдвиг 1
|
Сдвиг 2
|
Сдвиг 3
|
|
Передача без сдвига Сдвиг на 1 разряд Сдвиг на 2 разряда Сдвиг на 3 разряда
|
1 0 0 0
|
0 1 0 0
|
0 0
1
0
|
0 0 0
1
|
Требуемый результат получается за счет определенной схемы соединений ключей. В схеме рис. 2.42, предусмотрено автоматическое повторение зна�кового разряда и на выходы В передаются следующие коды:
при сдвиге на 0 разрядов: А3А2А1А0;
при сдвиге на 1 разряд: A3A3A2Ai;
при сдвиге на 2 разряда: А3А3АзА2;
при сдвиге на 3 разряда: А3А3А3А3.
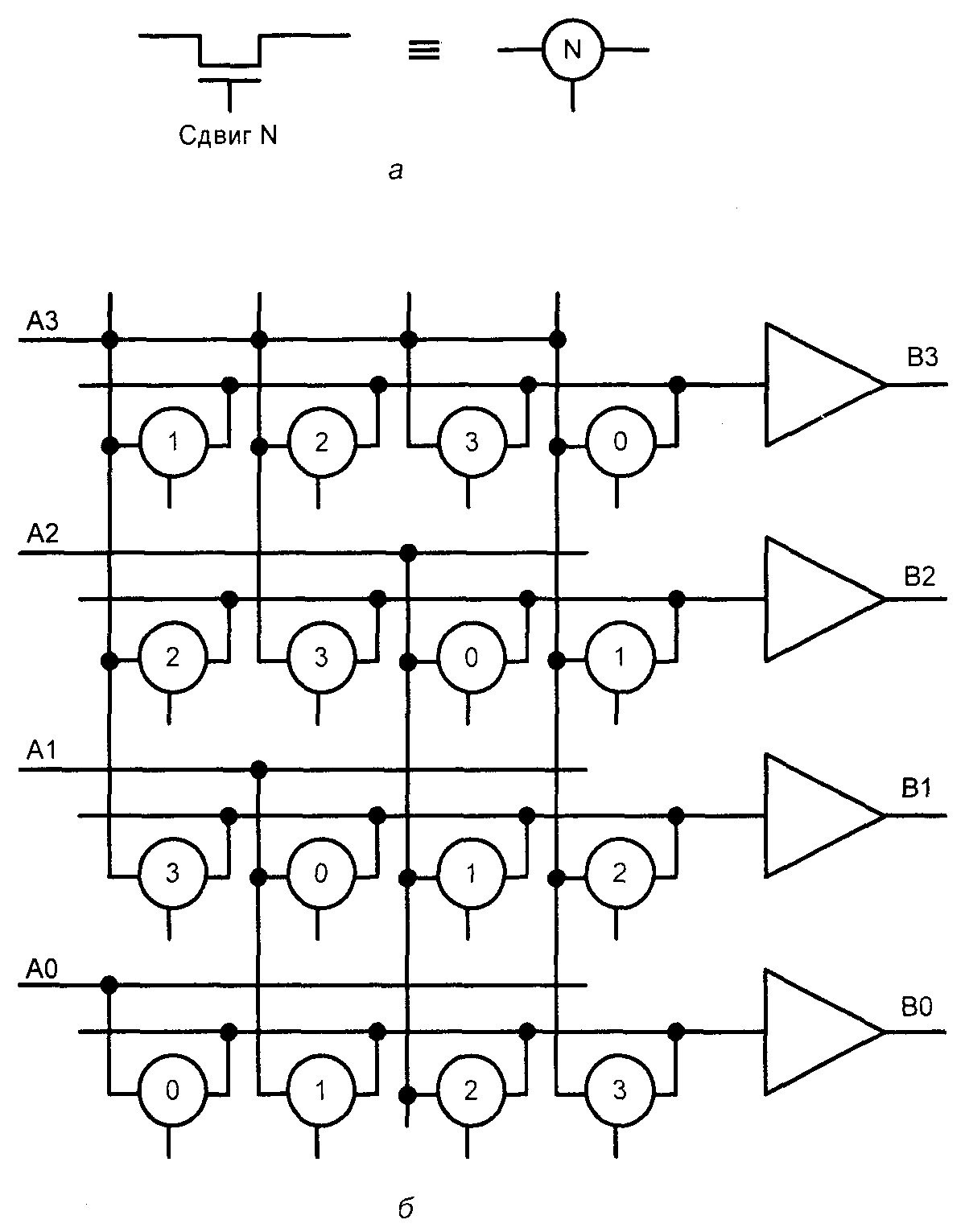
Рис. 2.42. Условное обозначение ключевых транзисторов, принятое при изображении структуры сдвигателя, управляемого кодом "1 из N" (а) и структура сдвигателя (б)
Сдвигатель типа Barrel Shifter отличается высоким быстродействием, т. к. сигнал сдвига замыкает для каждой передачи входного бита на выходной буфер цепь только из одного ключа. Однако это справедливо, если управ�ляющий код является кодом "1 из N". В большинстве случаев управляющие коды исходно вырабатываются как двоичные, и перед сдвигателем требуется включать дешифратор, что увеличивает как сложность схемы, так и задерж�ки в ее работе. В этих случаях, особенно при больших величинах макси�мально возможных сдвигов, преимущество по технико-экономическим по�казателям обычно оказывается на стороне сдвигателя, непосредственно управляемого двоичными кодами и называемого логарифмическим.
функциональные узлы комбинационного типа
141
Сдвигатель, управляемый двоичным кодом (логарифмический)
В отличие от предыдущего варианта этот сдвигатель в качестве основы име�ет не единую матрицу ключевых транзисторов, а схему, состоящую из не�скольких каскадов (ступеней). Число ступеней N связано со значением мак�симального сдвига S зависимостью N = log2S, что и объясняет название "логарифмический" применительно к данному типу сдвигателя. Требуемое значение величины сдвига образуется в этом сдвигателе как композиция нескольких сдвигов, каждый из которых равен числу 2', где i = 1, 2, 3.
Структура логарифмического сдвигателя показана на рис. 2.43 на примере четырехразрядного фрагмента.
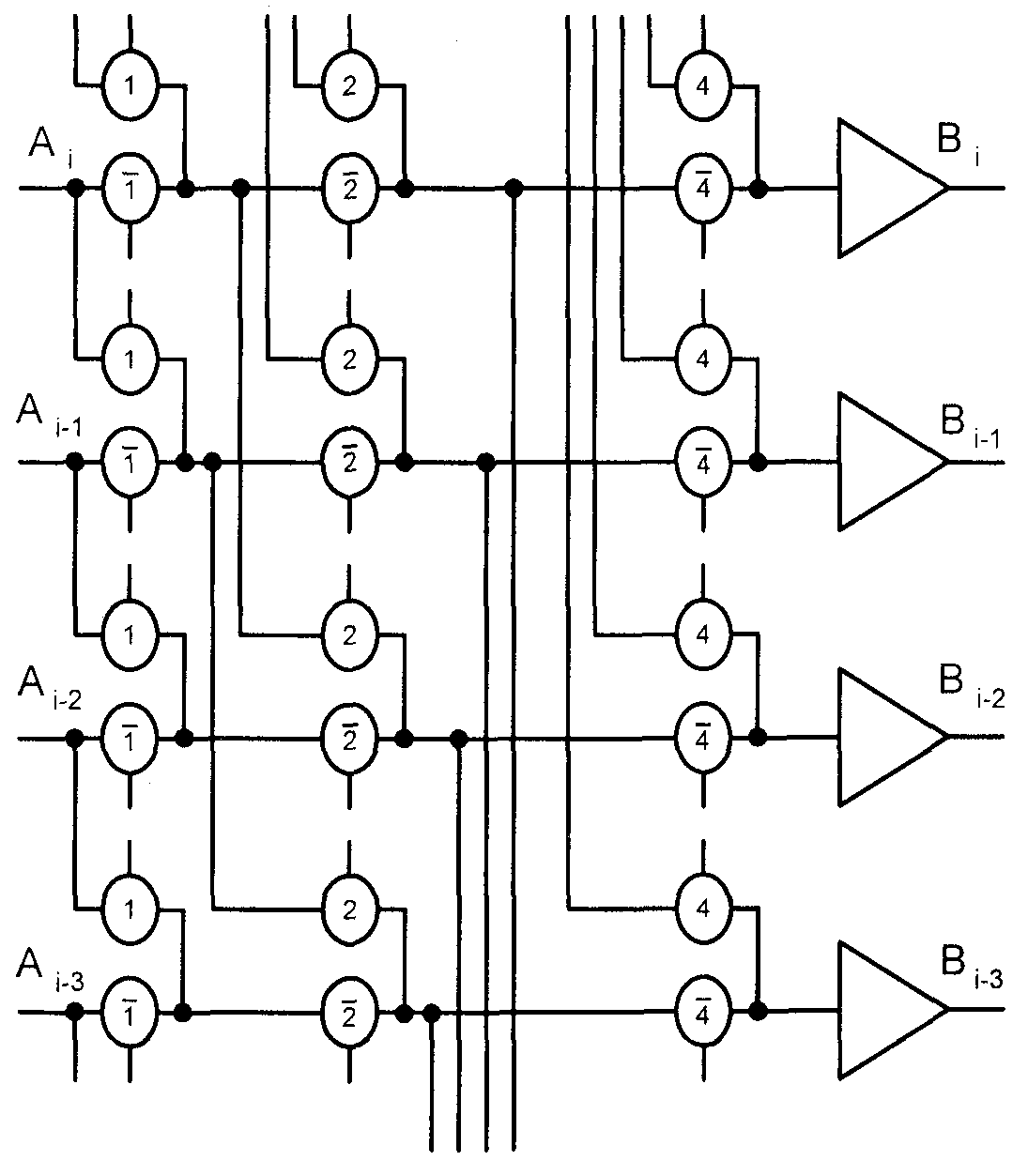
Рис. 2.43. Фрагмент структуры логарифмического сдвигателя
°означения сигналов управления ключевыми транзисторами совпадают с Принятыми на рис. 2.42, кроме того, на рисунке показаны и инверсные сиг-
142
Глава 2
налы. Как видно из схемы, сигналы от разрядов входного слова до входов выходных буферов проходят через цепочку последовательно включенных транзисторов, число которых равно log2S. Это замедляет процесс сдвига, а поскольку задержка цепочки из RC-звеньев, которая создается последова�тельно включенными пасс-транзисторами, зависит от их числа сильнее, чем по линейному закону, в длинные цепочки целесообразно вводить промежу�точные буферные каскады, разбивая цепочки на более короткие части.
Для иллюстрации работы сдвигателя рассмотрим сдвиг на 5 разрядов. В двоичном коде число 5 представляется кодом 101 = 1х22 + 0x2' + 1x2°, соответственно чему первая и третья ступени устанавливаются в режим сдвига, а вторая в режим пропуска сигнала без сдвига.
Сумматоры