Изучение процесса заряда и разряда конденсатора

МИНИСТЕРСТОВ ОБРАЗОВАНИЯ И НАУКИ АСТРАХАНСКОЙ ОБЛАСТИ

ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «АСТРАХАНСКИЙ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ ИНСТИТУТ»

Кафедра физика и математика, информационные технологии

ИЗУЧЕНИЕ ПРОЦЕССА ЗАРЯДА И РАЗРЯДА КОНДЕНСАТОРА

Методические указания к лабораторной работе по физике

Астрахань

2013

Составитель:

к.т.н., доцент Е.М. Евсина

Рецензенты:

к.п.н., доцент каф. общей физики АГУ С.А. Тишкова,

к.т.н., доцент П.Н. Садчиков

В работе содержатся основные теоретические сведения по теме «Электростатика».

Методические указания предназначены для самостоятельной подготовки студентов к выполнению лабораторной работы.

Лабораторная работа №2.1.

Изучение процесса заряда и разряда конденсатора

Цель работы:

1. Ознакомиться с процессом заряда и разряда конденсатора;
2. Экспериментально определить значение емкости конденсатора.

Оборудование:

1. Модульный учебный комплекс МУК-ЭМ1;
2. Генератор напряжений ГН1;
3. Стенд с объектами исследования СЗ-ЭМ01;
4. Осциллограф ОЦЛ2;
5. Комплект проводников.

КРАТКАЯ ТЕОРИЯ

Конденсатор — элемент электрической цепи переменного тока, служащий для накопления зарядов. Используется свойство снижения потенциала заряженного тела при приближении к нему другого тела с зарядом противоположного знака. Конденсатор представляет собой систему из двух изолированных друг от друга металлических проводников, между которыми находится диэлектрик. Сами проводники называют обкладками конденсатора. В зависимости от конфигурации обкладок различают:

а) плоский конденсатор – систему из двух плоских параллельно расположенных металлических пластин площадью S каждая. Расстояние между пластинами l много меньше их линейных размеров. В этом случае поле между пластинами можно считать однородным и пренебречь искажениями поля на краях (рис. 1);

Рис. 1.

Электрическое поле плоского конденсатора

б) сферический конденсатор, обкладки которого представляют собой две концентрические сферы;

в) цилиндрический конденсатор, у которого обкладками служат два коаксиальных цилиндра.

Обкладки конденсатора могут иметь и другую форму.

Основным параметром конденсатора является его электрическая емкость С. Она определяется зарядом, который способен удерживаться на одной из пластин конденсатора, когда разность потенциалов между пластинами равна 1 В:

С=Q/U.

(1)

Измеряется емкость в фарадах.

Для плоского конденсатора

(2)

где S – площадь пластин, d – расстояние между пластинами, - диэлектрическая проницаемость вещества между пластинами, - электрическая постоянная.

Для сферического конденсатора

(3)

где R и r – радиусы внутренней и внешней сфер. В частном случае, когда R = ,

(4)

Для цилиндрического конденсатора

(5)

где L – длина коаксиальных цилиндров, R и r – радиусы внутреннего и внешнего цилиндров.

Вторым важным параметром конденсатора является его электрическая прочность, т. е. максимальное напряжение, на которое рассчитан конденсатор. Прочность определяется, главным образом, толщиной слоя диэлектрика между пластинами. Однако чем больше эта толщина, тем больше объем и масса конденсатора. Кроме того, конденсатор характеризуется температурным коэффициентом емкости (ТКЕ), желательно минимальным, и тангенсом угла диэлектрических потерь tg (или добротностью 1/tg ).

Этой величиной учитывается выделение теплоты в конденсаторе при прохождении через него переменного тока. Она должна быть по возможности минимальной.

Свойства конденсатора в основном определяются диэлектриком. Конденсаторы могут быть воздушными (вакуумными), бумажными, слюдяными, керамическими, фторопластовыми (тефлоновыми), сегнетоэлектрическими и т. д. Чаще всего конденсатор изготавливают из двух металлических лент, между которыми проложен ленточный диэлектрик (рис.2, а). В металлопленочных конденсаторах на тонкую ленту диэлектрика напыляется с обеих сторон слой металла. Затем ленты скручиваются в рулон и укладываются в металлическую коробку. Обычный технический бумажный конденсатор состоит из двух полосок станиоля, изолированных друг от друга и от защитного корпуса бумажными лентами, пропитанными парафином. Полоски и ленты туго свернуты в пакеты небольшого размера.

Есть и другие типы конденсаторов. В радиотехнике широко применяются конденсаторы переменной емкости. В конденсаторах переменной емкости одна пластина (или группа пластин) смещается относительно другой пластины (группы пластин, рис. 2 б). В формуле емкости плоского конденсатора (1) величина S (для данного конденсатора) — не площадь пластин, а площадь взаимодействующей части пластин. Поэтому при относительном сдвиге пластин емкость меняется. Диэлектриком служит чаще всего воздух. Для воздушного конденсатора важно, чтобы пластины не задевали друг друга, поэтому расстояние d между пластинами сделать достаточно малым не удается. В результате емкость переменного воздушного конденсатора обычно не превышает 600 пФ. Для увеличения емкости или уменьшения габаритов конденсатора между пластинами прокладывают тонкую пленку фторопласта. Тогда пластины можно прижать друг к другу, обеспечив все же возможность их скольжения друг относительно друга. Для того чтобы емкость менялась по определенному закону (линейному, квадратичному, обратноквадратичному), подвижные пластинки делают специальной формы. Полупеременные керамические конденсаторы обычно имеют небольшую емкость; они используются в схемах для подстройки. Чтобы изменить емкость, нужно повернуть отверткой верхний диск относительно нижнего (рис. 2, в).

Электролитические конденсаторы обладают гораздо большей емкостью, чем рассмотренные выше. Их устройство напоминает устройство бумажных или пленочных конденсаторов (рис.1, а), но вместо изолирующей бумаги между металлическими лентами прокладывается пористая бумага, пропитанная проводящим раствором (электролитом), роль же изоляции выполняет тончайший слой оксида, покрывающий один из электродов (рис. 2, г). Такой конденсатор полярен. На него можно подавать напряжение только так, как показано на рисунке. При несоблюдении полярности кислород в результате электролиза уходит из оксидного слоя. Этот слой становится тоньше и пробивается. Поэтому электролитические конденсаторы нельзя использовать в цепях со знакопеременным напряжением. Чаще всего их ставят в сглаживающих фильтрах, выпрямителях.

Менее чувствительны к нарушению полярности оксидные конденсаторы без электролита, в которых поверх оксидного слоя напыляется слой металла — второй электрод (рис.1, д). Для изготовления электролитических и оксидных конденсаторов используется алюминиевая фольга, покрытая слоем оксида алюминия . Теперь применяют также тантал, титан или ниобий.

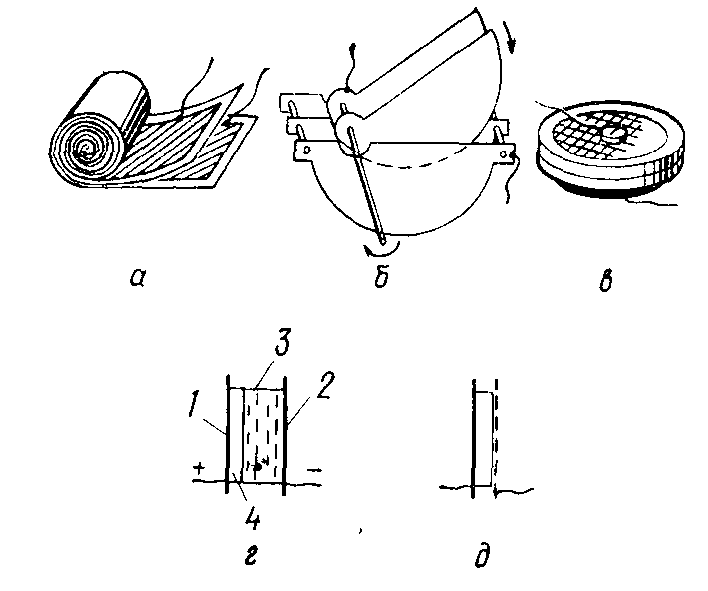
Рис.2.

Устройство конденсаторов: ( а — устройство бумажного конденсатора; б — конденсатор переменной емкости; в — подстроечный керамический конденсатор; г — электролитический конденсатор: 1, 2 — металлические электроды, 3 — электролит, 4 — оксидный слой; д — оксидный конденсатор)

.

Особое место занимают нелинейные конденсаторы, т. е. конденсаторы, в которых заряд и потенциал не пропорциональны друг другу. Иными словами, в формуле Q = CU коэффициент С является функцией от поданного напряжения: C(U). К нелинейным конденсаторам относятся вариконды и варикапы. Вариконды — конденсаторы, в которых в качестве диэлектрика используются керамические сегнетоэлектрики, обладающие очень большой диэлектрической проницаемостью (до 103—104), что обеспечивает малогабаритность конденсатора. Вариконд — управляемый конденсатор, его емкость зависит от величины управляющего напряжения U. Это используется в цепях автоматической настройки. Однако зависимость от температуры и сравнительно большие потери ограничивают область применения варикондов.

Конденсаторы различной емкости можно соединять в батареи двумя способами – либо последовательно (рис. 3, а) либо параллельно (рис.3, б). Суммарную электроемкость таких батарей называют эквивалентной электроемкостью. При разных способах соединения конденсаторов заряды и потенциалы между ними распределяются по-разному:

а) последовательное соединение конденсаторов

Рис. 3, а.

Последовательное соединение конденсаторов

(6)

б) параллельное соединение конденсаторов

Рис.3, б.

Параллельное соединение конденсаторов

(7)

Для того чтобы зарядить конденсатор до некоторой разности потенциалов между его обкладками, можно на одной из электронейтральных обкладок разделить заряды противоположных знаков и бесконечно малый заряд dq какого – либо знака перенести с одной обкладки на другую. При этом будет произведена работа, равная бесконечно малому изменению энергии конденсатора:

(7)

Подставив сюда значение разности потенциалов (см. определение электроемкости), получим Интегрируя это выражение при постоянной электроемкости, имеем

Используя определение электроемкости конденсатора, можно энергию заряженного конденсатора записать так:

(8)

Рассмотрим процессы заряда и разряда конденсатора. Если заряженный конденсатор замкнуть проводником, то по проводу потечет ток, и конденсатор будет разряжаться.

Пусть U – разность потенциалов между его обкладками, R – сопротивление цепи, через которую происходит разряд. Для мгновенных значений заряда q, силы тока I и напряжения U можно записать:

(9)

Знак «минус» взят потому, что заряд q на конденсаторе со временем убывает.

Полагаем, что мгновенное значение тока одно и то же во всех поперечных сечениях проводника, замыкающего конденсатор. Исключая силу тока I и напряжение U из уравнений (9), имеем

(10)

Интегрируя выражение (10), получаем

(11)

где В – постоянная интегрирования, которая определяется на начальных условий, т. е. при t = 0 заряд конденсатора q0:

(12)

Тогда имеем

(13)

Из выражения (13) следует, что заряд на конденсаторе при его разряде изменяется по экспоненциальному закону. По такому же закону изменяется и напряжение на конденсаторе (рис. 4, кривая 1):

(14)

где U0 - напряжение в начальный момент времени. Из выражения (13) следует, если , то

t = = RC

(15)

Величина имеет размерность времени и называется временем релаксации, т.е. это время за которое заряд конденсатора (напряжение на обкладках) изменится в е раз. Вообще релаксацией называется любой самопроизвольный процесс перехода системы в устойчивое равновесное состояние. В данном случае это процесс разряда конденсатора.

Рис. 4.

Зависимость U = f (t)

Для определения времени релаксации можно измерить время t1/2, за которое заряд (напряжение) (см. выражения (12), (13)) уменьшается до половины первоначальной величины: . Решая последнее выражение относительно t1/2, имеем t1/2 = ln2 = 0,693.

Закон изменения напряжения на конденсаторе при его заряде (без вывода) выглядит как

(16)

и на рис. 1 представлен кривой 2.

Методика проведения эксперимента

Полученные теоретические зависимости напряжения на конденсаторе при его разряде или заряде могут быть проверены экспериментально. Для этого следует измерить значения напряжения в разные моменты времени и результаты измерений изобразить в виде точек на координатной плоскости XOY, где Х=t, (операция линеаризации функции). Если экспериментальные точки в пределах точности измерений ложатся на прямую (рис. 5), то это подтверждает зависимости (14) и (16).

Рис. 5.

Экспериментальная зависимость

Для расчета ёмкости конденсатора можно воспользоваться полученным графиком. Для этого необходимо на линейном участке выбрать приращение t и найти соответствующее ему приращение , а затем воспользоваться формулой (17):

(17)

Для наблюдения процессов зарядки и разрядки конденсатора на осциллографе необходимо периодически подключать и отключать конденсатор от источника. Для этого можно использовать генератор прямоугольных импульсов. Период следования импульсов выбирается исходя из условия Тимп 4-6 .

Для исследования процессов зарядки и разрядки конденсатора используется модульный учебный комплекс МУК-ЭМ1(2).

Электрическая схема представлена на рис. 6. В качестве источника прямоугольного напряжения используется генератор ГН1. В качестве измерительного прибора используется осциллограф ОЦЛ2. Постоянный резистор и исследуемый конденсатор располагаются в стенде с объектами исследования С3-ЭМ01.

Рис. 6.

Принципиальная схема установка

Порядок выполнения работы:

1. Собрать электрическую схему рис. 6. На экране осциллографа получить изображение сигнала заряда и разряда конденсатора.

2. Перерисовать осциллограмму. Сравнить процессы разряда и заряда конденсатора. По осциллограмме измерить значение U0. На участке разряда конденсатора для 5-6 отсчетов времени найдите значения .

3. По полученным результатам построить график зависимости от t. Убедится, что в пределах точности измерений, экспериментальные точки ложатся на прямую.

4. Оценить ёмкость конденсатора по формуле (8).

5. Провести аналогичную процедуру измерений и расчётов, изменив сопротивление цепи R. Сопоставит полученные Вами значения ёмкости С.

Контрольные вопросы:

1. Устройство конденсатора, его основные параметры, типы.

2. Что называется электроемкостью, единицы измерения электроемкости. Виды конденсаторов и формулы емкости их определяющие.

3. Какова роль диэлектрического слоя в конденсаторе.

4. Как определяется емкость параллельно и последовательно соединенных конденсаторов.

5. На чем основан метод определения емкости конденсатора в данной работе? Что происходит с емкостью в процессе разрядки.

6. Приведите примеры использования энергии заряженного конденсатора.

7. Вывести формулу энергии конденсатора, назвать и дать определение всех физических величин входящих в данную формулу.

Литература

1. Зисман Г.А., Тодес О.М. Курс общей физики. – М.: Наука, 1989г, т.2

2. Детлаф А.А., Яворский В.М. Курс физики.- М.: ВШ, 1989, т.2.

1. Савельев И.В. Курс общей физики.- М.: Наука,1989, т.2
2. Бурсиан Э.В. Физические приборы.- М.: Просвещение,1984.

5. Комиссаров В.С. Методические указания к лабораторным занятиям по физике. 1998.

6. Андрейчик М.В. Учебно – методическое пособие по физике по курсу «Электричество» 2002.

7. Евсина Е.М., Соболева В.В. Учебно – методическое пособие к лабораторным работам по физике раздел «Электричество». – Астрахань, АИСИ, 2004 – 75 с. .

С3

С2

С1

С3

С2

С1

Изучение процесса заряда и разряда конденсатора