Настройка ПИД-регулятора на основе нечеткой логики

Лабораторная работа № 3.

Цель работы

Изучение принципов расчета начальных значений параметров ПИД-регулятора. Изучение принципов функционирования и правил настройки параметров ПИД-регулятора на основе нечеткой логики. Использование SCADA-системы TRACE MODE 6 для моделирования системы управления с ПИД-регулятором.

Задачи

Расчет начальных значений параметров ПИД-регулятора по методу Зиглера и Никольса. Настройка параметров ПИД-регулятора с использованием нечеткой логики. Моделирование системы управления с ПИД-регулятором с использованием SCADA-системы TRACE MODE 6.

Теоретическая часть

Впервые методику расчета параметров ПИД-регуляторы предложили Зиглер и Никольс в 1942 г. Эта методика очень проста и дает не очень хорошие результаты. Тем не менее она до сих пор часто используется на практике, хотя с тех пор появилось множество более точных методов. Фактически было предложено два метода настройки ПИД-регуляторов. Один из них основан на параметрах отклика объекта на единичный скачок, второй — на частотных характеристиках объекта управления.

Для расчета параметров ПИД-регулятора по отклику объекта на единичный скачок используется представление объекта в виде инерционного звена первого порядка с запаздыванием:

. (1)

Расчет параметров ПИД-регулятора производится по двум параметрам: а и N, где . Реакции объекта управления и замкнутой системы с ПИД-регулятором на единичное воздействие приведены на рис. 1. Там же показаны параметры a и L (запаздывание, эквивалентное N), используемые в расчетах.

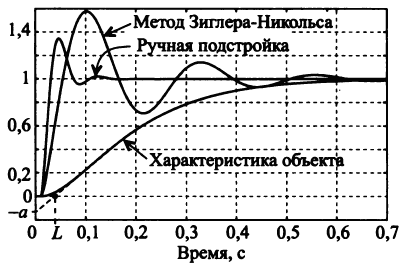
Рис. 1. Реакции объекта управления и замкнутой системы с ПИД-регулятором на единичное воздействие

Формулы для расчета коэффициентов ПИД-регулятора сведены в табл. 1.

Таблица 1. Формулы для расчета коэффициентов ПИД-регулятора по методу Зиглера-Никольса

Регулятор	Kп	Ти	Тд
П	1/a	-	-
ПИ	0.9/a	3N/Kп	-
ПИД	1.2/a	0.9N/Kп	0.5NKп

В табл.1 использованы следующие обозначения:

Kп – коэффициент передачи пропорционального звена ПИД-регулятора;

Ти – постоянная времени интегрирующего звена, обратная величина для его коэффициента передачи (Ти = 1/Kи);

Тд – постоянная времени дифференцирующего звена, равная его коэффициенту передачи (Тд = Kд).

После расчета параметров регулятора обычно требуется его подстройка для улучшения качества регулирования. Для этого используется различные методы, в том числе и настройка с использованием нечеткой логики.

Блок-схема нечеткого регулятора в общем случае принимает вид, изображенный на рис.2.

Как видно из данной схемы, формирование управляющих воздействий включает в себя следующие этапы:

а) получение отклонений управляемых координат и скоростей их изменения - ;

б) «фаззификация» этих данных, т.е. преобразование полученных значений к нечеткому виду, в форме лингвистических переменных;

в) определение нечетких (качественных) значений выходных переменных (в виде функций их принадлежности соответствующим нечетким подмножествам) на основе заранее сформулированных правил логического вывода, записанных в базе правил;

г) «дефаззификация», т.е вычисление реальных числовых значений выходов u1 , u2 , … , um , используемых для управления объектом.

Помимо варианта «чистого» использования нечеткого управления, существуют и другие варианты построения ИСУ с нечеткими регуляторами. Так, в классической теории регулирования широкое распространение получило использование ПИД-регулятора, выходной сигнал которого формулируется по формуле:

, (2)

где параметры Kп , Kи и Kд характеризуют удельный вес соответственно пропорциональной, интегральной и дифференциальной составляющей и должны выбираться исходя из заданных показателей качества регулирования (время регулирования, перерегулирование, затухание переходных процессов).

Таким образом, качество процессов управления при использовании ПИД-регуляторов существенно зависит от выбора его коэффициентов усиления Кп, Ки, Кд для пропорциональной, интегральной и дифференциальной составляющей соответственно. Большинство инженеров на практике настраивают эти коэффициенты вручную, методом проб и ошибок. Эта процедура является достаточно сложной и требует опыта проектирования систем управления. С другой стороны, наличие такого опыта позволяет построить процедуру автоматической настройки коэффициентов усиления ПИД-регулятора на основе алгоритмов нечеткой логики. Рассмотрим один из возможных способов решения данной задачи.

Допустим, что структурная схема адаптивной системы управления с эталонной моделью имеет следующий вид (рис.3).

Наличие интегральной составляющей обеспечивает нулевую статическую ошибку САУ; выбором коэффициентов Кп, Ки, Кд обеспечивают желаемые показатели качества переходных процессов. Будем учитывать три таких показателя – время достижения 10% от установившегося значения (t1); время нарастания, т.е. достижения 90% от установившегося значения (tн); перерегулирование ().

Будем полагать, что цель, поставленная перед нечетким регулятором, - обеспечить желаемые показатели качества системы t1* , tн*, * за счет подстройки параметров основного регулятора Кп, Ки, Кд. Для этого необходимо использовать правила, основанные на опыте и интуиции эксперта. При этом учитывается следующий опыт:

если коэффициент усиления Ки увеличивается, то время нарастания уменьшается, а перерегулирование возрастает;
если коэффициент усиления Кп увеличивается, то время нарастания сильно уменьшается, а перерегулирование возрастает;
если коэффициент усиления Кд увеличивается, то время нарастания сохраняется, а перерегулирование слегка возрастает;
чтобы уменьшить время достижения 10 % от установившегося значения, необходимо уменьшить коэффициент усиления Ки и одновременно увеличить коэффициент усиления Кп.

Будем рассматривать в качестве входов нечеткого регулятора отклонения =-, = -, = - , а под выходами нечеткого регулятора будем понимать настраиваемые значения коэффициентов усиления Кп, Ки, Кд основного регулятора. Базу правил нечеткого регулятора, построенную на основе мнений экспертов, представим в табл. 2.

Таблица 2. База правил.

0,75

1,25

0,75

0,9

1,2

0,9

1,1

0,5

1,6

0,8

1,9

-1,9

2,5

0,9

1,5

0,75

0,7

1,3

0,6

-0,4

1,4

0,6

1,4

1,2

0,7

1,25

1,8

0,95

1,8

1,25

0,75

0,5

1,25

0,8

0,55

0,95

0,8

0,6

0,8

-0,4

0,9

1,8

1,2

1,25

0,9

1,25

0,75

Здесь используются обозначения термов: NB – «отрицательное большое» (negative big), ZO – «около нуля, оптимальное» (zero, optimal), PB – «положительное большое» (positive big). Этим термам соответствуют функции принадлежности.

Поясним механизм составления таблицы 2. В каждой из клеток этой таблицы, составленной для различных значений переменной , записаны значения поправочных коэффициентов Sи, Sп, Sд , определяющих требуемый закон изменения параметров ПИД-регулятора в зависимости от значений входных лингвистических переменных нечеткого регулятора:

Ки = (1- Sи)* Ки ; Кп = (1- Sп)* Кп ; Кд = (1- Sд )* Кд .

Так, например:

ЕСЛИ (= NB И = NB И = NB ), ТО (Sи =0,5 И Sп =1,25 И Sд =1),

т.е. в случае затянутого, слабо демпфированного переходного процесса y(t) необходимо на 50% увеличить коэффициент усиления Ки, на 25% снизить коэффициент усиления Кп, сохраняя неизменным значение Кд.

ЕСЛИ (= PB И = PB И = ZO ), ТО (Sи =2,5 И Sп =0,9 И Sд =1), т.е. при наличии слишком форсированного переходного процесса y(t) необходимо резко уменьшить значение Ки, изменив даже его знак; несколько увеличить значение Кп, сохранив на том же уровне значение Кд.

Таким образом, измеренные отклонения , , (входы нечеткого регулятора) после фаззификации с помощью функций принадлежности подвергаются обработке с использованием записанных в табл. 2 правил вывода. Если на данном этапе применить метод Произведения, а для дефаззификации воспользоваться методом центра тяжести, то получим значения поправочных коэффициентов Sи, Sп, Sд.

Описание используемых программных комплексов

Запуск инструментальной системы TRACE MODE 6 производится двойным щелчком левой кнопки (ЛК) мыши по иконке рабочего стола Windows или из меню «ПУСК/Все программы/Trace Mode 6/TRACE MODE IDE 6».

Конечным результатом работы инструментальной системы TRACE MODE 6 является набор файлов, предназначенных для исполнения задач АСУ в мониторах реального времени на АРМах и в контроллерах. В лабораторной работе в качестве МРВ для АРМ будет использоваться профайлер с поддержкой графических экранов rtc.exe, расположенный в директории инструментальной системы TRACE MODE 6. Профайлер позволяет запускать на компьютере с установленной инструментальной системой один узел разработанного проекта.

Меры безопасности

Во время выполнения лабораторной работы необходимо:

соблюдать правила включения и выключения вычислительной техники;
не подключать кабели, разъемы и другую аппаратуру к компьютеру;
при включенном напряжении сети не отключать, не подключать и не трогать кабели, соединяющие различные устройства компьютера;
в случае обнаруженной неисправности в работе оборудования или нарушения правил техники безопасности сообщить руководителю лабораторной работы;
не пытаться самостоятельно устранить неисправности в работе аппаратуры;
по окончании работы приведите в порядок рабочее место.

ВНИМАНИЕ! При работе за компьютером необходимо помнить: к каждому рабочему месту подведено опасное для жизни напряжение. Поэтому во время работы надо быть предельно внимательным и соблюдать все требования техники безопасности!

Задание

6.1. Проект, созданный в ходе выполнения лабораторной работы № 2, подготовить для выполнения лабораторной работы № 3. Параметры объекта управления приведены в табл. 1 лабораторной работы № 2.

6.2. Программа на языке FBD должна реализовывать полную динамическую модель системы управления, т.е. содержать блок вычитания, блок ПИД-регулятора, блок объекта управления, соединенных в замкнутую систему.

6.3. Рассчитать начальные значения параметров ПИД-регулятора по методу Зиглера-Никольса.

6.3. Реализовать функционирование системы управления с полученными значениями параметров ПИД-регулятора в реальном времени. Задать уставку 100%, значения ограничений на управление задать примерно ±500%. Снять переходную характеристику системы управления как реакцию на ступенчатое изменение уставки.

6.4. По переходной характеристике системы определить значения показателей качества управления.

6.5. Рассчитать отклонения показателей качества управления от заданных значений. В качестве заданных показателей качества использовать: t1* = N+2; tн*= t1* + T; * = 20%. Рассчитать новые значения параметров ПИД-регулятора с использованием нечеткой логики.

6.6. Повторить п. 6.3 – 6.5. Убедиться в том, что отклонения показателей качества управления от заданных уменьшились. Процедуру повторять до тех пор, пока показатели качества не будут соответствовать заданным.

6.7. Задать ограничения на управление на уровне примерно ±50%. Снять переходную характеристику системы управления как реакцию на ступенчатое изменение уставки. Сделать выводы о характере влияния ограничения типа «насыщение» на качество управления.

Методика выполнения задания

7.1. Для выполнения п. 6.1. задания проделать следующее. Используя блоки Вычитание, PID, OBJ, составить модель системы управления. Создать необходимые аргументы программы, привязать их к каналам. Выполнить привязку входных и выходных сигналов блоков. Для блока OBJ параметры объекта управления – коэффициент передачи, постоянную времени, задержку, параметр помехи – задать константами в соответствии с вариантом задания.

7.2. Для выполнения п. 6.2 задания соединить блоки по схеме «уставка – блок вычитания – ПИД-регулятор – объект управления – обратная связь к блоку вычитания». Откомпилировать программу, при наличии ошибок устранить их. Запустить выполнение проекта с помощью МРВ.

7.3. Для выполнения п. 6.3 задания ввести значения уставки и параметров ПИД-регулятора и получить переходную характеристику для системы управления. Сделать скриншот переходной характеристики.

7.4. Для выполнения пп. 6.4, 6.5 задания по переходной характеристике системы управления определить значения показателей качества управления. При необходимости использовать функцию увеличения изображения для компонента построения графиков. Используя заданные значения показателей качества, рассчитать отклонения для показателей, построить функции принадлежности, определить значения лингвистических переменных и с помощью таблицы правил получить значения поправочных коэффициентов, затем рассчитать новые значения параметров ПИД-регулятора.

Требования к содержанию и оформлению отчета

Отчет по лабораторной работе должен содержать:

краткие теоретические сведения;
формулировку задания на лабораторную работу;
описание последовательности выполнения работы;
изображения рабочих окон, полученных в результате моделирования работы системы;
скриншоты для графиков переходных характеристик по всем этапам работы;
выводы по лабораторной работе.

Контрольные вопросы

9.1. Какие функции выполняет нечеткий регулятор?

9.2. От чего зависит качество управления при использовании ПИД-регулятора?

9.3. Какие этапы включает в себя процесс формирования управляющих воздействий?

9.4. Какие правила и опыт следует учитывать для того, чтобы обеспечить желаемые показатели качества системы , , ?

9.5. Как нужно воздействовать на коэффициенты усиления Кп, Ки, Кд , ЕСЛИ (= ZO И = ZO И = PB ), используя базу правил ?

Критерии оценки выполнения лабораторной работы

Лабораторная работа считается выполненной в том случае, если:

студент выполнил все задания в соответствии с представленной методикой;
результаты выполнения работы, представленные в виде отчета, соответствуют предъявленным к ним требованиям;
студент правильно ответил на все контрольные вопросы и может интерпретировать полученные результаты.

Литература

Рекомендуемая литература [1 - 4].

База правил

Фаззифи-кация

Механизм

вывода

Дефаззи-фикация

«Четкие» значения отклонений

Лингвистические переменные

«Четкие» значения выходов

Рис. 2. Блок-схема нечеткого регулятора

Рис.3. Структурная схема нечеткой адаптивной САУ с ПИД-регулятором

Кд

Кп

Ки

База правил

Функции принадлежности

Объект управления

ПИД-регулятор

Нечеткая логика

Эталонная модель

= NB

= ZO

= PB

Настройка ПИД-регулятора на основе нечеткой логики