РАЗРАБОТКА АЛГОРИТМА СТОХАСТИЧЕСКОГО ФОРМИРОВАНИЯ СИГНАЛОВ
КУРСОВАЯ РАБОТА
по дисциплине
«Технические средства и системы охраны»
на тему:
«РАЗРАБОТКА АЛГОРИТМА СТОХАСТИЧЕСКОГО ФОРМИРОВАНИЯ СИГНАЛОВ»
Содержание
|
Введение...................................................................................................................
|
4
|
|
1 Анализ угроз функционирования беспроводных систем передачи информации с кодовым разделением каналов................................................................
|
6
|
|
1.1 Общая характеристика и принципы функционирования CDMA.......................................................................................................................
|
6
|
|
1.2 Угрозы функционирования сетей с кодовым разделением каналов.............................................................................................................................
|
9
|
|
1.3 Анализ радиоэлектронных угроз...........................................................
|
11
|
|
1.4 Выводы по главе......................................................................................
|
13
|
|
2 Исследование методов защиты информации в беспроводных системах передачи информации с кодовым разделением каналов.........................................
|
14
|
|
2.1 Исследование методов защиты информации от радиоэлектронных угроз..........................................................................................................................
|
14
|
|
2.2 Исследование недостатков используемых ансамблей дискретных ортогональных сигналов.........................................................................................
|
15
|
|
2.3 Выводы по главе......................................................................................
|
19
|
|
3 Разработка алгоритма стохастического формирования сигналов....................
|
20
|
|
3.1 Анализ метода полного перебора коэффициентов бидиагональной симметрической матрицы.......................................................................................
|
20
|
|
3.2 Определение влияния знаковой структуры бидиагональной симметрической матрицы и абсолютной величины её элементов............................
|
22
|
|
3.3 Алгоритм построения ансамблей дискретных ортогональных многоуровневых сигналов и их математическое моделирование..............................................................................................................................
|
23
|
|
3.4 Вывод по главе.........................................................................................
|
25
|
|
Заключение...............................................................................................................
|
27
|
|
Список используемых источников.........................................................................
|
29
|
|
Приложение А..........................................................................................................
|
30
|
Введение
СDMA – технология на основе которой построены различные системы множественного доступа с кодовым разделением – стала, возможно, самой многообещающей, появившейся на мировом рынке. Десятилетия назад эта технология использовалась в военной связи, а сегодня известна всем как глобальный цифровой стандарт для коммерческих систем коммуникаций. Технология использования CDMA была протестирована, стандартизирована, лицензирована и запущена в производство большинством поставщиков беспроводного оборудования и давно применяется во всем мире [3]. В отличие от других методов доступа абонентов к сети, где энергия сигнала концентрируется на выбранных частотах или временных интервалах, сигналы CDMA распределены в непрерывном частотно-временном пространстве [4]. Фактически метод манипулирует и частотой, и временем, и энергией.
В настоящее время большое внимание уделяется безопасности в беспроводных сетях. Любая сеть является объектом существенного риска и проблем с точки зрения безопасности. В сетях с кодовым разделением каналов необходимо обеспечить повышение качества предоставляемых услуг на основе усиления их информационной защищенности, для гарантий безопасности имущественных прав и интересов клиентов, включая предотвращение нарушений прав личности, общества и государства на сохранение конфиденциальности информации циркулирующей в сети оператора [5].
К объектам защиты относятся информационные ресурсы, обрабатываемые в рамках инфраструктуры сети, а также информационные ресурсы самой инфраструктуры сети, влияющие на эффективность обеспечения информационной безопасности [5].
Исходя из вышесказанного, мы сформулировали цель работы – повышение защищённости информации в беспроводных системах путём разработки алгоритма стохастического формирования сигналов.
Для достижения цели, необходимо решить следующие задачи:
– провести анализ угроз функционирования беспроводных систем передачи информации с кодовым разделением каналов;
– исследовать методы защиты информации в беспроводных системах передачи информации с кодовым разделением каналов;
– разработать алгоритм стохастического формирования сигналов.
Актуальность темы: использования беспроводных систем с кодовым разделение каналов.
Объект исследования – беспроводная система с кодовым разделением каналов.
Предмет исследования – подсистема формирования радиосигнала.
1 Анализ угроз функционирования беспроводных систем передачи информации с кодовым разделением каналов
1.1 Общая характеристика и принципы функционирования CDMA
Принцип CDMA заключается в расширении спектра исходного информационного сигнала, которое может производиться двумя различными методами, которые называются следующим образом: “скачки по частоте” и “прямая последовательность” [3].
Так называемые “скачки по частоте” (или FH – Frequency Hopping) реализуются следующим образом: несущая частота в передатчике постоянно меняет свое значение в некоторых заданных пределах по псевдослучайному закону (коду), индивидуальному для каждого разговорного канала, через сравнительно небольшие интервалы времени. Приемник системы ведет себя аналогично, изменяя частоту гетеродина по точно такому же алгоритму, обеспечивая выделение и дальнейшую обработку только нужного канала [3].
Второй метод “прямой последовательности” (или DS – Direct Sequence), который основан на использовании шумоподобных сигналов и применяется в большинстве работающих и перспективных системах CDMA. Он предусматривает модуляцию информационного сигнала каждого абонента единственным и уникальным в своем роде псевдослучайным шумоподобным сигналом (он – то и является в данном случае кодом), который и расширяет спектр исходного информационного сигнала. В результате проведения описываемого процесса узкополосный информационный сигнал каждого пользователя расширяется во всю ширину частотного спектра, выделенного для пользователей сети (база сигнала при этом становится много больше). В приемнике сигнал восстанавливается с помощью идентичного кода, в результате чего восстанавливается исходный информационный сигнал. В то же самое время сигналы остальных пользователей для данного приемника продолжают оставаться расширенными и воспринимаются им лишь как белый шум, который является наиболее мягкой помехой, в наименьшей степени мешающей нормальной работе приемника [3].
В системах с частотным разделением каналов (как в FDMA, так и в TDMA) существует проблема так называемого "многократного использования" частотных каналов [3].
Чтобы не мешать друг другу, соседние базовые станции должны использовать разные каналы. Таким образом, если у базовой станции 6 соседей (наиболее часто рассматриваемый случай, при этом зону каждой базовой станции можно представить как шестиугольник, а всё вместе выглядит как пчелиные соты), то количество каналов, которые может использовать эта базовая станция в семь раз меньше чем общее количество каналов в отведённом для сети диапазоне. Это приводит к уменьшению ёмкости сети и необходимости увеличивать плотность установки базовой станции в густонаселённых районах. Для CDMA такой проблемы вообще нет. Все базовые станции работают на одном и том же канале. Таким образом, частотный ресурс используется более полно. Ёмкость CDMA сети обычно в несколько раз выше, чем TDMA, и на порядок выше чем FDMA сетей [3].
Для того, чтобы телефоны находящиеся близко к базовой станции не забивали своим сигналом более отдалённых абонентов, в CDMA предусмотрена плавная регулировка мощности, что приводит к значительному сокращению энергопотребления телефона вблизи базовой станции и, соответственно, увеличению времени работы телефона без подзарядки [3].
Одной из приятных особенностей CDMA сетей является возможность “мягкого” перехода от одной базовой станции к другой (soft handoff). При этом, возможна ситуация когда одного абонента “ведут” сразу несколько базовой станции. Абонент просто не заметит, что его “передали” другой базовой станции. Естественно, чтобы такое стало возможным, необходима прецизионная синхронизация базовой станции. В коммерческих системах это достигается использованием сигналов времени от GPS (Global Positioning System) американской спутниковой системы определения координат [3].
CDMA это практически полностью цифровой стандарт. Обычно все преобразования информационного сигнала происходят в цифровой форме, и только радиочасть аппарата является аналоговой, причём гораздо более простой, чем для других групп стандартов. Это позволяет практически весь телефон выполнить в виде одной микросхемы с большой степенью интеграции, тем самым значительно снизив стоимость телефона [3].
Цифровая сущность CDMA весьма располагает к использованию этой технологии для безпроводной передачи данных. В рассмотренном выше примере мы задали не очень высокую скорость, однако существующие реализации CDMA позволяют многократно увеличивать скорость передачи данных, правда за счет сокращения ёмкости сети [3].
Стандарты CDMA используют более современный кодек для оцифровки речи, что субъективно повышает качество передачи аналогового сигнала по сравнению с действующими TDMA стандартами [3].
Из минусов CDMA можно отметить необходимость использования достаточно широкой и неразрывной полосы, что не всегда возможно в современной обстановке дефицита частотного ресурса и большую сложность реализации данной технологии в “железе” [3].
В итоге получается что стандарт CDMA имеет следующие преимущества:
– более высокое качество связи по сравнению с другими стандартами связи;
– более высокая скорость передачи данных и соответственно более широкие возможности использования CDMA терминалов;
– меньшее энерго-потребление терминалов что продляет срок работы без подзарядки;
– большая емкость сети [3].
1.2 Угрозы функционирования сетей с кодовым разделением каналов
Связь – одна из наиболее динамично развивающихся отраслей инфраструктуры современного общества. Этому способствует постоянный рост спроса на услуги связи и информацию, а также достижения научно-технического прогресса в области электроники, волоконной оптики и вычислительной техники [4].
Информационная безопасностью – это защита интересов субъектов информационных отношений. Основные ее составляющие – конфиденциальность, целостность, доступность. Доступность – это возможность за приемлемое время получить требуемую информационную услугу. Под целостностью подразумевается актуальность и непротиворечивость информации, ее защищенность от разрушения и несанкционированного изменения [7].
Конфиденциальность – это защита от несанкционированного доступа к информации [7].
Информационная безопасность не сводится исключительно к защите от несанкционированного доступа к информации, это принципиально более широкое понятие. Субъект информационных отношений может пострадать (понести убытки и/или получить моральный ущерб) не только от несанкционированного доступа, но и от поломки системы, вызвавшей перерыв в работе [7].
Информационные системы создаются (приобретаются) для получения определенных информационных услуг. Если по тем или иным причинам предоставить эти услуги пользователям становится невозможно, это, очевидно, наносит ущерб всем субъектам информационных отношений [7].
Поэтому, не противопоставляя доступность остальным аспектам, мы выделяем ее как важнейший элемент информационной безопасности.
Особенно ярко ведущая роль доступности проявляется в разного рода системах управления – производством, транспортом и т.п. Внешне менее драматичные, но также весьма неприятные последствия – и материальные, и моральные – может иметь длительная недоступность информационных услуг, которыми пользуется большое количество людей [7].
Знание возможных угроз, а также уязвимых мест защиты, которые эти угрозы обычно эксплуатируют, необходимо для того, чтобы выбирать наиболее экономичные средства обеспечения безопасности [7].
Угроза – это потенциальная возможность определенным образом нарушить информационную безопасность [7].
Под угрозой информационной безопасности понимается действие или событие, которое может привезти к разрушению, искажению или несанкционированному использованию ресурсов сети, включая хранимую, передаваемую и обрабатываемую информацию, а также программные и аппаратные средства [7].
Классификация угроз информационной безопасности в зависимости от местонахождения источника возможной угрозы делятся на 2 группы: внешние и внутренние [8].
К внешним угрозам информационной безопасности относятся:
– деятельность политических и экономических структур, преступных групп и формирований, а также отдельных лиц внутри страны, направления против интересов граждан, государства и общества в целом и проявляющаяся в виде воздействий на беспроводные сети;
– стихийные бедствия и катастрофы.
К внутренним угрозам информационной безопасности относятся:
– нарушения установленных требований информационной безопасности (непреднамеренные либо преднамеренные), допускаемые обслуживающим персоналом и пользователями;
– отказы и неисправности технических средств обработки, хранения и передачи сообщений (данных), средств защиты и средств контроля эффективности принятых мер по защите, сбои программного обеспечения, программных средств защиты информации и программных средств контроля эффективности принятия мер по защите.
По способу реализации угрозы информационной безопасности подразделяются на следующие виды:
– организационные;
– программно – математические;
– физические;
– радиоэлектронные.
Через радиоэлектронные угрозы реализуются многие другие виды угроз.
Если радиоэлектронные угрозы не будут устранены возможна реализация организационных угроз например таких как:
– несанкционированный доступ обслуживающего персонала и пользователей к информационным ресурсам;
– манипулирование информацией (дезинформация, скрытие или искажение информации) [8].
Иметь представление о возможных угрозах, а также об уязвимых местах, которые эти угрозы обычно эксплуатируют, необходимо для того, чтобы выбирать наиболее экономичные средства обеспечения безопасности.
Реализация этих угроз может привести к серьезным последствиям. Нарушение требований по защите информации влечет за собой дисциплинарную, гражданско-правовую, административную или уголовную ответственность в соответствии с законодательством Российской Федерации. Это обосновывает необходимость реализовать защиту от радиоэлектронных угроз.
1.3 Анализ радиоэлектронных угроз
Перечень угроз служит основой для анализа реализации угроз и формулирования требований к защиты. Кроме выявления возможных угроз, целесообразно проведение анализа этих угроз на основе их классификации по ряду признаков. Угрозы, соответствующие каждому признаку классификации, позволяют детализировать отражаемое этим признаком требование.
К радиоэлектронным угрозам информационной безопасности относятся:
– перехват информации в технических каналах ее утечки;
– перехват и дешифрование информации в сетях передачи данных и линиях связи;
– внедрение электронных устройств перехвата информации в технические средства и помещения;
– навязывание ложной информации по сетям передачи данных и линиям связи;
– радиоэлектронное подавление линий связи и систем управления [8].
В данной курсовой работе нас интересует угроза:
– перехват и дешифрование информации в сетях передачи данных и линиях связи;
Выбор этой угрозы обоснован предметом исследования – подсистемой формирования радиосигнала, так как именно она осуществляет метод “прямой последовательности”, который основан на использовании шумоподобных сигналов которые повышают структурную скрытность сигнала.
Шифрованием называется процесс зашифрования или расшифрования данных.
Дешифрованием называется процесс преобразования закрытых данных в открытые при неизвестном ключе и, возможно, неизвестном алгоритме.
Защита данных с помощью шифрования — одно из возможных решений проблемы их безопасности. Зашифрованные данные становятся доступными только для того, кто знает, как их расшифровать, и поэтому похищение зашифрованных данных абсолютно бессмысленно для несанкционированных пользователей [10].
В отличии от шифрования, структурная скрытность должна противостоять мерам несанкционированного доступа, которые направлены на раскрытие формы сигнала и измерение его параметров при условии, что сигнал уже обнаружен и перехвачен. Можно говорить о том, что процессы шифрования и повышения структурной скрытности похожи, но реализуются на разных уровнях.
1.4 Выводы по главе
В данной главе были рассмотрена технология функционирования сетей с кодовым разделением каналов. А также были рассмотрены основные угрозы функционирования таких сетей. Был проведен анализ радиоэлектронных угроз, посредством чего была выявленная и обоснованна актуальная угроза для данной курсовой работы – перехват и дешифрование информации в сетях передачи данных и линиях связи.
2 Исследование методов защиты информации в беспроводных системах передачи информации с кодовым разделением каналов
2.1 Исследование методов защиты информации от радиоэлектронных угроз
Конфиденциальность передачи информации по радиоканалам может быть достигнута путем обеспечения:
– энергетической скрытности сигналов – переносчиков информации;
– структурной скрытности этих сигналов;
– информационной скрытности самого сообщения.
Информационная скрытность сообщения достигается в основном криптографическими методами [2].
Энергетическая и структурная скрытность являются важнейшими характеристиками сигнала, применяемого в системе радиосвязи. Энергетическая скрытность характеризует способность противостоять мерам, направленным на обнаружение сигнала разведывательным приёмным устройством. Так же может возникать задача определения параметров, в частности, нахождения структуры и метода формирования сигнала [9].
Под структурной (сигнальной) скрытностью понимают степень затруднения определения структуры обнаруженного сигнала. Сигнальная скрытность, в первую очередь, обеспечивается выбором сигнала, по возможности близким по внешнему виду к фону [9].
Одним из вариантов повышения защищенности беспроводных систем передачи информации в современных условиях, является применение эффективных способов сокрытия параметров (структуры) сигналов переносчиков за счет стохастического использования достаточно большого объема сигналов переносчиков, с фиксированным или изменяющимся периодом [1].
Заметим, что к сигналы переносчики, используемым в данном случае, кроме требований по скрытности предъявляются обычные требования, которым они должны удовлетворять для систем связи с расширенным спектром. Основными из них являются ортогональность сигналов, наличие «хороших» автокорреляционных и взаимокорреляционных свойств [1].
2.2 Исследование недостатков используемых ансамблей дискретных ортогональных сигналов
Исследования в области построения ансамблей дискретных ортогональных сигналов в настоящее время базируется на использовании известных дискретных ортогональных систем функций Радемахера, Уолша, Рида – Мюллера, Джеффи, Стиффлера, Велти и др., построенных на основе производных последовательностей, а так же применении систем последовательностей ортогональных кодов [1].
Большинство известных ансамблей дискретных ортогональных фазоманипулированных сигналов обладают рядом недостатков, к которым можно отнести следующие:
– они принадлежат к категории последовательностей, образующих ансамбли с малыми объемами (4х4, 8х8, 16х16);
– номенклатура длин последовательностей в пределах фиксированных числовых интервалов невелика;
– при резком увеличении объема ансамбля m > 64 ухудшаются взаимокорреляционные свойства [1].
Корреляционные свойства систем Уолша нельзя назвать удовлетворительными. Большинство автокорреляционной функции и взаимнокорреляционной функции последовательностей Уолша имеют большие боковые пики [1].
На рисунке 1 изображены автокорреляционной функции последовательностей Уолша при объёме системы N=8.
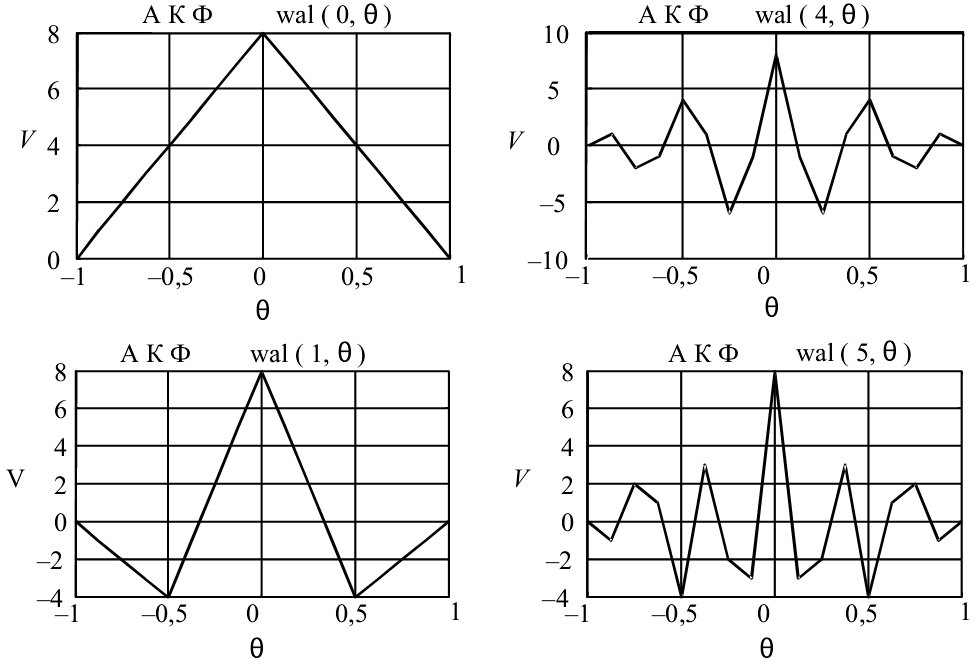
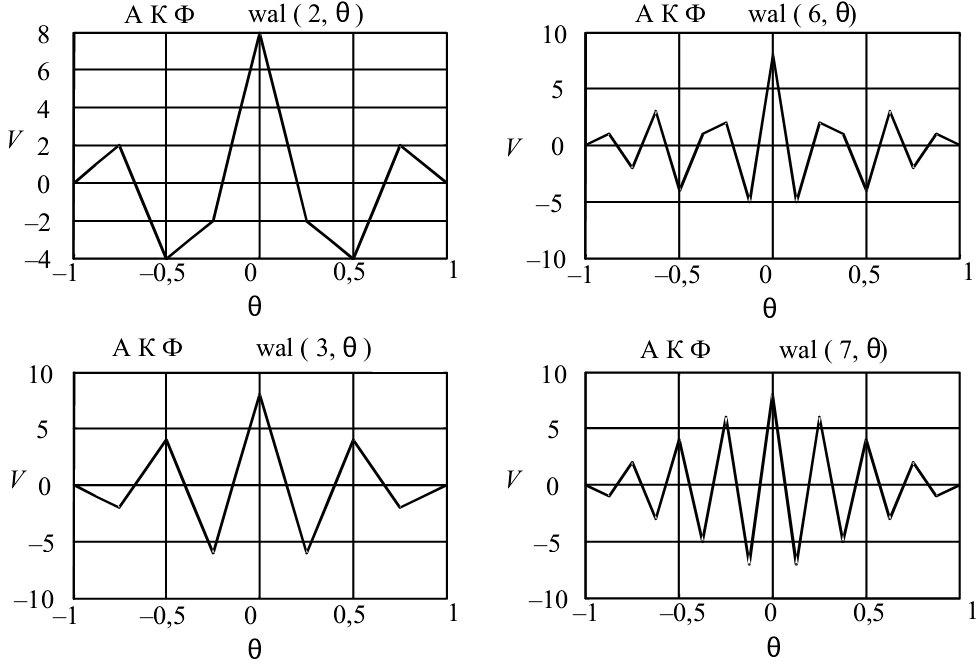
Рисунок 1 – Автокорреляционная функция Уолша
Как видно из рассмотрения рисунка 1, максимальные уровни боковых лепестков автокорреляционной функции (по модулю) составляют для , и значение , для , для и , а для функций Уолша с номером при значении основного корреляционного пика . Отметим, что при любом объёме функций Уолша , где z –целое число, последняя функция имеет вид меандра и, следовательно, уровень бокового лепестка при . Так при максимальный боковой лепесток , при , а при , принятом в стандарте CDMA, значение [1].
Уровень боковых лепестков взаимнокорреляционной функции функции Уолша также значителен, например боковой лепесток взаимнокорреляционной функции при объёме системы с равен . Таким образом, большинство автокорреляционной функции и взаимнокорреляционной функции последовательностей Уолша имеют большие боковые пики, что приводит к большому уровню междуканальных помех при использовании в качестве адресных сигналов непосредственно функций Уолша [1].
Плохие взаимокорреляционые свойства накладывают существенные ограничения на использование известных ансамблей дискретных ортогональных фазоманипулированных сигналов в качестве сигналов-переносчиков в системах передачи информации, к которым предъявляется ряд требований:
- применение сигналов – переносчиков с такой формой, что при заданной пиковой мощности Pmax, обеспечивается наибольшее возможное среднее значение блоков µ:
где µ0 – относительное число блоков, N – число элементов сигнала;
– выбор ансамбля сигналов, необходимо осуществлять с учетом минимальной ширины спектра у самого широкополосного сигнала входящего в ансамбль. В данном случае с точки зрения эффективности использования частотного диапазона оптимальным будет считаться ансамбль, имеющий минимальное значение Wэфф самого широкополосного сигнала;
– для обеспечения наибольшей помехоустойчивости следует использовать сигналы с хорошей равномерностью их спектральной плотности, поскольку в этом случае в используемом диапазоне нет характерных точек, где сигнал в большей степени проявляется. В этой связи характеристикой равномерности спектральной плотности xi(t) может являться максимальный выброс амплитудно-частотного спектра ;
– вследствие удобства осуществления синхронизации в m–ичной ортогональной системе связи путем выделения сигнала синхронизации непосредственно из принимаемой информации, желательным условием является обладание сигналами ансамбля функции автокорреляции с явно выраженным основным пиком, соответствующим моменту согласования фильтра [1].
Учитывая вышеизложенное, можно сделать вывод, что ансамбль дискретных ортогональных сигналов, используемый в качестве переносчика информации в m–ичной ортогональной системе может быть оценен векторной характеристикой:
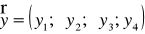
(2)
Значения параметров y1 – y4, исходя из выбранных характеристик, а также сформулированные к ансамблям дискретных ортогональных сигналов требования наглядно представлены в таблице 1.
Таблица 1 – Характеристики и требования к дискретным ортогональным сигналам
Продолжение таблицы 1
|
Выбранная
характеристика
|
|
|
|
|
|
Разработанные требования
|
|
|
|
|
Ещё одним недостатком известных ортогональных базисов является их плохая структурная скрытность, поскольку их количество ограничено (Уолша, Велти, Радемахера, Джеффи, Стифлера и др.), то оно может быть заранее известно злоумышленнику, поэтому необходима разработка нового способа повышения защищенности информации [1].
2.3 Выводы по главе
Конфиденциальность передачи информации по радиоканалам может быть достигнута путем обеспечения энергетической скрытности сигналов – переносчиков информации, структурной скрытности этих сигналов и информационной скрытности самого сообщения.
Исследования в области построения систем связи в настоящее время базируется на использовании известных ортогональных систем функций Радемахера, Уолша, Рида–Мюллера, Джеффи, Стиффлера, Велти и др. Большинство известных ансамблей обладают рядом недостатков, среди которых важнейшими являются плохие взаимокорреляционные свойства и ограниченность числа ансамблей, которые могут быть заранее известны злоумышленнику, что обосновывает выбор темы работы – разработка алгоритма стохастического формирования сигналов.
3 Разработка алгоритма стохастического формирования сигналов
3.1 Анализ метода полного перебора коэффициентов бидиагональной симметрической матрицы
Анализ известных методов построения ансамбля дискретных ортогональных сигналов позволяет сделать вывод, что метод на основе векторного синтеза ортогональных сигналов имеет наиболее широкие возможности по охватываемому количеству ортогональных базисов [2].
Поскольку существует тесная связь между энергетическим спектром сигнала и его автокорреляционной функцией, то применение позволяет охватить большее число ортогональных базисов с автокорреляционной функцией, изменяющихся в широких пределах [2].
Это обстоятельство определяет возможность применения метода на основе векторного синтеза ортогональных сигналов для решения задачи поиска большого числа ансамблей дискретных ортогональных многоуровневых сигналов с заданным диапазоном характеристик и, соответственно, разработки нового метода построения ансамблей дискретных ортогональных многоуровневых сигналов на его основе [2].
Наиболее простым путем решения задачи поиска большого числа ансамблей дискретных ортогональных многоуровневых сигналов с заданным диапазоном характеристик является полный перебор коэффициентов бидиагональной симметрической матрицы. При этом в первую очередь встает вопрос о границах перебора. То есть необходимо определить, в каких пределах должны изменяться коэффициенты бидиагональной симметрической матрицы, чтобы структура получаемых ансамблей дискретных ортогональных многоуровневых сигналов, равно как и их корреляционные свойства, были различны [2].
При изменении коэффициентов бидиагональной симметрической матрицы в широких пределах, характер зависимости уровня максимального бокового пика автокорреляционной функции и взаимнокорреляционной функции от коэффициентов бидиагональной симметрической матрицы может изменяться, а диапазон изменения – смещаться на величину K, при этом ширина диапазона изменения данной зависимости всегда остается неизменной. Следовательно, границы перебора коэффициентов исходной бидиагональной симметрической матрицы можно определить следующим образом:
(3)
где а – произвольное число.
Таким образом, при решении задачи поиска путем полного перебора коэффициентов бидиагональной симметрической матрицы размерности N=64 в диапазоне, определенном в (3) с дискретностью , при потребуется построить ансамблей ортогональных сигналов и рассчитать их корреляционные свойства. При этом с возрастанием размерности ансамблей дискретных ортогональных многоуровневых сигналов требуемое количество ансамблей для перебора будет возрастать согласно зависимости [2].
Если предположить, что на построение одного ансамблей дискретных ортогональных многоуровневых сигналов и расчет его корреляционных характеристик на ЭВМ требуется одна операция и производить полный перебор коэффициентов исходных бидиагональной симметрической матрицы будем на суперкомпьютере типа RENGER с производительностью 1014 операций в секунду, то на полный перебор всех вариантов коэффициентов бидиагональной симметрической матрицы для построения ансамблей дискретных ортогональных многоуровневых сигналов размерности N=64 потребуется:
(4)
Таким образом, задача поиска большого числа ансамблей дискретных ортогональных многоуровневых сигналов с заданным диапазоном характеристик не может быть решена путем полного перебора коэффициентов исходной бидиагональной симметрической матрицы в виду высокой вычислительной сложности [2].
3.2 Определение влияния знаковой структуры бидиагональной симметрической матрицы и абсолютной величины её элементов
Существует возможность подбора такой знаковой структуры коэффициентов бидиагональной симметрической матрицы, при которой можно получить наибольший период изменения данных коэффициентов для получения минимальных значений максимальных боковых пиков автокорреляционной функции. Таким образом, знаковая структура коэффициентов бидиагональной симметрической матрицы оказывает основное влияние на значение бокового пика автокорреляционной функции получаемых ансамблей дискретных ортогональных многоуровневых сигналов, а изменение абсолютных значения коэффициентов бидиагональной симметрической матрицы, оказывает влияние на значение бокового пика автокорреляционной функции получаемых ансамблей дискретных ортогональных многоуровневых сигналов в меньшей степени [2].
Следовательно, при построении получаемых ансамблей дискретных ортогональных многоуровневых сигналов в первую очередь целесообразно учитывать знаковую структуру получаемых ансамблей дискретных ортогональных многоуровневых сигналов, которая задается диагональными коэффициентами бидиагональной симметрической матрицы и в пределах которой обеспечивается минимизация бокового пика автокорреляционной функции получаемых ансамблей дискретных ортогональных многоуровневых сигналов. А затем в пределах выбранных знаковых структур необходимо изменять абсолютные значения коэффициентов бидиагональной симметрической матрицы, которые будут задавать различные получаемых ансамблей дискретных ортогональных многоуровневых сигналов [2].
Отбирая наилучшие знаковые структуры бидиагональной симметрической матрицы, можно добиться увеличения содержания ансамблей с хорошими автокорреляционными свойствами. При этом чтобы не производить предварительный полный перебор знаковых структур для требуемой размерности, необходимо наследовать знаковую структуру и амплитуду коэффициентов бидиагональной симметрической матрицы меньшей размерности [2].
3.3 Алгоритм построения ансамблей дискретных ортогональных многоуровневых сигналов и их математическое моделирование
Алгоритм построения и целенаправленного отбора ансамблей дискретных ортогональных многоуровневых сигналов с заданным диапазоном корреляционных характеристик разобьем на три этапа [2].
Первый этап. Задание начальных условий.
На данном этапе инициализируются следующие величины:
– m – степень для размерности формируемых ансамблей ;
– K – объем первоначального набора ансамблей (элементарных блоков).
Второй этап. Целенаправленный отбор.
Данный этап является основным и представляет собой цикл, в котором увеличивается размерность n блочной БДСМ в следующем порядке
Тело цикла представляет собой следующую последовательность действий:
– на основе ранее сгенерированной последовательности конструируется набор бидиагональной симметрической матрицы размерности n в количестве K единиц;
– рассчитываются собственные вектора каждой бидиагональной симметрической матрицы, тем самым, получая соответствующие им ансамблей дискретных ортогональных многоуровневых сигналов;
– производится расчет корреляционных характеристик полученных ансамблей дискретных ортогональных многоуровневых сигналов;
– производится отбор ансамблей дискретных ортогональных многоуровневых сигналов, чьи корреляционные свойства удовлетворяют заявленным требованиям;
– производится отбор бидиагональной симметрической матрицы, соответствующих отобранным ансамблей дискретных ортогональных многоуровневых сигналов [2];
– на основе отобранных бидиагональной симметрической матрицы формируется новая последовательность наборов коэффициентов увеличенной в двое размерности :
где , а M – количество отобранных бидиагональной симметрической матрицы. При этом переопределяется переменная K = L.
Третий этап. Завершающий. Вывод результатов. На данном этапе выводятся на экран корреляционные свойства отобранных результирующих ансамблей дискретных ортогональных многоуровневых сигналов [2].
Блок схема алгоритма представлена на рисунке 2.
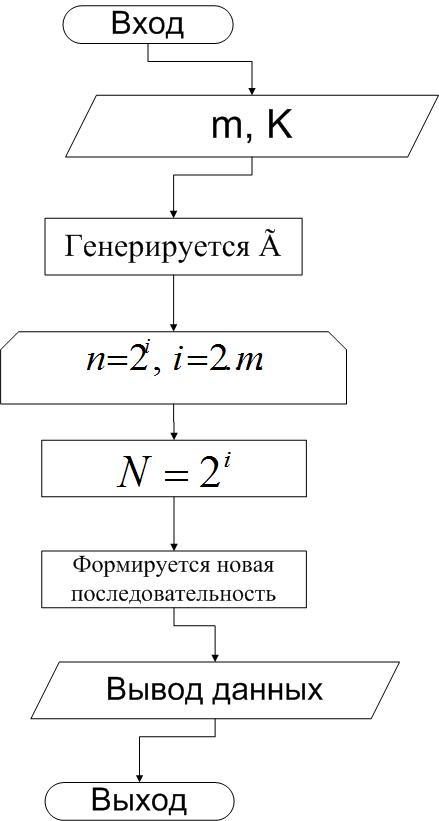
Рисунок 2 – Автокорреляционная функция Уолша
3.4 Выводы по главе
В главе была решена задача – разработка алгоритма стохастического формирования сигналов ( Приложение А).
Задача поиска большого числа ансамблей дискретных ортогональных сигналов с заданным диапазоном характеристик не может быть решена путем полного перебора коэффициентов исходной бидиагональной симметрической матрицы в виду высокой вычислительной сложности.
Результаты математического моделирования корреляционных свойств ансамблей дискретных ортогональных многоуровневых сигналов, получаемых методом случайного задания коэффициентов бидиагональной симметрической матрицы, показали нецелесообразность использования данного метода на практике в виду того, что с возрастанием размерности ансамблей дискретных ортогональных многоуровневых сигналов содержание ансамблей с «хорошими» автокорреляционными свойствами падает.
Отбирая наилучшие знаковые структуры бидиагональной симметрической матрицы, можно добиться увеличения содержания ансамблей с хорошими автокорреляционными свойствами. При этом чтобы не производить предварительный полный перебор знаковых структур для требуемой размерности, необходимо наследовать знаковую структуру и амплитуду коэффициентов бидиагональной симметрической матрицы меньшей размерности.
Заключение
Процесс защиты информации – это противостояние владельца информации, который хочет её защитить, и злоумышленника, стремящегося реализовать атаки на информацию.
Успеха попеременно достигает то одна, то другая Защищённые беспроводные сети передачи данных обладают развитыми подсистемами защиты информации, но технологии не стоят на месте и средства реализации угроз постоянно совершенствуются сторона.
Одним из важнейших аспектов проблемы обеспечения безопасности информации в беспроводных сетях является определение, анализ и классификация возможных угроз информационного обмена. В частности для мобильных сетей с кодовым разделением каналов главными угрозами являются прослушивание телефонных переговоров и различные виды манипуляции трафиком.
Конфиденциальность передачи информации по радиоканалам может быть достигнута путем обеспечения энергетической скрытности сигналов – переносчиков информации, структурной скрытности этих сигналов и информационной скрытности самого сообщения. Под структурной (сигнальной) скрытностью понимают степень затруднения определения структуры обнаруженного сигнала.
Системы с кодовым разделением каналов в настоящее время базируются на использовании известных дискретных ортогональных систем функций Радемахера, Уолша, Рида–Мюллера, Джеффи, Стиффлера, Велти и др. Большинство ансамблей обладают рядом недостатков, среди которых важнейшими являются плохие взаимокорреляционные свойства и ограниченность числа ансамблей, которые могут быть заранее известны злоумышленнику.
Все поставленные задачи в данной курсовой работе были решены и была достигнута цель работы – повышение защищённости информации в беспроводных системах путём разработки алгоритма стохастического формирования сигналов.
Предлагаемый алгоритм обеспечит основу для создания подсистемы формирования радиосигнала которая должна обеспечить повышение структурной скрытности что обеспечить достаточную защиту от возможных угроз.
Список использованных источников
- Д.В.Орёл Выпускная квалификационная работа исследование безопасности защищенных беспроводных телекоммуникационных сетей и разработка рекомендаций по повышению их защищенности 2008 г.
- З.В. Черняк Математическое моделирование ансамблей дискретных ортогональных многоуровневых сигналов с требуемыми корреляционными характеристиками 2010 г.
- CDMA-общие сведения – Forum – forum.motofan.ru/index.php?act=attach&type=post&id=2298
- Образовательный портал о технологиях мобильной связи – http://www.mobilla.info/mi_cdma.html
- Булана Л.В., Подгайная Е.И. Национальный авиационный университет, Методы обеспечения информационной бесопасности – http://www.rusnauka.com/3_ANR_2011/Informatica/4_78339.doc.htm
- Описание стандарта CDMA – http://dimitriy-od.narod.ru/IS_95_1/CDMA_1.htm
- Лаборатория Сетевой Безопасности – http://ypn.ru/106/analysis-of-threats-to-information-security/
- А.А. Малюк Угрозы информации и информационные угрозы. Подготовка кадров в области информационной безопасности – http://emag.iis.ru/arc/infosoc/emag.nsf/BPA/1d890f15704bb6c3c32575c4004debfc
- Исследование методов помехозащищенности радиотехнических систем – http://bibliofond.ru/view.aspx?id=668749
Приложение А
(обязательное)
Таблица А1 – Алгоритм стохастического формирования сигналов
|
Переработка аргументов эрмитовой матрицы
|
|
q=[100 1 100 .05 100 1 100 .0025 100 1 100 .05 100 1 100 .0001 100 1 100 .05 100 1 100 .0025 100 1 100 .05 100 1 100]';
degree=90;
step=100000;
n=length(q)+1;
phi=[-pi:(pi/180)*degree:pi]'; length_phi = length(phi);
length_q = length(q);
iterations=length_phi^length_q;
fprintf('Для матрицы размером %gx%g потребуется обработать %f вариантов.\n',n,n,iterations)
fprintf('При этом функция автокорреляции будет использована %f раз.\n',iterations*n)
|
|
Поиск лучшего АКФ
|
|
iter_int=1;
iter_vkf=1;
iter=0;
best_lm_AKF=1;
best_lm_VKF=1;
combs=nchoosek([1:n],2);
length_combs=length(combs);
for kk1=1:length_phi
for kk2=1:length_phi
for kk3=1:length_phi
for kk4=1:length_phi
|
Продолжение таблицы А1
|
for kk5=1:length_phi
for kk6=1:length_phi
for kk7=1:length_phi
for kk8=1:length_phi
for kk9=1:length_phi
for kk10=1:length_phi
for kk11=1:length_phi
for kk12=1:length_phi
for kk13=1:length_phi
for kk14=1:length_phi
for kk15=1:length_phi
for kk16=1:length_phi
for kk17=1:length_phi
for kk18=1:length_phi
for kk19=1:length_phi
for kk20=1:length_phi
for kk21=1:length_phi
for kk22=1:length_phi
for kk23=1:length_phi
for kk24=1:length_phi
for kk25=1:length_phi
for kk26=1:length_phi
for kk27=1:length_phi
for kk28=1:length_phi
for kk29=1:length_phi
for kk30=1:length_phi
for kk31=1:length_phi
iter=iter+1;
|
Продолжение таблицы А1
|
z=[q(1,1).*exp(i*phi(kk1,1)) q(2,1).*exp(i*phi(kk2,1)) q(3,1).*exp(i*phi(kk3,1))
q(4,1).*exp(i*phi(kk4,1)) q(5,1).*exp(i*phi(kk5,1)) q(6,1).*exp(i*phi(kk6,1)) q(7,1).*exp(i*phi(kk7,1)) q(8,1).*exp(i*phi(kk8,1)) q(9,1).*exp(i*phi(kk9,1)) q(10,1).*exp(i*phi(kk10,1)) q(11,1).*exp(i*phi(kk11,1)) q(12,1).*exp(i*phi(kk12,1)) q(13,1).*exp(i*phi(kk13,1)) q(14,1).*exp(i*phi(kk14,1)) q(15,1).*exp(i*phi(kk15,1)) q(16,1).*exp(i*phi(kk16,1)) q(17,1).*exp(i*phi(kk17,1)) q(18,1).*exp(i*phi(kk18,1)) q(19,1).*exp(i*phi(kk19,1)) q(20,1).*exp(i*phi(kk20,1)) q(21,1).*exp(i*phi(kk21,1)) q(22,1).*exp(i*phi(kk22,1)) q(23,1).*exp(i*phi(kk23,1)) q(24,1).*exp(i*phi(kk24,1)) q(25,1).*exp(i*phi(kk25,1)) q(26,1).*exp(i*phi(kk26,1)) q(27,1).*exp(i*phi(kk27,1)) q(28,1).*exp(i*phi(kk28,1)) q(29,1).*exp(i*phi(kk29,1)) q(30,1).*exp(i*phi(kk30,1)) q(31,1).*exp(i*phi(kk31,1)) ]';
ERMIT=diag(z,1)+diag(conj(z),-1);
[V,D]=eig(ERMIT);
% ищем боковой пик АКФ
for k=1:n
[AKF(1:2*n-1,k),lagsAKF]=xcorr(V(1:n,k),'coeff');
end
AKF(n,1:n)=0; %для поиска бокового максимума обнулим n-ю строку
max_AKF=max(max(abs(AKF)));
maximums_AKF(iter,1)=max_AKF;
if max_AKF<best_lm_AKF
best_lm_AKF=max_AKF;
best_kk_AKF=[kk1; kk2; kk3; kk4; kk5; kk6; kk7; kk8; kk9; kk10; kk11; kk12; kk13; kk14; kk15; kk16; kk17; kk18; kk19; kk20; kk21; kk22; kk23; kk24; kk25; kk26; kk27; kk28; kk29; kk30; kk31];
end
if max_AKF<=.3 % здесь меняется уровень бокового пика АКФ
bests_lm_AKF(iter_int,1)=max_AKF;
|
Продолжение таблицы А1
|
bests_kk_AKF(iter_int,1)=kk1;
bests_kk_AKF(iter_int,2)=kk2;
bests_kk_AKF(iter_int,3)=kk3;
bests_kk_AKF(iter_int,4)=kk4;
bests_kk_AKF(iter_int,5)=kk5;
bests_kk_AKF(iter_int,6)=kk6;
bests_kk_AKF(iter_int,7)=kk7;
bests_kk_AKF(iter_int,8)=kk8;
bests_kk_AKF(iter_int,9)=kk9;
bests_kk_AKF(iter_int,10)=kk10;
bests_kk_AKF(iter_int,11)=kk11;
bests_kk_AKF(iter_int,12)=kk12;
bests_kk_AKF(iter_int,13)=kk13;
bests_kk_AKF(iter_int,14)=kk14;
bests_kk_AKF(iter_int,15)=kk15;
bests_kk_AKF(iter_int,16)=kk16;
bests_kk_AKF(iter_int,17)=kk17;
bests_kk_AKF(iter_int,18)=kk18;
bests_kk_AKF(iter_int,19)=kk19;
bests_kk_AKF(iter_int,20)=kk20;
bests_kk_AKF(iter_int,21)=kk21;
bests_kk_AKF(iter_int,22)=kk22;
bests_kk_AKF(iter_int,23)=kk23;
bests_kk_AKF(iter_int,24)=kk24;
bests_kk_AKF(iter_int,25)=kk25;
bests_kk_AKF(iter_int,26)=kk26;
bests_kk_AKF(iter_int,27)=kk27;
bests_kk_AKF(iter_int,28)=kk28;
bests_kk_AKF(iter_int,29)=kk29;
bests_kk_AKF(iter_int,30)=kk30;
|
Продолжение таблицы А1
|
bests_kk_AKF(iter_int,31)=kk31;
|
|
Считаем ВКФ
|
|
for k=1:length_combs
var_one=V(1:n,combs(k,1));
var_two=V(1:n,combs(k,2));
[temp_vector,lagsVKF]=xcorr(var_one,var_two,'coeff');
VKF(1:2*n-1,k)=temp_vector;
end
max_VKF=max(max(abs(VKF)));
if max_VKF<best_lm_VKF
best_lm_VKF=max_VKF;
best_kk_VKF=[kk1; kk2; kk3; kk4; kk5; kk6; kk7; kk8; kk9; kk10; kk11; kk12; kk13; kk14; kk15; kk16; kk17; kk18; kk19; kk20; kk21; kk22; kk23; kk24; kk25; kk26; kk27; kk28; kk29; kk30; kk31];
end
if max_VKF<=.4 % здесь меняется уровень бокового пика BКФ
bests_lm_VKF(iter_vkf,1)=max_VKF;
bests_kk_VKF(iter_vkf,1)=kk1;
bests_kk_VKF(iter_vkf,2)=kk2;
bests_kk_VKF(iter_vkf,3)=kk3;
bests_kk_VKF(iter_vkf,4)=kk4;
bests_kk_VKF(iter_vkf,5)=kk5;
bests_kk_VKF(iter_vkf,6)=kk6;
bests_kk_VKF(iter_vkf,7)=kk7;
bests_kk_VKF(iter_vkf,8)=kk8;
bests_kk_VKF(iter_vkf,9)=kk9;
bests_kk_VKF(iter_vkf,10)=kk10;
bests_kk_VKF(iter_vkf,11)=kk11;
bests_kk_VKF(iter_vkf,12)=kk12;
bests_kk_VKF(iter_vkf,13)=kk13;
|
Продолжение таблицы А1
|
bests_kk_VKF(iter_vkf,14)=kk14;
bests_kk_VKF(iter_vkf,15)=kk15;
bests_kk_VKF(iter_vkf,16)=kk16;
bests_kk_VKF(iter_vkf,17)=kk17;
bests_kk_VKF(iter_vkf,18)=kk18;
bests_kk_VKF(iter_vkf,19)=kk19;
bests_kk_VKF(iter_vkf,20)=kk20;
bests_kk_VKF(iter_vkf,21)=kk21;
bests_kk_VKF(iter_vkf,22)=kk22;
bests_kk_VKF(iter_vkf,23)=kk23;
bests_kk_VKF(iter_vkf,24)=kk24;
bests_kk_VKF(iter_vkf,25)=kk25;
bests_kk_VKF(iter_vkf,26)=kk26;
bests_kk_VKF(iter_vkf,27)=kk27;
bests_kk_VKF(iter_vkf,28)=kk28;
bests_kk_VKF(iter_vkf,29)=kk29;
bests_kk_VKF(iter_vkf,30)=kk30;
bests_kk_VKF(iter_vkf,31)=kk31;
iter_vkf=iter_vkf+1;
end
iter_int=iter_int+1;
end
if iter==step
keyboard
end
end
end
end
end
end
|
Продолжение таблицы А1
|
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
%fprintf('Итерация: %g из %g\t лучший боковой пик АКФ: %g\t ВКФ: %g\n',iter,iterations,best_lm_AKF,best_lm_VKF)
%keyboard
end
%fprintf('Итерация: %g из %g\t лучший боковой пик АКФ: %g\t ВКФ: %g\n',iter,iterations,best_lm_AKF,best_lm_VKF)
%keyboard
end
%fprintf('Итерация: %g из %g\t лучший боковой пик АКФ: %g\t ВКФ: %g\n',iter,iterations,best_lm_AKF,best_lm_VKF)
|
Продолжение таблицы А1
|
%keyboard
end
%fprintf('Итерация: %g из %g\t лучший боковой пик АКФ: %g\t ВКФ: %g\n',iter,iterations,best_lm_AKF,best_lm_VKF)
%keyboard
end
fprintf('Итерация: %g из %g\t лучший боковой пик АКФ: %g\t ВКФ: %g\n',iter,iterations,best_lm_AKF,best_lm_VKF)
keyboard
end
%fprintf('Итерация: %g из %g\t лучший боковой пик АКФ: %g\t ВКФ: %g\n',iter,iterations,best_lm_AKF,best_lm_VKF)
%keyboard
end
|
|
Ищем из найденных лучших ВКФ лучший первый боковой пик АКФ
|
|
best_lm_AKF_first=1;
iter_int=1;
for h=1:length(bests_kk_VKF)
z=[q(1,1).*exp(i*phi(kk1,1)) q(2,1).*exp(i*phi(kk2,1)) q(3,1).*exp(i*phi(kk3,1)) q(4,1).*exp(i*phi(kk4,1)) q(5,1).*exp(i*phi(kk5,1)) q(6,1).*exp(i*phi(kk6,1))
q(7,1).*exp(i*phi(kk7,1)) q(8,1).*exp(i*phi(kk8,1)) q(9,1).*exp(i*phi(kk9,1)) q(10,1).*exp(i*phi(kk10,1)) q(11,1).*exp(i*phi(kk11,1)) q(12,1).*exp(i*phi(kk12,1)) q(13,1).*exp(i*phi(kk13,1)) q(14,1).*exp(i*phi(kk14,1)) q(15,1).*exp(i*phi(kk15,1)) q(16,1).*exp(i*phi(kk16,1)) q(17,1).*exp(i*phi(kk17,1)) q(18,1).*exp(i*phi(kk18,1)) q(19,1).*exp(i*phi(kk19,1)) q(20,1).*exp(i*phi(kk20,1)) q(21,1).*exp(i*phi(kk21,1)) q(22,1).*exp(i*phi(kk22,1)) q(23,1).*exp(i*phi(kk23,1)) q(24,1).*exp(i*phi(kk24,1)) q(25,1).*exp(i*phi(kk25,1)) q(26,1).*exp(i*phi(kk26,1)) q(27,1).*exp(i*phi(kk27,1)) q(28,1).*exp(i*phi(kk28,1)) q(29,1).*exp(i*phi(kk29,1)) q(30,1).*exp(i*phi(kk30,1)) q(31,1).*exp(i*phi(kk31,1)) ]';
ERMIT=diag(z,1)+diag(conj(z),-1);
|
Продолжение таблицы А1
|
[V,D]=eig(ERMIT);
for k=1:n
[AKF(1:2*n-1,k),lagsAKF]=xcorr(V(1:n,k),'coeff');
еnd
%AKF(n,1:n)=0; %для поиска бокового максимума обнулим n-ю строку
max_AKF=max(abs(AKF(n-1,1:n)));
maximums_AKF_first(h,1)=max_AKF;
if max_AKF<best_lm_AKF_first
best_lm_AKF_first=max_AKF;
best_kk_AKF_first=[ kk1; kk2; kk3; kk4; kk5; kk6; kk7; kk8; kk9; kk10; kk11; kk12; kk13; kk14; kk15; kk16; kk17; kk18; kk19; kk20; kk21; kk22; kk23; kk24; kk25; kk26; kk27; kk28; kk29; kk30; kk31];
end
if max_AKF<=.2501
bests_lm_AKF_first(iter_int,1)=max_AKF;
bests_kk_AKF_first(iter_int,1)=kk1;
bests_kk_AKF_first(iter_int,2)=kk2;
bests_kk_AKF_first(iter_int,3)=kk3;
bests_kk_AKF_first(iter_int,4)=kk4;
bests_kk_AKF_first(iter_int,5)=kk5;
bests_kk_AKF_first(iter_int,6)=kk6;
bests_kk_AKF_first(iter_int,7)=kk7;
bests_kk_AKF_first(iter_int,8)=kk8;
bests_kk_AKF_first(iter_int,9)=kk9;
bests_kk_AKF_first(iter_int,10)=kk10;
bests_kk_AKF_first(iter_int,11)=kk11;
bests_kk_AKF_first(iter_int,12)=kk12;
bests_kk_AKF_first(iter_int,13)=kk13;
bests_kk_AKF_first(iter_int,14)=kk14;
bests_kk_AKF_first(iter_int,15)=kk15;
|
Продолжение таблицы А1
|
bests_kk_AKF_first(iter_int,16)=kk16;
bests_kk_AKF_first(iter_int,17)=kk17;
bests_kk_AKF_first(iter_int,18)=kk18;
bests_kk_AKF_first(iter_int,19)=kk19;
bests_kk_AKF_first(iter_int,20)=kk20;
bests_kk_AKF_first(iter_int,21)=kk21;
bests_kk_AKF_first(iter_int,22)=kk22;
bests_kk_AKF_first(iter_int,23)=kk23;
bests_kk_AKF_first(iter_int,24)=kk24;
bests_kk_AKF_first(iter_int,25)=kk25;
bests_kk_AKF_first(iter_int,26)=kk26;
bests_kk_AKF_first(iter_int,27)=kk27;
bests_kk_AKF_first(iter_int,28)=kk28;
bests_kk_AKF_first(iter_int,29)=kk29;
bests_kk_AKF_first(iter_int,30)=kk30;
bests_kk_AKF_first(iter_int,31)=kk31;
iter_int=iter_int+1;
end
end
for h=1:length(bests_kk_VKF)
bests_phi_radian(h,1:n-1)=[phi(bests_kk_VKF(h,1),1) phi(bests_kk_VKF(h,2),1) phi(bests_kk_VKF(h,3),1)];
end
bests_phi_degree=bests_phi_radian.*180/pi;
|
EMBED Equation.3 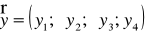
РАЗРАБОТКА АЛГОРИТМА СТОХАСТИЧЕСКОГО ФОРМИРОВАНИЯ СИГНАЛОВ