Квантовые компьютеры и сверхпроводящие компьютеры

РЕФЕРАТ

Квантовый компьютер — вычислительное устройство, работающее на основе квантовой механики. Квантовый компьютер принципиально отличается от классических компьютеров, работающих на основе классической механики.

Полноценный квантовый компьютер является пока гипотетическим устройством, сама возможность построения которого связана с серьёзным развитием квантовой теории в области многих частиц и сложных экспериментов, эта работа лежит на переднем краесовременной физики. Ограниченные (до 512 кубитов) квантовые компьютеры уже построены.

Первым практическим высокоуровневым языком программирования для такого вида компьютеров считается язык Quipper, основанный на Haskell.

Идея о квантовых вычислениях была высказана Юрием Маниным в 1980 году одна из первых моделей квантового компьютера была предложена Ричардом Фейнманом в 1981 году. Вскоре Пол Бениофф описал теоретические основы построения такого компьютера.

Необходимость в квантовом компьютере возникает тогда, когда мы пытаемся исследовать методами физики сложные многочастичные системы, подобные биологическим. Пространство квантовых состояний таких систем растет как экспонента от числа 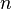составляющих их реальных частиц, что делает невозможным моделирование их поведения на классических компьютерах уже для 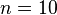. Поэтому Манин и Фейнман высказали идею построения квантового компьютера.

Квантовый компьютер использует для вычисления не обычные (классические) алгоритмы, а процессы квантовой природы, так называемые квантовые алгоритмы, использующие квантовомеханические эффекты, — такие как квантовый параллелизм и квантовая запутанность.

Если классический процессор в каждый момент может находиться ровно в одном из состояний 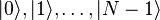(обозначения Дирака), то квантовый процессор в каждый момент находится одновременно во всех этих базисных состояниях, при этом в каждом состоянии 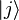— со своей комплексной амплитудой 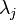. Это квантовое состояние называется «квантовой суперпозицией»

Тем не менее, с каждым годом исследователи объявляют о новых достижениях в области квантовых технологий, и надежда, что когда-нибудь квантовые компьютеры смогут превзойти обычные, продолжает крепнуть.

1998- Исследователям из Массачусетского технологического института удалось впервые распределить один кубит между тремя ядерными спинами в каждой молекуле жидкого аланина или молекулы трихлорэтилена. Такое распределение позволило использовать «запутанность» для неразрушающего анализа квантовой информации.

2000- В марте ученые из Национальной лаборатории в Лос-Аламосе объявили о создании 7-кубитного квантового компьютера в одной единственной капле жидкости.

2001- Демонстрация вычисления алгоритма Шора специалистами из IBM и Стэндфордского университета на 7-кубитном квантовом компьютере.

2005- В институте квантовой оптики и квантовой информации при Инсбрукском университете впервые удалось создать кубайт (сочетание 8 кубитов) с помощью ионных ловушек.

2007- Канадская компания D-Wave продемонстрировала первый 16-кубитный квантовый компьютер, способный решать целый ряд задач и головоломок, типа судоку.

С 2011 года D-Wave предлагает за $11 млн. долларов квантовый компьютер D-Wave One с 128-кубитным чипсетом, который выполняет только одну задачу – дискретную оптимизацию..

Но нужно сказать, что пока нет четкого определения, что понимать под квантовыми компьютерами. Разные компании и институты называют так совершенно несхожие разработки. К примеру, IBM экспериментирует с субатомными частицами, в которых двоичный код соответствует разным направлениям вращения частицы. В силу законов квантовой механики на субатомном уровне, квантовый бит может иметь промежуточное состояние.

Институт теоретической физики им. Ландау экспериментирует с миниатюрными сверхпроводимыми кольцами, в которых двоичный код соответствует разным направлениям тока, — квантовыми регистрами, которые переключаются с помощью магнитного поля.

Кубиты

Идея квантовых вычислений состоит в том, что квантовая система из L двухуровневых квантовых элементов (квантовых битов, кубитов) имеет 2L линейно независимых состояний, а значит, вследствие принципа квантовой суперпозиции, пространство состояний такого квантового регистра является 2L-мерным гильбертовым пространством. Операция в квантовых вычислениях соответствует повороту вектора состояния регистра в этом пространстве. Таким образом, квантовое вычислительное устройство размером L кубит фактически задействует одновременно 2L классических состояний.

Физическими системами, реализующими кубиты, могут быть любые объекты, имеющие два квантовых состояния: поляризационные состояния фотонов, электронные состояния изолированных атомов или ионов, спиновые состояния ядер атомов, и т. д.

Один классический бит может находиться в одном и только в одном из состояни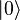й или 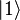. Квантовый бит, называемый кубитом, находится в состоянии 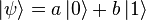, так что |a| и |b| — вероятности получить 0 или 1 соответственно при измерении этого состояния; 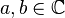; |a| + |b| = 1. Сразу после измерения кубит переходит в базовое квантовое состояние, соответствующее классическому результату.

Пример:

Имеется кубит в квантовом состоянии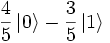

В этом случае, вероятность получить при измерении

0	составляет	(4/5)=16/25	= 64 %,
1		(-3/5)=9/25	= 36 %.

В данном случае, при измерении мы получили 0 с 64 % вероятностью.

В результате измерения кубит переходит в новое квантовое состояние 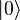, то есть, при следующем измерении этого кубита мы получим 0 со стопроцентной вероятностью (предполагается, что по умолчанию унитарная операция тождественна; в реальных системах это не всегда так).

Приведем для объяснения два примера из квантовой механики: 1) фотон находится в состоянии 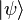суперпозиции двух поляризаций. Это состояние есть вектор в двумерной плоскости, систему координат в которой можно представлять как две перпендикулярные оси, так что 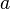и 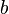есть проекции 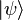на эти оси; измерение раз и навсегда коллапсирует состояние фотона в одно из состояни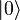й или 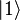, причём вероятность коллапса равна квадрату соответствующей проекции. Полная вероятность, получается, по теореме Пифагора.

Перейдем к системе из двух кубитов. Измерение каждого из них может дать 0 или 1. Поэтому у системы есть 4 классических состояния: 00, 01, 10 и 11. Аналогичные им базовые квантовые состояния: 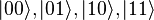. И наконец, общее квантовое состояние системы имеет вид 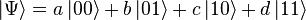. Теперь |a| — вероятность измерить 00 и т. д. Отметим, что |a|+|b|+|c|+|d|=1 как полная вероятность.

Если мы измерим только первый кубит квантовой системы, находящейся в состоянии 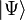, у нас получится:

С вероятностью 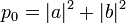первый кубит перейдет в состояние , а второй — в состояние ,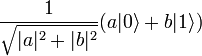
С вероятностью 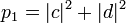первый кубит перейдет в состояние 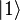, а второй — в состояние .

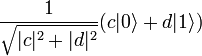В первом случае измерение даст состояние 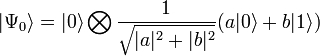, во втором — состояние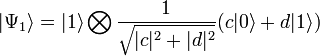

Мы снова видим, что результат такого измерения невозможно записать как вектор в гильбертовом пространстве состояний. Такое состояние, в котором участвует наше незнание о том, какой же результат получится на первом кубите, называют смешанным состоянием. В нашем случае такое смешанное состояние называют проекцией исходного состояния 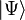на второй кубит, и записывают в виде матрицы плотности вида 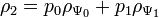где матрица плотности состояния 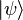определяется как .

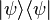В общем случае системы из L кубитов, у неё 2L классических состояний (00000…(L-нулей), …00001(L-цифр), … , 11111…(L-единиц)), каждое из которых может быть измерено с вероятностями 0—100 %.

Таким образом, одна операция над группой кубитов затрагивает все значения, которые она может принимать, в отличие от классического бита. Это и обеспечивает беспрецедентный параллелизм вычислений.

Вычисление

Упрощённая схема вычисления на квантовом компьютере выглядит так: берётся система кубитов, на которой записывается начальное состояние. Затем состояние системы или её подсистем изменяется посредством унитарных преобразований, выполняющих те или иные логические операции. В конце измеряется значение, и это результат работы компьютера. Роль проводов классического компьютера играют кубиты, а роль логических блоков классического компьютера играют унитарные преобразования. Такая концепция квантового процессора и квантовых логических вентилей была предложена в 1989 году Дэвидом Дойчем. Также Дэвид Дойч в 1995 году нашёл универсальный логический блок, с помощью которого можно выполнять любые квантовые вычисления.

Оказывается, что для построения любого вычисления достаточно двух базовых операций. Квантовая система даёт результат, только с некоторой вероятностью являющийся правильным. Но за счёт небольшого увеличения операций в алгоритме можно сколь угодно приблизить вероятность получения правильного результата к единице.

С помощью базовых квантовых операций можно симулировать работу обычных логических элементов, из которых сделаны обычные компьютеры. Поэтому любую задачу, которая решена сейчас, квантовый компьютер решит, и почти за такое же время. Следовательно, новая схема вычислений будет не слабее нынешней.

Чем же квантовый компьютер лучше классического? Большая часть современных ЭВМ работают по такой же схеме: n бит памяти хранят состояние и каждый такт времени изменяются процессором. В квантовом случае система из n кубитов находится в состоянии, являющимся суперпозицией всех базовых состояний, поэтому изменение системы касается всех 2n базовых состояний одновременно. Теоретически новая схема может работать намного (в экспоненциальное число раз) быстрее классической. Практически (квантовый) алгоритм Гровера поиска в базе данных показывает квадратичный прирост мощности против классических алгоритмов.

Алгоритмы

Алгоритм Гровера позволяет найти решение уравнения 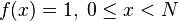за время .
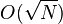Алгоритм Шора позволяет разложить натуральное число n на простые множители за полиномиальное от log(n) время.
Алгоритм Залки — Визнера позволяет моделировать унитарную эволюцию квантовой системы 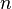частиц за почти линейное время с использованием 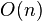кубит.
Алгоритм Дойча — Йожи позволяет «за одно вычисление» определить, является ли функция двоичной переменной f(n) постоянной (f1(n) = 0, f2(n) = 1 независимо отn) или «сбалансированной» (f3(0) = 0, f3(1) = 1; f4(0) = 1, f4(1) = 0).
Алгоритм Саймона решает проблему чёрного ящика экспоненциально быстрее, чем любой классический алгоритм, включая вероятностные алгоритмы.

Было показано, что не для всякого алгоритма возможно «квантовое ускорение». Более того, возможность получения квантового ускорения для произвольного классического алгоритма является большой редкостью.

Квантовая телепортация

Алгоритм телепортации реализует точный перенос состояния одного кубита (или системы) на другой. В простейшей схеме используются 3 кубита: телепортируемый кубит и запутанная пара, один кубит которой находится на другой стороне. Отметим, что в результате работы алгоритма первоначальное состояние источника разрушится — это пример действия общего принципа невозможности клонирования — невозможно создать точную копию квантового состояния, не разрушив оригинал. Не получится скопировать произвольное состояние, и телепортация — замена этой операции.

Телепортация позволяет передавать квантовое состояние системы с помощью обычных классических каналов связи. Таким образом, можно, в частности, получить связанное состояние системы, состоящей из подсистем, удалённых на большое расстояние.

Физические реализации квантовых компьютеров

Построение квантового компьютера в виде реального физического прибора является фундаментальной задачей физики XXI века. В настоящее время построены только ограниченные его варианты (в пределах 512 кубит). Вопрос о том, до какой степени возможно масштабирование такого устройства (так называемая «Проблема масштабирования»), является предметом новой интенсивно развивающейся области — многочастичной квантовой механики. Центральным здесь является вопрос о природе декогерентности (точнее, о коллапсе волновой функции), который пока остаётся открытым. Различные трактовки этого процесса можно найти в книгах.

Главные технологии для квантового компьютера:

Твердотельные квантовые точки на полупроводниках: в качестве логических кубитов используются либо зарядовые состояния (нахождение или отсутствиеэлектрона в определённой точке) либо направление электронного и/или ядерного спина в данной квантовой точке. Управление через внешние потенциалы илилазерным импульсом.
Сверхпроводящие элементы (джозефсоновские переходы, СКВИДы и др.). В качестве логических кубитов используются присутствие/отсутствие куперовской парыв определённой пространственной области. Управление: внешний потенциал/магнитный поток.
Ионы в вакуумных ловушках Пауля (или атомы в оптических ловушках). В качестве логических кубитов используются основное,/возбуждённое состояния внешнего электрона в ионе. Управление: классические лазерные импульсы вдоль оси ловушки или направленные на индивидуальные ионы + колебательные моды ионного ансамбля.
Смешанные технологии: использование заранее приготовленных запутанных состояний фотонов для управления атомными ансамблями или как элементы управления классическими вычислительными сетями.

На рубеже XXI века во многих научных лабораториях были созданы однокубитные квантовые процессоры (по существу, управляемые двухуровневые системы, о которых можно было предполагать возможность масштабирования на много кубитов).

В 2005 году группой Ю. Пашкина (кандидат физ.-мат. наук, старший научный сотрудник лаборатории сверхпроводимости г. Москвы) при помощи японских специалистов был построен двухкубитный квантовый процессор на сверхпроводящих элементах.

В ноябре 2009 года физикам из Национального института стандартов и технологий в США впервые удалось собрать программируемый квантовый компьютер, состоящий из двух кубит.

В феврале 2012 года компания IBM сообщила о достижении значительного прогресса в физической реализации квантовых вычислений с использованием сверхпроводящих кубитов которые, по мнению компании, позволят начать работы по созданию квантового компьютера.

В апреле 2012 года группе исследователей из Южно-Калифорнийского университета, Технологического университета Дельфта, университета штата Айова, калифорнийского, удалось построить двухкубитный квантовый компьютер на кристалле алмаза с примесями. Компьютер функционирует при комнатной температуре и теоретически является масштабируемым. В качестве двух логических кубитов использовались направления спина электрона и ядра азотасоответственно. Для обеспечения защиты от влияния декогерентности была разработана целая система, которая формировала импульс микроволнового излучения определённой длительности и формы. При помощи этого компьютера реализован алгоритм Гровера для четырёх вариантов перебора, что позволило получить правильный ответ с первой попытки в 95 % случаев.

В декабре 2012 года физики разработали фотонный квантовый компьютер.

Компьютер D-Wave

Канадская компания D-Wave Systems (англ.)русск. заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит (устройство получило название Orion). Информация об этом устройстве не отвечала требованиям достоверного научного сообщения, поэтому новость не получила научного признания. Более того, дальнейшие планы компании — создать уже в ближайшем будущем 1024-кубитный компьютер — вызвали скепсис у членов экспертного сообщества

В ноябре 2007 года та же компания D-Wave продемонстрировала работу образца 28-кубитного компьютера (устройство получило название Leda) онлайн на конференции, посвящённой суперкомпьютерам. Данная демонстрация также вызвала скепсис.

В январе 2008 года компания привлекла 17 млн. долларов США от международных инвесторов на поддержание своей деятельности (англ. product development, operations and business development activity).

В декабре 2008 года компания организовала проект распределённых вычислений AQUA@home (Adiabatic QUantum Algorithms), в котором тестируются алгоритмы, оптимизирующие вычисления на адиабатических сверхпроводящих квантовых компьютерах D-Wave.

8 декабря 2009 года на конференции NIPS научный сотрудник Google Hartmut Neven продемонстрировал на компьютере D-Wave работу программы распознавания образов.

Более подробно о компании D-Wave Systems, проводящихся в ней исследованиях и последних результатах можно узнать в блоге сооснователя компании Geordie Rose.

11 мая 2011 года представлен компьютер D-Wave One, созданный на базе 128-кубитного процессора.

С 20 мая 2011 года D-Wave Systems продаёт за $ 11 млн. долларов квантовый компьютер D-Wave One с 128-кубитным чипсетом, который выполняет только одну задачу — дискретную оптимизацию. Компьютер расположен в вычислительном центре Южно-Калифорнийского университета (университетский городок института информатики в Марина-дель-Рэе .Его рабочая температура составляет 20 мкК, компьютер тщательно экранирован от внешних электрических и магнитных полей.

25 мая 2011 года Lockheed Martin подписала многолетний контракт с D-Wave Systems, касающийся выполнения сложных вычислительных задач на квантовых процессорах. Контракт также включает в себя техническое обслуживание, сопутствующие услуги и покупку квантового компьютера D-Wave Onе.

В то же время, квантовые компьютеры D-Wave Systems подвергаются критике со стороны некоторых исследователей. Так, профессор (Associate Professor) Массачусетского Технологического Института Скотт Ааронсон считает, что D-Wave пока не смогла доказать ни того, что её компьютер решает какие-либо задачи быстрее, чем обычный компьютер, ни того, что используемые 128 кубитов удается ввести в состоянии квантовой запутанности. Если же кубиты не находятся в запутанном состоянии, то это не квантовый компьютер.

23 августа 2012 года было объявлено об успешном решении задачи о нахождении трехмерной формы белка по известной последовательности аминокислот в его составе с использованием 115 кубитов квантового компьютера D-Wave One из 128 имеющихся методом квантового отжига.

В декабре 2012 года представлен новый процессор Vesuvius, который объединяет 512 кубитов.

В мае 2013 года профессор Amherst College из канадской провинции Новая Шотландия Катерина МакГью (Catherine McGeoch) объявила о своих результатах сравнения компьютера D-Wave One (процессор Vesuvius) с четырёхпроцессорным компьютером на основе 2,4 ГГц чипа Intel с 16 Гб оперативной памяти. В первом тесте одну из задач класса QUBO, хорошо подходящую для структуры процессора, компьютер D-Wave One выполнил за 0,5 секунды, в то время как компьютеру с процессором Intel потребовалось 30 мин (выигрыш по скорости 3600 раз). Во втором тесте требовалась специальная программа для «перевода» задачи на язык компьютера D-Wave и скорость вычислений двух компьютеров была примерно равной. В третьем тесте, в котором также требовалась программа «перевода», компьютер D-Wave One за 30 минут нашёл решение 28 из 33 заданных задач, в то время как компьютер на процессоре Intel нашёл решение только для 9 задач.

Компьютеры D-Wave работают на принципе квантовой релаксации (Quantum Annealing)

В январе 2014 года учёные D-Wave опубликовали статью, в которой сообщается, что с помощью метода кубитовой туннельной спектроскопии ими было доказано наличие квантовой когерентности и квантового перепутывания в процессоре во время проведения вычислений.

Практическое применение квантовых компьютеров

Для практического применения пока не создано ни одного квантового компьютера, который бы удовлетворял всем вышеперечисленным условиям. Однако во многих развитых странах разработке квантовых компьютеров уделяется пристальное внимание и в такие программы ежегодно вкладываются десятки миллионов долларов.

На данный момент наибольший квантовый компьютер составлен всего из семи кубитов. Этого достаточно, чтобы реализовать алгоритм Шора и разложить число 15 на простые множители 3 и 5.

Если же говорить о возможных моделях квантовых компьютеров, то их, в принципе, довольно много. Первый квантовый компьютер, который был создан на практике, — это импульсный ядерный магнитно-резонансный (ЯМР) спектрометр высокого разрешения, хотя он, конечно же, как квантовый компьютер не рассматривался. Лишь когда появилась концепция квантового компьютера, ученые поняли, что ЯМР-спектрометр представляет собой вариант квантового компьютера.

В ЯМР-спектрометре спины ядер исследуемой молекулы образуют кубиты. Каждое ядро имеет свою частоту резонанса в данном магнитном поле. При воздействии импульсом на ядро на его резонансной частоте оно начинает эволюционировать, остальные же ядра не испытывают никакого воздействия. Для того чтобы заставить эволюционировать другое ядро, нужно взять иную резонансную частоту и дать импульс на ней. Таким образом, импульсное воздействие на ядра на резонансной частоте представляет собой селективное воздействие на кубиты. При этом в молекуле есть прямая связь между спинами, поэтому она является идеальной заготовкой для квантового компьютера, а сам спектрометр представляет собой квантовый процессор.

Первые эксперименты на ядерных спинах двух атомов водорода в молекулах 2,3-дибромотиофена SCH:(CBr)2:CH и на трех ядерных спинах — одном в атоме водорода H и двух в изотопах углерода C в молекулах трихлорэтилена CCl2:CHCl — были поставлены в 1997 году в Оксфорде (Великобритания).

В случае использования ЯМР-спектрометра важно, что для селективного воздействия на ядерные спины молекулы необходимо, чтобы они заметно различались по резонансным частотам. Позднее были осуществлены квантовые операции в ЯМР-спектрометре с числом кубитов 3, 5, 6 и 7.

Главным преимуществом ЯМР-спектрометра является то, что в нем можно использовать огромное количество одинаковых молекул. При этом каждая молекула (точнее, ядра атомов, из которых она состоит) представляет собой квантовую систему. Последовательности радиочастотных импульсов, выполняющие роль определенных квантовых логических вентилей, осуществляют унитарные преобразования состояний соответствующих ядерных спинов одновременно для всех молекул. То есть селективное воздействие на отдельный кубит заменяется одновременным обращением к соответствующим кубитам во всех молекулах большого ансамбля. Компьютер такого рода получил название ансамблевого (bulk-ensemble quantum computer) ЯМР квантового компьютера. Такие компьютеры могут работать при комнатной температуре, а время декогерентизации квантовых состояний ядерных спинов составляет несколько секунд.

В области ЯМР квантовых компьютеров на органических жидкостях к настоящему времени достигнуты наибольшие успехи. Они обусловлены в основном хорошо развитой импульсной техникой ЯМР-спектроскопии, обеспечивающей выполнение различных операций над когерентными суперпозициями состояний ядерных спинов, и возможностью использования для этого стандартных ЯМР-спектрометров, работающих при комнатной температуре.

Основным ограничением ЯМР квантовых компьютеров является сложность инициализации начального состояния в квантовом регистре. Дело в том, что в большом ансамбле молекул исходное состояние кубитов различно, что осложняет приведение системы к начальному состоянию.

Другое ограничение ЯМР квантовых компьютеров связано с тем, что измеряемый на выходе системы сигнал экспоненциально убывает с ростом числа кубитовL. Кроме того, число ядерных кубитов в отдельной молекуле с сильно различающимися резонансными частотами ограничено. Это приводит к тому, что ЯМР квантовые компьютеры не могут иметь больше десяти кубитов. Их следует рассматривать лишь как прототипы будущих квантовых компьютеров, полезные для отработки принципов квантовых вычислений и проверки квантовых алгоритмов.

Другой вариант квантового компьютера основан на использовании ионных ловушек, когда в роли кубитов выступает уровень энергии ионов, захваченных ионными ловушками, которые создаются в вакууме определенной конфигурацией электрического поля в условиях лазерного охлаждения их до сверхнизких температур. Первый прототип квантового компьютера, основанного на этом принципе, был предложен в 1995 году. Возможны и другие схемы квантовых компьютеров, разработка которых ведется в настоящее время. Однако пройдет еще как минимум десять лет, прежде чем настоящие квантовые компьютеры, наконец, будут созданы.

Квантовые компьютеры на сверхпроводящих фазовых кубитах

Понятия запутанности и суперпозиции введенные квантовой механикой дают возможность разрабатывать новую вычислительную архитектуру, называемую квантовым компьютером, который может экспоненциально превзойти любые возможные классические компьютеры. Такое повышение производительности сделает неразрешимые в настоящее время вычислительные задачи в достаточной степени разрешимыми. Такие проблемы включают в себя оптимизацию задачи коммивояжера, факторизацию и квантовые симуляторы, например, для медицинских исследований. Один из подходов к реализации квантового компьютера реализуется на основе сверхпроводящих фазовых джозефсоновских кубитов. Эксперименты показывают нарушение неравенства Белла при использовании этих кубитов (квантовых битов), т. е. показывают, что пара таких кубитов может быть помещена в состояние, которое показывает более сильные корреляции, чем это возможно для классической пары битов. Эти эксперименты являются значительной вехой для сверхпроводящих кубитов, поскольку они обеспечивают убедительные доказательства того, что архитектура квантовых компьютеров действительно сможет превзойти классическую систему. Кроме того, эти эксперименты демонстрируют первые нарушения неравенства Белла в системах в твердом состоянии и макроскопических квантовых системах. Поэтому они добавляют ценные свидетельства того, что новые идеи, предложенные квантовой механикой, действительны во всевозможных квантовых системах и не могут быть объяснены детерминистическими альтернативными теориями.

В 20-м веке информатизация труда выросла на порядок [Graham T.T. Molitor, 1982]. Это стало возможным с появлением персональных компьютеров и все более широким распространением и доступностью систем хранения и обмена информацией, таких как магнитные жесткие диски и Интернет. Экспоненциальный рост производительности труда и снижение цен на устройства сбора и создания информации привел к информационному потопу, что, по прогнозам, приведет к удвоению информационной базы в мире каждые несколько часов [Coles et al., 2006]. Чтобы справиться с этим потоком информации достаточно резко увеличить скорость обработки информации.

За последние 40 лет производительность вычислительных устройств удваивалась, примерно, каждые 18 месяцев. Эту тенденцию обычно называют законом Мура из-за статьи, написанной в 1965 году соучредителем Intel Гордоном Муром [Moore,1965]. Несмотря на то, что закон Мура, как ожидается, будет действовать, по крайней мере, еще десятилетия, важно подготовиться в более долгосрочной перспективе к будущему, когда транзисторы на основе кремния будут вытеснены.

Тезис Черча-Тьюринга

Тезис Черча-Тьюринга делает это еще более насущным. Тезис Чёрча — Тьюринга — фундаментальное эвристическое утверждение, существенное для многих областей науки, в том числе, для математической логики теории доказательств, информатики, кибернетики, дающее интуитивное понятие о вычислимости. Это утверждение было высказано Алонзо Чёрчем и Аланом Тьюрингом в середине 1930-х годов. В терминах теории рекурсии, это утверждение формулируется как совпадение классов вычислимых и частично рекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу, тезис гласит, что для любой интуитивно вычислимой функции существует вычисляющая её значения машина Тьюринга. Иногда в такой формулировке тезис Чёрча — Тьюринга фигурирует как тезис Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга. Тезис Чёрча — Тьюринга невозможно строго доказать или опровергнуть, поскольку он устанавливает эквивалентность между строго формализованным понятием частично вычислимой функции и неформальным понятием вычислимости. Позднее были сформулированы другие практические варианты утверждения: физический тезис Чёрча — Тьюринга: любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга. Проблемы, которые являются неразрешимыми, не разрешимы за полиномиальное время на современных компьютерах и останутся неразрешимыми на всех будущих классических компьютерах. К примерам таких проблем относятся факторизация, оптимизация путешествия коммивояжера, задача о скрытых подгруппах и т.д.

Алгоритм Deutsch-Josza

В 1992г. D. Deutsch и R. Jozsa предложили гипотетическую проблему, а также алгоритм ее решения, который показывает, что компьютер, который использует квантовые состояния для вычислений мог бы не подчиняться ограничению, наложенному тезисом Черча-Тьюринга [Deutsch и Jozsa, 1992]. Проблема – определение природы неизвестной функции вопросами оракулу, который оценивает функцию для данного входа. Функция действует на число n- битное и, как известно, результат или постоянный, то есть 0 (или 1) для всех возможных входов, или уравновешенный, то есть возвращается 0 для точно половины всех возможных входов и 1 для всех других. Классический компьютер, в худшем случае, должен был бы оценить функцию 2 в степени (n-1) + 1 раз, в то время как квантовый компьютер должен будет оценить функцию только однажды, чтобы определить с уверенностью результат будет уравновешен или постоянен. Это сделано одной оценкой значения функции, если состояние на входе представляет собой суперпозицию всех возможных 2 в степени n состояний, получаемых применением оператора Адамара. Если на выходе результат показывает амплитуды и для 0, и для 1, то функция уравновешена (сбалансирована), в противном случае - постоянна. Этот алгоритм подразумевает, что квантовый компьютер мог бы быть бесконечно быстрее, чем любой возможный классический компьютер для определенных классов проблем, которые слишком тяжелы для классических компьютеров.

Квантовые компьютеры и сверхпроводящие компьютеры