ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Лекция № 7 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Электростатика
Раздел электричества, который занимается физикой неподвижных зарядов, называется электростатикой. Известно, что в природе существуют два рода электрических зарядов – положительных и отрицательных. Электрические заряды состоят из дискретных зарядов, и равных по модулю 1,610-19 Кл. Обобщением большого количества опытных данных был установлен фундаментальный закон природы, закон сохранения заряда: в изолированной системе алгебраическая сумма зарядов, т.е. положительных и отрицательных остается постоянной. Изолированной или замкнутой системой называется система, не обменивающаяся зарядами с внешними телами.
Закон Кулона гласит: сила взаимодействия между двумя точечными зарядами, находящимися в вакууме пропорциональна величинам этих зарядов q1 и q2 и обратно пропорциональна квадрату расстояния r между ними.
, (7.1)
где k – коэффициент пропорциональности, зависящий от выбора системы единицы.
Силы, действующие между зарядами направлены по прямой, соединяющей заряды т.е. являются центральными. Для одноименных зарядов (q1 >0 и q2 >0) или (q1 < 0 и q2 < 0) сила F > 0 и для разноименных F < 0. В векторной форме закон Кулона записывается так:
, (7.2)
где - сила, действующая на заряд 2 со стороны заряда 1, - радиус- вектор, направленный от заряда 1 к заряду 2, . Таким образом, уравнение (7.2) кроме всего выражает, что одноименные заряды отталкиваются, а разноименные притягиваются.
Если взаимодействующие заряды находятся в какой- либо среде, то в знаменатель формулы (7.2) вводится множитель -безразмерная величина, характеризующая электрические свойства среды и называется диэлектрической проницаемостью среды. Для вакуума = 1. показывает во сколько раз сила взаимодействия между двумя зарядами в данной среде отличается от силы их взаимодействия в вакууме. Коэффициент в системе СИ равен:
, (7.3)
где 0 = 8,85 10-12 Кл2/(Нм2) или Ф/м и называется электрической постоянной.
Электростатическое поле. Напряженность поля. Согласно современным представлениям, взаимодействие между зарядами осуществляется через поле. Всякий заряд создает вокруг себя поле, которое обнаруживается тем, что на любой «пробный заряд», помещенный в это поле оказывается силовое воздействие. Заряд, применяемый для обнаружения поля, назван пробным. Он сам по себе мал, и своим присутствием не искажает то поле, в которое он внесен (вследствие возможного перераспределения создающих поле зарядов). Таким образом
, (7.4)
где F – сила, действующая со стороны поля на пробный заряд. Используя закон Кулона формулу (7.5) можно записать:
(7.5)
Если поле создается не одним зарядом, а системой точечных неподвижных зарядов, то напряженность поля равна векторной сумме напряженностей полей, которые создавали бы каждый из этих зарядов в отдельности:
, (7.6)
где ri – расстояние между зарядом qi и интересующей нас точкой поля. Сформулированное положение называют принципом суперпозиции электрических полей. Из него вытекает, что напряженность поля любой системы зарядов можно вычислить, представив ее как совокупность точечных зарядов, вклад каждого из которых можно определять по формуле (7.6).
Электрический диполь. Применим принцип суперпозиции для определения поля диполя. Электрическим диполем называют систему, состоящую из двух равных по модулю, но противоположных по знаку зарядов, расстояние между которыми мало по сравнению с расстоянием до рассматриваемых точек поля. Прямая, проходящая через оба заряда называется осью диполя.
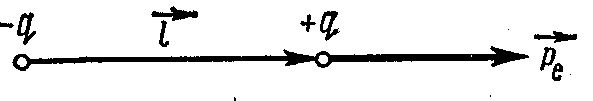
Рис. 7.1
Вектор, направленный от отрицательного заряда к положительному и равный расстоянию между ними называется плечом диполя (рис. 7.1). Важной характеристикой диполя является вектор , который называется электрическим моментом диполя и определяется произведением положительного заряда q и плечом диполя и совпадает по направлению с направлением вектора .
Графическое описание электрического поля. Графически электрическое поле можно изобразить с помощью так называемых силовых линий (линии напряженности), которые проводятся так, чтобы касательные к ним в каждой точке совпадали по направлению с вектором напряженности в этой же точке поля (рис.7.2). Для однородного поля, когда вектор напряженности в каждой точке постоянен по величине и по направлению, силовые
линии параллельны вектору напряженности. Линии напряженности не пересекаются, поскольку в каждой точке вектор имеет лишь одно направление. Если поле создается точечными зарядами, принято считать, что силовые линии исходят радиально от положительного заряда и входят в отрицательный заряд (рис. 7.3). Густота линий, т.е. число линий, проходящих через единичную площадку, расположенную перпендикулярно силовым линиям в данной точке, должна быть пропорциональна численному значению вектора в этой точке. Это дает возможность характеризовать значение напряженности.
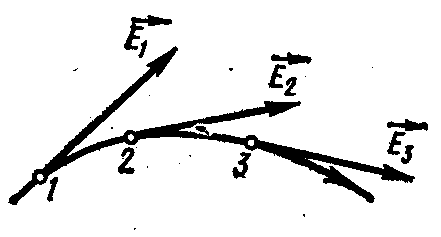
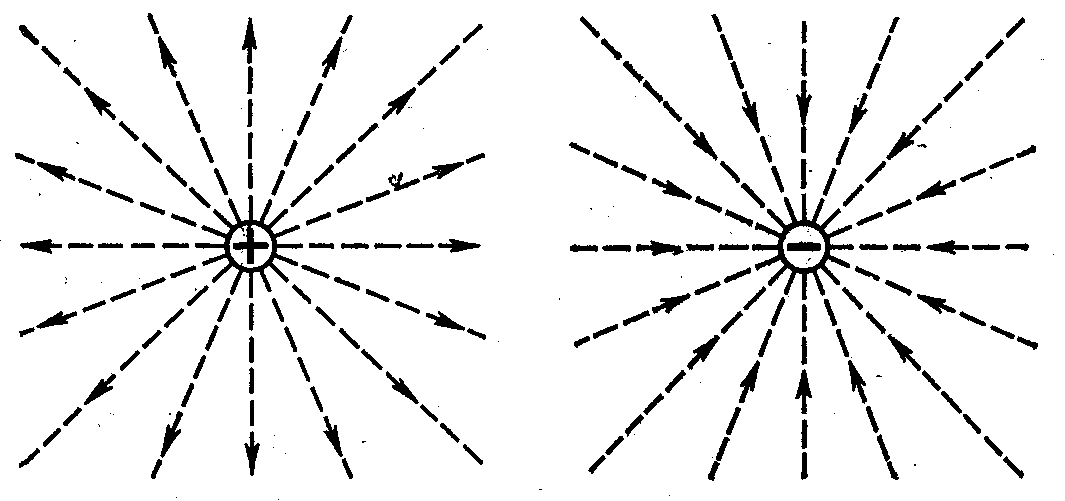
Рис.7.2 Рис.7.3
Теорема Гаусса. Для произвольной поверхности S поток вектора сквозь нее можно записать:
. (7.7)
Подставив значение Е для точечного заряда, последнюю формулу можно записать:
, (7.8)
где - телесный угол, опирающийся на элемент поверхности dS с вершиной в точке расположения заряда q. Интегрируя выражение (7.8) по всему телесному углу мы получим . Следует отметить, что в случае замкнутых поверхностей за положительное направление нормали берется внешняя нормаль, т.е. направленная наружу поверхности.
В случае, когда поле создается системой точечных зарядов q1, q2 qn то в соответствии с принципом суперпозиции полей имеем: .
Каждый интеграл в правой части равен qi /о, если заряд qi находится внутри замкнутой поверхности. Поэтому в правой части предыдущего уравнения мы должны записать алгебраическую сумму зарядов qi, находящихся внутри поверхности S. Таким образом, окончательно можно записать:
. (7.9)
Данное уравнение математически выражает теорему Гаусса: - поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри данной поверхности, деленной на 0. .
Работа, совершаемая при перемещении заряда в электростатическом поле. Пусть, в поле заряда q помещается заряд q0, который под действием сил поля заряда начнется перемещаться (рис.7.4). Элементарная работа, совершаемая при этом, будет равна: поскольку
,, или: . (7.10)
Из (7.10) следует, что работа по перемещению заряда в электростатическом поле не зависит от формы пути перехода, а зависит от положения начальной и конечной точек перемещения, т.е. электростатическое поле точечного заряда является потенциальным, а электростатические силы консервативными.
Работа, совершаемая при перемещении заряда в электростатическом поле по замкнутому пути, равна нулю, т.е. . Если перемещенный заряд, принять за единицу, то (7.14) можно записать:
, или . (7.11)
Этот интеграл называется циркуляцией вектора напряженности вдоль замкнутого контура.
Из теоремы о циркуляции вектора напряженности можно сделать несколько важных выводов: 1)Линии напряженности поля не могут быть замкнутыми. 2) Существование электростатического поля вида, показанного на рис. 7.5 невозможно.
|
Рис.7.4 |
Рис.7.5 |
В самом деле, если применить к этому полю теорему о циркуляции вектора по замкнутому контуру, показанному на рис. 457 пунктиром, то она была бы отлична от нуля, что противоречит теореме.
Потенциал электростатического поля. Запишем формулу (7.10) следующим образом:
, (7.12)
Работа консервативных сил равна убыли потенциальной энергии. При таком условии потенциальная энергия заряда q0, находящегося в поле заряда q на расстоянии r от него равна q0
. (7.13)
С другой стороны, последнюю формулу можно считать выражением энергии заряда q, находящегося в поле заряда q0. Таким образом, энергия, выражаемая формулой (4.13) является взаимной энергией зарядов q и q0 .Из этой формулы следует, что отношение W/q0 для данной точки поля не зависит от величины заряда q0. “то отношение служить энергетической характеристикой электростатического поля, которая называется потенциалом поля.
. (7.14)
Работу по перемещению заряда из одной точки в другую можно записать:
, (7.15)
т.е. работа по перемещению заряда в электрическом поле, равна произведению величины заряда на разность потенциалов в начальной и конечной точках перемещения.
Связь между потенциалом и напряженностью электрического поля .Работа по перемещению заряда q0 вдоль оси х на dx равна dA=q0 Eх dx. С другой стороны, та же работа равна dА=q0 d. Приравняв правые стороны этих выражений получим:
(7.16)
Рассуждая аналогичным образом, для осей y и z можем вектор записать так:
, (7.17)
где - единичные векторы, направленные соответственно вдоль осей х, у, z. Вспомнив определение градиента, последнее уравнение можно записать:
, или , (7.18)
Графически электростатические поля можно изобразить не только с помощью силовых линий, но и с помощью так называемых эквипотенциальных поверхностей. Эквипотенциальными поверхностями называются поверхности, на которых все точки имеют одинаковые потенциалы.
проводники в электрическом поле.
Если проводнику сообщить некоторый заряд или его поместить во внешнее электростатическое поле, то в обоих случаях на заряды проводника будет действовать электростатическое поле и они будут перемещаться внутри проводника. Этот процесс будет происходить до тех пор, пока внутри проводника поле не будет равно нулю и потенциал внутри проводника должен быть постоянным (=const). Напряженность на поверхности проводника в каждой точке должна быть направлена по нормали. В противном случае касательные составляющие привели бы заряды, находящиеся на поверхности в движение, и равновесие зарядов было бы нарушено.
Электроемкость уединенного проводника. Рассмотрим проводник, удаленный от других проводников, тел и зарядов в связи, с чем его можно рассматривать как уединенный проводник. Из опыта следует, что между зарядом и потенциалом существует зависимость
q = С. Величину
(7.19)
называют электроемкостью или просто емкостью уединенного проводника. Емкость зависит от формы и размеров проводника и не зависит от материала, агрегатного состояния и от размеров полостей внутри проводника. Емкость не зависит от заряда и потенциала проводника.
Конденсаторы. Система проводников, близко расположенных друг-другу и заряженных одинаковыми по величине, но противоположными по знаку зарядами называется конденсатором, а проводники – его обкладками. Емкость конденсатора определяется:
, (7.20)
где 1 - 2 –разность потенциалов между обкладками, q – заряд, расположенный на положительно заряженной обкладке конденсатора.
Энергия заряженного конденсатора Процесс зарядки конденсатора можно представить как последовательное перемещение бесконечно малых порций заряда dq с одной пластины на другую, в результате чего одна из пластин будет заряжаться положительно, а другая- отрицательно и между ними будет возникать постепенно возрастающая разность потенциалов U = q / С . При этом энергия конденсатора равна:
. (7.21) Здесь Е- напряженность электрического поля внутри конденсатора, a V= S d -его объем. Отсюда энергия единицы объема, или объемная плотность энергии электрического поля
(7.22)
В изотропном диэлектрике направления векторов и совпадают. Поэтому формулу для плотности энергии можно придать вид:
. (7.23)
Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика.
Электрическое смещение. Связанные заряды отличаются от сторонних лишь тем, что не могут покинуть пределы молекул, в состав которых они входят. В остальном же, их свойства не отличаются от свойств всех прочих зарядов. В частности они служат источником электрического поля. Вектор электростатической индукции пропорционален напряженности поля:
=0. (7.24)
Электрическим смещением называется величина, определяемая соотношением (7.24). Безразмерную величину =1+ называют относительной проницаемостью или просто диэлектрической проницаемостью среды. В анизотропных диэлектриках векторы и , вообще говоря, неколлинеарные. Единицей электрического смещения служит кулон на квадратный метр (Кл/м2). Источниками поля вектора служат только сторонние заряды. Поэтому линии смещения могут начинаться или заканчиваться лишь на сторонних зарядах. Через точки, в которых помещаются связанные заряды, линии смещения проходят, не прерываясь.
Осн. 2 [11-81, 84-97], 5 [154-194], 6 [148-179]
Доп. 15, 24 [140-166].
Контрольные вопросы:
1. При каких условиях силы взаимодействия двух заряженных тел можно найти по закону Кулона?
2. Чему равен поток напряженности электростатического поля в вакууме через замкнутую поверхность?
3. Расчет каких электростатических полей удобно производить на основе теоремы Остроградского-Гаусса?
4. Что можно сказать о напряженности и потенциале электростатического поля внутри и у поверхности проводника?
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ