Оптика. Волновое уравнение для электромагнитного поля
ЛЕКЦИЯ № 11 Оптика. Волновое уравнение для электромагнитного поля
Из теории Максвелла следует, что образование переменного во времени электрического поля всегда вызывает возникновение вихревого магнитного поля и, наоборот, переменное магнитное поле порождает вихревое электрическое поле. Эти поля неразрывно связаны, а их совокупность называют единым электромагнитным полем. Электромагнитное поле не может быть локализовано в определенном объеме пространства. Возбужденное в какой-либо области пространства переменное электрическое поле порождает переменное магнитное поле, которое в свою очередь, порождает переменное электрическое поле и так далее, то есть в пространстве возникает последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Данный процесс периодичен в пространстве и во времени, поэтому представляет собой волну, которая называется электромагнитной. Возможность существования электромагнитных волн вытекает из уравнения Максвелла. Вектор плотности потока электромагнитной энергии можно представить как векторное произведение и :
. (11.1)
Вектор называется вектором Умова- Пойнтинга.
Закон отражения света. Угол отражения равен углу падения ; лучи падающий и отраженный находятся в одной плоскости с нормалью к отражающей поверхности и восстановленной из точки падения луча (рис.11.1).
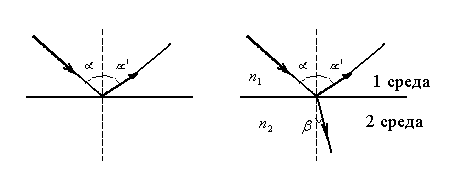
Рис.11.1 Рис.11. 2
Законы преломления света. А) Лучи падающий и преломленный лежат в одной плоскости с перпендикуляром, восстановленным в точке падения луча к границе раздела двух однородных и изотропных сред. Б) Отношения синуса угла падения к синусу угла преломления есть величина постоянная для этих двух сред, равная отношению скорости света в среде, откуда свет выходит к скорости света в среде, в которую входит (рис.11.2).
(11.2)
Так как скорость света в веществе связана со скоростью света в вакууме соотношением , то имеем следующие равенства:
и , (11.3)
где и - показатели преломления соответствующих веществ; напомним, что и - фазовые скорости световой волны.
Таким образом, закон преломления света может быть записан в следующем виде:
. (11.4)
Не приводя вывода запишем уравнение тонкой линзы:
, (11.5)
где - показатель преломления вещества линзы. Если , т.е. лучи падают на линзу параллельно главной оптической оси (рис.6.3), то они соберутся в фокусе , т.е. имеем:
, (11.6)
где величина определяет положение заднего фокуса, лежащего справа от линзы.
Если , т.е. изображение источника А лежит в ,то лучи выходят из линзы параллельным пучком (рис.11.3) и определяет положение переднего фокуса, лежащего слева от линзы. Необходимо помнить, что для двояковыпуклой линзы . С учетом этих равенств, уравнение тонкой линзы:
, (11.7)
где Ф иногда называют оптической силой линзы. Плоскость, проведенная через фокус, перпендикулярно главной оптической оси, называется фокальной. Параллельный пучок лучей, идущий под углом к главной оптической оси, сходится в фокальной плоскости. Ход лучей, как в собирающей, так и в рассеивающей линзах, изображен на рисунках 11.2 и 11.3.
Рис. 11.3 Рис.11.4
Обозначим величину предмета АВ через , а изображения АВ через Н, тогда линейное увеличение линзы будет:
. (11.8)
Фотометрические величины и их единицы.
Раздел оптики, занимающийся измерением интенсивности света и его источников, или же световых потоков и величин, связанных с ними, называется фотометрией. Интенсивность света характеризуют величиной переносимой энергии . Тогда потоком энергии излучения будет величина:
. (11.9)
Точечный источник света- это такой источник, размерами которого по сравнению с расстоянием до места наблюдения можно пренебречь. В однородной и изотропной среде световая волна, излучаемая точечным источником, будет сферической.
Сила света. Для характеристики точечных источников света применяется понятие: сила света , равная отношению потока излучения Ф к телесному углу (рис.11.5)
(11.10)
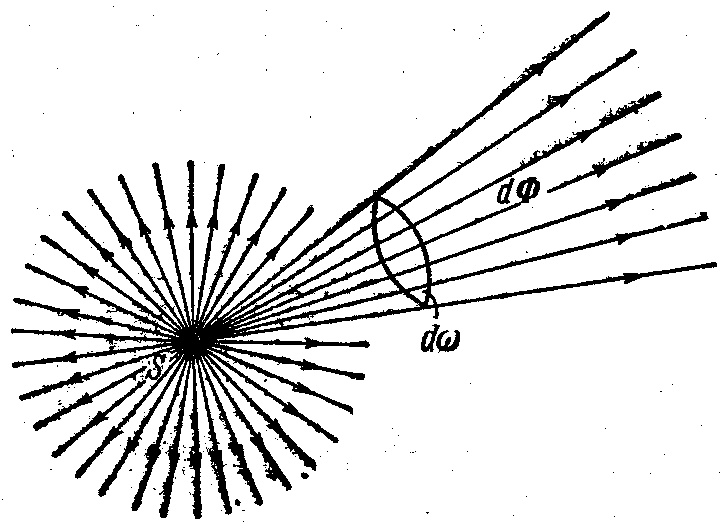
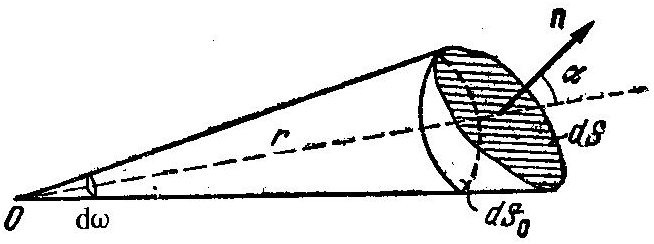
Рис.11.5. Рис.11.6
Мерой телесного угла является отношение площади участка, вырезаемого конусом на поверхности сферы, к квадрату его радиуса (рис.6.6)
.
За единицу телесного угла, принят телесный угол, опирающийся на участок поверхности сферы, площадь которого численно равна , т.е. площади квадрата со стороны равной . Эта единица называется стерадиан (ср). Как видно для произвольно ориентированной площадки , нормаль к которой составляет угол с радиусом , телесный угол определяется:
. (11.11) Если поток, излучаемый точечным источником, равномерный по всем направлениям, то такой источник называется изотропным и его сила света, равна
и , (11.12)
где есть полный телесный угол.
Единица силы света- кандела (кд) является одной из основных единиц Международной системы (СИ). Кандела – сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 5401012Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.
Единицей светового потока является люмен, т.е. 1 лм = 1кд1ср
Освещенность Е- величина, равная отношению светового потока , падающего на поверхность, к площади этой поверхности.
. (11.13)
Единицей освещенности является люкс (лк): .
.
Освещенность, создаваемую точечным источником можно выразить через силу света , расстояние и угол . На площадку падает поток , но , тогда
. (11.14)
Светимость - величина, равная отношению светового потока , испускаемого по всем направлениям, к площади этой поверхности
. (11.15)
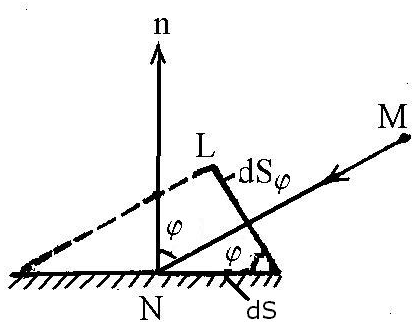
Яркость светящейся поверхности в некотором направлении, задаваемым углом и отсчитываемым от внешней нормали к излучающей поверхности , есть величина равная отношению силы света в этом направлении к площади проекции излучающей поверхности, на плоскость, перпендикулярную данному направлению (рис.11.7).
. (11.16)
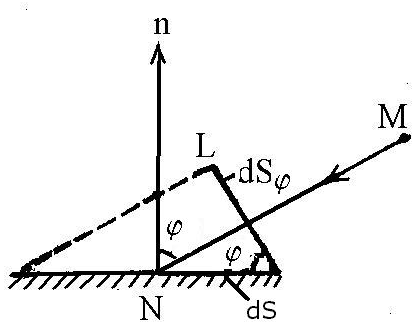
Рис.11.7
Единицей яркости служит кандела на квадратный метр (кд/м2). Обычно яркость протяженных источников различна в разных направлениях. Однако существуют источники, например, матовая поверхность, освещаемая внешним источником света, а также наше Солнце, для которых не зависит от направления наблюдения
, тогда (11.17)
это математическая запись закона Ламберта: сила света такого источника пропорциональна косинусу угла и максимальна в направлении нормали (.
Так как светимость является интегральной величиной, то для таких косинусных излучателей, у которых яркость по всем направлениям одинакова, между этими величинами существует простая связь:
. (11.18)
Волновая оптика
Существует оптические явления необъяснимые законами геометрической оптики. К ним относятся, например, кольца Ньютона и другие эксперименты, когда при падении света на экран, обнаруживается не равномерная его освещенность, а образования чередующихся полос максимальной и минимальной освещенности. В этих опытах наблюдается явление интерференции света – наложение друг на друга в какой-либо точке пространства когерентных световых волн и приводящие к перераспределению потока световых энергии (интенсивности) в соседних точках пространства.
Возмущение, распространяющееся только в одном направлении, называется «бегущей волной». Для случая распространения механического возмущения на струне было получено дифференциальное уравнение, называемое волновым. Оно в одномерном случае имеет следующий вид:
, (11.20)
где – смещение от положения равновесия точки с координатой x в зависимости времени t: S = f (x,t).
Уравнение (6.20) носит общий характер, т.е. оно применимо для бегущих волн любого происхождения. Так как при распространении электромагнитного возмущения функциями координаты x и времени t являются и , то для них по аналогии с выражением (11.20), можно записать:
. (11.21)
Уравнения (11.21) одномерные, то есть они определяют картину изменения
и . Явный вид этих функций зависит от начальных и граничных условий, накладываемых на них.Рещением волнового уравнения является гармоническая функция синуса или косинуса.
Получить когерентные волны можно только искусственным способом: для этого необходимо данную волну, испущенную отдельным атомом при помощи какого- либо оптического устройства разделить на две и более частей, а затем уже наблюдать результат их сложения в данной точке Р. Очевидно, что части одной и той же волны всегда будут когерентны между собой. Если эти две волны пройдут различный путь от точки их возникновения до точки их сложения, то между ними возникнет разность фаз. Рассмотрим два колебания:
, (11.22)
Разность фаз двух колебаний выражается формулой и остается постоянной во времени . Интерференционный максимум наблюдается при значении , т.е. для , где
Тогда имеем:
, отсюда (11.23)
интерференционный минимум наблюдается при значении , т.е. для . Тогда имеем , отсюда:
. (11.24)
Как видно из (11.20) и (6.21), образование в точке наблюдения и интенсивности (освещенности) зависит от того, четное или нечетное число полуволн укладывается на оптической разности хода.
Осн. 2 [93-291, 302-346], 4 [кн.4 с.41-53, 93-125],5 [333-339], 6 [297-316].
Доп. 242 [247-302].
Контрольные вопросы:
1. Какие свойства электромагнитных волн вам известны?
2. Какова связь между интенсивностью бегущей электромагнитной волны и вектором Умова-Пойнтинга?
3. Дайте определения законов геометрической оптики
4. Напишите формулу оптической силы тонкой линзы.
5. Что изучает фотометрия?
EMBED MSPhotoEd.3