Методы поиска отказов

PAGE 14

ЭКСПЛУАТАЦИЯ и ремонт ОБОРУДОВАНИЯ (5 курс)

ЛЕКЦИЯ №13

Учебные вопросы:

1. Последовательный поиск отказов с восстановлением объекта контроля.

2. Метод последовательных элементных проверок.

3. Прогнозирование технического состояния оборудования по результатам измерения сопротивления изоляции.

1. Последовательный поиск отказов с восстановлением объекта контроля

Метод последовательных поэлементных проверок

Рассмотрим задачу построения программы восстановления по минимуму математического ожидания затрат при условии, что имеется возможность проверки работоспособности объекта контроля.

Приближенный алгоритм при произвольных пересекающихся тестах заключается в следующем. Пусть к началу некоторого М-го шага процесса проверки проведена последовательность тестов: s(М-1)={t1,...,tM-1} и задача сводится к отысканию отказавших элементов подмножества W(М-1).

Алгоритм поиска заключается в следующем:

1) Проводится (если возможно) общий тест, чтобы определить есть ли в непроверенном подмножестве W(0) хотя бы один отказавший элемент. Если тест проходит успешно, то на этом процедура проверки прекращается, если тест проходит неуспешно, то начинается основная процедура.

2) Если глобальный тест проходит неуспешно, то для каждого теста ti вычисляется вероятность неуспешного исхода в проверяемом подмножестве:

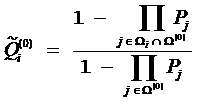при условии, что проведена последовательность тестов s(0).

Примечание. Достаточно вычислить лишь величины: 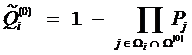, потому что в п.5 наибольшее значение имеют лишь относительные величины, а не абсолютные - .

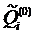3) Для каждого теста ti находят связанные с ним затраты Сi при условии, что уже проведена последовательность тестов s(0). Перед началом процесса проверки .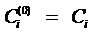

4) Для каждого теста ti определяется величина: .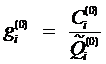

5) Выбираем такой тест tk для которого 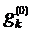минимально:.

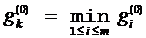6) Применяется тест tk, причем:

а) если тест завершается успешно, то процесс поиска отказавших элементов продолжается для оставшегося подмножества W(1)=W(0)\Wk;

б) тест заканчивается неуспешно, то возможны два случая:

- если тест контролирует работоспособность только одного элемента, то этот элемент заменяется годным и дальнейшее отыскание отказов производится в подмножестве W(1)=W(0)\Wk;

- если тест контролирует больше одного элемента, то дальнейший поиск отказов производится в подмножестве W(1)=Wk, причем для этого могут быть использованы лишь тесты tu, такие, что WkWu=Wk.

7) Фиксируется новая последовательность s(1) применяемых тестов, содержащая предыдущую последовательность s(0) и последний применяемый тест tk:s(1){s(0), tk}.

8) К подмножеству W(1), указанному в пункте 6 вновь применяется процедура проверки, начиная с пункта 1, если найденный отказавший элемент заменен на работоспособный, и начиная с пункта 2, если замена отказавшего элемента не проводилась, соответствующей заменой верхнего индекса (0) на индекс (1).

Процесс проверки продолжается до тех пор, пока не будут найдены и заменены годными все отказавшие элементы системы.

Пример 2. Система состоит из 8 элементов и может быть проверена 6-ю тестами, описание которых приводится в таблице 18.2. Известны затраты на проведение тестов: С1=1; с2=2; С3=1,2; С4=1,5; С5=2,5; С6=1,3, величина Сi не зависит от порядка применения теста.

Таблица 18.2 - Матрица тестов

Номер теста	Номер элемента
	1	2	3	4	5	6	7	8
1	1	1			1	1
2		1		1				1
3			1		1	1
4	1					1		1
5	1		1	1	1
6					1		1	1

Вероятности отказов элементов q1=0,1; q2=0,1; q3=0,2; q4=0,3; q5=0,1; q6=0,5; q7=0,5; q8=0,2; Количество отказавших элементов заранее неизвестно. Будем считать, что элементы 3, 4, и 7 неисправны, но тому, кто проводит проверку это неизвестно. Необходимо найти все отказавшие элементы при минимальных средних затратах на проведение необходимых для этого тестов.

РЕШЕНИЕ:

1) Вычисляем величины вероятностей неуспешного исхода 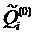в проверяемом подмножестве по формуле , и находим, что , , , , ,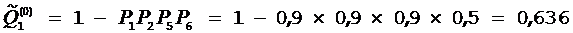

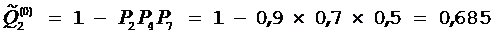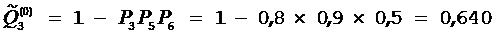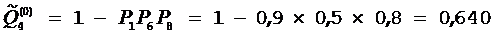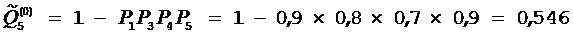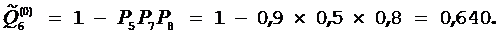
2) Определяем величину отношения стоимости проведения теста к величине вероятности неуспешного исхода 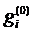, по формуле : ; ; ; ; ; ;

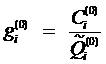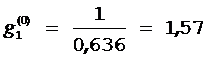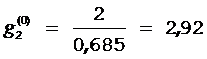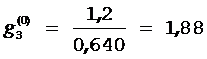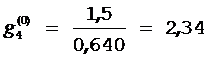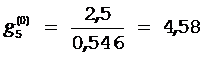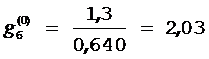Первым тестом должен быть тест t1, т. к. 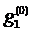минимально и равно 1,57.

Тест должен пройти успешно, т. к. в условии задачи мы определили элементы 3, 4 и 7 как отказавшие. В связи с этим задача сводится к обнаружению отказавших элементов в оставшемся подмножестве элементов W(1)={3,4,7,8}

3) Вычисляем величины 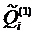по формуле 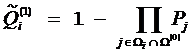, и находим, что , , , , .

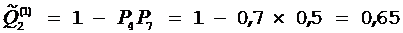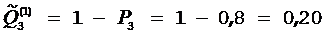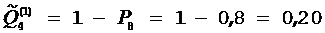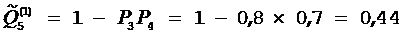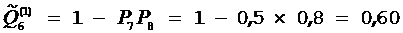4) Определяем новые значения

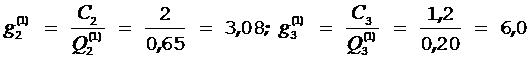
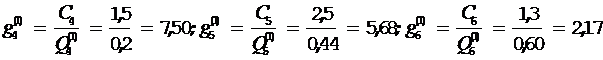
Минимальное значение 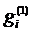имеет тест t6, проверяющий элементы 7 и 8. По условию задачи тест оказался неуспешным (неисправны элементы 3, 4 и 7). Для дальнейшего поиска отказов в подмножестве W1 может быть использован лишь тест t2, в результате применения которого (по условию данного примера) будет сделан вывод об отказе элементов 7 или 4. Получение более детальной информации о состоянии системы применением имеющихся тестов матрицы Т оказывается невозможным, следовательно, задача обнаружения всех отказавших элементов рассматриваемого объекта и замены их работоспособными не может быть выполнена.

ДОБАВЛЕНО

3.1 Метод последовательных поэлементных проверок

При использовании этого метода система рассматривается в виде последовательной цепочки элементов, выход каждого из которых приводит к отказу изделия. Для каждого элемента должны быть известны данные о надежности и времени проведения проверок.

Идея метода поэлементных проверок состоит том, что поиск отказавшего узла ведется путем диагностики каждого из элементов в определенной, заранее установленной, последовательности. При обнаружении отказавшего элемента поиск прекращается и производится замена отказавшегося элемента, а затем проверка работоспособности объекта. Если проверка показывает, что объект имеет еще один отказ, то поиск продолжается с той позиции, на которой был обнаружен отказывающий элемент. Операция продолжается, пока не будет обнаружен последний неисправный элемент.

Основная задача, решаемая при использовании метода последовательных поэлементных проверок, заключается в определении последовательности проверок. При этом в общем виде рассматривается объект, состоящий из N элементов, произвольным образом соединенных между собой, с известными интенсивностями отказов i , i=1,2,…N. Обычно предполагается, что неработоспособным может быть только один элемент. Известны также продолжительности проверок каждого элемента ti. Необходимо найти такую последовательность проверок, при которой среднее время поиска неисправности будет минимальным.

Имеющего в технической литературе [26,39] рекомендации по использованию метода предусматривают применение в качестве критерия оптимальности минимума отношения i /ti , где i = - коэффициент отказа i-го элемента или i/ .

Для обеспечения минимального среднего времени поиска отказавшего элемента проверки следует осуществлять в соответствии с последовательностью 1/t1<2/t2<…<N/tN, где порядковые номера от1 до N обозначают очередность проведения проверок.

3.2 Метод последовательных групповых проверок

Метод групповых проверок заключается в том, что путем проверки одного или нескольких параметров определяется часть изделия, в которой находится неисправный элемент, затем проводится другая серия проверок, позволяющая выявить следующую подгруппу элементов, включающую в себя неисправный элемент, и так далее до тех пор, пока последний не будет локализован и однозначно определен.

Если исходные данные по надежности элементов отсутствуют, то наиболее приемлемым методом поиска отказавшего элемента является метод половинного разбиения. Сущность метода заключается в том , что участок схемы с последовательно соединенными элементами делится на две равные части и равнозначно выбирается для проверки левая или правая ветвь. Если в результате проверки, например левой части схемы, окажется, что неисправный элемент находится в правой ветви, то для локализации отказавшегося элемента правая ветвь дополнительно делится на два равнозначных участка. Такое деление будет продолжаться до тех пор, пока не будет обнаружен отказавший элемент. Критерий половинного разбиения учитывает только одну из характеристик проверок – число элементов, охваченных проверкой. Он может дать оптимальное решение только при равных вероятностях отказов элементов и одинаковом времени проверок групп. Поскольку надежность элементов, входящих в систему, может отличатся, лучше использовать метод разбиения последовательной системы на две части с равными суммарными вероятностями отказа или интенсивностями отказов. Для практического использования метода вводят следующие ограничения: в системе может отказать только один элемент, время проверок различных групп элементов одинаково. В этом случае в качестве критерия оптимальности при проведении диагноза можно использовать выражение [Р() ] = min, где Р() – вероятность отрицательного исхода,

(3.1)

где r- число элементов, охваченных проверкой.

Подсчитав значение Р() для всех проверок и используя предложенный критерий, можно выбрать место первой проверки. После проведения первой проверки схема разбивается на две части, которые рассматриваются как самостоятельные объекты. Для каждого из них определяются коэффициенты отказа (сумма коэффициентов отказа должна быть равна 1), составляется перечень возможных проверок и выбирается проверка, для которой вероятности исходов близки к 0,5. Указанный процесс продолжается до однозначного определения отказавшего элемента.

3.3 Решение типовых примеров

Пример 1. Система автоматического управления технологическим процессом состоит из 14 элементов, соединенных в структурной схеме надежности последовательно (рис. 4.1)

Рис. 3.1. Структурная схема надежности системы автоматического управления

Выход каждого из элементов приводит к отказу системы. Заданы интенсивности отказов элементов (i 10-5 ч-1)

1 =7, 2 =3, 3 =4, 4 =5, 5 =4, 6 =5, 7 =6, 8 =1, 9 =1, 10 =2, 11 =1, 12 =2, 13 =2, 14 =1

Время поиска отказавшего элемента одинаково для всех проверок и составляет 5 мин. Используя метод последовательных поэлементных проверок, установить оптимальную последовательность диагностирования системы управления.

Решение. 1. Определяем суммарную интенсивность отказов системы

По формуле находим значение показателя i для всех элементов, в результате получаем 1 = 0,16, 2 = 0,068, 3 = 0,09, 4 = 0,11, 5 = 0,09, 6 = 0,11, 7 = 0,136, 8 = 0,022, 9 = 0,022, 10 = 0,045, 11 = 0,022, 12 = 0,045, 13 = 0,045, 14 = 0,022.

Определяем отношение i / ti, с учетом того, что ti = t = 5 мин

1 / t = 0,032, 2 / t = 0,0136, 3 / t = 0,018, 4 / t = 0,022, 5 / t = 0,018, 6 / t = 0,022, 7 / t = 0,028, 8 / t = 0,0046, 9 / t = 0,0046, 10 / t = 0,009, 11 / t = 0,0046, 12 / t = 0,009, 13 / t = 0,009, 14 / t = 0,0046.

В соответствии с принятым критерием оптимальности располагаем полученные отношения i / ti в порядке возрастания. Окончательно устанавливаем следующую последовательность проверок

8 9 11 14 10 12 13 2 3 5 4 6 7 1.

Пример 2. Основными элементами электропривода вентилятора (рис. 4.2) являются: аппарат защиты от токов короткого замыкания (1), вводное коммутационное устройство (2), силовые контакты магнитного пускателя (3), электродвигатель (4), устройство дистанционного включения и отключения электропривода (5), катушка магнитного пускателя (6).

Рис. 3.2. Функциональная схема электропривода вентилятора

Буквами А, Б, В, Г, Д, Е, Ж, З обозначены входные и выходные сигналы элементов. Известны коэффициенты отказов элементов 1 = 0,3 , 2 = 0,1 , 3 = 0,1 , 4 = 0,2 , 5 = 0,1 , 6 = 0,2 . Используя метод групповых проверок, требуется составить алгоритм поиска отказавшего элемента, обеспечивающий минимальное среднее количество проверок.

Решение. 1. Составляем перечень возможных проверок (табл. 4.1). В таблицу также для каждой проверки поместим вероятности отрицательного исхода

Таблица 3.1

Пk

Входной сигнал

Выходной сигнал

Проверяемые

элементы

Р()

П1

П2

П3

П4

П5

П6

П7

П8

П9

П10

П11

П12

П13

П14

П15

П16

П17

П18

П19

П20

ВЗ

ЕВ

ВЖ

ВЗ

ВЖ

ВЗ

ВЕ

ВЖ

ВЗ

1,2

1,2,3,5,6

1,2,5

1,2,5,6

2,5

2,5,6

2,3,5,6

2,3,4,5,6

5,6

3,5,6

3,4,5,6

3,6

3,4,6

3,4

0,3

0,4

0,8

0,5

0,7

0,1

0,2

0,4

0,5

0,7

0,1

0,2

0,1

0,2

0,3

0,4

0,6

0,3

0,5

0,3

Из анализа последнего столбца таблицы видно, что минимальное значение критерия соответствует проверкам П4, П9, П19.У проверки П9 4 элемента проверяется. Поэтому рассмотрение ведем по П4 и П19, имеющих по 3 элемента. Выбираем проверку П19 т.к. ее легче реализовать. При положительном исходе проверки П19 отказавший элемент будет находиться в группе, состоящей из 1, 2 и 5 элементов, а при отрицательном исходе – группе элементов 3, 6, 4.

Составляем перечни возможных проверок и вероятности их отрицательных исходов для вновь полученных групп, состоящих из 1, 2, 5 и 3, 6,4 элементов. Результаты показаны в табл. 3.2 и табл. 3.3. В этих таблицах Р() будет определяться суммой значений вероятностей отрицательного исхода ( для П1 : Р() = 0,3+0,3. Первое 0,3 взято из табл. 3.1, а второе 0,3 значение вероятности элемента).

Таблица3.2

Пk

Входной сигнал

Выходной сигнал

Проверяемые

элементы

Р()

П1

П2

П6

П7

ВЕ

ВЖ

1,2

2,5

0,6

0,8

0,2

0,4

Таблица 3.3

Пk

Входной сигнал

Выходной сигнал

Проверяемые

элементы

Р()

П11

П12

П18

П20

ВЗ

ВЖ

ВЗ

3,6

3,4

0,2

0,4

0,6

Проводим анализ материалов табл. 3.2 и 3.3. Данные табл. 3.2 свидетельствуют о том, что наиболее информативными являются проверки П1 и П7. Для обеих проверок = 0,1 . Выбираем проверку П1. При отрицательном исходе ее неисправен элемент 1, при положительном исходе – несправный элемент находится в группе элементов 2 и 5. Так как в последнем случае остается только 2 элемента, то дальнейшая последовательность проверок безразлична. Аналогичный подход применим при рассмотрении табл. 3.3.

Выбираем проверку П12 и П18. При положительном исходе проверки П12 нужно проверить элементы 3 и 6, при отрицательном – несправен элемент 4.

Строим алгоритм проверок

2. Метод последовательных элементных проверок.

Предполагается, что в системе, например, в процессе эксплуатации без постоянного наблюдения, может произойти несколько отказов. Имеется возможность провести полную проверку системы за некоторое время и проверку отдельных ее элементов (за время Сj каждого j-го элемента).

Процесс протекает следующим образом: проводится полная проверка, и если система оказывается неисправной, то последовательная проверка продолжается до тех пор, пока не будет найден отказавший элемент; обнаруженный элемент восстанавливается (ремонтируется, заменяется) и снова производится полная проверка. Если система продолжает оставаться неисправной, т. е. в ней есть еще хотя бы один отказавший элемент, то процедура продолжается.

Требуется найти такой порядок проверки элементов системы, что бы процесс поиска всех неисправных элементов протекал в среднем, минимальное время.

Предлагается следующий алгоритм:

1) Для каждого элемента вычисляются значения .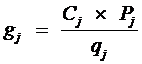

2) Элементы нумеруются в порядке возрастания 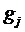. Полученный порядок и есть порядок оптимальных проверок.

ПРИМЕР 3. Рассмотрим схему, состоящую из пяти элементов, характеризующихся следующими показателями:

Показатели	Элементы
1	2	3	4	5
Вероятность безотказной работы, Рj	0,2	0,3	0,4	0,5	0,6
Время, Сj, мин.	10	20	10	5	10

Требуется определить в каком порядке следует проводить проверку для отыскания всех неисправных элементов.

РЕШЕНИЕ:

1) Вычисляем значение 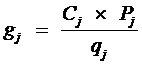. 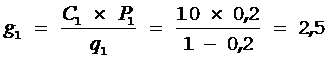; ; 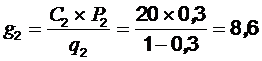; ; 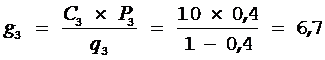; 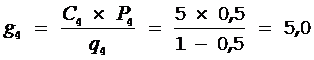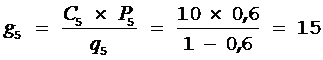Из расчетов видно, что для минимизации среднего времени отыскания неисправных элементов необходимо всегда проверять элементы данной системы в следующем порядке: 1, 4, 3, 2, 5.

3. Прогнозирование технического состояния оборудования по результатам измерения сопротивления изоляции

По результатам измерений сопротивления изоляции можно определить момент ожидаемого наступления предельного состояния изоляции. Рассмотрим эту методику на примерах.

Пример 1. Сопротивление изоляции участка электрической сети напряжением 220В в момент проведения измерений оказалась равным 4 Мом. Три последующих измерения были сделаны с интервалом в 6 месяцев и показали следующие значения: 3,4; 2,8; 2,2 Мом. Нам надо определить скорость изменения параметра и момент ожидаемого наступления предельного состояния изоляции.

1) Скорость изменения параметра технического состояния:

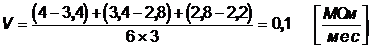2) Момент наступления предельного состояния (он определяется минимально допустимым значением сопротивления изоляции 1МОм, согласно требованиям ПТЭ и ПТБ):

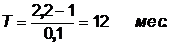
Через 12 месяцев состояние изоляции данного участка электрической сети окажется не удовлетворяющим установленным требованиям. По истечении указанного периода времени данный участок подлежит ремонту.

Пример 2. В результате измерения сопротивления изоляции электродвигателя были получены следующие значения:

Номер измерения, Ni	1	2	3	4	5
Результат измерения, Ri, МОм	100	75	50	30	10

Измерения производились один раз в месяц. Определим скорость изменения параметра и момент ожидаемого наступления предельного состояния изоляции.

1) Скорость изменения параметра технического состояния:

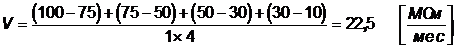2) Момент наступления предельного состояния (он определяется минимально допустимым значением сопротивления изоляции 0,5 МОм, согласно требованиям ПТЭ и ПТБ):

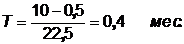
При такой скорости изменения сопротивления изоляции предельное состояние изоляции электродвигателя наступит через 0,4 месяца. Это необходимо иметь ввиду при составлении плана ремонта оборудования.

В общем виде скорость изменения параметра технического состояния может быть определено из выражения:

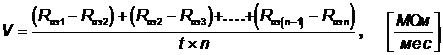где Rиз1, Rиз2, Rиз3, Rиз(n-1), Rизn - результаты измерений сопротивления изоляции, Мом;

t - интервал времени, через который проводились измерения, месяц;

n - количество измерений, не считая первое.

В общем виде момент наступления предельного состояния (он определяется минимально допустимым значением сопротивления изоляции для данного вида оборудования, согласно требованиям ПТЭ и ПТБ) может быть определен из выражения:

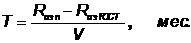где Rизn - результат последнего измерения сопротивления изоляции, Мом;

RизГОСТ - допустимое значение сопротивления изоляции электрооборудования согласно требованиям ГОСТа.

Литература

Ермолин Н.П., Жерихин И.П. Н Надежность электрических машин. Л.: Энергия, 1976.
Хорольский В.Я., Медведев А.А., Жданов В.Г. Задачник по эксплуатации электрооборудования. Ставрополь, 1997.

2 3 4 5 6 7 8 9 10 11 12 13 14

А Б В Г Д

Е Ж З

1 2 3 4

5 6

1,2,3,4,5,6

1,2,5

2,5

3,6

3,4,6

Методы поиска отказов