Розробка системи слідкування за напрямком цілі РЛС з моноконичним пеленгаційним пристроєм

АНОТАЦІЯ

Данна кваліфікаційна робота присвячена розробці системи слідкування за напрямком цілі РЛС з моноконичним пеленгаційним пристроєм.

В роботі на підставі вхідних даних розроблено функціональну структуру системи АСН, обговорено її призначення та принцип дії, побудована математична модель системи АСН, визначено бажаєму ЛАЧХ системи, а також здійснений аналіз залежності точності функціонування системи від параметрів алгоритму слідкування за напрямком цілі. На підставі отриманих результатів здійснено розрахунок основних параметрів, синтез корегуючого пристрою методом логарифмичних частотних характеристик, розрахунок показників якості системи в перехідному режимі.

ЗМІСТ

Перелік умовних позначень, символів, одиниць, скорочень і термінів …
Вступ ………………………………………………………………………….
1. Призначення, принцип дії та функціональна структура системи АСН...
1.1 Загальна характеристика системи АСН……………………………...
1.2. Принцип дії та функціональна структура системи автоматичного супроводження цілі за напрямком……………………………………….
1.3. Принцип дії та функціональна структура виконуючого пристрою
1.4. Особливості побудови завадозахищених моноімпульсних координаторів. Двоканальні приймальні пристрої з одночасним порівнянням сигналів з сумарно-різницевою обробкою (моноконічний приймальний пристрий)………………………………..
1.4.1 Трьохканальний приймальний пристрій з одним гетеродинним підсилювачем проміжної частоти……………………………………….
1.4.2 Функціональна схема системи автоматичного супроводження цілі за напрямком…………………………………………………………
2. Побудова математичної моделі системи автоматичного супроводження цілі за напрямком…………………………………………..
2.1 Математична модель пеленгаційного пристрою……………………
2.2 Математична модель виконавчого пристрою……………………….
3. Визначення бажаємої ЛАЧХ системи слідкування за напрямком цілі…
3.1 Побудова бажаної ЛАЧХ системи слідкування за напрямком цілі..
3.2 Визначення постійної часу форсуючої ланки……………………….
4. Синтез корегуючого пристрою системи………………………………….
4.1 Поняття про синтез корегуючого пристрою…………………………
4.2 Види корегуючих пристроїв…………………………………………..
4.3 Синтез корегуючого пристрою методом логарифмічних частотних характеристик……………………………………………………………...
4.4 Розрахунок показників якості системи в перехідному режимі…….
Висновок…………………………………………………………………...
Додаток 1…………………………………………………………………..
Додаток 2…………………………………………………………………..
Додаток 3………………………………………………………………….
Перелік посилань

ПЕРЕЛІК УМОВНИХ ПОЗНАЧЕНЬ, СИМВОЛІВ, ОДИНИЦЬ,

СКОРОЧЕНЬ І ТЕРМІНІВ

АКП	– автоматичний керуючий пристрій;
АСН	– система автоматичного супроводження за напрямком;
АХС	– антенно-хвилеводна система;
ВП	– виконуючий пристрій;
ВСП	– виділення сигналу помилки;
ВД	- виконавчий двигун;
ГППЧ	- головний підсилювач проміжної частоти;
ГКІ	– генератор комутуючих імпульсів;
ГОН	– генератор опорної напруги;
ДП	– динамічна помилка;
ЕКП	– еквивалентний керуючий пристрій;
ЕМП	– електромашинний підсилювач;
КП	– керуючий пристрій;
КК	- каскад комутації;
КСП	– канал сигналу помилки;
КД	- кутовий дискримінатор;
ПЕОМ	– персональна електронна обчислювальна машина;
ПСКП	- послідовний керуючий пристрій;
ПрКП	– паралельний керуючий пристрій;
ПП	- пеленгаційний пристрій;
ПФ	– передаточна функція;
САК	– система автоматичного керування.

ВСТУП

Продовження розвитку авіації і тактики її бойового застосування, розширення номенклатури літальних апаратів і їх льотно-тактичних характеристик в найбільш розвинених у військовому відношенні країн світу призвело до трансформації сучасної військової стратегії від орієнтації на масштабні загально-військові операції до переважного проведення повітряних та ракетних ударів у тому числі із застосуванням літаків з підвищеними маневреними можливостями [1]. Із урахуванням високих маневрових можливостей засобів повітряного нападу (літаки F – 22, СУ-37 розраховані на перевантаження до 10 одиниць) та розробками щодо їх підвищення (використання двигунів з керованим вектором тяги, розвиток концепції адаптивного крила) [2] зростають вимоги до ефективності використання ЗРК по маневруючим цілям. Однією з проблем, що виникають у зв'язку зі зростанням маневрових можливостей засобів повітряного нападу (ЗПН), є зрив супроводження цілі системами супроводження ЗРКособливо на малих дальностях. Відповідність рівня розвитку засобів ППО сучасним тактико-технічним характеристикам та способам бойового застосування ЗПН можливо досягти шляхом модернізації існуючих та під час створення нових ЗРК [3, 4].

Метою даної кваліфікаційної роботи є розробка дослідження структурної схеми пеленгаційного пристрою, а також системи автоматичного слідкування за напрямком з моноконічним пеленгаційним пристроєм.

Робота складається з вступу, чотирьох розділів і висновка.

Відповідно до поставленої задачі у першому розділі розглянути призначення, принципи дії та способи реалізації системи автоматичного слідкування за напрямком з моноконічним пеленгаційним пристроєм. Показано, що для нормальної роботи АСН потрібно здійснювати управління діаграмою спрямованості антени таким чином, щоб її головна пелюстка постійно з необхідною точністю слідкувала за зміною напрямку на джерело радіосигналу.

У другому розділі побудовані математичні моделі складових системи автоматичного слідкування за напрямком з моноконічним пеленгаційним пристроєм.

У третьому розділі визначена бажана логаріфмична частотна характеристика, при цьому побудова БЛАЧХ виконувалась на основі зв’язку параметрів типових ЛАЧХ, якими є частоти, нахили відрізків ЛАЧХ і коефіцієнтів підсилення, або частоти зрізу, з показниками якості САК.

У четвертому розділі розглянутий синтез корегуючого пристрою системи автоматичного слідкування за напрямком з моноконічним пеленгаційним пристроєм. Синтез КП здійснений методом логаріфмичних частотних характеристик, що має наглядність, дозволяє враховувати вимоги до якості САК. Проведено дослідження якості функціонування САК у переходному режимі шляхом моделювання на ПЕОМ. Отримані показники якості функціонування САК такі як перерегулювання, час регулювання тощо.

1. ПРИЗНАЧЕННЯ, ПРИНЦИП ДІЇ ТА ФУНКЦІОНАЛЬНА СТРУКТУРА СИСТЕМИ АСН

1.1. Загальна характеристика системи АСН

В радіотехнічних системах ЗРК приймання радіохвиль здійснюється, як правило, за допомогою гостроспрямованих антен, застосування яких забезпечує високу просторову вибірковість. В залежності від призначення системи і діапазону хвиль, які вона використовує, головна пелюстка діаграми спрямованості приймальній антени може мати ширину від декількох градусів до долей кутових хвилин.

В цьому випадку для здійснення постійного радіоконтакту із ціллю необхідно діючи на антену постійно повертати діаграму спрямованості таким чином, щоб її головна пелюстка постійно найбільш точніше супроводжувала ціль за кутовими координатами.

Якщо джерело радіосигналу рухоме, то потрібно здійснювати управління діаграмою спрямованості таким чином, щоб її головна пелюстка діаграми спрямованості постійно з необхідною точністю слідкувала за зміною напрямку на джерело випромінювання. Для здійснення такого управління застосовується спеціальна слідкуюча система, яка називається системою автоматичного слідкування за напрямком (АСН).

В ряді випадків виникає необхідність вступати в радіоконтакт не з одним, а з дкількома джерелами радіосигналів, які знаходяться на різних напрямках. В таких випадках за допомогою системи АСН організовується почергово супроводження всіх джерел, в процесі якого радіоконтакт з кожним з них (шляхом відповідного оріентування діаграми спрямованості) здійснюються на протязі порівнено коротких проміжків часу, розділених тривалими паузами. Під час паузи в прийомі сигналів від даного джерела здійснюється радіоконтакт з рештою джерел, взятими на супроводження.

1.2. Принцип дії та функціональна структура системи автоматичного супроводження цілі за напрямком.

Всяка система АСН складається з двох частин – пеленгаційного пристрою (ПП) і виконуючого пристрою (ВП) (рисунок 1.1). Кожен з цих пристроїв включає в себе декілька функціональних блоків, при цьому конкретна функціональна структура виконуючого пристрою суттєво залежить від способу управління діаграмою спрямованості антени.

Рисунок 1.1 – Загальна схема автоматичного супроводження за напрямком.

До складу ПП входять антено-фідерна система (АФС) та радіоприймальний пристрій (РПрП), за допомогою яких тим чи іншим шляхом створюються три канали обробки прийнятого радіосигналу – основний приймальний канал та два кутомірних пеленгаційних каналів – азимутальний та кутомісцевий.

В кутомірних каналах, що складають пеленгаційний пристрій з приймаємого антеною сигналу вилучається тільки інформація про напрямок проходу радіохвиль. Інша координатна і некоординатна інформація вилучається в основному приймальному каналі, що до складу ПП не входить.

ПП шляхом спеціальної обробки приймаємого сигналу в кутомірних каналах виконує таки функції:

1. Створює в просторі опорний (рівносигнальний) напрямок, котрий знаходиться в середині головної пелюстки діаграми спрямованості антени по основному приймальному каналу. Як правило опорний напрямок співпадає з напрямком головного максимуму, але є пеленгаційні пристрої, у яких опорний напрямок зміщений на невеликий кут відносно напрямку головного максимуму;

2. Виробляє в кожному кутомірному каналі сигнал кутового розузгодження, що характеризує величину (знак та абсолютне значення) кутового відхилення напрямку на джерело радіосигналу від обраного опорного напрямку у відповідній площині (кутомісцевій або азимутальний):

; (1.1)

, (1.2)

де – кутове відхилення в азимутальній площині, а – кутове відхилення в кутомісцевій площині. При малих кутах та можна вважати:

; (1.3)

, (1.4)

де та – нахилені азимути напрямку на джерело радіосигналу та опорного напрямку відповідно, а та – кути місця вказаних вище напрямків.

Друга частина системи АСН – виконуючий пристрій, служить для перетворення сигналу розузгодження в керуючий вплив, що прикладається до антени і забезпечує таку зміну орієнтації рівносигнального напрямку, при якій абсолютні величини кутових відхилень та зменшуються. Отже в основі принципу дії системи АСН лежить принцип управління по відхиленню, при наявності сигналів розузгодження виконуючий пристрій, діючи на антену намагається сумістити рівносигнальний напрямок ПП з напрямком на джерело радіосигналу.

За допомогою системи АСН можна здійснювати вимірювання кутових координат джерела сигналу, що супроводжується. Для цього достатньо ввести до складу системи супроводження датчики кутових положень.

В основі методів формування сигналів кутових розузгоджень лежить принцип порівняння двох (в кожному кутомірному каналі) сигналів, що формуються антеною або одночасно на двох різних виходах, або на одному її виході, але в різний час при періодичній зміні орієнтації діаграми спрямованості в просторі.

Порівняння сигналів, що формуються антеною, як раз і дозволяє ПП здійснити названі вище функції.

В якості опорного напрямку приймається такий напрямок приходу радіохвиль, при якому порівнювані сигнали виявляються однаковими (тому опорний напрямок і називається рівносигнальним). Якщо джерело радіосигналу зміщене відносно опорного (рівносигнального) напрямку, то різниця між порівнювальними сигналами використовується в кутомірних каналах ПП для формування сигналів кутових розузгоджень U1 та U2. Якщо джерело радіосигналу знаходиться на опорному (рівносигнальному) напрямку, то порівнювані сигнали виявляються однаковими, а сигнали кутових розузгоджень рівними нулю кутів та і значення кутових датчиків можна вважати виміреними значеннями (оцінками) кутових координат джерела випромінювання:

; (1.5)

(1.6)

де та – оцінки кутових координат джерела радіосигналу.

1.3. Принцип дії та функціональна структура виконуючого пристрою.

Виконуючий пристрій будь-якої системи АСН незалежно від його функціонального складу завжди вирішує одні й тиж задачі:

1. Обробляє сигнали кутових розузгоджень, що формуються ПП, з метою надання системі АСН потрібних показників якості, головним з яких є максимальна точність суміщення опорного напрямку з напрямком на джерело радіосигналу.

2. Формує керуючий вплив на антену, що забезпечує потрібну зміну орієнтації опорного напрямку.

Якщо система АСН використовується як слідкуючий вимірювач кутових координат супроводжуємого джерела радіосигналу, то і ВП вирішує третю задачу – формує оцінки кутових координат супроводжуємого джерела радіосигнала.

На функціональну структуру ВП впливає ще цілий ряд факторів, головними з яких є таки:

– спосіб управління орієнтацією опорного напрямку (механічний або електронний);

– характер радіоконтакту (безперервний або преривчастий) з боку приймальної антени з супроводжуємим джерелом радіосигналу;

– вид обробки сигналів кутових розузгоджень (аналогова або цифрова).

Якщо керування орієнтацією опорного напрямку здійснюється безперервно в часі шляхом обертання антени, встановленої на нерухомій основі, то в якості ВП частіше всього використовується азимутальний та кутомісцевий електромеханічні приводи антени з елементами послідовної та паралельної корекції, які забезпечують надання системі АСН потрібних показників якості.

Функціональна схема одного з каналів ВП такого типу наведена на рисунку 1.2.

Рисунок 1.2 – Функціональна схема одного з каналів ВП

Принцип роботи каналу ВП полягає у наступному:

напруга, яка знимається з керуючого пристрою підсилюється електромашинним підсилювачем (ЕМП) потужності. Вихід ЕМП потужності навантажений на якорну обмотку виконуючого двигуна (ВД), який представляе собою двигун постійного струму з незалежним збудженням. Якщо , на виході ЕМП з’явиться напруга, під впливом якої якір двигуна приводиться в обертання і через редуктор починає розвертатися антена. Обертання антени буде до тих пір, поки не стане рівному нулю помилка .

1.4. Особливості побудови завадозахищених моноімпульсних координаторів. Двоканальні приймальні пристрої з одночасним порівнянням сигналів з сумарно-різницевою обробкою (моноконічний приймальний пристрий).

Моноімпульсні координатори не чутливі до флуктуацій амплітуди сигналів, що приймаються. В цих координаторах можуть бути використані відомі схеми захисту від різних видів активних завад.

Захист моноімпульсних координаторів (МК) від пасивних завад викликає значні труднощі і досить проблематичній. Це пов’язано з тим, що використання в цих координаторах широко розповсюджених систем селекції рухомих цілей (СРЦ) веде до втрати інформації, яка в даному випадку міститься в амплітуді і фазі прийнятого сигналу.

Справа в тому, що в системі СРЦ сигнали обробляються у фазових детекторах (ФД), що веде до втрати інформації про кутове відхилення цілі відносно рівносигнального напрямку. На виході системи СРЦ з’являються відеоімпульси, промодульовані по амплітуді з частотою Доплера. Тому в амплітудних МК інформація про кутове положення цілі, яка міститься в амплітуді сигналу спотворюється.

Щоб зберегти інформацію про кутове положення цілі відносно РСН необхідно інформацію, яка міститься в амплітуді і фазі високочастотних сигналів, перетворити в амплітуду і фазу низкочастотної огинаючої приймаємих сигналів, які не руйнуються при обробці в системі СРЦ. Але тоді МК втрачає одне з важливих переваг – можливість визначати кутові координати цілі по одному імпульсу.

Але можливо побудувати ПП, в якому використовується моноімпульсний спосіб виявлення кутової інформації і забезпечується можливість використання системи СРЦ. При побудові схеми такого ПП використовуються принципи побудови й переваги трьохканальної моноімпульсної системи і двоканального координатора з коничним скануванням. Таки системи називають моноконичними.

Можлива структурна схема такого двоканального ПП з одночасним порівнюванням сигналів й сумарно-різницевою обробкою наведений на рисунку 1.3.

Рисунок 1.3 – Схема двоканального ПП з одночасним порівнюванням й сумарно-різницевою обробкою сигналів

Вхідним елементом є моноімпульсна антена з чотирма діаграмами спрямованості. На виході системи перетворення створюється сумарний і два різницевих сигнала і .

В подальшому трьохканальна моноімпульсна інформація перетворюється у двоканальну. В якості схеми додавання використовується круглий хвилевід з ортогональною характеристикою електричного поля (рисунок 1.4)

У ньому здійснюється просторове додавання різницевих сигналів і і створення сумарного різницевого сигналу

. (1.7)

Сигнал знимається з виходу круглого хвилеводу за допомогою модулятора – прямокутного хвилеводу, що обертається з частотою . В результаті обертання хвилеводу амплітуда сигналу змінюється за законом , а фаза огинаючої визначається напрямком поля у круглому хвилеводі, яка, у свою чергу, визначається величиною відхилення цілі від РСН:

. (1.8)

Сумарний і модульований загальний різницевий сигнали подаються на НВЧ – мостове зєднання, з виходу якого знимаються сигнали:

; (1.9)

, (1.10)

де .

Сигнали і представляють собою дві безперервні послідовності високочастотних сигналів, протифазно промодульованих по амплітуді з частотою . Амплітуда огинаючої цих сигналів пропорційна величині відхилення цілі від РСН, а фаза огинаючої вказує сторону відхилення цілі.

Таким чином розглянута схема забезпечує перетворення моноімпульсної інформації про кутове положення цілі, що міститься в амплітуді і фазі високочастотного сигналу, прийнятого різними діаграмами спрямованості, в інформацію, що міститься у амплітуді і фазі низькочастотної огинаючої послідовності сигналів.

Отримані на виході розглянутої схеми сигнали однакові сигналам двоканального ПП з коничним скануванням.

Після перетворення в змішувачах (ЗМ), підсилення у гетеродинних підсилювачах проміжної частоти (ГППЧ), обробки в системі СРЦ і детектування сигнали і поступають на пристрій сумарно-різницевої обробки, яка виконує сумарно-різніцеву обробку сигналів. На виході пристрою знимається напруга

(1.11)

Ця напруга подається на фазові детектори ФД і ФД на други входи яких подається сигнали з генератора опорної напруги (ГОН). З виходу ФД і ФД знимаються сигнали, пропорційні величині і напрямку відхилення цілі від РСН в азимутальній і кутомісцевій площіні.

1.4.1 Трьохканальний приймальний пристрій з одним гетеродинним підсилювачем проміжної частоти.

Задача забезпечення стабільності крутизни пеленгаційної характеристики може бути вирішена підсиленням сигналів всіх трьох каналів в одному головному підсилувачі проміжної частоти (ГППЧ).

На практиці можливи два шляхи реалізації цієї проблеми: частотне і часове ущільнення сигналів.

Схема частотного ущільнення сигналів наведена на рисунку 1.5.

Рисунок 1.5 – Схема частотного ущільнення сигналів в одному ГППЧ

На схему подаються сигнали , і на одній і тій же частоті fпр після попереднього ППЧ. На змішувачах ЗМ1, ЗМ2, ЗМ3 за допомогою гетеродинів Гет1, Гет2, Гет3 ці сигнали перетворюються на частоти f1 f2 f3 і поступають на широкосмуговий ГППЧ, де одночасно підсилюються. Потім на змішувачах ЗМ4, ЗМ5, ЗМ6 за допомогою гетеродинів Гет1, Гет2, Гет3 знову перетворюються на частоту fпр. Далі сигнали через вузькосмугові фільтри, що настроєні на частоту fпр, поступають для подальшого перетворення.

В розглянутої схемі є труднощі в забезпеченні якісного вихідного перетворення по частоті. В результаті підсилення в одному ГППЧ можуть з’явитися перехресні зв’язки між каналами, в результаті чого сумарний сигнал може потрапити в обідва різницевих канали. Для зменшення цього на виході кожного каналу схеми частотного ущільнення сигналів ставлять вузькосмугові фільтри, з коефіціентом прямокутності амплітудно-фазової характеристики близький до одиниці. З цією метою вузькосмугові фільтри виготовляються на високодобротних резонансних елементах, наприклад на кварцевих резонаторах. Цей метод добрий в тому, що зберігається структура сигналів, недолік у складності реалізації розв’язування сигналів у вихідної частині ГППЧ.

Схема часового ущільнення сигналів в одному ГППЧ наведена на рисунку 1.6.

Рисунок 1.6 – Схема часового ущільнення сигналів в одному ГППЧ

На вході і виході ГППЧ увімкнені каскади комутації (КК) відповідного каналу, добре екрановані, що керуються генератором комутуючих імпульсів (ГКІ). Він формує три зсунутих за часом послідовності імпульсів. Кожна з послідовностей керує вхідним і вихідним КК відповідного каналу. За час дії керуючого імпульсу вхідний сигнал проходить через ГППЧ і вихідний КК.

Перевагою цього методу є відсутність перехресних зв’язків між каналами, простота технічної реалізації.

Недоліком є порушення структури сигналу (якщо сигнал імпульсний, тоді змінюється його скважність, якщо безперервний – тоді він стає дискретним); виникають певні труднощі у використанні сумарного сигналу в якості опорного для виділення сигналу помилки по кутовим координатам.

1.4.2 Функціональна схема системи автоматичного супроводження цілі за напрямком

На вхід ПП з антени РЛС ЗРК, яка в загальному випадку є кутовим датчиком, поступають сигнали, що несуть інформацію про кутове положення цілі відносно РСН. Після підсилення і перетворення в приймальному пристрої ці сигнали поступають в канал сигналу помилки, де детектором виділяється їх огинаюча.

В цьому випадку ця огинаюча може бути представлена виразом

. (1.12)

В слідкуючих координаторах управління антеною можливе тільки в прямокутній системі координат, тому необхідно здійснити перехід від полярних координат цілі (, ) до декартових координат цілі (ц, ц). Ця задача вирішується в кутових дискримінаторах (КД).

Для формування декартової системи координат на КД подається дві опорні напруги синусоїдальній форми, що здвинуті одна відносно другої по фазі на /2. Для забезпечення узгодження системи координат, яка формується в КД, з прямокутною системою управління виконуючого пристрою, фази опорних напруг повинні бути жорстко пов’язані і синхронизовані з кутовими напрамками і швидкостями обертання діаграми спрямованості. Якщо діаграма спрямованості обертається проти часової стрелки з частотою ск і за початок відліку прийняти моменти часу, коли діаграма спрямованості знаходиться у крайньому правому положенні, тоді опорну напругу можна представити у такому вигляді:

(1.13)

. (1.14)

Якщо подавати на КД напругу сигналу помилки з виходу каналу сигналу помилки () і опорні напруги з ГОН (, ) фазові детектори КД сформують керуючу напругу:

, (1.14)

. (1.15)

Кожний КД чутливий тільки до однієй складової сигналу помилки, яка знаходиться в фазі з опорною напругою.

З урахуванням викладеного зобразимо функціональну схему системи АСН на рисунку 1.8.

Рисунок 1.8 – Функціональна схема системи АСН

2. ПОБУДОВА МАТЕМАТИЧНОЇ МОДЕЛІ СИСТЕМИ АВТОМАТИЧНОГО СУПРОВОДЖЕННЯ ЦІЛІ ЗА НАПРЯМКОМ.

2.1 Математична модель пеленгаційного пристрою

При побудові математичної моделі ПП його вхідними діяннями, будемо розглядати кутову координату цілі і кутове положення РСН , а вихідним діянням – напругу на виході ПП (фазового детектора) , що залежить від величини і напрямку кутового розузгодження між напрямком на ціль і РСН.

Розглянемо спрощену математичну модель ПП системи АСН, що безперервно супроводжує джерело імпульсного радіосигналу. В процесі супроводження сигнали кутових розузгоджень спочатку формуються у вигляді послідовності імпульсів і , амплітуди яких залежать від величин кутових розузгоджень і :

; (2.1)

, (2.2)

де Т – період слідування імпульсів приймаємого сигналу; кТ – моменти приходу імпульсів; – функція, яка визначає форму та тривалість одиночного імпульсу;

значення кутових відхилень і в моменти прийняття імпульсів;

, (2.3)

, (2.4)

і – дискретні біли шуми, що описують амплитудні флуктуації імпульсів.

Імпульсні сигнали кутових розузгоджень у вихідних ланцюгах каналів ПП перетворюються в безперервні сигнали і шляхом встановлення огинаючих їх амплітуд. В якості пристроїв виділення огинаючої використовують амплітудні імпульсні детектори з ємнісним навантаженням. У ході тривалості кожного імпульсу ємність навантаження детектора заряджається до напруги, рівній амплітуді імпульсу, а в проміжках між імпульсами повільно розряджається.

Знайдемо оператор, що пов’язує послідовність імпульсних сигналів розузгодження (і = 1, 2) з їх встановленими обвідними, враховуючи при цьому, що амплітудний імпульсний детектор достатньо точно реалізує функції ідеального встановлюючого пристрою нульового порядку.

При прийнятому допущенні напруга на виході амплітудних детекторів каналів ПП можуть бути представлени у вигляді:

(2.5)

де коефіціент передачи амплітудного детектора;

(2.6)

– перша зворотна різниця решітчатої функції , описуючи послідовність амплітуд імпульсного сигналу розузгодження . Підставляючи (2.6) в (2.5) і маючи порядок виконання операцій складання і обрахування різниці отримаємо:

(2.7)

Похідна від цього виразу має вигляд:

, (2.8)

де – послідовність амплітуд імпульсного сигналу розузгодження . З (2.8) отримаємо :

. (2.9)

Таким чином, якщо послідовність амплітуд сигналів розузгодження представити таким виразом як (2.9), то процес встановлення огинаючих послідовностей може бути наведений оператором .

Пеленгаційна характеристика для площини азимуту визначається залежністю величини вихідної напруги ПП як функції , яка є непарною функцією , симетричною відносно до початку координат і , при куті розузгодження рівному нулю. При малих кутах пеленгаційна характеристика лінійна і визначається виразами:

, (2.10)

, (2.11)

де – крутизна пеленгаційної характеристики.

В загальному випадку вигляд пеленгаційної характеристики і її крутизна залежить від відношення сигнал/щум на вході приймального пристрою. Із зменьшенням цього співвідношення величина зменшується. Крутизна пеленгаційної характеристики залежить від амплітуди радіосигналу.

Інерційні властивості ПП по відношенню до зміни кутового розузгодження характеризується операторним коєфіцієнтом передачи:

. (2.11)

При цьому у першому наближенні можна вважати рівною

, (2.12)

де – постійна часу ПП, що визначається інерційністю ФД, чи еквивалентною інерційністю каналу сигналу помилки в залежності від того, яка з вказаних інерційностей є більшей.

Для побудови математичної моделі імпульсного ПП представимо вихідні напруги у вигляді:

; (2.13)

, (2.14)

де – коефіціенти підсилення каналів в ПП, (і = 1, 2) ;

і – флуктуаційні складові вихідних напруг ПП;

і – функції, що описують послідовність значень кутових розузгоджень і в дискретні моменти часу які мають вигляд

(2.15)

(2.16)

Таким чином схему математичної моделі наприклад кутомісцевого каналу імпульсного ПП, що складена за виразами (2.1)…(2.16) можна зобразити на рисунку 2.1.

Рисунок 2.1 – Схема математичної моделі кутомісцевого каналу імпульсного ПП

2.2 Математична модель виконавчого пристрою

У якості вхідних величин для виконавчого пристрою візьмемо середне значення і повільно змінююча напруга зворотнього зв’язку , а в якості вихідної величини – середне значення пульсуючого струму в обмотці керування ЕМП.

Схема математичної моделі сумуючого підсилювача складемо відповідно з рівняннями [11]:

, (2.17)

, (2.18)

та наведена на рисунку 2.2.

Рисунок 2.2 – Схема математичної моделі сумуючого підсилювача

Для зручності математичного опису ЕМП у якості вихідної величини розглянемо ЕДС холостого ходу яка не залежна від струму навантаження. Знайдемо рівняння, яке пов’язує змінні у часі значення і при . Застосовуючи закон Кірхгофа для короткозамкненого ланцюга якоря ЕМП отримаємо:

. (2.18)

В операторній формі рівняння (2.18) має такий вигляд:

, (2.19)

де – стала часу поперечного кола.

Враховуючи те, що , а остаточно отримаємо рівняння для математичної моделі ЕМП в операторної формі (рисунок 2.3):

. (2.20)

Рисунок 2.3 – Схема математичної моделі ЕМП

При складанні математичної моделі двигуна постійного струму будемо враховувати, що він живитися від ЕМП. В цьому випадку в якості вхідної величини двигуна будемо розглядати величину ЕДС холостого ходу ЕМП . Для складання математичної моделі двигуна постійного струму скористаємося еквівалентної електричної схемой кола живлення якоря двигуна постійного струму з незалежним збудженням що зображена на рисунку 2.4.

Рисунок 2.4 – Еквівалентна електрична схема кола живлення якоря двигуна постійного струму з незалежним збудженням

Враховуючи закон Кірхгофа, запишемо диференціальне рівняння кола живлення якоря

, (2.21)

де і – активний опір та індуктивність джерела вхідного сигналу, , – повні активний опір та індуктивність кола живлення якоря; і – активний опір та індуктивність якірного кола двигуна; – ЕРС джерела вхідного сигналу, у даному випадку дорівнює .

Перейшовши до операторної форми запису отримаємо співвідношення, яке визначає струм в якорі

, (2.22)

де – електромагнітна стала часу двигуна (з урахуванням параметрів джерела живлення).

Для врахування динамічних властивостей навантаженого двигуна, до вала якого через редуктор під’єднаний об’єкт керування скористаємося рівнянням балансу потужностей

, (2.23)

де – обертальний момент і кутова швидкість об’єкта керування; J i Jок – моменти інерції якоря і об’єкта керування; добуток – потужність, яка розвивається на валу двигуна.

Якщо передаточне число редуктора дорівнює , то .

Перейдемо після виключення проміжних змінних – струму якоря і проти-ЕРС , одержимо диференціальне рівняння другого порядку з постійними коефіціентами:

, (2.24)

де – електромеханічна стала часу двигуна;

, – коефіцієнт підсилення двигуна і коефіцієнт демпфірування моменту сил опору.

Розв’язуючи рівняння (2.24) відносно , отримаємо

, (2.25)

де

, (2.26)

– оператор передачі двигуна.

Рівняння (2.25) і (2.26) дозволяють створити математичну модель двигуна, але найчастіше при розрахунках електромагнітною сталою можна знехтувати (), і тоді оператор передачі двигуна має вигляд:

. (2.27)

Отримаємо математичну модель двигуна, що зображена на рисунку 2.5.

Рисунок 2.5 – Схема математична модель двигуна постійного току з незалежним збудженням

До складу паралельного корегуючого пристрою (ПКП) розглядаємої електромеханічної слідкувальної системи входять тахогенератор постійного струму і фільтр. При математичному опису ПКП треба врахувати його вхідну кутову швидкість обертання (t) валу виконуючого двигуна, а вихідною величиною – напругу зворотнього зв’язку .

Рівняння разом з рівнянням встановлюює зв'язок між вхідною величиною ПКП (t) з його вихідною величиною – напругою зворотнього зв’язку . Математична модель тахогенератора є ідеальною диференціюючою ланкою.

Фільтр являє собою диференціюючу ланку, і тому напруга виникає лише за наявності прискорень обертання вала виконавчого двигуна. Внаслідок цього досягається плавна, без великих перевантажень, робота системи під час розгону та гальмування.

Схема математичної моделі ПКП наведена на рисунку 2.6.

Рисунок 2.6 – Схема математичної моделі ПКП

Система датчиків електромеханічної слідкувальної системи складається з двох сельсинів сельсина-датчика (СД) і сельсина-трансформатора (СТ). Сельсин-датчик підключений до мережі змінного струму, а з виходу СТ знімається напруга сигналу помилки:

, (2.28)

амплітуда якої визначається величиною, а фаза – знаком кута розузгодження між кутами повороту задавального і виконавчого валів. Якщо , то вихідна напруга СТ дорівнює нулю, при фаза вихідної напруги збігається з фазою напруги мережі, а при протилежна фазі напруги мережі. Тому математичну модель системи датчиків можна представити у вигляді підсилювальний ланки з коефіціентом підсилення Кдат.

При побудові математичної моделі електромеханічної слідкувальної системи для замикання зворотного зв’язку необхідно врахувати кінематичне рівняння, яке зв’язує швидкість обертання об’єкта керування з його кутом повороту

. (2.29)

Записуючи рівняння (2.29) в операторному вигляді і виражаючи вихідну величину системи , отримаємо

. (2.30)

При поєднанні лінеаризованих математичних моделей елементів системи, розглянутих вище, можна отримати математичну модель електромеханічної слідкувальної системи, схема якої наведена на рисунку 2.7.

Рисунок 2.7 – Схема математичної моделі електромеханічної слідкуючої системи з виконавчим двигуном постійного струму з незалежним збудженням

3. ВИЗНАЧЕННЯ БАЖАЄМОЇ ЛАЧХ СИСТЕМИ СЛІДКУВАННЯ ЗА НАПРЯМКОМ ЦІЛІ

3.1 Побудова бажаної ЛАЧХ системи слідкування за напрямком цілі

Побудова бажаної ЛАЧХ виконується на основі зв’язку параметрів типових ЛАЧХ, якими є частоти, нахили відрізків ЛАЧХ і коєфіцієнти підсилення, або частоти зрізу, з показниками якості системи автоматичного керування (САК).

Виходячи з призначення САК і аналізу діючих на неї діянь визначається діапазон значень задаючого діяння min … max, його максимально можливі щвидкості зміни і прискорення , а також спектральна щільність мішаючого діяння Sf0.

У відповідності з призначенням САК формуються умови до точності у вигляді допустимих значень систематичної динамічної помилки і дисперсії випадкової помилки, що викликається мішаючим діянням , а також встановлюються вимоги до показників якості перехідного процесу tp і .

На основі значень min … max , і згідно виразу

, (3.1)

де – помилка по положенню;

– помилка по швидкості;

– помилка по прискоренню;

– помилка по r – й похідної

для систематичної динамичної помилки:

(3.2)

розраховуються вимагаємі значення коєфіціентів помилок і = 0, 1, 2….

При розрахунку обирається порядок астатизму V, тобто номер першого коєфіціенту помилки не рівною нулю і помилка розподіляється між залишившимися похідними.

При виборі порядку астатизму можливе використовувати наступне. Якщо діапазон можливих значень задаючого діяння великий, тоді треба обирати систему з астатизмом першого порядку, щоб максимальна помилка системи повинна бути такою, щоб забезпечити надійне супроводження цілей, що супроводжуються. Як вже відомо, для цього для динамічної помилки повинне виконуватися умова:

де – максимальне значення дінамичної помилки; – ширина діаграми спрямованості за рівнем половинної потужності.

Згідно методу коефіціентів помилок динамична помилка розраховується виразом (3.1) де ,, – коефіцієнти помилок, – задаючий вплив.

Розглянута система має вид передаточної функції розімкненої САК:

Тоді коефіцієнти помилок будуть дорівнювати

; ; ; .

Тоді виходячи з формули (3.1) можна отримати

; , тоді

;

Отримане значення складової динамічної помилки для похідних задаючих дій буде дорівнювати:

;

рад/с2.

Так, як обидві складові не приймають максимальне значення, будем шукати параметри системи з таких умов:

;

Звідки отримаємо вираз для :

3.2 Визначення постійної часу форсуючої ланки

Розімкнена система автоматичного керування має вид:

. (3.3)

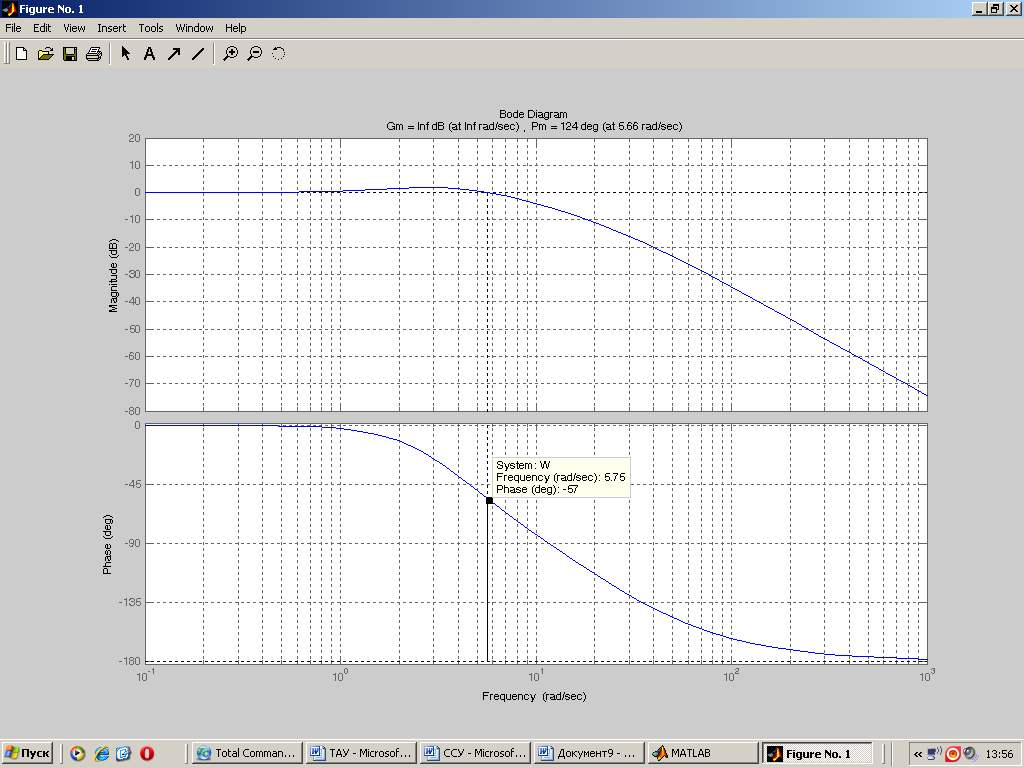
Визначаємо , виходячи з критерію мінімуму динамічної помилки по впливу, що заважає. Вона визначається виразом, що забезпечує необхідний запас стійкості системи. Як відомо в цьому випадку необхідно, щоб ЛАЧХ розімкненої системи проходила через вісь частот з нахилом – 20 дБ/дек на ділянці не менш 1 декади.

Візьмемо с, тоді с.

В цьому випадку ЛАЧХ розімкненої системи автоматичного керування має вигляд, зображений у Додатку 1. Як видно з рисунку запас по фазі складає 124, тобто замкнута САК стійка й тому отриману ЛАЧХ будемо вважати як бажану.

4. СИНТЕЗ КОРЕГУЮЧОГО ПРИСТРОЮ СИСТЕМИ

4.1 Поняття про синтез корегуючого пристрою

Керування системою автоматичного керування полягає в рішенні задачі раціональної побудови автоматичного керуючого пристрою (АКП), що відповідає комплексу різноманітних вимог, пов’язаних з різними характеристиками системи.

Цей комплекс вимог включає в себе вимоги до якості, надійності, умовам експлуатації, допустимим габаритам та ваги, роду енергії (електрична, пневматична, гідравлічна), величини споживаної потужності, технологічності виготовлення, вартості, економічної і бойової ефективності.

Перераховані вимоги досить різноманітні, тому конструювання системи автоматичного керування задовольняючого всьому їх комплексу представляє собою складну задачу, допускаючи різні варіанти її вирішення.

Процедура знаходження оператору автоматичного керуючого пристрою, що забезпечує управління при заданих вхідних впливах із заданою якістю, називається абстрактним синтезом системи автоматичного керування.

Після абстрактного синтезу, здійснюється вибір технічних засобів для його реалізації, складається функціональна електрична і принципіальна електрична схеми системи. При цьому з можливих технічних рішень обирається таке рішення, що найкращим чином забезпечує вирішення експлуатаційних, конструктивних вимог, а іноді формулюється рішення на розробку нових елементів системи автоматичного керування з потрібними вимогами.

Процедуру знаходження технічної реалізації системи автоматичного керування називають технічним синтезом.

Таким чином практика конструювання показує, що вже сам характер об’єкту управління і призначення системи автоматичного керування частіше всього заздалегідь визначає основні функціонально необхідні елементи автоматичного керуючого пристрою. Такими елементами є виконавчий і підсилюючий блок, сприймаючи блоки (датчики), порівнюючи пристрої. Таким чином можливе часткове або повне завдання функціональної структури САК.

При повністю заданій структурі системи вибір її параметрів здійснюється шляхом їх оптимізації за обраним критерієм якості, наприклад за критерієм мінімуму середньоквадратичної помилки.

Керуючий пристрій – це функціональний елемент САК, що забезпечує необхідну якість САК шляхом виправлення (корегування) властивостей вихідної не корегованої системи.

Задача синтезу САК в цьому випадку включає в себе математичне описування заданої частини системи, визначення оператору якості бажаної системи і на цій основі синтез корегую чого пристрою.

Під синтезом корегую чого пристрою розуміють визначення його виду, місця включення, передаточної функції, параметрів й технічної реалізації.

4.2 Види корегуючих пристроїв

Корегуючий пристрій застосовується для отримання запасів стійкості, придання необхідного порядку астатизму, отримання необхідної швидкодії і ефективної смуги пропускання.

Розглянемо деякі загальні характеристики КП, знання яких необхідне для рішення задачі їх вибору і синтезу.

Розглянемо послідовний корегуючий пристрій (ПКП), що вмикають безпосередньо після елементу порівняння або після попереднього підсилювача що наведений на рисунку 4.1.

Рисунок 4.1 – Схема вмикання послідовного корегуючого пристрою

Передаточну функцію системи в розімкненому стані при послідовному включенні КП можна записати як:

, 4.1)

де – передаточна функція вихідної не корегованої розімкненої САК.

Розглянемо паралельний корегуючий пристрій (ПрКП). Його можливо вмикати в коло місцевого зворотного зв’язку, частіше всього від’ємного. Як правило він об’єднує зворотним зв’язком виконуючий елемент або кінцевий каскад підсилення. На рисунку 4.2 зображений варіант вмикання ПрКП.

Рисунок 4.2 – Схема вмикання паралельного корегуючого пристрою

Передаточна функція розімкненої САК для ПрКП записується як:

. (4.2)

Обов’язковим елементом любого ПрКП є датчик сигналу місцевого зворотного зв’язку, якій приймає діяння й перетворює його в сигнал, зручний для подальшого використання. Так в електромеханічних САК в якості датчиків місцевого зворотного зв’язку використовують тахогенератори, які з’єднані з валами виконуючих двигунів.

Тахогенератори виробляють напругу, яка пропорційна швидкості вимірювання вихідної величини САК. Для здійснення більш повного перетворення вихідної величини в коло зворотного зв’язку послідовно з тахогенератором також ставиться пасивний чотириполюсник постійного струму. Важливою перевагою ПрКП є зменшення впливу зміни параметрів елементів, що охоплені зворотним зв’язком на якість системи.

Дійсно, комплексна частотна характеристика елементів, що охоплені зворотним звязком

де – комплексна частотна характеристика петлі місцевого зворотного зв’язку.

Як правило в достатньо широкому і важливому для якості системи діапазоні частот справедливі нерівності:

. (4.3)

Тоді в цьому діапазоні частот .

Таким чином при виконанні нерівності (4.3) умови ділянки кола з ПрКП визначаються тільки умовами цього КП.

Перевага ПрКП виявляється також в тому, що поданий на нього вихідний вплив системи має малий рівень перешкод, що містяться у ньому, так як вони придушені системою, що має вигляд фільтру низьких частот.

Однак треба мати на увазі, що при великому коефіцієнті підсилення петлі місцевого зворотного зв’язку, можлива втрата стійкості, тобто збудження в петлі місцевого зворотного зв’язку. Керування потужними САК як правило здійснюється з використанням ПрКП.

4.3 Синтез корегуючого пристрою методом логарифмічних частотних характеристик

Синтез КП методом логарифмічних частотних характеристик має простоту і наочність, дозволяє дуже легко враховувати вимоги до якості САК.

Виходячи з того, що передаточні функції САК із зворотними зв’язками знаходяться у взаємно однозначних відповідностях, тоді умови дії САК повністю визначаються любою з них, зокрема передаточною функцією розімкнутого кола R(p). Тому синтез КП можна проводити використовуючи передаточні функції і відповідні частотні характеристики розімкненої САК.

Тоді

. (4.4)

З виразу (4.4) отримуємо:

. (4.5)

Таким чином, як випливає з (4.5), процедура синтезу КП методом логарифмічних частотних характеристик включає наступні операції.

1. Побудову ЛАЧХ системи, що складається тільки з функціонально необхідних елементів, тобто некорегованої системи. Якщо порядки астатизму вихідної і бажаної системи однакові, тоді коефіцієнт підсилення вихідної системи при цьому береться рівним його бажаному значенню.

2. Побудову ЛАЧХ системи, що задовольняє умовам якості, тобто має бажані властивості. Таку систему називають бажаною, а її ЛАЧХ бажаною ЛАЧХ (БЛАЧХ).

3. Побудову на основі рівняння (4.5) ЛАЧХ ПрКП і визначення його передаточної функції.

4. Розробку схемної реалізації КП і розрахунок його параметрів.

При необхідності переходу від ПрКП до еквівалентного КП іншого виду здійснюється вибір місця вмикання КП, а також визначається його передаточна функція і розробляється схема реалізації.

4.4 Розрахунок показників якості системи в перехідному режимі

Частотний метод аналізу якості функціонування САК в перехідному режимі заснований на тому, що вигляд перехідної характеристики системи і частотних характеристик пов’язані між собою. Оскільки з частотних характеристик найбільш просто будуються логарифмічні частотні характеристики, саме вони і знайшли використання при аналізі якості функціонування САК в перехідному режимі.

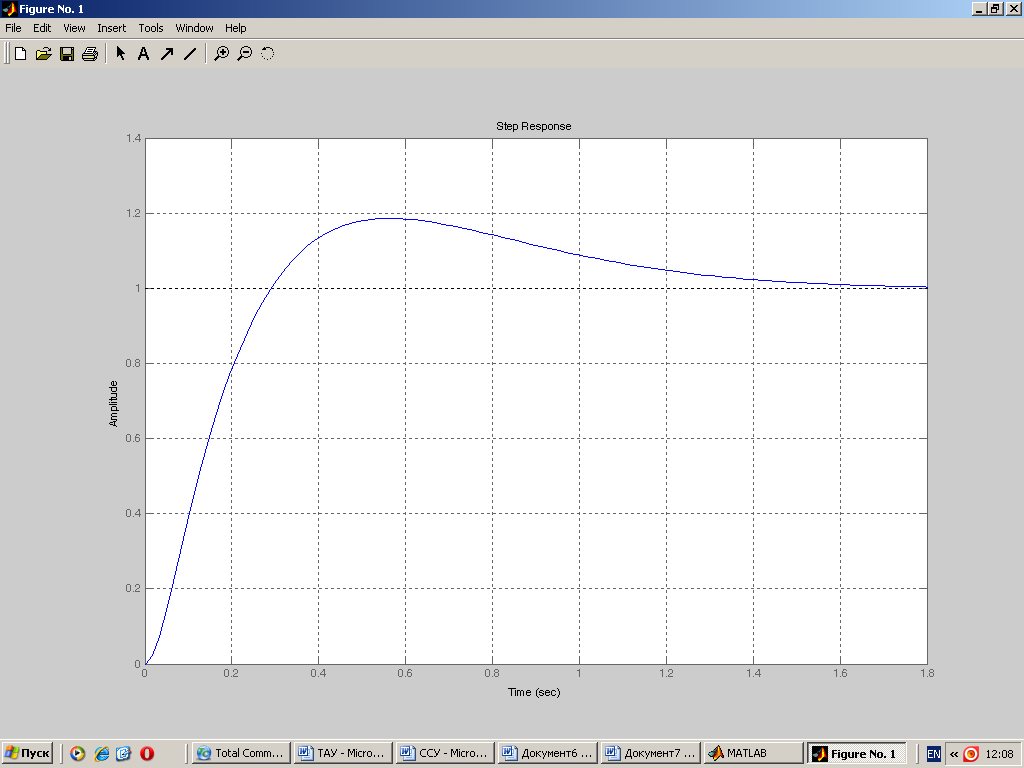
Показники якості функціонування системи супроводження цілі за кутовими координатами в перехідному режимі звичайно вводять на основі перехідної характеристики (Додаток 2).

Виділяють такі показники якості функціонування:

1. Перерегулювання , що визначається рівнянням

, (4.7)

де – максимальне значення перехідної характеристики;

– усталене значення перехідної характеристики.

2. Кількість максимумів перехідної характеристики N;

3. Час першого узгодження – час, по витіканню якого перехідна характеристика вперше досягла свого усталеного значення;

4. Час регулювання – час, по витіканню якого перехідна характеристика не виходить за межи смуги ± 5 % від усталеного значення.

Основним показником є величина перерегулювання і час регулювання . Перша величина характеризує ступінь коливальності, а друга – тривалість перехідного процесу.

Розраховане за формулою (4.7) значення перерегулювання становить

У реальних САК перерегулювання звичайно перебуває у діапазоні = 10 30 %, що задовільняє у нашому випадку.

За допомогою пакета прикладних програм Control System Toolbox Mathlab [9] отримана перехідна характеристика замкненої системи для значень параметрів алгоритму (Додаток 3) роботи системи супроводження цілі за кутовими координатами.

ВИСНОВОК

В кваліфікаційної роботі проведений аналіз якості системи супроводження цілі за кутовими координатами РЛС з моноконичним пеленгаційним пристроєм, яка включає:

– складання схеми математичної моделі системи супроводження цілі за кутовими координатами РЛС з моноконичним пеленгаційним пристроєм і її перетворення до оптимального для аналізу виду;

– аналіз стійкості системи;

– складання функціональної схеми системи АСН, принцип її дії;

– складання функціональної схеми ВП;

– розглянути особливості побудови завадозахищених моноімпульсних координаторів, двоканальні ПП з одночасним порівненням сигналів з сумарно-різницевою обробкою сигналів;

– визначена бажана ЛАЧХ системи, побудована БЛАЧХ розімкненої системи супроводження цілі за кутовими координатами;

– синтез КП системи. При дослідженні якості функціонування в перехідному режимі шляхом моделювання на ПЕОМ в пакеті прикладних програм Control System Toolbox Mathlab було визначено, що показники якості перехідного режиму є задовільними висунутим вимогам.

Додаток 1

ЛАЧХ і ЛФЧХ розімкненої системи автоматичного керування має

Додаток 2

Перехідна характеристика

Додаток 3

Програма розрахунку перехідної характеристики

>> K1=tf([115],[1 0])

Transfer function:

115

---

>> K2=tf([0.5 1],[10 1])

Transfer function:

0.5 s + 1

---------

10 s + 1

>> K3=tf([0 1],[0.03 1])

Transfer function:

----------

0.03 s + 1

>> R=K1*K2*K3

Transfer function:

57.5 s + 115

-----------------------

0.3 s^3 + 10.03 s^2 + s

>> W=feedback(R,1)

Transfer function:

57.5 s + 115

----------------------------------

0.3 s^3 + 10.03 s^2 + 58.5 s + 115

>> step(W), grid

ПЕРЕЛІК ПОСИЛАНЬ

Бабич В. Сверхманевренность истребителя. Зарубежное военное обозрение. - 1994, № 2.
Стрельніков В.І. Тенденції розвитку Військово-повітряних сил України з урахуванням досвіду воєнних конфліктів кінця XX сторіччя. Наука і оборона. -2002, № 2.
Кузьмук О.І. Збройні сили України на початку XXI сторіччя. Наука і оборона. - 2002, № 2.
Хисматулин В. Ш. Основи автоматики. - Харьков: ХВУ, 1998.
Системи автоматического управлення в вооружении войск ПВО. Часть 2. Типовьіе системи автоматического управлення радиотехнических устройств / Д. Д. Алексейчев, А. А. Казаков. - Харьков: ВИРТА ПВО, 1985.
Автоматическое управление и регулирование радиотехнических систем. Часть 1. Функциональнме структури и математическое описание систем автоматического управлення / Д. Д. Алексейчев, А. А. Казаков. - Харьков: ВИРТА ПВО, 1980.
Автоматическое управление и регулирование радиотехнических систем. Часть 2. Анализ и корекция САУ / Д. Д. Алексейчев, А. А. Козаков. - Харьков: ВИРТА ПВО, 1982.

8. Теоретические основи радиолокации / Я. Д. Ширман, В. Н. Голиков, И. Н. Бусигин и др.; под ред. Я. Д. Ширмана. - М.: Сов. Радно, 1970.

9. МАТLАВ Анализ, идентификация и моделирование систем. Спе-циальннй справочник / В. Дьяконов, В. Круглов. Санкт-Петербург, - 2002.

10. Системи керування. Ч.1. Типові системи автоматичного керування : навч. посіб. / А. О. Ковальчук, І. І. Сачук, О. О. Сосунов та ін.; за заг. ред. О. О. Сосунова. – Х. : ХУПС, 2012. – 316 с.: іл.

Рисунок 1.4 – Щодо пояснення формування загального різницевого сигналу кругової поляризації в пристрої сполучення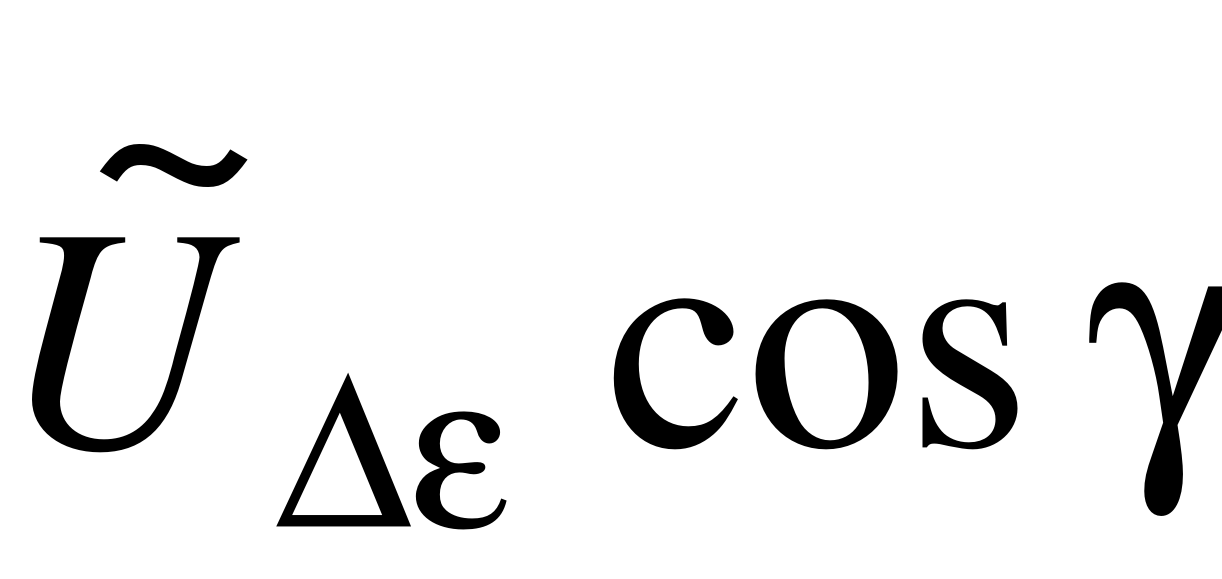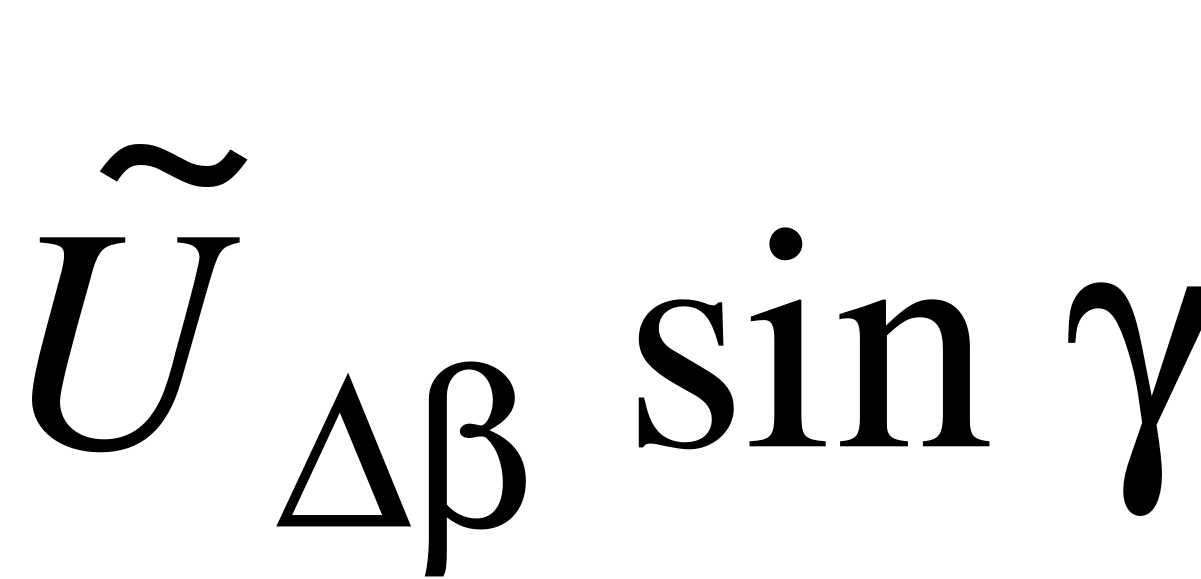

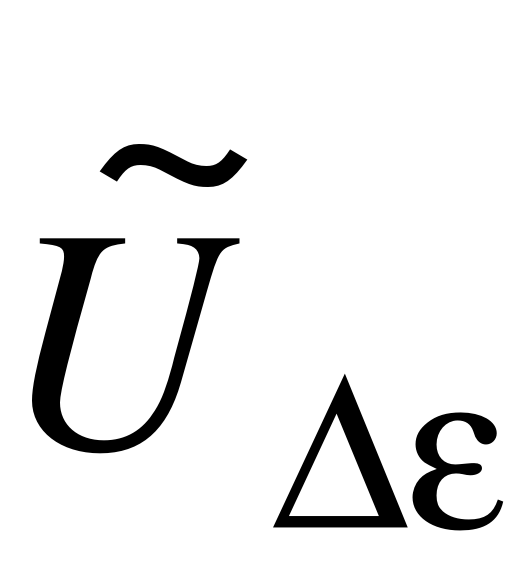
EMBED Equation.3

Напрямок площини

поляризації діелектричної

пластини

Розробка системи слідкування за напрямком цілі РЛС з моноконичним пеленгаційним пристроєм