Контроль коэффициента мощности
ЛЕКЦИЯ 12.
Контроль коэффициента мощности.
Коэффициент мощности как сдвиг фаз между векторами тока и напряжения определяют косвенно по показаниям различных при�боров или непосредственно с помощью фазометров.
Косвенный расчет коэффициента мощности в цепях однофазно�го тока выполняют по показаниям ваттметра, вольтметра и ампер�метра по формуле
.
В симметричных трехфазных системах коэффициент мощности можно рассчитать по результатам измерения активной мощности и линейных тока и напряжения по формуле
или по показаниям двух ваттметров, включенных по схеме, показанной на рис.11.9, используя формулу
.
При этом упрощает процесс определения коэффициента мощности по показаниям двух ваттметров номограмма, приведенная на рис.12.1.
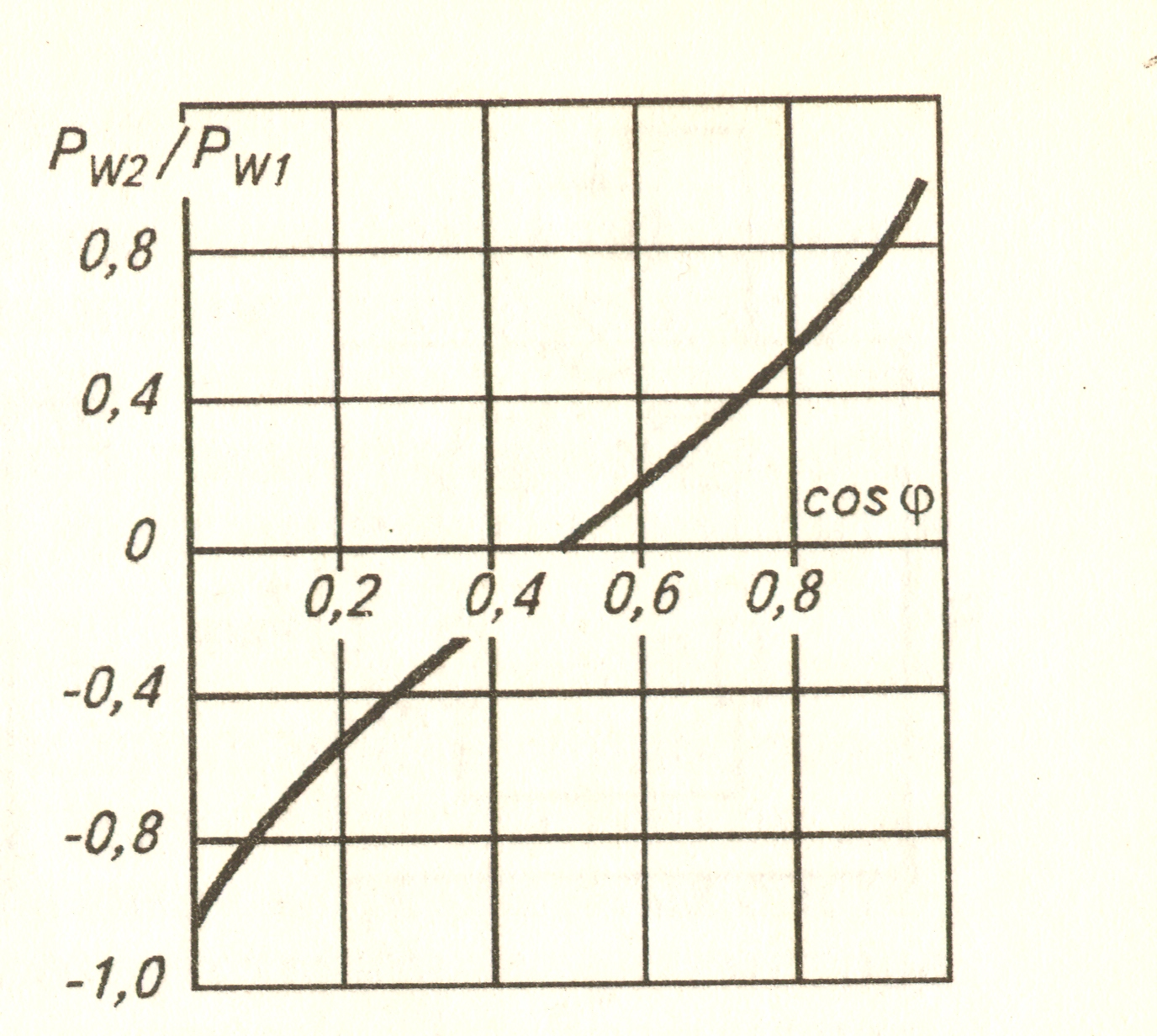
Рис.12.1. Номограмма для определения коэффициента мощности по
показаниям двух ваттметров, включенных по схеме, показанной
на рис. 11.9.
Угол , а соответственно, и коэффициент мощности можно определить при помощи электронно-лучевого осциллографа с использованием линейной или эллиптической развертки.
Непосредственно коэффициент мощности в одно- и трехфазных системах контролируют с помощью электродинамических, ферродинамических и электронных фазометров.
Электродинамический и ферродинамический фазометр представляет собой логометр, в цепи подвижных катушек которого включены элементы с разными реактивными сопротивлениями (рис.12.2,а). Известно, что функция преобразования такого прибора с учетом его векторной диаграммы (рис.12.2,б) имеет вид
,
поэтому его можно градуировать в единицах измерения или .
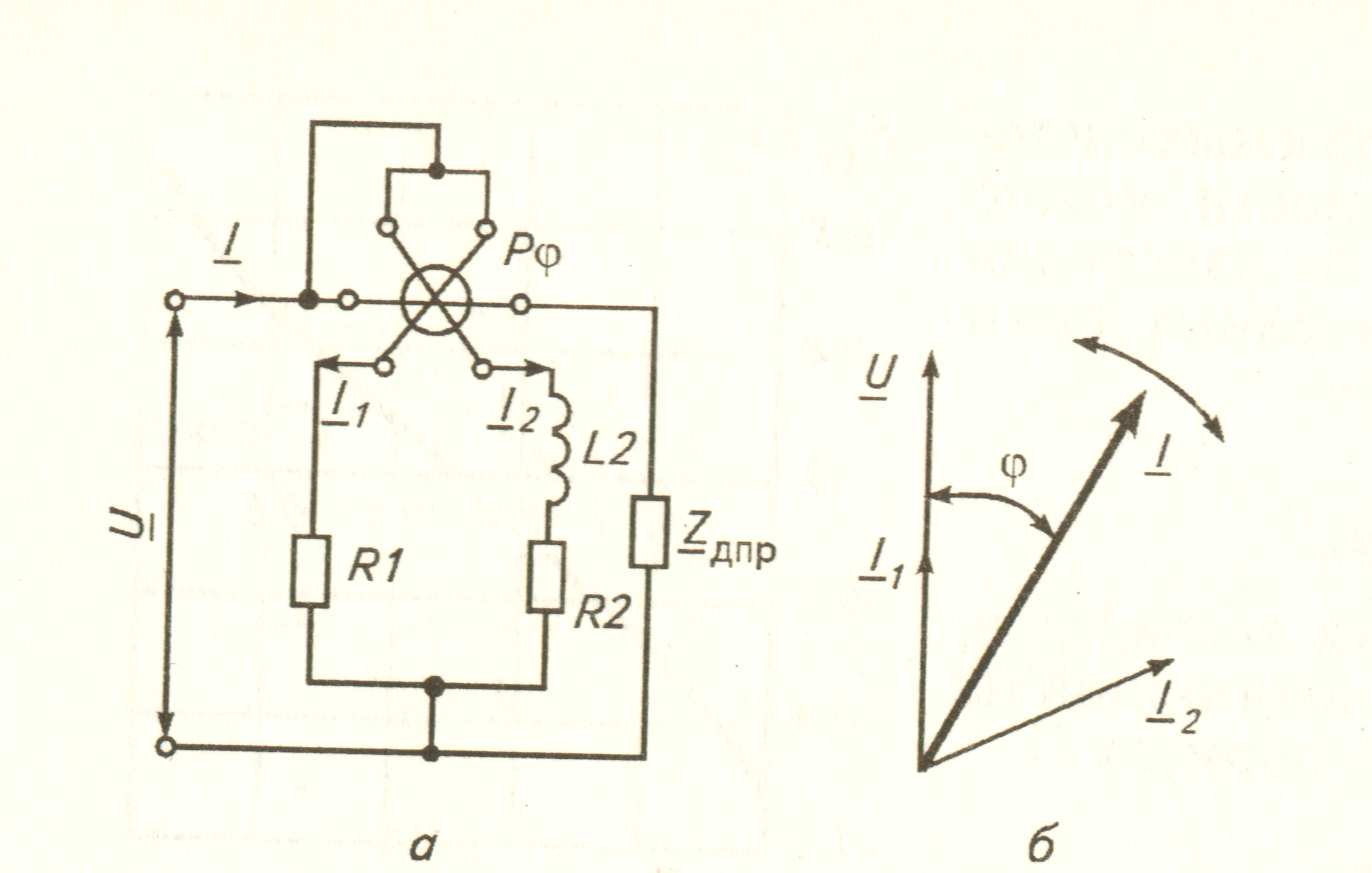
Рис.12.2. Измерение коэффициента мощности в однофазной цепи:
а – схема включения фазометра; б – векторная диаграмма цепи.
С использованием механизмов электродинамических и ферроди�намических логометров построены фазометры для трехфазных сис�тем. В таких приборах сдвиги между векторами токов в подвижных катушках получаются за счет сдвигов между токами и напряжениями в трехфазной системе. Схема включения трехфазного фазометра приведена на рисунке 12.3.
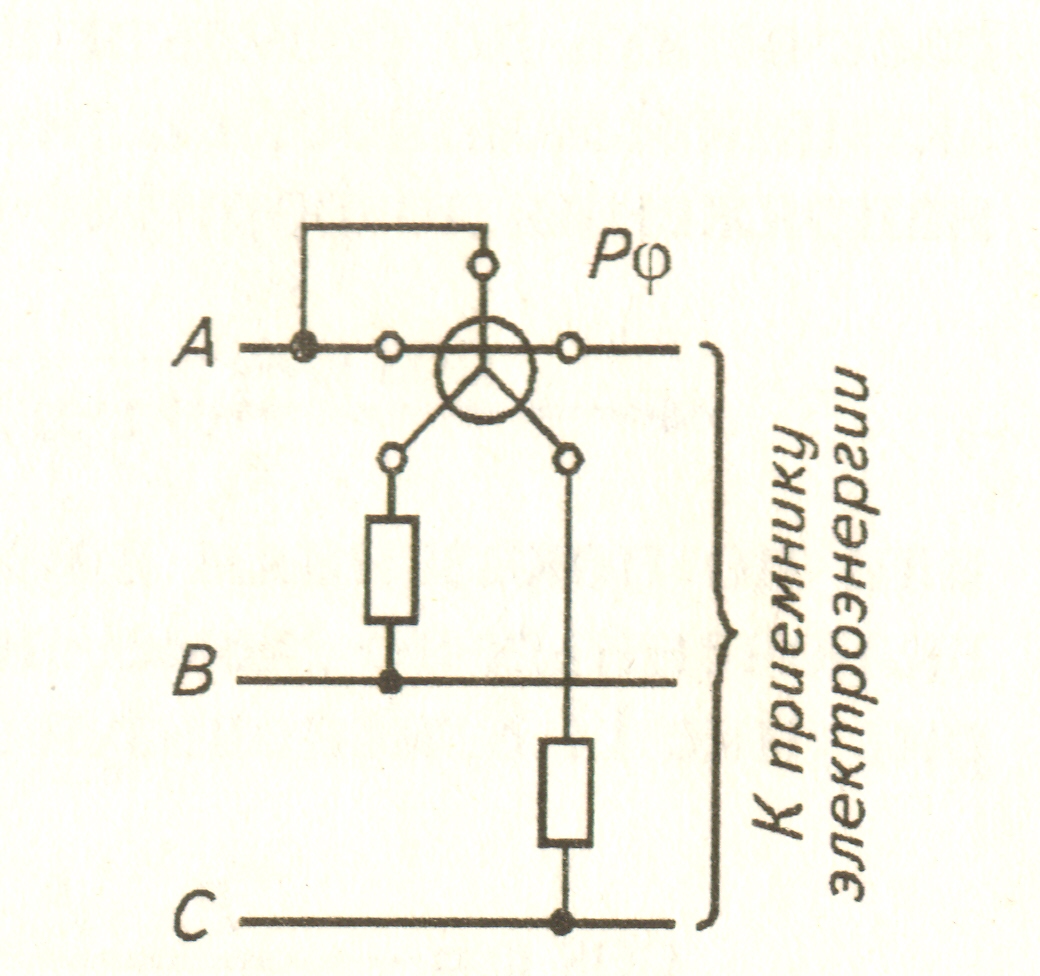
Рис.12.3. Схема включения фазометра в трехфазной системе.
Такие приборы обычно предназначены для непосредственного включения на напряжение 100 В. Для вклю�чения их в трехфазные системы используют измерительные транс�форматоры напряжения. Минимальные погрешности трехфазные фазометры имеют при работе в симметричных системах.
В электронных фазометрах (например, типа Ц302) фаза напря�жения преобразуется в постоянный ток, значение которого зависит от угла . Полученное напряжение постоянного тока подается на магнитоэлектрический прибор, проградуированный в единицах измерения угла или . Шкала такого фазометра равномерная, а его показания не зависят от частоты входного напряжения. Поэто�му прибор можно использовать в большом частотном диапазоне. Классы точности электронных фазометров обычно не ниже 2,5.
Измерение электрической энергии. Индукционные счетчики.
Как известно, электрическая энергия определяется выражением
,
где Р – мощность, потребляемая нагрузкой.
Энергия измеряется электрическими счетчиками. Для счетчиков переменного тока используются индукционные измерительные механизмы. Устройство счетчика индукционной системы показано на рис. 12.4.
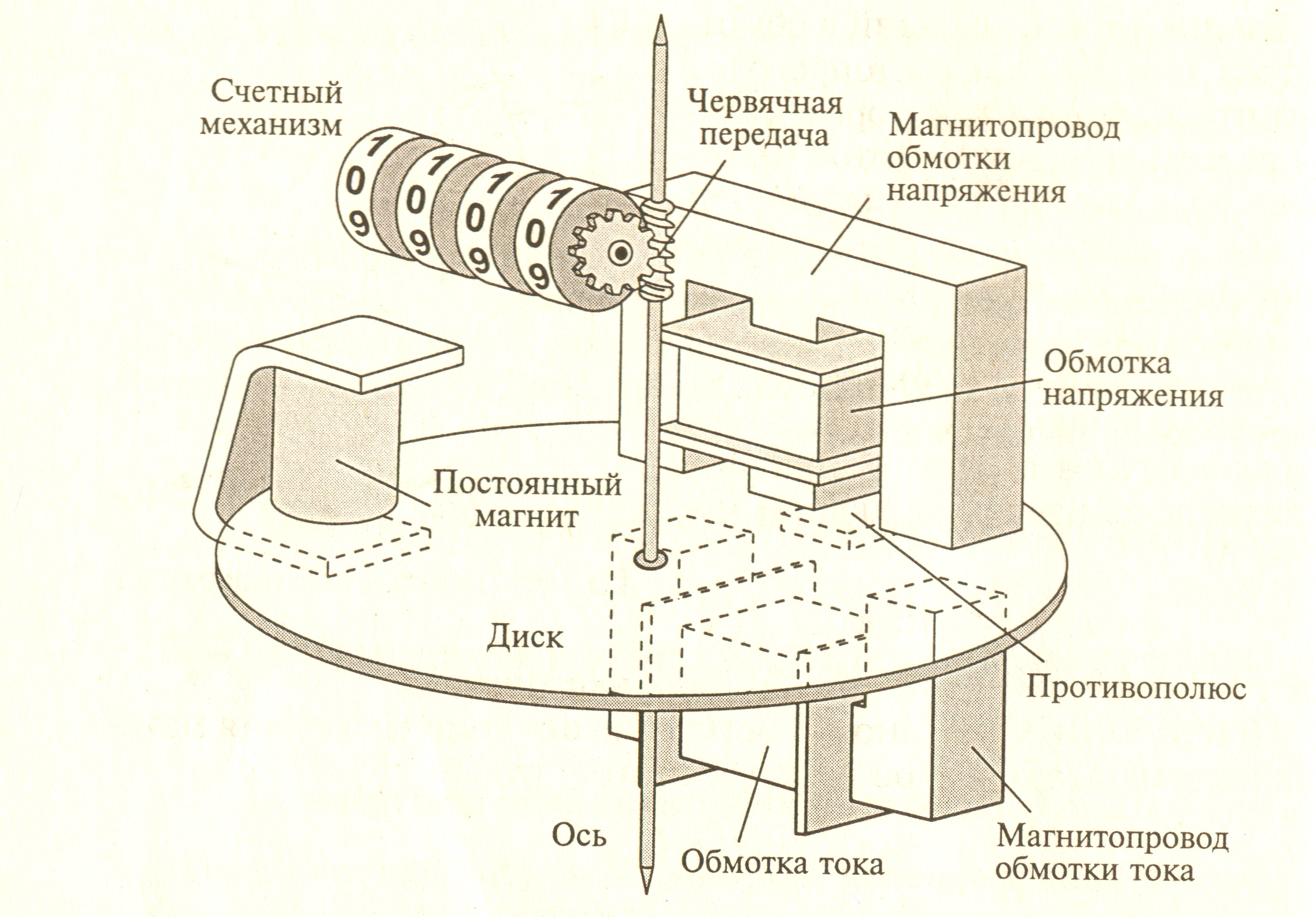
Рис.12.4. Упрощенная конструкция индукционного однофазного счетчика.
Схема (рис. 12.5) поясняет принцип действия этого прибора.
Основными элементами счетчика являются: электромагниты 1 и 2, называемые, соответственно, параллельным и последовательным электромагнитом; алюминиевый диск, укрепленный на оси; постоянный магнит; счетный механизм и др. Схемы включения счетчика и ваттметра одинаковы. Обмотка электромагнита 2 выполняется из небольшого числа витков относительно толстого провода и включается в цепь последовательно с нагрузкой. Обмотка электромагнита 1, имеющая большое число витков, выполняется из тонкого провода и включается параллельно нагрузке.
Ток I2 в последовательной цепи счетчика создает магнитный поток ФI, который проходит через сердечник электромагнита 2, через сердечник электромагнита 1 и дважды пересекает диск. Ток I1 в параллельной цепи счетчика создает потоки ФU и ФL. Первый пересекает диск в одном месте (в середине между полюсами электромагнита 2). Поток ФL замыкается через боковые стержни электромагнита 1, не пересекает диска и непосредственного участия в создании вращающего момента не принимает. Называется он нерабочим магнитным потоком параллельной цепи в отличие от потока ФU , называемого рабочим.
Из-за больших воздушных зазоров на пути потоков ФI и ФU можно с достаточным приближением считать зависимость между этими потоками и токами I2 и I1 линейной, т.е.
ФI = kI I2; ФU = kU I1 = kU .
где U1 – напряжение на параллельной обмотке; ZU – полное сопротивление параллельной обмотки.
Ввиду малости активного сопротивления параллельной обмотки по сравнению с ее индуктивным сопротивлением ХU можно принять ZUХU = 2fLU, где LU - индуктивность обмотки.
Тогда
ФU = kU U1 / 2fLU = .
Вращающие моменты от взаимодействия потока ФU и тока I1, и потока ФI и тока I2, определяют вращающий момент, действующий на подвижную часть. Вывод формулы вращающего момента давать не буду, а напишу сразу окончательную формулу вращающего момента, которая выглядит следующим образом:
Мвр = kвр U1 I2 sin ,
где kвр = с kI ; - сдвиг фаз между магнитными потоками ФU и ФI .
Если вектор тока I2 в последовательной обмотке отстает (предполагается индуктивный характер нагрузки) от вектора напряжения сети U1 на угол , то = / 2 - и sin = cos (добиваются специальными конструктивными мерами).
Тогда можно записать:
Мвр = kвр U1 I2 cos = kвр Р,
т.е. вращающий момент счетчика пропорционален мощности переменного тока.
Для создания противодействующего момента, называемого в счетчиках тормозным, применяется постоянный магнит, между полюсами которого находится диск. Тормозной момент Мт создается от взаимодействия поля постоянного магнита с током в диске, образующемся при вращении диска в поле магнита.
Мт = kт ,
где – угловая скорость диска.
При установившейся равномерной угловой скорости диска Мвр = Мт можно записать
kвр Р = kт или Рdt =( kт / kвр ) d .
Интегрируя это последнее равенство в пределах интервала времени t = t2 – t1, получим Pt = W = CN,
где W – энергия, израсходованная в цепи за интервал времени t; N – число оборотов диска за этот же интервал времени; С – постоянная счетчика энергии, равная:
С = 2 kт / kвр .
Отсчет энергии производится по показаниям счетного механизма – счетчика оборотов (рис. 12.4). Единице электрической энергии (обычно 1кВтч), регистрируемой счетным механизмом, соответствует определенное число оборотов подвижной части счетчика. Это соотношение, называемое передаточным числом А, указывается на счетчике.
Величина, обратная передаточному числу, т.е. отношение зарегистрированной энергии к числу оборотов диска, называется номинальной постоянной счетчика Сн (Сн = W / N). Значения А и Сн зависят только от конструкции счетного механизма и для данного счетчика остаются неизменными.
Под действительной постоянной счетчика С понимается количество энергии, действительно израсходованной в цепи за один оборот подвижной части. Эта энергия может быть измерена образцовыми приборами, например, ваттметром и секундомером.
Действительная постоянная в отличие от номинальной, зависит от режима работы счетчика, а также от внешних условий, например, температуры, частоты и т.д. Зная значение постоянных С и Сн , можно определить относительную погрешность счетчика по формуле
,
где – энергия, измеренная счетчиком, а W – действительное значение энергии, израсходованной в цепи.
По точности счетчики активной энергии делятся на классы точности 0.5, 1.0, 2.0, 2.5.
Совокупность двух или трех однофазных измерительных механизмов образуют трехфазный счетчик.
Промышленностью выпускаются счетчики типов:
Счетчики активной энергии СА3 - для трехпроводных цепей и СА4 для четырехпроводных цепей.
Электронные счетчики электрической энергии (ЭС).
ЭС обладают лучшими метрологическими характеристиками. В основу их работы положено использование статического преобразователя мощности в постоянное напряжение. При этом применяется двойная модуляция с преобразованием напряжения в частоту электрических импульсов и последующим интегрированием. Структурная схема ЭС активной энергии переменного тока (рис.12.6) содержит преобразователь мощности в напряжение (ПМН), преобразователь напряжения в частоту (ПНЧ) и счетчик импульсов (СИ).
ПМН содержит блоки широтно-импульсной (ШИМ) и амплитудно-импульсной (АИМ) модуляции. На вход блока ШИМ поступает напряжение, пропорциональное току нагрузки Iн, а на вход блока АИМ – напряжение на нагрузке Uн. С помощью схемы ШИМ напряжение U1 преобразуется в последовательность прямоугольных импульсов переменной длительности. С изменением величины U1 изменяется отношение разности длительностей импульсов Ти и интервалов между ними Тп к их сумме, т.е.
,
где k – постоянный коэффициент; ; - период следования импульсов.
Так как амплитуда импульсов в схеме АИМ изменяется пропорционально напряжению на нагрузке, а их длительность функционально связана с током нагрузки, в блоке АИМ производится перемножение входных сигналов. Среднее значение напряжения U3 на выходе схемы АИМ пропорционально активной мощности Рн. С помощью ПНЧ напряжение U3 преобразуется в частоту импуль�сов, которая, таким образом, пропорциональна мощности Рн.
Выходные импульсы ПНЧ подсчитываются счетчиком импульсов СИ, т. е. тем самым производится их интегрирование. Следователь�но, показания СИ пропорциональны активной энергии W.
Серийно выпускаемые в настоящее время электронные счетчики активной энергии переменного тока имеют класс точности 0,5 и выше.
PAGE 8
~U1 I1
2
~U2
1
1
1
N
S
Неподвижный
стержневой
магнитопровод
Неподвижный
П – образный
магнитопровод
Диск
Опора
Опора
Ось
Постоянный
магнит
Счетный
механизм
Рис. 12.5.
1
2
Контроль коэффициента мощности