Описание и минимизация логических функций

PAGE 2

Дисциплина «Микроконтроллеры в системах упарвления», 3-й курс, семестр 6. Модуль 1 – Тема 2

Модуль 1 – Тема 2 Описание и минимизация логических функций

2.1 Способы задания логических функций

Словесный. В словесной форме выражается взаимосвязь между аргументами функции и ее значениями.

Пример: функция трех аргументов принимает значение “1”, когда любые два или более аргументов функции равны “1”.

№ набора
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Табличный. Состоит в построении таблицы истинности, содержащей значения функции для всех наборов значений аргументов.

Количество наборов ,

где n – количество аргументов.

Аналитический. Функция задается в виде алгебраического уравнения, в котором логические переменные связаны логическими операциями. Используются две формы записи:

ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений аргументов. Каждое логическое произведение образуется таким набором аргументов, для которого функция равна 1. В данном примере по таблице истинности получаем такую запись в виде ДНФ:

;

КНФ – конъюнктивная нормальная форма - это логическое произведение логических сумм аргументов; для функции из примера получаем:

Если в каждом произведении в функции вида ДНФ присутствуют все аргументы функции, то такая запись называется СДНФ – совершенная ДНФ. Входящие в запись произведения называются минтермами.

Если в суммах функции вида КНФ участвуют все аргументы функций, то такая запись называется СКНФ – совершенная КНФ, а сами суммы - макстермами.

Функция может быть записана в КНФ в виде суммы произведений, но при этом каждое произведение характеризует нулевые значения функции.

4) Использование карт Карно

Карта Карно – это прямоугольная таблица, содержащая клеток, где - количество аргументов функции. В каждой клетке проставляют значение функции, соответствующее определенному минтерму. Правило расположения аргументов по таблице такое, что конъюнкции, соответствующие соседним клеткам, отличаются только одним аргументом. Пример заполнения карты Карно для функции двух аргументов, показан на рис. 2.1.


0	0	0
0	1	1
1	0	1
1	1	0
0	1
1	0

Рисунок 2.1 – Пример заполнения карты Карно для функции двух аргументов

Для каждого аргумента функции можно выделить область на карте Карно, в которой все клетки соответствуют произведениям с прямыми (т.е. неинверсными) значениями этого аргумента. Такие области принято отмечать чертой с указанием рассматриваемого аргумента.

Рис. 2.2. содержит пример заполнения карты Карно для функции трех аргументов. Цифры в правом углу клетки отмечают номер набора значений аргументов, соответствующего данной клетке. Как видно, в каждой клетке проставляется значение функции, соответствующее этому набору.

				№ набора
0	0	0	0	0
0	0	1	0	1
0	1	0	0	2
0	1	1	1	3
1	0	0	0	4
1	0	1	1	5
1	1	0	1	6
1	1	1	1	7

Рисунок 2.2 – Пример заполнения карты Карно для функции трех аргументов

2.2 Основы синтеза комбинационных схем

В процессе синтеза схемы комбинационного устройства выполняют следующие шаги:

по словесному описанию функции составляют таблицу истинности;
по таблице истинности формируют аналитическую запись или аналитическое выражение в ДНФ (КНФ);
выполняют минимизацию исходной логической функции:

а) с использованием алгебры логики (аналитически);

б) с помощью карт Карно.

по минимизированной функции строят принципиальную схему устройства в заданном или оптимальном логическом базисе.

Цель минимизации – получение логической функции с минимальным количеством операций. Благодаря минимизации некоторые аргументы функции могут быть исключены из записи логического уравнения.

Получение таблицы истинности и запись логической функции в виде алгебраического уравнения были рассмотрены ранее. Подробнее рассмотрим методы минимизации логических функций.

2.3 Минимизация в аналитическом виде

Аналитическая минимизация производится на основе законов Булевой алгебры, представленных в табл. 2.1.

Таблица 2.1

Закон алгебры логики	Запись для ДНФ	Запись для КНФ
Закон склеивания
Закон поглощения

Рассмотрим аналитическую запись исходной функции:

Последнее произведение можно сгруппировать с любым из трех предыдущих и использовать закон склеивания. Вводим избыточность на основе тождества

2.4 Минимизация с помощью карт Карно

Закон склеивания по карте Карно реализуется в том, что на карте прорисовываются прямоугольные контуры, содержащие единицы в строго соседних ячейках.

Логическая функция в минимизированной форме записывается на основе уравнений этих контуров путем исключением тех аргументов, которые изменяются в пределах контура (т.е. входят в соседние клетки в прямом и инверсном виде).

Правила формирования контуров:

количество клеток, входящих в контур – 2, 4, 8, 16;
одна клетка может входить в несколько контуров;
количество контуров должно быть минимальным, а их площадь
максимальна;
соседними считаются и те клетки, которые находятся на противоположных краях таблицы.

Минимизированная функция получается как сумма конъюнкций, описывающих эти контуры.

Минимизация функции из рассматриваемого примера на основе карты Карно показана на рис. 2.3.

Контур описывается функцией ;

контур – ; контур – ;

Минимизированная функция имеет вид

Рисунок 2.3 – Пример минимизации логической функции трех аргументов

Размещение аргументов относительно карты Карно может быть любым, но следует соблюдать правило о соседних клетках (см. рис. 2.4).

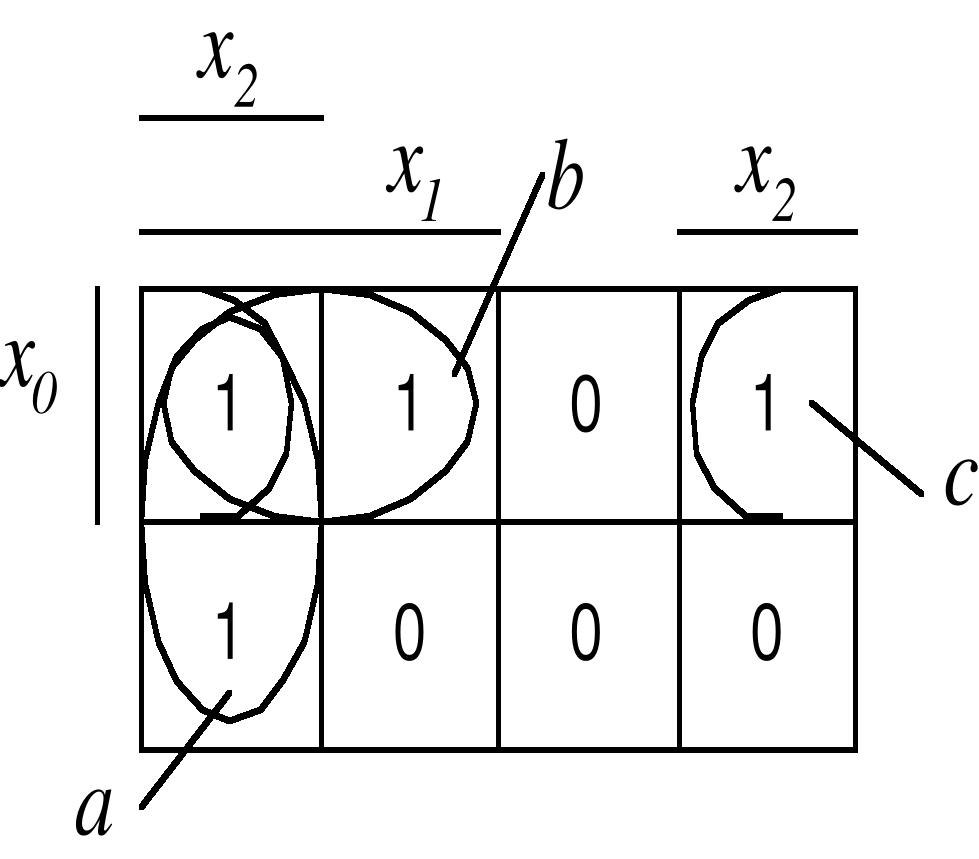
Рисунок 2.4 – Варианты заполнения карты Карно для функции из примера

Контура описываются такими уравнениями: контур ; контур ; контур . Результирующая функция имеет аналогичный вид:

Пример размещения аргументов на карте Карно для функции четырех аргументов показан на рис. 2.5:

Рисунок 2.5 – Пример карты Карно для функции четырех аргументов

2.5 Реализация функции в заданном логическом базисе

Наиболее простой является реализация функции в базисе (И, ИЛИ, НЕ). Реализация оптимальным набором элементов означает, что можно использовать элементы с любым необходимым количеством входов (до восьми); схема устройства для функции из рассматриваемого примера показана на рис. 2.6.

Рисунок 2.6 – Реализация функции из примера в базисе (И, ИЛИ, НЕ).

Для построения схемы в базисе (И-НЕ) необходимо преобразовать логическое уравнение, используя двойное отрицание и правило де Моргана

Как видно, полученное выражение содержит только операции конъюнкции и инверсии, что согласуется с заданным логическим базисом. Схема устройства в соответствии с этим выражением представлена на рис. 2.7.

Рисунок 2.7 – Реализация функции из примера в базисе (И-НЕ).

Если требуется реализовать функцию из однотипных элементов в определенном базисе (например, (И-НЕ)), то трехвходовый элемент на рис.2.7 нужно заменить группой двухвходовых в соответствии с выражением:

Реализация этого выражения представлена на рис.2.8.

Рисунок 2.8 – Реализация функции из примера в базисе (И-НЕ)
только на двухвходовых элементах 2И-НЕ.

Правильный выбор логического базиса для реализации логической функции, как правило, позволяет сократить количество микросхем при изготовлении физического цифрового устройства.

Автор конспекта доцент каф. 301 Джулгаков В.Г.

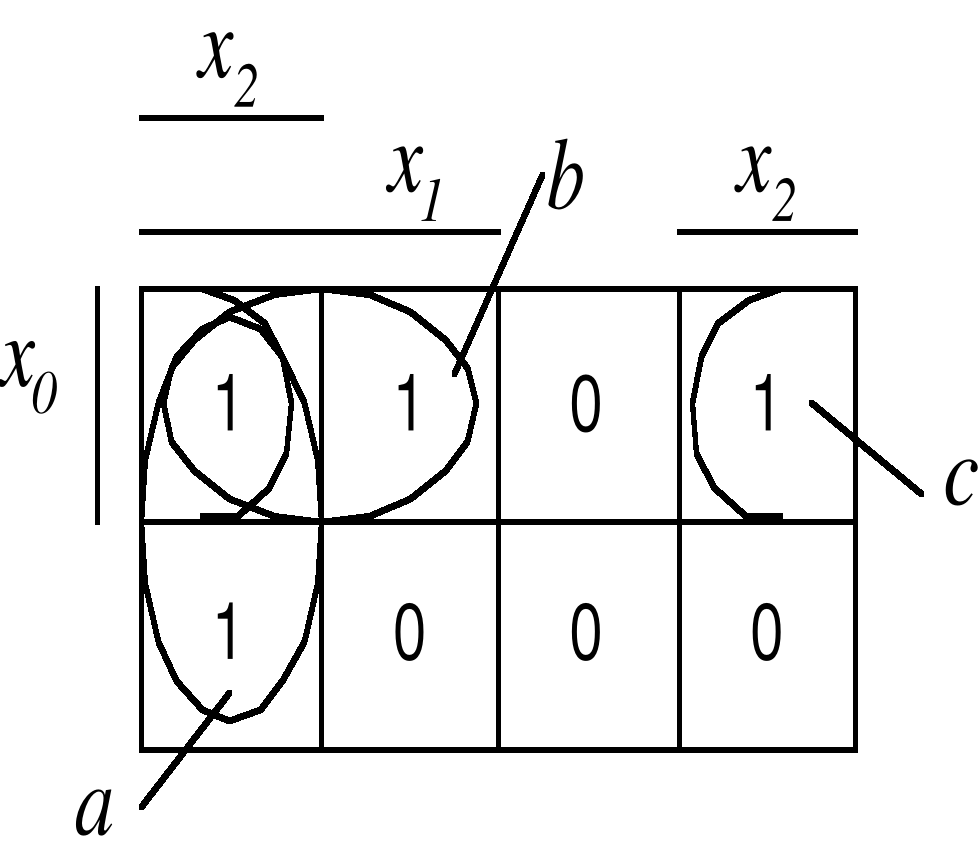
EMBED Visio.Drawing.5

Описание и минимизация логических функций