Имитационное моделирование

PAGE 8

Моделирование

Моделирование является общепризнанным средством познания действительности. Этот процесс состоит из двух больших этапов: разработки модели и анализа разработанной модели. Моделирование позволяет исследовать суть сложных процессов и явлений с помощью экспериментов не с реальной системой, а с ее моделью. Известно, что для принятия разумного решения по организации работы системы не обязательно знание всех характеристик системы, всегда достаточен анализ ее упрошенного, приближенного представления.

В области создания новых систем моделирование является средством исследования важных характеристик будущей системы на самых ранних стадиях ее разработки. С помощью моделирования возможно исследовать узкие места будущей системы, оценить производительность, стоимость, пропускную способность — все главные ее характеристики еще до того, как система будет создана. С помощью моделей разрабатываются оптимальные операционные планы и расписания функционирования существующих сложных систем. В организационных системах имитационное моделирование становится основным инструментом сравнения различных вариантов управляющих решений и поиска наиболее эффективного из них как для решений внутри цеха, организации, фирмы, так и на макроэкономическом уровне.

Модели сложных систем строятся в виде программ, выполняемых на компьютере. Компьютерное моделирование существует почти 50 лет, оно возникло с появлением первых компьютеров. С тех пор сложились две перекрывающиеся области компьютерного моделирования, которые можно охарактеризовать как математическое моделирование и имитационное моделирование.

Математическое моделирование связано, в основном, с разработкой математических моделей физических явлений, с созданием и обоснованием численных методов. Существует академическая трактовка моделирования как области вычислительной математики, которая является традиционной для активности прикладных математиков. В России сложилась сильная школа в этой области: НИИ Математического Моделирования РАН — головная организация, Научный Совет РАН по проблеме "Математическое моделирование", издается журнал "Математическое моделирование" (www.imamod.ru).

Имитационное моделирование — это разработка и выполнение на компьютере программной системы, отражающей поведение и структуру моделируемого объекта. Компьютерный эксперимент с моделью состоит в выполнении на компьютере данной программы с разными значениями параметров (исходных данных) и анализе результатов этих выполнений.

Проблемы разработки имитационных моделей

Имитационное моделирование — очень обширная область. Можно по-разному подходить к классификации решаемых в ней задач. В соответствии с одной из классификаций эта область насчитывает в настоящее время четыре основных направления:

моделирование динамических систем,
дискретно-событийное моделирование,
системная динамика
агентное моделирование.

В каждом из этих направлений развиваются свои инструментальные средства, упрощающие разработку моделей и их анализ. Данные направления (кроме агентного моделирования) базируются на концепциях и парадигмах, которые появились и были зафиксированы в инструментальных пакетах моделирования несколько десятилетий назад и с тех пор не менялись.

Моделирование динамических систем

Направлено на исследование сложных объектов, поведение которых описывается системами алгебро-дифференциальных уравнений. Инженерным подходом к моделированию таких объектов 40 лет назад была сборка блок-схем из решающих блоков аналоговых компьютеров: интеграторов, усилителей и сумматоров, токи и напряжения в которых представляли переменные и параметры моделируемой системы. Этот подход и сейчас является основным в моделировании динамических систем, только решающие блоки являются не аппаратными, а программными. Он реализован, например, в инструментальной среде Simulink.

Дискретно-событийное моделирование

В нем рассматриваются системы с дискретными событиями. Для создания имитационной модели такой системы моделируемая система приводится к потоку заявок, которые обрабатываются активными приборами. Например, для моделирования процесса обслуживания физических лиц в банке физические лица представляются в виде потока заявок, а работники банка, обслуживающие их представляются активными приборами. Идеология дискретно-событийного моделирования была сформулирована более 40 лет назад и реализована в среде моделирования GPSS, которая с некоторыми модификациями до сих пор используется для обучения имитационному моделированию.

Системная динамика.

Системная динамика – это направление в изучении сложных систем, исследующее их поведение во времени и в зависимости от структуры элементов системы и взаимодействия между ними. В том числе: причинно-следственных связей, петель обратных связей, задержек реакции, влияния среды и других. Основоположником системной динамики является американский ученый Джей Форрестер. Дж. Форрестер применил принципы обратной связи, существующей в системах автоматического регулирования, для демонстрации того, что динамика функционирования сложных систем, в первую очередь производственных и социальных, существенно зависит от структуры связей и временных задержек в принятии решений и действиях, которые имеются в системе. В 1958 году он предложил использовать для компьютерного моделирования сложных систем потоковые диаграммы, отражающих причинно-следственные связи в сложной системе,

В настоящее время системная динамика превратилась в зрелую науку. Общество системной динамики (The- System Dynamics Society, www.systemdynamics.org) является официальным форумом системных аналитиков во всем мире. Ежеквартально выходит журнал System Dynamics Review, ежегодно созываются несколько международных конференций по этим проблемам. Системная динамика как методология и инструмент исследования сложных экономических и социальных процессов изучается во многих бизнес-школах по всему миру..

Агентное моделирование

Агентное моделирование (agent-based model (ABM)) — метод имитационного моделирования, исследующий поведение децентрализованных агентов и то, как такое поведение определяет поведение всей системы в целом. В отличие от системной динамики аналитик определяет поведение агентов на индивидуальном уровне, а глобальное поведение возникает как результат деятельности множества агентов (моделирование «снизу вверх»).

Агентное моделирование включает в себя элементы теории игр, сложных систем, мультиагентных систем и эволюционного программирования, методы Монте-Карло, использует случайные числа.

Существует множество определений понятия агента. Общим во всех этих определениях является то, что агент — это некоторая сущность, которая обладает активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, может взаимодействовать с окружением и другими агентами, а также может изменяться (эволюционировать). Многоагентные (или просто агентные) модели используются для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами, а наоборот, эти глобальные правила и законы являются результатом индивидуальной активности членов группы. Цель агентных моделей — получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении ее отдельных активных объектов и взаимодействии этих объектов в системе.

При создании агентной модели логика поведения агентов и их взаимодействие не всегда могут быть выражены чисто графическими средствами, здесь часто приходится использовать программный код. Для агентного моделирования используются пакеты Swarm и RePast. Примером агентной модели является модель развития города.

В современном мире информационных технологий десятилетие сравнимо с веком прогресса в традиционных технологиях, Но в имитационном моделировании почти без изменения применяются идеи и решения 60-х годов прошлого века. На базе этих идей еще в прошлом веке были разработаны программные средства, которые с незначительными изменениями применяются до сих пор. Разработка имитационных модели с использованием этих программ является весьма сложной и трудоемкой задачей, доступной только высококвалифицированным специалистам и требующей больших временных затрат. Один из разработчиков имитационных моделей Роберт. Шеннон писал: «разработка даже простых моделей требует 5—6 человеко-месяцев и стоит порядка 30 ООО долларов, а сложных — на два порядка больше». Иными словами, трудоемкость построения сложной имитационной модели традиционными методами оценивается в сотню человеко-лет.

Имитационное моделирование традиционными методами реально используется узким кругом профессионалов, которые должны иметь не только глубокие знания в той прикладной области, для которой строится модель, но также глубокие знания в программировании, теории вероятностей и статистике.

Кроме того, проблемы анализа современных реальных систем часто требуют разработки моделей, не укладывающихся в рамки одной единственной парадигмы моделирования. Например, при моделировании системы с преобладающим дискретным типом событий может потребоваться введение переменных, описывающих непрерывные характеристики среды. В парадигму блочной модели потоков данных совершенно не вписываются дискретно-событийные системы, В системно-динамической модели часто возникает необходимость учета дискретных событий или моделирования индивидуальных свойств объектов из разнородных групп. Поэтому использование указанных выше программных средств не отвечает современным требованиям,.

AnyLogic — инструмент имитационного моделирования нового поколения

AnyLogic - программное обеспечение для имитационного моделирования нового поколения, разработано российской компанией The AnyLogic Company (бывшая «Экс Джей Текнолоджис»,- англ. XJ Technologies). Этот инструмент существенно упрощает разработку моделей и их анализ.

Пакет AnyLogic создан с использованием последних достижений информационных технологий: объектно-ориентированный подход, элементы стандарта UML, языка программирования Java, и т.д. Первая версия пакета (Anylogic 4.0) была выпущена в 2000г. К настоящему времени выпущена версия Anylogic 6.9.

Пакет поддерживает все известные методы имитационного моделирования:

Моделирование динамических систем
системная динамика;
дискретно-событийное моделирование;
агентное моделирование.

Рост производительности компьютеров и достижения в информационных технологиях, использованные в AnyLogic, сделали возможным реализацию агентных моделей, содержащих десятки и даже сотни тысяч активных агентов

С помощью AnyLogic стало возможным разрабатывать модели в следующих областях:

производство;
логистика и цепочки поставок;
рынок и конкуренция;
бизнес-процессы и сфера обслуживания;
здравоохранение и фармацевтика;
управление активами и проектами;
телекоммуникации и информационные системы;
социальные и экологические системы;
пешеходная динамика;
оборона.

Модели. Наука и искусство моделирования

Моделирование состоит из трех этапов:

анализ реального явления и построение его упрошенной модели,
анализ построенной модели формальными средствами (например, с помощью компьютера),
интерпретация результатов, полученных на модели, в терминах реального явления.

Первый и третий этапы не могут быть формализованы, их выполнение требует интуиции, творческого воображения и понимания сути изучаемого явления, т. е. качеств, присущих работникам искусства.

1.1. Модели процессов и систем

Современная концепция научного исследования состоит в том, что реальные объекты заменяются их упрощенными представлениями, абстракциями, выбираемыми таким образом, чтобы в них была отражена суть явления, те свойства исходных объектов, которые существенны для решения поставленной проблемы. Построенный в результате упрощения объект называется моделью.

Модель — это упрошенный аналог реального объекта или явления, представляющий законы поведения входящих в объект частей и их связи. Построение модели и ее анализ называется моделированием. В научной работе моделирование является одним из главных элементов научного познания.

В практической деятельности цель построения модели — решение некоторой проблемы реального мира, которую дорого либо невозможно решать, экспериментируя с реальным объектом.

Обычно исходная проблема состоит в анализе существующего или предполагаемого объекта для принятия решения по его управлению. Например, таким объектом может быть географически распределенная система поставщиков сырья, заводов, складов готовой продукции и их транспортные связи. Другой пример — порт для разгрузки танкеров с несколькими терминалами, емкостями для загрузки нефти, пулом нефтеналивных цистерн для вывоза нефти.

При построении модели как заменителя реальной системы выделяются те аспекты, которые существенны для решения проблемы, и игнорируются те аспекты, которые усложняют проблему, делают анализ очень сложным или вообще невозможным. Проблема анализа всегда ставится в мире реальных объектов. В примере с портом это может быть проблема оптимального использования существующих ресурсов (организация движения танкеров в акватории порта и использования железнодорожных нефтеналивных цистерн) для организации перекачки нефти из танкеров и ее отправки потребителям.

Принимать решения по управлению ресурсами, перестраивая реальную систему, экономически нецелесообразно. Другой путь решения — сформулировать эту проблему для модели, которую составят схема порта, объемы нефтеналивных емкостей, скорости разгрузки, средняя интенсивность прибытия танкеров, среднее время оборачиваемости цистерн и т. п..

Реальные объекты и ситуации обычно сложны, и модели нужны для того, чтобы ограничить эту сложность, дать возможность понять ситуацию, понять тенденции изменения ситуации (спрогнозировать будущее поведение анализируемой системы), принять решение по изменению будущего поведения системы и проверить его. Если модель отражает свойства системы, существенные для решения конкретной проблемы, то анализ модели позволяет вывести характеристики, которые объяснят известные и предскажут новые свойства исследуемой реальной системы без экспериментов с самой системой. С помощью моделирования получено множество впечатляющих результатов в науке, технике и на производстве.

1.2. Моделирование для поддержки принятия управленческих решений

Принятие разумных решений по рациональной организации и управлению современными системами становится невозможным на основе обычного здравого смысла или интуиции из-за возрастающей сложности систем. Еще в 1969 г. известный ученый, родоначальник системной динамики Джей Форрестер отмечал, что на основе интуиции для управления сложными системами чаще выбираются неверные решения, чем верные , и это происходит потому, что в сложной системе причинно-следственные отношения ее параметров не являются простыми и ясными. В литературе имеется большое число примеров, показывающих, что люди неспособны предвидеть результат их воздействий в сложных системах. Примером может служить каскадное развитие аварий в энергосистемах Северо-Запада США 16 августа 2003 г. и в Московском регионе 25 мая 2005 г., приведших к миллиардным потерям и затронувшим миллионы людей.

Повышение производительности и надежности, уменьшение стоимости и рисков, оценка чувствительности системы к изменениям параметров, оптимизация структуры — все эти проблемы встают как при эксплуатации существующих, так и при проектировании новых технических и организационных систем. Трудность понимания причинно-следственных зависимостей в сложной системе приводит к неэффективной организации систем, ошибкам в их проектировании, большим затратам на устранение ошибок. Сегодня моделирование становится единственным практическим эффективным средством нахождения путей оптимального (либо приемлемого) решения проблем в сложных системах, средством поддержки принятия ответственных решений.

Моделирование особенно важно именно тогда, когда система состоит из многих параллельно функционирующих во времени и взаимодействующих подсистем. Такие системы наиболее часто встречаются в жизни. Каждый человек мыслит последовательно, даже очень умный человек в конкретный момент времени обычно может думать только об одном деле. Поэтому понимание одновременного развития во времени многих влияющих друг на друга процессов является для человека трудной задачей. Имитационная модель помогает понять сложные системы, предсказать их поведение и развитие процессов в различных ситуациях и, наконец, дает возможность изменять параметры и даже структуру модели, чтобы направить эти процессы в желаемое русло. Модели позволяют оценить эффект планируемых изменений, выполнить сравнительный анализ качества возможных вариантов решений. Такое моделирование может осуществляться в реальном времени, что позволяет использовать его результаты в различных технологиях (от оперативного управления до тренинга персонала).

1.3. Уровни абстракции и адекватность модели

Основной парадокс моделирования состоит в том, что изучается упрощенная модель системы, а полученные выводы применяются к исходной реальной системе со всеми ее сложностями. Является ли такая подмена правомерной?

При изучении естественных объектов исследователь абстрагируется от несущественных, случайных деталей, которые не просто усложняют, но могут и затемнить само явление. Например, при анализе нефтеналивного порта удобно говорить о танкерах как о емкостях, из которых производится перекачка определенного объема нефти с некоторой скоростью, а не как о кораблях с каютами, определенной численностью экипажа и т. п. Поскольку все абстракции неполны и неточны, можно говорить только о приближенном соответствии реальности тех результатов, которые получены исследованием моделей. Соответствие модели моделируемому объекту или явлению при решении конкретной проблемы называется адекватностью. Адекватность определяет возможность использования приближенных результатов, полученных на модели, для решения практической проблемы реального мира. Часто адекватность модели определяется рядом условий и ограничений на сущности реального мира, и для того чтобы использовать результаты анализа, полученные на модели, необходимо тщательно проверять (или даже обеспечивать) эти ограничения и условия при функционировании реальной системы (например, чтобы сделать процессы в обществе управляемыми, создается вертикаль власти). Поскольку адекватность модели определяется только возможностью использования модели для решения конкретной проблемы, адекватная модель не обязательно должна досконально отображать процессы, происходящие в моделируемой системе (или, что то же самое, модель не обязательно должна отображать "физически правильную" картину мира).

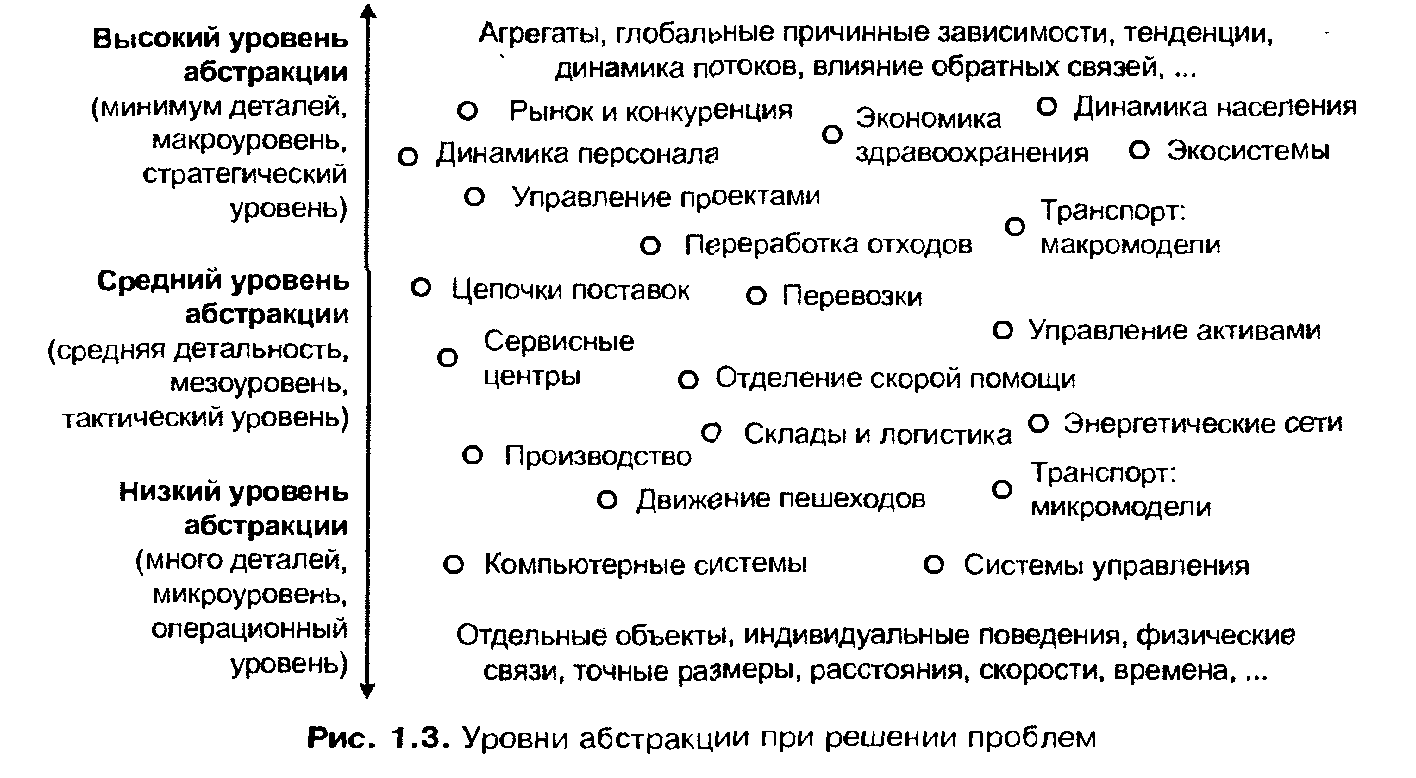
На рис. 1.3 представлена шкала уровней абстракции и примеры проблем моделирования в конкретных областях, приблизительно расставленные на этой шкале. На нижнем уровне абстракции решаются проблемы, в которых важны отдельные физические объекты, их индивидуальное поведение и физические связи, точные размеры, расстояния, времена. Примерами моделей, относящихся к этому уровню абстракции, являются модели движения пешеходов, модели движения механических систем и их систем управления. На среднем уровне обычно решаются проблемы массового производства и обслуживания, здесь представляются отдельные объекты, но их физическими размерами пренебрегают; значения скоростей и времен усредняются или используются их стохастические значения. Примерами моделей на этом уровне абстракции являются модели массового обслуживания, модели движения транспорта, модели управления ресурсами. Высокий уровень абстракции используется при разработке моделей сложных систем, в которых исследователь абстрагируется от индивидуальных объектов и их поведений, рассматривая только совокупности объектов и их интегральные, агрегированные характеристики, тенденции изменения значений, влияние на динамику системы причинных обратных связей. Модели рынка и динамики народонаселения, экологические модели и классические модели распространения эпидемий построены на этом уровне абстракции.

Для каждой цели исследования даже одного и того же объекта реального мира должна быть построена своя модель, которая соответствует этой цели. Для решения конкретной задачи будет удобна модель, адекватно отражающая структуру объекта и законы, по которым он функционирует на выбранном уровне абстракции. Например, очевидно, что планеты не материальные точки, но при такой абстракции в рамках ньютоновской теории тяготения можно достаточно точно предсказать характеристики движения планет. Однако эта модель требует уточнения для расчета траекторий спутников и ракет. Для решения проблемы оптимального использования транспорта необходимы подробные карты, расстояния и времена. То, что Земля на карте представляется плоской, не существенно для решения транспортных проблем.

Хотя существуют устоявшиеся подходы к выбору уровня абстракции и разумные объяснения данного выбора для построения достаточно адекватных моделей при решении многих типов проблем, все же общей методики построения модели с требуемым уровнем адекватности не существует. В качестве рекомендации по выбору уровня абстракции можно сказать лишь следующее. Нужно начать с наиболее простой модели, отражающей только самые существенные (с точки зрения исследователя) аспекты моделируемой системы. После обнаружения неадекватности модели, т. е. неприменимости ее к решению поставленной проблемы, отдельные подструктуры и процессы модели следует реализовать более детально, на более низком уровне абстракции. Можно быть уверенным, что разработка последовательности усложняющихся все более подробных моделей может привести к обеспечению приемлемой адекватности при решении любой конкретной задачи.

о моделируемом объекте. Например, никакая модель не может представить все характеристики планеты Земля. С другой стороны, очевидно также, что любая конкретная задача не потребует для своего решения знания всех этих характеристик.

Конечно, можно построить модели, которые абстрагируются от существенных аспектов реальности. Такие модели будут неадекватными, а выводы, полученные на основе этих моделей, будут неверными.

Очевидно, что никакая модель никогда не дает полных знаний

1.4. Моделирование как наука и искусство

Моделирование как вид профессиональной деятельности связано с анализом реальных систем и процессов самой разной природы. Специалист по моделированию при разработке модели в конкретной области должен связать словарь этой области с терминологией моделирования, выделить подсистемы и их связи в реальной системе, определить параметры подсистем и их зависимости, выбрать подходящий уровень абстракции при построении модели каждой подсистемы. Он должен грамотно выбрать подходящий математический аппарат и корректно его использовать, уметь реализовать элементы модели, их связи и логические отношения подходящими средствами в среде моделирования, понимать ограничения при интерпретации результатов моделирования, владеть методами верификации и калибровки моделей. Все это делает моделирование серьезной научной деятельностью.

Но моделирование является также и искусством, причем в значительно большей мере, чем им является, например, программирование. Универсального общего способа построения адекватных моделей не существует. Хотя для многих физических явлений давно разработаны адекватные модели, достаточные для решения широкого класса задач анализа динамических систем (например, связь скорости, расстояния и времени при анализе свободного перемещения объектов в пространстве), однако для производственных, социальных, биологических систем, а также многих технических систем при конструировании модели нужно проявить изобретательность, знание математики, понимание процессов в системе, сути абстрагирования и т. п. По-строение модели — созидательная креативная деятельность сродни искусству, она требует интуиции, глубокого проникновения в природу явления и решаемой проблемы.

Виды моделей

Модели можно классифицировать по различным признакам: статические и динамические, непрерывные и дискретные, детерминированные и стохастические, аналитические и имитационные и т. д.

2.1. Статические и динамические модели

Статические модели оперируют характеристиками и объектами, не изменяющимися во времени. В динамических моделях, которые обычно более сложны, изменение параметров во времени является существенным. Модель нефтеналивного порта является динамической: в ней моделируется поведение во времени отдельных объектов системы: движение танкеров в акватории порта, движение цистерн на причале, уровень нефти в накопителях.

Статические модели обычно имеют дело с установившимися процессами, уравнениями балансового типа, с предельными стационарными характеристиками. Моделирование динамических систем состоит в имитации правил перехода системы из одного состояния в другое с течением времени. Под состоянием системы понимается набор значений существенных параметров и переменных системы. Изменение состояния системы во времени в динамических системах — это изменение значений переменных системы в соответствии с законами, определяющими связи переменных и их зависимости друг от друга во времени.

Пакет AnyLogic поддерживает разработку и анализ динамических моделей. Этот инструмент содержит средства для аналитического задания уравнений, описывающих изменение переменных во времени, дает возможность учета модельного времени и содержит средства его продвижения, здесь также имеется язык для выражения логики и описания прогресса систем под влиянием любого типа событий, в частности, исчерпания таймаута — заданного интервала времени.

2.2. Непрерывные, дискретные и гибридные модели

Реальные физические объекты функционируют в непрерывном времени, и для изучения многих проблем физических систем их модели должны быть непрерывными. Состояние таких моделей изменяется непрерывно во времени. Это модели движения в реальных координатах, модели химического производства и т. п. Процессы движения объектов и процессы перекачки нефти в модели нефтеналивного порта являются непрерывными.

На более высоком уровне абстракции для многих систем адекватными являются модели, в которых переходы системы из одного состояния в другое можно считать мгновенными, происходящими в дискретные моменты времени. Такие системы называются дискретными. Примером мгновенного перехода является изменение числа клиентов банка или количества покупателей в магазине. Очевидно, что дискретные системы — это абстракция, процессы в природе не происходят мгновенно. В реальный магазин реальный покупатель входит в течение некоторого времени, он может застрять в дверях, колеблясь, войти или нет, и всегда существует непрерывная последовательность его положения во время прохождения дверей магазина. Однако при построении модели магазина для оценки, например, средней длины очереди в кассу при заданном потоке покупателей и известных характеристиках обслуживания кассиром клиентов можно абстрагироваться от этих второстепенных явлений и считать систему дискретной: результаты анализа полученной дискретной модели обычно достаточно точны для принятия обоснованных управленческих решений для подобных систем. В модели нефтеналивного порта мгновенными можно считать, например, переходы светофоров на входе в гавань из состояния "запрещено" в состояние "разрешено". На еще более высоком уровне абстракции при анализе систем также используются непрерывные модели, что характерно для системной динамики. Потоки машин на автострадах, потребительский спрос, распространение инфекции среди населения часто удобно описывать с помощью взаимозависимостей непрерывных переменных, описывающих количества, интенсивности изменения этих количеств, степени влияния одних количеств на другие. Соотношения таких переменных выражаются обычно дифференциальными уравнениями.

Во многих случаях в реальных системах присутствуют оба типа процессов, и если оба они являются существенными для анализа системы, то и в модели одни процессы должны представляться как непрерывные, другие — как дискретные. Такие модели со смешанным типом процессов называются гибридными. Например, если при анализе функционирования магазина существенным является не только количество покупателей, но и пространственное их положение и перемещение покупателей, то модель в этом случае должна представлять смесь непрерывных и дискретных процессов, т. е. это гибридная модель. Другим примером может служить модель функционирования крупного банка. Поток инвестиций, получение и выдача кредитов в нормальном режиме описывается набором дифференциальных и алгебраических уравнений, т. е. модель является непрерывной. Однако существуют ситуации, например дефолт (дискретное событие), в результате чего возникает паника у населения, и с этого момента система описывается совершенно другой непрерывной моделью. Модель данного процесса на том уровне абстракции, на котором мы хотим адекватно описать оба режима работы банка и переход между режимами, должна включать как описание непрерывных процессов, так и дискретные события, а также их взаимозависимости.

Пакет AnyLogic поддерживает описание как непрерывных, так и дискретных процессов, а также строить гибридные модели.. AnyLogic позволяет реализовать модель, фактически, на любом уровне абстракции (детальности). Выполнение гибридных моделей в AnyLogic основано на современных результатах теории гибридных динамических систем.

2.3. Детерминированные и стохастические модели

При моделировании сложных реальных систем исследователь часто сталкивается с ситуациями, в которых случайные воздействия играют существенную роль. Стохастические модели, в отличие от детерминированных, учитывают вероятностный характер параметров моделируемого объекта. Например, в модели нефтеналивного порта не могут быть определены точно моменты прихода в порт танкеров. Данные моменты являются случайными величинами, потому модель эта является стохастической: значения переменных величин модели, которые зависят от реализаций случайных величин, сами становятся случайными величинами. Анализ подобных моделей выполняется на компьютере на основе статистики, набираемой в ходе имитационных экспериментов при многократном прогоне модели для различных значений исходных случайных величин, выбранных в соответствии с их статистическими характеристиками.

AnyLogic содержит средства для генерации случайных величин и статистической обработки результатов компьютерных экспериментов. AnyLogic включает генераторы случайных чисел для множества распределений. Разработчик модели может использовать также свой собственный генератор случайных величин, построенный в соответствии с данными наблюдений над реальной системой.

2.4. Аналитические и имитационные модели

Использование абстракций при решении проблем с помощью моделей часто состоит в применении того или иного математического аппарата. Простейшими математическими моделями являются алгебраические соотношения, и анализ модели часто сводится к аналитическому решению этих уравнений. Некоторые динамические системы можно описать в замкнутой форме, например, в виде систем линейных дифференциальных и алгебраических уравнений и получить решение аналитически. Такое моделирование называется аналитическим. При аналитическом моделировании процессы функционирования исследуемой системы записываются в виде алгебраических, интегральных, дифференциальных уравнений и логических соотношений, и в некоторых случаях анализ этих соотношений можно выполнить с помощью аналитических преобразований. Современным средством поддержки аналитического моделирования являются электронные таблицы типа MS Excel.

Однако использование чисто аналитических методов при моделировании реальных систем сталкивается с серьезными трудностями: классические математические модели, допускающие аналитическое решение, в большинстве случаев к реальным задачам неприменимы. Например, в модели нефтеналивного порта построить аналитическую формулу для оценки коэффициента использования оборудования невозможно хотя бы потому, что в системе существуют стохастические процессы, есть приоритеты обработки заявок на использование ресурсов, внутренний параллелизм в обрабатывающих подсистемах, прерывания работы и т. п. Даже если аналитическую модель удается построить, для реальных систем они часто являются существенно нелинейными, и чисто математические соотношения в них обычно дополняются логико-семантическими операциями, а для них аналитического решения не существует. Поэтому при анализе систем часто стоит выбор между моделью, которая является реалистическим аналогом реальной ситуации, но не разрешимой аналитически, и более простой, но неадекватной моделью, математический анализ которой возможен.

При имитационном моделировании структура моделируемой системы — ее подсистемы и связи — непосредственно представлена структурой модели, а процесс функционирования подсистем, выраженный в виде правил и уравнений, связывающих переменные, имитируется на компьютере. AnyLogic — это среда имитационного моделирования. Разнообразные средства спецификации и анализа результатов, имеющиеся в AnyLogic, позволяют строить модели, имитирующие работу моделируемой системы фактически с любой желаемой степенью адекватности, и выполнять анализ модели на компьютере без проведения аналитических преобразований.

Имитационное моделирование

3.1. Что такое имитационное моделирование

Имитационное моделирование — это разработка и выполнение на компьютере программной системы, отражающей структуру и функционирование (поведение) моделируемого объекта или явления во времени. Такую программную систему называют имитационной моделью этого объекта или явления. Объекты и сущности имитационной модели представляют объекты и сущности реального мира, а связи структурных единиц объекта моделирования отражаются в интерфейсных связях соответствующих объектов модели. Таким образом, имитационная модель — это упрощенное подобие реальной системы, либо существующей, либо той, которую предполагается создать в будущем. Имитационная модель обычно представляется компьютерной программой, выполнение программы можно считать имитацией поведения исходной системы во времени.

В русскоязычной литературе термин "моделирование" соответствует американскому "modeling" и имеет смысл создание модели и ее анализ, причем под термином "модель" понимается объект любой природы, упрощенно представляющий исследуемую систему. Слова "имитационное моделирование" и "вычислительный (компьютерный) эксперимент" соответствуют англоязычному термину "simulation". Эти термины подразумевают разработку модели именно как компьютерной программы и исполнение этой программы на компьютере.

Итак, имитационное моделирование — это деятельность по разработке программных моделей реальных или гипотетических систем, выполнение этих программ на компьютере и анализ результатов компьютерных экспериментов по исследованию поведения моделей. Имитационное моделирование имеет существенные преимущества перед аналитическим моделированием в тех случаях, когда:

отношения между переменными в модели нелинейны, и поэтому аналитические модели трудно или невозможно построить;
модель содержит стохастические компоненты;
для понимания поведения системы требуется визуализация динамики происходящих в ней процессов;
модель содержит много параллельно функционирующих взаимодействующих компонентов.

Во многих случаях имитационное моделирование — это единственный способ получить представление о поведении сложной системы и провести ее анализ.

Имитационное моделирование