Генетический алгоритм (ГА)
Введение
Генетический алгоритм (ГА) — адаптивный поисковый метод, основанный на се лекции лучших элементов в популяции, подобно эволюционной теории Ч.Дарвина. Свои принципы и терминологию ГА заимствуют из естественной генетики.
Основой для возникновения генетических алгоритмов послужи ли модель биологической эволюции и методы случайного поиска. Основоположниками теории ГА являются Д.Холланд и его коллеги. Изначально он разрабатывался для распознавания образов и оптимизации.
Эволюционный поиск представляет собой последовательное преобразование одного конечного нечетко го множества промежуточных решений в другое. Само преобразование можно назвать алгоритмом генетического поиска, или ГА.
Цели ГА:
абстрактно и формально объяснять адаптацию процессов в есте ственной системе и интеллектуальной исследовательской системе;
моделировать естественные эволюционные процессы для эффек тивного решения оптимизационных задач.
ГА балансируют между эффективностью и качеством решений за счет «выживания сильнейших альтернативных решений» в неопределенных и нечетких условиях.
От других оптимизационных и поисковых процедур ГА отличаются следующим:
работают в основном не с параметрами задачи, а с закодированным множеством параметров;
осуществляют поиск не путем улучшения одного решения, а путем использования сразу нескольких альтернатив на заданном множе стве решений;
используют целевую функцию, а не ее различные приращения для оценки качества принятия решений;
применяют не детерминированные, а вероятностные правила ана лиза оптимизационных задач.
ГА для обработки выбирает множество нату ральных параметров оптимизационной проблемы и кодирует их в по следовательность конечной длины в некотором алфавите. Он работаеют до тех пор, пока не будет выполнено заданное число генераций (ите раций алгоритма) или на некоторой генерации будет получено решение определенного качества, или когда найден локальный оптимум, т. е. возникла преждевременная сходимость и алгоритм не может найти вы ход из этого состояния. В отличие от других методов оптимизации ГА анализируют различные области пространства решений одновременно и поэтому они более приспособлены к нахож дению новых областей с лучшими значениями целевой функции.
Определения и понятия ГА
ГА работает на осно ве начальной информации, в качестве которой выступает популяция альтернативных решений Р.
Популяция Рt = {P1, ..., PNp} – множество элементов Pt, t = 0,1,2... – номер генерации ГА, Np – размер популяции. Каждый элемент этой популяции Pi – одна или несколько хромосом (особей, индивидуальностей) – альтернативных упо рядоченных или неупорядоченных решений. Хромосомы состоят из генов Pi = {g1,…,gv} (элементы, части закодированного решения), и позиции генов в хромосоме называются локус (лоци) для одной позиции, т. е. ген – подэлемент (элемент в хромосоме), локус – позиция в хромосоме, аллель – функциональное значение гена.
Гены могут иметь числовые или функциональные значения. Эти значения берутся из некоторого алфавита. Генети ческий материал элементов обычно кодируется на основе двоичного алфавита {0,1}, но можно использовать буквенные, де сятичные и др. алфавиты.
Пример. Закодированная хромосома длиной девять на основе двоичного алфавита: Pi = (001001101).
В ГА используются родительские элементы (родители), выбиранные из популяции на основе заданных пра вил для смешиванися (скрещивания) для получения потомков. Потомки и родители в результате генерации, т. е. одного цикла (подцикла) эволюции, создают новую популяцию. Генерация – процесс реализации одной итерации алгоритма, называется поколением.
Эволюция популя ции – чередование поколений, в которых хромосомы изменяют свои значения так, чтобы каждое новое поколение наилучшим спосо бом приспосабливалось к внешней среде. Тогда общая генетическая упаковка называется генотипом, а организм формируется посредством связи генетической упаковки с окружающей средой и называется фе нотипом.
Каждый элемент в популяции имеет определенный уровень ка чества, характеризующийся значением целевой функции (функция полезности, приспособленности или пригодности, фитнесс-функции, fitness). Она используется для сравнения альтернативных решений между собой и выбора лучших.
Основная задача ГА – оптимизация целевой функции. Т.е. ГА анализируют популяцию хромосом, представляющих комби нацию элементов из некоторого множества, и оптимизируют целевую функцию, оценивая каждую хромосому. Они ана лизируют и преобразовывают популяции хромосом на основе механиз ма натуральной эволюции. Каждая популяция обладает наследственной изменчивостью,т. е. возможностью случайных откло нений от наиболее вероятного среднего значения целевой функции.
Отклонения описываются нормальным законом распределения случай ных величин. При этом наследственные признаки закрепляются, если они имеют приспособительный характер, т. е. обеспечивают популяции лучшие условия существования и размножения.
Процесс эволюции начинается с начальной популяции, т.е. с создания начального множества конкурирующих между собой решений оптимизационной задачи. Затем эти «родительские» решения создают «потомков» путем случайных и направленных изменений. После этого оценивается эффективность этих решений, и они подвергаются селекции. Принцип «выживания сильнейших» заключается в удалении наименее приспособленных решений.
Традиционные оптимизационные алгоритмы для нахождения луч шего решения используют большое количество допущений при оценке целевой функции. Эволюционный подход не требует таких допущений, что расширяет класс задач, решаемых только с помощью ГА.
ГА актуален при решении практи ческих задач, таких, например, как адаптация к изменяющейся окру жающей среде.
При использовании традиционных методов все вычисления начится заново, приводя к большим затратам машинного времени. При эволюционном подходе популяцию можно анализировать, дополнять и видоизменять приме нительно к изменяющимся условиям, не используя полный перебор. ГА хороши для быстрого полученния достаточно хороших решений.
При решении практических задач с помощью ГА выполняют 4-е предварительных этапа:
выбор способа представления решения;
разработка операторов случайных изменений;
определение способов «выживания» решений;
создание начальной популяции альтернативных решений.
На 1-ом этапе для представления решения в формальном виде требуется структура, позволяющая кодировать любое воз можное решение и производить его оценку. Математически доказано, что не существует идеальной структуры представления, так что для создания хорошей структуры требуется анализ, перебор и эвристиче ские подходы. Возможный вариант представления должен позволять проведение различных перестановок в альтернативных решениях. Для их оценки необходимо определить способ вычисления целевой функции.
На 2-ом этапе выбирается случайный оператор (операторы) для генерации потомков. Например, он может быть аналогичен половому и бесполому размножениям. При половом – два родителя обмениваются генетическим материалом, используемом для создания потомка. Бесполое размножение — это клонирование, при котором происходят различные му тации при передаче информации от родителя к потомку. Или же использовать материал от трех или более родителей, проводить голосование при выборе родителей и пр.
Успех ГА зависит от взаимодействия между собой схемы представления, методов случай ных изменений и способа определения целевой функции, поэтому иногда целесообразно использовать направленные методы.
Примеры способа представления пере становок при решении оптимизационных задач:
1. Используем одного родителя (альтернативное решение) и получать одного потомка. Этот способ всегда генери рует реальное решение.
2. Используем 2-х родителей, случай но выберем точку перестановки и для образования потомка возьмем первый сегмент у первого родителя, а второй сегмент — у второго. Этот способ может генерировать недопустимые решения и следует «восстанавливать» допустимые решения перед их оценкой.
На 3-ем этапе задаются правила вы живания решений для создания потомства. Существует множество способов проведения селекции альтернативных решений, оставляющих только решения с максимальным значением целевой функции, устраняя все остальные. Такое правило часто оказывается малоэффективным при решении сложных технических задач, т.к. иногда лучшие решения происходят от худших, а не только от самых лучших.
Чем «лучше» решение, тем. больше вероятность его выживания.
На 4-ом этапе создается начальная попу ляция. При неполноте исходных данных о проблеме решения могут случайным образом выбираться из всего множества альтернатив. Это реализуется генерацией случайных внутрихромосомных перестановок, каждая из которых представляет собой определенное решение. При создании начальной популяции лучше всего использовать знания о решаемой задаче. Например, эти знания могут быть получены из опыта разработчика, существующих стандартов и библиотек алгорит мов решения задач данного класса.
Эффективность генетического алгоритма — степень реали зации запланированных действий алгоритма и достижение требуемых значений целевой функции. Эффективность во многом определяется структурой и составом начальной популяции. При создании начального множества решений популяция формируется на основе 4-х основных принципов:
«одеяло» — генерирование полной популяции, включая все воз можные решения в некоторой заданной проблемной области;
«дробовик» — случайный выбор альтернатив из всей области решений данной задачи;
«фокусировка» — случайный выбор допустимых альтер натив из заданной области решений поставленной задачи;
«комбинирование» — различные комбинации совместных реализа циях первых трех принципов.
Популяция обязательно является конечным множеством.
Генетические операторы
В каждой генерации ГА хромосомы явля ются результатом применения некоторых генетических операторов.
Оператор — языковая конструкция, представляющая один шаг из последовательности действий или набора описаний алгоритма.
ГА состоит из набора генетических операторов.
Генетический оператор (ГО) — средство отображения одного множества на другое. Т.е. это конструкция, представляющая один шаг из последовательности действий ГА.
Селекция
Оператор репродукции (селекция) — это процесс, посредством которого хромосомы (альтернативные решения), имеющие более высо кое значение целевой функции, получают большую возможность для воспроизводства (репродукции) потомков, чем «худшие» хромосомы. Элементы, выбранные для репродукции, обмениваются генетическим материалом, создавая аналогичных или различных потомков.
Существует множество операторов репродукции, таких как:
Селекция на основе рулетки — простой и широко исполь зуемый в простом ГА метод, в котором каждому элементу популяции соответствует зона на колесе рулетки, пропорционально соразмерная с величиной целе вой функции. При повороте колеса рулетки каждый эле мент имеет некоторую вероятность выбора для селекции. Элемент с большим значением целевой функции имеет большую вероятность для выбора.
Селекция на основе заданной шкалы — метод, в котором популяция предвари тельно сортируется от «лучшей» к «худшей» на основе заданного критерия. Каждому элементу назначается определенное число и селекция выполняется согласно этому числу.
Элитная селекция— метод, выбирающий лучшие (элитные) элементы на основе сравнения значений целевой функции. Далее они вступают в различные преобразования, после которых снова выбираются элитные элементы. Процесс продолжается аналогично до тех пор, пока продолжают появляться элитные элементы.
Турнирная селекция — метод, в котором некоторое число элементов (соглас но размеру «турнира») выбирается случайно или направленно из популяции, и лучшие элементы в этой группе на основе заданного турнира определяются для дальнейшего эволюционного поиска.
Оператор репродукции считается эффективным, если он создает возможность перехода из одной подобласти альтернативных решений области поиска в другую. Это повышает вероятность нахождения гло бального оптимума целевой функции. Выделяют два основных типа реализации оператора репродукции:
случайный выбор хромосом;
выбор хромосом на основе значений целевой функции.
При случайном выборе хромосом частота R образования родитель ских пар не зависит от значения целевой функции хромосом Рtk и полностью определяется численностью популяции N:
где — коэффициент селекции, принимающий значение от 1 до 4 в зависимости от усло вий внешней среды.
Другой способ реализации оператора репродукции связан с ис пользованием значений целевой функции. Существуют две основные стратегии. Стратегия — это оптимальный набор правил и приемов, позволяющих реализовать общую цель, достигнуть глобальных и локальных целей решаемой задачи. В первой предпочтение отдается хромосомам с близкими и «лучшими» (наибольшими при максимиза ции и наименьшими — при минимизации) значениями целевой функ ции. Во второй — хромосомам, со значениями целевой функции, сильно различающимися между собой.
Для реализации 1-ой стратегии с максимизацией целевой функ ции с вероятностью
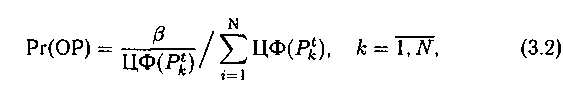
выбирают разные хромосомы. Здесь ЦФ — целевая функция, ОР —оператор репродукции, моделирующий естественный процесс селекции, Рr(ОР) — вероятность выбора хромосом для репродукции.
Вторая стратегия реализуется следующим образом: часть хромосом выбирается слу чайным образом, а вторая — с вероятностью, заданной предыдущей формулой.
Если ЦФ(Рtk) < ЦФср, где ЦФср — среднее значение целевой функ ции в популяции, то оператор репродукции моделирует естественный отбор. Выбор случайных и сильно отличающихся хромосом повышает генетическое разнообразие популяции, что повышает скорость сходи мости ГА на начальном этапе оптимизации и часто позволяет выходить из локальных оптимумов.
Существуют и другие методы селекции, условно разделенные на три группы. К первой отнесятся вероятностные методы. Ко второй — детер минированные методы. К третьей — различные комбинации методов из 1-ой и 2-ой групп.
Основной трудностью решения инженерных оптимизационных задач с большим количеством локальных оптимумов является пред варительная сходимость алгоритмов, т.е. попадание решения в один, не самый лучший, локальный оптимум при наличии их большого количества. Различные методы селекции и их модификации позволяют в некоторых случаях решать про блему предварительной сходимости алгоритмов. Исследователи ГА применяю комбинированные методы селекции с использованием пред варительных знаний о решаемых задачах и предварительных резуль татах.
Кроссинговер
Опе ратор кроссинговера (скрещивания)— языковая конструкция, позволяющая на основе преобразования (скрещивания) хромосом родителей (или их ча стей) создавать хромосомы потомков. Существуют различные oneраторы кроссинговера, т.к. в основном их структура определяет эффективность ГА. Рассмотрим основные операторы кроссинговера и их модификации:
1. Простой (одноточечный) оператор кроссинговера. Перед его началом работы случайным образом определяется точка оператора кроссинговера (разрезающая точ ка оператора кроссинговера), определяющая место в двух хромосомах, где они должны быть «разрезаны».
Например, пусть популяция Р состоит из хромосом P1 и P2, являющиеся родителями Р={P1, P2}, где P1 = (11111) и P2 = (00000). Пусть случайным образом точка оператора кроссинговера расположится между вторым и третьим генами. Тогда, меняя элементы после точки оператора кроссинговера между двумя родителями, создаются 2 новых потомка P’1 и P’2:
|
P1:
|
1
|
1
|
1
|
1
|
1
|
|
P2:
|
0
|
0
|
0
|
0
|
0
|
|
P’1:
|
1
|
1
|
0
|
0
|
0
|
|
P’2:
|
0
|
0
|
1
|
1
|
1
|
2. Двухточечный оператор кроссинговера. В каждой хромосо ме случайным образом определяются 2 точки оператора кроссинговера, и хромосомы обмениваются участками, расположенными между этими точками опе ратора кроссинговера. Например:
|
P1:
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
P2:
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
P’1:
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
|
P’2:
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
Существует много модификаций двухточечного оператора кроссинговера. Развитием двухточечного оператора кроссинговера является много точечный (N-точечный) оператор кроссинговера, действующий по аналогии с ним. Отметим, что увеличении кол-ва «разрезающих» точек может уменьшиться качество родительских свойств.
Пример трехточечного оператора кроссинговера:
|
P1:
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
P2:
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
P’1:
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
|
P’2:
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
3. Упорядоченный оператор кроссинговера. «Разрезаю щая» точка выбирается случайно. Далее левый сегмент P1 копируется в P’1. Остальные позиции P’1 заполняются из P2 в упорядоченном виде (например, слева направо) исключая элементы, уже попавшие в P2. Например:
|
P1:
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
|
P2:
|
G
|
A
|
B
|
E
|
C
|
D
|
F
|
H
|
|
P’1:
|
A
|
B
|
C
|
D
|
G
|
E
|
F
|
H
|
P’2 можно получать различными способами. Например, копируя в левый сегмент P’2 левый сегмент P2, а далее указанным выше методом. Тогда
4. Частично-соответствующий оператор кроссинговера. «Разрезаю щая» точка выбирается произвольно. Далее анализируются сегменты в родительских хромосомах и устанавливается частичное соответствие между элементами 1-го и 2-го родителей с формированием потомков. При этом правый сегмент P2 переносится в правый сегмент P’1, левый сегмент P1 переносится в левый сегмент P’1 с заменой повторяющихся генов на отсутствующие гены из правой части P2 в правой части P1. Например:
|
P1:
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
|
P2:
|
E
|
C
|
I
|
A
|
D
|
H
|
J
|
B
|
F
|
G
|
|
P’1:
|
A
|
H
|
C
|
D
|
E
|
I
|
J
|
B
|
F
|
G
|
Аналогично
|
P1:
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
|
P2:
|
E
|
C
|
I
|
A
|
D
|
H
|
J
|
B
|
F
|
G
|
|
P’2:
|
E
|
C
|
F
|
A
|
D
|
B
|
G
|
H
|
I
|
J
|
5. Циклический оператор кроссинговера выполняет рекомбинации согласно циклам, которые существуют при установлении соответствия между генами первого и второго родителей. Например:
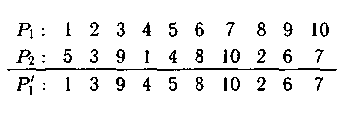
P’1 запол няется, начиная с первой позиции, копируя элемент с первой пози ции P1. Элементу 1 в P1 соответствует элемент 5 в P2. Следовательно, имеем первый путь в цикле (1,5). Элементу 5 в P1 соответствует элемент 4 в P2, откуда второй путь в первом цикле (1,5; 5,4). Про должая далее, получим, что элементу 4 в P1 соответствует элемент 1 в P2. Следовательно, сформирован первый цикл (1,5; 5,4; 4,1). Согласно этому циклу элемент 5 переходит в пятую позицию P’1, а элемент 4 — в четвертую позицию.
Сформируем второй цикл. Элемент 2 в P1 соответствует элементу 3 в P2. Продолжая аналогично, получим второй цикл (2,3; 3,9; 9,6; 6,8; 8,2) и третий (7,10; 10,7) циклы.
Следовательно, в P’1 элемент 3 расположен во втором локусе, т. е. на второй позиции, элемент 9 — в третьем, элемент 6 — в девятом, элемент 8 — в шестом, элемент 2 — в восьмом, элемент 10 — в седьмом и элемент 7 — в десятом локусах. Циклический оператор кроссинго вера и его модификации эффективны для решения ком бинаторно-логических задач, задач на графах и гиперграфах и других оптимизационных задач.
6. Универсальный оператор кроссинговера популярен для решения различных задач теории распи саний. Вместо использования «разрезающих» точкек в универ сальный оператор кроссинговера вводят двоичную маску, длина ко торой равна длине заданных хромосом. Первый потомок получается сложением первого родителя с маской на основе следующих правил: (0 + 0 = 0, 0+1 = 1+0 =1, 1 + 1=0). Второй потомок получается аналогичным образом. Для каждого элемента в P1 и P2 гены меняются, как показано в примере:
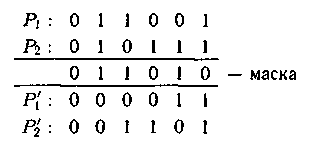
Маска задается или выбирается случайно с заданной вероятностью или на основе генератора случайных чисел. При этом чередование 0 и 1 в маске происходит с вероятностью и 50%. Иногда используется параметризированный универсальный опе ратор кроссинговера, где маска выбирается с вероятностью для 1 или 0 выше, чем 50%. Такой вид маски эффективен, когда хромосомы кодируются в двоичном алфавите.
7. Для решения оптимизационных задач исполь зуются классы алгоритмов, называемы «жадными». Та кой алгоритм на каждом шаге делает локально оптимальный выбор, в надежде, что итоговое решение будет оптимальным. Это не всегда так, но для многих задач такие эвристические алгоритмы дают оптимальный результат. К оптимизационной задаче применим принцип «жадного» выбора, если последовательность ло кально-оптимальных («жадных») выборов дает оптимальное решение.
«Жадный» оператор — это языковая конструкция, создающая новые решения на основе частичного выбора на каждом шаге преобразования локально-оптимального значения целевой функции. Он может быть реализован на двух и более хромосомах, а в пределе — на всей популяции.
Пример «жадного» оператора кроссинговера для нахождения пути с минимальной/максимальной стоимо стью на графе:
- Для всех хромосом популяции вычисляется целевая функция (сто имость пути между всеми вершинами графа). Выбирается заданное число родительских хромосом и случайным образом на одной из хромосом определяется точка «жадного» оператора кроссинговера.
- В выбранной хромосоме для n-го гена, расположенного слева от точки «жадного» оператора кроссинговера, определяется значение частичной целевой функции (например, стоимость пути от выбранного гена к ближайшему, находящемуся справа гену). Анало гично определению стоимости пути от n-го гена во всех остальных хромосомах, выбранных для «жадного» оператора кроссинговера.
- В хромосому «потомок» выбирают тот ген, у которого значение целевой функции выше/ниже при максимизации/минимизации значений целевой функции.
4. Процесс продолжается аналогично, до построения хромосомы «по томок». Если в процессе реализации появляется цикл или тупик, то выбираются нерассмотренные гены с лучшими значениями целевой функции.
Например, пусть задан граф G = (X,U), X = {а, b, с, d,e} в виде матрицы. Построим популяцию Р, состоящую из трех родительских хромосом Р = { P1, P2, P3}, где P1 : abcde; P2 : bdeca; P3 : ebadc. Элементы матрицы определяют стоимость пути между любыми двумя вершинами графа, а каждый ген в хромосоме кодируется номером вершины графа:
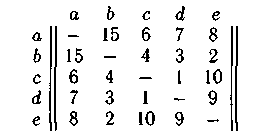
Согласно алгоритму выберем точку «жадного» оператора кроссинговера между генами b и с в хромосоме P1. Теперь выбор (b – с) дает значение целевой функции, равное 4 (см. матрицу), выбор (b — d) (в хромосоме P2) определяет целевую функцию со значением 3, а выбор (6 — а) (в хромосоме Рз) определяет целевую функцию, равную 15. При минимизации целевой функции выберем путь (b — d). Продолжая, по лучим путь реализации «жадного» оператора кроссинговера (рис. 3.1). Итак, хромосома потомка P’: bdcae имеет суммарную целевую функ цию, равную 18: 3 + 1 + 6 + 8 = 18, а целевая функция родителей для P1 равна 15 + 4 + 1 + 9 = 29, для Р2 равна 3 + 9 + 10 + 6 = 28 и для P3 равна 2+ 15 + 7+ 1 =25.
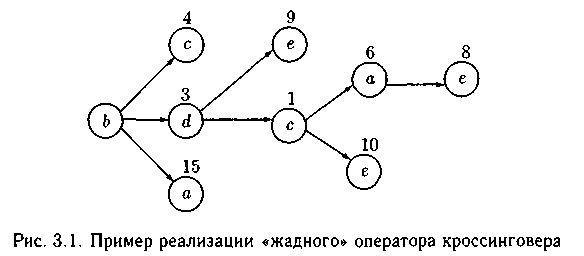
Стратегию «жадного» оператора кроссинговера можно выполнять различными способами, ориентированными на решение заданного класса задач.
Рассмотрим различные варианты выбора пары хромосом для скре щивания. Вероятность скрещивания РЛ|Х(ОК) лучших хромосом с худ шими по значению целевой функции, должна уменьшаться при эволю ции поколений: ОК — оператор кроссинговера.
Вероятность скрещивания лучших хромосом должна увеличиваться на последних этапах оператора кроссинговера для закрепления желае мых признаков в хромосомах.
8. Другие методы выбора пар хромосом для скре щивания. Например, «близкое» родство, «дальнее» родство, выбор на основе кода Грея и пр.
«Близкое родство». Здесь вероятность выбора хромосом, подлежа щих скрещиванию, запишется так:
— для первой хромосомы Pi
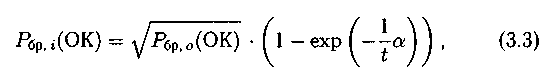
где Рбр.i(ОК) — вероятность выбора хромосомы на основе близкого родства;
— для второй хромосомы Pj вероятность Рбр.i(ОК) задается пользо вателем.
Затем вычисляется Хэммингово расстояние dist(Pi, Pj) между выбранными хромосомами текущей популяции. Например, рассмотрим, две хромосомы, каждая из которых задается конкретными значениями семи переменных: x1, x2, x3, x4, x5, x6, x7; пусть в первом случае ими будут 0, 1,0, 1, 1,0, 1, а во втором 1, 1,0, 1, 0, 0, 0. Запишем данные совокупности значений x1, x2, …, x7 одну под другой:
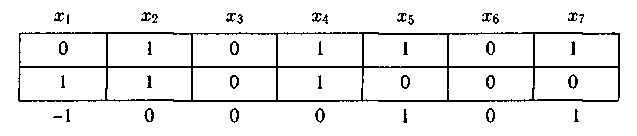
Вычислим разность между каждым элементом первой строки и соответствующим элементом второй строки. Запишем результаты под второй строкой. Теперь вычислим сумму «абсолютных значений» по лученных результатов. Эта сумма равна 3, т.е. расстояние Хэмминга между указанными выше точками (или величинами) [0, 1, 0, 1, 1,0, 1] и [1, 1,0, 1, 0,0, 0] равно 3:
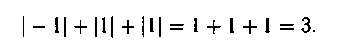
В общем случае рассмотрим две хромосомы (x’1, x’2, …, x’n) и (x1, x2, …, xn); обобщенным расстоянием Хэмминга между этими дву мя хромосомами называется скаляр
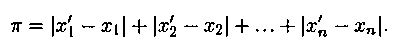
Хромосомы рекомендуются для скрещивания, если хеммингово рас стояние между ними dist(Pi, Pj) > R, где R — радиус скрещивания, задаваемый лицом, принимающим решение, или определяется как ближайшее меньшее целое от разности значений целевых функций ЦФ(Рг) - ЦФ(Р;'), деленное на два.
Вероятности Рвр, i(OK) и PePtj(OK) возрастают на конечных стадиях работы оператора кроссинговера.
«Дальнее»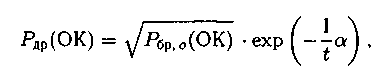
родство определяется условием
где Рдр^(ОК) — вероятность выбора хромосом при «дальнем» родстве на начальных стадиях работы генетических алгоритмов, с учетом осо бенностей вычисляется для первой и второй хромосомы.
Хромосомы Pi и Pj подлежат скрещиванию, если хеммингово расстояние между ними dist(Pi,Pj) > R. Вероятность Рдр>ДОК) и Pflp,j(OK) уменьшается на конечных стадиях поиска оптимального решения.
Код Грея — это двоичный код, последовательные значения кото рого отличаются только одним двоичным разрядом. Код Грея может использоваться для хромосом, представленных в двоичном виде. На пример: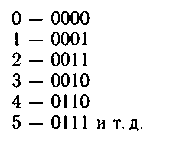
Такое кодирование альтернативных решений позволяет решать во просы «взбалтывания» популяции; оно эффективно на начальных ста диях генетического алгоритма.
Мутация
В биологии процессы преобразования по пуляции происходят толчками на основе точковые мутации. В ГА точковые мутация необходима для предотвращения потери генетического материала. Они не влияет на размер и строения хромосом, а изменяют взаимное расположение генов в хромосоме.
Оператор мутации — языковая конструкция, позволяющая на основе преобразования родительской хромосомы (или ее части) создавать хромосому потомка.
Оператор мутации состоит из двух этапов:
- В хромосоме A = (a1, a2, a3,..., aL-2, aL-1, aL) определяются слу чайным образом две позиции (например, a2 и aL-1).
- Гены, соответствующие выбранным позициям, переставляются, формируя новую хромосому А' = (a1, aL-1, a3,..., aL-2, a2, aL).
Основные операторы мутации:
– одноточечный опе ратором мутации: случайно выбиранный ген в родительской хромосоме меняется местами с геном, расположенным правее:
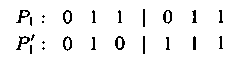
Здесь и далее P1 — родительская хромосома, а P'1 — хромосома-потомок после применения оператора мутации.
– при двухточечном операторе мутаёции задаются или случайно выбираются 2 точки разреза. Затем между собой перестановляются гены, расположенные справа от точек разреза:
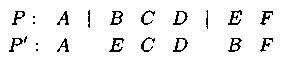
При многоточеч ном или n-точечном операторе мутации последовательно обмениваются гены, расположенные правее точек разрезов друг с другом в порядке их расположения. Ген, расположенный правее последней точки разреза, переходит на место первого:
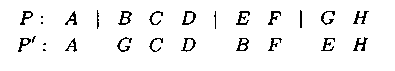
Строительный блок — совокупность смежных ген. Строительные блоки — это тесно связанные между собой гены (части альтернативных решений), которые нежелательно изменять при выполнении генетических операторов. Из них можно создавать альтернативные оптимальные или квазиоптимальные решения.
Пример: при четном кол-ве точек разреза ме няются местами гены, расположенные справа и слева от выбранных точек:
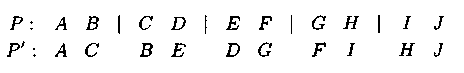
Пример: при нечетном кол-ве точек потомок получается после обмена участ ками хромосом, расположенных между четными точками разреза:
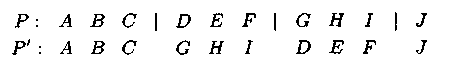
– оператор мутации, использующий знания о ре шаемой задаче, заключается в перестановке местами любых выбранных генов в хромосоме, причем точка(ки) разреза определяются преднамерено.
– в позиционном операторе мутации 2 точки разреза выбирают ся случайно, а затем ген, соответствующий 2-ой точке мутации, размещается в позицию перед геном, соответствующим 1-ой точке:
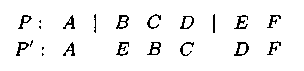
Инверсия
Оператор инверсии – языковая конструкция, позволяющая на основе инвертирования родительской хромосомы (или ее части) создавать хромосому потом ка. При его реализации случайным образом определяется одна или несколько точек разреза (инверсии), внутри которых элементы инвер тируются.
Генетический оператор инверсии состоит из следующих шагов:
- Хромосома В = b1, b2, ..., bL выбирается случайным образом из текущей популяции.
- Два числа y'1 и y'2 выбираются случайным образом из множества {0,1,2,..., L + 1}, причем считается, что y'1 = min{ y'1, y'2} и y'2= тах{ y'1, y'2}.
- Новая хромосома формируется из В путем инверсии сегмента, который лежит справа от позиции y'1 и слева от позиции y'2 в хромосоме В. Тогда после применения оператора инверсии получаем:
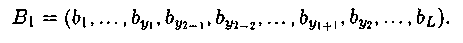
Для одноточечного оператора инверсии:
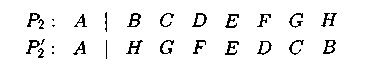
Здесь P2 — родительская хромосома, Р2' — хромосома-потомок после применения оператора инверсии.
Например, для двухточечного оператора инверсии:
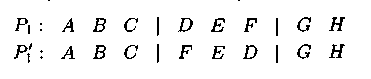
Здесь P1 — родительская хромосома, P'1 — хромосома-потомок после применения двухточечного оператора инверсии.
Существует специальный оператор инверсии, в котором точки инверсии определяются с заданной вероятностью для каждой новой создаваемой хромосомы в популяции.
Транслока ция
Оператор транслока ции — это языковая конструкция, позволяющая на основе скрещивания и инвертирования из пары родительских хромосом (или их частей) создавать две хромосомы потомков. Транслока ция представляетсобой комбинацию операторов кроссинговера и инверсии. При ее реализации случайным образом производится один разрез в каждой хромосоме. При формировании потомка P'1 берется левая часть до разрыва из родителя P1 и инверсия правой части до разрыва из P2. При создании P'2 берется левая часть P2 и инверсия правой части P1. Пример:
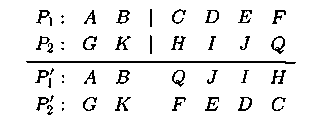
Транслокация – самый новый из генетических операторов, насчитывающий >10 разновидностей.
Транспозиция
Оператор транспозиции — языковая конструкция, позволя ющая на основе преобразования и инвертирования выделяемой части родительской хромосомы создавать хромосому потомка. Пример:
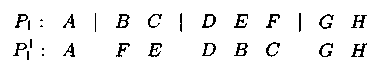
Определенным или случайным образом выберем 3 точки разреза. Для получения хромосомы-потомока P'1 в родительской хромосоме P1 строительный блок DEF инвертируем и вставляется в точку разреза между генами А и В. Существует большое кол-во модификаций оператора транспозиции.
Сегрегация
Оператор сегрегации – языковая конструк ция, позволяющая на основе выбора строительных блоков из хромосом-родителей (или их частей) создавать хромосомы-потомки. Оператор сегрегации реализуется на некотором наборе хромосом различными способами.
Пример: пусть существует популяция Р, состоящая из четырех родительских хро мосом:
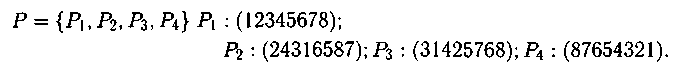
В каждой хромосоме выделим по 2 строительных блока: в P1 — 23 и 67, в P2 — 1 и 4, в P3 — 768 и 425, в P4 — 54 и 87. Тогда потомок P'1 можно сформировать, взяв первые строительные блоки из каждой родительской хромосомы популяции: (23176854). Потомок P'2: (67442587) является нереальным (недопустимым).
Удаление
Оператор удаления – языковая конструкция, позволяющая на основе удаления строительных блоков из хромосом родителей (или их частей) создавать хромосомы потомков.
При его реализации заданным или случайным образом опреде ляется точка(и) разреза. Справа от точки опера тора удаления (между двумя точками) удаляются гены или их строительные блоки с вычислением изменения значения целевой функции. Потомок преобразуется так, чтобы соответствующее альтернативное решение стало реальным.
Вставка
Оператор вставки – языковая конструкция, поз воляющая на основе вставки строительных блоков в хромосомы роди телей создавать хромосомы потомков.
При его реализации направленным или случайным образом созда ется хромосома-донор, состоящая из строительных блоков, которые желательно разместить в другие хромосомы популяции. Для ре ализации оператора вставки направленным или случайным образом определяется хромосома, в которой ставится точка(ки) разреза. Далее анализируются др. хромосомы в популяции для определения альтернативных вставок. Затем производится пробная вставка строи тельных блоков с вычислением изменения значения целевой функции и получением реальных решений. Новые строительные блоки вставля ются в хромосому справа от точки оператора вставки (между его двумя точками).
Операторы удаления и вставки могут изменять размер хромосом. Для предотвращения изменеия эти операторы можно применять совместно.
На конечном этапе поиска целесообразно близкие решения оценивать по определенным критерием, (поиск реше ние среди лучших Рtk.
Редукция
Оператор редукции — языковая конструкция, позволяющая на основе анализа популяции после смены одного или нескольких поколений уменьшить размер до заданного кол-ва. Он необходим для устранения неудачных хромосомов и/или сохранения постоянного размера попу ляции. Следовательно, встает проблема нахождение компромисса между разнообразием генетического материала и качеством решений. Поэтому, сначала формируется репродукционная группа из всех решений, образующих популяцию, а затем выполняют отбор решений в следующую популяцию.
Численность новой популяции
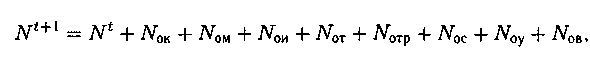
где
Nt+1 — численность новой популяции;
N1 — численность популяции на предыдущем шаге (поколении) t;
N0K, N0M, N0И, N0Т, N0ТР, N0С N0У, N0B — потомки, полученные в резуль тате применения операторов: кроссинговера, мутации, инверсии, транслокации, транспозиции, сегрегации, удаления, вставки. Оператор редукции может применяться после каждого оператора или после всех при каждой генерации ГА. Выделяют две основных схемы редукции (отбора).
1. Элитная схема редукции: в группу удаления из популяции включаются хромосомы Рtk+1Рt и только те потомки, для которых выполняется условие:
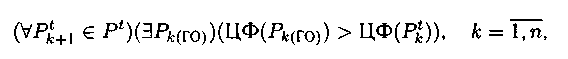
где Рk(ГО) – потомки (решения), полученные после применения гене тического оператора.
2. Последовательная схема редукции позволяет варьировать мето ды выбора хромосом для удаления из популяции:
случайный выбор (позволяет разнообразить генофонд на ранних этапах рвыполнения ГА. Вероятность этого выбора должна снижаться с каждым поколением);
выбор «лучших» и «худших»;
«близкое» родство;
«дальнее» родство;
на основе кода Грея для бинарных хромосом;
на основе расстояние Хэмминга;
на основе «турнира».
По аналогии с оператором репродукции моди фикацированные операторы редукции осуществляют:
1) равновероятностный отбор с вероятностью
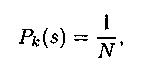
где N — размер популяции;
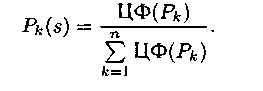
2) пропорциональный отбор с вероятностью
Т.о. редукция на ранних ста диях выполняет случайный отбор хромосом (без учета значений их ЦФ(Рk)). На заключительных – при отборе значения ЦФ(Рk) становится определяющиям фактором: чем больше значение целевой функции экземпляра, тем выше вероятность его отбора в следующую попу ляцию. На заключительной стадии уменьшаестя случайность выбора и увеличивается его направленность.
Рекомбинация
Оператор ре комбинации — языковая конструкция, определяющая как новая генерация хромосом будет построена из родителей и потомков. Т.е. это технология анализа и преобразования популяции при переходе из одной генерации в другую. Существует много разновидностей рекомбинации:
1) перемещение родителей в потомки после реализации каждого генетического оператора;
2) перемещение части популяции после каждой генерации.
Часто в ГА задается параметр W(P), управляющий этим процессом. Так, Np(1 - W(P)) элементов в популяции Р, выбранных случайно, могут «выжить» в следующей генерации; Np — размер популяции. Величина W(P) = 0 означает, что вся предыдущая популяция перемещается в новую популяцию при каждой генерации. При дальнейшей реализации ГА лучшие или отобранные элементы из родителей и потомков будут выбираться для формирования новой популяции.
В задачах используются следующие механизмы и мо дели этого процесса:
Ml — вытеснение (crowding factor). Этот механизм определя ет способ и порядок замены родительских хромосом из генерации t хромосомами потомками после генерации t+ 1. Механизм реали зован так, что стремится удалять «похожие» хромосомы из популяции и оставлять отличающиеся.
М2 — разделение (sharing). Этот механизм вводит зависимость значения ЦФ хромосомы от их распределения в попу ляции и поисковом пространстве, что позволяет копиям родитель ских хромосом (или близких к ним) не появляться в популяциях.
МЗ — введение идентификаторов (tagging). Специальным хромо сомам присваиваются метки. Операторы ГА применяются только к помеченным хромосомам.
Оператор редукции является частным случаем опера тора рекомбинации.
Вероятность
В ГА часто используется вероятность, определяющая процент общего числа генов в популяции, изменяющихся в каждой генерации. Для оптимизационных задач вероятность оператора кроссинговера обычно прини мают в пределах от 0,6 до 0,99; вероятность оператора мутации — 0,6; инверсии — от 0,1 до 0,5); транслокации — от 0,1 до 0,5; транспозиции — от 0,1 до 0,5; сегрегации — от 0,6 до 0,99; удаления — от 0,6 до 0,99; встав ки – от 0,6 до 0,99.
Генетический алгоритм (ГА)