Методы нахождения корней системы нелинейных уравнений

Тема 4.

Методы нахождения корней системы нелинейных уравнений.

Для уточнения корней систем нелинейных уравнений наиболее часто используют методы итерации, Зейделя и метод Ньютона. Как и в случае уточнения корней одного нелинейного уравнения для систем требуется определение хорошего начального приближения (отделение корня), гарантирующего сходимость метода и высокую скорость сходимости. Для системы из 2 уравнений это можно сделать графически, но для систем высоких порядков удовлетворительных методов отделения корней не существует.

Дана система n нелинейных уравнений с n неизвестными:

,

, (1)

.

.

.

,

Где , - нелинейные функции, определенные и непрерывные в некоторой области , или в векторном виде:

(2)

где , .

Требуется найти такой вектор , который при подстановке в систему (1) превращает каждое уравнение в векторное числовое равенство.

Замечание.

Проблема решения системы (1) возникает при решении многих прикладных задач, например, поиска безусловного экстремума функций многих переменных с помощью необходимых условий [23], при применении неявных методов интегрирования обыкновенных дифференциальных уравнений [28] и т.д.

Метод простых итераций.

В методе простой итерации система (1) приводится к эквивалентной системе вида , где , или

(3)

Полагая известным начальное приближение для корня , построим итерационный процесс , k=0,1,2,…, или

(4)

в методе простой итерации вектор погрешности испытывает линейное преобразование, или, иначе, метод имеет первый порядок сходимости.

Теорема 3.13 (о достаточном условии сходимости метода простых итераций).

Пусть функции и , i=1,…,n, непрерывны в области G, причем выполнено неравенство:

, (5)

где q –некоторая постоянная.

Если последовательные приближения , k=0,1,… не выходят из области G, то процесс последовательных приближений сходятся и вектор x* является в области G единственным решением системы (3).

Замечание.

Вместо условия (5) можно также использовать:

(6)

Метод итераций Зейделя.

Нередко сходимость метода простой итерации можно улучшить, если вновь вычисленные значения компонент вектора неизвестных немедленно включить в расчет. В этом случае итерационный процесс имеет вид:

, i=1,…,n (7)

Сходимость этого процесса также линейная.

Условием окончания итераций, методами итерации и Зейделя является достижение заранее заданной точности .

Если

Пример 1.

Расположенные в первом квадранте, методом простых итераций с точностью до =0,001.

Преобразуем систему к виду (3) так, чтобы выполнилось условие сходимости:

Найдем частные производные:

,

,

Здесь принято . Далее воспользуемся методикой решения задачи.

1. Для выбора начального приближения найдем координаты точек пересечения кривых, соответствующих первому и второму уравнениям.

(рис 3.17)

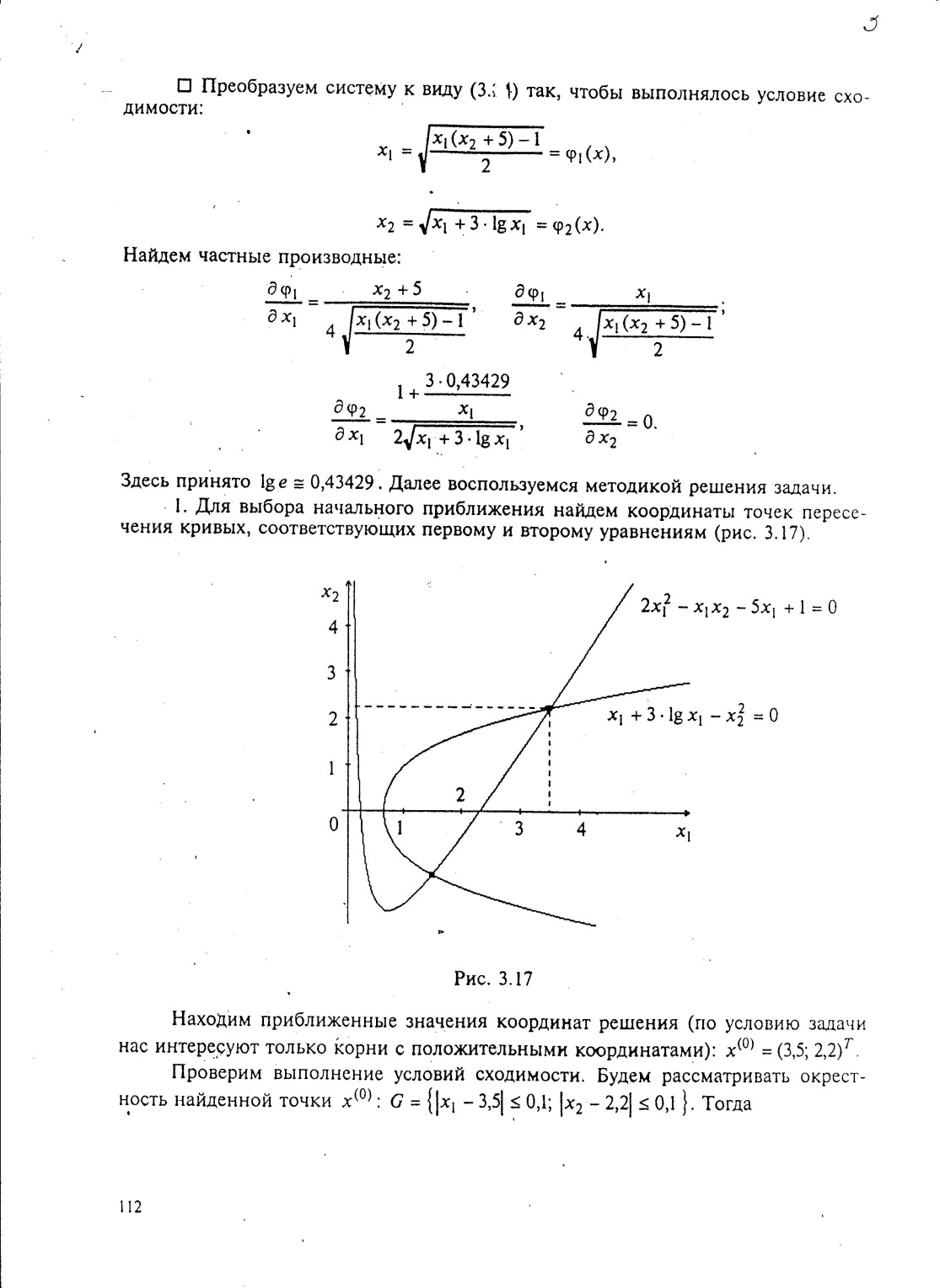
Находим приближенные значения координат решения (по условию задачи нас интересуют только корни с положительными координатами): .

Проверим выполнение условий сходимости. Будем рассматривать окрестность найденной точки . Тогда

;

;

Следовательно, можно получить оценки:

Очевидно, условие (5) выполняется. Если последовательные приближения не будут выходить из области G, то согласно теореме 3.13 итерационный процесс будет сходящимся. В поставленной задаче =0,001.

2,3 Выполним расчеты по формуле (4):

, k=0,1,…,

А результаты поместим в таблицу 3.17:

k	0	1	2	3	4
	3,500	3,4785	3,4837	3,4848	3,4957
	3,500	2,2654	2,2589	2,26049	2,26082
(k+1)	-	0,0654	0,0065	0,00159	0,0009

Заметим, что величина (k+1) при увеличении номера итерации уменьшается, что характерно для любого сходящегося процесса. Найдено приближенное решение:

. При этом , .

Метод Ньютона

Основная идея метода Ньютона — решение системы нелинейных уравнений сводится к решению последовательности линейных задач, дающих в пределе решение исходной задачи. Линейная задача получается путем выделения из нелинейных уравнений главной линейной части.

Рассмотрим погрешность вычисления корня на k-ой итерации , где . Полагая, что функции fi непрерывны и дифференцируемы в окрестности корня и - малые величины, разложим в ряд Тейлора, сохранив лишь линейную часть разложения. Получим систему уравнений:

, i=1,…,n (8)

Линейную относительно компонент вектора погрешностей. Если использовать эту систему для отыскания компонент вектора погрешностей, то в силу приближенности системы (8) – оставлена, лишь линейная часть – найденное значение вектора погрешности будет лишь приближенным. Тогда при подстановке полученного решения в соотношение будем иметь вместо x* приближенное уточненное значение корня, которое обозначим через x(k+1). Используя запись системы (8) в виде:

Где J(x) – матрица производных системы функций fi(x) (матрицы Якоби), можем записать итерационный процесс для нахождения вектора x:

, k=0,1,…, (9)

Где

- матрица Якоби

Так как процесс вычисления обратной матрицы является трудоемким, преобразуем (9) следующим образом:

, k=0,1,…

Где - поправка к текущему приближению x(k)

Умножим последнее выражение слева на матрицу Якоби W(x(k)):

, k=0,1,…

В результате получена система линейных алгебраических уравнений относительно поправки :

(10)

1. Вычислить следующее приближение:

(11)

1. Если , процесс закончить и положить . Если , то положить и перейти к пункту 2

Итерационный процесс метода Ньютона сходится, если определитель матрицы Якоби на k-й итерации J(k)0. Требуется, однако, хорошее отделение корня, но достаточное условие сходимости слишком громоздко, чтобы им воспользоваться на практике.

1. К недостаткам метода Ньютона следует отнести:

- необходимость задавать достаточно хорошее начальное приближение;

- отсутствие глобальной сходимости для многих задач;

- необходимость вычисления матрицы Якоби на каждой итерации;

- необходимость решения на каждой итерации системы линейных уравнений, которая может быть плохо обусловленной.

Достоинством метода является квадратичная сходимость из хорошего начального приближения при условии невырожденности матрицы Якоби.

Пример 3.19. Решить систему:

Методом Ньютона с точностью =0,001.

Очевидно, корнями системы являются ; . Найдем приближенно второй корень x*2.

1. Зададим начальное приближение . В поставленной задаче =0,001. Положим k=0.
2. Составим систему (10). Так как , то система

имеет вид .

Для системы из двух уравнений поправку можно найти по формулам:

(11)

(12)

Отсюда . Для вычисления x(k), k=0,1,… здесь и далее используется метод Гаусса единственного деления.

1. Вычислим
2. Так как , то положим k=1 и перейдем к пункту 2.
3. Составим систему :

. Отсюда

1. Вычислим
2. Так как, то положим k=2 и перейдем к пункту 5. Результаты дальнейших вычислений приведены в таблице 3.19.

k	0	1	2	3	4	5
	1	-0,625	-0,091911	-0,002653	-0,0000023	0,0000
	5	3,625	3,091911	3,002653	3,0000023	3,0000
(k+1)	-	1,625	0,5333	0,089258	0,0026507	0,0000023

Найденное приближенное решение . Из анализа решения приведенного в таблице 3.19, следует, что количество верных знаков на каждой итерации удваивается, что соответствует квадратичной сходимости.

Методы нахождения корней системы нелинейных уравнений