Численные методы решения обыкновенных дифференциальных уравнений

Тема 7

Численные методы решения

обыкновенных дифференциальных уравнений

В главе рассматриваются различные методы решения задачи Коши и краевой задачи для обыкновенных дифференциальных уравнений. Подробно рассмотрены метод Эйлера и ошибки, возникающие при его реализации на компьютерах; семейство одношаговых методов Рунге - Кутты, многошаговые методы. В качестве примеров методов решения краевой задачи излагаются методы стрельбы и разностный.

Основы теории обыкновенных

дифференциальных уравнений

Обыкновенным дифференциальным уравнением называется уравнение вида

(3.1)

связывающее одну независимую переменную , искомую функцию и ее производные вплоть до n-го порядка. Порядком обыкновенного дифференциального уравнения называется порядок старшей производной от искомой функции.

Дифференциальное уравнение называется линейным, если оно имеет вид

Так, например, - линейное дифференциальное уравнение второго порядка; - нелинейное уравнение.

Общим интегралом уравнения (3.1) называют функцию

(3.2)

связывающую независимую переменную , искомую функцию и п постоянных интегрирования с помощью уравнения . Таким образом, функция входит в функцию (3.2) неявным образом, причем число постоянных интегрирования равно порядку уравнения.

Общим решением обыкновенного дифференциального уравнения называется функция

(3.3)

связывающая независимую переменную и п постоянных интегрирования, иначе говоря, уравнение (3.3) определяет функцию явным образом.

Для определения постоянных интегрирования задаются дополнительные условия. Их число равно числу постоянных интегрирования. Если в дополнительные условия подставить функцию (3.2) и решить полученную систему относительно постоянных интегрирования а затем полученные решения подставить в (3.2), то получим частный интеграл .

Аналогичные процедуры с общим решением (3.3) дают частное решение

Если все дополнительные условия задаются более чем в одной точке , то совокупность обыкновенного дифференциального уравнения и дополнительных условий называют задачей Коши для рассматриваемого дифференциального уравнения. В этом случае дополнительные условия называют начальными условиями.

Если дополнительные условия задаются более чем в одной граничной точке расчетной области, то совокупность обыкновенного дифференциального уравнения и дополнительных условий называют краевой задачей для рассматриваемого уравнения, а дополнительные условия - граничными или краевыми условиями.

Таким образом, если задать числа то задача Коши для уравнения (3.1) имеет вид

Порядок старшей производной в начальных условиях не превышает , где - порядок дифференциального уравнения.

Если старшая производная в уравнении выражается как функция переменных и производных более низкого порядка, то уравнение называют разрешенным относительно старшей производной и оно записывается в виде

Во многих практических приложениях независимая переменная обозначается через и имеет смысл времени, задача Коши называется «начальной».

Актуальность задачи Коши для многих областей науки и техники явилась причиной разработки для ее решения большого количества методов. Рассматриваются две группы численных методов решения задачи Коши.

- Одношаговые методы, в которых для нахождения решения в некоторой точке отрезка используется информация лишь в одной предыдущей точке. К этим методам относятся методы Эйлера и Рунге - Кутты.

- Многошаговые методы, в которых для отыскания решения в некоторой точке используется информация о решении в нескольких предыдущих точках. К таким методам относится метод Адамса.

Рассмотрим применение этих методов к дифференциальным уравнениям первого порядка. Алгоритм для случая системы дифференциальных уравнений легко получается из алгоритма для решения одного уравнения, более высокого порядка которое приводят к системе 1-го порядка, обозначая:

тогда,

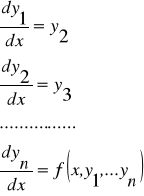
Пример

Записать в нормальной форме Коши

Обозначим:

Понятие о методе конечных разностей.

Порядок разностной схемы

Численное решение обыкновенных дифференциальных уравнений и уравнений в частных производных во многих случаях осуществляется методом конечных разностей. Метод конечных разностей сводит решение дифференциальных уравнений к решению линейных или нелинейных уравнений с достаточно разреженными матрицами. При этом построение решения в методе сеток осуществляется в три этапа.

- Область непрерывного изменения аргумента (или аргументов) заменяется конечным дискретным множеством точек, называемых разностной сеткой. В разностной сетке выделяются внутренние и граничные узлы. Решение разыскивается во внутренних узлах, а в граничных узлах значение искомой функции задается при аппроксимации граничных условий исходной дифференциальной задачи. Функция дискретного аргумента, определенная на разностной сетке, называется сеточной функцией.

- Дифференциальные уравнения и граничные условия заменяются по определенным правилам своими разностными аналогами. Разностные операторы, соответствующие дифференциальному уравнению, записываются во внутренних узлах сетки. Разностные операторы, соответствующие граничным условиям, записываются в граничных узлах. В результате получается система алгебраических уравнений, число которых пропорционально числу внутренних узлов разностной сетки.

- Осуществляется решение системы алгебраических уравнений каким-либо из известных методов. В большинстве случаев получаемая система уравнений является системой линейных алгебраических уравнений очень большого порядка (как правило, ), но с весьма разреженной матрицей.

Методы сеток делятся на явные и неявные:

- Явные – когда значение на шаге определяется явно:

, где -некоторая функция, зависящая от конкретного метода (кроме последней рассчитанной точки ) могут использоваться еще предыдущих значений;

- Неявные – когда искомая величина входит как в левую, так и в правую часть:

Явные и неявные методы делятся на 1-шаговые и многошаговые:

В одношаговых – для расчета очередной точки требуется информация только о последней рассчитанной точке ;

В шаговых – требуется информация о предыдущих точках.

В случае нелинейных систем итерационные процедуры, как правило, сводят их к линейным системам.

Продемонстрируем эти этапы на примере решения задачи Коши для простейшего линейного уравнения первого порядка. Пусть требуется найти решение задачи Коши на интервале (0, 1) для уравнения

(3.4)

Непрерывный интервал можно заменить множеством точек . Расстояние между точками называется шагом разностной сетки. В общем случае эти шаги могут быть переменными. Рассмотрим случай постоянного шага и примем . Заменим дифференциальное уравнение разностным в точке :

(3.5)

Таким образом, первая производная аппроксимирована односторонней разностью вперед с первым порядком точности. Перепишем уравнение (3.5) в виде

(3.6)

Здесь Из (3.6) следует, что

. (3.7)

Из рекуррентного соотношения (3.7) имеем точное решение разностного уравнения (3.6)

(3.8)

Очевидно, что точное решение разностных уравнений можно получить лишь для простейших случаев. Точное решение задачи (3.4) имеет вид

. (3.9)

Определим погрешность разностного решения. Имеем

. (3.10)

Предполагая шаг разностной схемы малым, представим член в виде

Подставляя это выражение в (3.10), получим

. (3.11)

Таким образом, величина погрешности имеет первый порядок точности и совпадает в данном случае с порядком аппроксимации производной. В общем случае порядок погрешности решения определяется не только порядком аппроксимации дифференциального уравнения, но и порядком аппроксимации граничных условий.

Говорят, что разностная схема (3.5) имеет первый порядок точности на интервале. Можно показать, что на шаге эта разностная схема имеет второй порядок точности. Представим точное решение в виде ряда Тейлора в точке. Имеем

. (3.12)

Поскольку

,

то

. (3.13)

Из соотношений (3.7) и (3.13) следует, что погрешность на шаге имеет порядок . Очевидно, что погрешность на интервале выше на порядок, так как она накапливается по мере увеличения числа шагов. Отметим еще, что погрешность решения стремится к нулю при , т. е. решение разностной задачи сходится к точному. Однако для сходимости необходимы не только аппроксимация дифференциального уравнения, но и устойчивость разностной схемы.

Численный метод называется устойчивым, если численные результаты непрерывно зависят от входных данных и если погрешность остается ограниченной при заданных приделах изменения параметров численного алгоритма (шагов сетки, числа итераций).

Сходимость является основной проблемой, от которой зависит точность всей задачи.

Численный алгоритм называется сходящимся, если при стремлении его параметров к предельным значениям, например при , (итерационный шаг при - число итераций), результаты стремятся к точному решению.

Метод Эйлера.

Метод Эйлера с пересчетом

Метод Эйлера является простейшим методом решения задачи Коши и имеет невысокую точность, поэтому на практике его используют достаточно редко. Однако на его основе в дальнейшем легче объяснить алгоритмы более эффективных (и, как правило, более сложных) методов и способы построения и исследования этих алгоритмов.

Пусть дано дифференциальное уравнение

(1)

с начальным условием

.

Выбрав достаточно малый шаг , построим систему равноотстоящих точек

. (2)

Искомую интегральную кривую , проходящую через точку , приближенно заменим (рис. 28) ломаной ,

с вершинами , звенья которой прямолинейны между прямыми и имеют подъем

(3)

(так называемая ломаная Эйлера).

Таким образом, звенья ломаной Эйлера в каждой вершине имеют направление, совпадающее с направлением уд интегральной кривой уравнения (1), проходящей через точку.

Из формулы (3) вытекает, что значения могут быть определены (метод Эйлера) по формулам

. (4)

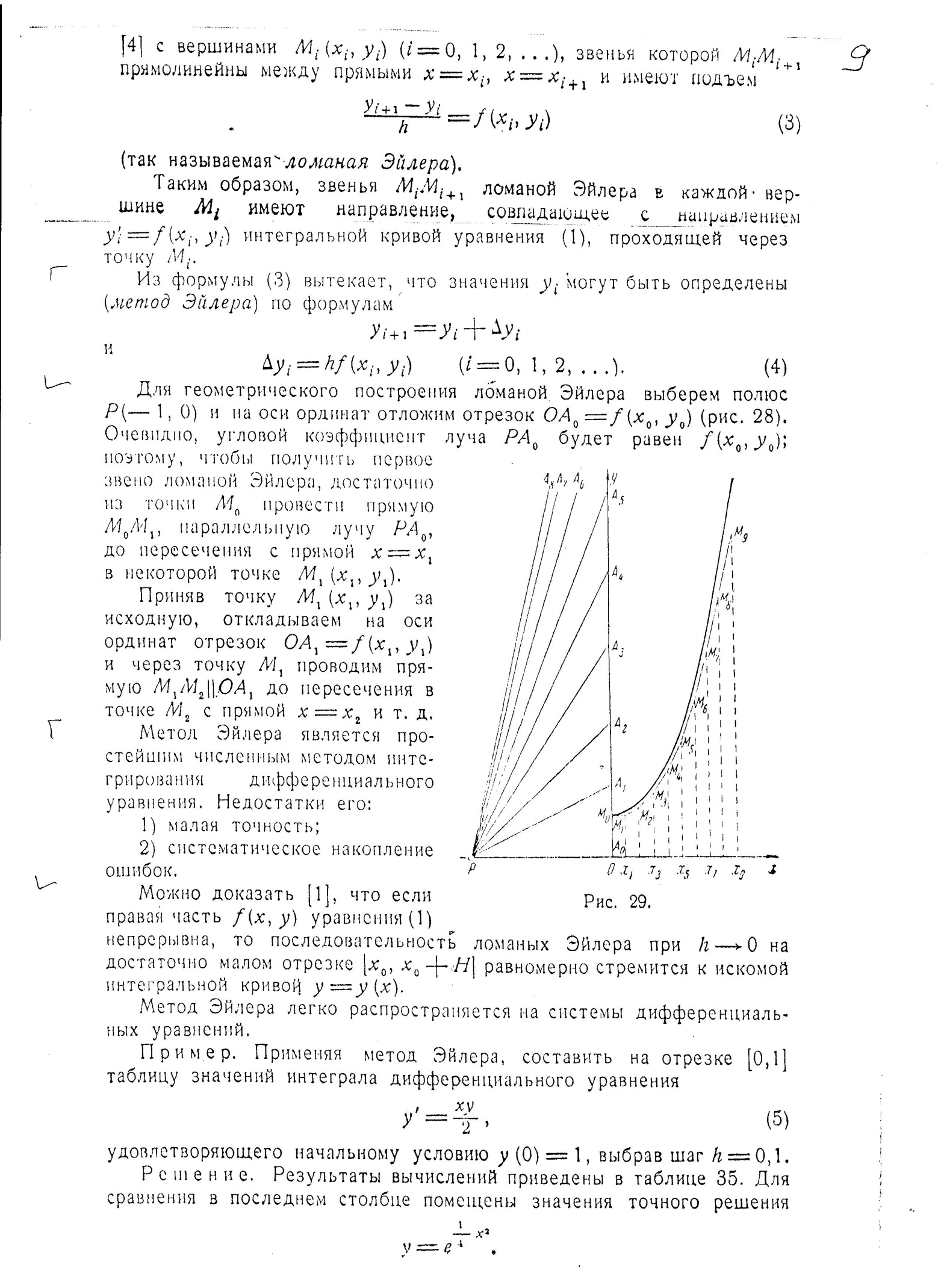
Для геометрического построения ломаной Эйлера выберем полюс и на оси ординат отложим отрезок (рис. 28). Очевидно, угловой коэффициент луча будет равен ; поэтому, чтобы получить первое звено ломаной Эйлера, достаточно из точки , провести прямую , параллельную лучу, до пересечения с прямой в некоторой точке .

Приняв точку за исходную, откладываем на оси ординат отрезок и через точку проводим прямую до пересечения в точке с прямой и т. д.

Метод Эйлера является простейшим численным методом интегрирования дифференциального уравнения. Недостатки его:

1. малая точность;
2. систематическое накопление ошибок.

Можно доказать, что если правая часть уравнения (1) непрерывна, то последовательность ломаных Эйлера при на достаточно малом отрезкеравномерно стремится к искомой интегральной кривой.

Метод Эйлера легко распространяется на системы дифференциальных уравнений.

Пример. Применяя метод Эйлера, составить на отрезке [0,1] таблицу значений интеграла дифференциального уравнения

, (5)

удовлетворяющего начальному условию , выбрав шаг .

Решение. Результаты вычислений приведены в таблице 35. Для сравнения в последнем столбце помещены значения точного решения

.

Из приведенной таблицы видно, что абсолютная погрешность значения составляет . Отсюда относительная погрешность примерно равна 3%.

Для сравнения приводим график точного решения (выделенный жирной линией) и соответствующую ломаную Эйлера (рис. 29).

Метод Эйлера, вообще говоря, обладает, малой точностью и дает сравнительно удовлетворительные результаты (в смысле погрешности) лишь при малых значениях . Это обстоятельство понятно, так как по существу метод Эйлера заключается в том, что интеграл дифференциального уравнения (1) на каждом частичном отрезке представляется двумя членами ряда Тейлора

,

т.е. для этого отрезка имеется погрешность порядка .

Таблица 35

Интегрирование дифференциального уравнения (5) методом Эйлера

					Точное значение
0 1 2 3 4 5 6 7 8 9 10	0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	1 1 1,005 1,0151 1,0303 1,0509 1,0772 1,1095 1,1483 1,1942 1,2479	0 0,5 0,1005 0,1523 0,2067 0,2627 0,3232 0,3883 0,4593 0,5374	0 0,005 0,0101 0,0152 0,0206 0,0263 0,0323 0,0388 0,0459 0,0537	1 1,0025 1,0100 1,0227 1,0408 1,0645 1,0942 1,1303 1,1735 1,2244 1,2840

Кроме того, при вычислении значений на следующем отрезке исходные данные не являются точными и содержат погрешности, зависящие от неточности предшествующих вычислений.

Существует несколько модификаций метода Эйлера. Остановимся на одной из них – методе Эйлера с пересчетом, который называют также методом Эйлера – Коши.

Подобные схемы часто называют схемами типа прогноз – корректор (предиктор – корректор). Сначала определяется «грубое приближение» решения

,

исходя из которого находится направление поля интегральных кривых

.

Затем решение уточняют, приближенно полагают

(5)

Усовершенствованный метод Эйлера – Коши можно еще более уточнить, применяя итерационную обработку каждого значения . А именно, исходя из грубого приближения

,

построим итерационный процесс

. (7)

Итерацию продолжаем до тех пор, пока некоторые два последовательных приближения и не совпадут между собой в соответствующих десятичных знаках. После этого полагаем

,

где - общая часть приближений и .

Если алгоритм уточнения численного значения искомого решения после трех - четырех итераций не приводит к совпадению требуемого числа десятичных знаков, то следует уменьшить шаг вычисления .

Отметим в заключение, что метод Эйлера с итерационной обработкой ординат дает на каждом шаге погрешность порядка и нередко применяется в вычислительной практике.

Пример 2. Применяя метод итерационной обработки, с точностью до четырех совпадающих десятичных знаков найти значение

интеграла дифференциального уравнения

.

Решение. Примем шаг

.

Применяя итерационный процесс (7) и учитывая, что

,

последовательно будем иметь

Следовательно, удержав запасной знак, можно положить

.

Аналогично, приняв и за исходные данные и принимая во внимание, что

,

С помощью того же итерационного процесса (7) получим

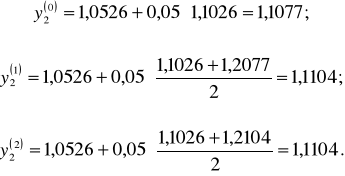
Отсюда

.

Для сравнения приводим точное значение

Интегрирование дифференциального уравнения методом

Эйлера с последующей итерацией значений

					Точное значение
0 1 2 3 4 5 6 7 8 9 10	0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	1 1,0025 1,0100 1,0227 1,0408 1,0646 1,0943 1,1305 1,1738 1,2248 1,2812	0 0,0501 0,1010 0,1534 0,2082 0,2661 0,3283 0,3957 0,4695 0,5512	0 0,0050 0,0101 0,0153 0,0208 0,0266 0,0328 0,0396 0,0470 0,0551	1 1,0025 1,0100 1,0227 1,0408 1,0645 1,0942 1,1303 1,1735 1,2244 1,2840

Метод Рунге – Кутты

Метод Рунге — Кутты позволяет строить схемы различного порядка точности. Основная идея метода состоит в построении специального алгоритма – такого, чтобы приращение функции на шаге совпадало с приращением , которое определяется из ряда Тейлора (3.15) с учетом возможно большего числа членов. При этом вторые и следующие производные определяются не дифференцированием, а путем многократного вычисления функции в некоторых промежуточных точках между и .

Пусть дано дифференциальное уравнение первого порядка

(1)

с начальным условием

Выберем шаг и для кратности введем обозначения и .

Рассмотрим числа:

(2)

Согласно обычному методу Рунге – Кутта, последовательные значения искомой функции определяются по формуле

,

где

. (3)

Формула (9) имеет четвертый порядок точности. Получены также формулы типа Рунге – Кутта с иными порядками точности.

Для вычисления по формуле (3) удобно пользоваться схемой, приведенной в таблице 39.

Эффективная оценка погрешности метода Рунге - Кутта затруднительна. Поэтому для определения правильности выбора шага h на практике обычно на каждом этапе из двух шагов применяют двойной пересчет. А именно, исходя из текущего верного значения , вычисляют величину двумя способами: один раз с шагом h, а другой раз с двойным шагом . Если расхождение полученных значений не превышает допустимой погрешности, то шаг h для данного этапа выбран правильно и полученное с его помощью значение можно принять за . В противном случае шаг уменьшаю в два раза.

Схема метода Рунге – Кутта

0
-	-	-	-
1

Метод Рунге - Кутта обладает значительной точностью и, несмотря на свою трудоемкость, широко используется при численном решении дифференциальных уравнений с помощью электронных вычислительных машин. Кроме того, важным преимуществом этого метода является возможность применения «переменного шага».

Пример 1. Методом Рунге - Кутта вычислить на отрезке [0; 0,5] интеграл дифференциального уравнения

(10)

приняв шаг h = 0,1.

Решение. Покажем начало процесса.

Вычисление .

Последовательно имеем

Отсюда

и, следовательно,

.

Аналогично вычисляются дальнейшие приближения. Результаты вычислений приведены в таблице 40.

Таким образом, у (0,5) = 1,7974.

Для сравнения приводим точное решение:

,

откуда

Метод Рунге – Кутта применим также для приближенного решения систем обыкновенных дифференциальных уравнений.

Таблица 40

Интегрирование дифференциального уравнения (10)

методом Рунге – Кутта

0	0 0,05 0,05 0,1	1 1,05 1,055 1,1105	0,1 0,11 0,1105 0,1210
1	0,1 0,15 0,15 0,2	1,1103 1,1708 1,1763 1,2429	0,1210 0,1321 0,1326 0,1443
2	0,2 0,25 0,25 0,3	1,2427 1,3149 1,3209 1,3998	0,1443 0,1565 0,1571 0,1700
3	0,3 0,35 0,35 0,4	1,3996 1,4846 1,4904 1,5836	0,1700 0,1835 0,1840 0,1984
4	0,4 0,45 0,45 0,5	1,5836 1,6828 1,6902 1,7976	0,1984 0,2133 0,2140 0,2298
5	0,5	1,7974

Многошаговый метод Адамса

В предыдущих схемах решение в точке вычисляется с использованием решения только в одной точке . Логично предположить, что можно повысить точность метода, если использовать информацию о поведении решения в предыдущих точках . Такие методы получили название многошаговых.

Общая схема построения многошаговых методов выглядит следующим образом. Пусть нам известно приближенное решение.

Изложим метод Адамса применительно к уравнению первого порядка

(1)

с начальным условием

(2)

Пусть - система равноотстоящих значений с шагом h и . Очевидно, имеем

. (3)

В силу второй интерполяционной формулы Ньютона с точностью до разностей четвертого порядка получаем:

, (4)

где

,

или

, (4’)

Подставляя выражение (4') в формулу (3) и учитывая, что

будем иметь

.

Отсюда получаем экстраполяционную формулу Адамса

. (5)

Для начала процесса нужны четыре начальных значения:

так называемый начальный отрезок, который определяется, исходя из начального условия (2), каким–нибудь численным методом.

Можно, например, использовать метод Рунге – Кутта или разложение в ряд Тейлора

.,

где (или с соответствующим изменением нумерации). Зная эти значения, из уравнения (1) можно найти значения производных

и составить таблицу разностей:

(6)

Дальнейшие значения искомого решения можно шаг за шагом вычислять по формуле Адамса, пополняя по мере необходимости таблицу разностей (6).

Для работы на электронных счетных машинах формулу Адамса (5) выгодно применять в раскрытом виде. Учитывая, что

после приведения подобных членов имеем

,

причем

Таким образом, метод Адамса имеет четвертый порядок точности на интервале. Чтобы начать счет по схеме Адамса, необходимо знать решение в четырех начальных точках .

По существу, интерполяционный многочлен в формуле (3.32) используется вне области интерполяции, т. е. в данном случае это экстраполяционный многочлен. Однако, поскольку интервал мал, ошибка за счет экстраполяции невелика. Недостающие значения функции вычисляются в точках , как правило, по методу Рунге – Кутты соответствующего порядка. Это является недостатком метода, так как увеличивает объем программы для компьютера. Преимущество многошаговых методов заключается в том, что на каждом шаге правая часть дифференциального уравнения вычисляется только один раз, а в методе Рунге – Кутты четвертого порядка точности на каждом шаге функция вычисляется четыре раза.

Достоинство метода Адамса по сравнению с методом Рунге – Кутты заключается в простоте оценки остаточного члена метода.

Метод Адамса распространяется и на системы дифференциальных уравнений 1-го порядка.

Пример 1. Методом Адамса найти на отрезке [0,1] интеграл уравнении

.

Решение. Примем шаг . Для начала процесса используем значения, найденные методом Рунге - Кутта (см. §7, пример 1), т. е.

.

Дальнейшие вычисления располагаем в двух бланках: основном (таблица 42) и вспомогательном (таблица 43).

Если правая часть дифференциального уравнения сложна, то в основном бланке приходится вводить промежуточные графы. При заполнении вспомогательного бланка используются согласно формуле (5) наклонные строки.

Таблица 42

Основной бланк для интегрирования дифференциального уравнения

методом Адамса

0 1 2 3 4 5 6 7 8 9 10	0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	1 1,1103 1,2427 1,3996 1,5834 1,7971 2,0440 2,3273 2,6508 3,0190 3,4362	0,1838 0,2137 0,2469 0,2833 0,3235 0,3682 0,4172	0,1000 0,1210 0,1443 0,1700 0,1983 0,2297 0,2644 0,3027 0,3451 0,3919	210 233 257 283 314 347 383 424 468	23 24 26 31 33 36 41 44	1 2 5 2 3 5 3	1 1,1103 1,2428 1,3997 1,5836 1,7974 2,0442 2,3275 2,6511 3,0192 3,4366

Вспомогательный бланк для интегрирования дифференциального

уравнения методом Адамса

	3	4	5	6	7	8	9
	0,1700 128 10 0	0,1983 142 11 1	0,2297 157 13 2	0,2644 174 14 1	0,3027 192 15 1	0,3451 212 17 2	0,3919 234 18 1
	0,1838	0,2137	0,2469	0,2833	0,3235	0,3682	0,4172

В последнем столбце приведены для сравнения точные значения решения

.

Отсюда видно, что максимальная ошибка приближенного решения у не превосходит четырех единиц последнего десятичного разряда.

Неявные схемы

Рассмотрим следующую разностную схему для численного решения уравнения (3.14) при условии, что вычислено значение функции u в точке . Имеем

, (3.34)

где s — параметр разностной схемы такой, что . Говорят, что разностная схема является явной, если правая часть дифференциального уравнения записывается в известной точке . Схема называется неявной, если правая часть дифференциального уравнения записывается в неизвестной точке . Схема называется полуявной (полунеявной), если правая часть с определенными весами записывается в известной и неизвестной точках. В соответствии с этими терминами схема (3.34) является явной при s = 1, неявной при s = 0 и полуявной (полунеявной) при . В явных схемах решение в точке определяется непосредственно из алгебраических соотношений с известными коэффициентами. Все рассмотренные выше схемы методов Эйлера, Рунге - Кутты, Адамса (кроме схемы метода Эйлера с пересчетом) являются явными. В неявных и полунеявных схемах при для нахождения решения в точке необходимо решить в общем случае нелинейное уравнение (3.34).

Нелинейное уравнение (3.34) можно разрешить различными методами, например, методами простой итерации, дихотомии, Ньютона и т. д. В рассматриваемом случае логично использовать метод простой итерации, поскольку нелинейное уравнение (3.34) уже разрешено относительно. Тогда, если номер итерации обозначить верхним индексом, итерационный процесс можно записать в виде

. (3.35)

Известно, что сходимость метода простой итерации зависит от выбора начального приближения. В рассматриваемом случае в качестве можно выбрать значение или какое-либо другое, например, значение, вычисленное по методу Эйлера, достаточно близкое к искомому значению . Вычисления по формуле (3.35) продолжаются до получения заданной точности .

Таким образом, очевидно, что при расчете на шаге явные схемы требуют значительно меньшего числа операций, чем неявные. Однако неявные схемы значительно более устойчивы, чем явные. Поэтому в неявных схемах ограничения на шаг разностной схемы, связанные с устойчивостью, как правило, менее жесткие, чем в явных. В результате может оказаться, что общее число операции при заданной точности и при расчетах на интервале интегрирования в неявных схемах меньше чем в явных.

Численные методы решения обыкновенных дифференциальных уравнений