Приближение функций

Тема 5

Приближение функций.

§ 1 Постановка задачи об аппроксимации функций

Для практических приложений важными являются следующие задачи. Первая состоит в замене некоторой функции, заданный аналитически или таблично, другой функцией, близкой к исходной, но более простой и удобной для вычислений. Например, замена функции многочленом позволяет получать простые формулы численного интегрирования и дифференцирования; замена таблицы приближающей функцией позволяет получать значения в ее промежуточных точках. Эти примеры можно продолжить и дальше.

Возникает также и вторая задача - восстановление функции на некотором отрезке по заданным на этом отрезке значениям функции в дискретном множестве точек. Отметим также, что теория приближения функций является важным вспомогательным аппаратом при численном решении дифференциальных уравнений.

В общем случае при постановке задачи приближения необходимо действовать по следующему алгоритму.

• Определить, какой класс приближенных функций необходимо выбрать. Ответ на такой вопрос зависит от вида приближаемой функции и целей, для которых в дальнейшем будет использоваться приближающая функция. Широко используются следующие классы функций: многочлены, тригонометрические функции, показательные функции и др.

• Выбрать критерий близости исходной и приближающей функций. В качестве критерия можно выбрать, например, точное совпадение приближаемой и приближающей функций в узловых точках (лагранжева интерполяция); минимум суммы квадратов отклонения в узловых точках (метод наименьших квадратов) и др. Как и при выборе класса приближающих функций, выбор критерия близости исходной и приближающей функций определяется целью построения приближающей функции и может существенно повлиять на результаты. При аппроксимации экспериментальных результатов целесообразно использовать среднеквадратичное приближение. На рис. 2.1 показаны два варианта приближения функций: кривая I соответствует лагранжевой интерполяции, а кривая II — среднеквадратичному приближению. Здесь точками обозначены точные значения функции . По рис. 2.1 видно, что кривая II не проходит через узлы интерполяции, а сглаживает

расчетные или экспериментальные погрешности.

• Необходимо указать правило, позволяющее с заданной степенью точности получить значение функции в промежутках между узлами, в частности, ответить на вопросы, какие узлы использовать для построения приближения функции и как их расположить.

§ 2 Постановка задачи интерполяции

Простейшая задача интерполирования заключается в следующем. На отрезке [а, b] заданы точки которые

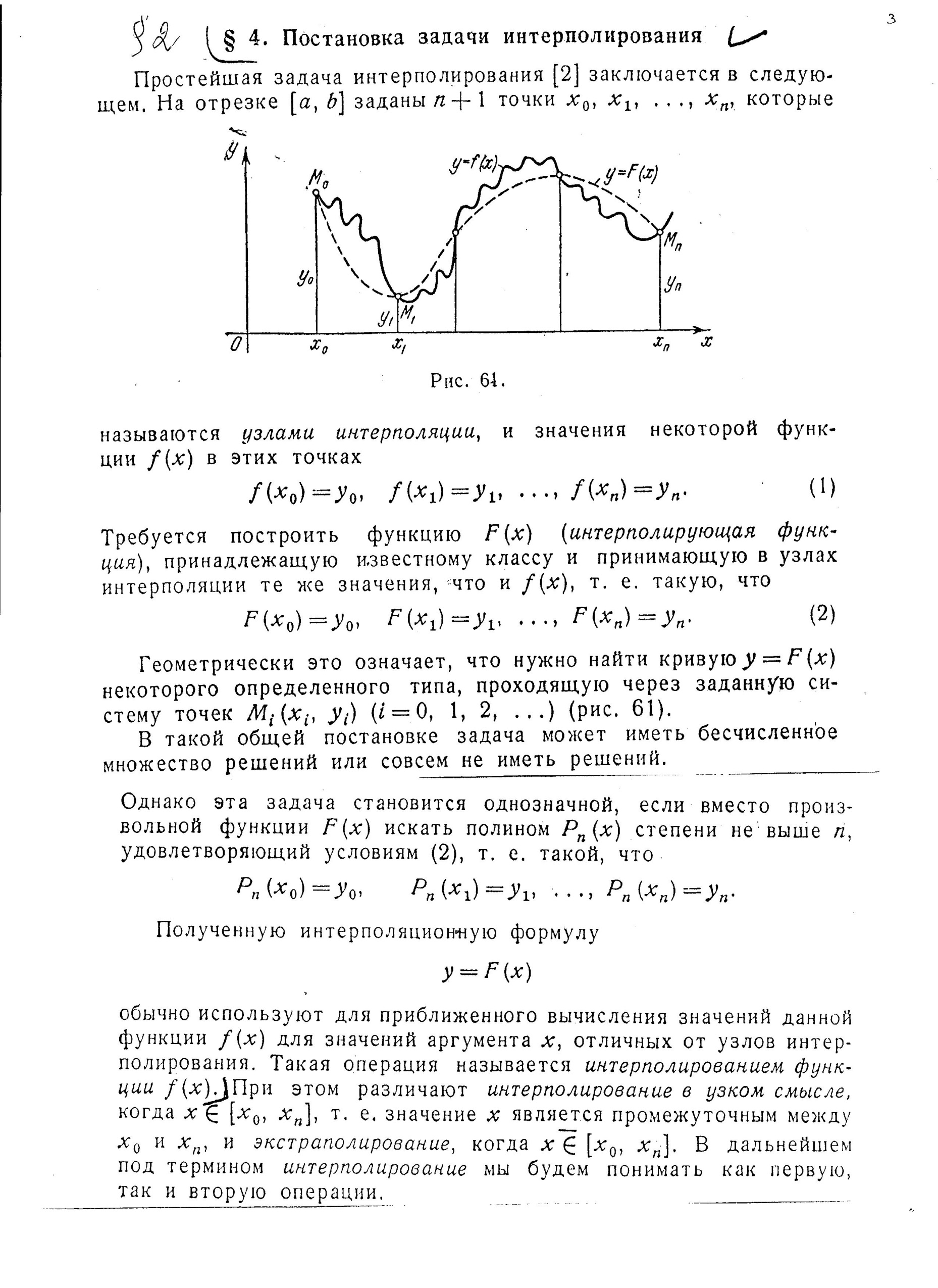
называются узлами интерполяции, и значения некоторой функции в этих точках

. (1)

Требуется построить функцию (интерполирующая функция), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что ит. е. такую, что

. (2)

Геометрически это означает, что нужно найти кривую некоторого определенного типа, проходящую через заданную систему точек (рис. 61).

В такой общей постановке задача может иметь бесчисленное множество решений или совсем не иметь решений.

Однако эта задача становится однозначной, если вместо произвольной функции искать полином степени не выше n, удовлетворяющий условиям (2), т. е. такой, что

Полученную интерполяционную формулу

обычно используют для приближенного вычисления значений данной функции для значений аргумента , отличных от узлов интерполирования. Такая операция называется интерполированием функции . При этом различают интерполирование в узком смысле, когда , т. е. значение х является промежуточным между и , и экстраполирование, когда . В дальнейшем под термином интерполирование мы будем понимать как первую, так и вторую операции.

§ 12 Интерполяционная формула Лагранжа

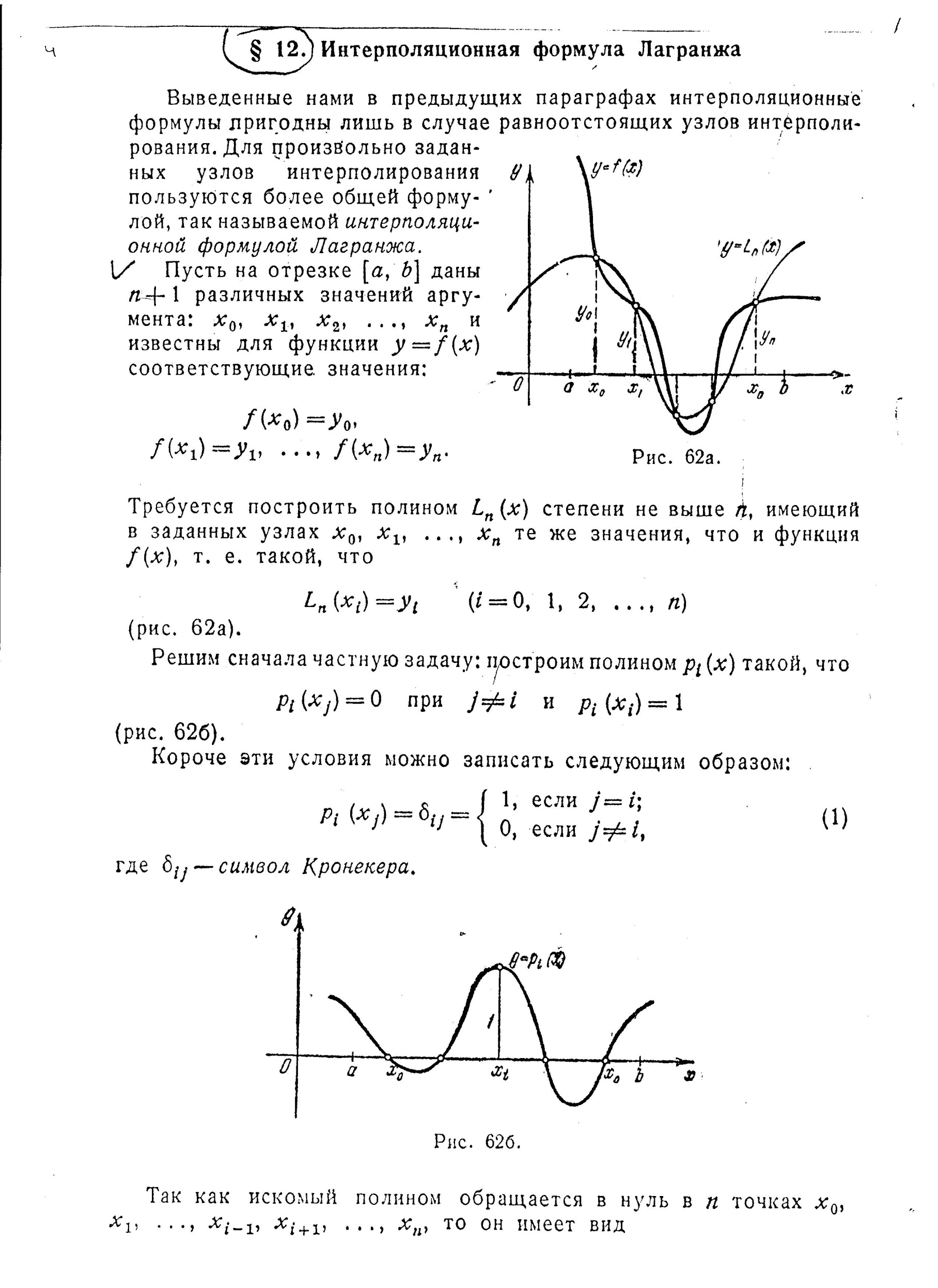
Выведенные нами в предыдущих параграфах интерполяционные формулы пригодны лишь в случае равноотстоящих узлов интерполирования. Для произвольно заданных узлов интерполирования пользуются более общей формулой, так называемой интерполяционной формулой Лагранжа.

Пусть на отрезке [а, b] даны различных значений аргумента и известны для функции соответствующие, значения:

Требуется построить полином степени не выше n, имеющий в заданных узлах те же значения, что и функция , т. е. такой, что

(рис. 62а).

Решим сначала частную задачу: простроим полином такой, что

при и

(рис. 62б).

Короче эти условия можно записать следующим образом:

(1)

где - символ Кронекера.

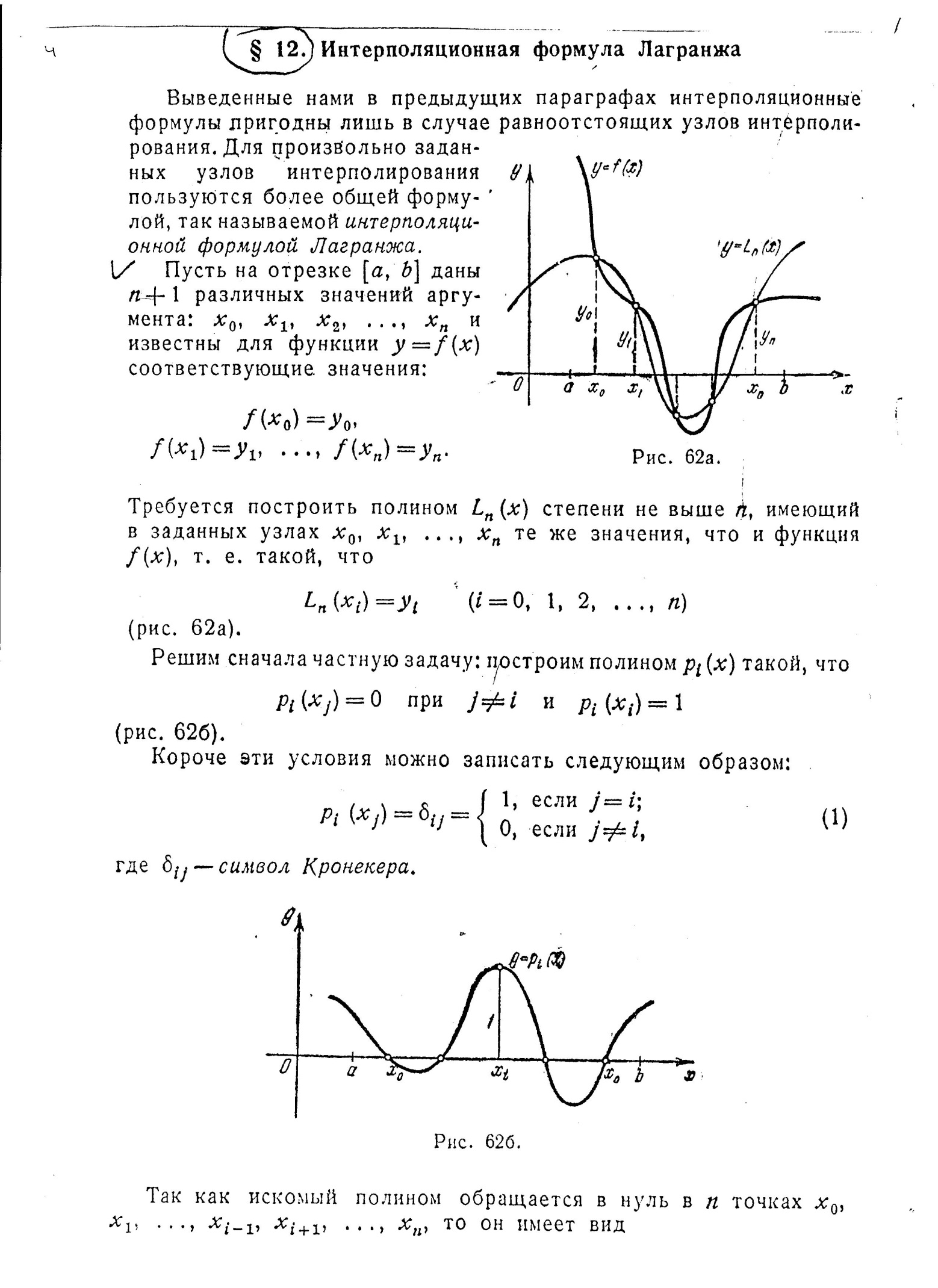
Так как искомый полином обращается в нуль в n точках , то он имеет вид

, (2)

где - постоянный коэффициент. Полагая в формуле (2) и учитывая, что , получим:

Отсюда

Подставив это значение в формулу (2), будем иметь

. (3)

Теперь перейдем к решению общей задачи: к отысканию полинома , удовлетворяющего указанным выше условиям . Этот полином имеет следующий вид:

(4)

В самом деле, во-первых, очевидно, степень построенного полинома не выше n и, во-вторых,- в силу условия (1) имеем:

Подставив в формулу (4) значение из (3), получим:

. (5)

Это и есть интерполяционная формула Лагранжа.

Для записи полинома удобно пользоваться таблицей

Таблица 4.1

Здесь - произведение элементов строки, - произведение элементов главной диагонали, .

Тогда многочлен Лагранжа может быть записан в форме

(4.18)

Основные достоинства записи интерполяционного многочлена в форме Лагранжа:

- число операций, необходимых для построения многочлена, пропорционально и является наименьшим для всех форм записи.

- формула (5) в явном виде содержит значения функции в узлах, что бывает удобно при некоторых вычислениях, например для формул численного интегрирования.

- формула (5) применима как для равноотстоящих и для неравноотстоящих узлов.

- многочлен Лагранжа особенно удобен, когда значения функции меняются, а узлы неизменны, что имеет место во многих экспериментальных исследованиях.

Недостатки:

- с изменением числа узлов, все вычисления необходимо проводить заново, это не удобно на практике, затрудняет проведение оценок точности, получающихся в процессе расчета.

т.к., например – пусть задан узел можно построить:

1 многочлен n-й степени

многочлен - степени

- степени < n, опирающихся на некоторые из узлов.

Теоретически максимальная точность обеспечивает многочлен более высокой степени, однако на практике наиболее часто используется многочлен невысоких степеней, во избежание погрешностей при расчетах коэффициент при больших степенях многочлена.

Пример 4.1. Построить многочлен Лагранжа третьей степени для сеточной функции, заданной табл. 4.2. Вычислить значение функции в точке . Для записи многочлена использовать формулу (4.18).

Таблица 4.2

0	1	2	3
2	3	4	5
7	5	8	7

1. Построим многочлен Лагранжа. Для этого составим табл. 4.3, соответствующую табл. 4.1.

Таблица 4.3

	-1	-2	-3	7
1		-1	-2	5
2	1		-1	8
3	2	1		7

По формуле (4.18) получаем:

2. Вычислим значение функции в заданной точке: .

Погрешность интерполяции многочленами Лагранжа

При определении значения для функции с помощью многочлена Лагранжа возникает погрешность или остаточное слагаемое :

(4.19)

Здесь предполагается, что используется глобальный способ интерполяции и что. Последнее предположение требуется для применения соответствующих теорем математического анализа, однако, приведенное ниже соотношение для может использоваться и для сеточных функций.

На основе указанных предположений доказано, что при интерполяции функции , заданной в общем случае на неравномерной сетке , интерполяционным многочленом Лагранжа для произвольного значения возникает погрешность

, (4.20)

где - многочлен -й степени, а .

Поскольку точно найти нельзя (из-за неопределенности точки ), то при проведении вычислений обычно находятся только приближенные оценки погрешностей интерполяции, которые являются априорными.

Оценка погрешности интерполяции в некоторой произвольной фиксированной точке имеет вид

, (4.21)

где .

Оценка максимальной погрешности интерполяции в любой точке , т.е. на всем отрезке:

. (4.22)

Пример 4.2. С какой точностью можно вычислить значение , если вычисления производить на основе интерполяционного многочлена Лагранжа первой и второй степени, а в качестве сеточной функции принять

Так как требуется вычислить погрешность только в одной точке , то необходимо использовать формулу (4.21).

Найдем оценку погрешности в точке для . В качестве "окна" линейной интерполяции выбираем отрезок . Определим величину :

Тогда .

Найдем оценку погрешности в точке для . В качестве "окна" квадратичной интерполяции выбираем отрезок . Определим величину :

Тогда

Погрешность для многочлена получилась больше погрешности для многочлена , что обусловлено величиной .

§ 17. О наилучшем выборе узлов интерполирования

Анализируя формулу (4.21) из с. 135, мы видим, что погрешность формулы Лагранжа представляет собой, с точностью до числовой постоянной, произведение двух множителей, из которых один, , зависит от свойств функции и не поддается регулированию, а величина другого, , определяется исключительно выбором узлов интерполирования.

При неудачном расположении узлов интерполирования верхняя грань модуля погрешности может быть весьма большой. Например, если мы сконцентрируем узлы вблизи одного конца отрезка [а, b], то при вообще говоря, будет велик в точках х, близких к другому концу отрезка. Поэтому возникает задача о наиболее рациональном выборе узлов интерполирования (при заданном числе узлов n) с тем, чтобы находящаяся в нашей власти часть погрешности – полином имел наименьшее максимальное значение по абсолютной величине на отрезке [а,b], или, как коротко говорят, «наименее отклонялся от нуля на [а, b]». Эта задача была решена русским математиком П. Л. Чебышевым, который доказал, что наилучший выбор в указанном смысле узлов интерполирования дается формулой

где

- нули так называемого полинома Чебышева . В этом случае мы будем иметь:

Интересно отметить, что эти узлы не являются равноотстоящими, а сгущаются около концов отрезка. Даже при таком подборе узлов в общем случае нельзя гарантировать, что абсолютная величина погрешности будет сколь угодно мала при достаточно большом n.

Если функция задана таблично и аналитическое выражение ее неизвестно, то оценка погрешности интерполяционного полинома, строго говоря, является невозможной. Действительно, для данного полинома теоретически можно построить бесчисленное множество различных функций, совпадающих с этим полиномом в данной системе узлов. Таким образом, в промежуточных точках отклонение интерполяционного полинома от функции может быть каким угодно.

Тема 5 продолжение

Интерполяционный полином Ньютона

Часто приходится рассматривать функции заданные табличными значениями для системы равноотстоящих точек , где

Введем понятие конечных разностей последовательности , определяются соотношениями

Вообще, справедливо утверждение: если

- полином n-й степени, то , где .

Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной таблицы разностей (таблица 33) или диагональной таблицы разностей (таблица 34)

Таблица 33 Таблица 34

Горизонтальная таблица разностей Диагональная таблица разностей

Заметим, что для вычисления n-й разности , нужно знать членов данной последовательности.

§ 5. Первая интерполяционная формула Ньютона

Пусть для функции заданы значения для равноотстоящих значений независимой переменной: , где h – шаг интерполяции. Требуется подобрать полином степени не выше n, принимающий в точках значения

. (1)

Условия (1) эквивалентны тому, что

будем искать полином в виде

. (2)

Введем понятие обобщенной степени.

Обобщенной n – степенью числа х называется произведение n сомножителей, 1-й = х, а каждый следующий на h меньше предыдущего, где h – фиксированное число:

Пользуясь обобщенной степенью, выражение (1) запишем так:

. (2’)

Наша задача состоит в определении коэффициентов полинома . Полагая в выражении (2'), получим:

Чтобы найти коэффициент , составим первую конечную разность

Полагая в последнем выражении , получим:

откуда

Для определения коэффициента составим конечную разность второго порядка

Положив , получим:

;

откуда

Последовательно продолжая этот процесс, мы обнаружим, что

где положено

Подставляя найденные значения коэффициентов в выражение (2,), получим интерполяционный полином Ньютона

. (3)

Для практического использования интерполяционную формулу Ньютона (3) обычно записывают в несколько преобразовательном виде. Для этого введем новую переменную по формуле

тогда

Подставляя эти выражения в формулу (3), получим:

, (4)

где представляет собой число шагов, необходимых для достижения точки x, исходя из точки. Это и есть окончательный вид первой интерполяционной формулы Ньютона.

Формулу (4) выгодно использовать для интерполирования функции в окрестности начального значения , где q мало по абсолютной величине.

Если в формуле (4) положить , то получим формулу линейного интерполирования:

При n=2 , будем иметь формулу параболического или квадратичного интерполирования:

Пример.

Построим на отрезке [2,5; 2,6] интерполированный полином Ньютона для функции , шаг h=0,05.

3,5

3,55

3,6

3,65

3,7

33,115

34,813

36,598

38,475

40,447

1,698

1,785

1,877

1,972

0,087

0,092

0,095

0,005

0,003

Таблица значений х, у задана, достроим ее до таблицы разности т.к. почти постоянны примем , полином 3 степени

где .

§ 6. Вторая интерполяционная формула Ньютона

Первая интерполяционная формула Ньютона практически неудобна для интерполирования функции вблизи конца таблица. В этом случае обычно применяется вторая интерполяционная формула Ньютона. Выводом этой формулы мы и займемся.

Пусть имеем систему значений функции

для равноотстоящих значений аргумента

Построим интерполирующий полином следующего вида:

или, используя обобщенную степень, получаем:

(1)

Наша задача состоит в определении коэффициентов таким образом, чтобы были выполнены равенства

Для этого необходимо и достаточно, чтобы

(2)

Положим в формуле (1). Тогда будем иметь:

следовательно,

Далее, берем от левой и правой частей формулы (1) конечные разности первого порядка

Отсюда, полагая и учитывая соотношения (2), будем иметь:

Следовательно,

Аналогично составив вторую разность от , получим:

Полагая , находим:

и, таким образом,

Характер закономерности коэффициентов достаточно ясен. Применяя метод математической индукции, можно строго доказать, что

. (3)

Подставляя эти значения в формулу (1), будем иметь окончательно:

(4)

Формула (4) носит название второй интерполяционной формулы Ньютона.

Введем более удобную запись формулы (4). Пусть

тогда

Подставив эти значения в формулу (4), получим:

(4’)

Это и есть обычный вид второй интерполяционной формулы Ньютона. Для приближенного вычисления значений функции у полагают:

Пример 1. Дана таблица значений семизначных логарифмов

1000

1010

1020

1030

1040

1050

3,0000000

3,0043214

3,0086002

3,0128372

3,0170333

3,0211893

Найти .

Решение. Составляем таблицу разностей (таблица 41).

Таблица 41

Конечные разности функции

1000

1010

1020

1030

1040

1050

3,0000000

3,0043214

3,0086002

3,0128372

3,0170333

3,0211893

43214

42788

42370

41961

41560

- 426

- 418

- 409

- 401

Примем

тогда

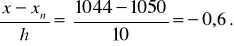
Используя подчеркнутые разности, в силу формулы (4’) будем иметь:

В полученном результате все знаки верные.

Как первая, так и вторая интерполяционные формулы Ньютона могут быть использованы для экстраполирования функции, т. е. для нахождения значений функции у для значений аргументов х, лежащих вне пределов таблицы. Если и близко к , то применяют 1-ю формулу, тогда , если или близко к , то 2-ю формулу, причем .

Таким образом 1-я формула используется для интерполирования вперед, и экстраполирования назад, 2-я формула – наоборот интерполируется назад, экстраполируется вперед.

Оценка погрешности

Воспользуемся формулой, как и для Лагранжевой интерполяции

учитывая, что узлы равноотстоящие, заменим в формуле на , получим остаточный член первой первой интерполяционной формулы Ньютона

, (1)

где — некоторое промежуточное значение между узлами интерполирования и рассматриваемой точкой . Заметим, что для случая интерполирования в узком смысле слова ;

Обычно при практических вычислениях интерполяционная формула Ньютона обрывается на членах, содержащих такие разности, которые в пределах заданной точности можно считать постоянными.

Предполагая, что почти постоянны для функции и h достаточно мало, и учитывая, что

приближенно можно положить:

В этом случае остаточный член первой интерполяционной формулы Ньютона равен

На практике для повышения точности интерполяционного многочлена, как правило, уменьшают шаг таблицы, оставляя неизменной степень интерполирующего многочлена. Для того чтобы уменьшить влияние колебательных свойств интерполяционного многочлена, используют линейную или квадратичную интерполяцию.

Приближение методом наименьших квадратов

До сих пор мы рассматривали интерполяцию – т.е. значения приближаемой и приближающей функций совпадают в узлах. Достаточно часто, например, при аппроксимации большого числа экспериментальных точек, найденных с некоторой погрешностью, интерполяция становится неразумной. В этом случае целесообразно строить приближающую функцию таким образом, чтобы сгладить влияние погрешности измерения и числа точек эксперимента. Такое сглаживание реализуется при построении приближающей функции по методу наименьших квадратов. Вид приближающей функции может быть произвольным, далее рассмотрен случай, когда приближающая функция является многочленом. При этом добиваются минимизации суммы квадратов отклонений значений приближаемой и приближающей функций в узлах сетки. Эта сумма называется квадратичным отклонением.

Пусть функция задана таблично в узлах

При точечном квадратичном аппроксимировании за меру отклонения полинома

(1)

от данной функции на множестве точек принимают величину

, (2)

называемую квадратичным отклонением (способ наименьших квадратов).

Для построения аппроксимирующего полинома требуется подобрать коэффициенты так, чтобы величина S была наименьшей. Предполагаем, что . В случае коэффициенты можно определить из системы уравнений

(3)

причем , и приходим к разобранной выше проблеме интерполирования функций. При система (3), вообще говори, несовместна. Кроме того, следует иметь в виду, что во многих случаях значения функции определяются экспериментально и содержат ошибки, поэтому сама постановка вопроса о точном решении системы (3) теряет смысл.

Для решения нашей задачи аппроксимирования воспользуемся общим приемом дифференциального исчисления. А именно, найдем частные производные от величины

где по всем переменным .

Приравнивая эти частные производные нулю, получим для определения неизвестных систему уравнений с неизвестными:

(4)

Введем обозначения:

Преобразуя, систему (4) и используя введенные обозначения, будем иметь

(5)

где .

Можно доказать, что если среди точек нет совпадающих и , то определитель системы (5) отличен от нуля, и, следовательно, эта система имеет единственное решение [3]. Полином (1) с такими коэффициентами будет обладать минимальным квадратичным отклонением .

Если , то аппроксимирующий полипом совпадает с полиномом Лагранжа для системы точек , причем . На практике обычно бывает, что степень полинома "значительно меньше числа точек и поэтому построение точного интерполяционного полинома, вообще говори, невозможно. Таким образом, аппроксимирование функций представляет собой более общий процесс, чем интерполирование. При работе на счетно - электронных машинах для решения линейной системы (5) выгодно использовать итерационные методы. В частности, так как матрица системы (5) положительно определенная, то для этой системы будет сходящимся процесс Зейделя. Следовательно, система (5) с увеличением степени приближающего многочлена становится плохо обусловленной и решение ее связано с большой потерей точности. Поэтому в методе наименьших квадратов, как правило, используют приближающий многочлен не выше третьей степени. При необходимости построения многочленов большей степени применяют приемы, позволяющие повысить обусловленность системы (5); обычно таких приемов два. В первом используют систему точек, позволяющую разбить систему (5) на две подсистемы меньшего порядка, во втором — систему ортогональных многочленов.

Как отмечалось, метод наименьших квадратов широко применяется для сглаживания экспериментальных кривых, полученных с некоторой погрешностью. Если степень аппроксимирующего многочлена равна числу точек, то среднеквадратичный многочлен совпадает с интерполяционным. Поэтому хорошее сглаживание будет при m « n . Но если m очень мало, то для описания сложной кривой коэффициентов может не хватить. Чтобы выбрать оптимальную степень многочлена, строят многочлен по методу наименьших квадратов некоторой степени m, вычисляют квадратичное отклонение S и сравнивают его с известной величиной погрешности .

Если S » е, т. е. математическая ошибка существенно превышает ошибку экспериментальных данных, то степень приближающего многочлена недостаточна для описания кривой. Если лее S « , то старшие коэффициенты аппроксимации физически недостоверны. Хорошее сглаживание получается в том случае, когда S . В этом случае степень приближающего многочлена оптимальна. Обычно начинают построение приближающего многочлена для случая m = 1 и увеличивают его степень до тех пор, пока отклонение S не станет примерно равным . Если при этом m « n, то приближающий многочлен выбран верно. Если это условие не соблюдается, то следует поискать более удачный вид приближающей функции.

Пример. Подобрать аппроксимирующий полином второй степени для данных:

	0,78	1,56	2,34	3,12	3,81
	2,50	1,20	1,12	2,25	4,28

Решение. Вычисления которые нам нужно произвести, расположим по схеме (для m = 2, n = 4), приведенной в таблице 1.

Для данного примера получает таблицу 2 (вычисления проводятся с тремя десятичными знаками).

Таблица 1

Схема способа наименьших квадратов

Таблица 2

Вычисления по способу наименьших квадратов

0,78

1,56

2,34

3,12

3,81

0,608

2,434

5,476

9,734

14,516

0,475

3,796

12,813

30,371

55,306

0,370

5,922

29,982

94,759

210,717

2,50

1,20

1,12

2,25

4,28

1,950

1,872

2,621

7,020

16,307

1,520

2,921

6,133

21,902

62,128

11,61

32,768

102,761

341,750

11,35

29,770

94,604

Отсюда, система для определения коэффициентов имеет вид

(6)

Решив систему (6), будем иметь:

Следовательно, искомый полином есть

. (7)

Сравним исходные значения для у с соответствующими значениями , полученными из приближенной формулы (7). Соответствующие результаты приведены в таблице 3.

Таблица 3

Погрешности вычисления по способу

наименьших квадратов

0,78

1,56

2,34

3,12

3,81

2,50

1,20

1,12

2,25

4,28

2,505

1,194

1,110

2,252

4,288

+ 0,005

- 0,006

- 0,010

+ 0,002

+ 0,008

Приближение функций